Одна из этих задач может вам попасться на реальном ОГЭ в этом году, поэтому нужно подготовиться и прорешать парочку из них заранее, потому как очень много теории привлечено к решению.
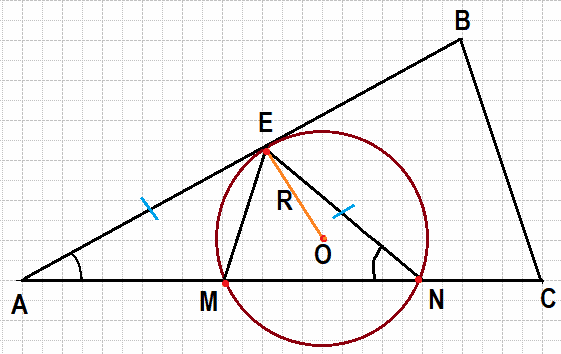
Для начала, нужно построить рисунок и сделать дополнительные построения - соединить точки, в которых окружность касается и пересекает стороны треугольника. Получим вписанный в окружность треугольник. А мы знаем, что по следствию из теоремы синусов мы можем найти радиус окружности, в которую вписан треугольник.
Теорема синусов, вернее ее следствие: a/sin α = 2R. Вот этот R и надо найти по условию задачи, а для этого нужно знать сторону и угол. Ищем их.
Сразу видим, что может пригодиться теорема о касательной и секущей (Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть). Теорему и формулу учите, ее не будет в справочных материалах ОГЭ.
Еще будет нужна теорема косинусов: а2=b2 + c2 - 2bc cos α , по ней найдем как раз стороны вписанного треугольника и по пути кое-что узнаем про угол;
основное тригонометрическое тождество: sin2α + cos2α = 1 пригодится, потому что мы знаем косинус, а нам нужен будет синус.
Формулы теоремы синусов, косинусов и основное тригонометрическое тождество будут у вас напечатаны на экзаменационных листах в качестве справочных материалов, нужно лишь знать название и уметь пользоваться. Можете посмотреть в демо, как это будет выглядеть >>
Итак, приступим к решению с разными числовыми значениями. Решения к каждой задаче под катом.
Задачи ОГЭ по геометрии с развернутым ответом
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{15}}4$.
Решение:
Найдем AE по теореме о касательной и секущей. Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 4*15
АE = $\sqrt{4\ast15}$= $\sqrt{60}$
Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{60}$2 +42 - 2*$\sqrt{60}$*4*$\frac{\sqrt{15}}4$= 60+16-2*$\sqrt{60}$*$\sqrt{15}$=76-2*30=16
EM = $\sqrt{16}$ =4
Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{60}$2 +152 - 2*$\sqrt{60}$*15*$\frac{\sqrt{15}}4$=60+225-($\sqrt{900}$*15)/2=285-225=60
EN = $\sqrt{60}$
В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где где AE = EN = $\sqrt{60}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.
$\sin\angle ENA^2+\cos\angle ENA^2=1\\\sin\angle ENA^2+{(\frac{\sqrt{15}}4)}^2=1\\\sin\angle ENA^2=1-{(\frac{\sqrt{15}}4)}^2\;\;\\\sin\angle ENA^2=1-\frac{15}{16}\\\sin\angle ENA^2=\frac1{16}\\\sin\angle ENA=\frac14$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\ast\sin\angle ENA}=\frac4{2\ast{\displaystyle\frac14}}=8$
Ответ: 8
F41EBF
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 21 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*21
АE = $\sqrt{12\ast21}$= $\sqrt{252}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{252}$2 +122 - 2*$\sqrt{252}$*12*$\frac{\sqrt7}4$= 252+144-2*$\sqrt{252}$*12*$\frac{\sqrt7}4$=396-252=$\sqrt{144}$
EM = $\sqrt{144}$ =12Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{252}$2 +212 - 2*$\sqrt{252}$*21*$\frac{\sqrt7}4$=252+441-441=252
EN = $\sqrt{252}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt7}4\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt7}4\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac7{16}\\\sin\angle ENA^2\;=\;\frac9{16}\\\sin\angle ENA^\;=\frac34\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac{12}{2{\displaystyle\frac34}}=\frac{48}6=8$
Ответ: 8
23C5ED
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 8*30
АE = $\sqrt{8\ast30}$= $\sqrt{240}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{240}$2 +82 - 2*$\sqrt{240}$*8*$\frac{\sqrt{15}}4$=240+64-240=64
EM = 8Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{240}$2 +302 - 2*$\sqrt{240}$*30*$\frac{\sqrt{15}}4$=240+900-900=240
EN = $\sqrt{240}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{15}}4\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{15}}4\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{15}{16}\\\sin\angle ENA^2\;=\;\frac1{16}\\\sin\angle ENA\;=\frac14\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac8{2{\displaystyle\frac14}}=\frac{32}2=16$
Ответ: 16
1D3A90
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 22 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*22
АE = $\sqrt{18\ast22}$= $\sqrt{396}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{396}$2 +182 - 2*$\sqrt{396}$*18*$\frac{\sqrt{11}}6$=396+324-396=324
EM = 18Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{396}$2 +222 - 2*$\sqrt{396}$*22*$\frac{\sqrt{11}}6$=396+484-484=396
EN = $\sqrt{396}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{11}}6\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{11}}6\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{11}{36}\\\sin\angle ENA^2\;=\;\frac{25}{36}\\\sin\angle ENA\;=\frac56\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac18{2{\displaystyle\frac56}}=\frac{21.6}2=10.8$
Ответ: 10.8
35C690
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt5}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*40
АE = $\sqrt{18\ast40}$= $\sqrt{720}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{720}$2 +182 - 2*$\sqrt{720}$*18*$\frac{\sqrt{5}}3$=720+324-720=324
EM = 18Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{720}$2 +402 - 2*$\sqrt{720}$*40*$\frac{\sqrt{5}}3$=720+1600-1600=720
EN = $\sqrt{720}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt5}3\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt5}3\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac59\\\sin\angle ENA^2\;=\;\frac49\\\sin\angle ENA\;=\frac23\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac18{2{\displaystyle\frac23}}=\frac{54}4=13.5$
Ответ: 13.5
CCD611
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 35 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{35}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*35
АE = $\sqrt{9\ast35}$= $\sqrt{315}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{315}$2 +92 - 2*$\sqrt{315}$*9*$\frac{\sqrt{35}}6$=315+81-315=81
EM = 9Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{315}$2 +352 - 2*$\sqrt{315}$*35*$\frac{\sqrt{35}}6$=315+1225-1225=315
EN = $\sqrt{315}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{35}}6\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{35}}6\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{35}{36}\\\sin\angle ENA^2\;=\;\frac1{36}\\\sin\angle ENA\;=\frac16\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac9{2{\displaystyle\frac16}}=\frac{54}2=27$
Ответ: 27
65B0A0
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 45 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*45
АE = $\sqrt{12\ast45}$= $\sqrt{540}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{540}$2 +122 - 2*$\sqrt{540}$*12*$\frac{\sqrt{15}}4$=540+144-540=144
EM = 12Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{540}$2 +452 - 2*$\sqrt{540}$*45*$\frac{\sqrt{15}}4$=540+2025-2025=540
EN = $\sqrt{540}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = $\sqrt{540}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{15}}4\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{15}}4\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{15}{16}\\\sin\angle ENA^2\;=\;\frac1{16}\\\sin\angle ENA\;=\frac14\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac{12}{2{\displaystyle\frac14}}=\frac{48}2=24$
Ответ: 24
36C43D
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{2\sqrt2}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*32
АE = $\sqrt{9\ast32}$= $\sqrt{288}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{288}$2 +92 - 2*$\sqrt{288}$*9*$\frac{2\sqrt2}3$=288+81-288=81
EM = 9Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{288}$2 +322 - 2*$\sqrt{288}$*32*$\frac{2\sqrt2}3$=288+1024-1024=288
EN = $\sqrt{288}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = $\sqrt{288}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{2\sqrt2}3\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{2\sqrt2}3\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac89\\\sin\angle ENA^2\;=\;\frac13\\\sin\angle ENA\;=\frac13\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac9{2{\displaystyle\frac13}}=\frac{27}2=13,5$
Ответ: 13,5
A077B6
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 24 и 42 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 24*42
АE = $\sqrt{24\ast42}$= $\sqrt{1008}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{1008}$2 +242 - 2*$\sqrt{1008}$*24*$\frac{\sqrt7}4$=1008+576-1008=576
EM = 24Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{1008}$2 +422 - 2*$\sqrt{1008}$*42*$\frac{\sqrt7}4$=1008+1764-1764=1008
EN = $\sqrt{1008}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = $\sqrt{1008}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt7}4\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt7}4\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac7{16}\\\sin\angle ENA^2\;=\;\frac9{16}\\\sin\angle ENA\;=\frac34\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac{24}{2{\displaystyle\frac34}}=\frac{96}3=32$
Ответ: 32
973563
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 36 и 44 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 36*44
АE = $\sqrt{36\ast44}$= $\sqrt{1584}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{1584}$2 +362 - 2*$\sqrt{1584}$*36*$\frac{\sqrt11}6$=1584+1296-1584=1296
EM = 36Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{1584}$2 +442 - 2*$\sqrt{1584}$*44*$\frac{\sqrt11}6$=1584+1936-1936=1584
EN = $\sqrt{1584}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = $\sqrt{1584}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{11}}6\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{11}}6\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{11}{36}\\\sin\angle ENA^2\;=\;\frac{25}{36}\\\sin\angle ENA\;=\frac56\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac{36}{2{\displaystyle\frac56}}=\frac{216}{10}=21.6$
Ответ: 21.6
A142B2
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 16 и 39 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{39}}8$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 16*39
АE = $\sqrt{16\ast39}$= $\sqrt{624}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = $\sqrt{624}$2 +162 - 2*$\sqrt{624}$*16*$\frac{\sqrt{39}}8$=624+256-624=256
EM = 16Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = $\sqrt{624}$2 +392 - 2*$\sqrt{624}$*39*$\frac{\sqrt{39}}8$=624+1521-1521=624
EN = $\sqrt{624}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = $\sqrt{624}$. В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle ENA^2+\cos\angle ENA^2\;=1\\\sin\angle ENA^2+\left(\frac{\sqrt{39}}8\right)^2\;=1\\\sin\angle ENA^2=1-\left(\frac{\sqrt{39}}8\right)^2\\\sin\angle ENA^2\;=\;1\;-\;\frac{39}{64}\\\sin\angle ENA^2\;=\;\frac{25}{64}\\\sin\angle ENA\;=\frac58\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\sin\angle ENA}=\frac{39}{2{\displaystyle\frac58}}=\frac{312}{10}=31.2$
Ответ: 31.2
553368
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$\frac{\sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*11
АE = $\sqrt{9\ast11}$= 3$\sqrt{11}$Рассмотрим △АЕМ. По теореме косинусов найдем EM:
EM2 = AE2+AM2 - 2AE*AM*cos∠BAC
EM2 = 32$\sqrt{11}$2 +92 - 2*3$\sqrt{11}$*9*$\frac{\sqrt{11}}6$=9*11+81-11*9=81
EM = 9Рассмотрим △АЕN. По теореме косинусов найдем EN:
EN2 = AE2+AN2 - 2AE*AN*cos∠BAC
EN2 = 32$\sqrt{11}$2 +112 - 2*3$\sqrt{11}$*11*$\frac{\sqrt{11}}6$=32$\sqrt{11}$2 +121-121 = 32$\sqrt{11}$2
EN = 3$\sqrt{11}$В △AEN стороны AE и EN равны, значит △AEN равнобедренный, где AE = EN = 3$\sqrt{11}$ . В равнобедренном треугольнике углы при основании равны, значит ∠BAC = ∠ENA.
Из основного тригонометрического тождества найдем sin∠ENA.$\sin\angle B\;A\;C^2+\cos\angle B\;A\;C^2=1\\\sin\angle B\;A\;C^2=1-\cos\angle B\;A\;C^2\\\sin\angle B\;A\;C^2=1-\frac{\sqrt{11}}6^2\\\sin\angle B\;A\;C^2\;=\;1-\frac{11}{36}\\\sin\angle B\;A\;C^2\;=\frac{25}{36}\\\sin\angle B\;A\;C\;=\;\frac56\\\\\\\\$
По теореме синусов найдем радиус описанной вокруг треугольника окружности:
$R=\frac{EM}{2\ast\sin\angle\;B\;A\;C}\;\;=\frac9{2\ast{\displaystyle\frac56}}=5.4\\\\\\\\$
Ответ: 5.4
B83171