Механика: Динамика. Задания ЕГЭ по физике из банка ФИПИ с ответами

Все задания из банка ФИПИ в КЭС Механика. Динамика к ЕГЭ по физике.

Задания из банка ФИПИ с ответами к ЕГЭ по физике

1.2 Динамика 1.2.1 Инерциальные системы отсчёта. Первый закон Ньютона. Принцип относительности Галилея 1.2.2 Масса тела. Плотность вещества 1.2.3 Сила. Принцип суперпозиции сил 1.2.4 Второй закон Ньютона: для материальной точки в ИСО 1.2.5 Третий закон Ньютона для материальных точек 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела. 1.2.7 Сила упругости. Закон Гука 1.2.8 Сила трения. Сухое трение. Сила трения скольжения. Сила трения покоя. Коэффициент трения 1.2.9 Давление

Формулы которые вам пригодятся в этом разделе:

Плотность тела
`ρ = m/V `

Сила трения
Fтр. = μmg

Формула ускорения
a=Δv/Δt

Законы Ньютона
F действия = -F противодействия (разница знаков показывает напрвления векторов сил)
F=ma (1 Н = 1 кг·м/с2)

Кинетическая энергия
`Ek=(mV^2)/2`

Формула взаимного притяжения тел
`F=(G*m1*m2)/R^2`

Центростремительное ускорение
`a_n = (v^2)/R`
При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение возрастают и наоборот!

Закон Гука
`F упр = k ·Δℓ`

Сила трения
Fтр. = µN, где Fтр.макс - модуль максимальной силы трения покоя, µ- коэффициент пропорциональности, называемый коэффициентом трения покоя.

Выбор ответов из предложенных вариантов (9)

Выберите один или несколько правильных ответов.
Необходимо собрать экспериментальную установку, с помощью которой можно определить плотность алюминия. Для этого школьник взял стакан с водой и алюминиевый шарик с крючком.

Какое дополнительное оборудование необходимо использовать для проведения этого эксперимента? Из приведённого ниже перечня оборудования выберите две позиции.

1) электронные весы
2) мензурка
3) секундомер
4) термометр
5) пружина

В ответе запишите номера выбранных позиций.
КЭС: 1.2.2 Масса тела. Плотность вещества
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

12

Необходимо будет замерить объем вытесненной воды, для этого используем мензурку. Необходимо будет знать вес шарика, используем весы.
`ρ = m/V `

Номер: 60DF4D

Выберите один или несколько правильных ответов.
Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?

1) деревянная рейка
2) динамометр
3) мензурка
4) пластмассовая рейка
5) линейка

В ответ запишите номера выбранных предметов.
КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

12

Берем рейку из дерева, берем динамометр, для измерения силы.

Номер: 9F7170

Выберите один или несколько правильных ответов. ²⁰²⁴
Необходимо собрать экспериментальную установку, с помощью которой можно определить плотность меди. Для этого школьник взял динамометр и мензурку. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения эксперимента?

1) алюминиевый шарик
2) термометр
3) секундомер
4) стакан с водой
5) медный шарик

В ответ запишите номера выбранного оборудования.

КЭС: 1.2 Динамика
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

45

Берем медный шарик, так как плотность находим для меди. Берем воду, чтобы узнать объем шарика в воде и разницу сил притяжения в воде и без нее.

Номер: 48DF11

Выберите один или несколько правильных ответов.
Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.

1) Сила Архимеда, действующая на тело, полностью погружённое в жидкость, прямо пропорциональна объёму тела.
2) Теплопередача путём конвекции наблюдается в жидкостях и газах.
3) При последовательном соединении резисторов напряжения на всех резисторах одинаковы.
4) Вследствие интерференции электромагнитных волн происходит перераспределение энергии в пространстве: энергия концентрируется в максимумах и не поступает в минимумы интерференции.
5) Заряды атомных ядер изотопов химического элемента различны, но массы их одинаковы.

КЭС: 1.1 Кинематика
1.2 Динамика
1.3 Статика
1.4 Законы сохранения в механике
1.5 Механические колебания и волны
2.1 Молекулярная физика
2.2 Термодинамика
3.1 Электрическое поле
3.2 Законы постоянного тока
3.3 Магнитное поле
3.4 Электромагнитная индукция
3.5 Электромагнитные колебания и волны
3.6 Оптика
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

124

Номер: AA8BDA

Выберите один или несколько правильных ответов.
Мальчик поднимает вверх гирю массой 10 кг, действуя на неё постоянной силой 120 Н, направленной вертикально вверх. Из приведённого ниже списка выберите два правильных утверждения.

1) Вес гири равен 120 Н и направлен вверх.
2) Гиря действует на руку мальчика с силой 100 Н, направленной вниз.
3) Равнодействующая сил, действующих на гирю, равна 240 Н и направлена вверх.
4) Ускорение гири равно 2 м/с².
5) Если мальчик приложит к гире направленную вертикально силу 90 Н, он не сможет её поднять.

КЭС: 1.2.5 Третий закон Ньютона для материальных точек
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

45

1) сила от вес гири направлена вниз и равна 100 Н (10 кг).
2) Гиря действует на руку мальчика с силой 120 Н, согласно закону Ньютона.
3) 120-100=20 Н равнодействующая сила. Направлена вверх.
4) F=ma
a=F/m=20/10=2 м/с²
5) Да, когда мальчик прикладывает силу в 90 Н, направленную вверх, то совместно с силой тяжести в 100 Н, направленной вниз, получаем равнодействующую в 100 - 90 = -10 Н. То есть подъемной силы не хватает.

Номер: 7D140C

Выберите один или несколько правильных ответов.

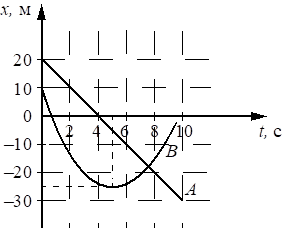
ЕГЭ физика

На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся вдоль оси Ох. Выберите все верные утверждения о характере движения тел.

1) В момент времени t = 5 с импульс тела В был равен 0.
2) В момент времени t = 4 с проекция скорости тела А на ось Ох была равна 0.
3) Тело В движется равномерно.
4) Импульс тела А с течением времени не изменяется.
5) За время от 3 до 9 с тело В прошло путь 15 м.

КЭС: 1.2.1 Инерциальные системы отсчёта. Первый закон Ньютона. Принцип относительности Галилея
1.2.2 Масса тела. Плотность вещества
1.2.3 Сила. Принцип суперпозиции сил
1.2.4 Второй закон Ньютона: для материальной точки в ИСО
1.2.5 Третий закон Ньютона для материальных точек
1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

14

1) Импульс тела p = mV, то есть минимальный импульс возникает при скорости равной 0. При этом видно что по графику скорость в точке 5 секунд равна нулю, так как поменялся вектор скорости, направление.

4) Движение тела A равномерное, то есть V=const, а значит импульс неизменный.

Номер: AF1AB8

Выберите один или несколько правильных ответов.
Школьники изучали движение небольшого бруска массой 400 г по горизонтальной шероховатой поверхности под действием горизонтальной постоянной силы, равной по модулю 2,1 Н. Зависимость скорости бруска от времени приведена в таблице. Выберите все верные утверждения на основании анализа представленной таблицы.

Время t, с	0	1	2	3	4	5	6
Скорость u, м/с	0	2	4	6	8	10	12

1) Сумма сил, действующих на брусок, равна нулю.
2) Ускорение бруска равно 2 м/с².
3) Коэффициент трения бруска о поверхность μ = 0,2.
4) Брусок движется равномерно.
5) В момент времени 3 с кинетическая энергия бруска равна 7,2 Дж.

КЭС: 1.2 Динамика
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

25

1) Сумма сил, действующих на брусок, равна нулю. a=Δv/Δt. Изменение скорости 2 м/с за 1 с, значит ускорение равно 2 м/с.
F=ma, получается равнодействующая сила равна F=0,4*2=0,8 Н НЕВЕРНО
2) Ускорение бруска равно a=Δv/Δt. Изменение скорости 2 м/с за 1 с, значит ускорение равно 2 м/с. ВЕРНО
3) Коэффициент трения бруска о поверхность μ = 0,2.
Проверим:
Fтр. = μF
μ = Fтр./F = 2.1/4=0,525 НЕВЕРНО
4) Брусок движется равномерно. НЕВЕРНО (ранее выяснили, что есть ускорение)
5) В момент времени 3 с кинетическая энергия бруска равна 7,2 Дж.
Кинетическая энергия равна при скорости 6 м/с:
`Ek=(mV^2)/2`
`Ek=(0,4*6^2)/2=(14,4)/2=7,2`Дж ВЕРНО

Номер: 92D622

Выберите один или несколько правильных ответов.
В лабораторной работе изучали движение небольшого бруска массой 400 г по горизонтальной шероховатой поверхности под действием горизонтальной постоянной силы, равной по модулю 1,6 Н. Зависимость скорости бруска от времени приведена в таблице. Выберите все верные утверждения на основании анализа представленной таблицы.

Время t, с	0	1	2	3	4	5	6
Скорость u, м/с	0	0,5	1,0	1,5	2,0	2,5	3,0

1) Равнодействующая сил, действующих на брусок, равна 0,2 Н.
2) Ускорение бруска равно 3 м/с².
3) Коэффициент трения бруска о поверхность m=0,2.
4) Брусок движется равноускоренно.
5) В момент времени 2с кинетическая энергия бруска равна 0,6Дж.

КЭС: 1.2 Динамика
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

14

1) Равнодействующая сил, действующих на брусок, равна 0,2 Н. Проверим:
a=Δv/Δt= 0,5/1=0,5 м/с²
F=ma=0,4*0,5=0,2 Н равнодействующая сил. ВЕРНО.
2) Ускорение бруска равно 3 м/с². Проверим:
a=Δv/Δt= 0,5/1=0,5 м/с²НЕВЕРНО
3) Коэффициент трения бруска о поверхность m=0,2.
Проверим:
Fтр. = μF
μ = Fтр./F = 1,6/4=0,4 НЕВЕРНО
4) Брусок движется равноускоренно. ВЕРНО (ранее выяснили, что есть ускорение a=Δv/Δt= 0,5/1=0,5 м/с²)
5) В момент времени 2с кинетическая энергия бруска равна 0,6Дж.
Кинетическая энергия равна при скорости 1 м/с (2 секунда):
`Ek=(mV^2)/2`
`Ek=(0,4*1^2)/2=(0,4)/2=0,2`Дж НЕВЕРНО

Номер: 29B3AD

1) Сила, с которой гиря действует на мальчика, равна 100 Н и направлена вертикально вниз.
2) Гиря действует на руку мальчика с силой 120 Н, направленной вертикально вниз.
3) Равнодействующая сил, действующих на гирю, равна 20 Н и направлена вертикально вверх.
4) Ускорение гири равно 8 м/с².
5) Если мальчик приложит к гире силу 102 Н, направленную вертикально вверх, он не сможет её поднять.

КЭС: 1.2 Динамика
Тип ответа: Выбор ответов из предложенных вариантов

Ответ:

23

1) сила действия равна силе противодействия. Сила воздействует с силой 120 Н. Утверждение 1 НЕВЕРНО.
2) Гиря действует на руку мальчика с силой 120 Н, согласно закону Ньютона. ВЕРНО
3) 120-100=20 Н равнодействующая сила. Направлена вверх.
4) F=ma
a=F/m=20/10=2 м/с²НЕВЕРНО
5) Да, когда мальчик прикладывает силу в 90 Н, направленную вверх, то совместно с силой тяжести в 100 Н, направленной вниз, получаем равнодействующую в 102 -100 = 2 Н. То есть подъемной силы хватает. НЕВЕРНО

Номер: 698D8C

Краткий ответ (65)

Впишите правильный ответ.
Два маленьких шарика массой m каждый находятся на расстоянии 40 см друг от друга. Каково расстояние между шариками вдвое большей массы, если модуль сил гравитационного взаимодействия между ними такой же, как и между первыми двумя шариками?

см

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

80

`F=(G*m_1*m_2)/R^2`

Произведем расчет для других масс, при условии что силы равны:

`(G*m_1^2)/R_1^2 = (G*m_2^2)/R_2^2` при условии 2m1 = m2 получаем (m1 - первоначальная масса шариков, m2 - шарики большей массы):

`(m_1^2)/R_1^2 = ((2*m_1)^2)/R_2^2`

`(m_1^2)/R_1^2 = (4*m_1^2)/R_2^2`

`1/R_1^2 = 4/R_2^2`

`4R_1^2 = R_2^2`

`R_1^2 = (R_2^2)/4`

`R_1 = sqrt((R_2^2)/4)`

`R_1 = (R_2)/2`

тогда `R_2=2*R_1`

2*40=80 см

Номер: 9F5549

Впишите правильный ответ. ²⁰²⁴
Космический аппарат, обращающийся вокруг Луны по круговой орбите, перешёл на другую круговую орбиту бóльшего радиуса. Как изменились в результате этого перехода центростремительное ускорение, с которым аппарат движется по орбите, и его период обращения вокруг Луны?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Центростремительное ускорение / Период обращения аппарата вокруг Луны

КЭС:
1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

21

Центростремительное ускорение
`a_n = (v^2)/R` При увеличении радиуса ускорение уменьшилось

При угловая скорость уменьшилась из-за сокращения углового перемещения в единицу времени, окружность стала больше, время обращения больше стало больше.

Номер: F4D3FF

Впишите правильный ответ.
В инерциальной системе отсчёта сила, равная по модулю 16 Н, сообщает телу массой m ускорение `veca`.
Чему равен модуль силы, под действием которой тело массой `m/2` будет иметь в этой системе отсчёта ускорение `veca/4`?

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

2

F=ma
a = 16/m, из этой формулы необходимо получить ускорение a/4, то есть правую часть надо также поделить на 4

a/4 = 16/4m = 4/m. Кроме того, наша масса m2 по условию в два раза меньше. Если знаменатель в два раза меньше, то числитель тоже надо уменьшить в два раза.

Получаем a/4=2/m_2 , то есть из соотношения видно, что сила стала равна 2Н

Номер: 2622F3

Впишите правильный ответ.

Определите показания динамометра (см. рисунок), если погрешность прямого измерения силы равна цене деления динамометра. Динамометр проградуирован в ньютонах.

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

1,80,1

Номер: 189A00

Впишите правильный ответ.
Определите показания динамометра (см. рисунок), если погрешность прямого измерения силы равна цене деления динамометра. Динамометр проградуирован в ньютонах.

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

3,80,1

Номер: 96260C

Впишите правильный ответ.
В результате перехода искусственного спутника Земли с одной круговой орбиты на другую его центростремительное ускорение увеличивается. Как изменяются в результате этого перехода скорость движения спутника по орбите и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость движения спутника по орбите/ Период обращения спутника вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

12

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение возрастают.

Период вращения спутника
`T=(2πR)/v`
Исходя из заключения выше, увеличение скорости и уменьшение радиуса повлечет уменьшение периода обращения.

Номер: FB9B74

Впишите правильный ответ.
Камень подбросили вверх. Как меняются по мере подъёма ускорение камня и его кинетическая энергия? Сопротивление воздуха не учитывать.

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не меняется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Ускорение камня / Кинетическая энергия камня

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

32

Ускорение не меняется, оно равно гравитационной постоянной g.
Кинетическая энергия уменьшается, так как при подъеме уменьшается скорость.

Номер: 010677

Впишите правильный ответ.
В инерциальной системе отсчёта сила, модуль которой равен 16 Н, сообщает телу массой m ускорение `veca`. Каков модуль силы, которая сообщает телу массой 4m в этой системе отсчёта ускорение `veca/2`?

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

32

F=ma
a = 16/m, из этой формулы необходимо получить ускорение a/2, то есть правую часть надо также поделить на 2

a/2 = 16/2m = 8/m. Кроме того, наша масса m2 по условию в четыре раза увеличилась. Если знаменатель в четыре раза больше, то числитель тоже надо увеличить в 4 раза дабы сохранить пропорции.

Получаем a/2=32/m_2 , то есть из соотношения видно, что сила стала равна 32Н

Номер: 242172

Впишите правильный ответ.
В инерциальной системе отсчёта некоторая сила сообщает телу массой 8 кг ускорение 5 м/с². Какова масса тела, которому та же сила сообщает в той же системе отсчёта ускорение 4 м/с²?

кг

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

10

F=ma
F=5*8=40 Н (1Н = 1 кг*м/с2)

После нахождения силы составим уравнение с неизвестной массой

40=4*m

Найдем массу.

m=40/4=10 кг

Номер: 249978

Впишите правильный ответ.
Два одинаковых маленьких шарика притягиваются друг к другу с силами, равными по модулю 0,16 Н. Каким станет модуль сил их гравитационного взаимодействия, если расстояние между шариками уменьшить в 1,5 раза?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

0,36

`F=(G*m_1*m_2)/R^2`

Произведем расчет для разных расстояний:
при условии R1 = 1.5*R2 получаем:

`(G*m_1^2)/(R_1/(1,5))^2 = (2,25*G*m_1^2)/R_1^2`

При этом первоначально формула имела вид до изменения расстояний:

`(G*m_1^2)/R_1^2` То есть во втором случае сила увеличилась в 2,25 раза. Нетрудно вычислить вариант с изменением расстояния:

0,16*2,25=0,36 Н

Номер: 5E7E7C

Впишите правильный ответ.
В результате перехода спутника Земли с одной круговой орбиты на другую скорость его движения уменьшается. Как изменяются при этом центростремительное ускорение спутника и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Центростремительное ускорение спутника/ Период обращения спутника вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

21

Центростремительное ускорение
`a_n = (v^2)/R` При увеличении орбиты (радиуса R), скорость спутника и центростремительное ускорение уменьшаются.

Период вращения спутника
`T=(2πR)/v`
Исходя из заключения выше, уменьшение скорости и увеличение радиуса повлечет увеличение периода обращения.

Номер: AFD87F

Впишите правильный ответ.
Определите показания динамометра (см. рисунок), если погрешность прямого измерения силы равна цене деления динамометра. Шкала динамометра проградуирована в ньютонах (Н).

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

1,80,1

Номер: 699675

Впишите правильный ответ.
Две планеты обращаются по круговым орбитам вокруг звезды. Модули сил притяжения планет к звезде одинаковы. У первой из планет радиус орбиты в шесть раз больше, чем у второй. Каково отношение `m_1/m_2`
массы первой планеты к массе второй планеты?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

36

`F=(G*m_1*m_2)/R^2`

Примем для планет массу m1 и m2, а для планеты m3, тогда

`(G*m_1*m_3)/(6R)^2=(G*m_2*m_3)/R^2`

`(G*m_1*m_3)/36R^2=(G*m_2*m_3)/R^2`

Сокращаем однородные показатели:

`(m_1)/36=(m_2)`

`36=(m_1)/(m_2)`

Номер: 3FB779

Впишите правильный ответ.
В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличилась. Как изменились в результате этого перехода центростремительное ускорение спутника и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Центростремительное ускорение спутника /Период обращения спутника вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

Номер: 470EB5

Впишите правильный ответ.
Камень брошен вверх под углом к горизонту. Сопротивление воздуха пренебрежимо малó. Как меняются по мере подъёма камня модуль ускорения и модуль импульса камня?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль ускорения камня /Модуль импульса камня

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

32

Ускорение камня связано с гравитационной постоянной и его модуль остается неизменным.

Импульс с подъемом уменьшается, так как уменьшается скорость.

Номер: D443B8

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

1,40,1

Номер: 5CDAB8

Впишите правильный ответ.
Высота круговой орбиты искусственного спутника над поверхностью Земли уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника и период его обращения?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость спутника/ Период обращения спутника

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

Номер: A431BF

Впишите правильный ответ. ²⁰²⁴
Запишите показания динамометра с учётом абсолютной погрешности измерений. Абсолютная погрешность прямого измерения равна цене деления динамометра. Шкала проградуирована в ньютонах (Н).

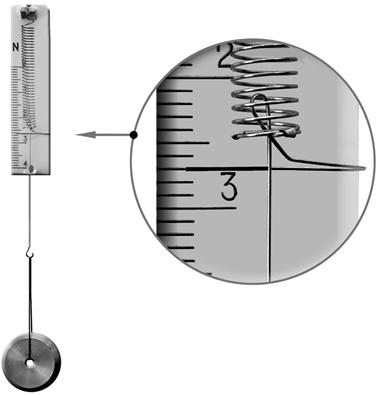
ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

2,70,1

Номер: 8E40BE

Впишите правильный ответ.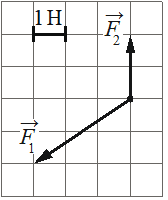
ЕГЭ физика

На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Определите модуль равнодействующей этих сил.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

3

Сложение векторов производим путем построения. Из конца одного вектора строим второй. Результата сложения векторов будет номинал от последнего вектора, до точки начала координат.

Номер: 1E061B

Впишите правильный ответ.

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 36 раз меньше, чем для второй. Каково отношение `R_1/R_2` радиусов орбит первой и второй планет?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

6

`F=(G*m_1*m_2)/R^2`

Примем для планет массу m1 = m2 = m, а для планеты m3, тогда

`36*(G*m*m_3)/R_1^2=(G*m*m_3)/R_2^2`

Сокращаем однородные показатели:

`36/R_1^2 = 1/R_2^2`

`36=R_1^2/R_2^2`

`6=R_1/R_2`

Номер: 9AE31E

Впишите правильный ответ.
В результате перехода искусственного спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода скорость движения спутника по орбите и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость движения спутника по орбите/ Период обращения спутника вокруг Земли

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

Номер: 607C12

Впишите правильный ответ. ²⁰²⁴
В инерциальной системе отсчёта сила величиной 70 Н сообщает телу массой 10 кг некоторое ускорение. Сила какой величины сообщит телу массой 9 кг в этой же системе отсчёта такое же ускорение?

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

63

F=ma
F=10*a=70 Н (1Н = 1 кг*м/с2)

a = 70/10=7 м/с²

После нахождения ускорение составим уравнение с неизвестной F

F=9*7=63 Н

Номер: 19872D

Впишите правильный ответ.
В результате перехода с одной круговой орбиты на другую кинетическая энергия спутника Земли увеличилась. Как изменились в результате этого перехода радиус орбиты спутника и его центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Радиус орбиты спутника/ Центростремительное ускорение спутника

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

21

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение увеличиваются.

Номер: C30E2B

Впишите правильный ответ.
В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличилась. Как изменились в результате этого перехода потенциальная энергия спутника в поле тяжести Земли и его центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Потенциальная энергия спутника/ Центростремительное ускорение спутника

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

21

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение увеличиваются.

Потенциальная энергия уменьшилась, так как радиус стал меньше. Еп.=mgh где h = R

Номер: BDFED1

Впишите правильный ответ.
При переходе с одной круговой орбиты на другую скорость движения искусственного спутника Земли уменьшается. Как изменяются в результате этого перехода центростремительное ускорение спутника и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Центростремительное ускорение/ Период обращения вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

Номер: 9810DD

Впишите правильный ответ.
В инерциальной системе отсчёта сила величиной 9 Н сообщает телу массой 3 кг ускорение `veca`.
Какой должна быть масса тела, чтобы сила, равная 18 Н, сообщала ему в той же системе отсчёта ускорение `4veca`?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

1,5

F=ma
a = 9/3, из этой формулы ускорение `veca = 3` м/с²

Необходимо получить ускорение `4veca = 3*4=12` м/с²при силе 18Н

Рассчитаем массу:

m=F/a=18/12=1,5 кг

Номер: 41AB52

Впишите правильный ответ.
Высота полёта искусственного спутника над Землёй увеличилась с 300 до 400 км. Как изменились при этом период обращения спутника и скорость его движения по орбите?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Период обращения спутника/ Скорость движения спутника по орбите

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

12

Центростремительное ускорение
`a_n = (v^2)/R` При увеличении орбиты (радиуса R), скорость спутника и центростремительное ускорение уменьшаются.

Период вращения спутника
`T=(2πR)/v`
Исходя из заключения выше, уменьшение скорости и увеличение радиуса повлечет увеличение периода обращения.

Номер: 4DEC5A

Впишите правильный ответ.
В инерциальной системе отсчёта сила 50 Н сообщает телу массой 5 кг некоторое ускорение. Какая сила сообщит телу массой 9 кг в этой системе отсчёта в 2 раза большее ускорение?

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

180

F=ma
F=5*a=50 Н (1Н = 1 кг*м/с2)

a = 50/5=10 м/с²

После нахождения ускорение составим уравнение с неизвестной F, по той же формуле F=ma, при этом ускорение возьмем в два раза больше

F=9*(2*10)=180 Н

Номер: 414B58

Впишите правильный ответ.
Расстояние от искусственного спутника до поверхности Земли равно двум радиусам Земли. Во сколько раз увеличится сила притяжения спутника к Земле, если расстояние от него до поверхности Земли станет равным одному радиусу Земли?

в
раз(а)

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

2.25

Первоначально расстояние между спутником и Землей равно 3 радиусам, берем расстояние от центра земли.

`F_1=(G*m_с*m_з)/(3R)^2`

`F_1=(G*m_с*m_з)/9R^2`

В случае если расстояние между спутником и землей будет 1 радиус, то

`F_2=(G*m_с*m_з)/(2R)^2`

`F_2=(G*m_с*m_з)/4R^2`

Из уравнения выше `F_1/F_2 = ((G*m_с*m_з)/4R^2)/((G*m_с*m_з)/9R^2)=9/4=2,25`

Номер: AC8852

Впишите правильный ответ. ²⁰²⁴
При исследовании зависимости модуля силы упругости Fупр от удлинения пружины были получены следующие данные.

Fупр, Н 2,5 5,0 10,0 12,5
Δx, м 0,01 0,02 0,04 0,05

Определите по результатам исследования жёсткость пружины.

H/м

КЭС: 1.2.7 Сила упругости. Закон Гука
Тип ответа: Краткий ответ

Ответ:

250

`F_упр.= k ·Δℓ`
`k = (F_упр.)/(Δℓ)`
`k = (5-2,5)/(0,02-0,01)=250 Н/м

Номер: C97E5E

Впишите правильный ответ.
Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 Н. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них 2m, а расстояние между их центрами 2r?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

0,2

Используем формулу
`F=(G*m_1*m_2)/R^2 = (G*m_1^2)/R^2` , при `m_1=m_2`

Произведем расчет для других показателей:
при условии `m_1=m_2 = 2m` и R = 2r получаем:

`(G*(2m)^2)/((2r)^2) = (G*4m^2)/(4r^2)=(G*m^2)/(r^2)`

То есть получается если мы будем увеличивать пропорционально как массу, так и расстояние между шариками, то сила будет оставаться прежней.

Номер: A129A4

Впишите правильный ответ.
В инерциальной системе отсчёта сила 50 Н сообщает телу массой 5 кг некоторое ускорение. Какая сила сообщит телу массой 8 кг в этой системе отсчёта такое же ускорение?

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

80

F=ma
F=5*a=50 Н (1Н = 1 кг*м/с2)

a = 50/5=10 м/с²

После нахождения ускорение составим уравнение с неизвестной F, по той же формуле F=ma

F=8*10=80 Н

Номер: C6B6AB

Впишите правильный ответ.
В инерциальной системе отсчёта сила, модуль которой равен 100 Н, сообщает некоторому телу ускорение 10 м/с². Каков модуль силы, которая сообщит этому телу ускорение 7 м/с² в этой системе отсчёта?

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

70

F=ma
100=m*10 (1Н = 1 кг*м/с²), находим массу m
m = 100/10=10 кг

После нахождения массы составим уравнение с неизвестной силой F, по той же формуле F=ma
F=7*10=70 Н

Номер: 64F9A6

Впишите правильный ответ.
В результате перехода искусственного спутника Земли с одной круговой орбиты на другую скорость его движения по орбите увеличилась. Как изменились в результате этого перехода радиус орбиты спутника и его период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Радиус орбиты спутника/ Период обращения спутника вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

22

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение увеличиваются.

Период вращения спутника
`T=(2πR)/v`
Исходя из заключения выше, увеличение скорости и уменьшение радиуса повлечет уменьшение периода обращения.

Номер: 82BCA1

Впишите правильный ответ.
Два маленьких шарика массой m каждый находятся на расстоянии r друг от друга и притягиваются друг к другу с силой 8 Н. Какова сила гравитационного притяжения двух других шариков, если масса одного 2m, масса другого `m/2`, а расстояние между их центрами 2r?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

2

Используем формулу
`F=(G*m_1*m_2)/r^2 = (G*m^2)/r^2`, при `m_1=m_2=m`

Произведем расчет для других показателей:
при условии `m_1=2m`, `m_2 = m/2` и r = 2r получаем:

`(G*(2m*m/2))/((2r)^2) = (G*m^2)/(4r^2)=1/4(G*m^2)/(r^2)`

То есть получается если мы будем менять условия согласно задания, то сила будет иметь коэффициент 1/4.

Тогда 8*1/4= 2 H

Номер: 41BBCF

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

4,70,1

Номер: 42A6C3

Впишите правильный ответ.
Искусственный спутник Земли перешёл с одной круговой орбиты на другую так, что на новой орбите его центростремительное ускорение увеличилось. Как изменились при этом сила притяжения спутника к Земле и скорость его движения по орбите?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Сила притяжения спутника к Земле/Скорость движения спутника по орбите

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

11

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение увеличиваются.

Сила притяжения
`F=(G*m_1*m_2)/r^2` Сила увеличилась, так как знаменатель уменьшился.

Номер: 29F6CD

Впишите правильный ответ.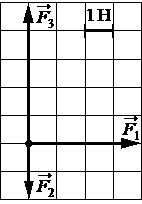
ЕГЭ физика

На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона
клетки соответствует 1 Н. Определите модуль равнодействующей приложенных сил.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

5

Сложение векторов производим путем построения. Из конца одного вектора строим второй. Результата сложения векторов будет номинал от последнего вектора, до точки начала координат.

3²+4²=x²
`x=sqrt(9+16)`
x=5

Номер: 9B55C6

Впишите правильный ответ.
В инерциальной системе отсчёта сила `vecF` сообщает телу массой 3 кг ускорение `veca`.
Какой должна быть масса тела, чтобы вдвое меньшая сила сообщала ему в той же системе отсчёта ускорение `1/4 veca`?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

6

F=ma
F = 3*a

Уменьшим силу в два раза сохраняя пропорции

F/2=3a/2

F/2=1,5a При силе в два раза меньше, масса при том же ускорении будет 1,5 кг.

Нам надо получить 1/4а, для этого чтобы уменьшить влияние ускорения на силу в 4 раза (снизив его), необходимо компенсировать правую часть увеличением массы в 4 раза.

`F/2=6a_2` где `a_2=1/4a`

Получается масса равна 6 кг.

Номер: 82C6CD

Впишите правильный ответ.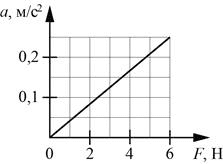
ЕГЭ физика

На графике приведена зависимость ускорения бруска, скользящего без трения по горизонтальной поверхности, от величины приложенной к нему горизонтальной силы. Систему отсчёта считать инерциальной. Чему равна масса бруска?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

20

F=ma ⇒ m=F/a
Ищем удобную точку на графике и считаем:
6/0,25=24 кг

Номер: 4D1B9A

Впишите правильный ответ.
В инерциальной системе отсчёта сила 50 Н сообщает телу массой 5 кг некоторое ускорение. Какова масса тела, которому сила 60 Н сообщает такое же ускорение?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

6

F=ma
F=5*a=50 Н (1Н = 1 кг*м/с2)

a = 50/5=10 м/с²

После нахождения ускорение составим уравнение с неизвестной m, по той же формуле F=ma

F=m*10=60 Н

m=60/10=6 кг

Номер: F65695

Впишите правильный ответ.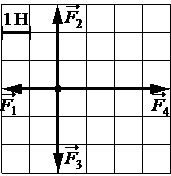
ЕГЭ физика

На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

2

Сложение векторов производим путем построения. Из конца одного вектора строим второй. Результата сложения векторов будет номинал от последнего вектора, до точки начала координат.

Номер: 12E192

Впишите правильный ответ.
Под действием силы величиной 6 Н пружина удлинилась на 3 см. Чему равна величина силы, под действием которой удлинение этой пружины составит 4,5 см?

КЭС: 1.2.7 Сила упругости. Закон Гука
Тип ответа: Краткий ответ

Ответ:

9

По закону Гука
`F_упр.= k ·Δℓ`
`k = (F_упр.)/(Δℓ)`
`k = 6/3=2 Н/м

`F_упр.= 2 * 4,5`
`F_упр.= 9` Н

Номер: 26769F

Впишите правильный ответ.
Два маленьких шарика массой m каждый находятся на расстоянии r друг от друга и притягиваются друг к другу с силой 32 Н. Каков модуль сил гравитационного притяжения друг к другу двух других шариков, если масса каждого из них равна `m/2`, а расстояние между ними равно 2r?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

2

Используем формулу
`F=(G*m_1*m_2)/r^2 = (G*m^2)/r^2`, при `m_1=m_2=m`

Произведем расчет для других показателей:
при условии `m_1=m_2 = m/2` и r = 2r получаем:

`(G*(m/2)^2)/((2r)^2) = (G*m^2/4)/(4r^2)=1/16(G*m^2)/(r^2)`

То есть получается если мы будем менять условия согласно задания, то сила будет меньше на коэффициент 1/16, то есть в 16 раз.

Тогда 32/16=2 Н

Номер: D9079D

Впишите правильный ответ. ²⁰²⁴
При исследовании зависимости модуля силы трения скольжения F_тр→ от модуля нормальной составляющей силы реакции опоры N→
были получены следующие данные.

Fтр, Н 0,8 1,6 2,4 3,2
N, Н 2,0 4,0 6,0 8,0

Определите по результатам исследования коэффициент трения скольжения.

КЭС: 1.2.8 Сила трения. Сухое трение. Сила трения скольжения. Сила трения покоя. Коэффициент трения
Тип ответа: Краткий ответ

Ответ:

0,4

Сила трения
Fтр. = µN, где Fтр.макс - модуль максимальной силы трения покоя, µ- коэффициент пропорциональности, называемый коэффициентом трения.

1,6 = µ*4
µ = (1,6)/4 = 0,4

Номер: 318091

Впишите правильный ответ.

ЕГЭ физика

На рисунке изображены лабораторный динамометр и линейка. Шкала динамометра проградуирована в ньютонах, шкала линейки проградуирована в сантиметрах. Какой должна быть масса груза, подвешенного к пружине динамометра, чтобы пружина растянулась на 7,5 см?

КЭС: 1.2.7 Сила упругости. Закон Гука
Тип ответа: Краткий ответ

Ответ:

75

Значение по динамометру должно быть равно 0,75 Н, то есть 75 грамм

Номер: 8CF69C

Впишите правильный ответ.
У поверхности Луны на космонавта действует сила тяготения 120 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии двух лунных радиусов от её центра?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

30

Используем формулу
`F=(G*m_1*m_2)/r^2 `

если увеличить радиус в два раза, то знаменатель увеличится в 4 раза, а само значение F уменьшится в 4 раза, тогда:

120/4=30 Н

Номер: BA66EA

Впишите правильный ответ.
Космический исследовательский зонд обращается по круговой орбите вокруг Марса. В результате перехода на другую круговую орбиту центростремительное ускорение зонда уменьшилось. Как изменились при этом переходе период обращения зонда вокруг Марса и его кинетическая энергия?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Период обращения зонда/ Кинетическая энергия зонда

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

Номер: DCFBE7

Впишите правильный ответ.
В инерциальной системе отсчёта сила `vecF` сообщает телу массой 4 кг ускорение `veca`.
Какова должна быть масса тела, чтобы вдвое меньшая сила сообщала ему в 4 раза большее ускорение?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

0,5

F=ma
F = 4*a

Уменьшим силу в два раза сохраняя пропорции двух частей равенства

F/2=4a/2

F/2=2a При силе в два раза меньше, масса при том же ускорении будет 2 кг.

Нам надо получить 4а, для этого чтобы увеличить влияние ускорения на силу в 4 раза (повышая его), необходимо компенсировать правую часть уменьшением массы в 4 раза.

`F/2=2/4*a_2` где `a_2=4a`

`F/2=0,5*a_2`

Получается масса равна 0,5 кг.

Номер: C644EA

Впишите правильный ответ.
ЕГЭ физика

При помощи динамометра измеряют силу тяжести, действующую на пластину
(см. рисунок). Динамометр проградуирован в ньютонах. Абсолютная погрешность прямого измерения силы динамометром равна цене деления. Какова сила тяжести, действующая на пластину, по показаниям динамометра?

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

1,60,1

Номер: E11CE9

Впишите правильный ответ.
Динамометр с прикреплённым к нему бруском тянут влево, как показано на рисунке. Брусок движется с постоянной скоростью. Абсолютная погрешность измерения силы при помощи динамометра равна цене деления прибора. Запишите значение силы трения скольжения, действующей на брусок, с учётом абсолютной погрешности измерений.

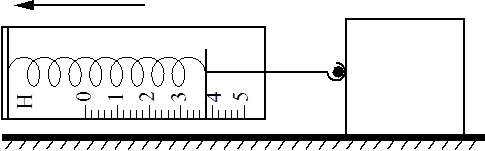
ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

3,80,2

Номер: EDAAE9

Впишите правильный ответ.
Космический исследовательский зонд обращается по круговой орбите вокруг Марса. В результате перехода на другую круговую орбиту центростремительное ускорение зонда увеличилось. Как изменились при этом переходе скорость зонда и период обращения зонда вокруг Марса?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость зонда/ Период обращения зонда

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

12

Центростремительное ускорение
`a_n = (v^2)/R` При уменьшении орбиты (радиуса R), скорость спутника и центростремительное ускорение увеличиваются.

Период обращения спутника
`T=(2πR)/v`
Исходя из заключения выше, увеличение скорости и уменьшение радиуса повлечет уменьшение периода обращения.

Номер: 7EC464

Впишите правильный ответ. ²⁰²⁴
В инерциальной системе отсчёта некоторая сила сообщает телу массой 5 кг ускорение, равное по модулю 3 м/с². Определите модуль ускорения, которое сообщит та же сила в той же системе отсчёта телу массой 7,5 кг.

м/с²

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

2

F=ma
F=5*3=15 Н (1Н = 1 кг*м/с2)

После нахождения силы составим уравнение с неизвестной a, по той же формуле F=ma

15=7.5*a

a=15/7.5=2 м/с²

Номер: 19F564

Впишите правильный ответ.
Два маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с гравитационной силой 0,3 Н. Каков модуль сил гравитационного притяжения друг к другу двух других шариков, если масса одного из них равна 3m, масса другого – `m/3`, а расстояние между их центрами равно `r/3`?

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

2,7

Используем формулу
`F=(G*m_1*m_2)/r^2 = (G*m^2)/r^2`, при `m_1=m_2=m`

Произведем расчет для других показателей:
при условии `m_1=3m`, `m_2 = m/3` и r = r/3 получаем:

`(G*(3m* m/3)^2)/((r/3)^2) = (G*m^2)/(r^2/9)=9(G*m^2)/(r^2)`

То есть получается если мы будем менять условия согласно задания, то сила будет больше на коэффициент 9, то есть в 9 раз.

Тогда 0,3*9=2,7 Н

Номер: C0B561

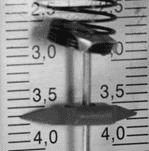
ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

3,60,1

Номер: E92765

Впишите правильный ответ.
В инерциальной системе отсчёта некоторая сила сообщает телу массой 8 кг ускорение 5 м/с². Какое ускорение в той же системе отсчёта сообщит та же сила телу массой 5 кг?

м/с²

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

8

F=ma
F=8*5=40 Н (1Н = 1 кг*м/с2)

После нахождения силы составим уравнение с неизвестной a, по той же формуле F=ma

40=5*a

a=40/5=8 м/с²

Номер: E24869

Впишите правильный ответ.
Определите показания динамометра (см. рисунок), если абсолютная погрешность прямого измерения силы равна цене деления динамометра. Динамометр проградуирован в ньютонах.

ЕГЭ физика

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

2,20,1

Номер: 55563B

Впишите правильный ответ.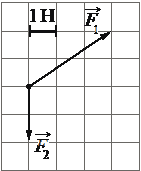
ЕГЭ физика

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

Номер: 5E2935

Впишите правильный ответ.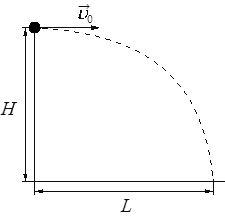
ЕГЭ физика

Шарик, брошенный горизонтально с высоты H с начальной скоростью vecυ_0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок). Как изменятся дальность полёта L и скорость шарика в момент падения, если, не меняя начальной скорости шарика, увеличить высоту H? Сопротивлением воздуха пренебречь.

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Дальность полета/ Скорость шарика в момент падения

КЭС: 1.2 Динамика
Тип ответа: Краткий ответ

Ответ:

11

Если пренебречь сопротивлением воздуха, то получается по горизонтали шарик может лететь сколь угодно долго, если будет позволять высота. В итоге дальность полета по горизонту при увеличении высоты увеличиться.

Скорость в момент приземления увеличиться, так как повышение потенциальной энергии за счет высоты вызовет увеличение кинетической энергии при падении. А кинетическая энергия как известно характеризуется в том числе и скоростью.

Номер: C89B35

Впишите правильный ответ.
Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом центростремительное ускорение, с которым спутник движется по орбите, и его период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Центростремительное ускорение/ Период обращения спутника вокруг Земли

КЭС: 1.2.6 Закон всемирного тяготения. Сила тяжести. Центр тяжести тела.
Тип ответа: Краткий ответ

Ответ:

21

Центростремительное ускорение
`a_n = (v^2)/R` При увеличении орбиты (радиуса R), скорость спутника и центростремительное ускорение уменьшаются.

Период обращения спутника
`T=(2πR)/v`
Исходя из заключения выше, уменьшении скорости и увеличении радиуса повлечет увеличение периода обращения.

Номер: E1173A

Впишите правильный ответ.
Пакет, в котором находится 200 гаек, положили на весы. Весы показали 60 г. Чему равна масса одной гайки по результатам этих измерений, если погрешность весов равна ±10 г? Массу самого пакета не учитывать.

Ответ: ( ± ) г.

Ответ:

0,300,05

m = 60/200=0,30 г

Найдем погрешность

10/200=0,05 г

Обратите внимание, что в ответ вписываем не 0,3, а 0,30, для того, чтобы показать точность соизмеримую с вычисленной погрешностью.

Номер: 6FB53E

Впишите правильный ответ.
ЕГЭ физика

Определите показания динамометра (см. рисунок), если погрешность прямого измерения силы равна цене деления динамометра. Шкала динамометра проградуирована в Н.

Ответ: ( ± ) Н.

КЭС: 1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Краткий ответ

Ответ:

2,10,1

Номер: AAC78C

Впишите правильный ответ.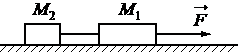
ЕГЭ физика

Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы `vecF`, приложенной к грузу М₁ = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы `vecF`
равен 12 H. Чему равна масса второго груза М₂?

кг

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

1

Два груза массами M₁ и M₂ движутся под действием силы F = 12 Н, следовательно, оба груза движутся с ускорением.
`F=a(M_1+M_2)` ⇒ `a=F/(M_1+M_2)`

Сила натяжения нити T возникает в результате силы трения последнего груза, направленной в противоположную сторону силе F. Так как ускорение последнего груза также равно a, а его масса равна M₂, то из второго закона Ньютона (при обрыве нити) имеем `T=aM_2` или в виде
`T=F/(M_1+M_2)*M_2`
откуда
`M_2=T/(F-T)*M_1`
`M_2=4/(12-4)*2=1` кг

Номер: 1DEB4C

Впишите правильный ответ.
Даны следующие зависимости величин:

А) зависимость пути, пройденного телом при равномерном движении,
от времени;

Б) зависимость объёма постоянной массы идеального газа от абсолютной температуры в изохорном процессе;

В) зависимость электроёмкости плоского конденсатора с расстоянием d между пластинами от площади пластин.

Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

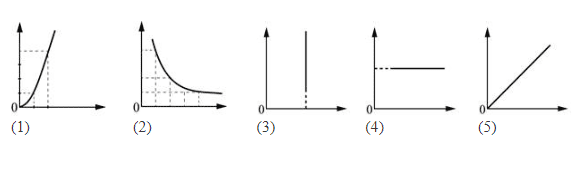
А Б В
Ответ:

Ответ:

545

1) зависимость пути, пройденного телом при равномерном движении,
от времени; S=М*н. График под номером 5

2) В изохорном процессе объём постоянен, горизонтальная линия. График 4.

3) Зависимость электроёмкости плоского конденсатора с расстоянием d между пластинами от площади пластин имеет вид: `С= εε_0 * S/d`. График под номером 5

Номер: A89B4F

Впишите правильный ответ.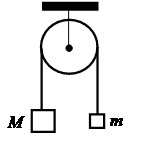
ЕГЭ физика

Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускоренно. Через t = 1 с после начала движения скорость правого груза направлена вверх и равна 4 м/с. Определите силу натяжения нити, если масса левого груза М = 1 кг. Трением пренебречь.

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Тип ответа: Краткий ответ

Ответ:

6

Получается ускорение равно 4 м/с², так как именно такая скорость 4 м/с у груза через 1 секунду.

То есть получается у нас по закону Ньютона появилась постоянная сила со стороны более тяжелого груза, которая равна:

F=ma

F=1*4= 4 Н

При этом гравитационная постоянная для левого груза (1 кг) равно g, и также в том же направлении есть ускорение 4 м/с²

То есть у нас для левого груза ускорение равно 10-4=6 м/с²

Оно снижается за счет того, что в противоположном направлении действует правый груз.

Найдем силу по закону Ньютона.

F=ma

F=0,6*10=6 Н (Это и будет натяжение нити)

Номер: 150AE7

Установление соответствия (3)

Установите соответствие и впишите ответ.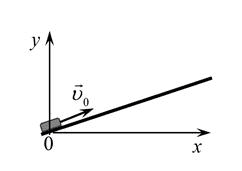
ЕГЭ физика

После удара шайба начала скользить вверх по гладкой наклонной плоскости со скоростью vecυ_0,
как показано на рисунке. В момент t₀
шайба возвращается в исходное положение. Графики А и Б отображают изменение с течением времени физических величин, характеризующих движение шайбы.

Установите соответствие между графиками и физическими величинами, изменение которых со временем эти графики могут отображать.

К каждой позиции первого столбца подберите соответствующую позицию
из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ
А)
ЕГЭ физика

Б)
ЕГЭ физика

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) кинетическая энергия Е_к
2) проекция скорости V_x
3) потенциальная энергия Е_п
4) проекция ускорения а_х

А Б

КЭС: 1.2 Динамика
Тип ответа: Установление соответствия

Ответ:

42

А) Проекция ускорения будет одной и той же на всем промежутке времени. И всегда напаравлена в одну сторону.

Б) Скорость вначале падет, потом возрастает, но уже с другим знаком.

Номер: F9DC54

Установите соответствие и впишите ответ.
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой
х(t) = 10 + 5t – 3t² (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их изменения во времени.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) проекция υ_x(t) скорости тела
Б) проекция F_x(t)
равнодействующей сил, приложенных к телу

ФОРМУЛЫ
1) 5 – 6t
2) –1,2
3) –3
4) 10 + 5t

А Б

КЭС: 1.1.6 Равноускоренное прямолинейное движение
1.2.3 Сила. Принцип суперпозиции сил
Тип ответа: Установление соответствия

Ответ:

12

А) Производная от формул будет проекцией скорости.

Б) Корень производной будет характеризовать равнодействующую силу.

Номер: B28492

Установите соответствие и впишите ответ. ²⁰²⁴

ЕГЭ физика

После удара в момент времени t=0
шайба начала скользить вверх по гладкой наклонной плоскости с начальной скоростью υ→0,
как показано на рисунке. В момент времени t0 шайба вернулась в исходное положение. Графики А и Б отображают изменение с течением времени физических величин, характеризующих движение шайбы.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ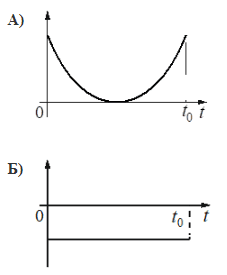
ЕГЭ физика

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) проекция скорости v_x
2) проекция ускорения а_у
3) кинетическая энергия Е_к
4) полная механическая энергия Е_мех

А Б

КЭС: 1.2 Динамика
Тип ответа: Установление соответствия

Ответ:

32

А) С падением скорости падала и кинетическая энергия. После верхней точки, при возрастании скорости энергия опять стала расти. График квадратичной функции является параболой.

Кинетическая энергия
`Ek=(mV^2)/2`

Б) Ускорение было постоянным на всем промежутке времени.

Номер: FFF839

Развернутый ответ (31)

Дайте развернутый ответ.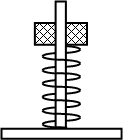
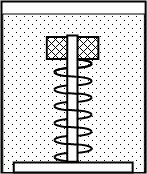
ЕГЭ физика

Пирамидка №1 Пирамидка №2

Два деревянных кольца детских пирамидок №1 и №2, способных без трения скользить по оси, соединили с основаниями двумя одинаковыми лёгкими пружинками (см. рисунок). Пирамидку №2 поместили в прочный сосуд с водой, прикрепив основание к его дну. Обе пирамидки покоятся относительно Земли. Как изменится по сравнению с этим случаем (увеличится, уменьшится или останется прежней) длина пружин пирамидок № 1 и № 2 во время свободного падения с балкона высокого дома? Сопротивлением воздуха пренебречь. Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.

КЭС: 1.2 Динамика

Решение:

На кольцо в первом случае действует сила упругости пружины Fy1 , сила тяжести кольца mg . Во втором случае на тело действует сила Архимеда Fарх , сила упругости Fy2 и сила тяжести mg . Пусть плотность дерева ρ, объём кольца V, а плотность воды ρ0 . Тогда сила тяжести равна ρgV , а сила Архимеда ρ0gV . Так как ρ0 > ρ , то сила Архимеда по модулю больше, чем сила тяжести. Сделаем рисунок с расстановкой сил.

ЕГЭ физика

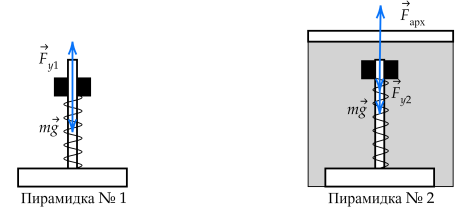
В первом случае пружина сжата, а во втором растянута (из-за того, что сила Архимеда больше силы тяжести кольца). Запишем второй закон Ньютона для двух пирамидок во время покоя относительно Земли:

`vec(F_(y1)) +m vecg = m veca`,
`vec(F_(y2))+ mg+ vecF_(арх) = m veca`,
так как ускорение a равно нулю, то спроецировав на вертикальную ось получим:

`F_(y1) = mg`
`F_(y2) = F_(арх)− mg`
Модули сил упругости равны:

`F_(y1) = k|l_1− l_0| F_(y2) = k|l_2− l_0|`,

где k – жёсткость пружины, l0 – длина недеформированной пружины.
При свободном падении тело испытывает состояние невесомости: невесомы стали и кольцо, и вода. Сила Архимеда равна весу вытесненной жидкости, когда пирамидка находится в состоянии невесомости, то вес вытесненной жидкости также равен нулю, следовательно, сила Архимеда стала равна нулю. Вес всех предметов стал равен нулю и перестал действовать на пружины и они вернулись в недеформированное состояние: пружина 1 растянулась, пружина 2 – сжалась

Номер: 746AB3

Дайте развернутый ответ.

ЕГЭ физика

Пирамидка №1 Пирамидка №2

Два деревянных кольца детских пирамидок № 1 и № 2, способных без трения скользить по оси, соединили с основаниями двумя одинаковыми лёгкими пружинками (см. рисунок). Пирамидку № 2 поместили в прочный сосуд с глицерином, прикрепив основание к его дну. Обе пирамидки покоятся относительно Земли. Плотность глицерина больше плотности дерева. Как изменится по сравнению с этим случаем (увеличится, уменьшится или останется прежней) длина пружин пирамидок № 1 и № 2 во время свободного падения с балкона высокого дома? Сопротивлением воздуха пренебречь. Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.

КЭС: 1.2 Динамика

Решение:

ЕГЭ физика

В первом случае пружина сжата, а во втором растянута (из-за того, что сила Архимеда больше силы тяжести кольца). Запишем второй закон Ньютона для двух пирамидок во время покоя относительно Земли:

`vec(F_(y1)) +m vecg = m veca`,
`vec(F_(y2))+ mg+ vecF_(арх) = m veca`,
так как ускорение a равно нулю, то спроецировав на вертикальную ось получим:

`F_(y1) = mg`
`F_(y2) = F_(арх)− mg`
Модули сил упругости равны:

`F_(y1) = k|l_1− l_0| F_(y2) = k|l_2− l_0|`,

где k – жёсткость пружины, l0 – длина недеформированной пружины.
При свободном падении тело испытывает состояние невесомости: невесомы стали и кольцо, и вода. Сила Архимеда равна весу вытесненной жидкости, когда пирамидка находится в состоянии невесомости, то вес вытесненной жидкости также равен нулю, следовательно, сила Архимеда стала равна нулю. Вес всех предметов стал равен нулю и перестал действовать на пружины и они вернулись в недеформированное состояние: пружина 1 растянулась, пружина 2 – сжалась

Номер: 1A1FBB

Дайте развернутый ответ.
Лёгкая нить, привязанная к грузу массой m=0,4 кг, перекинута через идеальный неподвижный блок. К правому концу нити приложена постоянная сила `vecF`.
Левая часть нити вертикальна, а правая наклонена под углом α=30° к горизонту (см. рисунок).

Постройте график зависимости модуля силы реакции стола N от F на отрезке 0≤F≤10 Н. Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения. Сделайте рисунок с указанием сил, приложенных к грузу.

ЕГЭ физика

КЭС: 1.2 Динамика

Решение:

ЕГЭ физика

В начале сила натяжения нити, равная силе F будет меньше, чем сила mg = 4 Н, поэтому по второму закону Ньютона

F − mg + N = ma
пока тело покоится, ускорение равно нулю, при F = 0, N = mg = 4 Н.
При силе от 0 до 4 Н, N =mg − F
При силе больше 4 Н, груз начнет отрываться от стола и двигаться с ускорением, а сила реакции опоры станет равна 0.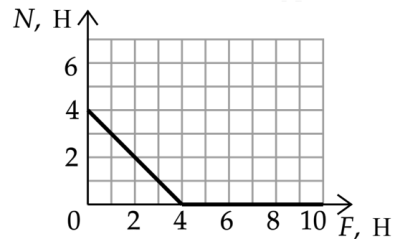

ЕГЭ физика

Номер: 170B54

Дайте развернутый ответ.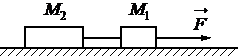
ЕГЭ физика

Два груза, связанных нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием горизонтальной силы `vecF`, приложенной к грузу массой М₁ = 2 кг (см. рисунок). Максимальная сила F, при которой нить ещё не обрывается, равна 18 Н. Известно, что нить может выдержать нагрузку не более 10 Н. Чему равна масса второго груза?

КЭС: 1.2 Динамика

Решение:

2,5

Грузы движутся с ускорением. Грузы связаны нерастяжимой и невесомой нитью, следовательно, силы натяжения нити одинаковы и грузы движутся с одинаковыми ускорениями. Поверхность гладкая, значит, силой трения пренебрегаем.

Запишем для каждого груза второй закон Ньютона в проекциях на горизонтальную ось, направленную в сторону движения грузов:

`F − T = M_1*a`
`T = M_2*a`

ЕГЭ физика

Сложим два уравнения системы и выразим ускорение грузов:

`F = (M_1 + M_2)/a` ⇒ `a = F/(M_1+M_2)`

Из второго уравнения системы выразим силу натяжения нити с учетом выражения для ускорения грузов:

`T = a*M_2 = (F*M_2)/(M_1 + M2)

Выразим массу второго груза:

`M_2 = T *M_1/(F − T) = 2*10/(18-10) = 2,5 кг`

Номер: 7DEBA4

Дайте развернутый ответ.
Груз массой 200 г подвешен на пружине жёсткостью 100 Н/м к потолку лифта. Лифт равноускоренно движется вниз, набирая скорость. Каково ускорение лифта, если удлинение пружины постоянно и равно 1,5 см?

КЭС: 1.2 Динамика

Решение:

2,5

Вначале узнаем силу оказываемую на пружину.
1,5 см = 0,015 м

При жесткости пружины 100 Н/м получается.

`F упр. = k ·Δℓ`
`k = (F_(упр.))/Δℓ`

так как у нас удлинение 0,015, то 0,015/1 это та часть силы, которая приложена к пружине если сравнивать ее с силой которая оттягивает эту пружину на 1 метр, а эта сила равна 100 Н, тогда:

100*0,015=1,5 Н сила воздействия на пружину.

При этом эту силу можно выразить через закон Ньютона.

F=m*(g-a), (так как лифт ускоряется вниз, то это будет уменьшать усилие на пружину то есть из гравитационной постоянной вычтем ускорение лифта) То есть ускорение вниз как бы помогает уменьшить гравитационную постоянную, сокращая ее значение, за счет перемещения вниз.

g - a = F/m = 1,5/0,2=7,5 м/с²

a = 10 - 7,5 = 2,5 м/с²

Номер: C961A9

Дайте развернутый ответ.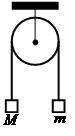
ЕГЭ физика

Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускоренно. Через t=1 с после начала движения скорость правого груза (массой m = 1 кг) была направлена вертикально вверх и равна 4 м/с. Определите силу натяжения нити. Трением пренебречь.

КЭС: 1.2 Динамика

Решение:

Получается ускорение равно 4 м/с², так как именно такая скорость 4 м/с у груза (ов) через 1 секунду.

То есть получается у нас по закону Ньютона появилась дополнительная постоянная сила:

F=ma

F=1*4= 4 Н

При этом нить удерживала груз под воздействием веса, который характеризуется гравитационной постоянной g = 10 м/с²и появилось ускорение в 4 м/с² , которое добавилось к g.

То есть по закону Ньютона: F=m(g+a) =1*10+4=14 Н

Номер: 4F0963

Дайте развернутый ответ.
Лёгкая нить, привязанная к грузу массой m=0,3 кг, перекинута через идеальный неподвижный блок. К правому концу нити приложена постоянная сила `vecF`.
Левая часть нити вертикальна, а правая наклонена под углом α=30° к горизонту (см. рисунок).

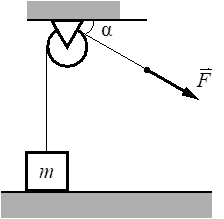
ЕГЭ физика

КЭС: 1.2 Динамика

Решение:

ЕГЭ физика

В начале сила натяжения нити, равная силе F будет меньше, чем сила mg = 3 Н, поэтому по второму закону Ньютона

F − mg + N = ma
пока тело покоится, ускорение равно нулю, при F = 0, N = mg = 3 Н.
При силе от 0 до 3 Н, N =mg − F
При силе больше 3 Н, груз начнет отрываться от стола и двигаться с ускорением, а сила реакции опоры станет равна 0.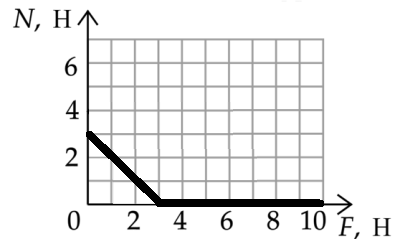

ЕГЭ физика

Номер: 36B168

Дайте развернутый ответ.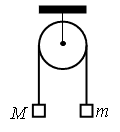
ЕГЭ физика

Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок
(см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускоренно. Опустившись на 2 м, левый груз приобрёл скорость 4 м/с. Определите силу натяжения нити, если масса правого груза m = 1 кг. Трением пренебречь.

КЭС: 1.2 Динамика

Решение:

Получается ускорение равно

`S=(V^2 - V_0^2)/(2a)`

`2=4^2/(2a)`

`2a=16/2`

a = 4 м/с²

То есть получается у нас по закону Ньютона появилась дополнительная постоянная сила, так как появилось ускорение:

F=ma

F=1*4= 4 Н

При этом нить удерживала правый груз под воздействием веса, который характеризуется гравитационной постоянной g = 10 м/с²и появилось ускорение в 4 м/с² , которое добавилось к g.

То есть по закону Ньютона: F=m(g+a) =1*(10+4)=14 Н натяжение нити.

Номер: 873381

Дайте развернутый ответ.
Имеется недеформированная пружина длиной L = 20 см и жёсткостью k = 30 Н/м, груз массой m = 0,2 кг, а также вращающийся с частотой ν = 1 Гц массивный диск. На каком максимальном расстоянии от центра диска можно положить на него груз, прикрепив его пружиной к центру диска, чтобы груз оставался неподвижным относительно диска? Коэффициент трения между грузом и диском μ = 0,3. Размерами груза пренебречь. Сделайте схематический рисунок с указанием сил, действующих на груз.

КЭС: 1.2 Динамика

Решение:

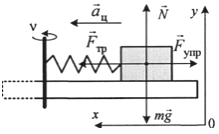
ЕГЭ физика

На груз действуют четыре силы: сила тяжести mg, нормальная составляющая силы реакции опоры N, сила упругости F и сила трения Fтp. По условию задачи груз должен находится на минимальном расстоянии от центра диска; значит, пружина должна быть сжата, сила упругости направлена вправо (см. рисунок), а сила трения – влево. Поскольку пружина максимально сжата, а груз при этом находится в покое относительно диска, сила трения покоя принимает максимальное значение:
Fтр=μN. (1)
Второй закон Ньютона в проекциях на оси инерциальной системы отсчёта ху имеет вид:
Ох: ац = Fтp – Fynp; (2)
Оу: 0 = N – mg (3)

Сила упругости определяется законом Гука:
Fупр=k∆x (4)

Центростремительное ускорение груза выражается формулой

`а_ц = 4π^2*ν^2*Rmin`. (5)

Из формул (1)–(5) получаем: `4π^2*ν^2*R_min*m = μmg – к * ∆х`, где Rmin = L – ∆х.
Окончательно получим: `R_min = (kL + μmg)/(k - 4π^2*ν^2*m) ≈ 0,29` м
Ответ: Rmin = 0,29 м

Номер: 0DDE03

Дайте развернутый ответ.
ЕГЭ физика

Груз массой М = 800 г соединён невесомой и нерастяжимой нитью, перекинутой через гладкий невесомый блок, с бруском массой m = 400 г. К этому бруску на лёгкой пружине жёсткостью k = 80 Н/м подвешен второй такой же брусок. Длина нерастянутой пружины l = 10 см, коэффициент трения груза о поверхность стола μ = 0,2. Определите длину пружины при движении брусков, считая, что при этом движении она постоянна. Сделайте рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.

КЭС: 1.2 Динамика

Решение:

1. Задачу будем решать в инерциальной системе отсчета, связанной с поверхностью стола.

2. Будем применять для грузов и бруска законы Ньютона, справедливые для материальных точек, поскольку тела движутся поступательно.

3. Трением в оси блока и трением о воздух, а также массой блока пренебрежем.

4. Так как нить нерастяжима и длина пружины постоянна, ускорения обоих брусков и груза равны по модулю:

`|veca_1|= |veca_2|= |veca_3|= a`.
5. На рисунке показаны силы, действующие на бруски и груз.

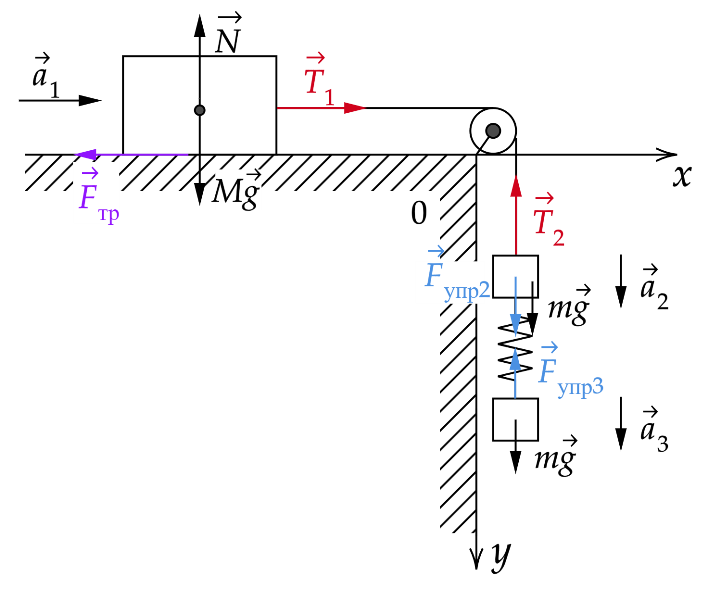
ЕГЭ физика

6. Так как блок и нити невесомы, а трение отсутствует, то модули сил натяжения нити, действующих на груз и верхний брусок, одинаковы:

`|vecT_1|= |vecT_2|=T`
7. Равны по модулю и силы

`|vecF_(упр2)|= |vecF_(упр3)|`
так как пружина легкая.

Решение
Рисунок с указанием сил показан в обосновании. Запишем второй закон Ньютона для каждого из тел. Тело массой M :

`M vecg+ vecT_1+ vecF_(тр)+ vecN = M veca1`,

Верхний груз массой m :

`m vecg+ vecT_2+ vecF_(упр2) = m veca_2`,

Нижний груз массой m :

`m vecg+ vecF_(упр3) = m veca_3`,

спроецируем второй закон Ньютона M на вертикальную и горизонтальную оси, с учетом 4 и 6 пункта обоснования:

Mg = N
T − F тр =Ma,

Сила трения скольжения равна:

Fтр = μN = μMg.
T − μMg = Ma

Спроецируем второй закон Ньютона для тел m , с учётом, что Fупр = kΔl здесь Δl – удлинение пружины.

Верхний груз массой m :

mg + kΔl− T = ma

Нижний груз массой m :

mg − kΔl = ma

Получаем систем уравнений:

`{(T − μMg = Ma),(mg +kΔl − T = ma),(mg − kΔl = ma):}`

Сложим 3 уравнения:

`a = (2mg - μMg)/(M + 2m) = (2⋅0,4 кг *10Н/(кг)-0,2*0,8 кг*10 Н/(кг))/(0,8 кг +2 ⋅0,4 кг)= 4 Н/(кг)`

Из последнего уравнения системы

`Δl = m(g-a)/k= (0,4 кг(10 Н/(кг)-4Н/(кг)))/(80 Н/м)= 0,03` м

тогда общая длина пружины

L = l + Δl = 0,1 м+ 0,03 м = 0,13 м

Номер: 6F7274

Дайте развернутый ответ.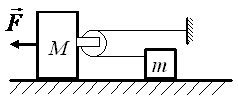
ЕГЭ физика

К бруску массой М прикреплён лёгкий блок (см. рисунок), через него переброшена лёгкая нерастяжимая нить, один конец которой привязан
к стене, а к другому прикреплено тело массой m. На брусок действует сила F. Определите ускорение бруска. Свободные куски нити горизонтальны и лежат в одной вертикальной плоскости, тела двигаются вдоль одной прямой. Массой блока и нити, а также трением пренебречь. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика

Решение:

Систему отсчёта, связанную с Землёй, будем считать инерциальной. Запишем второй закон Ньютона в проекциях на горизонтальную ось для тела и бруска:

`ma_1=T_1`
`M*a_2=F - T_4`

где a₁, a₂— ускорения тела и бруска,
Т1 — сила натяжения нити,
Т4 — сила, с которой блок действует на брусок.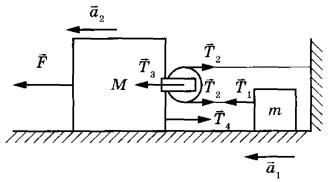

ЕГЭ физика

Запишем второй закон Ньютона для невесомого блока:

`0 = T_3 - 2T_2`,

где
T₃ — сила, с которой брусок действует на блок,
T₂ — сила натяжения нити, действующая на блок.

Ускорение бруска массой M в 2 раза меньше ускорения тела массой m, так как за одно и то же время перемещение тела в 2 раза больше перемещения бруска: a₁=2a₂.

Приходим к системе уравнений:

`{(F-2T=Ma_2), (T=m*2a_2):}`

откуда

`a_2=F/(M+4m)`

`a_1=2a_2=(2F)/(M+4m)`

Обоснование

1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).

2. Брусок и тело движутся поступательно, поэтому описываем их моделью материальной точки независимо от их размеров.

3. Из пп. 1 и 2 следует, что движение бруска и тела в ИСО описывается вторым законом Ньютона.

4. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.

5. Нить нерастяжима, поэтому модули ускорений подвижного блока и тела m при их прямолинейном поступательном движении отличаются в 2 раза.

Номер: 04DCB4

Дайте развернутый ответ.
На горизонтальном столе лежит деревянный брусок. Коэффициент трения между поверхностью стола и бруском μ = 0,1. Если приложить к бруску силу, направленную вверх под углом α = 45° к горизонту, то брусок будет двигаться по столу равномерно прямолинейно. С каким ускорением будет двигаться этот брусок по столу, если приложить к нему такую же по модулю силу, направленную вверх под углом β = 30° к горизонту? Сделайте рисунок с указанием сил, действующих на брусок.

КЭС: 1.2 Динамика

Решение:

Запишем второй закон Ньютона:

`vecF +vecN+ vecFтр+ m vecg = m veca`.
Так как движения равномерное, то ускорение равно 0, тогда второй закон Ньютона на оси Ox и Oy имеет вид:

`{ (Ox F cosα − Fтр = 0), (Oy N +F sin α= mg):}`

Сила трения равна Fтр = μN

{ (Ox F cosα − μN = 0 (1)), (Oy N +F sin α= mg (2)):}`

Тогда отсюда можно выразить F

`F = μmg/(cosα+ μ*sinα)`. (3)

Во втором случае второй закон Ньютона имеет вид:

`{ (Ox F cosβ − μN_1 = ma (4)), (Oy N_1+ F sinα = mg (5)):}`

Откуда

`a= (F (cosβ +μ sinβ))/m − μg`

Или с учетом (3)

`a= (μg(cosβ+ μsin β))/(cosα+μsin-α) - μg = (0,1⋅10 * (cos30+ 0,1⋅sin30))/(cos45+0,1⋅sin45) - 0,1⋅10 ≈ 0,18`м/с²

Номер: A0A0B3

Дайте развернутый ответ.

На шероховатой наклонной плоскости, образующей с горизонтом угол α = 30°, лежит маленькая шайба массой m = 500 г. Минимальное значение модуля силы `vecF`, приложенной в горизонтальном направлении вдоль плоскости (см. рисунок), при котором шайба начинает скользить по наклонной плоскости, равно 1,7 Н. Чему равен коэффициент трения скольжения μ шайбы о плоскость?

ЕГЭ физика

КЭС: 1.2 Динамика

Решение:

Дано: m = 500 г = 0,5 кг; μ = 0,7; α = 30

Найти: F - ?

Обоснование:
1) Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2) При описании движения шайбы используем модель материальной точки.
3) На тело действуют: сила тяжести, сила реакции опоры, силы трения и минимальная сила F. В ИСО, связанной с Землёй, возможно применение второго закона Ньютона.

Решение:

Брусок сдвинется с места при условии, если сила трения достигнет своего максимального значения, равного силе трения скольжения: Fтр = μN

До начала скольжения брусок находился в состоянии покоя, то по второму закону Ньютона:

`vecF + m vecg + vecN+ vecFтр = 0` (2)

В проекции на ось Ox:

F - Fтр = 0 (3)
F трх = F (4)

В проекции на ось Oy:

F_тру - mg sinα = 0 (5)
F_тру = mg sinα (6)

В проекции на ось Oz:

N - mg cosα = 0 (7)
N = mg cosα (8)
`F_(тр) = sqrt(F_(трх)^2+F_(тру)^2)` (9)

Подставим (4), (6) и (1) в (9):

`μN =sqrt(F^2+(mg sinα)^2) `

Подставим (8) в (10):

`μmg cosα=sqrt(F^2+(mg sinα)^2)`

`F = sqrt((μmg cosα)^2-(mg sinα)^2) `

`F = mg sqrt(μ^2 cosα^2 - sinα^2) `

`F = 0,5 *10 sqrt((0,7)^2 cos30^2 - sin30^2) `

Ответ: F = 1,7 H

Номер: 45D010

Дайте развернутый ответ. ²⁰²⁴
ЕГЭ физика

На гладком горизонтальном столе лежит доска массой М = 1 кг и длиной L = 50 см. На левом краю доски находится маленький брусок массой m = 200 г. Брусок и доска связаны невесомой нерастяжимой нитью, перекинутой через невесомый гладкий блок, закреплённый на стене (отрезки нити, не лежащие на блоке, горизонтальны). Коэффициент трения между бруском и доской μ = 0,2. Брусок начинают тянуть вправо горизонтальной силой F = 1,2 Н. Через какое время t после начала движения брусок соскользнёт с доски? Сделайте рисунок с указанием сил, действующих на тела. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика
Тип ответа: Развернутый ответ

Решение:

ЕГЭ физика

Изобразим силы, действующие на каждый груз и определяющие их движение в горизонтальном направлении.

Сила трения между грузами действует в направлении, препятствующем их отдельному перемещению. Поэтому на груз m (далее m2) будет действовать сила трения Fтр.2 , направленная вправо.

Относительно груза m2, груз M (далее m1) будет двигаться вправо. Поэтому со стороны груза m2 на груз m1 будет действовать сила трения Fтр.1 , направленная влево. По третьему закону Ньютона, Fтр.1 = - Fтр.2 . Кроме того, на каждый из грузов будут действовать силы натяжения нити. Поскольку нить и блок невесомы, то модули обеих сил натяжения равны между собой.

Движение грузов подчиняются второму закону Ньютона. В проекциях на ось x неподвижной инерциальной системы координат получим систему уравнений.

`{(m_1a_1=F-T-F_(тр.1)),(-m_2a_2 = F_(тр.2)-T):}`

Поскольку нить нерастяжима, то a₁ = a₂ = a₃ . Используем соотношение
Fтр =mNд ,

где Fд – сила нормального давления груза m2 на груз m1.
По III закону Ньютона Fд = N, где N = m2g – сила нормальной реакции, действующая со стороны нижнего бруска на верхний.

Тогда уравнения движения грузов будут иметь следующий вид.

`{(m_1a_1=F-T-μm_2g),(-m_2a = μm_2g-T):}`

Исключая из этой системы силу натяжения T, найдем a.

`a=(F-2μm_2g)/(m_1+m_2) = (1,2-2*0,2*0,2*10)/(1+0,2)≈0,3`м/с²

Теперь осталось узнать за какое время с этим ускорением пройдет половину доски, так как путь сократится, вследствие того, что груз едет по самой доске.

`s=v0*t+(at^2)/2`

`s=t+(at^2)/2`

`s=t(1+(a^2)/2)`

`t=s/(1+(a^2)/2)`

`t=(0,25)/(1+(0,3^2)/2)`

`t=(0,25)/(1+(0,3^2)/2) = 0,23 с`

Номер: C6A611

Дайте развернутый ответ.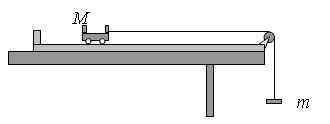
ЕГЭ физика

В установке, изображённой на рисунке, масса грузика m подобрана так, что первоначально покоящаяся тележка после толчка вправо движется равномерно по поверхности трибометра. С каким ускорением будет двигаться тележка, если её толкнуть влево? Масса грузика m в 9 раз меньше массы тележки M. Массами блока и нити пренебречь. Нить нерастяжима. Силу сопротивления движению тележки считать постоянной и одинаковой в обоих случаях.

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО

Решение:

Систему отсчёта, связанную с Землёй, считаем инерциальной. Тогда при равномерном движении тележки сила сопротивления равна по модулю силе тяжести груза: F1=mg. Согласно второму закону Ньютона ускорение груза и тележки после толчка влево соответственно:

`a_г=(mg-T)/m`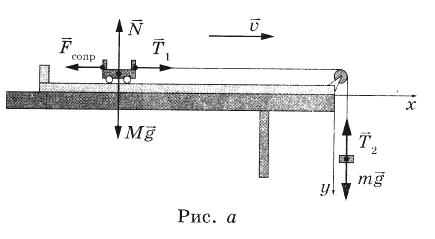

ЕГЭ физика

`a_т=(T+F_1)/m`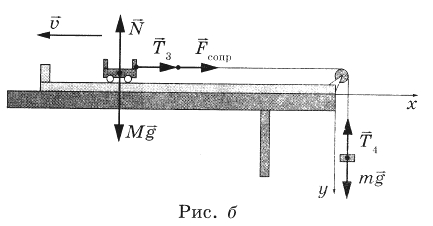

где T — сила натяжения нити. Нить нерастяжима, следовательно `a_г = a_т`, и `(mg-T)/m=(T+F_1)/m`, откуда:

`T = (mMg-mF_1)/M`

Учитывая, что `F_1=mg`, получаем:

`T = (M-m)/(M+m) * mg = (9-1)/10 = 0,8 mg`

Тогда

`a_т=(2mg)/(m+M) = 2mg/10m = 0,2g = 2` м/с²

Ответ: 2 м/с²

Номер: 89181B

Дайте развернутый ответ.

К бруску массой М = 2 кг прикреплён лёгкий блок (см. рисунок), через него переброшена лёгкая нерастяжимая нить, один конец которой привязан к стене,
а к другому прикреплено тело массой m = 0,75 кг. На брусок действует сила F = 10 Н. Определите ускорение бруска. Свободные куски нити горизонтальны
и лежат в одной вертикальной плоскости, тела двигаются вдоль одной прямой. Массой блока и нити, а также трением пренебречь.

Решение:

4

Обоснование

3. Из пп. 1 и 2 следует, что движение бруска и тела в ИСО описывается вторым законом Ньютона.

5. Нить нерастяжима, поэтому модули ускорений подвижного блока и тела m при их прямолинейном поступательном движении отличаются в 2 раза.

ЕГЭ физика

Систему отсчёта, связанную с Землёй, будем считать инерциальной. Запишем второй закон Ньютона в проекциях на горизонтальную ось для тела и бруска:

`ma_1=T_1`

`Ma_2 = F - T_4`

где — ускорения тела и бруска, Т1 — сила натяжения нити, Т4 — сила, с которой блок действует на брусок.

Запишем второй закон Ньютона для невесомого блока:

`0 = T_3-2*T_2`,

где T3 — сила, с которой брусок действует на блок, T2 — сила натяжения нити, действующая на блок.

Поскольку нить невесома, то |T1|=|T2|=|T|. По третьему закону Ньютона

T3=-T4 или |T3|=|T4|.

Ускорение бруска массой M в 2 раза меньше ускорения тела массой m, так как за одно и то же время перемещение тела в 2 раза больше перемещения бруска: .

Приходим к системе уравнений:

{(F-2T=Ma_2),(T = m*2a_2):}

откуда

`a_2=F/(M+4m)`

`a_1=2a_2=(2F)/(M+4m) = (2*10)/2+4*0,75=4`

Ответ: 4 м/с2

Номер: 087023

Дайте развернутый ответ. 2024
ЕГЭ физика

Если в установке, изображённой на рисунке, первоначально покоящуюся тележку толкнуть влево, то она движется с ускорением 2 м/с2. Если же тележку толкнуть вправо, то она движется равномерно. Найдите массу грузика на нити, если масса тележки равна 450 г. Массами блока и нити пренебречь. Нить нерастяжима. Модуль силы сопротивления движению тележки считать постоянным и одинаковым в обоих случаях, трением в оси блока пренебречь. Сделайте рисунки с указанием сил, действующих на тела в обоих случаях. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика
Тип ответа: Развернутый ответ

Решение:

Систему отсчёта, связанную с Землёй, считаем инерциальной. Тогда при равномерном движении тележки сила сопротивления равна по модулю силе тяжести груза: F1=mg. Согласно второму закону Ньютона ускорение груза и тележки после толчка влево соответственно:

`{(T1=T2=0),(T1-F_сопр.=0),(mg-T_2=0):}`

ЕГЭ физика

Из неё получаем, что `F_сопр. = mg`, где F сопр. - модуль силы сопротивления. После толчка влево скорость тележки направлена влево (см. рис. б), а её ускорение направлено вправо. Ускорение груза направлено вниз. С учётом второго закона Ньютона получаем систему уравнений

`{(T3=T4=0),(T3+F_сопр.=M a_т),(mg - T_4=m a_г):}`

ЕГЭ физика

Отсюда получим `a_т = (T+F_сопр.)/M` и `а_г = (mg-T)/m`

, где T - модуль силы натяжения нити. Нить нерастяжима, и поэтому `а_г=а_т` и `(Т+F_сопр)/M = (mg-T)/m`, откуда

`T = (mMg-mF_сопр)/(m+M)`.

Учитывая, что `F_сопр = mg`, получаем:

`T = (M-m)/(m+M) * mg`. Тогда a=a2=g-T/m=(2mg)/(m+M)`, откуда

`M/m = 2g/a -1 = 9`. То есть тележка в 9 раз тяжелее груза. Вычисляем массу груза:

450/9=50 г

Номер: 309C22

Дайте развернутый ответ.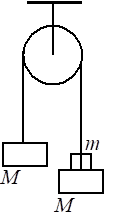
ЕГЭ физика

Два одинаковых бруска массой М = 500 г связаны между собой невесомой нерастяжимой нитью, перекинутой через невесомый гладкий блок, неподвижно закреплённый на потолке (см. рисунок).
На один из брусков кладут груз массой m = 100 г, и система приходит в движение. С какой силой F груз будет давить на брусок? Сделайте схематический рисунок с указанием сил, действующих на бруски и груз. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика

Решение:

0,91

Груз на одном из брусков можно назвать разницей двух тел. 100 г = 1 Н

Инерционная масса всей системы равна массе двух тел + брусок, это (500+500+100)= 1100г = 1,1 кг. При этом получаем силу воздействия равной разнице тел (100 г = 1 Н), эта сила создает ускорение:

По закону Ньютона F=ma посчитаем ускорение

1=1,1*a

a = (1)/(1,1) ≈ 0,9 м/с²

Но, в нашем случае брусок лежит на грузе и притягивается с ускорением g = 10 м/с². И вот за счет того, что брусок уже имеет в этом направлении ускорение посчитанное ранее, а именно 0,9 м/с², мы можем узнать какое ускорение воздействует на брусок от груза:

10-0,9=9,1 м/с²

Это будет разница ускорения от груза и бруска, так как брусок как бы уходит из под груза, несколько снижая воздействие груза, на разницу ускорений выраженных опять же через закон Ньютона.

F=ma

F=0,1*9,1 = 0,91 Н

Номер: E068D9

Дайте развернутый ответ.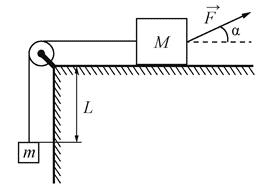
ЕГЭ физика

На горизонтальном столе находится брусок массой М = 1 кг, соединённый невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок, с грузом массой m = 500 г. На брусок действует сила `vecF`, направленная под углом α = 30° к горизонту (см. рисунок), F = 9 Н. В момент начала движения груз находился на расстоянии L = 32 см от края стола. Какую скорость V будет иметь груз в тот момент, когда он поднимется до края стола, если коэффициент трения между бруском и столом μ = 0,3? Сделайте схематический рисунок с указанием сил, действующих на брусок и груз. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика

Решение:

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Учитывая, что нить нерастяжима, блок идеальный, делаем вывод, что все тела движутся с одинаковым ускорением
5. Учитывая, что нить невесома, блок идеальный, делаем вывод, что силы натяжения, приложенные к телам, равны по модулю.
6. Так как тела движутся с ускорением, то описывать их движение будем с использованием формул кинематики равноускоренного движения.

Решение

Расставим силы, действующие на тела.

ЕГЭ физика
Здесь N – сила реакции опоры, T1 и T2 – силы натяжения нити, Fтр – сила трения, a1 и a2 – ускорения бруска M и груза m соответственно.
Запишем второй закон Ньютона для каждого из тел

`vecF +vecF_тр+vecT_1+vecN +M vecg =M vec a_1,`

`vecT_2+ m vecg =m veca_1`.
Спроецируем вторые законы Ньютона на оси x и y

`{(x F cosα − T1 − F_тр = Ma_1), (y N − Mg +F sin α= 0), (y T_2− mg = ma_2):}`

Так как нить невесома и нерастяжима, то
a1 = a2 = a,
T1 = T2 = T.

Тогда

`{( x F cosα− T − Fтр = Ma), (y N =Mg − F sinα), (y T − mg = ma):}`

Сила трения скольжения же равна

Fтр = μN.

Тогда систему уравнений можно записать в виде

`{( x F cosα− T − μ(Mg − F sinα)= Ma), (y T − mg = ma):}`

⇒ F cosα − mg − μ(Mg − F sinα)= a(M + m ). (1)

Движение груза по вертикали описывается уравнением:

`h vec(t)= vecv_0 * t+ (vecat^2)/2`,

где v0 = 0 – начальная скорость тела.

А скорость тела по вертикали

`vec v = vec v_0+ vec at`

Спроецируем два уравнения кинематики

`y = (at^2)/2`

v = at

Отсюда

`v = sqrt(2aL)`, (2)

где L – начальное расстояние от поверхности стола до грузика.
Объединим (1) и (2)

`v = sqrt(2L (F cosα-mg-μ(Mg-F sin∝))/(M +m) )= sqrt(2⋅0,32 (9⋅cos30-0,5⋅10-0,3(10-9⋅sin-30∘))/(1+ 0,5)) ≈0,7 м/с`

Номер: 8CF4D1

Дайте развернутый ответ.
ЕГЭ физика

По неподвижной гладкой наклонной плоскости с углом α = 30° движутся два одинаковых бруска массой m = 0,25 кг каждый, скреплённые между собой лёгкой пружиной с жёсткостью k = 100 Н/м. Верхний брусок соединён невесомой нерастяжимой нитью, перекинутой через идеальный блок, с грузом массой М = 2 кг (см. рисунок). Чему равна длина пружины l в нерастянутом состоянии, если при движении брусков её длина постоянна и равна L = 15 см? Сделайте рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.

КЭС: 1.2 Динамика

Решение:

Будем считать систему связанную с Землей, инерциальной. Все три тела движутся поступательно, поэтому их можно считать материальными точками. На левый брусок действуют сила тяжести, сила упругости, сила реакции опоры. На правый брусок действуют сила тяжести, сила упругости, сила реакции опоры, сила натяжения нити. На груз действуют сила тяжести и сила натяжения нити. Учитывая, что длина пружины во время движения не меняется, нить нерастяжима и невесома, делаем вывод, что все тела движутся с одинаковым ускорением, силы упругости равны по модулю, силы натяжения равны по модулю. Для ИСО можно применить второй закон Ньютона для каждого тела.

Перейдем к решению. Изобразим все силы, действующие на
каждое из трех тел. Выберем ось Ох вдоль наклонной
плоскости, ось Оу— вертикально вниз.
ЕГЭ физика

Запишем второй закон Ньютона для каждого тела.

`{(ma=F_(y1)+N+mg),(ma=F_(y2)+N+mg+T),(Ma=Mg+T):}`

В проекциях на выбранные оси:

`{(ma=F_y-mg sin∝),(ma=T-F_y-mg sin∝),(Ma=Mg-T):}`

Решая эту систему уравнений, находим ускорение, с которым
движется данная система тел

`a =g (M-2m sin∝)/(2m+M)`

Из закона Гука следует, что Fy =k(L-l), а сила упругости:

`F_y=(M-2msin∝)/(2m-M)`

Тогда длина растянутой
пружины равна тогда сила упругости равна.

`l=L - (Mmg (1+sin∝)/(2m+M)k) = 0.15 - (2*0.25*10(1+0.5))/((2*0.25+2)*100)=0,12 м = 0,12 см`

Ответ: 12 см.

Номер: 8D9256

Дайте развернутый ответ.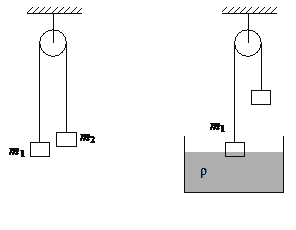
ЕГЭ физика

Два груза подвешены за нерастяжимую и невесомую нить к идеальному блоку, как показано на рисунке. При этом первый груз массой m1 движется из состояния покоя вниз с ускорением. Если первый груз опустить в жидкость плотностью ρ, находящуюся в сосуде большого объёма, система будет находиться в равновесии. При этом объём погружённой в жидкость части груза равен V. Определите ускорение первого груза. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика

Решение:

При опускании в воду система уравновешивается, значит получается, что m1 если учесть силу Архимеда, то m1 равно m2. Нетрудно посчитать массу, зная плотность и объем.

Δm=ρ*V (Это можно назвать разницей масс двух тел)

F=ma

Инерционная масса равна массе двух тел, это (m1+m1-ρ*V). При этом получаем силу воздействия на эту массу Δm=ρ*V которая характеризуется силой Архимеда, и которая придает ускорение, тогда составим равенство:

ρ*V=(m1+m1-ρ*V)*a

a = (ρ*V)/(m1+m1-ρ*V) = 1/((2m1)/(ρ*V)-1)

Номер: 2593A8

Дайте развернутый ответ.
Небольшой брусок массой m = 100 г, скользящий по гладкой горизонтальной поверхности, абсолютно не упруго сталкивается с неподвижным телом массой М = 2m . При дальнейшем поступательном движении тела налетают на недеформированную пружину, одним концом прикреплённую к стене (см. рисунок). Через какое время t после абсолютно неупругого удара бруски вернутся в точку столкновения? Скорость движения бруска до столкновения υ = 2 м/с, жёсткость пружины k = 30 Н/м, а расстояние от точки столкновения до пружины L = 10 см.

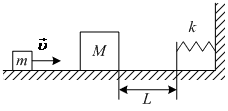
ЕГЭ физика

Решение:

Обоснование

1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Брусок и тело движутся поступательно, поэтому описываем их моделью материальной точки как до, так и после столкновения независимо от их размеров.
3. По условию трение отсутствует, и поэтому все внешние силы (силы тяжести и силы реакции опоры), действующие на тела
и, направлены вертикально и уравновешивают друг друга отдельно для каждого тела. Следовательно, в ИСО сохраняется импульс системы «брусок + тело » при их столкновении.
4. Когда брусок и тело движутся, касаясь пружины, механическая энергия системы тел «брусок и тело + пружина» равна

E_(мех) = ((m+M)v^2)/2 + (kx^2)/2

Изменение механической энергии системы тел в ИСО равно работе всех непотенциальных сил, приложенных к телам системы. В данной задаче единственной такой силой является сила реакции опоры, действующая на брусок
+ тело со стороны стола. Но из-за отсутствия трения эта сила вертикальна, а составное тело ( m+M ) движется горизонтально, поэтому работа силы реакции опоры равна нулю и Емех
сохраняется в ИСО.

Решение:

1. В процессе абсолютно неупругого столкновения сохраняется суммарный импульс системы тел: mv = (m+M)v1, где v1- скорость тел после столкновения.

2. Так как поверхность гладкая, то трения нет и движение тел от момента удара до момента касания свободного конца пружины будет равномерным: `L = v_1t_1`, где t_1 - время движения на этом участке.

3. После касания пружины и до отрыва от неё тела будут двигаться, совершая гармоническое колебание. До отрыва пройдёт время t2=T/2, где T - период колебаний груза на пружине:

T = 2π sqrt((m+M)/k).

4. Отрыв тел от пружины произойдёт в точке касания пружины. По закону сохранения механической энергии при гармонических колебаниях скорость тел в точке отрыва равна
. Дальнейшее движение тел будет равномерным. Поэтому полное время движения тел до точки столкновения

t = 2t1 + t2 = (2L)/(v1) + T/2 = 2L(m+M)/mv + π sqrt ((m+M)/k)

Учитывая, что M = 2m, получим `t = (6L)/v + π sqrt(3m/k) = (6*0.1)/2 + 3.14 * sqrt((3*0.1)/30) = 0.614` c

Ответ: t = 0,614 с.

Номер: 3ECDA4

Дайте развернутый ответ. ²⁰²⁴
ЕГЭ физика

На горизонтальном столе находится брусок массой М = 1 кг, соединённый невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок, с грузом массой m = 500 г. На брусок действует сила величиной F = 9 Н, направленная под углом α = 30° к горизонту (см. рисунок). В момент начала движения груз находится на расстоянии L = 40 см от края стола. Через какое время t груз поднимется до края стола, если коэффициент трения между бруском и столом m = 0,3? Сделайте схематический рисунок с указанием сил, действующих на брусок и груз. Трением в оси блока и трением о воздух пренебречь. Обоснуйте применимость законов, используемых для решения задачи.

КЭС:
1.2 Динамика
Тип ответа: Развернутый ответ

Решение:

Обоснование

Решение

Расставим силы, действующие на тела.

ЕГЭ физика
Ответ:

Номер: 24D9C3

Дайте развернутый ответ.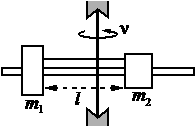
ЕГЭ физика

На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m₁ = 200 г и m₂ = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.

Решение:

Дано: m1 = 200 г = 0,2 кг; m2 = 300 г = 0,3 кг; l = 20 см = 0,2 м; v = 600 об/мин = 10 об/ч

Найти: T - ?

Обоснование:
1) Рассмотрим задачу в системе отсчёта, связанной со стре Будем считать эту систему отсчёта инерциальной (ИСО).
2) Невесомый стержень и грузы образуют твёрдое тело (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3) Так как нить лёгкая, то можно считать T1 = T2 = T.
4) На тело действуют: сила тяжести, сила реакции опоры, силы натяжения нити. На основе пунктов 1 и 2 возможно применение второго закона Ньютона.

Решение:
По второму закону Ньютона для первого тела:
`T = m_1a_1` (1)

Для второго тела:

`T = m_2a_2 `(2)

`a = V^2/r` (3)

Подставим (4) в (3):

`a = (4π^2r^2v^2)/r = 4π^2rv^2` (5)

Так как нить нерастяжима, то сумма радиусов, по которым движутся тела, равна длине нити:
`l = r_1 +r_2` (6)
`r_2 = l - r_1` (7)

Подставим r1 и r2 в ускорения тел (5):

`a_1 = 4π^2r_1v^2` (8)
`a_2 = 4π^2v^2(l-r_1)` (9)

Приравняем (1) и (2) и подставим (8) и (9):

`4π^2r_1v^2m_1=4π^2v^2m_2(l-r_1)` (10)

`r_1=(4π^2v^2m_2l)/(4π^2v^2m_1+4π^2v^2m_2)` (11)

`r_1=(m_2l)/(m_1+m_2)` (12)

Подставим (12) в (8):

`a=(4π^2v^2m_2l)/(m_1+m_2)` (13)

Подставим (13) в (1):

`T = (4π^2v^2m_2lm_1)/(m_1+m_2)` (14)

`T = (4 (3,14)^2*10^2*0,2_2*0,3*0,2)/(0,2+0,3)=95` (14)

Ответ: T = 95 Н

Номер: 48129F

Дайте развернутый ответ.

ЕГЭ физика
Небольшая шайба массой m=10
г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14
м, скользит по его внутренней поверхности. На высоте h=0,18 м
она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок
с указанием сил, действующих на шайбу в точке А.

КЭС: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО

Решение:

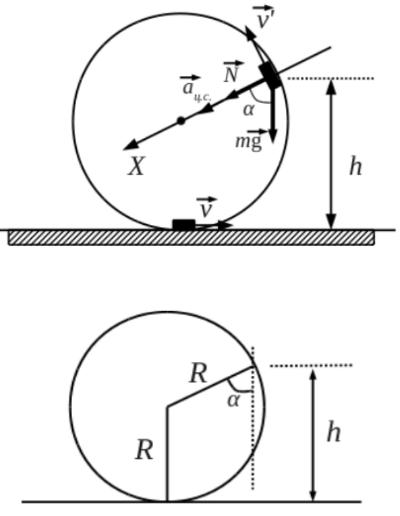
ЕГЭ физика

Дано: m = 10 г = 0,01 кг; h = 0,18 м; R = 0,14 м

Найти: Eк0 - ?

Обоснование:
1) Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2) Шайба имеет малые размеры по сравнению с кольцом, поэтому описываем её моделью материальной точки.
3) При движении шайбы по поверхности кольца на тело действуют потенциальные силы: тяжести и реакции опоры, перпендикулярная поверхности сферы (трения нет, так как поверхность гладкая). Поэтому работа силы реакции опоры при движении тела равна нулю. Механическая энергия тела при движении по поверхности сферы для шайбы сохраняется.
4) Поскольку тело описывается моделью материальной точки, условие отрыва этого тела от поверхности сферы формулируется на основе второго закона Ньютона. В момент отрыва обращается в нуль сила реакции опоры.
5) Для материальной точки применимы законы движения по окружности.

Решение:

В точке A шайба отрывается от кольца, поэтому сила реакции опоры обращается в ноль. Выполняется второй закон Ньютона в проекции на ось, направленную к центру окружности:

`mg cos∝ = ma` (1)

`a = (V^2)/R` (2)

Подставим (2) в (1):

`mg cos∝ = (mV^2)/R` (3)

`V^2 = Rg cos∝` (4)

`E_(k0) = (mV^2)/2` (5)

Подставим (4) в (5):

`E_(k0) = (mRgcos∝)/2` (6)

Из рисунка получим:
h =R + R cos∝ (7)

R cos∝ = h - R (8)

Подставим (8) в (6):

`E_(k0) = (mg(h-R))/2` (9)

`E_(k0) = (0.01*10(0.18-0.14))/2` (10)

`E_(k0) = 0,002` Дж (11)

Ответ: Формула = 0,002 Дж

Номер: 582E9A

Дайте развернутый ответ.
На шероховатом горизонтальном диске, вращающемся вокруг вертикальной оси, покоится небольшое тело. Расстояние от оси вращения до тела r = 25 см. Угловую скорость вращения диска начали медленно увеличивать. Каков коэффициент трения μ между телом и диском, если тело начало скользить по диску при угловой скорости ω = 4 рад/с? Сделайте рисунок с указанием сил, действующих на тело.

КЭС: 1.2 Динамика

Решение:

0,4

Изобразим силы, действующие на тело в начале скольжения по поверхности диска:

ЕГЭ физика

По второму закону Ньютона `N = mg + F_тр = ma`

В проекции на координатные оси:

Fтр = ma,
N = mg.

При равномерном движении по окружности `a =ω^2*r` сила трения скольжения `F_тр = μN` Объединяя формулы, получаем:

`μmg = mω^2*r`

`μ = (ω^2*r)/g = (4^2*0,25)/10 =0,4`

Ответ:0,4

Номер: AB3A90

Дайте развернутый ответ. ²⁰²⁴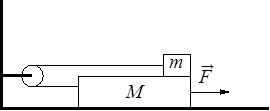
ЕГЭ физика

На горизонтальном неподвижном столе лежит доска массой М = 0,8 кг. На доске находится маленький брусок массой m = 200 г. Брусок и доска связаны невесомой нерастяжимой нитью, перекинутой через невесомый блок, закреплённый на стене (отрезки нити, не лежащие на блоке, горизонтальны). Коэффициент трения между бруском и доской μ1 = 0,5, между столом и доской μ2 = 0,3. Доску тянут вправо горизонтальной силой F→ . Чему равен модуль силы F→, если модуль ускорения бруска относительно стола а = 1 м/с2? Трением в оси блока пренебречь. Сделайте рисунок с указанием сил, действующих на тела. Обоснуйте применимость законов, используемых для решения задачи.

КЭС: 1.2 Динамика
Тип ответа: Развернутый ответ

Решение:

6

ЕГЭ физика

Изобразим силы, действующие на каждый груз и определяющие их движение в горизонтальном направлении.

Здесь T – сила натяжения нити, N1 – сила реакции опоры доски, N2 – сила реакции опоры стола, Fтр1 – сила трения между доской и бруском, Fтр2 – сила трения между столом и доской.
Ускорения доски и бруска равны, так как они связаны нерастяжимой нитью.
Запишем второй закон Ньютона для доски и бруска

F+ T + Fтр1+ Fтр2 +N2 + N1+ Mg = Ma,

T+ Fтр1 +N1 + mg =ma.

Здесь a – ускорение.
Сила трения равна:

Fтр = μN. (1)
Спроецируем второй закон Ньютона на вертикальную ось:

`N_1 = mg`

`N_2 = N1+ Mg = mg + Mg`

Спроецируем второй закон Ньютона на горизонтальную ось, с учётом (1):

`{(F − T − μ_2(m + M ) g − μ1mg = Ma),(T − μ_1 mg = ma):}`

Сложим два уравнения:

`F − μ_2*(m + M )g− 2μ_1*mg = a(M + m) ⇒ F − μ_2*Mg − Ma = ma + μ_2*mg +2μ_1*mg`

Отсюда выразим F :

F = ma + mg(μ_2+2μ_1) + M(μ_2g+a) = 0,2*1+0,2*10*(0,3+2*0,5)+0,8(0,3*10+1)=0,2 +2*1,3 + 3,2= 6 H

Номер: DB33E7

Дайте развернутый ответ.
ЕГЭ физика

На шероховатой наклонной плоскости, образующей с горизонтом угол α=30°, лежит маленькая шайба массой m=500 г. Коэффициент трения шайбы о плоскость μ = 0,7. Какую минимальную силу Fmin в горизонтальном направлении вдоль плоскости надо приложить к шайбе, чтобы она сдвинулась с места?

КЭС: 1.2 Динамика

Решение:

1,7 Н

Систему отсчета связанную с Землей считаем инерциальной. Введем Декартову систему координат (xyz), как показано на рисунке. На шайбу действует сила трения, сила нормальной реакции опоры и сила тяжести. Поскольку шайба по условию задачи первоначально покоится, это означает, что μ>tg∝. Шайба сдвинется в том случае, когда сила трения покоя достигнет своего максимального значения, равного силе трения скольжения.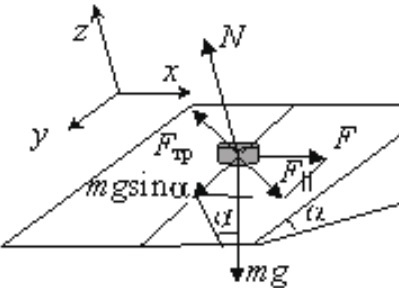

ЕГЭ физика (1)
Поскольку до начала скольжения шайба находилась в покое, то согласно второму закону Ньютона

F+mg+N+Fтр =0 (2)

Запишем второй закон Ньютона в проекциях на ось z:

N - mg cos∝ = 0 (3)

Обозначим составляющую равнодействующих двух сил: силы тяжести mg и силы F, направленную вдоль наклонной плоскости, как силу F. Из (2) следует, что в момент начала движения сила трения направлена противоположно силе F и равна ей по модулю (см. рисунок). Проекция силы тяжести на ось у равна mg sin∝. По теореме Пифагора.

`Fтр = (mg sin∝)^2 +F^2` (4)

Решая систему уравнений (1) (3) (4), получим:

`Fmin=m*g sqrt((μ*cos∝)^2-(sin∝)^2) = 0,5*10 sqrt((0,75*0,7)^2 - 0,25^2) ≈ 1,7`

Ответ: Fmin ≈ 1,7 Н

Номер: 9F9E6D

Дайте развернутый ответ.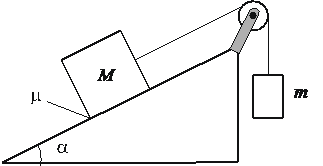
ЕГЭ физика

Грузы массами M=1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через невесомый блок, вращающийся без трения (см. рисунок). Груз массой M покоится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α=30°, коэффициент трения μ=0,3). Чему равно минимальное значение массы m, при котором система грузов остаётся в состоянии покоя? Сделайте рисунок с указанием сил, действующих на грузы.

КЭС: 1.2 Динамика

Решение:

Обоснование:
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Учитывая, что нить нерастяжима и невесома, блок идеальный, делаем вывод, что все тела движутся с одинаковым ускорением, силы натяжения, приложенные к телам, равны по модулю.

Решение:

Введем оси, как показано на рисунке

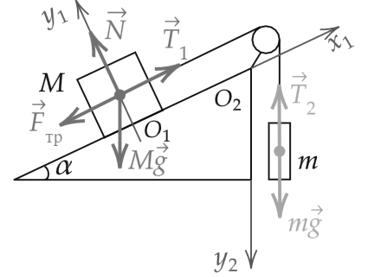
ЕГЭ физика

Запишем второй закон Ньютона для тела массой M

`M vecg+ vecT1+ vecF_(тр) +vecN_1 = M vec a_1`,
где T1 – сила натяжения нити, Fтр – сила трения, N1 – сила реакции опоры, a1 – ускорение тела.
Запишем второй закон Ньютона для тела массой m

`m vecg+ vec T_2 =m veca_2`,
где T2 – сила натяжения нити, a2 – ускорение тела.
Так как система находится в равновесии, то ускорение тел равно 0. Спроецируем второй закон Ньютона на введенные оси для каждого из тел

`{(O_1 x_1 T_1− Mg sinα − F_тр = 0 (1)), (O_1 y_1 N − Mg cosα = 0 (2)), (O_2 y_2 mg − T_2 = 0 (3)):}

Так как нить невесомая и нерастяжимая, то T1 = T2 , кроме того тело покоится, а значит Fтр ≤ μN
Тогда сложив (1) с (3) получим

`mg − Mg sinα − F_(тр) = 0 ⇒ F_(тр) = mg − Mg sinα`

Из (2)

`N =Mg cosα`

Так как F тр. ≤ μN , то

`mg − Mg sinα ≤ μMg cosα`

Выразим массу груза.

`m ≤ M (sinα+μ-cosα) ≤ 1 * (0,5+0,3*sqrt(3)/2) ≤ 0,76`кг

Номер: 5D4738

Дайте развернутый ответ.
Под действием постоянной горизонтальной силы `vecF` клин массой M = 1 кг движется по гладкой горизонтальной поверхности стола. По шероховатой поверхности клина, составляющей угол α = 30° с горизонтом, равномерно (относительно клина) скользит вниз брусок массой m = 0,2 кг. Коэффициент трения между бруском и клином µ = 0,6. Найдите модуль ускорения клина. Сопротивлением воздуха пренебречь. Сделайте рисунок с указанием сил, действующих на брусок. Обоснуйте применимость законов, используемых для решения задачи.

ЕГЭ физика

КЭС: 1.2 Динамика

Решение:

Обоснование:
1) Рассмотрим систему отсчета, связанную с Землей и будем считать ее инерциальной.
2) Так как клин и брусок двигаются поступательно, значит можем описывать их моделями материальной точки.
3) Согласно пп. 1 и 2 можем применить второй закон Ньютона для бруска и клина.
4) Так как брусок движется равномерно относительно клина, значит относительно Земли брусок и клин двигаются с одинаковым ускорением.

Решение задания:

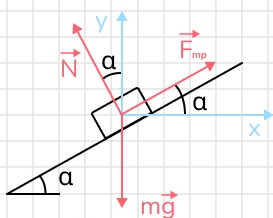
ЕГЭ физика

Запишем второй закон Ньютона для бруска в проекциях на ось ОХ и ОУ соответственно:

`ma = F_тр * cos α - N sin α` (1)

`0 = N * cos α + sin α - mg` (2)

Используем закон Амонтона-Кулона для скользящего бруска:

F тр = μN

Подставим (3) в (1) и (2):

`ma = μN * cos α - N sin α` (4)

`ma = μN * cos α - N sin α` (5)

Поделим (4) на (5):

`a/g = (μ * cos α - sin α)/(cos α + μ * sin α)`

`a = g * (μ * cos α - sin α)/(cos α + μ * sin α)`

`a = 10 * (0,6 * cos 30 - sin 30)/(cos 30 + 0,6 * sin 30) = 0,168` м/с²

Номер: AB0739

Дайте развернутый ответ.
Два тела подвешены за нерастяжимую и невесомую нить к идеальному блоку, как показано на рисунке. При этом первое тело массой m1 = 500 г движется из состояния покоя вниз с ускорением а. Если первое тело опустить в воду с плотностью ρ = 1000 кг/м³, находящуюся в большом объёме, система будет находиться в равновесии. При этом объём погруженной в воду части тела равен V = 1,5⋅10⁻⁴м³. Сделайте рисунки с указанием сил, действующих на тела в обоих случаях. Определите ускорение а первого тела.

ЕГЭ физика

КЭС: 1.2 Динамика

Решение:

1,8

При опускании в воду система уравновешивается, значит получается, что m1 если учесть силу Архимеда, то m1 равно m2. Нетрудно посчитать массу, зная плотность и объем.

m=ρ*V = 1000 * 1,5⋅10⁻⁴ = 0,15 кг = 1,5 Н (Это можно назвать разницей масс двух тел)

F=ma

Инерционная масса равна массе двух тел, это (500+500-150)= 850 г = 0,85 кг. При этом получаем силу воздействия на эту массу 1,5 Н которая характеризуется силой Архимеда, и которая придает ускорение, тогда составим равенство:

1,5=0,85*a

a = (1,5)/(0,85)=1,76 ≈ 1,8 м/с²

Номер: 82C08B

: Обновлено: 26 августа 2024

ЕГЭ по физике 2025. Теория и задания ФИПИ с ответами