Все задания из банка ФИПИ в КЭС Механика. Статика к ЕГЭ по физике.
Задания из банка ФИПИ с ответами к ЕГЭ по физике
1.3 Статика 1.3.1 Момент силы относительно оси вращения 1.3.2 Центр масс тела. Центр масс системы материальных точек 1.3.3 Условия равновесия твёрдого тела в ИСО 1.3.4 Закон Паскаля 1.3.5 Давление в жидкости, покоящейся в ИСО 1.3.6 Закон Архимеда. Условия плавания тел
Выбор ответов из предложенных вариантов (13)
Выберите один или несколько правильных ответов.
Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
1) Сила Архимеда, действующая на тело, полностью погружённое в жидкость, прямо пропорциональна объёму тела.
2) Теплопередача путём конвекции наблюдается в жидкостях и газах.
3) При последовательном соединении резисторов напряжения на всех резисторах одинаковы.
4) Вследствие интерференции электромагнитных волн происходит перераспределение энергии в пространстве: энергия концентрируется в максимумах и не поступает в минимумы интерференции.
5) Заряды атомных ядер изотопов химического элемента различны,
но массы их одинаковы.
КЭС: 1.1 Кинематика
1.2 Динамика
1.3 Статика
1.4 Законы сохранения в механике
1.5 Механические колебания и волны
2.1 Молекулярная физика
2.2 Термодинамика
3.1 Электрическое поле
3.2 Законы постоянного тока
3.3 Магнитное поле
3.4 Электромагнитная индукция
3.5 Электромагнитные колебания и волны
3.6 Оптика
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
124
Сила Архимеда зависит от объема тела. Конвекция проявляется в жидкости и газах. При последовательном подключении сопротивлений напряжение падает на каждом последующем.
Номер: AA8BDA
Выберите один или несколько правильных ответов.
Необходимо собрать экспериментальную установку, с помощью которой можно определить плотность бензина. Для этого школьник взял стакан с бензином и динамометр.
Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) калориметр
2) мензурка
3) стальной цилиндр с крючком
4) термометр
5) пружина
В ответе запишите номера выбранного оборудования.
КЭС: 1.3 Статика
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
23
берем мензурку и приспособление для того чтобы ее подвесить
Номер: F68A6A
Выберите один или несколько правильных ответов.
Необходимо собрать экспериментальную установку, с помощью которой можно определить плотность керосина. Для этого школьник взял пустую мензурку и металлический цилиндр с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) стакан с бензином
2) линейка
3) стакан с керосином
4) динамометр
5) термометр
В ответе запишите номера выбранных предметов.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
34
берем сам керосин и динамометр
Номер: 830760
Выберите один или несколько правильных ответов.
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и лёгкой жидкости эфира (плотность эфира ρэ=0,72
г/см3), при постоянной температуре.
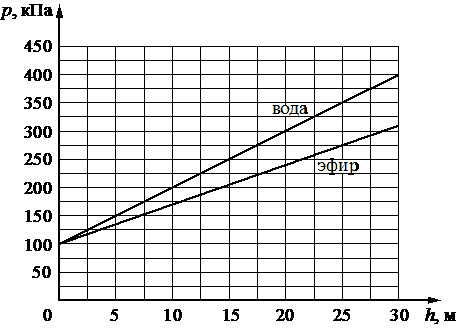
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) С глубиной погружения давление в воде возрастает быстрее.
2) В воде давление возрастёт вдвое на глубине 20 м.
3) Плотность оливкового масла 0,92 г/см3, график аналогичной зависимости давления от глубины для масла окажется между зависимостью для эфира и осью абсцисс.
4) По мере подъёма из воды давление падает до нуля.
5) Плотность ртути 13,59 г/см3, график аналогичной зависимости давления от глубины для ртути окажется между зависимостью для воды и осью ординат (вертикальной осью).
КЭС: 1.3.5 Давление в жидкости, покоящейся в ИСО
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
15
Номер: B2D13F
Выберите один или несколько правильных ответов.
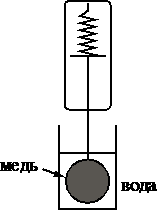
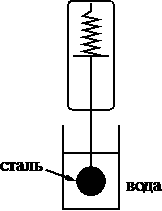
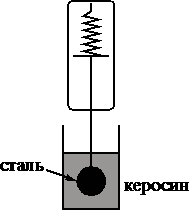
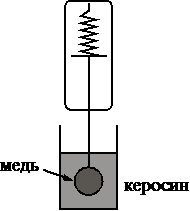
Необходимо экспериментально проверить, зависит ли сила Архимеда, действующая на тело, полностью погружённое в жидкость, от его объёма. Какие две установки следует использовать для проведения такого исследования?
1) 
2) 
3) 
4) 
5) 
В ответе запишите номера выбранных установок.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
24
Берем тело из одного материала, берем одну жидкость в которую погружать, но разные объемы для тела.
Номер: CC1C3E
Выберите один или несколько правильных ответов.
Необходимо собрать экспериментальную установку, с помощью которой можно определить плотность алюминия. Для этого школьник взял стакан с водой и алюминиевый шарик. Какие две позиции из приведенного ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) электронные весы
2) мензурка
3) линейка
4) термометр
5) пружина
В ответ запишите номера выбранного оборудования.
КЭС: 1.3 Статика
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
12
Мензурка для измерения объема вытесненной жидкости. Электронные весы чтобы измерить массу шарика.
Номер: 9AF830
Выберите один или несколько правильных ответов.
Изучая на практике закон Архимеда, учащиеся опускали цилиндр объёмом V = 10 см3 в различные жидкости (см. таблицу) и измеряли объём цилиндра, погружённый в жидкость. По результатам измерений была построена обобщённая зависимость объёма погружённой части цилиндра Vпогр от плотности жидкости ρ (см. рисунок).
|
Жидкость |
Бензин |
Спирт |
Вода |
Глицерин |
Хлороформ |
Бромоформ |
Дийодметан |
|
ρ, г/см3 |
0,71 |
0,79 |
1,0 |
1,26 |
1,49 |
2,89 |
3,25 |
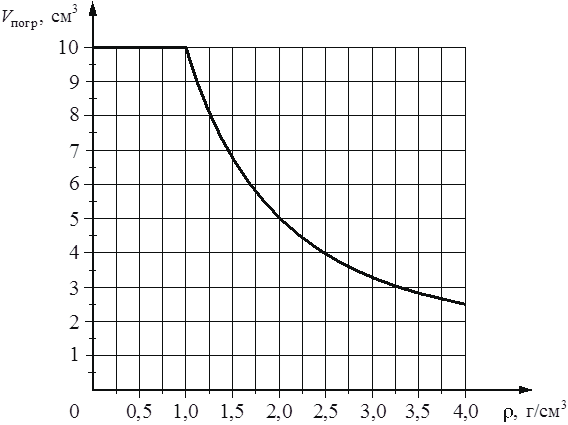
Выберите два верных утверждения, согласующихся с результатами, представленными на рисунке и в таблице.
1) Цилиндр плавает в бромоформе
2) Цилиндр тонет в глицерине
3) При возрастании плотности жидкостей до 1 г/см3 сила Архимеда, действующая на цилиндр, опущенный в жидкость, возрастает.
4) При возрастании плотности жидкости от 1,5 до 3,25 г/см3 сила Архимеда убывает
5) На цилиндр, плавающий в глицерине, действует выталкивающая сила, составляющая около 80 мН
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
13
Условно можно увидеть, что плотность цилиндра соразмерна с плотностью воды, то есть в этой жидкости объем вытесненной жидкости равен объему цилиндра. Цилиндр как бы и тонет и плавает в воде, то есть может находиться в ее объеме. При увеличении плотности жидкости он начинает плавать, при уменьшении плотности, - тонуть.
Номер: B29D40
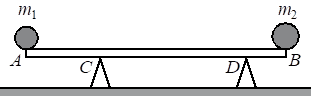
Выберите один или несколько правильных ответов.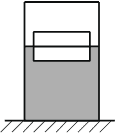
Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Из приведённого ниже списка выберите два правильных утверждения.
1) Если воду заменить на керосин, то глубина погружения брусков уменьшится.
2) Сила Архимеда, действующая на бруски, равна 20 Н.
3) Плотность материала, из которого изготовлены бруски, равна 500 кг/м3.
4) Если на верхний брусок положить груз массой 0,7 кг, то бруски утонут.
5) Если в стопку добавить ещё два таких же бруска, то глубина её погружения увеличится на 10 см.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
23
Если бруски плавают по середине, то их плотность равна половине плотности в 1000 кг/м3 (воды) 1000/2=500 кг/м3
Сила Архимеда равна масса жидкости в объеме погруженного тела. Определим погруженный объем.
1 кг при плотности 500 кг/м3 в займет объем V = 1/500 = 0,002 м3
Получается в этом объеме масса воды m = 0,002 *1000 = 2 кг = 20 H
Номер: 664373
Выберите один или несколько правильных ответов. 2024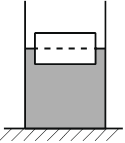
Брусок толщиной 6 см и массой 1 кг плавает в воде так, что уровень воды приходится на середину бруска
(см. рисунок). Из приведённого ниже списка выберите все верные утверждения.
1) Сила Архимеда, действующая на брусок, равна 20 Н.
2) Если воду заменить на керосин, то глубина погружения бруска уменьшится.
3) Если воду заменить на керосин, то сила Архимеда, действующая на брусок, не изменится.
4) Плотность материала, из которого изготовлен брусок, равна 1000 кг/м3.
5) Если на брусок положить сверху ещё один такой же брусок, то глубина погружения увеличится на 3 см.
КЭС: 1.3 Статика
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
35
При замене на керосин тело глубже погрузиться в жидкость, но керосин сам по себе менее плотный по сравнению с водой. Эти величины обратно пропорциональны, поэтому сила Архимеда останется прежней.
Полная высота брусков составляет 6+6 см, Если добавить еще 6 см, то 12+6 = 18 см. При этом половина 18/2=9 см
9-6=3 см разница погружения при условии если положить еще один брусок сверху.
Номер: EEB120
Выберите один или несколько правильных ответов.
Изучая на практике закон Архимеда, учащиеся опускали цилиндр объёмом V = 10 см3 в различные жидкости (см. таблицу) и измеряли объём погружённой в жидкость части цилиндра. По результатам исследования была построена обобщённая зависимость объёма погружённой части цилиндра Vпогр от плотности жидкости ρ (см. рисунок).
|
Жидкость |
Бензин |
Спирт |
Вода |
Глицерин |
Хлороформ |
Бромоформ |
Дийодметан |
|
ρ, г/см3 |
0,71 |
0,79 |
1,0 |
1,26 |
1,49 |
2,89 |
3,25 |
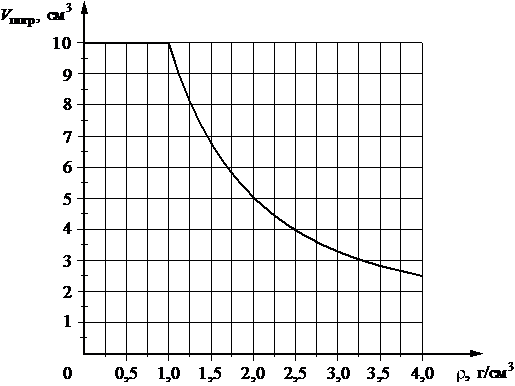
Выберите два верных утверждения, согласующихся с результатами, представленными на рисунке и в таблице.
1) Цилиндр плавает в глицерине.
2) Цилиндр, опущенный в спирт, плавает у поверхности.
3) В глицерине на плавающий цилиндр действует выталкивающая сила, примерно в 2,6 раза бо́льшая, чем в дийодметане.
4) В дийодметане на плавающий цилиндр действует выталкивающая сила, составляющая около 70 мН.
5) На цилиндр, плавающий в хлороформе, действует выталкивающая сила, составляющая около 0,1 Н.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
15
Плотность цилиндра составляет порядка 1000 кг/м3 так как именно с этого показателя график погружаемого объема в жидкости не полный, то есть меньше объема тела, значит часть цилиндра выступает над поверхностью жидкости.
Плотность хлороформа 1490 кг/м3, при этом погружение цилиндра составило 6,5 см3, тогда:
1490/1000=0,0149 кг/см3
Если взять 6,5 см3 , то 0,0149*6,5=0,098 кг ≈ 1Н
Номер: E6072A
Выберите один или несколько правильных ответов.
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
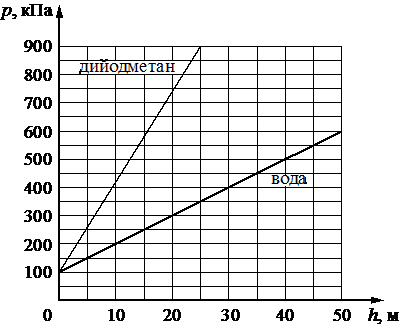
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
2) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
3) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
4) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
5) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
КЭС: 1.3.5 Давление в жидкости, покоящейся в ИСО
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
25
По графику подтверждается утверждение 2
Масло имеет меньшую плотность, значит нарастание давление по сравнению с водой будет не столь значимое, утверждение 5.
Номер: 368EAC
Выберите один или несколько правильных ответов.
Ученик помещал цилиндр объёмом V=10 см3, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объём погружённой в жидкость части цилиндра Vпогр. По результатам измерений была получена зависимость объёма погружённой части цилиндра Vпогр от плотности жидкости ρ (см. рисунок).
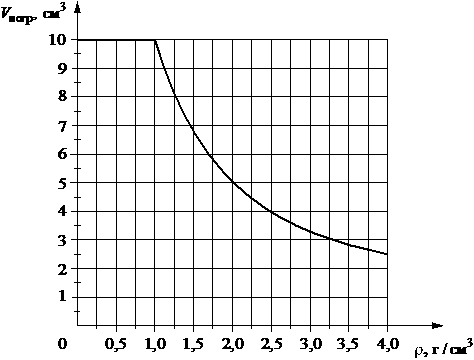
|
Жидкость |
Бензин |
Спирт |
Вода |
Глицерин |
Хлороформ |
Бромоформ |
Дийодметан |
|
ρ, г/см3 |
0,71 |
0,79 |
1,0 |
1,26 |
1,49 |
2,89 |
3,25 |
Выберите два верных утверждения, согласующихся с данными, представленными на рисунке и в таблице.
1) Цилиндр тонет в спирте.
2) Цилиндр плавает во всех жидкостях, указанных в таблице.
3) В бензине и спирте сила Архимеда, действующая на цилиндр, одинакова.
4) При плавании цилиндра в хлороформе и дийодметане сила Архимеда, действующая на него, одинакова.
5) На цилиндр, плавающий в бромоформе, действует выталкивающая сила около 35 мН.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
14
Так как объем вытесненной жидкости равен объему цилиндра, значит весь цилиндр погружается в спирт, то есть он в нем тонет.
Цилиндр плавает и хлороформе и в дийодметане. При замене одной жидкости на другую (1,49 на 3,25 по плотности г/см3), тело глубже погрузиться в жидкость, но номинал выталкивающей силы останется прежним, так как объем и масса для этих случаев обратно пропорциональны, поэтому сила Архимеда останется прежней.
Номер: FE64EC
Выберите один или несколько правильных ответов.
Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними
(см. рисунок). Из приведённого ниже списка выберите два правильных утверждения.
1) Если воду заменить на подсолнечное масло, то глубина погружения брусков уменьшится.
2) Сила Архимеда, действующая на бруски, равна 10 Н.
3) Плотность материала, из которого изготовлены бруски, равна 500 кг/м3.
4) Если на верхний брусок поставить гирю массой 1,5 кг, то бруски не утонут.
5) Если в стопку добавить ещё три таких же бруска, то глубина её погружения увеличится на 15 см.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Выбор ответов из предложенных вариантов
Ответ:
34
Плотность брусков равна половине плотности жидкости в которой они плавают, то есть воды. 1000/2=500 кг/м3
При массе в 1 кг и плотности 500 кг/м3 брусок будет занимать объем:
V=m/ρ= 1/500=0,002 м3, тогда в этом объеме масса воды будет m=ρV=1000*0,002=2 кг, что больше груза на 2-1 кг = 1 кг, то есть 1 кг это сила Архимеда с каждого бруска если его погрузить в воду полностью.
1+1-1,5=0,5 кг. Разница в силе будет 0,5 кг, что позволит брускам с дополнительным грузом держаться на поверхности.
Номер: 7552E3
Краткий ответ (41)
Впишите правильный ответ.
В сосуд глубиной 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равно дополнительное к атмосферному давление столба воды на плоское дно сосуда?
кПа
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
1,8
Гидростатическое давление
P = phg = 1000*(0,2-0,02)*10=1000*1,8=1800=1,8 кПа
Номер: F120FE
Впишите правильный ответ. 2024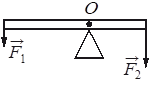
Невесомый рычаг находится в равновесии (см. рисунок). Модуль силы F2 = 12 Н, её плечо равно 10 см. Каков модуль силы F1→, если её плечо равно 15 см?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
8
Золотое правило механики
F1*l1 = F2*l2
F1*0,15 = 12*0,1
F1 = (12*0,1)/0,15 = 8 Н
Номер: 5E50FD
Впишите правильный ответ.
Полый стальной шар массой 10 кг плавает на поверхности озера. Объём шара равен 15 дм3. Чему равна сила Архимеда, действующая на шар?
Н
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
100
1 вариант
Так как шар плавает и не тонет, то сила Архимеда уравновешивает силу тяжести, действующую на шар:
F=mg=10*10=100 Н
2 вариант ("собака укусила сама себя за хвост;) размышление от нашего сайта")
При объеме 15 дм3, масса воды в шаре была бы в 1 дм3=1кг, значит он весил бы 15 кг. То есть если бы шар весил 15 кг, то он находился бы в взвешенном состоянии, не тонул бы и не всплывал.
Получается плотность шара ниже воды в 1,5 раза, так как `15/10=1,5`.
В нашем случае складывается ситуация, когда сила Архимеда будет выталкивать часть шара над поверхностью. Причем погруженная часть тела будет выталкиваться с разностью плотностей воды и шара и эта разность должна быть равна массе шара над поверхностью
`V_(погр.) *p_в - V_(погр.) *p_ш = V_(над водой) * p_ш`
Из соотношения 1,5 получается.
`V_(погр.) *1,5 * p_ш - V_(погр.) *p_ш = V_(над водой) * p_ш`
`0,5 V_погруж * p_ш = V_(над водой) * p_ш` то есть 2 части в воде и 1 часть над ней.
`15/3*2=10` кг выталкивающая сила. 10 кг = 100Н
Из этих размышлений можно зато узнать сколько под водой, сколько над водой!
Номер: 176001
Впишите правильный ответ.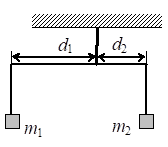
Коромысло весов, к которому подвешены на нитях два груза (см. рисунок), находится в равновесии. Массу первого груза увеличили в 2 раза. Во сколько раз нужно уменьшить плечо d1, чтобы равновесие сохранилось? (Коромысло и нити считать невесомыми.)
в
раз(а)
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
2
Золотое правило механики
F1*l1 = F2*l2
в два раза увеличив силу, надо уменьшить в 2 раза плечо
Номер: 109B0A
Впишите правильный ответ.
На поверхности воды плавает прямоугольный брусок из древесины плотностью 400 кг/м3. Брусок заменили на другой брусок той же массы и с той же площадью основания, но из древесины плотностью 600 кг/м3. Как при этом изменились глубина погружения бруска и действующая на него сила Архимеда?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могу повторяться.
Глубина погружения бруска/ Сила Архимеда
КЭС: 1.3.5 Давление в жидкости, покоящейся в ИСО
Тип ответа: Краткий ответ
Ответ:
33
Решение:
Оба бруска будут плавать в воде, так как их плотность меньше, чем плотность воды. Если тело плавает, то по второму закону Ньютона сила Архимеда равна силе тяжести: Fарх = mg. Так как сила тяжести брусков не изменилась, то и сила Архимеда осталась той же: Fарх = ρжФормулаgФормулаVпогр
Сила Архимеда не изменилась, плотность жидкости ρж осталась той же, поэтому объём погруженной части тела Vпогр не изменяется (3).
Vпогр = SФормулаh, где h - глубина погруженной части бруска. Поскольку площадь основания не изменилась, то и глубина осталась той же (3).
Номер: CCDA00
Впишите правильный ответ.
Невесомый рычаг находится в равновесии (см. рисунок). Сила F1 = 8 Н, её плечо равно 20 см. Каков модуль силы `vecF_2`, если её плечо равно 16 см?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
10
Золотое правило механики
F1*l1 = F2*l2
F2*0,16 = 8*0,2
F1 = (8*0,2)/0,16 = 10 Н
Номер: C7E001
Впишите правильный ответ.
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется пять установок, каждая из которых состоит из ёмкости с жидкостью и сплошного шарика. Какие две из перечисленных в таблице установок необходимы ученику для того, чтобы опытным путём исследовать зависимость силы Архимеда от объёма шарика?
|
№№ установки |
Жидкость, налитая |
Объём шарика |
Масса шарика |
|
1 |
вода |
30 см3 |
234 г |
|
2 |
вода |
20 см3 |
156 г |
|
3 |
керосин |
20 см3 |
267 г |
|
4 |
подсолнечное масло |
30 см3 |
234 г |
|
5 |
керосин |
30 см3 |
267 г |
Запишите в ответе номера выбранных установок.
Ответ:
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
35
Взяли одну и ту же жидкость для погружения, одну и ту же массу шариков, но разные объемы.
Номер: E41101
Впишите правильный ответ.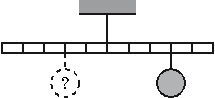
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
кг
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
0,3
Золотое правило механики
F1*l1 = F2*l2
F2*2 = 0,2*3
F1 = (3*0,2)/2 = 0,3 кг
Номер: D52A7D
Впишите правильный ответ.
Ученик выполнял лабораторную работу по исследованию условий равновесия лёгкого рычага, к которому приложены силы `vecF_1` и `vecF_2`. Результаты, которые он получил, представлены в таблице. l1 и l2 –плечи сил.
|
F1, Н |
l1, м |
F2, Н |
l2, м |
|
40 |
0,8 |
? |
0,2 |
Каков модуль силы `vecF_2`, если рычаг находится в равновесии?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
160
Золотое правило механики
F1*l1 = F2*l2
F2*0,2 = 40*0,8
F2 = (40*0,8)/0,2 = 160 H
Номер: A74573
Впишите правильный ответ.
На лодку, плавающую в воде, действует сила Архимеда величиной 2150 Н. Чему равна масса лодки?
кг
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
215
Вся массы лодки выталкивается из воды силой Архимеда, значит:
2150 H = 215 кг
Номер: ED57BF
Впишите правильный ответ.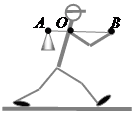
Человек несёт груз на лёгкой палке (см. рисунок). Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
см
КЭС: 1.3.2 Центр масс тела. Центр масс системы материальных точек
Тип ответа: Краткий ответ
Ответ:
30
Золотое правило механики
F1*l1 = F2*l2
30*0,8 = 80*OA
OA = (30*0,8)/80 = 0,3 = 30 см
Номер: 43BD11
Впишите правильный ответ.
На поверхности подсолнечного масла плавает деревянный шарик, частично погружённый в жидкость. Как изменятся сила Архимеда, действующая
на шарик, и глубина погружения шарика, если он будет плавать в воде?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила Архимеда/ Глубина погружения шарика в жидкость
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
32
Сила Архимеда не изменится, она будет равна массе шарика в том и другом случае. Погружение станет меньше, так как плотность среды выше.
Номер: E2791B
Впишите правильный ответ.
Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Н
КЭС: 1.3.5 Давление в жидкости, покоящейся в ИСО
Тип ответа: Краткий ответ
Ответ:
16
Гидростатическое давление
P = phg
p = 800 г/м3 плотность керосина
10 см2 = 0,001 м2 площадь заплаты.
P = phg = 0,8*2*10*0,001=16 H
Номер: 0EFE20
Впишите правильный ответ.
Момент первой силы, действующей на рычаг, равен 50 Н⋅м. Какой должна быть вторая сила, чтобы рычаг находился в равновесии, если её плечо равно 0,5 м?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
100
Крутящий момент
M = F*l
Нам надо создать крутящий момент 50 Н*м при плече 0,5
При плече 1 метр у нас 50 Н.
При плече 0,5 тогда
x*0,5=50
x=50/0,5=100 Н
Номер: 0BA328
Впишите правильный ответ.
На поверхности пресной воды плотностью ρ1 = 1000 кг/м3 плавает деревянный брусок. Как изменятся масса вытесненной бруском жидкости и действующая на него сила Архимеда, если этот брусок будет плавать на поверхности керосина плотностью ρ2 = 800 кг/м3?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Масса вытесненной бруском жидкости/ Сила Архимеда
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
33
Масса вытесненной жидкости останется та же. Несмотря на увеличение объема вытесненной жидкости, массе ее останется прежней.
Сила Архимеда равна массе бруска.
Номер: 10BE25
Впишите правильный ответ.
Ученик выполнял лабораторную работу по исследованию условий равновесия рычага под действием двух сил: `vecF_1` и `vecF_2`. Результаты, которые он получил, представлены в таблице. l1 и l2 –плечи сил.
|
F1, Н |
l1, м |
F2, Н |
l2, м |
|
40 |
0,4 |
? |
0,8 |
Какова сила F2, если рычаг находится в равновесии?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
20
Золотое правило механики
F1*l1 = F2*l2
F2*0,8 = 40*0,4
F2 = (40*0,4)/0,8 = 20 H
Номер: 3FFC2F
Впишите правильный ответ.
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется пять установок, состоящих из ёмкости с жидкостью и сплошного шарика. Какие две из перечисленных в таблице установок необходимы ученику для того, чтобы на опыте обнаружить, зависит ли сила Архимеда от плотности материала шарика?
|
№ установки |
Жидкость, налитая |
Объём шарика |
Материал, из которого сделан шарик |
|
1 |
вода |
30 см3 |
сталь |
|
2 |
вода |
20 см3 |
алюминий |
|
3 |
керосин |
20 см3 |
алюминий |
|
4 |
подсолнечное масло |
30 см3 |
сталь |
|
5 |
вода |
30 см3 |
алюминий |
Запишите в таблицу номера выбранных установок.
Ответ:
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
15
Нужны одинаковые жидкости, объемы шаров, но разные материалы.
Номер: A6D7D1
Впишите правильный ответ.
Деревянный шарик плавает в керосине. Как изменятся масса вытесненной жидкости и глубина погружения шарика в жидкость, если он будет плавать
в воде?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Масса вытесненной жидкости/ Глубина погружения шарика в жидкость
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
32
Масса не изменится, так как меньшая вытесненная жидкость будет весить столько же, массе тела. Именно поэтому и сила Архимеда будет равна для двух случаев.
Номер: E7DBDE
Впишите правильный ответ. 2024
Ученик выполнял лабораторную работу по исследованию условий равновесия рычага под действием двух сил: F1→ и F2→, плечи которых равны соответственно l1 и l2. Он внёс результаты измерений в таблицу.
F1, Н l1, м F2, Н l2, м
? 0,4 20 1,2
Определите модуль силы F1→, если рычаг находится в равновесии. Массой рычага пренебречь.
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
60
Золотое правило механики
F1*l1 = F2*l2
F1*0,4 = 20*1,2
F1 = (20*1,2)/0,4 = 60 H
Номер: 99BD56
Впишите правильный ответ.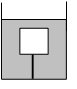
Водонепроницаемая коробка массой 0,2 кг привязана ниткой ко дну сосуда с водой (см. рисунок). На коробку действует сила Архимеда, равная 10 Н. Определите силу натяжения нити.
Н
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
8
0,2 кг = 2 Н
10-2=8 Н сила выталкивающая коробку, равная натяжению нити.
Номер: 92E953
Впишите правильный ответ.
На кусок алюминия массой 0,54 кг при полном погружении в воду действует сила Архимеда, равная 2 Н. Чему равна при этом масса вытесненной воды?
кг
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
0,2
Масса воды равна силе Архимеда в объеме тела. Так как тело все погрузилось, то берем 2 Н, то есть 0,2 кг
Номер: 2EF7AF
Впишите правильный ответ.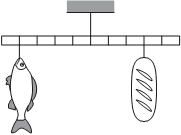
Мальчик взвесил рыбу на самодельных весах из лёгкой удочки (см. рисунок). В качестве гири он использовал батон хлеба массой 1 кг. Определите массу рыбы.
кг
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
0,75
Золотое правило механики
F1*l1 = F2*l2
F1*4 = 1*3
F1 = 3/4 = 0,75 кг
Номер: A55FAE
Впишите правильный ответ.
Деревянный кубик имеет ребро длиной 2 см. Определите архимедову силу, действующую на кубик при его полном погружении в воду.
Н
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
0,08
Объем куба:
0,02*0,02*0,02=0,000008 м3
ρ воды = 1000*0,000008=0,008 кг = 0,08 Н
Номер: EB02A8
Впишите правильный ответ.
Деревянный шарик плавает в стакане с водой. Как изменятся сила тяжести, действующая на шарик, и глубина погружения шарика в жидкость, если он будет плавать в подсолнечном масле?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила тяжести, действующая на шарик/ Глубина погружения шарика в жидкость
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
31
Гравитационная составляющая не изменится, так не зависит от силы Архимеда, а вот погружение увеличится, так как плотность масла меньше.
Номер: 45DEC1
Впишите правильный ответ.
Определите давление керосина в открытой цистерне на глубине 1,5 м. Атмосферное давление не учитывать.
кПа
КЭС: 1.3.4 Закон Паскаля
Тип ответа: Краткий ответ
Ответ:
12
Гидростатическое давление
P = phg
p = 800 г/м3 плотность керосина
P = phg = 0,8*1,5*10=12 кПа
Номер: 2A56CC
Впишите правильный ответ.
Ученик выполнял лабораторную работу по исследованию условий равновесия рычага под действием двух сил: `vecF_1` и `vecF_2` , плечи которых равны соответственно l1 и l2. Он занёс результаты измерений в таблицу.
|
F1, Н |
l1, м |
F2, Н |
l2, м |
|
? |
0,3 |
50 |
0,6 |
Какова сила F1, если рычаг находится в равновесии?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
100
Золотое правило механики
F1*l1 = F2*l2
F1*0,3 = 50*0,6
F1 = (50*0,6)/0,3 = 100 H
Номер: 8093C0
Впишите правильный ответ.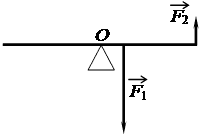
На тонкий рычаг действуют силы так, как показано на рисунке. Сила F1 = 10 H; сила F2 = 2,5 H. Рычаг находится в равновесии.
С какой силой рычаг давит на опору в точке О? Массой рычага пренебречь.
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
7,5
При проекции сил на ось y: 10-2,5=7,5 H
Номер: 2A8C90
Впишите правильный ответ. 2024
Медный кубик, подвешенный на нити, полностью погружён в воду и не касается дна сосуда. Ребро кубика равно 3 см. Определите силу Архимеда, действующую на кубик.
Н
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
0,27
Сила Архимеда рана массе воды в объеме куба. Объем куба:
0,03*0,03*0,03=0,000027 м3
ρ воды = 1000*0,000027=0,027 кг = 0,27 Н
Номер: 17FFEA
Впишите правильный ответ.
В первом опыте на поверхности воды плавает деревянный брусок, частично погружённый в жидкость. Во втором опыте брусок заменили на другой – той же плотности и массы, но большей высоты.
Как изменятся сила Архимеда, действующая на брусок, и масса вытесненной воды при переходе от первого опыта ко второму?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила Архимеда/ Масса вытесненной воды
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
33
При изменении формы тела все параметры сил останутся прежними.
Для размышления: Увеличивая высоту, сохраняя плотность и массу, изменяем основание. Ведь изменение высоты повлечет изменение основания, но при изменении основания объем погруженного тела в воде не изменится, даже если оно будет погружено глубже чем ранее.
Номер: 72E162
Впишите правильный ответ.
Ученик выполнял лабораторную работу по исследованию условий равновесия рычага под действием двух сил: `vecF_1` и `vecF_2`. l1 и l2 – плечи сил. Результаты, которые он получил, занесены в таблицу.
|
F1, Н |
l1, м |
F2, Н |
l2, м |
|
20 |
0,4 |
5 |
? |
Каково плечо силы l2, если рычаг находится в равновесии?
м
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
1,6
Золотое правило механики
F1*l1 = F2*l2
l2*5 = 20*0,4
l2 = (20*0,4)/5 = 1,6
Номер: A34464
Впишите правильный ответ.
Деревянный шарик плавает в воде. Как изменятся сила тяжести, действующая на шарик, и глубина погружения шарика в жидкость, если он будет плавать в керосине?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила тяжести/ Глубина погружения шарика в жидкость
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
31
Сила тяжести не изменится, так как она не связана с силой Архимеда. Погружение увеличится, так как плотность стала меньше и одна и та же масса должно занимать больший объем погруженного тела.
Номер: 6AAD61
Впишите правильный ответ.
Стальной кубик, висящий на нити, целиком погружён в воду и не касается дна сосуда. Верхняя и нижняя грани кубика горизонтальны. Как изменятся давление воды на нижнюю грань кубика и модуль силы натяжения нити, если приподнять кубик, оставив его целиком в воде? Воду считать несжимаемой.
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Давление воды на нижнюю грань кубика/ Модуль силы натяжения нити
КЭС: 1.3.4 Закон Паскаля
Тип ответа: Краткий ответ
Ответ:
23
Гидростатическое давление станет меньше, то есть на грань давление уменьшится. Натяжение нити не изменится ибо оно характеризуется силой притяжения и силой Архимеда.
Номер: 07E032
Впишите правильный ответ.
Гидростатическое давление, создаваемое водой на дне озера, без учёта давления атмосферы равно 4·105 Па. Какова глубина озера?
м
КЭС: 1.3.5 Давление в жидкости, покоящейся в ИСО
Тип ответа: Краткий ответ
Ответ:
40
Гидростатическое давление
P = phg
400000 = 1000*h*10
h = 400000*10000=40 м
Номер: B08038
Впишите правильный ответ.
Деревянный шарик плавает в керосине. Как изменятся сила тяжести и сила Архимеда, действующие на шарик, если он будет плавать в воде?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила тяжести, действующая на шарик/ Сила Архимеда, действующая на шарик
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
33
Сила тяжести никак не изменится, а значит и сила Архимеда, ведь она равна массе выталкиваемого тела.
Номер: FA548D
Впишите правильный ответ.
Даны следующие зависимости величин:
А) зависимость пути, пройденного телом при равномерном движении, от времени;
Б) зависимость объёма постоянной массы идеального газа от абсолютной температуры в изохорном процессе;
В) зависимость электроёмкости плоского конденсатора с расстоянием d между пластинами от площади пластин.
Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
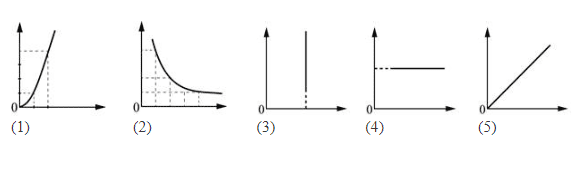
А Б В
Ответ:
КЭС: 1.1 Кинематика
1.2 Динамика
1.3 Статика
1.4 Законы сохранения в механике
1.5 Механические колебания и волны
2.1 Молекулярная физика
2.2 Термодинамика
3.1 Электрическое поле
3.2 Законы постоянного тока
3.3 Магнитное поле
3.4 Электромагнитная индукция
3.5 Электромагнитные колебания и волны
3.6 Оптика
Тип ответа: Краткий ответ
Ответ:
545
Номер: A89B4F
Впишите правильный ответ.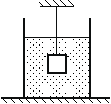
Груз массой m = 2,0 кг и объёмом V = 10–3 м3, подвешенный на тонкой нити, целиком погружён в жидкость и не касается дна сосуда (см. рисунок). Модуль силы натяжения нити Т = 12 Н. Найдите плотность жидкости.
кг/м3
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
800
Сила Архимеда равна массе жидкости в объеме тела:
12 Н = 1,2 кг это натяжение которое остается на нити после противодействия силе Архимеда.
2-1,2 = 0,8 кг сила Архимеда
Нам известно, что эта сила образовалась от погружения тела объемом V = 10–3 м3
То есть 1 дм3, значит 1 м3 жидкости будет весить 0,8*1000=800 кг/м3 что и является плотностью жидкости.
Номер: 16C3B9
Впишите правильный ответ.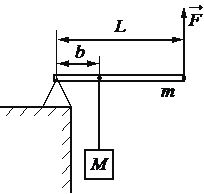
Груз поднимают с помощью рычага (см. рисунок). Рычаг состоит из шарнира без трения и однородного стержня массой m=20
кг и длиной L=4 м. Расстояние от оси шарнира до точки подвеса груза равно b=1 м. Какую вертикальную силу надо приложить к концу рычага, чтобы медленно поднимать груз массой M=80 кг?
Н
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
300
Чтобы рычаг находился в горизонтальном положении, необходимо равенство моментов, движущих рычаг вниз и вверх. Моменты сил, направленные вниз, это груз массой M с моментом M*g*b и сама балка mg*L/2 с моментом (здесь m – масса рычага, а величина L/2 говорит о том, что вес балки, создающий ее момент, отсчитывается от ее центра). Момент силы, направленный вверх, равен F*L. Получаем уравнение:
`Mgb + mg * L/2 = FL`
`F = Mgb/L + mg/2`
`F = (80*10*1)/40 +(20*10)/2 = 300 Н`
Номер: D795BB
Впишите правильный ответ.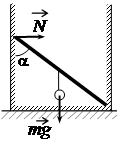
Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N→, действующей на стержень со стороны левой стенки ящика?
Н
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
5
Поскольку стержень находится в равновесии, можем расписать условие равновесия в проекции на горизонтальную ось:
N1 - N = 0, где N1 - сила реакции опоры, действующая на левый конец стержня.
N1 = N (1)
Запишем уравнение моментов относительно оси, проходящей через нижнюю точку стержня в точке её касания стенки:
mg*0.5Lsin∝=N1 cos∝ (2)
Подставим (1) во (2):
mg*0,5Lsin∝=NL*cos∝
`N = (mg*0,5Lsin∝)/(L*cos∝)`
`N = (1*10*0,5*sin45)/(cos45)`
`N = (5*sin45)/(cos45)`
Ответ: N = 5 H
Номер: 37D2BB
Впишите правильный ответ.
На поверхности воды плавает деревянный брусок, частично погружённый в жидкость. Как изменятся сила Архимеда, действующая на брусок, и глубина погружения бруска, если он будет плавать в подсолнечном масле?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Сила Архимеда/Глубина погружения бруска
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
31
Сила Архимеда не изменится, она будет равна массе бруска. Глубина погружения станет больше, так как плотность жидкости меньше.
Номер: 8247AC
Впишите правильный ответ.
Школьник изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеются пять установок, состоящие из ёмкостей с различными жидкостями и сплошных шариков различного объёма, и сделанных из разного материала, (см. таблицу). Какие две установки необходимо использовать ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?
|
№ установки |
Жидкость, налитая в ёмкость |
Объём шарика |
Материал, из которого сделан шарик |
|
1 |
керосин |
30 см3 |
сталь |
|
2 |
вода |
20 см3 |
дерево |
|
3 |
керосин |
20 см3 |
дерево |
|
4 |
подсолнечное масло |
30 см3 |
сталь |
|
5 |
вода |
30 см3 |
дерево |
В ответ запишите номера выбранных установок.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Тип ответа: Краткий ответ
Ответ:
25
Одна жидкость, разный объем.
Номер: FB279F
Впишите правильный ответ.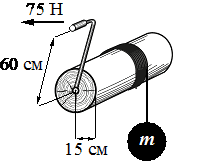
Длина рукоятки ворота 60 см, радиус вала 15 см (см. рисунок). Какую максимальную массу m можно равномерно поднимать при помощи ворота, прикладывая к рукоятке силу 75 Н? Трением пренебречь.
кг
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Тип ответа: Краткий ответ
Ответ:
30
Золотое правило механики
F1*l1 = F2*l2
0,6*75 = 0,15*F
`F = (0,6*75)/0,15 = 300 Н = 30 кг`
Номер: 523C36
Развернутый ответ (24)
Дайте развернутый ответ. 2024
В стакан налита вода, а поверх неё – керосин. Однородный шар плавает, погружённый в обе жидкости. При этом четверть объёма шара находится в воде. Найдите плотность материала шара.
КЭС: 1.3 Статика
Тип ответа: Развернутый ответ
Решение:
850
Решение 1
По условию объем погруженной части шарика в воду равен 1/4 объема, следовательно, в керосин будет погружена 3/4 от объема шарика. На шарик действуют силы Архимеда со стороны керосина и воды, направленные вверх, и сила тяжести, направленная вниз. Так как шарик находится в равновесии, то Fа1+Fа2-mg=0 Сила Архимеда со стороны керосина Fа1 = ρk*g*3/4gV со стороны воды Fа2 = ρk*g*1/4gV масса шарика m = ρV. Объединяя формулы, находим плотность шарика:
`ρ = (3*ρ_k+ρ_в)/4 = (3*800+1000)/4=850` кг*м3
Решение 2 (от нашего сайта)
Найдем плотность шара с учетом условия, что он плавает в воде. Так как 1/4 шара условно держит над водой 3/4 шара, то его плотность получилась в 4 раза ниже плотности воды.
ρ воды = 1000 кг*м3
ρ керосина = 800 кг*м3
ρ шара без учета керосина =1000 : 4 = 250 кг*м3
Однако эта плотность занижена из-за того, что на 3/4 шара действует сила Архимеда керосина.
То есть если 3/4 шара плавают в керосине, то можно считать, что у них плотность 800+250=1050 кг/м3
Получается у шара условная неравномерная плотность:
1050 кг/м3 на 75%
250 кг/м3 и на 25%
Вот и найдем теперь плотность шара, представив что его плотность все же однородная, из среднестатистического значения, где 1 часть это 25 процентов, то есть 1/4 шара.
`(3*1050+250)/4= 850` кг/м3
Ответ: 850 кг/м3
Номер: 29960D
Дайте развернутый ответ.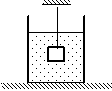
Груз массой m = 2,0 кг и объёмом V = 10–3 м3, подвешенный на тонкой нити, целиком погружён в жидкость и не касается дна сосуда (см. рисунок). Плотность жидкости ρ = 700 кг/м3. Найдите модуль силы натяжения нити.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
13
На груз действует сила тяжести и сила Архимеда
T = Fт-Fа
Fа = ρV = 700*10–3 = 0,7 кг = 7 H
T = 20-7=13 H
Ответ: 13H
Номер: E9B775
Дайте развернутый ответ.
Однородный деревянный шар массой m = 1,6 кг лежит в сосуде с водой, касаясь дна и не касаясь стенок сосуда, так, что половина шара находится в воде. Определите плотность дерева, если шар давит на дно сосуда с силой F = 6 Н. Сделайте рисунок с указанием сил, действующих на шар.
КЭС: 1.3 Статика
Тип ответа: Развернутый ответ
Решение:
800
Решение 1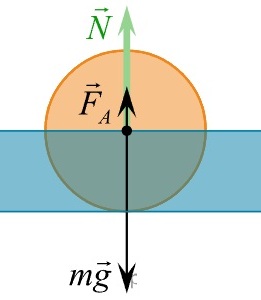
Сила, с которой шар давит на дно, равна по модулю силе реакции опоры по третьему закону Ньютона F = N. Изобразим силы, действующие на деревянный шар (см. рис).
Шар находится в равновесии, следовательно Т+Fа = mg, Сила Архимеда при погружении шара наполовину Fа = ρg V/2, Объем шара V = m/ρ. Объединив формулы, находим плотность дерева, из которого изготовлен шар:
`ρ ш = (ρв*gm)/(2(mg-N))=(1000*10*1,6)/(2(1,6*10-6)) = 800`кг/м3
Ответ: 800 кг/м3
Решение 2 (от нашего сайта)
Нарисуем рисунок с действием всех сил на шар.
Силу Архимеда можно найти как разность между силой действующей на дно и массой шара.
Fа = 16-6=10 H
То есть для половины шара действует сила 10 Н, а для всего шара действовала бы сила 2*10=20H
Значит объем шара равен 2 дм3 или 2*10-3 м3
Так как масса воды в 1 дм3 (1*10-3 м3) равна 1 кг = 10 Н
Зная объем и массу, можем найти плотность.
ρ = 1,6/2*10-3 = 800 кг/м3
Ответ: 800 кг/м3
Номер: DB692A
Дайте развернутый ответ.
Однородный цилиндр объёмом 4·10–4 м3 подвешен на нити и наполовину погружён в воду. Какова плотность материала цилиндра, если сила натяжения нити F = 3 Н?
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
1250
Решение 1
Нарисуем рисунок с приложенными силами.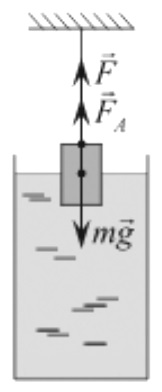
Из условия равновесия:
F+Fа-mg = 0
При этом сила Архимеда:
`Fа = 1/2*ρV_ц`
При этом масса цилиндра равна:
m = F+Fа
отсюда можно выразить плотность:
`ρ = (F+Fа)/V= (3+0,5*10^3*4*10^-4)/(4*10^-4) =1250`кг/м3
Ответ:1250 кг/м3
Решение 2 (от нашего сайта)
Если половина цилиндра погружена в воду, то в воде находится объем: 4:2·10–4 м3 = 2·10–4 м3
То есть сила Архимеда для цилиндра погруженного в воду равна 1000 * 2·10–4= 0,2 кг = 2 H.
Получается если бы цилиндр висел только на нити, без погружения, то натяжение нити и значит масса груза была бы равна 3+2=5H, то есть выталкивающая силы бы не действовала. Теперь зная массу и объем, можем найти плотность цилиндра:
ρ = 0,5/4·10–4 = 1250 кг/м3
Ответ:1250 кг/м3
Номер: 1F1FD6
Дайте развернутый ответ.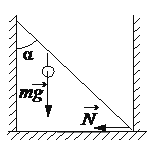
Невесомый стержень длиной 3 м, находящийся в ящике с гладкими дном и стенками, составляет с вертикалью угол α = 45º (см. рисунок). К стержню на расстоянии 1 м от левого его конца подвешен на нити шар массой 3 кг. Каков модуль силы нормальной реакции `vecN`правой стенки ящика, действующей на нижний конец стержня?
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
34,64
Решение.
1. Поскольку стержень находится в равновесии (см. рисунок),
N2-N=0. (1)
mg-N1=0 (2)
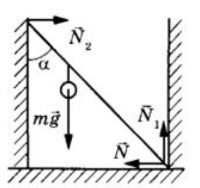
2. Запишем уравнение моментов относительно оси, проходящей через нижнюю точку стержня в точке её касания стенки:
mgl sin∝ - N2Lcos∝ = 0, (3)
где l — расстояние от левого конца стержня до точки подвеса шара, L — длина стержня.
4. Решая систему уравнений (1)-(3), получим выражение для модуля силы N:
`N = N_2=(mgl*sin∝)/(L*cos∝) = (mgl*tg∝)/L`
`N = (3*10*2*sqrt(3))/(3) ≈ 34,64`
Ответ: 34,64 H
Номер: 36135B
Дайте развернутый ответ.
Плоская льдина плавает в воде, выступая над её поверхностью на h = 0,04 м. Определите массу льдины, если площадь её поверхности S = 2500 см². Плотность льда равна 900 кг/м3.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
90
Решение 1
Пусть высота льдины H , тогда высота погруженной части H − h , а объём тела HS . На тело действует сила Архимеда Fа и сила тяжести mg .
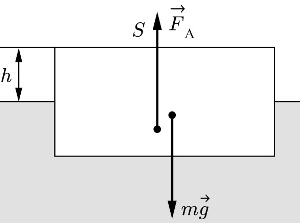
Запишем второй закон Ньютона для тела, находящегося в равновесии
FA − mg = 0
Силу Архимеда можно найти по формуле:
`FA = ρgV_п`,
где ρ – плотность жидкости, Vп = (H − h)S – объём погруженной части.
Масса груза равна
`m = ρ_лHS`.
`ρ(H − h)= ρ_лH ⇒ H = ρ/(ρ − ρ_л)*h`.
Тогда масса
`m = (ρ*ρ_л)/(ρ− ρ_л)*hS = (1000 *900)/(1000-900)*0,04*2500*10^-4=90`кг
Ответ:90 кг
Решение 2 (от нашего сайта)
Сила Архимеда равна массе воды в объеме тела погруженного в жидкость. Нам надо узнать погруженный объем. Начнем с вычисления глубины погружения.
Разность масс между льдом и водой в погруженном объеме тела будет обеспечивать плавучесть части над водой. В итоге если объем над водой
V над водой = 0,04*0,25=0,01 м3
Что по массе при плотности 900 кг/м3 составит
m=900*0,01=9 кг
Получается при разности масс льда и воды в соотношении 900/1000=9/10=0,9 то есть на каждые 9 частей льда, можно удерживать на плаву 10 часть. Значит объем под водой в 9 раз больше, нежели над поверхностью, а значит и масса в 9 раз больше.
Тогда получается масса льдины 9+9*9=90 кг
Ответ:90 кг
Номер: 7733A6
Дайте развернутый ответ.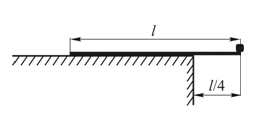
Деревянная линейка длиной l=60 см выдвинута за край стола на 1/4 часть своей длины. При этом она не опрокидывается, если на её правом конце лежит груз массой не более 250 г (см. рисунок). На какое расстояние можно выдвинуть вправо за край стола эту линейку, если на её правом конце лежит груз массой 125 г?
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
0,2
Решение.
1. Пусть M — масса линейки, m — масса груза. При максимальной массе груза, который неподвижен относительно линейки, сила реакции стола действует на линейку только по краю стола.
2. Запишем уравнение моментов для первого случая относительно оси вращения, проходящей через край стола перпендикулярно плоскости рисунка:
`Mg(l/4) = m_1g(l/4)`(1)
3. Уравнение моментов для второго случая относительно оси вращения, проходящей через край стола перпендикулярно плоскости рисунка:
`(Mgl)/6 = (m_2gl)/3` , (2)
где m2 — искомая масса второго груза.
4. Решая уравнения (1) и (2), получим:
`x =(m_1*l)/(2(m_1+m_2)) = (0,25*6)/(2(0,25+0,125))=0,2 м`
Ответ: 0,2 м
Номер: B938AE
Дайте развернутый ответ.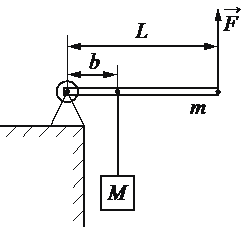
Груз массой M=75 кг медленно поднимают с помощью рычага, приложив вертикальную силу `vecF` (см. рисунок). Рычаг, сделанный из однородного стержня массой m=10 кг и длиной L=4 м, шарнирно закреплён. Определите модуль силы `vecF , если расстояние b от оси шарнира до точки подвеса груза равно 1,6 м. Считать, что трение в шарнире отсутствует.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
350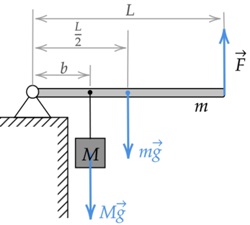
Запишем правило моментов относительно точки закрепления шарнира. Так как груз находится в равновесии, то алгебраическая сумма моментов действующих на него сил равна нулю:
`M_(Mg) + M_F + M_(mg) = 0`
`FL − Mgb − mg L/2 = 0`
`Mgb =F L− mg L/2`
Выразим F :
`F = Mg b/L + (m*g)/2= 75*10*(1,6)/4+(10*10)/2=350` Н
Ответ: 350 Н
Номер: 2E71C0
Дайте развернутый ответ. 2024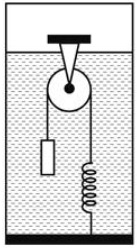
На рисунке показана система тел, состоящая из неподвижного блока с перекинутой через него лёгкой и нерастяжимой нитью, к концам которой привязаны тяжёлое тело объёмом V = 100 см3 и лёгкая пружина жёсткостью k = 100 Н/м. Эта система погружена в сосуд с жидкостью плотностью ρ = 900 кг/м3. Нижний конец пружины прикреплён ко дну сосуда. Как и на сколько изменится сила натяжения нити, действующая на пружину, если всю жидкость вылить из сосуда? Считать, что трение в оси блока отсутствует.
КЭС: 1.3 Статика
Тип ответа: Развернутый ответ
Решение:
9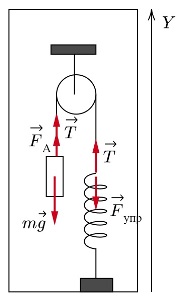
Если убрать всю жидкость, то пропадет сила Архимеда, которая была противоположно направлена относительно силы гравитации mg.
Это как раз и будет изменение для натяжения нити.
ΔT = Fa = ρ*g*V= 900*10*0,0001=9 Н
Ответ: 9 Н
Номер: 62CDEC
Дайте развернутый ответ.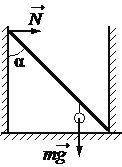
Невесомый стержень длиной 3 м, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К стержню на расстоянии 1 м от его правого конца подвешен на нити шар массой 3 кг. Каков модуль силы реакции опоры N→, действующей на стержень со стороны левой стенки ящика?
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
17,32
Решение.
1. Поскольку стержень находится в равновесии (см. рисунок),
N2-N = 0. (1)
mg-N1=0 (2)
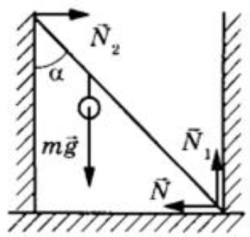
2. Запишем уравнение моментов относительно оси, проходящей через нижнюю точку стержня в точке её касания стенки:
m*glsinα - N2L*cosα=0, (3)
где l — расстояние от правого конца стержня до точки подвеса шара (3-1=2), L — длина стержня.
4. Решая систему уравнений (1)-(3), получим выражение для модуля силы N:
`N = N2=(m*g*l*sin∝)/(L*cos∝)=(m*g*l*tg∝)/L`
`N = (3*10*1*sqrt(3))/3=17,32`H
Ответ:17,32 H
Номер: F9BE3E
Дайте развернутый ответ.
Два небольших массивных шара массами m1=0,2 кг и m2=0,3 кг закреплены на концах невесомого стержня AB, лежащего горизонтально на опорах C и D. Длина стержня AB L=1 м, а расстояние AC равно 0,2 м. Сила давления стержня на опору D в 2 раза больше, чем на опору C. Каково расстояние между опорами CD? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стрежень и шары».
Обоснуйте применимость законов, используемых для решения задачи.
КЭС: 1.3 Статика
Решение:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Стержень будем описывать моделью абсолютно твердого тела - его форма и размеры неизменны, расстояние между любыми двумя точками остаются неизменным.
3. Движение абсолютно твердого тела можно описать совокупностью движений - поступательного и вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного движения). Также применим третий закон Ньютона для описания взаимодействия между стержнем и опорами.
5. Размеры шариков малы по сравнению с размером стержня, поэтому будем описывать шарики моделью материальной точки.
Решение
На твердое тело, образованное двумя шарами и стержнем действует силы тяжести первого и второго шаров m1g и m2g , а также силы реакции опоры N1 и N2 . По условию силы давления на опоры отличаются в 2 раза. По третьему закону Ньютона силы давления на опору равны силе реакции опоры в этой точке, значит, 2N1 = N2 Запишем второй закон Ньютона и правило моментов относительно точки B.
Момент силы можно найти по формуле: M = Fl , где F - сила, а l - её плечо до рассматриваемой оси вращения.
`{(N_1 + N_2− m1g − m2g = 0),(N_1(1-0,2) + N_2(x)− m1g*1 = 0):}`
где x – DB и плечо силы N2.
Так как N2 = 2N1 , то систему уравнений можно переписать в виде
`{(N_1 + 2N_1− m1g − m2g = 0),(N_1(0,8) + 2N_1(x)− m1g*1 = 0):}`
`{(3N_1 = m1g + m2g),(N_1 (0,8 + 2x) = m1g):}`
Поделим второе уравнение на первое, левую часть на левую, правую на правую, - чтобы сократить N1
`(3N_1)/(N_1 (0,8 + 2x)) = (m_1g + m_2g)/(m_1g)`
`3/(0,8 + 2x) = 1+(m2g)/(m1g)`
`3/(0,8 + 2x) = 1 +(0,3*10)/(0,2*10)`
`3/(0,8 + 2x) = 2,5`
`2,5(0,8 + 2x) = 3`
`2 + 5x = 3 `
5x = 3-2
x = 0,2
DB = 0,2
Отсюда AB =1-0,2-0,2 = 0,6 м
Ответ: 0,6 м
Номер: 652146
Дайте развернутый ответ.
Гладкий цилиндр лежит между двумя плоскостями, одна из которых вертикальна, а линия их пересечения горизонтальна (см. рисунок). Сила давления цилиндра на вертикальную стенку равна 10 Н и в n = 3 раза меньше, чем сила давления на цилиндр со стороны другой плоскости. Определите массу цилиндра. Сделайте рисунок, на котором укажите силы, действующие на цилиндр.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
Решение.
1. Поскольку цилиндр гладкий, силы трения отсутствуют. Все действующие на цилиндр силы проходят через его центр масс, поэтому момент сил относительно оси, проходящей через его центр масс, равен нулю.
2. Для того чтобы цилиндр в этом случае находился в равновесии, необходимо, чтобы векторная сумма сил, действующих на него, была равна нулю. Поэтому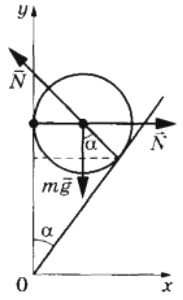
3. С учётом того, что `N_1=n10=30`: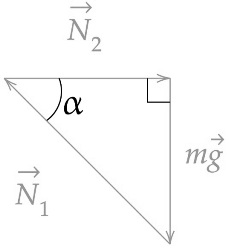
Можно составить уравнение исходя из теоремы Пифагора
`30^2=10^2+mg^2`
`mg^2 = 30^2-10^2`
`mg^2 = 800`
`mg ≈ 28`
m ≈ 2,8 кг
Ответ: 2,8
Номер: 0CDBF9
Дайте развернутый ответ.
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Стержень будем описывать моделью абсолютно твердого тела - его форма и размеры неизменны, расстояние между любыми двумя точками остаются неизменным.
3. Движение абсолютно твердого тела можно описать совокопнустью движений - поступательного и вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного движения)
Решение
Сделаем рисунок с указанием сил, действующих на стержень
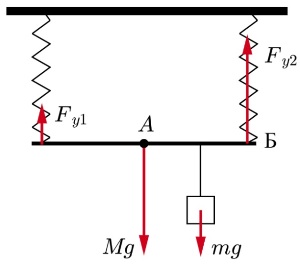
Момент силы можно найти по формуле: M =F*l , где F - сила, а l - её плечо до рассматриваемой оси вращения. Тогда правило моментов относительно точки A
`F_(y1) L/2 + m*g*(L/2 − d) = F_(y2) L/2`
Здесь: Fy1 L/2 - момент силы упругости левой пружинки относительно точки А, mg * (L/2− d) - момент силы тяжести груза относительно точки А,
Fy2 L/2 - момент силы упругости правой пружинки относительно точки А.
Кроме того, по условию стержень расположен горизонтально (растяжения пружин равно) и жёсткость левой пружины в 2 раза меньше правой Fy1 = kx - сила упругости левой пружины, Fy2 =2kx - сила упругости правой пружины, где k – жёсткость левой пружины, x – удлинение пружины. Тогда правило моментов запишется в виде:
`k*x*L/2 + mg(L/2 − d) = 2kx*L/2⇒ kx = (mg(L−2d))/L`
Также по правилу моментов относительно точки Б
`kxL = Mg L/2 + mgd`
Здесь:
kxL - силы упругости левой пружинки относительно точки Б,
Mg L/2 - момент силы тяжести стержня относительно точки Б,
mgd - момент силы тяжести груза относительно точки Б.
Тогда
`2mg (L− 2d)= MgL + 2mgd ⇒ M = (2(kxL-mgd))/(gL) = 3` кг
Ответ: 3 кг.
Номер: EB0004
Дайте развернутый ответ.
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S=100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h=5 см. Найдите силу натяжения нити T.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
1. Условие равновесия шара в первом случае:
`F_(a1) = T + mg (1)`
где `F_(a1) = ρV_1g`– сила Архимеда, действующая на шар в первом случае,
`V_1`– объём части шара, погружённой в воду в первом случае (в данной задаче это объём всего шара),
m – масса шара и ρ– плотность воды.
2. Условие равновесия шара во втором случае:
`F_(a2) = mg (2)`
где `F_(a2) = ρV_2g`– сила Архимеда, действующая на шар во втором случае,
`V_2`– объём части шара, погруженной в воду во втором случае.
3. Вычтем из уравнения уравнение и, учитывая, что получим:
`T = ρg(V_1-V_2) = ρgSh = 10^3*10*100*10^-4*0,05 =5`H
Ответ: T = 5Н
Номер: 328102
Дайте развернутый ответ.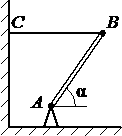
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы `vecF`, действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
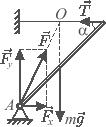
Стержень находится в равновесии под действием сил, изображенных на рисунке, где
mg — сила тяжести,
T — сила натяжения нити,
Fx и Fy — составляющие силы реакции шарнира вдоль горизонтальной и вертикальной осей, соответственно. Условия равновесия стержня имеют вид:
для сил:
`F_x=T`,
`F_y=mg`,
для моментов сил относительно точки A:
`mg*l/2*cos∝ =T*l*sin∝`
где — длина стержня. Учитывая, что
`F=sqrt(F_x^2 +F_y^2)`,
получаем:
`F = mgsqrt(1+1/4ctg^2∝) ≈ 11` Н.
Ответ 11 Н.
Дополнение
Поскольку линии действия сил mg и T пересекаются в точке O, линия действия силы F также должна проходить через эту точку, что позволяет до решения задачи однозначно определить направление силы реакции шарнира.
Номер: 904771
Дайте развернутый ответ.
Гладкий цилиндр лежит между двумя плоскостями, одна из которых вертикальна, а линия их пересечения горизонтальна (см. рисунок). Сила давления цилиндра на вертикальную стенку в n=√3 раза превышает силу тяжести, действующую на шар. Найдите угол α между плоскостями. Сделайте рисунок, на котором укажите силы, действующие на цилиндр.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
Решение.
1. Поскольку цилиндр гладкий, силы трения отсутствуют. Все действующие на цилиндр силы проходят через его центр масс, поэтому момент сил относительно оси, проходящей через его центр масс, равен нулю.
2. Для того чтобы цилиндр в этом случае находился в равновесии, необходимо, чтобы векторная сумма сил, действующих на него, была равна нулю. Поэтому
`N_1-Ncos∝=0`
`Nsin∝-mg=0`
3. Решая систему уравнений с учётом того, что `N_1=nmg`, получим:
`tg∝ = mg/N_1 = 1/n`
`∝=arctg(1/n) = arctg (1/sqrt(3))=30`
Ответ: 30
Номер: A69E10
Дайте развернутый ответ.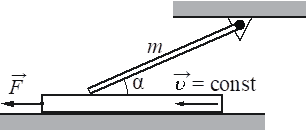
Однородный тонкий стержень массой m одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную горизонтальную доску, образуя с ней угол α=30 °.
Под действием горизонтальной силы `vecF` доска движется поступательно влево с постоянной скоростью (см. рисунок). Стержень при этом неподвижен. Найдите m, если F=2 Н, а коэффициент трения стержня по доске μ=0,2. Сделайте рисунок с указанием сил, действующих на стержень и доску. Трением доски по опоре и трением в шарнире пренебречь.
Обоснуйте применимость законов, используемых для решения задачи.
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Решение:
1. В инерциальной системе отсчёта связанной с Землёй, доска движется поступательно с постоянной скоростью. Поэтому сумма проекций на ось всех сил, приложенных к доске, равна нулю:
F=Fтр
2. Показаны все силы, приложенные к стержню. Силы реакции шарнира и доски представлены горизонтальными и вертикальными составляющими: и соответственно.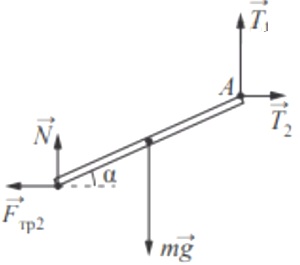
По третьему закону Ньютона получается что силы трения у доски у бруска и сила которая тянет доску одинаковы.
F=Fтр1=Fтр2
3. По условию задачи стержень покоится, поэтому сумма моментов сил относительно оси шарнира равна нулю. Обозначив длину стержня L через запишем это условие:
`mg * L/2 cos∝ - F_(тр2) * L sin∝ - N*L*cos∝ = 0`
4. Доска движется относительно стержня, поэтому сила трения является силой трения скольжения:
`F_(тр2) = μ*N`, тогда подставляя в уравнение выше получаем:
`mg * L/2 cos∝ - μ*N * L * sin∝ - N*L*cos∝ = 0`
Теперь выражаем N:
`N = (mg)/(2(1+μtg∝))`
Отсюда: F = Fтр1=Fтр2=μ*N.
В итоге сила нам известна, известен коэффициент трения, вместо N подставляем выражение с массой, которую необходимо найти.
`F = (μmg)/(2(1+μtg∝))`
`2 = (0,2*m*10)/(2(1+0,2 *tg30))`
`2 = (2*m)/(2+0,4 *tg30)`
`2m = 2(2+0,4 *tg30)`
`m = 2+0,4 *tg30`
`m = 2+0,4 *1/sqrt(3)`
m ≈ 2+1,33≈3,33
Ответ:3,3 кг
Номер: D59EAC
Дайте развернутый ответ.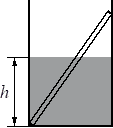
В гладкий высокий стакан радиусом 4 см поставили тонкую однородную палочку длиной 10 см и массой 1,8 г. До какой высоты h надо налить в стакан жидкость, плотность которой составляет 0,75 плотности материала палочки, чтобы модуль силы, с которой верхний конец палочки давит на стенку стакана, равнялся 0,008 Н? Сделайте рисунок с указанием сил, действующих на палочку.
Обоснуйте применимость законов, используемых для решения задачи.
КЭС: 1.3.6 Закон Архимеда. Условия плавания тел
Решение:
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Описываем спицу моделью твердого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Движение твердого тела можно описать совокупностью движений - поступательного и вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного движения).
5. Так как поверхность гладкая, то трение отсутствует и на доску действует сила реакции опоры со стороны дна сосуда направленная перпендикулярно поверхности, также действует сила реакции опоры, направленная со со стороны левой стенки вправо.
1. Высота конца палочки относительно дна стакана
`H = sqrt(l^2-4R^2) = sqrt(0,1^2 - 4*0,04^2) = 0,06`м,
где l — длина палочки, R — радиус стакана.
2. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на h/H- от своего объема, то есть
`Fa = ρ_ж (h/H * V) g = ρ_ж/ρ*h/H*mg`,
где
V — объём палочки,
ρ — её плотность,
ρж— плотность жидкости.
3. Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через точку приложения сил F2 и F1.
Итак, поскольку палочка покоится, сумма приложенных к ней сил равна нулю. Поэтому можно записать правило моментов так, чтобы исключить из него упоминание неизвестных сил F1 и F2, т. е. записать это правило относительно точки откуда исходят эти силы:
`mgR-F_a(h/2*ctg∝) - NH =0`,
где `ctg∝ = (2R)/H`. Отсюда можно выразить h:
`mgR-NH = F_a(h/2*ctg∝)`
`N = mg*R/H-F_a(h/(2H)*ctg∝) =mg*R/H(1-ρ_ж/ρ(h/H)^2)`
`(NH)/(mgR)=1-ρ_ж/ρ(h/H)^2`
`ρ_ж/ρ(h/H)^2 = 1-(NH)/(mgR)`
`0,75(h/H)^2 = 1-(0,008*0,06)/(0,0018*10*0,04)`
`0,75(h/H)^2 = 1-(0,00048)/(0,001)`
`0,75(h/H)^2 = 1-0,48`
`(h/H)^2 = (0,52)/(0,75)`
`(h/H)^2 = 0,7`
`h^2 ≈ 0,7*H^2`
`h^2 ≈ 0,7*(0,06)^2`
h≈ 0,05 м ≈ 5 см
Ответ: 5 см
Номер: 7018C7
Дайте развернутый ответ.
В гладкий высокий стакан радиусом 4 см поставили однородную тонкую палочку длиной 10 см и массой 0,9 г, после чего в стакан налили до высоты h=4 см жидкость, плотность которой составляет 0,75 плотности материала палочки. Найдите силу F, с которой верхний конец палочки давит на стенку стакана. Сделайте рисунок с указанием сил, действующих на палочку.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Описываем спицу моделью твердого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Движение твердого тела можно описать совокупностью движений - поступательного и вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного движения).
5. Так как поверхность гладкая, то трение отсутствует и на доску действует сила реакции опоры со стороны дна сосуда направленная перпендикулярно поверхности, также действует сила реакции опоры, направленная со со стороны левой стенки вправо.

1. Высота конца палочки относительно дна стакана
`H = sqrt(l^2-4R^2) = sqrt(0,1^2 - 4*0,04^2) = 0,06`м,
где l — длина палочки, R — радиус стакана.
2. Сила Архимеда
`Fa = ρ_ж (h/H * V) g = ρ_ж/ρ*h/H*mg`,
где
V — объём палочки,
ρ — её плотность,
ρж— плотность жидкости.
3. Поскольку палочка покоится, сумма приложенных к ней сил равна нулю. Поэтому можно записать правило моментов так, чтобы исключить из него упоминание неизвестных сил F1 и F2, т. е. записать это правило относительно оси, проходящей перпендикулярно рисунку через нижний конец палочки:
`mgR-F_a(h/2*ctg∝) - NH =0`,
где `ctg∝ = (2R)/H`. Отсюда получаем:
`N = mg*R/H-F_a(h/(2H)*ctg∝) =mg*R/H(1-ρ_ж/ρ(h/H)^2)`
`N = 9*10^-4*10*(0,04)/(0,06)(1-0,75*(0,04^2)/(0,06^2)) =4*10^-3`
По третьему закону Ньютона, N = F, поэтому, `F=4*10^-3`Н.
Ответ:`4*10^-3`Н
Номер: 7823C1
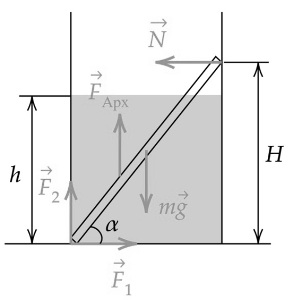
Дайте развернутый ответ.
Железный шар массой 2,5 кг подвешен на нити и полностью погружён в воду (см. рисунок). Нить образует с вертикалью угол α = 30о. Определите силу, с которой шар действует на нить. Трением шара о стенку пренебречь. Сделайте схематический рисунок с указанием сил, действующих на шар.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
25
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Описываем тело моделью твердого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Движение твердого тела можно описать совокупностью движений - поступательного и вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для поступательного движения, другое - для вращательного движения.
4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Также применимо правило моментов (условие равновесия твёрдого тела относительно вращательного движения).
5. Шар целиком погружён в жидкость и отсутствует трение между шаром и стенкой сосуда. Значит, все вешние силы, действующие на шар, кроме силы натяжения нити, действуют по прямым, проходящим через центр шара. Значит, сумма моментов этих сил относительно оси, проходящей через центр шара, равна нулю. При равновесии шара в ИСО сумма моментов всех внешних сил равна нулю. следовательно, и момент силы натяжения нити, относительно оси, проходящей через центр шара, тоже равен нулю, поэтому сила натяжения нити действует по прямой, проходящей через центр шара.
Решение
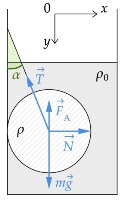
Второй закон Ньютона в этом случае
`F_A +mg+T = ma`, где
Fа – сила Архимеда, T – сила натяжения нити, a – ускорение тела.
Так как тело покоится, то его ускорение равно 0.
Запишем второй закон Ньютона на ось y
`F_А − mg +T*cosα = 0` (1)
С учетом того, что сила Архимеда равна
`F_А = ρ_0gV = ρ_0g*m/ρ` (2)
ρ0 – плотность жидкости, V – объем погруженной части тела, ρ – плотность стали (7800 кг/m3).
Выразим из (1) силу натяжения нити T, с учетом (2)
`T = (mg-(ρ_0g*m/ρ))/cosα = (mg(ρ-ρ_0))/(ρ cosα) = (2,5*10 (7800-1000))/(7800 sqrt(3)/2) ≈170000/6755 ≈ 25` Н
Ответ: 25 H
Номер: 6AB9E6
Дайте развернутый ответ.
Невесомый стержень АВ с двумя малыми грузиками массами m1 = 200 г и m2 = 100 г, расположенными в точках C и B соответственно, шарнирно закреплён в точке А. Груз массой M = 100 г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии: если стержень отклонён от вертикали на угол α = 30°, а нить составляет угол с вертикалью, равный β = 30°. Расстояние АС = b = 25 см. Определите длину l стержня АВ. Сделайте рисунок с указанием сил, действующих на груз M и стержень.
КЭС: 1.3.1 Момент силы относительно оси вращения
1.3.2 Центр масс тела. Центр масс системы материальных точек
1.3.3 Условия равновесия твёрдого тела в ИСО
1.3.4 Закон Паскаля
1.3.5 Давление в жидкости, покоящейся в ИСО
1.3.6 Закон Архимеда. Условия плавания тел
Решение:
68,3
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Любое движение твёрдого тела является суперпозицией поступательного и вращательного движений. Поэтому условий равновесия твёрдого тела в ИСО ровно два; одно для поступательного движения, другое — для вращательного движения.
4. В качестве оси, относительно которой будем считать сумму моментов сил, действующих на стержень, выберем ось, проходящую перпендикулярно плоскости рисунка через точку шарнирного крепления (точку А).
5. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.
Решение.
1. Введём декартову систему координат хОу, как показано на рисунке. Поскольку груз М находится в равновесии, согласно второму закону Ньютона
t1-Mg=0. (1)
2. На стержень с грузами m1 и m2 действуют силы m1g b m2g, а также сила натяжения нити T2. Поскольку нить невесома, а блок идеален, то
|T1|=|T2|=|T3|
Кроме того, на стержень действует сила F со стороны шарнира. Запишем условие равенства нулю суммы моментов этих сил относительно оси вращения, проходящей через точку A — точку шарнирного закрепления стержня:
`m_1g*b*sinα + m_2g*l*sinα-T*AD=0`(2)
3. Решая систему уравнений (1) и (2), с учётом
AD = l sin φ = l (α+β)
получим:
`l = (m_1*b*sinα)/(M sin (α+β)-m_2*sinα)`
`l = (200*25*1/2)/(100*sqrt(3)/2-100*1/2) ≈ 68,3`см
Ответ: 68,3 см
Номер: BBC367
Дайте развернутый ответ.
Цилиндр массой m = 1 кг и радиусом R = 20 см, на который намотана нерастяжимая невесомая нить, положили на наклонную плоскость, а конец нити прикрепили к вертикальной стенке. Нить не скользит
по цилиндру, параллельна наклонной плоскости и перпендикулярна оси цилиндра (см. рисунок). Коэффициент трения между цилиндром и плоскостью μ = 0,5. При каком максимальном угле наклона плоскости к горизонту α цилиндр будет находиться в равновесии? Сделайте схематический рисунок с указанием сил, действующих на цилиндр.
Обоснуйте применимость законов, используемых для решения задачи.
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Решение:
45

Обоснование. 1. Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать эту систему отсчета инерциальной (ИСО).
2. Описываем цилиндр моделью твердого тела (форма и размеры тела неизменны, расстояние между двумя точками тела остается неизменным ).
3. Любое движение твердого тела является суперпозицией поступательного и вращательного движений. Поэтому условий равновесия твердого тела в ИСО ровно два: одно −для поступательного движения, другое − для вращательного движения.
4. В качестве оси, относительно которой будем считать сумму моментов сил, действующих на цилиндр, выберем ось, проходящую перпендикулярно плоскости рисунка через точку касания цилиндра плоскости А.
5. Нить невесома, поэтому модуль силы натяжения нити в любой ее точке один и тот же.
6. Между цилиндром и поверхностью наклонной плоскости действует сила трения, которая в предельном случае равна
Fтр = μN
Перейдем к решению. Изобразим все силы, действующие на цилиндр: сила тяжести mg, сила реакции опоры N, сила трения Fтр, сила натяжения нити Т.
Запишем правило моментов относительно точки А:
mg*sin∝*R-T*2R=0
Тогда получаем, что T = (mg*sin∝)/2
Применим второй закон Ньютона, учитывая, что ускорение равно 0:
N+T+mg+Fтр=0
Найдем проекцию на оси:
ox: T+Fтр-mg*sin∝ = 0
oy: N - mg*cos∝ = 0
Учитывая, что в предельном случае сила трения равна Fтр=N получаем:
2μ*cos∝ = sin∝
Объединяя уравнения, получаем:
`∝ =arctg2μ=arctg(2*0,5) = 45º`
Откуда находим предельный угол наклона плоскости
Данный угол действительно будет максимальным, поскольку при увеличении угла наклона сила трения уменьшится, горизонтальная составляющая силы тяжести увеличится, сила натяжения нити увеличится, в результате чего равновесие нарушится.
Ответ: 45°.
Номер: CFC86C
Дайте развернутый ответ.
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень массой M = 2 кг и длиной L = 40 см. Если к этому стержню подвесить груз на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, а растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 3 раза меньше, чем у правой. Чему равна масса m подвешенного груза? Сделайте рисунок с указанием сил, использованных в решении задачи.
КЭС: 1.3 Статика
Решение:
4
1. По закону Гука модуль силы упругости равен F =kΔl. Так как растяжения пружин одинаковы, то
`F2/F1=k2/k1=3`, где F1, F2 – модули сил упругости левой и правой пружин соответственно.
2. Условия равновесия стержня с грузом имеют вид
F1+F2=Mg+mg
По закону сохранения моментов сил относительно точки равновесия O, имеем:
`F_1*L/2+mg*(L/2-d) = F_2*L/2`
3. Объединяя пункты 1 и 2, получаем систему уравнений:
`{(4F_1=Mg+mg),(mg*(L/2-d) = F_1*L):}`
4. Из системы уравнений пункта 3 получаем
`m = (ML)/(L-4d) = (2*0,4)/(0,4-0,2)=4`кг
Ответ: 4 кг
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Любое движение твёрдого тела является суперпозицией поступательного и вращательного движений. Поэтому условий равновесия твёрдого тела в ИСО ровно два; одно для поступательного движения, другое — для вращательного движения.
4. Сумма приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого тела относительно поступательного движения). Поэтому сумма моментов этих сил относительно любых двух параллельных осей одна и та же. Для удобства выберем ось, проходящую перпендикулярно плоскости рисунка через центр масс стержня (точку О).
Номер: DEAB32
Дайте развернутый ответ.
Невесомый стержень АВ с двумя малыми грузиками массами m1 = 100 г и m2 = 200 г, расположенными в точках C и B соответственно, шарнирно закреплён в точке А. Груз массой M = 200 г подвешен к идеальному блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол a = 45°, а нить составляет угол с вертикалью, равный b = 15°. Расстояние АС = b = 25 см. Определите длину l стержня АВ, пренебрегая трением в шарнире. Сделайте рисунок с указанием сил, действующих на груз M и стержень.
Обоснуйте применимость законов, используемых для решения задачи.
КЭС: 1.3.3 Условия равновесия твёрдого тела в ИСО
Решение:
57
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
3. Любое движение твёрдого тела является суперпозицией поступательного и вращательного движений. Поэтому условий равновесия твёрдого тела в ИСО ровно два; одно для поступательного движения, другое — для вращательного движения.
4. В качестве оси, относительно которой будем считать сумму моментов сил, действующих на стержень, выберем ось, проходящую перпендикулярно плоскости рисунка через точку шарнирного крепления (точку А).
5. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.

Решение.
1. Введём декартову систему координат хОу, как показано на рисунке. Поскольку груз М находится в равновесии, согласно второму закону Ньютона
t1-Mg=0. (1)
2. На стержень с грузами m1 и m2 действуют силы m1g b m2g, а также сила натяжения нити T2. Поскольку нить невесома, а блок идеален, то
|T1|=|T2|=|T3|
Кроме того, на стержень действует сила F со стороны шарнира. Запишем условие равенства нулю суммы моментов этих сил относительно оси вращения, проходящей через точку A — точку шарнирного закрепления стержня:
`m_1g*b*sinα + m_2g*l*sinα-T*AD=0`(2)
3. Решая систему уравнений (1) и (2), с учётом
AD = l sin φ = l (α+β)
получим:
`l = (m_1*b*sinα)/(M sin (α+β)-m_2*sinα)`
`l = (100*25*sin45)/(200*sin (45+15)-200*sin45)=(100*10*25*1/sqrt(2))/(200*sqrt(3)/2-200*sqrt(2)/2) =1768/(173-141) ≈ 57`см
Ответ: 57 см
Номер: 27EF85

