Задания 6-й линейки ЕГЭ по информатике из разных источников, в том числе с реальных ЕГЭ
Шаблон на Python:
from turtle import * # Импортируем модуль turtle для визуализации пути Черепахи
tracer(0) # Отключаем анимацию для мгновенного отображения
screensize(2000, 2000) # Устанавливаем размер холста
k = 12 # Масштабный коэффициент для увеличения видимости
# Размечаем сетку целочисленных координат
up() # Поднимаем хвост, чтобы не рисовать при перемещении
for x in range(-15, 6): # Проходим по всем целым x от -15 до 5 (цифры подбором)
for y in range(-5, 26): # Проходим по всем целым y от -5 до 25
goto(x * k, y * k) # Перемещаемся к координатам (x*k, y*k)
dot(4, 'blue') if x * y % 5 == 0 else dot(2, 'grey') # Синие точки для координат, где x*y делится на 5, серые для остальных. Можно просто оставить черные точки с размером dot(4)
# Начинаем рисовать основную фигуру
goto(0, 0) # Возвращаемся в начало координат
lt(90) # Поворачиваем налево на 90°, потому что в питоне черепаха изначально головой вдоль оси х (голова теперь вдоль оси Y)
down() # Опускаем хвост, черепаха готова к рисованию
# Задаем алгоритм из задания
for _ in range(2): # цикл
fd(14 * k) # вперед
lt(270) # влево
bk(12 * k) # назад
rt(90) # вправо
up() # хвост вверх
down() # хвост вниз
update() # Обновляем холст после отрисовки
done() # Завершаем работу, оставляя окно открытымЗадания №6 ЕГЭ по информатике
ЕГЭ 2026. Демо
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 14 Налево 270 Назад 12 Направо 90]
Поднять хвост
Вперёд 9 Направо 90 Назад 7 Налево 90
Опустить хвост
Повтори 2 [Вперёд 13 Направо 90 Вперёд 6 Направо 90]
Определите, сколько точек с целочисленными координатами находятся внутри области, ограниченной линией, заданной алгоритмом, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
k = 12
up()
for x in range(-15, 6):
for y in range(-5, 26):
goto(x * k, y * k)
dot(4, 'blue') if x * y % 5 == 0 else dot(2, 'grey')
goto(0, 0)
lt(90)
down()
for _ in range(2):
fd(14 * k)
lt(270)
bk(12 * k)
rt(90)
up()
fd(9 * k)
rt(90)
bk(7 * k)
lt(90)
down()
for _ in range(2):
fd(13 * k)
rt(90)
fd(6 * k)
rt(90)
update()
done()
Программа нарисует картинку
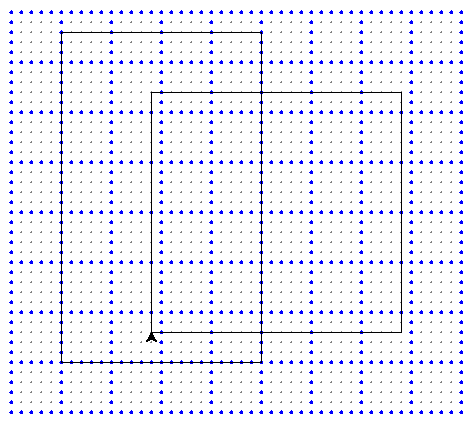
Из неё легко определяем количество точеr внутри объединения прямоугольников, включая точки на линиях $$15 \cdot 13 + 8 \cdot 7 = 251$$
Ответ: 251
ЕГЭ 2026. Статград. 23.10.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 15 Направо 90 Вперёд 23 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 7 [Вперёд 252 Направо 90 Вперёд 398 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая точки на линиях.
Решение:
Нарисуем область пересечения фигур:
Python
from turtle import *
tracer(0)
screensize(1000, 1300)
up()
lt(90)
k = 7
for x in range(-25, 31):
for y in range(-25, 21):
goto(x * k, y * k)
dot(3, 'red') if x * y % 5 == 0 else dot(2, 'green')
goto(0, 0)
down()
pensize(3)
for _ in range(7):
fd(15 * k)
rt(90)
fd(23 * k)
rt(90)
up()
fd(3 * k)
rt(90)
fd(5 * k)
lt(90)
down()
for _ in range(7):
fd(252 * k)
rt(90)
fd(398 * k)
rt(90)
ht()
update()
done()
Видим, что пересечением является прямоугольник со сторонами \(18\) и \(12.\) По формуле Эйлера теперь легко можно найти количество точек, лежащих внутри объединения фигур, включая точки на границах: $$16 \cdot 24 + 253 \cdot 399 - 19 \cdot 13 = 101084$$
Ответ: 101084
Основная волна. Пересдача. 03.07.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 40 Направо 90 Вперёд 46 Направо 90]
Поднять хвост
Вперёд 19 Направо 90 Вперёд 19 Налево 90
Опустить хвост
Повтори 5 [Вперёд 37 Направо 90 Вперёд 19 Направо 90]
Определите, сколько точек с целочисленными координатами находятся внутри объединения фигур, ограниченного заданными алгоритмом линиями, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
k = 10
up()
for x in range(-20, 46):
for y in range(-50, 6):
goto(x * k, y * k)
dot(4, 'blue') if x * y % 5 == 0 else dot(3, 'grey')
goto(0, 0)
down()
pensize(2)
for _ in range(5):
fd(40 * k)
rt(90)
fd(46 * k)
rt(90)
up()
fd(19 * k)
rt(90)
fd(19 * k)
lt(90)
down()
for _ in range(5):
fd(37 * k)
rt(90)
fd(19 * k)
rt(90)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
$$N = 41 \cdot 47 + 16 \cdot 20 = 2247$$
Ответ: 2247
Основная волна. Резерв. 23.06.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 37 Направо 90 Вперёд 44 Направо 90]
Поднять хвост
Назад 18 Направо 90 Вперёд 29 Налево 90
Опустить хвост
Повтори 5 [Вперёд 31 Направо 90 Вперёд 35 Направо 90]
Определите, сколько точек с целочисленными координатами находятся внутри пересечения фигур, ограниченного заданными алгоритмом линиями, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
k = 10
up()
for x in range(-5, 61):
for y in range(-50, 26):
goto(x * k, y * k)
dot(4, 'blue') if x * y % 5 == 0 else dot(3, 'grey')
goto(0, 0)
down()
pensize(2)
for _ in range(5):
fd(37 * k)
rt(90)
fd(44 * k)
rt(90)
up()
bk(18 * k)
rt(90)
fd(29 * k)
lt(90)
down()
for _ in range(5):
fd(31 * k)
rt(90)
fd(35 * k)
rt(90)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
$$N = 14 \cdot 16 = 224$$
Ответ: 224
Основная волна. Резерв. 19.06.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 3 [Вперёд 39 Направо 90 Вперёд 48 Направо 90]
Поднять хвост
Вперёд 27 Направо 90 Вперёд 24 Налево 90
Опустить хвост
Повтори 3 [Вперёд 29 Направо 90 Вперёд 18 Направо 90]
Определите площадь объединения фигур, ограниченного заданными алгоритмом линиями.
Решение:
Python
from turtle import *
tracer(0)
screensize(3000, 3000)
k = 8
up()
lt(90)
for x in range(-5, 51):
for y in range(-25, 41):
goto(x * k, y * k)
dot(3, 'blue') if x * y % 5 == 0 else dot(2, 'grey')
goto(0, 0)
down()
pensize(2)
for _ in range(3):
fd(39 * k)
rt(90)
fd(48 * k)
rt(90)
up()
fd(27 * k)
rt(90)
fd(24 * k)
lt(90)
down()
for _ in range(3):
fd(29 * k)
rt(90)
fd(18 * k)
rt(90)
update()
done()
Рисунок, который получается после выполнения программы:
$$S = 39 \cdot 48 + 29 \cdot 18 - 18 \cdot 12 = 2178$$
Ответ: 2178
Основная волна. 11.06.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 20 Налево 270 Вперёд 12 Направо 90]
Поднять хвост
Вперёд 9 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 2 [Вперёд 13 Направо 90 Вперёд 6 Направо 90]
Определите, сколько точек с целочисленными координатами находятся внутри области, ограниченной линией, заданной алгоритмом, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(3000, 3000)
k = 10
up()
lt(90)
for x in range(-5, 21):
for y in range(-5, 26):
goto(x * k, y * k)
dot(3, 'blue') if x * y % 5 == 0 else dot(2, 'grey')
goto(0, 0)
down()
pensize(2)
for _ in range(2):
fd(20 * k)
lt(270)
fd(12 * k)
rt(90)
up()
fd(9 * k)
rt(90)
fd(7 * k)
lt(90)
down()
for _ in range(2):
fd(13 * k)
rt(90)
fd(6 * k)
rt(90)
update()
done()
Рисунок, который получается после выполнения программы:
Количество точек внутри области объединения равно $$13 \cdot 21 + 7 \cdot 14 - 6 \cdot 12 = 299$$
Ответ: 299
Основная волна. 10.06.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 24 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Вперёд 7 Направо 90 Вперёд 7 Направо 90
Опустить хвост
Повтори 2 [Вперёд 30 Направо 90 Вперёд 27 Направо 90]
Определите, сколько точек с целочисленными координатами находятся внутри области, ограниченной линией, заданной алгоритмом, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
k = 10
lt(90)
up()
for x in range(-5, 41):
for y in range(-40, 6):
goto(x * k, y * k)
dot(4, 'blue') if x * y % 5 == 0 else dot(3, 'grey')
goto(0, 0)
down()
rt(90)
for _ in range(2):
fd(24 * k)
rt(90)
fd(20 * k)
rt(90)
up()
fd(7 * k)
rt(90)
fd(7 * k)
lt(90)
down()
for _ in range(2):
fd(30 * k)
rt(90)
fd(27 * k)
rt(90)
update()
done()
Рисунок, который получается после выполнения программы:
Количество точек внутри области объединения равно $$25 \cdot 21 + 31 \cdot 28 - 18 \cdot 14 = 1141$$
Ответ: 1141
Апробация. 14.05.2025-1
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Направо 90 Повтори 7 [Вперёд 11 Направо 45 Вперёд 8 Направо 135]
Определите, сколько точек с целочисленными координатами находятся внутри области, ограниченной линией, заданной алгоритмом. Точки на линии учитывать не следует.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
k = 25
lt(90)
up()
for x in range(-5, 21):
for y in range(-10, 6):
goto(x * k, y * k)
dot(4, 'blue') if x * y % 5 == 0 else dot(3, 'grey')
goto(0, 0)
down()
rt(90)
for _ in range(7):
fd(11 * k)
rt(45)
fd(8 * k)
rt(135)
update()
done()
Рисунок, который получается после выполнения программы:
Количество точек внутри параллелограмма равно \(5 \cdot 10 = 50.\)
Ответ: 50
ЕГКР. 19.04.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 28 Направо 90 Вперёд 18 Направо 90]
Поднять хвост
Вперёд 14 Направо 90 Вперёд 10 Налево 90
Опустить хвост
Повтори 2 [Вперёд 30 Направо 90 Вперёд 7 Направо 90]
Определите, сколько точек с целочисленными координатами находится внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая точки на линиях.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
up()
k = 8
for x in range(-5, 21):
for y in range(-5, 46):
goto(x * k, y * k)
dot(3, 'blue') if x * y % 5 == 0 else dot(2, 'gray')
goto(0, 0)
down()
lt(90)
pensize(2)
for _ in range(2):
fd(28 * k)
rt(90)
fd(18 * k)
rt(90)
up()
fd(14 * k)
rt(90)
fd(10)
lt(90)
down()
for _ in range(2):
fd(30 * k)
rt(90)
fd(7 * k)
rt(90)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
Количество точек внутри объединения фигур, равно \(19 \cdot 29 + 16 \cdot 8 = 679.\)
Ответ: 679
Досрочный экзамен. 08.04.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд \(n\) (где \(n\) — целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Направо \(m\) (где \(m\) — целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке. Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Направо 30 Повтори 3 [Направо 150 Вперёд 6 Направо 30 Вперёд 12]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, которая ограничена линией, заданной алгоритмом. Точки на линии учитывать не следует.
Решение:
Python
from turtle import *
tracer(0)
screensize(2000, 2000)
lt(90)
k = 20
up()
for x in range(-10, 6):
for y in range(-20, 6):
goto(x * k, y * k)
dot(3, 'red') if x * y % 5 == 0 else dot(2, 'green')
goto(0, 0)
down()
rt(30)
for _ in range(3):
rt(150)
fd(6 * k)
rt(30)
fd(12 * k)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
Черепаха нарисовала параллелограмм, две стороны которого параллельны оси ординат, две другие наклонены к оси абсцисс под углом \(60^\circ\) и проходящие через начало координат \((0, \, 0)\) и точку \((0, \, -6)\). Уравнение этих прямых \(y = \sqrt{3} x\) и \(y = \sqrt{3} x - 6.\) Понятно, что кроме указанных точек, никакие другие с целочисленными координатами не будут лежать на этих прямых. Из рисунка видно, что внутри параллелограмма находятся \(5\) столбцов с точками по \(6\) в каждом. Всего \(5 \cdot 6 = 30\) точек. Можно проверить это программно:
print(sum(-6 < x < 0 and 3 ** 0.5 * x - 6 < y < 3 ** 0.5 * x for x in range(-10, 10) for y in range(-17, 0)))Ответ: 30
Апробация. 05.03.2025-2
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 3 [Вперёд 27 Направо 90 Вперёд 12 Направо 90]
Поднять хвост
Вперёд 4 Направо 90 Вперёд 6 Налево 90
Опустить хвост
Повтори 3 [Вперёд 83 Направо 90 Вперёд 77 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого объединения.
Решение:
Python
from turtle import *
tracer(0)
screensize(1000, 1300)
up()
lt(90)
k = 7
for x in range(-75, 16):
for y in range(-65, 31):
goto(x * k, y * k)
dot(3, 'red') if x * y % 5 == 0 else dot(2, 'green')
goto(0, 0)
down()
pensize(3)
for _ in range(3):
fd(27 * k)
rt(90)
fd(12 * k)
rt(90)
up()
fd(4 * k)
rt(90)
fd(6 * k)
lt(90)
down()
for _ in range(3):
fd(83 * k)
rt(90)
fd(77 * k)
rt(90)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
Количество точек с целочисленными координатами, находящиеся внутри объединения фигур, включая точки на границах этого объединения \(N = 78 \cdot 84 + 13 \cdot 28 - 7 \cdot 24 = 6748.\)
Ответ: 6748
Апробация. 05.03.2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 10 Направо 90 Вперёд 16 Направо 90]
Поднять хвост
Вперёд 4 Направо 90 Вперёд 6 Налево 90
Опустить хвост
Повтори 4 [Вперёд 73 Направо 90 Вперёд 67 Направо 90]
Определите площадь пересечения фигур, нарисованных при помощи алгоритма.
Решение:
Python
from turtle import *
tracer(0)
screensize(1000, 1300)
up()
lt(90)
k = 7
for x in range(-5, 81):
for y in range(-5, 86):
goto(x * k, y * k)
dot(3, 'red') if x * y % 5 == 0 else dot(2, 'green')
goto(0, 0)
down()
pensize(3)
for _ in range(4):
fd(10 * k)
rt(90)
fd(16 * k)
rt(90)
up()
fd(4 * k)
rt(90)
fd(6 * k)
lt(90)
down()
for _ in range(4):
fd(73 * k)
rt(90)
fd(67 * k)
rt(90)
ht()
update()
done()
Рисунок, который получается после выполнения программы:
Площадь пересечения фигур \(S = 10 \cdot 6 = 10.\)
Ответ: 60
Шастин. 7.6.2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 3 [Вперёд 10 Направо 90 Вперёд 15 Направо 90]
Поднять хвост
Вперёд 4 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 2 [Вперёд 80 Направо 90 Вперёд 60 Направо 90]
Определите периметр области объединения фигур, заданных алгоритмом линиями. В ответе укажите только число.
Решение:
...
Ответ: -
Шастин. 5.6.2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 31 Направо 90 Вперёд 16 Направо 90]
Повтори 2 [Вперёд 7 Направо 90 Вперёд 40 Направо 90]
Поднять хвост
Вперёд 13 Направо 90 Вперёд 6 Налево 90
Опустить хвост
Повтори 2 [Вперёд 100 Направо 90 Вперёд 50 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор из трёх пересекающихся прямоугольников. Определите наибольшую из площадей пересечения любых двух прямоугольников. В ответе запишите только число — наибольшую площадь в условных единицах.
Решение:
...
Ответ: -
Шастин. 3.6.2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 50 Налево 90]
Поднять хвост
Вперёд 50 Налево 135
Опустить хвост
Повтори 2 [Вперёд 102 Налево 120 Вперёд 182 Налево 60]
Определите площадь области пересечения фигур, ограниченных заданными алгоритмом линиями. В ответе укажите только число.
Решение:
...
Ответ: -
Шастин. 1.6.2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Направо 30 Повтори 11 [Вперёд 11 Направо 120 Вперёд 11 Направо 60]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, которая ограничена линией, заданной алгоритмом, включая точки на линиях.
Решение:
...
Ответ: -
Статград. Профиль. 12.05.2025-1
Исполнитель Чертёжник передвигается по плоскости и оставляет след в виде линии. Чертёжник может выполнять две команды: Точка \((x, y)\) \((x\) и \(y\) – числа) и Вектор \((a, b)\) \((a\) и \(b\) – числа). По команде Точка \((x, y)\) Чертёжник перемещается в точку с координатами \((x, y).\) По команде Вектор \((a, b)\) Чертёжник смещается на вектор \((a, b),\) то есть переходит из точки с координатами \((x, y)\) в точку с координатами \((x + a, y + b).\) В начальный момент Чертёжник находится в начале координат.
Чертёжник выполнил следующую программу:
Вектор \((4, 1)\) Вектор \((1, 4)\) Вектор \((-4, -1)\) Точка \((0, 0)\)
Определите площадь фигуры, полученной при этом построении.
Решение:
...
Ответ: -
Статград. База. 12.05.2025-1
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 2 команды: Вперёд \(n\) (где \(n\) — целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Направо \(m\) (где \(m\) — целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке. Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 13 [Вперёд 17 Налево 90 Вперёд 15 Налево 90]
Поднять хвост
Вперёд 10 Налево 90 Вперёд 10 Направо 90
Опустить хвост
Повтори 40 [Вперёд 100 Направо 90 Вперёд 200 Направо 90]
Определите периметр области объединения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Демо-2025
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 22 Направо 90 Вперёд 6 Направо 90]
Поднять хвост
Вперёд 1 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 9 [Вперёд 53 Направо 90 Вперёд 75 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Шастин. 7.05.2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Вперёд 30 Налево 60 Вперёд 24 Направо 240
Вперёд 54 Налево 120 Вперёд 24 Налево 60
Поднять хвост
Вперёд 30 Направо 90 Вперёд 20 Налево 90
Опустить хвост
Повтори 17 [Вперёд 6 Налево 90 Вперёд 80 Налево 90]
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями. В ответе запишите целую часть получившегося числа.
Решение:
...
Ответ: -
Статград. 01.04.2025-1
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 2 команды: Вперёд \(n\) (где \(n\) — целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Направо \(m\) (где \(m\) — целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке. Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Направо 270
Повтори 2 [Вперёд 8 Направо 120]
Направо 120
Повтори 2 [Направо 120 Вперёд 3 Направо 240]
Направо 240
Повтори 2 [Вперёд 14 Направо 120]
Определите площадь фигуры, нарисованной при помощи алгоритма. В ответе укажите целую часть полученного числа.
Решение:
...
Ответ: -
Шастин. 13.03.2025
(Л. Шастин) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Вправо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Влево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 36 Вправо 90 Вперёд 41 Вправо 90]
Поднять хвост
Вправо 90 Вперёд 20 Влево 90 Вперёд 20
Опустить хвост
Повтори 4 [Вперёд 25 Вправо 90]
Поднять хвост
Вперёд 7 Влево 90 Вперёд 7 Вправо 90
Опустить хвост
Повтори 7 [Вперёд 16 Вправо 90]
Определите, сколько точек с целочисленными координатами будут находиться на пересечении всех нарисованных фигур, включая точки на линиях.
Решение:
...
Ответ: -
ЕГКР. 21.12.2024
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 8 [Вперёд 16 Направо 90 Вперёд 22 Направо 90]
Поднять хвост
Вперёд 5 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 8 [Вперёд 52 Направо 90 Вперёд 77 Направо 90]
Определите площадь области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Статград. 04.03.2025
Исполнитель Чертёжник передвигается по плоскости и оставляет след в виде линии. Чертёжник может выполнять две команды: Точка \((x,~y)\) (\(x\) и \(y\) – числа) и Вектор \((a,~b)\) (\(a\) и \(b\) – числа). По команде Точка \((x,~y)\) Чертёжник перемещается в точку с координатами (\(x\), \(y\)). По команде Вектор \((a,~b)\) Чертёжник смещается на вектор \((a,~b),\) то есть переходит из точки с координатами \((x,~y)\) в точку с координатами \((x + a, y + b).\) В начальный момент Чертёжник находится в начале координат.
Чертёжник выполнил следующую программу:
Вектор \((3, 1)\) Вектор \((–2, 6)\) Точка \((0, 0)\)
Определите площадь фигуры, полученной при этом построении. В ответе запишите целую часть числа, полученного при умножении найденной площади на \(100.\)
Решение:
...
Ответ: -
Статград. 28.01.2025-1
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять две команды: Вперёд \(n\) (\(n\) – число) и Направо \(m\) (\(m\) – число). По команде Вперёд \(n\) Черепаха перемещается вперёд на \(n\) условных единиц. По команде Направо \(m\) Черепаха поворачивается на месте на \(m\) градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения.
Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что заданная последовательность из \(S\) команд повторится \(k\) раз.
Черепаха выполнила следующую программу:
Повтори 3 [Вперёд 19 Направо 90 Вперёд 3 Направо 90]
Повтори 3 [Вперёд 5 Направо 90 Вперёд 11 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор непересекающихся прямоугольников. Определите наибольшее количество точек с целочисленными координатами, находящихся внутри одного из этих прямоугольников. Точки, находящиеся на линиях, не учитывать.
Решение:
...
Ответ: -
Статград. 17.12.2024-1
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять две команды: Вперёд \(n\) (\(n\) – число) и Направо \(m\) (\(m\) – число). По команде Вперёд \(n\) Черепаха перемещается вперёд на \(n\) условных единиц. По команде Направо \(m\) Черепаха поворачивается на месте на \(m\) градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения.
Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что заданная последовательность из \(S\) команд повторится \(k\) раз.
В начальный момент на поле находятся две Черепахи. Первая Черепаха находится в начале координат и направлена вверх (вдоль положительного направления оси ординат). Вторая Черепаха находится в неизвестной точке поля и направлена вправо (вдоль положительного направления оси абсцисс). Каждая Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 15 Направо 90 Вперёд 8 Направо 90]
Определите максимально возможное количество точек с целочисленными координатами, которые могут оказаться внутри пересечения фигур, нарисованных двумя Черепахами. Точки, находящиеся на линиях, не учитывать.
Решение:
...
Ответ: -
Статград. 24.10.2024-2
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять три команды: Вперёд \(n\) (\(n\) – число), Направо \(m\) (\(m\) – число) и Налево \(m\) (\(m\) – число). По команде Вперёд \(n\) Черепаха перемещается вперёд на \(n\) условных единиц. По команде Направо \(m\) Черепаха поворачивается на месте на \(m\) градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения. По команде Налево \(m\) Черепаха поворачивается на месте на \(m\) градусов против часовой стрелки, при этом соответственно меняется направление дальнейшего движения. В начальный момент Черепаха находится в начале координат и направлена вверх (вдоль положительного направления оси ординат). Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что заданная последовательность из \(S\) команд повторится \(k\) раз.
Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 24 Направо 90 Вперёд 10 Направо 90]
Вперёд 3 Налево 90 Вперёд 13 Направо 90
Повтори 2 [Вперёд 9 Направо 90 Вперёд 32 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор непересекающихся прямоугольников. Определите наибольшую из площадей этих прямоугольников. В ответе запишите только число – наибольшую площадь в условных единицах.
Решение:
...
Ответ: -
Статград. 24.10.2024-1
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять три команды: Вперёд \(n\) (\(n\) – число), Направо \(m\) (\(m\) – число) и Налево \(m\) (\(m\) – число). По команде Вперёд \(n\) Черепаха перемещается вперёд на \(n\) условных единиц. По команде Направо \(m\) Черепаха поворачивается на месте на \(m\) градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения. По команде Налево \(m\) Черепаха поворачивается на месте на \(m\) градусов против часовой стрелки, при этом соответственно меняется направление дальнейшего движения. В начальный момент Черепаха находится в начале координат и направлена вверх (вдоль положительного направления оси ординат). Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что заданная последовательность из \(S\) команд повторится \(k\) раз.
Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 23 Направо 90 Вперёд 10 Направо 90]
Вперёд 3 Налево 90 Вперёд 12 Направо 90
Повтори 2 [Вперёд 9 Направо 90 Вперёд 32 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор непересекающихся прямоугольников. Определите наибольшую из площадей этих прямоугольников. В ответе запишите только число – наибольшую площадь в условных единицах.
Решение:
...
Ответ: -
Шастин. 9.2.2025
(Л. Шастин) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 777 [Вперёд 25 Налево 90 Вперёд 34 Налево 90]
Поднять хвост
Вперёд 12 Налево 90 Вперёд 17 Направо 90
Опустить хвост
Повтори 1996 [Вперёд 25 Налево 90 Вперёд 17 Налево 90]
Определите площадь области объединения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Шастин. 19.01.2025
(Л. Шастин) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 27 Направо 90 Вперёд 21 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 4 [Вперёд 73 Направо 90 Вперёд 91 Направо 90]
Определите площадь области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Шастин. 18.12.2024
(K. Шастин) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) — целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) — целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где m — целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) — целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори K [Команда1 Команда2 ...Команда$]
означает, что последовательность из \(S\) команд повторится \(K\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Назад 4 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 4 [Вперёд 8 Налево 90 Вперёд 12 Налево 90]
Поднять хвост
Вперёд 10
Опустить хвост
Повтори 4 [Вперёд 12 Направо 90]
Определите, какое максимальное количество точек может находиться внутри объединения любых двух из получившихся фигур, ограниченного заданными алгоритмом линиями, включая точки на линиях.
Решение:
...
Ответ: -
Шастин. 30.11.2024
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) — целое число), вызывающее передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) — целое число), вызывающее передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) — целое число), вызывающее направление движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) — целое число), вызывающее изменение направления движения на \(m\) градусов против часовой стрелки.
Запись Повтори \(k\) [Команда1 Команда2 ... КомандаS] означает, что последовательность из \(S\) команд повторяется \(k\) раз.
Черепахе был дан для исполнения следующий алгоритм:
Вперед 25 Направо 45 Вперед 50
Поднять хвост
Назад 50 Направо 45 Вперед 15 Налево 90 Вперед 30
Опустить хвост
Направо 180 Вперед 60 Назад 5 Направо 90 Вперед 31
Определить площадь получившегося четырёхугольника, ограниченного заданными алгоритмом линиями. В ответе запишите целую часть получившегося числа.
Решение:
...
Ответ: -
Шастин. 6.11.2024
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 16 Налево 90 Вперёд 20 Налево 90]
Поднять хвост
Вперёд 4 Налево 90 Вперёд 8 Направо 180
Опустить хвост
Повтори 3 [Вперёд 35 Налево 90 Вперёд 6 Налево 90]
Определите периметр области объединения фигур, ограниченных заданным алгоритмом линиями.
Решение:
...
Ответ: -
Шастин. 18.10.2024
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 15 Налево 90 Вперёд 25 Налево 90]
Поднять хвост
Вперёд 4 Налево 90 Вперёд 12 Налево 90
Опустить хвост
Повтори 6 [Вперёд 38 Направо 90 Вперёд 22 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданным алгоритмом линиями.
Решение:
...
Ответ: -
Шастин. 4.10.2024
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 50 Направо 90 Вперёд 35 Направо 90]
Поднять хвост
Вперёд 5 Направо 90 Вперёд 10 Налево 90
Опустить хвост
Повтори 4 [Вперёд 35 Направо 90 Вперёд 17 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданным алгоритмом линиями, включая точки на границах этого объединения.
Решение:
...
Ответ: -
Шастин. 19.09.2024
(Л. Шастин) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 11 Направо 90 Вперёд 17 Направо 90]
Поднять хвост
Вперёд 7 Налево 90 Назад 1 Направо 90
Опустить хвост
Повтори 2 [Вперёд 15 Направо 90 Вперёд 7 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченного заданными алгоритмом линиями, включая точки на линиях.
Решение:
...
Ответ: -
Шастин. 29.08.2024
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 8 Направо 90 Вперёд 11 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри получившейся фигуры, включая точки на линиях.
Решение:
...
Ответ: -
Поляков-7638
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 12 Направо 90 Вперёд 6 Направо 90]
Поднять хвост
Вперёд 1 Направо 90 Вперёд 3 Налево 90
Опустить хвост
Повтори 9 [Вперёд 53 Направо 90 Вперёд 75 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Поляков-7542
(ЕГЭ-2024) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперед 6 Направо 90 Вперед 12 Направо 90]
Поднять хвост
Вперед 1 Направо 90 Вперед 3 Налево 90
Опустить хвост
Повтори 2 [Вперед 77 Направо 90 Вперед 45 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Поляков-7541
(ЕГЭ-2024) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 10 [Вперёд 22 Направо 90 Вперед 16 Направо 90]
Поднять хвост
Вперед 1 Направо 90 Вперёд 1 Налево 90
Опустить хвост
Повтори 10 [Вперёд 72 Направо 90 Вперёд 79 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Поляков-7515
(ЕГЭ-2024) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 3 [Вперёд 7 Направо 90 Вперёд 12 Направо 90]
Поднять хвост
Вперёд 4 Направо 90 Вперёд 6 Налево 90
Опустить хвост
Повтори 4 [Вперёд 83 Направо 90 Вперёд 77 Направо 90]
Повтори 2 [Вперед 77 Направо 90 Вперед 45 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого объединения.
Решение:
...
Ответ: -
Поляков-7459
(ЕГЭ-2024) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 28 Направо 90 Вперёд 26 Направо 90]
Поднять хвост
Вперёд 8 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 4 [Вперёд 67 Направо 90 Вперёд 98 Направо 90]
Определите площадь пересечения фигур, ограниченных заданными алгоритмом линиями.
Решение:
...
Ответ: -
Поляков-7410
(Е. Джобс) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Направо 45
Повтори 10 раз [ Направо 45 Вперед 203 Направо 45 ]
Поднять хвост
Назад 40
Направо 45
Опустить хвост
Повтори 5 раз [ Вперед 20 Налево 90 ]
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданными алгоритмом линиями, не включая точки на линиях.
Решение:
...
Ответ: -
Поляков-7369
(Е. Джобс) Исполнитель Кузнечик действует на числовой прямой. У исполнителя существует три команды: Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) единиц вправо по оси ординат; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) ячеек влево по оси ординат; Перекрасить закрашивает не закрашенную клетку или отменяет закраску закрашенной клетки там, где в данный момент находится исполнитель. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Кузнечику был дан для исполнения следующий алгоритм:
Повторить 27 [
Вперед 5
Перекрасить
Назад 3
Перекрасить
Назад 3
]
Определите, сколько клеток будет закрашено после выполнения следующего алгоритма.
Решение:
...
Ответ: -
Поляков-7368
(Е. Джобс) Исполнитель Кузнечик действует на числовой прямой. У исполнителя существует три команды: Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) единиц вправо по числовой оси; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) ячеек влево по числовой оси; Закрасить закрашивает ячейку, в которой находится Кузнечик. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Кузнечику был дан для исполнения следующий алгоритм:
Повтори 11 [
Вперед 2
Закрасить
Назад 4
Закрасить
Вперед 2
Вперед 2 ]
Определите, сколько клеток будет закрашено после выполнения следующего алгоритма.
Решение:
...
Ответ: -
Поляков-7367
(Е. Джобс) Исполнитель Кузнечик действует на числовой прямой. У исполнителя существует три команды: Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) единиц вправо по оси ординат; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) ячеек влево по оси ординат; Перекрасить закрашивает не закрашенную клетку или отменяет закраску закрашенной клетки там, где в данный момент находится исполнитель. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Кузнечику был дан для исполнения следующий алгоритм:
Повтори 7 [
Повтори 2 [ Вперед 3 ]
Перекрасить
Назад 4
Перекрасить ]
Определите, сколько клеток будет закрашено после выполнения следующего алгоритма.
Решение:
...
Ответ: -
Поляков-7366
(Е. Джобс) Исполнитель Кузнечик действует на числовой прямой. У исполнителя существует три команды: Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) единиц вправо по числовой оси; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение Кузнечика на \(n\) ячеек влево по числовой оси; Закрасить закрашивает ячейку, в которой находится Кузнечик. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз. Кузнечику был дан для исполнения следующий алгоритм:
Повтори 7 [
Повтори 2 [ Вперед 3 ]
Закрасить
Назад 4
Закрасить ]
Определите, сколько клеток будет закрашено после выполнения следующего алгоритма.
Решение:
...
Ответ: -
Поляков-7365
(Е. Джобс) Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на \((a, \,b)\) (где \(a, \, b\) — целые числа), перемещающую Чертёжника из точки с координатами \((x, \, y)\) в точку с координатами \((x+a, \, y+b).\) Если числа \(a, \, b\) положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами \((4, \, 2),\) то команда Сместиться на \((2, \,-3)\) переместит Чертёжника в точку \((6, \,-1).\) Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 [
Сместиться на (60, 156)
Сместиться на (140, -153)
Сместиться в (71, 80)
Сместиться на (-111, 77) ]
Определите количество точек с целочисленными координатами, лежащих на линии, нарисованной Чертёжником.
Решение:
...
Ответ: -
Поляков-7364
(Е. Джобс) Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на \((a, \, b)\) (где \(a, \, b\) — целые числа), перемещающую Чертёжника из точки с координатами \((x, \, y)\) в точку с координатами \((x+a, \, y+b).\) Если числа \(a, \, b\) положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами \((4, \, 2),\) то команда Сместиться на \((2, \,-3)\) переместит Чертёжника в точку \((6, \,-1).\) Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 [
Сместиться на (6, 15)
Сместиться на (4, -6)
Сместиться в (2, 2)
Сместиться на (3, 9) ]
Определите количество точек с целочисленными координатами, лежащих на линии, нарисованной Чертёжником.
Решение:
...
Ответ: -
Поляков-7363
(Е. Джобс) Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на \((a, \, b)\) (где \(a, \, b\) — целые числа), перемещающую Чертёжника из точки с координатами \((x, \, y)\) в точку с координатами \((x+a, \, y+b).\) Если числа \(a, \, b\) положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами \((4, \, 2),\) то команда Сместиться на \((2, \,-3)\) переместит Чертёжника в точку \((6, \, -1).\) Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из \(S\) команд повторится \(k\) раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 [
Сместиться на (6, 15)
Сместиться на (-5, -5)
Сместиться в (2, 2)
Сместиться на (-1, -10) ]
Определите количество точек с целочисленными координатами, лежащих на линии, нарисованной Чертёжником.
Решение:
...
Ответ: -
