Линейка заданий с уравнениями с развернутым ответом входит в так называемый джентельменский набор - набор заданий, которые нужно уметь решать обязательно, чтобы не завалить ЕГЭ по профильной математике. А раз нужно - учимся их решать. На ЕГЭ могут попасться следующие прототипы заданий этой линейки.
Прототипы уравнений с развернутым ответом к ЕГЭ по профильной математике
Тригонометрические квадратные уравнения
а) Решите уравнение
`6sin^2x — 5sinх-4=0`
6) Найдите его корни, принадлежащие отрезку `[-(7π)/2;-(3π)/2]`
Решение:
a) Пусть sinx = t
`-1≤t≤1`
`6t^2-5t-4=0`
`D= 5-4*6*(-4)=121`
`t_1=(5+11)/12=4/3`
`sinx=4/3 > 1`
нет решений
или
`t_2 = (5-11)/12=-1/2`
`sinx=-1/2`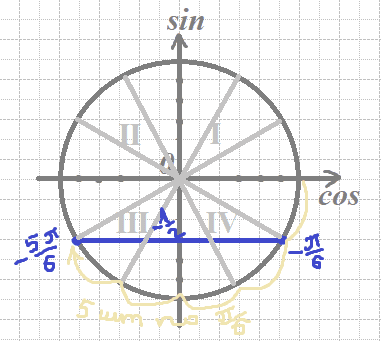
`x=-π/6 + 2πn`; n∈Z
или
`x=-(5π)/6+2πn`; n∈Z
б) Отберем корни с помощью окружности:
По условию отрезок `[-(7π)/2;-(3π)/2]`.
`π/2` - это четверть круга. Идем от крайней правой точки на окружности 7 раз по четвертинке по часовой стрелке, получим `-(7π)/2` в самом верху. Так как надо дойти до `-(3π)/2`, а оно по модулю меньше, теперь шагаем обратно (против часовой). Проходим четвертинку назад, получаем `-3π`, еще четверть `-(5π)/2`, еще четверть `-2π`, и еще четверть (вернулись вверх) `-(3π)/2`.
`sinx=-1/2` по решению из пункта а.
На вертикальной оси (она соответствует синусу) откладываем точку `-1/2`. Проводим линию до пересечения с окружностью.
Наш синус соответствует шагу `π/6`, но от `-2π` по часовой, а от `-3π` против.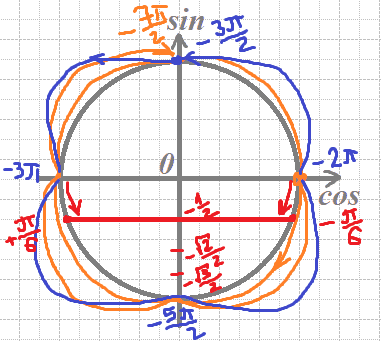
Получим число:
`x = -3π+π/6 = -(17π)/6`
`x = -2π-π/6 = -(13π)/6`
Ответ: а) `-π/6+2πn`; `-(5π)/6+2πn`; n∈Z
б) `-(13π)/6`; `-(17π)/6`
а) Решите уравнение
`6cos^2x+5sinх-2=0`
6) Найдите его корни, принадлежащие отрезку `[-(5π)/2; -π]`
Решение:
а) `6*(1-sin^2x)+5*sinx-2=0`
`6-6sin^2x+5sinx-2=0`
`-6sin^2x+5sinx+4=0`
Пусть `sinx=t`
`-6t^2+5t+4=0`
`D=25+96=121`
`t_1=(-5+11)/-12 = -1/2`
`sinx=-1/2`
`x=-π/6+2πn`; n∈Z
`x=-(5π)/6+2πn`; n∈Z
или
`t_2=(-16)/-12=4/3`
`sinx=4/3>1`
нет решений
б) Отберем корни с помощью окружности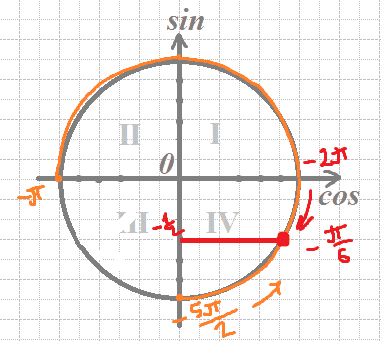
Получим числа:
`x=-2π-π/6=-(13π)/6`
Ответ: а) `-π/6+2πn`, `-5π/6+2πn`; n∈Z
б) `-(13π)/6`
а) Решите уравнение
`8sinx+4cos^2х=7`
6) Найдите его корни, принадлежащие отрезку `[-(3π)/2;-π/2]`
Решение:
a) `8sinx+4*(1-sin^2x)-7=0`
`8sinx+4-4sin^2x-7=0`
`-4sin^2x+8sinx-3=0`
Пусть `sinx=t`
`-4t^2+8t-3=0`
`D=64-4*(-4)*(-3)=16`
`t_1=(-8+4)/-8=1/2`
`sinx=1/2`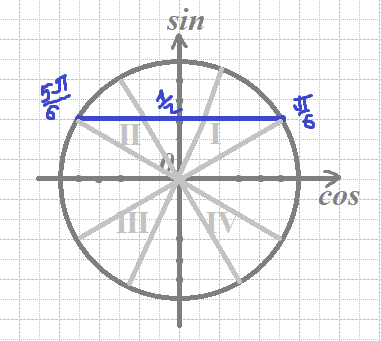
`x_1=π/6+2πn`; n∈Z
или
`x_2=(5π)/6+2πn`; n∈Z
или
`t_2=(-8-4)/-8=1,5`
`sinx=1,5>1`
нет решений
б) Отберем корни с помощью окружности: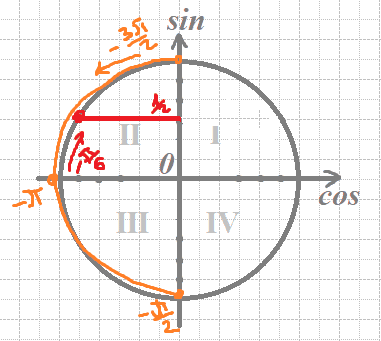
`sinx=1/2`
Получим числа:
`x=-π-π/6=-(6π)/6-π/6=-(7π)/6`
Ответ: а) `π/6 + 2πn`, `(5π)/6+2πn`; n∈Z
б) `-(7π)/6`
а) Решите уравнение
`2sin^2x+4=3sqrt(3)sin(3π/2+x)`
6) Найдите его корни, принадлежащие отрезку `[-(5π)/2;-π]`
Решение:
a) `2sin^2x+4=-3sqrt(3)*cosx`
`2*(1-cos^2x)+4=-3sqrt(3)*cosx`
`2-2cos^2x+4+3sqrt(3)*cosx=0`
`-2cos^2x+3sqrt(3)*cosx+6=0`
Пусть `cosx=t`
`-2t^2+3sqrt(3)*t+6=0`
`D=27+48=75`
`t_1=(-3sqrt3+sqrt75)/(-4)`
`t_1=-sqrt3/2`
`cosx=-sqrt3/2`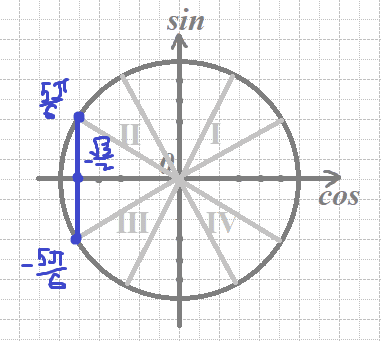
`x=±(5π)/6+2πn`; n∈Z
или
`t_2=(-3sqrt3-sqrt75)/(-4)`
`t_2=2sqrt3`
`cosx=2sqrt3>1`
нет решений
б) Отберем корни с помощью окружности: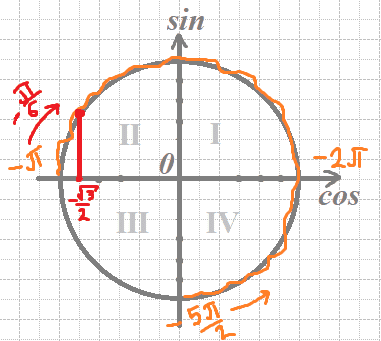
Получим числа:
`x=-π-π/6=-(6π)/6-π/6=(-7π)/6`
Ответ: а) `±5π/6+2πn`; n∈Z
б) `-(7π)/6`
а) Решите уравнение
`cos^2x-cos2x=0,75`
6) Найдите его корни, принадлежащие отрезку `[-2π;-π/2]`
Решение:
a) `cos^2x-(2cos^2x-1)=0.75`
`cos^2x-2cos^2x+1=0.75`
`-cos^2=-0.25` |*(-1)
`cos^2x=1/4`
`cosx=1/2`
или
`cosx=-1/2`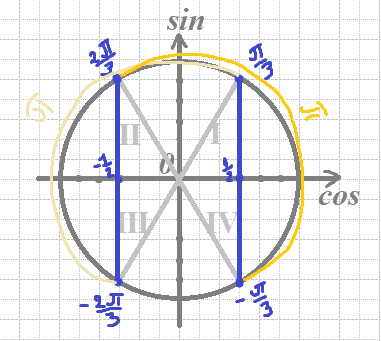
`x=±π/3+πn`; n∈Z
б) Отберем корни с помощью окружности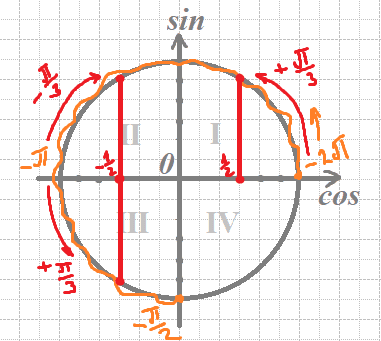
Получим числа:
`x=-2π+π/3=-(2*3*π)/3+π/3=(-5π)/3`
`x=-π-π/3=(4π)/3`
`x=-π+π/3=-(2π)/3`
Ответ: а) `±π/3+πn`; n∈Z
б) `(-5π)/3`; `(4π)/3`; `-(2π)/3`
а) Решите уравнение
`cos^2x-cos2x=0,5`
6) Найдите его корни, принадлежащие отрезку `[-(3π)/2;-π/2]`
Решение:
а) `cos^2x-(cos^2x-sin^2x)=1/2`
`sin^2x=1/2`
`sinx=sqrt(1/2)=1/sqrt(2)*sqrt(2)/sqrt(2)=sqrt(2)/2`
или
`sinx=-sqrt(1/2)=-1/sqrt(2)*sqrt(2)/sqrt(2)=-sqrt(2)/2`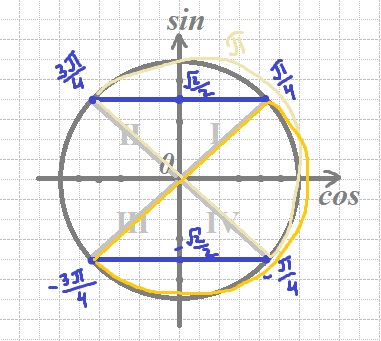
`x=±π/4+πn`; n∈Z
б) Отберем корни с помощью окружности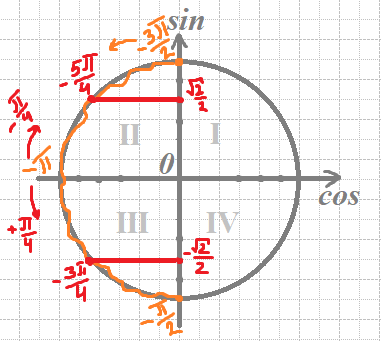
Получим числа:
`x=-π+π/4=(-3π)/4`
`x=-π-π/4=(-5π)/4`
Ответ: а) `x=±π/4+πn`; n∈Z
б) `-(3π)/4`; `-(5π)/4`
а) Решите уравнение
`3сos2х-5sinx+1=0`
6) Найдите его корни, принадлежащие отрезку `[π;(5π)/2]`
Решение:
а) `3*(1-2sin^2x)-5*sinx+1=0`
`3-6sin^2x-5sinx+1=0`
`3-6sin^2x-5sinx+1=0`
`-6sin^2x-5sinx+4=0`
Пусть `sinx=t`
`-6t^2-5t+4=0`
`D=25-4*(-6)*4=121`
`t_1=(5+11)/-12=16/-12=4/3`
`sinx=-4/3<1`
нет решений
или
`t_2=(5-11)/-12=(-6)/-12=1/2`
`sinx=1/2`
`x_1=π/6+2πn`; n∈Z
или
`x_2=(5π)/6+2πn`; n∈Z
б) Отберем корни с помощью окружности
Получим числа:
`x=2π+π/6=(13π)/6`
Ответ: а) `π/6+2πn`; n∈Z; `(5π)/6+2πn`; n∈Z
б) `(13π)/6`
а) Решите уравнение
`2сos2х+8sinx+3=0`
6) Найдите его корни, принадлежащие отрезку `[-(3π)/2;π]`
Решение:
a) `2*(1-2sin^2x)+8sinx+3=0`
`2-4sin^2x+8sinx+3=0`
`-4sin^2x+8sinx+5=0`
Пусть `sinx=t`
`-4t^2+8t+5=0`
`D=64-4*(-4)*5=144`
`t_1=(-8+12)/-8=-1/2`
`sinx=-1/2`
`x_1=-π/6+2πn`; n∈Z
или
`x_1=(-5π)/6+2πn`; n∈Z
или
`t_2=(-8-12)/-8=5/2`
`sinx=5/2>1`
нет решений
б) Отберем корни с помощью окружности
Получим числа:
`x=-π/2-π/3=-(3π)/(2*3)-(2π)/(3*2)=(-5π)/6`
`x=-π/2+π/3=-π/6`
Ответ: а) `-π/6+2πn`; n∈Z; `(-5π)/6+2πn`; n∈Z.
б) `(-5π)/6`; `-π/6`
а) Решите уравнение
`6sin^2х+5sin(π/2-x)-2=0`
6) Найдите его корни, принадлежащие отрезку `[-5π;-(7π)/2]`
Решение:
а) `6sin^2x+5cosx-2=0`
`6*(1-cos^2x)+5cosx-2=0`
`6-6cos^2x+5cosx+4=0`
Пусть `cosx=t`
`-6t^2+5t+4=0`
`D=25-4*(-6)*4=121`
`t_1=(-5+11)/-12=6/-12=1/2`
`cosx=-1/2`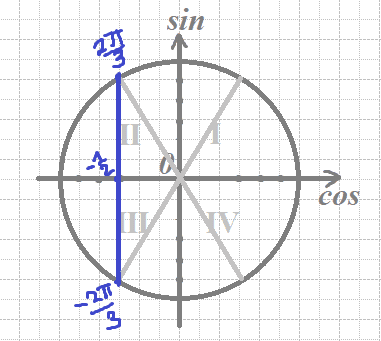
`x=±(2π)/3+2πn`; n∈Z
или
`t_2=(-5-11)/-12=-16/-12=4/3`
`cosx=4/3>1`
нет решений
б) Отберем корни с помощью окружности
Получим числа:
`x=-5π+π/3=(-14π)/3`
Ответ: а) `±(2π)/3+2πn`; n∈Z
б) `(-14π)/3`
а) Решите уравнение
`2sin^2х+cosx-1=0`
6) Найдите его корни, принадлежащие отрезку `[-5π;-4π]`
Решение:
а) `2*(1-cos^2x)+cosx-1=0`
`2-2cos^2x+cosx-1=0`
`-2cos^2+cosx+1=0`
Пусть `cosx=t`
`-2t^2+t+1=0`
`D=1^2-4*(-2)*1=9`
`t_1=(-1-3)/-4=(-4)/(-4)=1`
`cosx=1`
`x=2πn`; n∈Z
или
`t_2=(-1+3)/-4=2/(-4)=-1/2`
`cosx=-1/2`
`x=±(2π)/3+2πn`; n∈Z
б) Отберем корни с помощью окружности
Получим числа:
`x=-4π`
`x=-5π+π/3=-(14π)/3`
Ответ: а) `2πn`; n∈Z, `±(2π)/3+2πn`; n∈Z
б) `-4π`, `-(14π)/3`
а) Решите уравнение
`2sqrt(2)cosx+2-cos2x=0`
6) Найдите его корни, принадлежащие отрезку `[5π;(13π)/2]`
Решение:
a) `2sqrt(2)cosx+2-(2cos^2x-1)=0`
`2sqrt(2)cosx+2-2cos^2x+1=0`
`-2cos^2x+2sqrt(2)cosx+3=0`
Пусть `cosx=t`
`-2t^2+2sqrt(2)t+3=0`
`D=(2sqrt(2))^2-4*(-2)*3=8+24=32`
`t=(-2sqrt(2)±sqrt(32))/-4=(-2sqrt(2)±sqrt(16*2))/-4=(-2sqrt(2)±4sqrt(2))/-4`
`t_1=sqrt(2)/2`
`cosx=-sqrt(2)/2`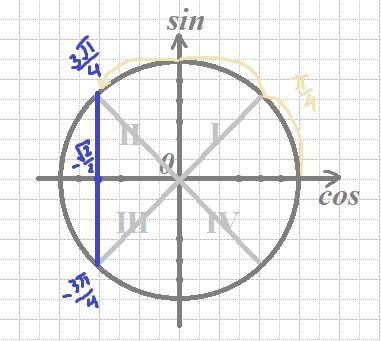
`x=±(3π)/4+2πn`; n∈Z
или
`t_2=(-6sqrt2)/-4=(3sqrt2)/2`
`cosx=(3sqrt2)/2>1`
нет решений
б) Отберем корни с помощью окружности
Получим числа:
`x=5π+π/4=(21π)/4`
Ответ: а) `±(3π)/4+2πn`; n∈Z
б) `(21π)/4`
а) Решите уравнение
`2cos2x+8sin(π/2-х)-3=0`
6) Найдите его корни, принадлежащие отрезку `[(7π)/2;5π]`
Решение:
a) `2co2x+8cosx-3=0`
`2*(2cos^2x-1)+8cosx-3=0`
`4cos^2x-2+8cosx-3=0`
`4cos^2x+8cosx-5=0`
`Пусть cosx=t`
`4t^2+8t-5=0`
`D=64-4*4*(-5)=144`
`t_1=(-8+12)/8=4/8=1/2`
`cosx=1/2`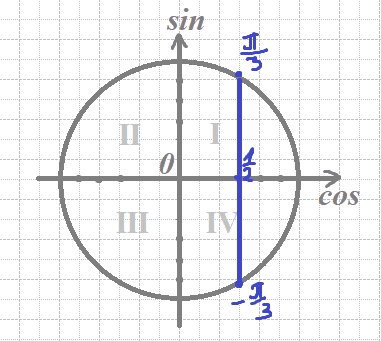
`x=±π/3+2πn`; n∈Z
или
`t_2=(-20)/8=-5/2`
`cosx=-5/2<-1`
нет решений
б) Отберем корни с помощью окружности
Получим числа:
`x=4π+π/3=(13π)/3`
`x=4π-π/3=(11π)/3`
Ответ: а) `±π/3+2πn`; n∈Z
б) `(13π)/3`; `(11π)/3`
а) Решите уравнение
`6cos^2(x-π/2)+11sin((3π)/2+х)-10=0`
б) Найдите его корни, принадлежащие отрезку `[-3π;-(3π)/2]`
Решение:
a) `6(sinx)^2+11*(-cosx)-10=0`
`6sin^2x-11cosx-10=0`
`6(1-cos^2x)-11cosx-10=0`
`6-6cos^2x-11cosx-10=0`
`-6cos^2x-11cosx-4=0`
Пусть `cosx=t`
`-6t^2-11t-4=0`
`D=121-4*(-6)*(-4)=25`
`t_1=(11+5)/(-12)=-4/3`
`cosx=-4/3<-1`
нет решений
или
`t_2=(11-5)/(-12)=-1/2`
`cosx=-1/2`
`x=±(2π)/3+2πn`; n∈Z
б) Отберем корни с помощью окружности
Получим числа:
`x=-3π+π/3=(-8π)/3`
Ответ: а) `±(2π)/3+2πn`; n∈Z
б) `(-8π)/3`
а) Решите уравнение
`6sin^2(x+(3π)/2)=13cos(x+(5π)/2)+13`
6) Найдите его корни, принадлежащие отрезку `[-3π;(-3π)/2]`
Решение:
a) `6*(-cosx)^2=13*(-sinx)+13`
`6cos^2x+13sinx-13=0`
`6(1-sin^2x)+13sinx-13=0`
`6-6sin^2x+13sinx-7=0`
`-6sin^2x+13sinx-7=0`
Пусть `sinx=t`
`-6t^2+13t-7=0`
`D=169-168=1`
`t_1=(-13+1)/(-12)=1`
`sinx=1`
`x=π/2+2πn`; n∈Z
или
`t_2=(-13-1)/(-12)=7/6`
sinx=7/6>1
нет решений
б) Отберем корни с помощью окружности
Получим числа:
`x=(-3π)/2`
Ответ: а) `π/2+2πn`; n∈Z
б) `(-3π)/2`
а) Решите уравнение
`cos4x-cos2x=0`
6) Найдите его корни, принадлежащие отрезку `[π/2;2π]`
Решение:
а) `2(cos^2)2x-1-cos2x=0`
Пусть `cos2x=t`
`2t^2-t-1=0`
`D=1+8=9`
`t_1=(1+3)/4`
`t_1=1`
`cos2x=1`
`2x=2πn`; n∈Z | /2
`x=πn`; n∈Z
или
`t_2=-1/2`
`cos2x=-1/2`
`2x=±(2π)/3+2πn`; n∈Z |/2
`x=±π/3+2πn`; n∈Z
б) Отберем корни с помощью прямой:
Для `x=πn`; n∈Z
Если n=0, то x=0 ∉
n=1, то x=π ∈
n=2, то x=2π ∈
n=3, то x=3π ∉
Для `x=π/3+πn`; n∈Z
Если n=0, то `x=π/3` ∉
n=1, то `x=(4π)/3` ∈
n=2, то `x=(7π)/3` ∉
Для `x=-π/3+πn`; n∈Z
Если n=0, то `x=-π/3` ∉
n=1, то `x=(2π)/3` ∈
n=2, то `x=(5π)/3` ∈
n=3, то `x=(2π)/2` ∉
Ответ: а) `πn`, `±π/3+2πn`; n∈Z
б) `π`; `2π`; `(2π)/3`; `(4π)/3`; `(5π)/3`
а) Решите уравнение
`cos4x-sin2x=0`
6) Найдите его корни, принадлежащие отрезку `[π/2;2π]`
Решение:
а) `2cos^2-1-cos2x=0`
Пусть `cos2x=t`
`2t^2-t-1=0`
`D=1+8=9`
`t=(1±3)/4`
`t_1=1`
`cos2x=1`
`2x=2πn`; n∈Z
`x=πn`; n∈Z
`t_2=-1/2`
`cos2x=-1/2`
`2x=±(2π)/3+2πn`; n∈Z
`x=±π/3+πn`; n∈Z
б) Отберем корни с помощью прямой:
Для `x=πn`; n∈Z
Если n=0, то x=0 ∉
n=1, то `x=π∈`
n=2, то `x=2π` ∈
n=3, то `x=3π` ∉
Для `x=π/3+πn`; n∈Z
Если n=0, то `x=π/3` ∉
n=1, то `x=(4π)/3` ∈
n=2, то `x=(7π)/3` ∉
Для `x=-π/3+πn`; n∈Z
Если n=0, то `x=-π/3` ∉
n=1, то `x=(2π)/3` ∈
n=2, то `x=(5π)/3` ∈
n=3, то `x=(8π)/2` ∉
Ответ:
а) Решите уравнение
`5-2cosx = 5sqrt2 sin(x/2)`
6) Найдите его корни, принадлежащие отрезку `[-(5π)/2;-π]`
Решение:
...
Ответ:
а) Решите уравнение
`2cos^2 x+(sqrt3-2)sinx-2+sqrt3=0`
6) Найдите его корни, принадлежащие отрезку `[2π;3π]`
Решение:
...
Ответ:
а) Решите уравнение
`2cos^2x+(2-sqrt2)sinx+sqrt2-2 =0`
6) Найдите его корни, принадлежащие отрезку `[-3π;-2π]`
Решение:
...
Ответ:
Тригонометрические уравнения, вынос общего
...
Могут быть совершенно новые прототипы, ранее не встречавшиеся на ЕГЭ, как и среди любых других заданий с развернутым ответом.
