Задачи на равномерное движение по окружности к ОГЭ по физике с ответами, ФИПИ

Все задания на равномерное движение по окружности к ОГЭ по физике с ответами из открытого банка заданий ФИПИ. 26 + 5 штук на данный момент.

Основные формулы:

`a_(цс)=v^2/R=omega^2R` - центростремительное ускорение [м/с²]
`T=(2pi)/omega=(2πR)/υ=t/n` - период обращения (время, за которое тело проходит 1 полный оборот), t - время [с], n - количество оборотов [-].
`ν=n/t`- частота вращения (число полных оборотов за единицу времени)
`omega=(Deltavarphi)/(Deltat)=(2pi)/T=2pinu` - угловая скорость [рад/с]
`v=omegaR` - связь линейной и угловой скоростей

КЭС 1.6 Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления ускорения. Формула, связывающая период и частоту обращения

Все задания на равномерное движение по окружности

За 1 мин. пропеллер вентилятора совершает 1200 оборотов. Чему равна частота вращения лопастей вентилятора?

Ответ: ___________________________ 1с.

Ответ:

*пояснение 1200/60=20 об/с

Номер: 4EE106

За 4 мин. пропеллер вентилятора совершает 480 оборотов. Чему равна частота вращения лопастей вентилятора?

Ответ: ___________________________ 1с.

Ответ:

Номер: 4070BA

Муха сидела на равномерно вращающемся диске в точке А, а затем перелетела в точку В и села там (см. рисунок). Как в результате этого перемещения изменились линейная скорость мухи и частота её обращения на диске вокруг оси О?

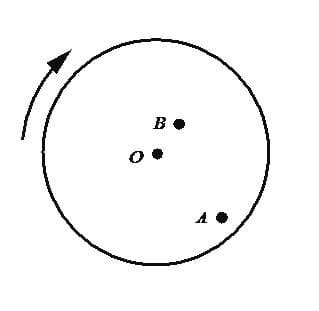
ОГЭ по физике

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Линейная скорость мухи Частота обращения мухи

Ответ:

2 3

Номер: 226314

За 2 мин. пропеллер вентилятора совершает 2400 оборотов. Чему равна частота вращения лопастей вентилятора?

Ответ: _________________________ 1с.

Ответ:

*пояснение 2400/2=1200об/мин
1200 /60=20 об/с

Номер: 4BE6D0

За 1 мин. пропеллер вентилятора совершает 1200 оборотов. Чему равен период вращения лопастей вентилятора?

Ответ:

0,05

*пояснение. Так как частота вращения 1200/60=20 Гц, то период 1/частоте, то есть 1/20=0,05 с надо для того, чтобы вентилятор сделал один оборот.

Номер: 537ADD

Тело движется по окружности вокруг точки О с постоянной по модулю скоростью. Какая из стрелок – 1, 2, 3 или 4 – указывает направление ускорения этого тела в точке А?

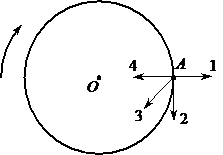
ОГЭ по физике

Ответ:

Номер: 0E9DC0

За 4 мин. пропеллер вентилятора совершает 480 оборотов. Чему равен период вращения лопастей вентилятора?

Ответ:

0,5

*пояснение 480/4=120 об/мин 120/60=2 об/с. То есть один период равный 1 обороту совершается за 1/2 =0,5 с

Номер: 102DC1

Радиус окружности, по которой движется тело, увеличили в 4 раза, линейную скорость тела увеличили в √2 раза. Во сколько раз уменьшилось центростремительное ускорение тела?

в ___ раз(а)

Ответ:

2

*пояснение F=(mV²)/r
Если увеличим радиус в 4 раза, то уменьшим силу в 4 раза. Если увеличим скорость в √2 раза, то увеличим силу в 2 раза. То есть уменьшение равно 4/2, итого получается уменьшение центростремительного ускорения в 2 раза.

Номер: F7869E

Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, большего радиуса. Как при этом изменились сила тяготения, действующая на корабль со стороны Земли,
и период обращения корабля вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Сила тяготения Период обращения корабля

Ответ:

2 1

Номер: F5B8EA

Радиус окружности, по которой движется тело, уменьшили в 2 раза, его линейную скорость тоже уменьшили в 2 раза. Во сколько раз уменьшилось центростремительное ускорение тела?

в ___ раз(а)

Ответ:

2

*пояснение F=(mV²)/r Если уменьшим радиус в два раза, то увеличим силу в 2 раза, если уменьшим скорость в 2 раза, то уменьшим силу в 4 раза. То есть уменьшение равно 4/2, итого получается уменьшение в 2 раза.

Номер: 83C331

Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, меньшего радиуса. Как изменились в результате этого перехода модуль скорости корабля и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль скорости корабля Период обращения корабля вокруг Земли

Ответ:

1 2

Номер: 709280

На равномерно вращающемся диске жук переместился из точки А в точку В (см. рисунок). Как при этом изменились линейная скорость жука и частота его обращения вокруг оси O?

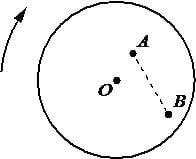
ОГЭ по физике

Для каждой величины определите соответствующий характер изменения:

1) увеличилась
2) уменьшилась
3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость Частота

Ответ:

1 3

Номер: 11DF89

Радиус окружности, по которой движется тело, увеличили в 2 раза, линейную скорость тела тоже увеличили в 2 раза. Во сколько раз увеличилось центростремительное ускорение тела?

в ___ раз(а)

Ответ:

2

*пояснение F=(mV²)/r
Если увеличить радиус в два раза, то уменьшим силу в 2 раза, если увеличить скорость в 2 раза, то увеличим силу в 4 раза. Итого получается разделить на 2 и умножить на 4, то есть в 2 раза.

Номер: C8FB81

Радиус окружности, по которой движется тело, увеличили в 2 раза, линейную скорость тела увеличили в 4 раза. Во сколько раз увеличилось центростремительное ускорение тела?

в ___ раз(а)

Ответ:

8

*пояснение F=(mV²)/r
Если увеличить радиус в два раза, то уменьшим силу в 2 раза, если увеличить скорость в 4 раза, то увеличим силу в 16 раз. Итого получается разделить на 2 и умножить на 16, то есть в 8 раз.

Номер: E18D8C

Дайте развернутый ответ.
Шарик на нити длиной 50 см вращается по окружности с частотой 120 об/мин. Чему равна линейная скорость шарика?

Ответ:

Дано: r = 50 см; H=120 об/мин
Найти: V-? м/с
Решение:
P=2∏r=2*3,14*0,5=3,14 м периметр окружности
`V=S/t=120*3,14/60=6,28` м/с
Ответ: 6,28 м/с

Номер: 6A1D7B

Тело движется по криволинейной траектории (см. рисунок), причём на участке АБ его скорость неизменна по модулю и равна 2 м/с, а на участке ВГ равна 4 м/с. Для радиусов кривизны траектории в точках 1, 2 и 3 выполняется соотношение R1 > R2 > R3.

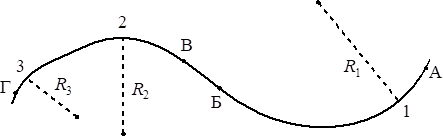
ОГЭ по физике

Используя текст и рисунок, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Во всех точках участка АБ ускорение тела направлено перпендикулярно вектору скорости.
2) Во всех точках траектории ускорение тела направлено по касательной к траектории.
3) Центростремительное ускорение тела в точке 1 в 4 раза меньше центростремительного ускорения в точке 2.
4) В точке 3 центростремительное ускорение тела имеет наибольшее значение.
5) На участке БВ тело двигалось равномерно и прямолинейно.

Ответ:

1 4

Номер: 61CC1A

Дайте развернутый ответ.
Диск радиусом 30 см равномерно вращается относительно оси, проходящей через его центр, с частотой 60 обмин. Чему равна линейная скорость точек диска, наиболее удалённых от его центра?

Ответ:

Дано: r=30 см; H= 60 об/мин
Найти: V - ?
Решение:
P=2∏r=2*3,14*0,3=1,88 м периметр окружности
`V=S/t=(1,88*60)/60=1,88 м/с`
Ответ: 1,88 м/с

Номер: 760E25

В таблице указаны некоторые характеристики планет Солнечной системы. Все параметры в таблице, кроме плотности и числа спутников, указаны в отношении к аналогичным данным Земли.

Планета	Диаметр, относительно Земли	Масса, относительно Земли	Орбитальный радиус, относительно Земли	Период обращения, земных лет	Сутки, относительно Земли	Плотность, кг/м³	Спутники
Планеты земной группы
Меркурий	0,382	0,06	0,38	0,241	58,6	5427	Нет
Венера	0,949	0,82	0,72	0,615	243	5243	Нет
Земля	1,0	1,0	1,0	1,0	1,0	5515	1
Марс	0,53	0,11	1,52	1,88	1,03	3933	2
Планеты-гиганты
Юпитер	11,2	318	5,20	11,86	0,414	1326	67
Сатурн	9,41	95	9,54	29,46	0,426	687	62
Уран	3,98	14,6	19,22	84,01	0,718	1270	27
Нептун	3,81	17,2	30,06	164,79	0,671	1638	13

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) По мере удаления от Солнца период обращения планет увеличивается.
2) Чем меньше плотность планеты, тем больше спутников она имеет.
3) Самую большую плотность из планет Солнечной системы имеет Земля.
4) По мере удаления от Солнца увеличивается радиус планет.
5) Для планет-гигантов характерны более длительные сутки по сравнению
с планетами земной группы.

Ответ:

1 3

Номер: A7D02E

Тело движется по криволинейной траектории (см. рисунок), причём на участке АБ его скорость неизменна по модулю и равна 2 мс, а на участке ВГ равна 4 мс. Для радиусов кривизны траектории в точках 1, 2 и 3 выполняется соотношение R1 > R2 > R3.

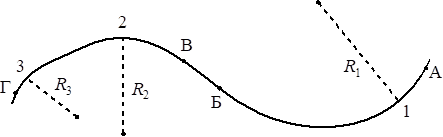
ОГЭ по физике

Используя текст и рисунок, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) На участке АБ ускорение тела равно нулю.
2) На участке ВГ вектор скорости тела не изменяется.
3) Центростремительное ускорение в точке 1 меньше центростремительного ускорения в точке 2.
4) Во всех точках траектории вектор скорости тела направлен по касательной к траектории.
5) На участке БВ скорость тела постоянна.

Ответ:

3 4

Номер: 9DA75F

В таблице указаны некоторые характеристики планет Солнечной системы. Все параметры в таблице, кроме плотности, указаны в отношении к аналогичным данным Земли.

Планета	Диаметр, относительно Земли	Масса, относительно Земли	Орбитальный радиус, относительно Земли	Период обращения, земных лет	Сутки, относительно Земли	Плотность, кг/м³	Спутники
Планеты земной группы
Меркурий	0,382	0,06	0,38	0,241	58,6	5427	Нет
Венера	0,949	0,82	0,72	0,615	243	5243	Нет
Земля	1,0	1,0	1,0	1,0	1,0	5515	1
Марс	0,53	0,11	1,52	1,88	1,03	3933	2
Планеты-гиганты
Юпитер	11,2	318	5,20	11,86	0,414	1326	67
Сатурн	9,41	95	9,54	29,46	0,426	687	62
Уран	3,98	14,6	19,22	84,01	0,718	1270	27
Нептун	3,81	17,2	30,06	164,79	0,671	1638	13

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) По мере удаления от Солнца масса планет увеличивается.
2) Плотность планет земной группы больше плотности планет-гигантов.
3) Самый маленький период обращения вокруг своей оси имеет Венера.
4) Время, проходимое планетой по её орбите, характеризует сутки на данной планете.
5) Для планет-гигантов характерно наличие большого количества спутников.

Ответ:

2 5

Номер: D06A97

Дайте развернутый ответ.
Автомобиль равномерно движется по закруглённому участку дороги длиной 50 м и радиусом кривизны, равным 20 м. Сколько времени затратит автомобиль на преодоление этого участка, если центростремительное ускорение автомобиля равно 5 м/с²?

Ответ:

Дано: a = 5 м/с²; R = 20 м; S = 50 м
Найти: t - ? c;
Решение:
`a=v^2/R`
S=v*t
`S/sqrt(a*R) = 50/(5*20) = 50/sqrt100 = 50/10=5` c
Ответ: 5 c

Номер: EF7C9A

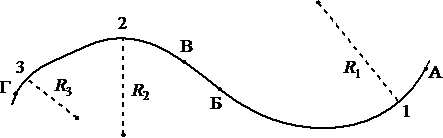
ОГЭ по физике

Используя текст и рисунок, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) На участке АБ вектор ускорения тела не изменяется.
2) На участке ВГ вектор скорости тела не изменяется.
3) Центростремительное ускорение в точке 1 меньше центростремительного ускорения в точке 3.
4) Во всех точках траектории вектор скорости тела направлен по касательной к траектории.
5) На участке БВ скорость тела не изменяется.

Ответ:

3 4

Номер: A05C87

Задачи повышенной сложности

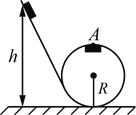
Дайте развернутый ответ.
Маленькая шайба движется по наклонному жёлобу, переходящему в вертикальную окружность радиусом R = 0,2 м. С какой минимальной высоты h шайба должна начинать движение, чтобы в верхней точке окружности не оторваться от жёлоба? Трением пренебречь.

КЭС: 1.5 Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления ускорения. Формула, связывающая период и частоту обращения
1.18 Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения

Ответ:

Дано: R = 0,2 м
Найти: h - ?
Решение:
В верхней точке центробежная сила должна быть уравновешена силой от массы, тогда
mV²/R = mg
V²/R = g
V²=Rg
V = √2 м/с
Однако это скорость должна быть обеспечена на высоте в верхней точке окружности, то есть если спроецировать на высоту на горке, это скорость уже должна быть в точке проекции по горизонтали на спуске, получается надо найти прирост высоты относительно этой проекции, где тело имело скорость равную 0.
mV²/R = mg(h-2R)
R/2 = h - 2R
h = R/2 +2R = 2,5R
h = 2,5*0,2 = 0,5 м
Ответ: 0,5 м

Номер: 2446BC

Дайте развернутый ответ.
С какой скоростью должен лететь самолёт в наивысшей точке «мёртвой петли» радиусом 1 км, чтобы лётчик оказался в невесомости?

КЭС: 1.5 Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления ускорения. Формула, связывающая период и частоту обращения
1.9 Второй закон Ньютона. Сонаправленность вектора ускорения тела и вектора силы, действующей на тело

Ответ:

Дано: R = 1 км
Найти: V-?
Решение:
В высшей точке «мёртвой петли» на летчика действует сила тяжести F=mg и противоположна ей центростремительная (центробежная) сила, равная ma, где - центробежное ускорение. Чтобы летчик оказался в состоянии невесомости данные силы должны уравновешивать друг друга, тогда,
mg - mV²/R = 0
откуда скорость V равна
V = √gR = √10*1000 = 100 м/с
Ответ: 100 м/с

Номер: BF6C13

Дайте развернутый ответ.
Маленькая шайба движется по наклонному жёлобу, переходящему в окружность. Минимальная высота h, с которой шайба начинает движение и не отрывается от жёлоба в верхней точке окружности радиуса R, равна 0,5 м. Чему равен радиус окружности? Трением пренебречь.

Ответ:

Дано: высота с которой шайба начинает движение — $h=0,5$ м.

Найти: радиус окружности — $R-?$

Решение. Поскольку трением можно пренебречь, то при описании движения шайбы можно использовать закон сохранения энергии. В начале пути полная механическая энергия шайбы равна ее потенциальной энергии

$E_1=mgh$.

В точке А полная механическая энергия равна сумме потенциальной и кинетической энергии (шайба движется с некоторой скоростью, ведь она не должна остановиться и упасть по условию задачи)

$E_2=mgH+\frac{mv^2}{2}$.

Высота, на которую поднимается на высоту $H=2R$, поэтому

$E_2=2mgR+\frac{mv^2}{2}$.

При движении шарика на него будут действовать две силы: реакции и тяжести. Причем, если шарик отрывается, то в момент отрыва сила реакции на него перестает действовать и он начнет движение только под действием силы тяжести. Можно сказать, что в момент отрыва будет выполняться равенство

$mg=ma_c\Rightarrow a_c=g$,

$\frac{v^2}{R}=g$,

$v^2=gR$.

Вернемся к закону сохранения энергии и найдем из него квадрат скорости, т.к. $E_1=E_2$, то

$mgh=2mgR+\frac{mv^2}{2}$.

Сокращаем массу

$gh=2gR+\frac{v^2}{2}$.

Умножим обе части уравнения на 2

$2gh=4gR+v^2$.

Переносим выражение $4gR$ в одну сторону и выносим общий множитель $2g$ за скобки

$v^2=2g(h-2R)$.

Составляем уравнение, приравниваем правые части для выражений квадрата скорости

$gR=2g(h-2R)$.

Сокращаем $g$ и находим радиус

$R=2(h-2R)$,

$R=2h — 4R$,

$5R=2h \Rightarrow R=\frac{2h}{5}=0,2$ м.

Ответ: радиус окружности 0,2 м.

Номер: E3ED28

Дайте развернутый ответ.
Самолёт совершает «мёртвую петлю». Чему равен радиус петли, если лётчик в верхней точке петли оказывается в состоянии невесомости при скорости 100 м/с?

КЭС: 1.5 Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления ускорения. Формула, связывающая период и частоту обращения
1.9 Второй закон Ньютона. Сонаправленность вектора ускорения тела и вектора силы, действующей на тело

Ответ:

Дано: вес летчика в верхней точке — $P=0$; скорость летчика — $v=100$ м/с.

Найти: радиус петли — $R$.

Решение. При равномерном движении по окружности возникает ускорение называемое центростремительным. Вес тела вычисляется по формуле

$\vec{P}=m(\vec{g}-\vec{a})$.

Согласно условию задачи вес летчика в верхней точке равен нулю, это возможно тогда, когда $m(\vec{g}=\vec{a})$. Отсюда следует, что модуль центростремительного ускорения в верхней точке будет равен $g$. Модуль центростремительного ускорения вычисляется по формуле

$a=\frac{v^2}{R}$.

Отсюда находим радиус окружности

$R=\frac{v^2}{a}=\frac{v^2}{g}$,

$R=\frac{100^2}{10}=1000$ м $=1$ км.

Ответ: радиус «мёртвой петли» 1 км.

Номер: B7143F

КЭС 1 Механические явления

Установите соответствие между формулами для расчёта физических величин при равномерном движении тела по окружности и названиями этих величин. В формулах использованы обозначения: T – период обращения; R – радиус окружности.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФОРМУЛЫ
А) `1/T`
Б) `(2πR)/T`

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) линейная скорость
2) центростремительное ускорение
3) пройденный путь
4) частота обращения

А Б

Ответ:

4 1

Номер: F2BFF1

Установите соответствие между формулами для расчёта физических величин при равномерном движении тела по окружности и названиями этих величин. В формулах использованы обозначения: R – радиус окружности; T – период обращения.

ФОРМУЛЫ
А) `(2πR)/T`
Б) `1/T`

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) центростремительное ускорение
2) линейная скорость
3) пройденный путь
4) частота обращения

А Б

Ответ:

2 4

Номер: A8E4FB

Установите соответствие между формулами для расчёта физических величин при равномерном движении тела по окружности и названиями этих величин. В формулах использованы обозначения: R – радиус окружности; `υ` – линейная cкорость.

ФОРМУЛЫ
А) `(2πR)/υ`
Б) `υ^2/R`

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) период обращения
2) центростремительное ускорение
3) пройденный путь
4) частота обращения

А Б

Ответ:

1 2

Номер: 7091B2

Установите соответствие между формулами для расчёта физических величин при равномерном движении тела по окружности и названиями этих величин. В формулах использованы обозначения: `ν` – частота обращения; Т – период обращения.

ФОРМУЛЫ
А) `1/ν`
Б) `1/T`

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) линейная скорость
2) период обращения
3) частота обращения
4) центростремительное ускорение

А Б

Ответ:

2 3

Номер: 8363D9

ФОРМУЛЫ
А) `(2πR)/T`
Б) `1/T`

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) линейная скорость
2) центростремительное ускорение
3) длина волны
4) частота обращения

А Б

Ответ:

1 4

Номер: 8CCC96

: Обновлено: 03 января 2024

ОГЭ по физике 2024, все задания ФИПИ с ответами