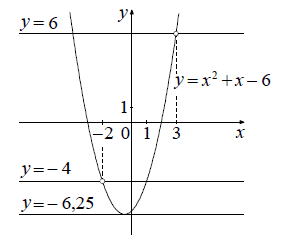Итак, ДЕМО версия ОГЭ по математике. Напоминаю, что нужно правильно решить минимум 2 задания из геометрии, иначе экзамен не засчитают.

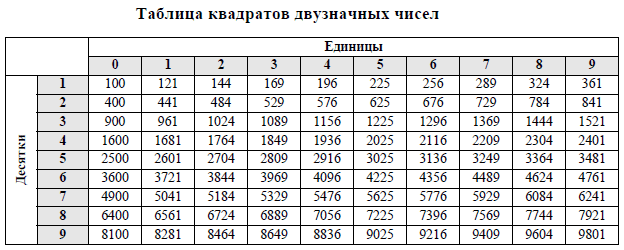
Справочные материалы по математике

Справочные материалы с прошлых лет остались те же. К этим справочным данным будет доступ и у вас на ОГЭ, заучивать их не нужно, нужно уметь ими пользоваться.

Инструкция по выполнению работы

   Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.
   На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
   Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.
   Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.
   Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.
   Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
   Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
   При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
   Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
   При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ и линейкой.
   Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
   После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.

Желаем успеха!

Часть 1

Ответами к заданиям 1–19 являются число или последовательность цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Если ответом является последовательность цифр, то запишите её без пробелов и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.

Прочитайте внимательно текст и выполните задания 1–5.

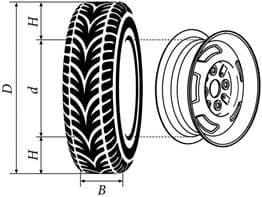
                     Рис. 1                                     Рис. 2

Автомобильное колесо представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). В приведённом примере ширина шины равна 195 мм, а высота боковины равна 65 % от 195, то есть 126,75 мм.
Буква обозначает тип конструкции шины. Буква R означает, что шина радиальная, то есть нити каркаса в шине расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За буквой указан диаметр диска d в дюймах. На рисунке шина рассчитана на диск диаметром 15 дюймов. В одном дюйме 25,4 мм.
Таким образом, зная маркировку шины, можно найти общий диаметр колеса D.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.

1  Завод допускает установку шин разных размеров. В таблице показаны разрешённые размеры шин.

Ширина шины (мм)	Диаметр диска (дюймы)
	13	14	15
165	165/70	165/65	—
175	175/65	175/65; 175/60	—
185	185/65; 185/60	185/60	185/55
195	195/60	195/55	195/55; 195/50

Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.  

Ответ:

185

 2  На сколько миллиметров радиус колеса с шиной 205/55 R14 больше, чем
радиус колеса с шиной 165/65 R14?

Ответ:     .

Ответ:

5,5

 3  На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами 195/50 R15?

Ответ:       .

Ответ:

14,8

 4  Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Ответ:        .

Ответ:

561,2

 5  На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами 175/60 R14? Результат округлите до десятых.

Ответ:         .

Ответ:

0,8

Задания 1-5

 6  Представьте выражение 3/5 − 2/7  в виде дроби со знаменателем 70. В ответ запишите числитель полученной дроби.

Ответ:          .

Ответ:

22

 7  Одно из чисел 5/9 ; 11/9; 13/9; 14/9  отмечено на прямой точкой.

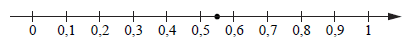
Какое это число?

Ответ:    .

Ответ:

1 (видимо, имеется в виду номер ответа по порядку)

 8  Найдите значение выражения `(a^(14) ⋅ (b^4)^3)/(a⋅b)^(12)` при a = 3 и `b = sqrt3` .

Ответ:          .

Ответ:

9

 9  Решите уравнение 2x² − 3x + 1 = 0.

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ:          .

Ответ:

0,5

 10  В магазине канцтоваров в продаже 100 ручек: 37 красных, 8 зелёных, 17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка окажется красной или чёрной.

Ответ:         .

Ответ:

0,56

 11  Установите соответствие между функциями и их графиками.

ФУНКЦИИ
А) y=− x² −x+5
Б) y=−`3/4 x − 1`
В) y=−`12/x`

ГРАФИКИ
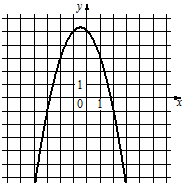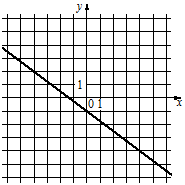1)2)3)

В таблице под каждой буквой укажите соответствующий номер.

            А Б В
Ответ: 

Ответ:

123

 12  Энергия заряженного конденсатора W (в джоулях) вычисляется по формуле `W=(CU^2)/2` где C — ёмкость конденсатора (в фарадах), а U — разность потенциалов на обкладках конденсатора (в вольтах). Найдите энергию конденсатора ёмкостью 10⁻⁴ фарад, если разность потенциалов на обкладках конденсатора равна 12 вольт. Ответ дайте в джоулях.

Ответ:   .

Ответ:

0,0072

 13  Найдите множество решений системы неравенств:
_{ -8+4x > 0,
   4-3x > -8.

1) нет решений
2) ( − ∞; 4)
3) ( 2; + ∞)
4) ( 2; 4 )

Ответ:  

Ответ:

4

 14  Камень бросают в глубокое ущелье. За первую секунду он пролетает 6 м, а за каждую следующую секунду на 10 м больше, чем за предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые 5 секунд?

Ответ:               .

Ответ:

130

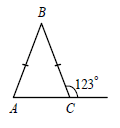 15  равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Ответ:        .

Ответ:

66 (у ФИПИ ошибка, они дали ответ к углу ABC, его и нужно было найти)

 16 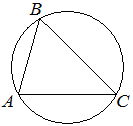 В треугольнике ABC угол C равен 45° , AB = 6 2 . Найдите радиус окружности, описанной около этого треугольника.

Ответ:       .

Ответ:

6

  17 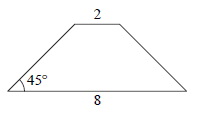 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

Ответ:     .

Ответ:

15

 18 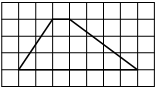 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Ответ:             .

Ответ:

4

 19  Какие из следующих утверждений являются истинными высказываниями?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ:          .

Ответ:

13 <или> 31

Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.

Часть 2

При выполнении заданий 20–25 используйте БЛАНК ОТВЕТОВ № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

 20  Решите уравнение `−12/(x^2−7x−8)≤0`.

 

Решение:

Исходное неравенство принимает вид `12/((x+1)(x-8))≥0`,
откуда x < −1; x > 8 .
Ответ: (− ∞; −1) ; (8; +∞) .

 21  Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61 % кислоты. Сколько процентов кислоты содержится в первом растворе?

Решение:

Пусть концентрация кислоты в первом сосуде равна c₁%, а во втором — c₂%.
Получаем систему уравнений:
{ `(10c_1+16c_2)/26=55`,
   `(c_1+c_2)/2=61`

{ `10c_1+16c_2=1430`,
    `c_1+c_2=122`
откуда c₁ = 87 , c₂ = 35.
Ответ: 87

 22  Постройте график функции `у=(x^4-13x^2+36)/((x-3)(x+2))` и определите, при каких значениях с прямая y =c имеет с графиком ровно одну общую точку.

Решение:

Разложим числитель дроби на множители:

x⁴ −13x² + 36 = (x² − 4)(x² − 9) = ( x − 2)( x + 2)( x − 3)( x + 3).

При x ≠ −2 и x ≠ 3 функция принимает вид:

y = x² + x − 6;

её график — парабола, из которой выколоты точки ( −2; −4) и (3; 6).



Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых выколотая. Вершина параболы имеет координаты ( −0,5; −6,25).

Поэтому c = −6,25, c = −4 или c = 6.

Ответ: c=−6,25; c = −4; c = 6.

Примечание ГДЗответ.ру: к заданиям 23,24 и 25 рисунок на ОГЭ не прилагается, вам нужно сделать его в ходе решения.

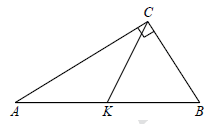
 23  В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6, BC=8. Найдите медиану CK этого треугольника.

Решение:

$CK=\frac12AB=\frac12\sqrt{AC^2+BC^2}=\frac12\sqrt{36+64}=5$

Ответ: 5.

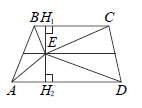
 24  На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.

Доказательство:

Проведём через точку E высоту H₁H₂ трапеции.
По теореме Фалеса средняя линия разделит высоту пополам.
Пусть EH₁ = EH₂ = h . Тогда сумма площадей треугольников BEC и AED равна
`h*(BC)/2+h*(AD)/2=h*(BC+AD)/2`
При этом площадь трапеции равна `2h ⋅ (BC + AD)/2` , что как раз вдвое больше найденной суммы площадей треугольников.

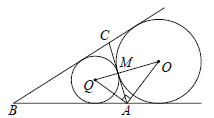
 25  Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Решение:

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC.
Точка касания M окружностей делит AC пополам.
Лучи A Q и AO — биссектрисы смежных углов, значит, угол OAQ прямой.
Из прямоугольного треугольника OAQ получаем: AM 2 = MQ ⋅ MO .
Следовательно,
$QM=\frac{AM^2}{OM}=\frac92=4,5$
Ответ: 4,5.

Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.

ВСЕ задания

Система оценивания ОГЭ по математике 9 класс

Часть 1

За правильный ответ на каждое из заданий 1–19 ставится 1 балл.

Критерии оценивания выполнения заданий с развёрнутым ответом

Часть 2

Задание 20.

Обоснованно получен верный ответ 2
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учётом дальнейшие шаги выполнены верно - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл 2

Задание 21. 

Ход решения задачи верный, получен верный ответ - 2 балла
Верно составлена математическая модель задачи (в алгебраической или иной форме), однако решение до конца не доведено или содержит ошибки
ИЛИ
Решение в целом верное, но содержит несущественные недостатки или вычислительные ошибки - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл 2

Задание 22. 

График построен верно, верно найдены искомые значения параметра - 2 балла
График построен верно, но искомые значения параметра найдены неверно или не найдены - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл 2

Задание 23.  

Ход решения верный, все его шаги выполнены правильно, получен верный ответ - 2 балла
Решение в целом верное, но содержит несущественные недостатки или вычислительные ошибки - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл 2

Задание 24.

Доказательство верное, все шаги обоснованы - 2 балла
Доказательство в целом верное, но содержит несущественные недостатки - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл - 2

Задание  25.

Ход решения верный, получен верный ответ - 2 балла
Решение в целом верное, но содержит несущественные недостатки или вычислительные ошибки - 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов
Максимальный балл - 2

Баллы и оценка по пятибалльной системе

19 заданий с кратким ответом - по 1 баллу за каждое.
6 заданий с развернутым ответом, по 2 балла максимум за каждое.
Всего за тестовую часть можно получить 19 баллов, за развернутую - 12.

0-7 баллов - оценка 2
8-14 баллов (из них минимум 2 балла по геометрии) - оценка 3
15-21 балл (из них минимум 2 балла по геометрии) - оценка 4
22-31 (из них минимум 2 балла по геометрии) - оценка 5

То есть по факту на оценку 4 можно правильно выполнить всего 15 заданий тестовой части, из них 2 задания по геометрии, правда, в профильный класс с таким результатом не возьмут.

Рекомендуемы порог приема в профильные классы для физико-математического профиля - 19 баллов, из них не менее 7 по геометрии (это хотя бы по 1 баллу за каждое задание, ведь их всего 7).

Уже сдали ОГЭ по математике? Пишите в комментариях, какие у вас были задания!