Если прорешаете все эти прототипы, сможете решить любое задание с кратким ответом по планиметрии на реальном ЕГЭ. Обратные и очень близкие типы c mathege не выделяем в прототип, так что могут быть варианты (например, буквы другие, а рисунок тот же).
Площадь треугольника через угол `S_△=1/2*a*c*sinβ`, где β-угол между сторонами a и c.
Площадь треугольника через высоту `S_△=1/2*a*h_a`.
Площадь треугольника через радиус описанной окружности `S_△=(ABC)/(4R)`
Площадь прямоугольного треугольника: `S = (a*b)/2`
Площадь многоугольника через радиус вписанной окружности `S=pr`, где p - полупериметр, r - радиус.
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
`S_(больш.△)/S_(мал.△)=k^2`- отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Радиус окружности, вписанной в равносторонний треугольник `r =(sqrt3*a)/6`; `r =1/3*h`
Радиус окружности описанной около равностороннего треугольника `R =(sqrt3*a)/3`; `R =2/3*h`
Высота равностороннего треугольника `h=(sqrt3*a)/3`
Радиус окружности описанной около прямоугольного треугольника `R = c/2`
Свойства острых углов прямоугольного треугольника
sinA = cosB
sinB = cosA
tgA = ctgB
tgB = ctgA
Тригонометрические формулы: `sin^2α+cos^2α=1`
`1+tg^2α=1/cos^2α`
`1+ctg^2α=1/sin^2α`
`tgα*ctgα=1`
Теорема Пифагора
`c^2=a^2+b^2`
Свойство медианы: в прямоугольном треугольнике медиана, проведенная к гипотенузе. равна половине гипотенузы.
Площадь трапеции `S = (a+b)/2 * h`
Средняя линия трапеции: лежит на серединах сторон; параллельна основаниям; равна полусумме оснований.
Средняя линия треугольника равна половине основания.
В трапеции сумма углов, прилежащих к боковой стороне, равна 180º
Площадь трапеции `S = (a+b)/2 * h`
В трапеции сумма углов, прилегающих к боковой поверхности, равна 180 градусам.
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
Площадь параллелограмма равна произведению основания на высоту `S = ah_a`
Площадь параллелограмма через угол `S=ac*sinα`
Накрест лежащие углы равны при параллельных прямых (из 1 признака параллельности).
Площадь ромба равна половине произведения диагоналей: `S = (d1*d2)/2`
Площадь ромба через радиус вписанной окружности `S_(ромба) =2ar`
Признак описанного четырёхугольника – суммы противоположных сторон равны a+c = b+d
Все прототипы задания ЕГЭ по планиметрии с кратким ответом (168 шт.)
Треугольники
В треугольнике 𝐴𝐵𝐶 угол A равен 37°, стороны AC и BC равны. Найдите угол C. Ответ дайте в градусах.
Решение:
Сумма углов треугольника 180°. В равнобедренном треугольнике углы при основании одинаковы.
∠C=180-37-37=106°
Ответ: 106
Номер: 8286C4
В треугольнике ABC угол C равен 102°, стороны AC и BC равны. Найдите угол A. Ответ дайте в градусах.

Решение:
Сумма углов треугольника 180°. В равнобедренном треугольнике углы при основании одинаковы.
∠A=(180-102)/2=39°
Ответ: 39
Номер: 7AFD6F
В треугольнике 𝐴𝐵𝐶 AD — биссектриса, угол C равен 104°, угол CAD равен 5°. Найдите угол B. Ответ дайте в градусах.
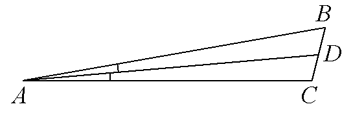
Решение:
Биссектриса делит угол пополам ⇒
∠A=5*2=10°
Сумма углов треугольника 180°.
∠B=180-104-10=66°
Ответ: 66
Номер: 1A845D
В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
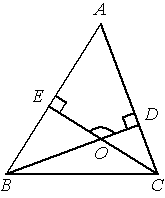
Решение:
Сумма внутренних углов четырёхугольника равна 360°.
Рассмотрим четырехугольник ADOE.
∠DOE=360-90-90-56=124°
Ответ: 124
Номер: A4D931
В треугольнике ABC угол C равен 58° , биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.
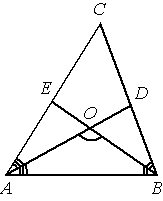
Решение:
∠A+∠B=180-58=122°
`1/2∠A+1/2∠B=122/2=61`°
∠AOB=180-61=119°
Ответ: 119
Номер: 540F92
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.

Решение:
Формула площади треугольника через угол
`S_△=1/2*a*c*sinβ`, где β-угол между сторонами a и c.
`S_(△ABC)=1/2*11*11*sin30°=1/2*11*11*1/2=30,25`
Ответ: 30,25
Номер: 21470A
Впишите правильный ответ.
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
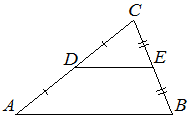
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
Средняя линия равна половине основания, а высота - половине высоты, при этом, исходя из формулы площади треугольника
`S_(ABC)=1/2*AB*h=24`
`S_(CDE)=1/2*1/2AB*1/2h=(1/2*AB*h)*1/4`
То есть площадь меньше в 4 раза.
24/4=6
Ответ: 6
Второе решение:
`S_(больш.△)/S_(мал.△)=k^2`- отношение площадей подобных треугольников равно квадрату коэффициента подобия.
DE — средняя линия, значит k=2
`S_(△ABC)/S_(△CDE)=2^2`
`S_(△CDE)=24/4=6`
Ответ: 6
Номер: F34697
Впишите правильный ответ.
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
Средняя линия равна половине основания, а высота - половине высоты, при этом, исходя из формулы площади
`S_(ABC)=1/2*AB*h=24`
`S_(DCE)=1/2*1/2 AB*1/2 h=1/2*1/4*AB*h`
То есть площадь маленького треугольника меньше в 4 раза. То есть площадь трапеции равна `3/4=0,75` от площади треугольника
24*0,75=18
Ответ: 18
Второе решение:
`S_(больш.△)/S_(мал.△)=k^2`- отношение площадей подобных треугольников равно квадрату коэффициента подобия.
DE — средняя линия, значит k=2
`S_(△ABC)/S_(△CDE)=2^2`
`S_(△CDE)=24/4=6`
`S_(ABED)=24-6=18`
Ответ: 18
Номер: 5B3F1A
В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.
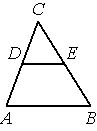
Решение:
`S_(больш.△)/S_(мал.△)=k^2`- отношение площадей подобных треугольников равно квадрату коэффициента подобия.
DE — средняя линия, значит k=2
`S_(△ABC)/S_(△CDE)=2^2`
`S_(△ABC)=24*4=96`
Ответ: 96
Номер: 509E9A
Две стороны треугольника равны 21 и 28. Высота, опущенная на бо́льшую из этих сторон, равна 15. Найдите высоту, опущенную на меньшую из этих сторон треугольника.
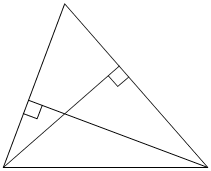
Решение:
Формула площади треугольника через высоту
`S_△=1/2*a*h_a`
`S_△=1/2*28*15=210`
Пусть x - вторая высота
`210=1/2*21*x` | :21
`10=1/2*x`
`х=20`
Ответ: 20
Номер: CA58AE
Впишите правильный ответ.
В треугольнике ABC сторона AB равна `3sqrt2`, угол C равен 135°. Найдите радиус описанной около этого треугольника окружности.
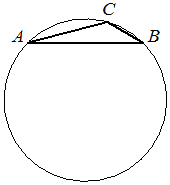
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
По теореме синусов:
`(AB)/(sinC)=2R`
`(3sqrt2)/(sqrt2/2)=2R`
2R =6
R=3
Ответ: 3
Номер: 1DD37A
В треугольнике ABC AB=BC, AC=14, высота CH равна 7. Найдите синус угла ACB.
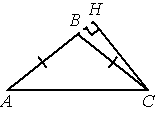
Решение:
1) ΔAHC
`sin∠A = 7/14 = 1/2 = 0,5`
2) sin∠ACB = 0,5
Ответ: 0,5
Номер: 387739
В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC.
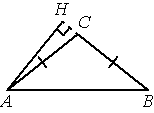
Решение:
1) ΔABH
`sin∠B = 8/20 = 4/10 = 0,4`
2) sin∠BAC = 0,4
Ответ: 0,4
Номер: B26F8E
В треугольнике ABC AC=BC, AB=15, AH — высота, BH=6. Найдите косинус угла BAC.
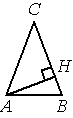
Решение:
1) ∠A =∠B
2) ΔABH
`сos∠B = 6/15 = 2/15 = 0,4`
2) cos∠BAC = 0,4
Ответ: 0,4
Номер: C18485
В треугольнике ABC AC=BC , высота CH равна 19,2, cosA=7/25. Найдите AC.
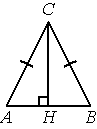
Решение:
1) `sin^2α + (7/25)^2=1`
`sin^2A + (49/625)^2=1`
`sin^2A = 576/625`
`sinA = 24/25`
2) `sinA = 24/25=(19,2)/(AC)`
`AC = (25*19,2*0,8)/24 =20`
Ответ: 20
Номер: 244628
В треугольнике ABC AC=BC=20 , AB=28. Найдите cosA.
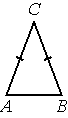
Решение:
`cosA = (AH)/(AC)=14/20=7/10=0,7`
Ответ: 0,7
Номер: 565E4B
В равностороннем треугольнике ABC высота CH равна 45√3. Найдите AB.
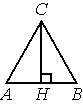
Решение:
Высота равностороннего треугольника
`h=(sqrt3*a)/3`
`45sqrt3=(sqrt3*AB)/2`| :3
`AB=45*2=90`
Ответ: 90
Номер: 7CD17A
В треугольнике ABC угол C равен 90°, BC=12, cosB=3/5. Найдите AB.
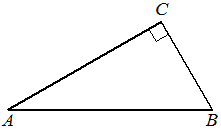
Решение:
`cosB = 3/5 = 12/(AB)`
`AB=(5*12)/3=20`
Ответ: 20
Номер: D74EE5
В треугольнике ABC угол C равен 90°, BC=6, AB=10. Найдите sinB.
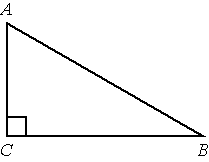
Решение:
1) `10^2=6^2+AC^2`
`100=36+AC^2`
`AC^2 =64`
AC =8
2) `sinB=8/10=0,8`
Ответ: 0,8
Номер: 27BB40
Впишите правильный ответ.
В треугольнике 𝐴𝐵𝐶 угол C равен 90°, AB=10 , BC=√19. Найдите cosA.

КЭС: 5.1.1 Треугольник
Решение:
Находим неизвестный катет по теореме Пифагора.
`10^2=sqrt(19)^2+x^2`
`x^2=10^2-sqrt(19)^2`
`x^2 = 81`
`х=9`
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
`cosA=9/10=0,9`
Ответ: 0,9
Номер: A33A46
В треугольнике 𝐴𝐵𝐶 угол C равен 90°, sinA=0,8. Найдите sinB.

Решение:
`sin^2B+cos^2B=1`
`sin^2B+0,64=1`
`sin^2B=0,36`
`sinB=0,6`
Ответ: 0,6
Номер: CD84BB
В треугольнике ABC угол C равен 90°, AC=6 , tgA=√5/2. Найдите AB.
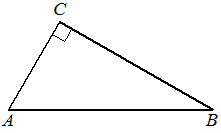
Решение:
`1+tg^2α=1/(cos^2α)`
1) `1+5/4=1/(cos^2A)`
`9/4=1/(cos^2A)`
`cos^2A =4/9`
`cosA = 2/3`
2) `cosA = 2/3 =6/(AB)`
`AB = 9`
Ответ: 9
Номер: 58D926
В треугольнике ABC CD — медиана, угол C равен 90° , угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.
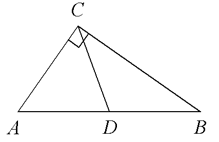
Решение:
Свойство медианы. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы
1) ∠BCD = 35°
2) ∠ACD = 90 - 35 = 55°
Ответ: 55
Номер: 5B17F7
Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14° . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
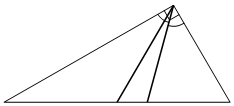
Решение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
1) ∠BCK=45º
2) ∠ACM=90-45-14=31º
3) ∠A = 31º так как ΔACM равнобедренный.
Ответ: 31
Номер: CAC0BA
В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14° . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
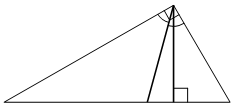
Решение:
1) ∠BCH=45-14=31º
2) ΔBCH: ∠B = 180-90-31=59º
3) ΔABC: ∠A = 180-90-59=31º
Ответ: 31
Номер: 70BEF2
Острые углы прямоугольного треугольника равны 84° и 6° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
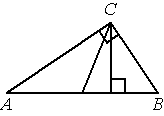
Решение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
1) ΔBCH: ∠BCH=180-90-84=6º
2) ∠ACM =6 так как ΔACM равнобедренный
3) ∠MСH = 90-6-6=78º
Ответ: 78
Номер: F1150D
В треугольнике 𝐴𝐵𝐶: ∠𝐶=90°, 𝐵𝐶=4√3, 𝐴𝐶=4. Найдите sin𝐵.

Решение:
1) Находим гипотенузу по теореме Пифагора
`AB^2=4^2+(4sqrt3)^2`
`AB^2=64`
`AB=8`
2) `sinB=4/8=1/2=0,5`
Ответ: 0,5
ЕГЭ 2015
В треугольнике 𝐴𝐵𝐶 𝐴𝐵=𝐵𝐶. Внешний угол при вершине 𝐵 равен 94°. Найдите угол 𝐶. Ответ дайте в градусах.
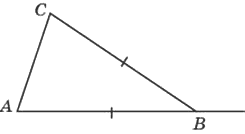
Решение:
Смежные углы вместе составляют 180°
∠Bвнутр.=180-94=86°
Сумма углов треугольника 180°. В равнобедренном треугольнике углы при основании одинаковы.
∠C=(180-86)/2=47°
Ответ: 47
mathege, ЕГЭ 2018
Боковые стороны равнобедренного треугольника равны 136, основание равно 128. Найдите радиус вписанной окружности.
Решение:
Формула площади треугольника через высоту
`S_△=1/2*a*h_a`
Формула площади треугольника через радиус вписанной окружности
S=pr, где p - полупериметр, r - радиус
Построим высоту CH и найдем ее по теореме Пифагора из △ACH.
1362=642+CH2
CH2=1362-642
CH2=(136-64)(136+64)
CH2=72*200
CH2=36*400
CH=6*20=120
`1/2*a*h_a=pr`
`1/2*128*120=(136*2+128)/2*r`
`64*120=200*r`
`r=(64*120)/200`
`r=(64*6)/10`
`r=38,4`
Ответ: 38,4
mathege, ЕГЭ 2014
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
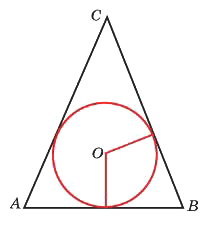
Решение:
Отрезки касательных к окружности, проведенные из одной точки, равны, и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
1) АС=11
2) АВ = 1+1=2
3) P = 11+11+2=24
Ответ: 24
mathege, ЕГЭ 2017
В прямоугольном треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐴𝐵=4, tg𝐴=0,75. Найдите 𝐴𝐶.
Решение:
Тригонометрические формулы
`1+tg^2α=1/(cos^2α)`
1) `1+(3/4)^2=1/(cos^2A)`
`1/(cos^2A)=1/1+9/16`
`1/(cos^2A)=25/16`
`cos^2A=16/25`
`cosA=4/5`
2) `cosA=4/5 =(AC)/4`
`AC = (4*4)/5=16/5=3,2`
Ответ: 3,2
ЕГЭ 2016
Острый угол 𝐵 прямоугольного треугольника равен 66°. Найдите угол между биссектрисой 𝐶𝐷 и медианой 𝐶𝑀, проведёнными из вершины прямого угла. Ответ дайте в градусах.
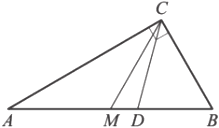
Решение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
1) ∠BCD=45º
2) ∠A=180-90-66=24º
3) ∠ACM=24º так как ΔACM равнобедренный
4) ∠MСD=90-45-24=21º
Ответ: 21
mathege, ЕГЭ 2017
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 10°, внешний угол при вершине 𝐵 равен 31°. Найдите угол 𝐶. Ответ дайте в градусах.
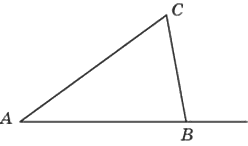
Решение:
Смежные углы вместе составляют 180°
∠Bвнутр.=180-31=149°
Сумма углов треугольника 180°.
∠C=180-149-10=21°
Ответ: 21
mathege
В треугольнике 𝐴𝐵𝐶 стороны 𝐴𝐶 и 𝐵𝐶 равны, угол 𝐶 равен 134°, угол 𝐶𝐵𝐷− внешний. Найдите угол 𝐶𝐵𝐷. Ответ дайте в градусах.
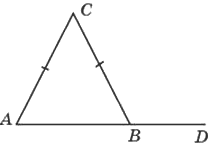
Решение:
Сумма углов треугольника 180°. В равнобедренном треугольнике углы при основании одинаковы.
∠Bвнутр.=(180-134)/2=23°
Смежные углы вместе составляют 180°
∠Bвнеш.=180-23=157°
Ответ: 157
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 60°, 𝐶𝐻 — высота, угол 𝐵𝐶𝐻 равен 19°. Найдите угол 𝐴𝐶𝐵. Ответ дайте в градусах.
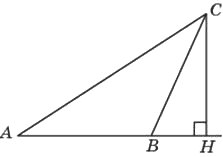
Решение:
Сумма углов треугольника 180°.
Рассмотрим △ACH.
∠ACH=180-90-60=30°
∠ACB=30-19=11°
Ответ: 11
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=𝐵𝐶, 𝐴𝐷− высота, угол 𝐵𝐴𝐷 равен 34°. Найдите угол 𝐶. Ответ дайте в градусах.
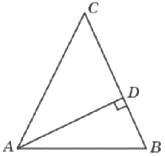
Решение:
Сумма углов треугольника 180°.
Рассмотрим △ABD.
∠ABD=180-90-34=56°
В равнобедренном треугольнике углы при основании одинаковы.
∠A=∠B=56°
∠C=180-56-56=68°
Ответ: 68
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 50°, 𝐴𝐷 — биссектриса, угол 𝐵𝐴𝐷 равен 63°. Найдите угол 𝐴𝐷𝐵. Ответ дайте в градусах.
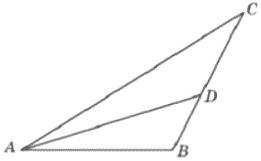
Решение:
Сумма углов треугольника 180°.
Рассмотрим △ADC.
∠ADC=180-63-50=67°
Смежные углы вместе составляют 180°
∠ADB=180-67=113°
Ответ: 113
mathege
Два угла треугольника равны 53° и 48°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
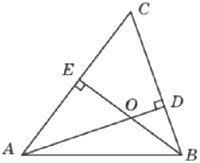
Решение:
Сумма углов треугольника 180°.
∠C=180-53-48=79°
Сумма внутренних углов четырёхугольника равна 360°.
∠EOD=360-79-90-90=101°
Ответ: 101
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 100°, угол 𝐶 равен 13°. На продолжении стороны 𝐴𝐵 за точку 𝐵 отложен отрезок 𝐵𝐷, равный стороне 𝐵𝐶. Найдите угол 𝐷 треугольника 𝐵𝐶𝐷. Ответ дайте в градусах.
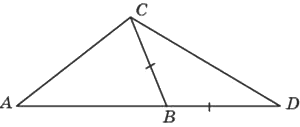
Решение:
Сумма углов треугольника 180°.
Рассмотрим △ABC.
∠B=180-100-13=67°
Смежные углы вместе составляют 180°
∠Bвнеш.=180-67=113°
В равнобедренном треугольнике углы при основании одинаковы.
∠BDC=(180-113)/2=67/2=33,5°
Ответ: 33,5
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 60°, угол 𝐵 равен 53°. 𝐴𝐷, 𝐵𝐸 и 𝐶𝐹− биссектрисы, пересекающиеся в точке 𝑂. Найдите угол 𝐴𝑂𝐹. Ответ дайте в градусах.
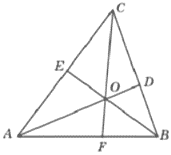
Решение:
∠C=180-60-53=67°, CF - биссектриса ⇒ ∠ACF=67/2=33,5°
△AFC: ∠AFC=180-60-33,5=86,5°
△AOF: ∠AOF=180-30-86,5=63,5°
Ответ: 63,5
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 21°, угол 𝐵 равен 81°. 𝐴𝐷, 𝐵𝐸 и 𝐶𝐹− высоты, пересекающиеся в точке 𝑂. Найдите угол 𝐴𝑂𝐹. Ответ дайте в градусах.

Решение:
∠BAD=180-90-81=9°
∠AOF=180-90-9=81°
Ответ: 81
mathege
В треугольнике 𝐴𝐵𝐶 𝐶𝐻 — высота, 𝐴𝐷 — биссектриса, 𝑂 — точка пересечения прямых 𝐶𝐻 и 𝐴𝐷, угол 𝐵𝐴𝐷 равен 42°. Найдите угол 𝐴𝑂𝐶. Ответ дайте в градусах.
Решение:
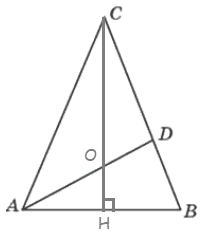
𝐴𝐷 — биссектриса ⇒ ∠CAO=∠BAD=42°
△ACH: ∠ACH=180-90-84=6°
△AOC: ∠AOC=180-42-6=132°
Ответ: 132
mathege 47548
В треугольнике 𝐴𝐵𝐶 проведена биссектриса 𝐴𝐷 и 𝐴𝐵=𝐴𝐷=𝐶𝐷. Найдите меньший угол треугольника 𝐴𝐵𝐶. Ответ дайте в градусах.
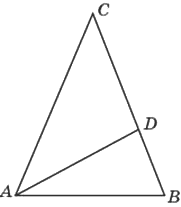
Решение:
С - меньший угол, так как противолежащая сторона самая короткая. Примем угол C за х.
∠C=∠CAD=∠DAB=х
△ABC: ∠B=180-3х
△ABD: ∠B=(180-х)/2
180-3х=(180-х)/2
360-6х=180-х
5х=180
х=36
Ответ: 36
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐵 равен 50°, угол 𝐶 равен 77°, 𝐴𝐷− биссектриса, 𝐸− такая точка на 𝐴𝐵, что 𝐴𝐸=𝐴𝐶. Найдите угол 𝐵𝐷𝐸. Ответ дайте в градусах.
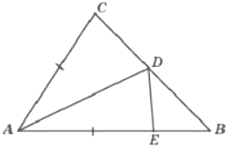
Решение:
Сумма углов треугольника 180°.
Рассмотрим △ABC.
∠A=180-77-50=53°
△ACD=△ADE по 1 признаку (по двум сторонам и углу между ними) ⇒
∠AED=77°
Смежные углы вместе составляют 180°
∠BED=180-77=103°
△BDE: ∠BDE=180-103-50=27°
Ответ: 27
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 17°, угол 𝐵 равен 46°, 𝐶𝐷− биссектриса внешнего угла при вершине 𝐶, причем точка 𝐷 лежит на прямой 𝐴𝐵. На продолжении стороны 𝐴𝐶 за точку 𝐶 выбрана такая точка 𝐸, что 𝐶𝐸=𝐶𝐵. Найдите угол 𝐵𝐷𝐸. Ответ дайте в градусах.
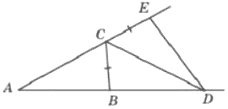
Решение:
△ABC: ∠C=180-17-46=117°
∠Cвнеш.=180-117=63°, CD - биссектриса ⇒ ∠BCD=63/2=31,5°
∠Bвнеш.=180-46=134°
∠BDC=180-134-31,5=14,5°
△BCD=△CED по 1 признаку (по двум сторонам и углу между ними) ⇒
∠CDE=∠BDC=14,5°
∠BDE=14,5*2=29°
Ответ: 29
mathege
Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.
Решение:
Сумма углов треугольника 180°.
2х+3х+4х=180°
9х=180
х=20
2х=2*20=40°
Ответ: 40
mathege
Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.
Решение:
Формула площади треугольника через угол
`S_△=1/2*a*c*sinβ`, где β-угол между сторонами a и c.
`S_(△ABC)=1/2*2*21*sin30°=21*1/2=10,5`
Ответ: 10,5
mathege
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

Решение:
Формула площади треугольника через высоту
`S_△=1/2*a*h_a`
Проведем высоту CH, получим прямоугольный △ACH
По теореме Пифагора
52=32+CH2
CH2=25-9
CH2=16
CH=4
`S_(△ABC)=1/2*6*4=12`
Ответ: 12
mathege
Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
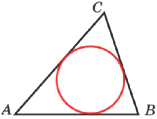
Решение:
Формула площади треугольника через радиус вписанной окружности
S=pr, где p - полупериметр, r - радиус
`S=76/2*8=38*8=304`
Ответ: 304
mathege
Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
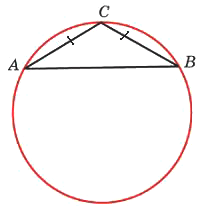
Решение:
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
∠A=(180-120)/2=30°
`7/(sin30°)=2R`
`7/(1/2)=2R`
14=2R=d
Ответ: 14
mathege
Боковые стороны равнобедренного треугольника равны 104, основание равно 192. Найдите радиус описанной окружности этого треугольника.
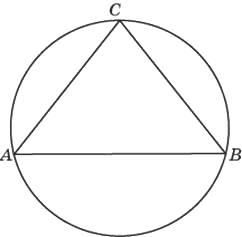
Решение:
Площадь треугольника через радиус описанной окружности
`S_△=(ABC)/(4R)`
Проведем высоту CH.
△ACH: По теореме Пифагора
`104^2=96^2+CH^2`
`CH^2=104^2-96^2`
`CH^2=(104-96)(104+96)`
`CH^2=8*200`
`CH^2=1600`
`CH=40`
`S_(△ABC)=1/2*192*40=96*40`
`(ABC)/(4R)=96*40`
`(104*104*192)/4R=96*40`
`4R=(104*104*192)/(96*40)`
`R=(104*104*192)/(96*40*4)`
`R=(26*26*2)/10`
`R=1352/10`
`R=135,2`
Ответ: 135,2
mathege
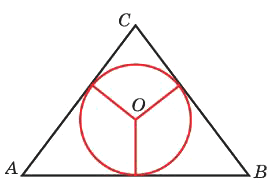
К окружности, вписанной в треугольник 𝐴𝐵𝐶, проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника.
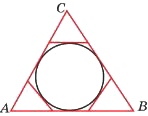
Решение:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.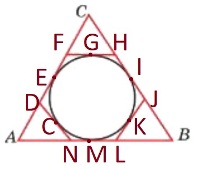
1) `P_(CFH) = 8 = CF+CH+FG+GH` (FG=EF, GH=IH)
2) `P_(ADN) = 23 = AD+AN+DO+ON` (DO=DE, ON=NM)
3) `P_(JBL) = 78 = JB+BL+LK+KJ` (LK=ML, KJ=IJ)
4) `P_(ABC) = CF+CH+FG+GH +AD+AN+DO+ON+JB+BL+LK+KJ = 8+23+78=109`
Ответ: 109
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=𝐵𝐶=2√2, угол 𝐶 равен 135°. Найдите высоту 𝐴𝐻.
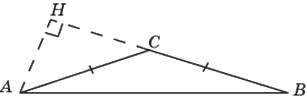
Решение:
1) ∠ACH =180-135=45º
2) ∠HAC = 180-90-45=45º ⇒ ΔAHC прямоугольный и равнобедренный
3) Пусть AH = x = CH
`(2sqrt2)^2=x^2+x^2`
`8=2 x^2`
`x^2 = 4`
`x = 2`
Ответ: 2
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=𝐵𝐶=2√2, угол 𝐶 равен 45°. Найдите высоту 𝐴𝐻.
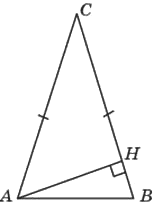
Решение:
1) ∠CAH =180-90-45=45º ⇒ ΔCAH прямоугольный и равнобедренный
2) Пусть CH = x = AH
`(2sqrt(2))^6=x^2+x^2`
`8=2 x^2`
`x^2 = 4`
x = 2
Ответ: 2
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=𝐵𝐶, угол 𝐶 равен 120°, 𝐴𝐵=2√3. Найдите 𝐴𝐶.

Решение:
ΔACH:
`sin60º = sqrt3/(AC)`
`sqrt3/2 = sqrt3/(AC)`
`AC = (sqrt3*2)/sqrt3 = 2`
Ответ: 2
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=𝐵𝐶, 𝐴𝐵=40, высота 𝐶𝐻 равна 20√3. Найдите угол 𝐶. Ответ дайте в градусах.

Решение:
1)`AC = sqrt(20^2+(20sqrt3)^2) = 40`
2) `sin∠ACH = 20/40=1/2` ⇒ ∠ACH = 30º
3) ∠C = 2*30=60º
Ответ: 60
mathege
Больший угол равнобедренного треугольника равен 164°. Найдите меньший угол. Ответ дайте в градусах.
Решение:

`(180-164)/2 = 8`
Ответ: 8
mathege
Один угол равнобедренного треугольника на 90° больше другого. Найдите меньший угол. Ответ дайте в градусах.
Решение:

α +α+α+90=180º
3α = 90º
α = 30º
Ответ: 30
mathege
Сторона правильного треугольника равна 6√3. Найдите радиус окружности, вписанной в этот треугольник.
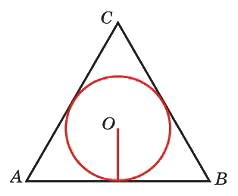
Решение:
Радиус окружности, вписанной в равносторонний треугольник
`r =(sqrt3*a)/6`
`r =1/3*h`
`r =(sqrt3*6sqrt3)/6=sqrt9=3`
Ответ: 3
mathege
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 138.

Решение:
Радиус окружности вписанной в равносторонний треугольник
`r =(sqrt3*a)/6`
`r =1/3*h`
`r =1/3*138=46`
Ответ: 46
mathege
Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.
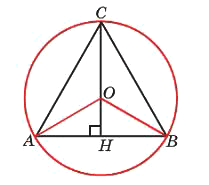
Решение:
Радиус окружности описанной около равностороннего треугольника
`R =(sqrt3*a)/3`
`R =2/3*h`
`R =2/3*33=2*11=22`
Ответ: 22
mathege
Сторона правильного треугольника равна 22√3. Найдите радиус окружности, описанной около этого треугольника.
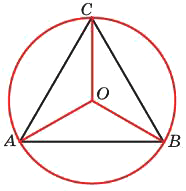
Решение:
Радиус окружности описанной около равностороннего треугольника
`R =(sqrt3*a)/3`
`R =2/3*h`
`R =(sqrt3*22*sqrt3)/3=(22*sqrt9)/3=22`
Ответ: 22
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶=8, cos𝐴=0,5. Найдите высоту 𝐶𝐻.
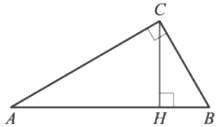
Решение:
Свойства острых углов прямоугольного треугольника
sinA = cosB
sinB = cosA
tgA = ctgB
tgB = ctgA
ΔBCH
`sinB = 1/2=CH/8`
CH=4
Ответ: 4
mathege 27273
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐴𝐵=4√15, cos𝐴=0,25. Найдите высоту 𝐶𝐻

Решение:
`sin^2α+cos^2α=1`
1) ΔABC
`cosA = 1/4=(AC)/(4sqrt(15)) ⇒ AC = sqrt15`
2) `sin^2A+1/16=1`
`sin^2A=15/16`
`sinA=sqrt15/4`
3) ΔACH
`sinA=sqrt15/4=(CH)/sqrt15`
`CH = 15/4=3,75`
Ответ: 3,75
mathege 27264
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐶𝐻− высота, 𝐴𝐵=27, sin𝐴=2/3. Найдите 𝐴𝐻.

Решение:
`sin^2α+cos^2α=1`
1) `4/9+cos^2A =1`
`cos^2A =5/9`
`cos^2A =sqrt5/3`
2) ΔABC:
`cosA = sqrt5/3=(AC)/27 ⇒ AC = 9*sqrt5`
3) ΔACH:
`cosA = sqrt5/3=(AH)/(9sqrt5) ⇒ AH = 15`
Ответ: 15
mathege 27263
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐶𝐻− высота, 𝐵𝐶=7, tg𝐴=`(4sqrt33)/33`. Найдите 𝐵𝐻.

Решение:
Тригонометрические формулы
`sin^2∝+cos^2∝=1`
`1+tg^2∝=1/(cos^2∝)`
1) `1+tg^2A=1/(cos^2A)`
`1/1+(16*33)/33^2=1/(cos^2A)`
`49/33=1/(cos^2A)`
`cos^2A=33/49`
`cosA=sqrt(33)/7=sinB`
2) `33/49+cos^2B=1`
`cos^2B=16/49`
`cosB=4/7`
3) ΔBCH
`cosB=4/7=(BH)/7 ⇒ BH = 4`
Ответ: 4
mathege 27274
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐶𝐻− высота, 𝐴𝐵=13, tg𝐴=5. Найдите 𝐵𝐻.

Решение:
`1+tg^2∝=1/(cos^2∝)`
1) `1+25=1/(cos^2A)`
`26=1/(cos^2A)`
`cos^2A = 1/26`
`cosA = 1/sqrt(26)`
2) ΔABC
`cosA = 1/sqrt26 = (AC)/13 ⇒ AC=13/sqrt26`
3) ΔACH
`cosA = 1/sqrt26 = AH*sqrt26/13 ⇒ 1/sqrt26 = (sqrt26*AH)/13 ⇒ sqrt26*AH = 13/sqrt26`
AH = 0,5
4) BH=13-0,5=12,5
Ответ: 12,5
mathege
В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐶𝐻− высота, 𝐵𝐶=3, sin𝐴=1/6. Найдите 𝐴𝐻.

Решение:
Тригонометрические формулы
`1+tg^2∝=1/(cos^2∝)`
Свойства острых углов прямоугольного треугольника
sinA = cosB
sinB = cosA
tgA = ctgB
tgB = ctgA
1) `sinA = 1/6 = 3/AB ⇒ AB=18`
2) `18^2=3^2+AC^2`
`324=9+AC^2`
`AC^2 = 315`
`AC = sqrt(9*35)=3sqrt35`
3) `1/36+cos^2A=1`
`cos^2A=35/36`
`cosA=sqrt35/6`
4) ΔACH
`cosA=sqrt35/6 = (AH)/(3sqrt35)`
`AH = 17,5`
2 способ:
1) `sinA = 1/6 = 3/AB ⇒ AB=18`
2) ΔBCH: `cosB=1/6 =(BH)/3`
BH=0,5
3) AH=18-0,5=17,5
Ответ: 17,5
mathege
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
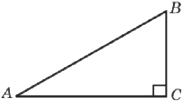
Решение:
Площадь прямоугольного треугольника:
`S = (a*b)/2`
Теорема Пифагора
`c^2=a^2+b^2`
1) `10^2=6^2+AC^2`
`100=36+AC^2`
`AC^2 = 64`
`AC = 8`
2) `S = (6*8)/2=24`
Ответ: 24
mathege
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Решение:
Площадь прямоугольного треугольника:
`S = (a*b)/2`
Теорема Пифагора
`c^2=a^2+b^2`
1) `S = 24/1=(x*(x+2))/2`
2) `x^2+2x=48`
`x^2+2x-48=0`
`x_1=-8`
`x_2=6`
Ответ: 6
mathege
Один острый угол прямоугольного треугольника на 32° больше другого. Найдите больший острый угол. Ответ дайте в градусах.

Решение:
∝+∝-32+90=180°
2∝=122°
∝=61°
Ответ: 61
mathege
Гипотенуза прямоугольного треугольника равна 28. Найдите радиус описанной окружности этого треугольника.
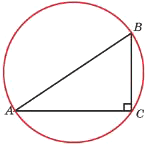
Решение:
Радиус окружности описанной около прямоугольного треугольника
`R = c/2`
`R = 28/2=14`
Ответ: 14
mathege
Острый угол прямоугольного треугольника равен 56°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
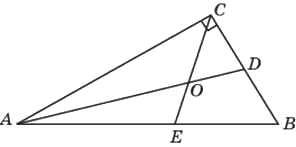
Решение:
1) ∠AOC = 180-45-28=107°
2) ∠AOE = 180-107 = 73°
Ответ: 73
mathege
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
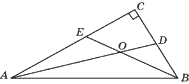
Решение:
1) ∠A + ∠B =90º
2) `1/2 ∠A +1/2 ∠B =45º`
3) ∠AOB = 180-45=135º
4) ∠AOE = 180-135=45º
Ответ: 45
mathege
В треугольнике 𝐴𝐵𝐶 𝐴𝐶=37,5, 𝐵𝐶=20, угол 𝐶 равен 90°. Найдите радиус вписанной окружности.
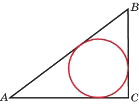
Решение:
Площадь треугольника через радиус
S=pr, p - полупериметр
Площадь прямоугольного треугольника
`S = (a*b)/2`
1) `S = (37,5*20)/10=375`
2) `AB^2=20^2+(75/2)^2`
`AB^2=400+5625/4`
`AB^2=7225/4`
`AB=42,5`
3) `p = (42,5+37,5+20)/2 =50`
4) `r = 375/50=7,5`
Ответ: 7,5
mathege
Катеты равнобедренного прямоугольного треугольника равны 82+41√2. Найдите радиус окружности, вписанной в этот треугольник.

Решение:
Площадь треугольника через радиус S=pr, p - полупериметр
1) `AB^2=41^2*(2+sqrt2)^2+41^2*(2+sqrt2)^2=2*41^2*(2+sqrt2)^2`
`AB^2=41sqrt2*(2+sqrt2)^2=82*sqrt2+82`
2) `S =(41*(2+sqrt2)*41*(2+sqrt2))/2=(41^2*(2+sqrt2)^2)/2`
3) `p=(82+82sqrt2+82+41sqrt2+82+41sqrt2)/2=(3*82+4*41sqrt2)/2`
4) `r=(41^2*(2+sqrt2)^2)/(3*2*41+4*41*sqrt2)=(41^2*(4+4sqrt2+2))/(41*(6+4*sqrt2)=41`
Ответ: 41
mathege
Прямоугольник
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Решение:
1) `x*2x=18`
`2x^2=18`
`x^2=9`
`x=3`
2) P = 2*3+2*6=18
Ответ: 18
mathege
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.

Решение:
1) `P = 2x+2(x+3)=18`
`2x+2x+6=18`
`4x=12`
`x=3`
2) S = 3*6=18
Ответ: 18
mathege
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
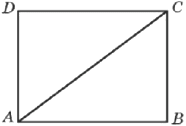
Решение:
1) `(5x)^2=(4x)^2+6^2`
`25^2=16x^2+36`
`9x^2=36`
`x^2=4`
`x=2`
2) `S=6*8=48`
Ответ: 48
mathege
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.

Решение:
1) `P =2*AD+2*CD=42`
`AD+CD=21`
2) CD=x
AD=21-x
3) `S_(abcd)=x*(21-x)=98`
`-x^2+21*x-98=0`
`x^2+21*x+98=0`
`x_1=7`
`x_2=14`
БОльшая сторона 14
Ответ: 14
mathege
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
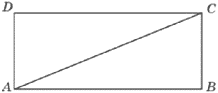
Решение:
1) `2*AD+2*CD=34` | :2
`AD+CD=17`
`CD=17-x`
2) `S_(abcd)=x*(17-x)=60`
`-x^2+17x-60=0` |:(-1)
`x^2-17x+60=0`
`x_1=12`
`x_2=5`
3) ΔACD:
`AC^2=5^2+12^2`
`AC^2=169`
`AC=13`
Ответ: 13
mathege
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Решение:
1) P=2AB+2BC=28
AB+BC=14
Пусть AB=x, тогда BC = 14 - x
2) `10^2=x^2+(14-x)^2`
`100=x^2+196-28x+x^2`
`2x^2-28x+96=0`
`x^2-14x+48=0`
`x_1=6`
`x_2=8`
3) S=6*8=48
Ответ: 48
mathege
Параллелограмм
Один угол параллелограмма больше другого на 40°. Найдите меньший угол. Ответ дайте в градусах.
Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
∝+∝+40=180
2∝ = 140
∝ =70°
Ответ: 70
Номер: 2E0A28
Один угол параллелограмма больше другого на 52°. Найдите больший угол. Ответ дайте в градусах.

Решение:
В параллелограмме сумма углов прилегающих к любой стороне равна 180 градусам.
∝+∝-52=180
2∝ = 232
∝ = 116
Ответ: 116
Номер: 3C09A9
Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.
Решение:
Площадь параллелограмма равна произведению основания на высоту.
`S = 5*3=15`
`S = 10*h_(10)=15`
`h_(10) = 15/10=1,5`
Ответ: 1,5
Номер: D254F2
Площадь параллелограмма 𝐴𝐵𝐶𝐷 равна 132. Точка G — середина стороны CD. Найдите площадь трапеции ABGD.
Решение:
Если из середины G провести параллельную прямую стороне CB, то она также будет делить АB пополам.
Площадь такого параллелограмма будет равна `132/2=66`
При этом GB будет диагональю правой половины и делит ее тоже пополам.
Тогда:
`S_(ABGD) = 66+33=99`
Ответ: 99
Номер: 2695F1
Впишите правильный ответ.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AD. Найдите площадь трапеции BCDE .
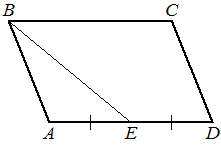
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
Площадь параллелограмма равна
S=AD*h
Площадь трапеции
S=`(AD+ED)/2*h=(1,5AD)/2 * h` = 0,75AD*h
То есть 0,75 от площади параллелограмма равна площадь трапеции
28*0,75=21
Ответ: 21
Номер: F12D1C
В ромбе 𝐴𝐵𝐶𝐷 угол CDA равен 78°. Найдите угол ACB. Ответ дайте в градусах.
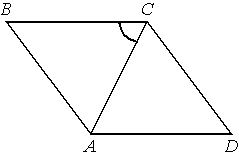
Решение:
1) ∠B = 78
2) AB=BC
⇒ ΔABC равнобедренный
3) `∠ACB =(180-78)/2=51`
Ответ: 51
Номер: 257EE0
Угол между стороной и диагональю ромба равен 54°. Найдите острый угол ромба.

Решение:
1) BC=AB
⇒ ΔABC равнобедренный.
⇒ ∠BAC = 54
2) ∠B = 180-2*54=180-108=72
Ответ: 72
mathege, ЕГЭ 2019
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Решение:
x - одна сторона
x+3 - вторая сторона
P = 46 = 2x+2(x+3)
46 = 2x+2x+6
40=4*x
x=10
Ответ: 10
mathege
Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах.

Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
1) ∠A + ∠B = 180°
3x+7x=180°
10x=180°
x = 18°
2) ∠B = 7*18=126°
Ответ: 126
mathege
Две стороны параллелограмма относятся как 3:4, а его периметр равен 70. Найдите большую сторону параллелограмма.

Решение:
Примем одну сторону за 3x, вторую за 4x.
1) `P_(ABCD)=70=2*4x+2*3x`
`14x=70`
`x=5`
2) BC=4*5=20
Ответ: 20
mathege
Сумма двух углов параллелограмма равна 100°. Найдите один из оставшихся углов. Ответ дайте в градусах.

Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
1) ∠A+∠C=100° ⇒
∠A=1/2*100=50°
2) ∠B=180-50-130°
Ответ: 130
mathege
Площадь параллелограмма равна 12, две его стороны равны 4 и 8. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению основания на высоту.
`S = 8*h_8=12`
`S = 8*h_4=12`
`h_4 = 3`
Ответ: 3
mathege
Площадь параллелограмма 𝐴𝐵𝐶𝐷 равна 155. Точка 𝐸 — середина стороны 𝐶𝐷. Найдите площадь треугольника 𝐴𝐷𝐸.
Решение:
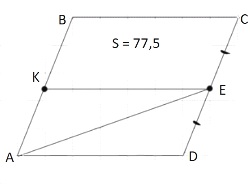
Если из середины Е провести параллельную прямую стороне AB, то она также будет делить АB пополам. Если провести диагональ то это будет искомый треугольник и половина половины.
`S_(ADE) = 155/4 = 38,75`
Ответ: 38,75
mathege
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
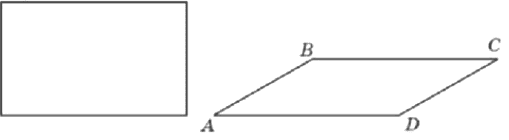
Решение:
Площадь параллелограмма равна
`S = ac*sin∝`
1) `S_(прям.) = ab`
2) `S_(пар.) = 1/2 ab = sinA * ab` | :ab
`sinA = 1/2 = 30°`
Ответ: 30
mathege
Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
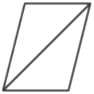
Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
1) ∠A = 26+34=60º
2) ∠A +∠B = 180º
60 + ∠B = 180º
∠B = 180-60=120º
Ответ: 120
mathege
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 10. Найдите его большую сторону.
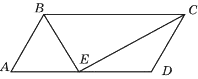
Решение:
Накрест лежащие углы равны при параллельных прямых (из 1 признака параллельности)
1) ∠AEB = ∠CBE
∠CED = ∠BCE
⇒ ΔABE равнобедренный
ΔСDЕ равнобедренный
2) AD=10+10=20
Ответ: 20
mathege
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2:7, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
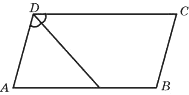
Решение:
Накрест лежащие углы равны при параллельных прямых (из 1 признака параллельности)
1) ∠CDK = ∠AKD
⇒ ΔADK равнобедренный
⇒ AD = 2x
2) P = 33 = 2*2x+2*9x
33 = 22x
x=1,5
3) СD = 9*1,5=13,5
Ответ: 13,5
mathege
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
1) ∠A+∠B = 180
2∝ + 2∝ = 180 |:2
∝ + ß = 90
2) ∠AOB = 180 - (∝ + ß) = 180 -90 = 90
Ответ: 90
mathege
Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
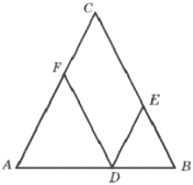
Решение:
1) FC+CE=10
2) ∠A=∠B=∝
∠FDA=∝ (соответ.)
∠BDE=∝
3) `P_(CFDE) = FC+CE +FC+CE =20`
Ответ: 20
mathege
В параллелограмме 𝐴𝐵𝐶𝐷 известно, что 𝐴𝐵=2, 𝐴𝐷=9, sin𝐴=4/9. Найдите большую высоту параллелограмма.
Решение:
Площадь параллелограмма
S = ah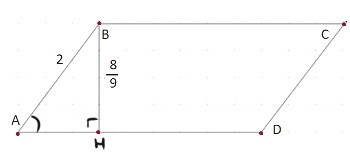
1) ΔABH:
`sinA = 4/9=(BH)/2`
`BH = 4*2/9=8/9`
2) `S_(ABCD) = 9 * 8/9 = 8`
`S_(ABCD) = 8 = 2*h`
`h = 8/2=4`
Ответ: 4
mathege
Площадь параллелограмма 𝐴𝐵𝐶𝐷 равна 14. Найдите площадь параллелограмма 𝐴′𝐵′𝐶′𝐷′, вершинами которого являются середины сторон данного параллелограмма.
Решение:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
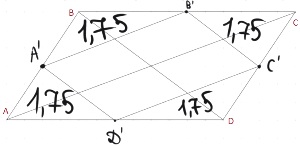
1) `S_(ABC) = 1/2*14=7`
`S_(ACD) = 7`
2) `S_(ABD)/S_(A’BB’) = 2^2`
`S_(A’BB’) =7/4=1,75`
3) `S_(A’B’С’D’) =14-4*7/4=7`
Ответ: 7
mathege
Ромб
Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения диагоналей:
`S = (d_1*d_2)/2`
`S = (4*12)/2=24`
Ответ: 24
mathege
Найдите высоту ромба, сторона которого равна 11√3, а острый угол равен 60°.
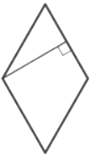
Решение:
`sin60 = (AH)/(11sqrt3)`
`sqrt3/2=(AH)/(11sqrt3)`
`AH=16,5`
Ответ: 16,5
mathege
Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
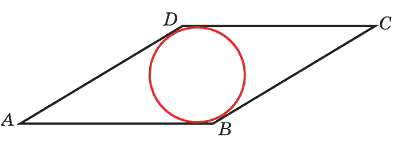
Решение:
Площадь ромба через радиус вписанной окружности
`S_(ромба) =2ar`
Площадь параллелограмма через угол
`S=ac*sinα`
`S_(ромба) = 2*20*r=20*20*1/2`
2r=10
r=5
Ответ: 5
mathege
Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

Решение:
Площадь параллелограмма (основание на высоту):
S = ah
1) ΔADH:
`sin30 = 2/(AD)`
`1/2=2/(AD)`
`AD = 4`
2) CD = 4, так как стороны у ромба равны
3) `S_(ABCD)=4*2=8`
Ответ: 8
mathege
Площадь ромба равна 867. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.

Решение:
Площадь ромба равна половине произведения диагоналей:
`S = (d1*d2)/2`
1) BD=x
AC=6x
2) `S_(ромба) = 867 = (x*6*x)/2`
`6x^2=867*2`
`3x^2=867`
`x^2=289`
`x= 17`
Ответ: 17
mathege
Найдите большую диагональ ромба, сторона которого равна 11√3, а острый угол равен 60°.
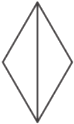
Решение:
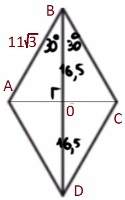
1) ΔABO
`cos30 = (BO)/(11sqrt3)`
`sqrt3/2=(BO)/(11sqrt3)`
`BO = 16,5`
2) BD=2*16,5=33
Ответ: 33
mathege
Диагонали ромба относятся как 1:9. Периметр ромба равен 164. Найдите высоту ромба.
Решение:
Площадь ромба равна половине произведения диагоналей:
`S = (d1*d2)/2`
1) Пусть
AC = 2x
BD = 18x
2) `P_(ABCD)=164=4CD`
CD =41
3) ΔCOD:
`41^2=x^2+(9x)^2`
`1681=x^2+81x^2`
`x^2 = 1681/82=41/2`
4) `S_(ромба) = (2x*18x)/2=18x^2=18*41/2=369`
5) `S_(ромба) =369=41*h`
`h = 369/41=9`
Ответ: 9
mathege
Квадрат
Найдите площадь квадрата, если его диагональ равна 1.
Решение:
1)`1^2=x^2+x^2`
`1=2x^2`
`x^2=1/2`
`x_1=1/sqrt2`
x2 - отрицательный корень не рассматриваем.
2) `S_(abcd) = x*x=1/sqrt(2)*1/sqrt(2)=1/sqrt(4)=0,5`
Ответ: 0,5
mathege
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Решение:
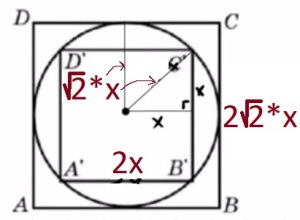
1) `R^2=x^2+x^2`
`R^2=2x^2`
`R=sqrt(2)x`
2) `S_(мал) = (2x)^2=4x^2`
`S_(мал) = (2sqrt(2)x)^2=8x^2`
`8/4=2`- в 2 раза
Ответ: 2
mathege
Трапеция
Основания трапеции равны 2 и 4. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Средняя линия треугольника равна половине основания.
Точку пересечения DB и EF обозначим символом К, тогда
`EK=1/2*4=2`
Ответ: 2
mathege, ЕГЭ 2019
Основания трапеции равны 8 и 34, площадь равна 168. Найдите её высоту.
Решение:
Площадь трапеции
`S = (a+b)/2 * h`
`S = (8+34)/2 * h`
`168 = 21 * h`
`h = 168/21=8`
Ответ: 8
mathege
Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Решение:
Площадь трапеции
`S = (a+b)/2 * h`
Средняя линия трапеции равна полусумме оснований.
`150=(a+b)/2 * 10`
`(a+b)/2 = 15`
`EF = 15`
Ответ: 15
mathege
Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Решение:
Средняя линия трапеции равна половине суммы оснований.
Пусть средняя линия равна MN, а меньшее и большее основание DC и AB.
`MN = 28 = (AB+DC)/2`
`AB+18=56`
`AB=38`
Ответ: 38
mathege
Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50°? Ответ дайте в градусах.
Решение:
В трапеции сумма углов, прилежащих к боковой стороне, равна 180º.
∝+∝-50º=180º
2∝=230º
∝=115º
Ответ: 115
mathege
Высота, опущенная из вершины тупого угла на большее основание равнобедренной трапеции, делит его на отрезки равные 10 и 4. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия трапеции равна половине суммы оснований.
Пусть средняя линия равна MN, а меньшее и большее основание DC и AB .
DC = 10-4=6
AB = 10+4=14
`MN =(6+14)/2=10`
Ответ: 10
mathege
Основания трапеции равны 27 и 83. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение:
Средняя линия треугольника равна половине основания.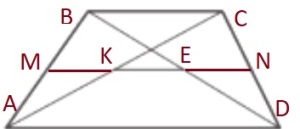
Пусть средняя линия трапеции равна MN, а меньшее и большее основание BC и AD.
1) Найдем среднюю линию трапеции
`MN = (27+83)/2=110/2=55`
2) Если продлить отрезок, то получим среднюю линию для треугольников с вершинами BC и основанием AD, а также среднюю линию трапеции BCAD.
При этом средняя линия треугольников равна ME=KN:
ME=KN = 83/2=41,5
3) В искомом отрезке одна средняя линия треугольника накладывается на другую именно по этому отрезку KE, тогда:
KE = 41,5 + 41,5 - 55 = 83-55= 28 искомый отрезок.
Ответ: 28
2 способ:
1) `MN = (27+83)/2=110/2=55`
2) `MK=1/2BC=1/2*27=13,5`
`EN=1/2BC=13,5`
3) `KE=55-2*13,5=55-27=28`
Ответ: 28
mathege
Основания равнобедренной трапеции равны 14 и 26, а её боковые стороны равны 10. Найдите площадь трапеции.
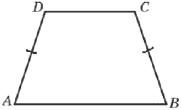
Решение:
Проведем высоту из верхних вершин основания трапеции, скажем DK и СH.
1) `AK = (26-14)/2=6`
2) ΔADK:
`10^2=6^2+DK^2`
`100=36+DK^2`
`DK^2 = 64`
`DK = 8`
3) `S_(ABCD)=(14+26)/2*8=160`
Ответ: 160
mathege
Найдите площадь прямоугольной трапеции, основания которой равны 2 и 14, большая боковая сторона составляет с основанием угол 45°.
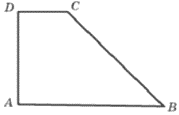
Решение:
Площадь трапеции
`S = (a+b)/2 * h`
Проведем высоту CH из точки С к стороне AB - это высота трапеции и треугольника
1)∠BCH = 180-90-45=45°
ΔBCH прямоугольный и равнобедренный.
CH = 14-2=12
2) `S = (2+14)/2*12=8*12=96`
Ответ: 96
mathege
Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение:
Площадь трапеции
`S = (a+b)/2 * h`
Проведем высоту DH из D к AB - это высота трапеции и получившегося треугольника
1) ∠ADN = 150-90=60°
2) ΔADN:
`cos∠ADN = (DH)/(AD)`
`cos60 = (DH)/8`
`cos60 =1/2`
`DH = 8*1/2 = 4`
3) `S = (10+20)/2 * 4 = 60`
Ответ: 60
mathege
Основания равнобедренной трапеции равны 12 и 18, а её площадь равна 60. Найдите периметр трапеции.

Решение:
Площадь трапеции
`S = (a+b)/2 * h`
Проведем высоту DH из D к AB - это высота трапеции и получившегося треугольника
1) `AH - (18-12)/2=3`
2)`S = (12+18)/2 * DH=60`
15*DH = 60
DH = 4
3) AD = 5
4) `P_(ABCD) = 12+18+2*5=40`
Ответ: 40
mathege
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
Решение:
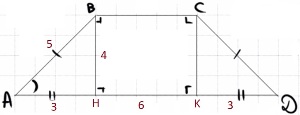
1) `AH=(12-6)/2=3`
2) ΔABH
`5^2=3^2+BH^2`
`BH^2 = 16`
`BH = 4`
3) `sinA = 4/5 = 0,8`
Ответ: 0,8
mathege
Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
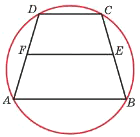
Решение:
Если трапеция вписана в окружность, значит это равнобедренная трапеция.
1) `FE = 21 = (AB+CD)/2` ⇒
AB+CD=42
2) `P_(ABCD) = AB+CD+BC+AD = 52`
AB+CD =42, BC+AD=?
BC+AD=10
3) `BC=AD`
`BC = 10/2=5`
Ответ: 5
mathege
В равнобедренной трапеции основания равны 29 и 50, острый угол равен 60°. Найдите её периметр.

Решение:
Проведем высоту из B к AD, - BH (высота трапеции и получившегося треугольника)
1) `AH = (50-29)/2`
2) ΔABH:
`cosA=(AH)/(AB)`
`1/2=(10,5)/(AB)`
`AB = 21`
3) P = 29+50+2*21=121
Ответ: 121
mathege
В трапеции 𝐴𝐵𝐶𝐷 меньшее основание 𝐵𝐶 равно 4, прямая 𝐵𝐸 параллельна боковой стороне 𝐶𝐷. Найдите периметр трапеции 𝐴𝐵𝐶𝐷, если периметр треугольника 𝐴𝐵𝐸 равен 15.
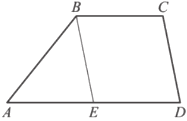
Решение:
1) `P_(ABE) = AB+BC+CD = 15`
2) AB+BC+CD=a+b+c, BC=DE=4
`P_(ABCD) = AB+BC+CD+AE+DE = 15+4+4=23`
Ответ: 23
mathege
Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
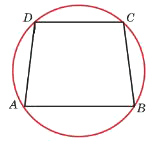
Решение:
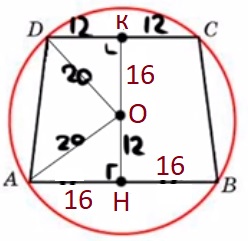
1) ΔDOK:
`20^2=12^2+KO^2`
`KO^2=256`
`KO=16`
ΔAOH:
`20^2=OH^2+16^2`
`OH = 12`
2) KH = 16+12=28
Ответ: 28
mathege
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите её среднюю линию.
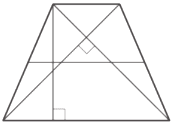
Решение:
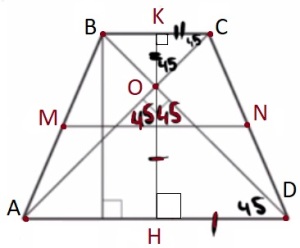
1) ∠BOC=90°
∠KOC=45°
∠OCK=45°
ΔOCK равнобедренный CK=KO
2) Аналогично получается OH=DH
3) KH - высота
KH=OK+OH
|| ||
CK DH = полусумма оснований
KH = CK+DH = OK + OH = MN = 46
Ответ: 46
mathege
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 38. Найдите радиус описанной окружности этой трапеции.
Решение:
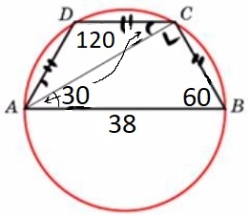
В трапеции сумма углов, прилегающих к боковой поверхности, равна 180 градусам.
Теорема синусов
`a/sinα = b/sinβ =c/sinϒ = 2R`, где R - радиус описанной окружности.
1) ∠D = 180-60=120 = ∠С
2) `∠ACD = 180-120/2=30º`
`∠ACB = 120-30=90º`
3) ΔABC
`(AB)/sinC=2R`
`38/1=2R`
`R = 19`
Ответ: 19
mathege
Окружность
В четырёхугольник 𝐴𝐵𝐶𝐷 вписана окружность, 𝐴𝐵=13, 𝐵𝐶=7 и 𝐴𝐷=11. Найдите четвёртую сторону четырёхугольника.
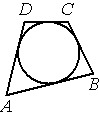
Решение:
Признаком описанного четырехугольника является свойство, когда суммы противоположных сторон равны.
AB +CD = BC + DA
11+7=13+CD
18=13+CD
CD =5
Ответ: 5
Номер: 31765C
В четырёхугольник 𝐴𝐵𝐶𝐷 вписана окружность, AB=22, CD=17. Найдите периметр четырёхугольника 𝐴𝐵𝐶𝐷.
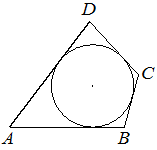
Решение:
Признаком описанного четырехугольника является свойство, когда суммы противоположных сторон равны.
AB +CD = BC + DA
1) BC+AD=22+17=39
2) BC + DA = AB +CD = 22 + 17 =39
`P_(ABCD) = AB +CD + BC + DA = 39+39=78`
Ответ: 78
Номер: CB8C97
Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.

Решение:
Признаком описанного четырехугольника является свойство, когда сумма противоположных сторон равна.
AB +CD = BC + DA
Средняя линия трапеции равна половине суммы оснований.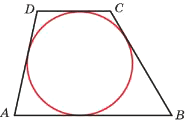
1) AB+CD=15+22=BC+AD
BC+AD=37
2) Ср. линия = `(BC+AD)/2=37/2=18,5`
Ответ: 18,5
Номер: F6F40C
Периметр прямоугольной трапеции, описанной около окружности, равен 40, её большая боковая сторона равна 11. Найдите радиус окружности.

Решение:
Признак описанного четырёхугольника – суммы противоположных сторон равны
a+c = b+d
P = AB + CD + AD + BC = 40 => AB + CD = 20
AB = 20 – 11 = 9
`R = 9/2 = 4,5`
Ответ: 4,5
Номер: 47EA41
Два угла вписанного в окружность четырёхугольника равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
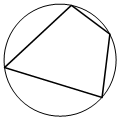
Решение:
Признак вписанного четырехугольника
∠A + ∠C = 180°
∠B + ∠D = 180°
∠C = 180 – 56 = 124°
∠D = 180 – 77 = 103°
Ответ: 103
Номер: C3174D
Впишите правильный ответ.
Два угла вписанного в окружность четырёхугольника равны 99 и 117. Найдите бо́льший из оставшихся углов. Ответ дайте в градусах.
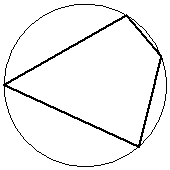
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
Во вписанной четырехугольнике противоположные углы равны 180 градусам, значит
180-99=81º
Ответ: 81
Номер: A9DCC5
Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности. Ответ дайте в градусах.
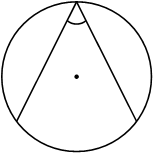
Решение:
Вписанный угол равен половине дуги, на которую он опирается
Дуга `BC = 1/5 * 360 = 72 °`
`∠d = 72 * 1/2 = 36°`
Ответ: 36
Номер: 343A64
Впишите правильный ответ.
Найдите центральный угол, если он на 28° больше острого вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.
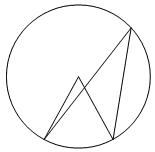
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*28°=56°
Ответ: 56
Номер: 907C53
Впишите правильный ответ.
Центральный угол на 32° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*32°=64°, то есть центральный как раз 32
Ответ: 32
Номер: 30B4E7
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите вписанный угол ACB. Ответ дайте в градусах.
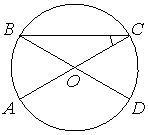
Решение:
∠BOC = 114°
△BOC – р/б
`∠OCB = (180-114)/2 = 33°`
Ответ: 33
Номер: 29D9FB
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 41°. Найдите величину угла AOD. Ответ дайте в градусах.
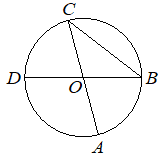
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
CO=OB из условия, так как это половина диаметра, то есть радиус. Значит треугольник OCB равнобедренный, а углы у основания равны.
Тогда угол вершины этого треугольника
∠COB = 180-2*41= 98º
При этом ∠AOD=∠COB = 98º
Ответ: 98
Номер: 80A34C
На окружности отмечены точки A, B и C. Дуга окружности AC, не содержащая точку B, составляет 200°. Дуга окружности BC, не содержащая точку A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.
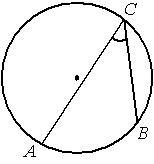
Решение:
Вписанный угол равен половине дуги, на которую он опирается
Дуга AB = 360 -200 -80 = 80°
`∠ACB = 80/2 = 40°`
Ответ: 40
Номер: 65729E
Четырёхугольник 𝐴𝐵𝐶𝐷 вписан в окружность. Угол 𝐴𝐵𝐷 равен 61°, угол CAD равен 37°. Найдите угол ABC. Ответ дайте в градусах.
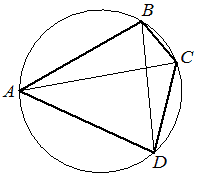
Решение:
Вписанный угол равен половине дуги, на которую он опирается
дуга CD = 2*37 = 74°
дуга AD = 2 * 61 = 122°
дуга AC= 122 + 74 = 196°
`∠ABC = 1/2 * 196 = 98°`
Ответ: 98
Номер: 3CF402
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 98°, угол CAD равен 44°. Найдите угол ABD. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
Вписанные в окружность углы опирающиеся на одну и ту же дугу равны, тогда
∠CAD=∠CBD=44°
∠ABС-∠CBD=∠ABD=98°-44°=54°
Ответ: 54
Номер: 9C6FBB
Четырёхугольник 𝐴𝐵𝐶𝐷 вписан в окружность. Угол 𝐴𝐵𝐶 равен 82°, угол 𝐴𝐵𝐷 равен 47°. Найдите угол 𝐶𝐴𝐷. Ответ дайте в градусах.
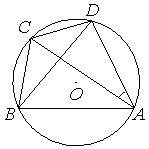
Решение:
Вписанный угол равен половине дуги, на которую он опирается
∠CBD = 82 – 47 = 35°
Дуга CD = 2 * 35 = 70°
`∠ CAD = 1/2 * 70 = 35°`
Ответ: 35
Номер: F62324
Угол 𝐴𝐶𝑂 равен 27°, где 𝑂 − центр окружности. Его сторона 𝐶𝐴 касается окружности. Сторона 𝐶𝑂 пересекает окружность в точке 𝐵 (см. рис.). Найдите величину меньшей дуги 𝐴𝐵 окружности. Ответ дайте в градусах.
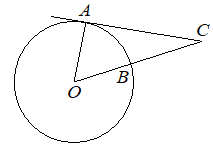
Решение:
Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Центральный угол равен градусной мере дуги, на которую он опирается.
∠AOC = 180 – 90 – 27 = 63°
Дуга AB = 63°
Ответ: 63
Номер: A6532B
Впишите правильный ответ.
Найдите величину угла 𝐴𝐶𝑂, если его сторона 𝐶𝐴 касается окружности с центром O, отрезок CO пересекает окружность в точке B (см. рисунок), а дуга AB окружности, заключённая внутри этого угла, равна 66°. Ответ дайте в градусах.

КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
АС-касательная, тогда ∠СAO=90º Градусная мера дуги указывает на то, что ∠AOB=66º, тогда
∠ACO=180º-90º-66º=24º
Ответ: 24
Номер: 84E9F2
Угол 𝐴𝐶𝑂 равен 28°. Его сторона 𝐶𝐴 касается окружности с центром в точке 𝑂. Сторона 𝐶𝑂 пересекает окружность в точках 𝐵 и 𝐷 (см. рис.). Найдите градусную меру дуги 𝐴𝐷 окружности, заключённой внутри этого угла. Ответ дайте в градусах.
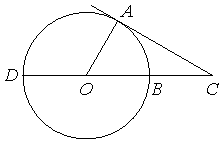
Решение:
∠AOC = 180 – 90 – 28 = 62°
∠AOD = 180 – 62 = 118°
Дуга AD = 118°
Ответ: 118
Номер: 292C86
Угол 𝐴𝐶𝐵 равен 54°. Градусная мера дуги 𝐴𝐵 окружности, не содержащей точек 𝐷 и 𝐸 равна 138°. Найдите угол 𝐷𝐴𝐸. Ответ дайте в градусах.
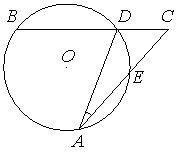
Решение:
Вписанный угол равен половине дуги, на которую он опирается
`∠BDA = 1/2 * 138 = 69°`
∠ADC = 180 – 69 = 111°
∠DAC = 180 – 111 – 54 = 15°
Ответ: 15
Номер: 6328DF
Через концы 𝐴 и 𝐵 дуги окружности с центром 𝑂 проведены касательные 𝐴𝐶 и 𝐵𝐶. Меньшая дуга 𝐴𝐵 равна 58°. Найдите угол 𝐴𝐶𝐵. Ответ дайте в градусах.
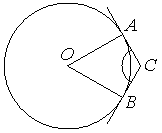
Решение:
Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Центральный угол равен градусной мере дуги, на которую он опирается.
Сумма углов четырехугольника 360°
∠AOB = 58°
∠ACB = 360 – 90 – 90 – 58 = 122°
Ответ: 122
Номер: 0EB251
Хорда 𝐴𝐵 стягивает дугу окружности в 92°. Найдите угол 𝐴𝐵𝐶 между этой хордой и касательной к окружности, проведённой через точку 𝐵. Ответ дайте в градусах.
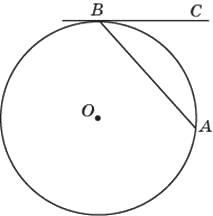
Решение:
Угол между касательной и хордой
`a=(дуга AB)/2`
`∠ABC = 92/2 = 46°`
Ответ: 46
mathege, ЕГЭ 2018
Четырёхугольник 𝐴𝐵𝐶𝐷 вписан в окружность. Угол 𝐵𝐴𝐷 равен 58°. Найдите угол 𝐵𝐶𝐷. Ответ дайте в градусах.
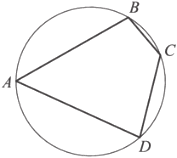
Решение:
Признак вписанного четырехугольника
∠A + ∠C = 180°
∠B + ∠D = 180°
∠A + ∠C = 180°
58 + ∠C = 180°
∠C = 122°
Ответ: 122
mathege, ЕГЭ 2017
Угол 𝐴𝐵𝐷 равен 53°. Угол 𝐵𝐶𝐴 равен 38°. Найдите вписанный угол 𝐵𝐶𝐷. Ответ дайте в градусах.
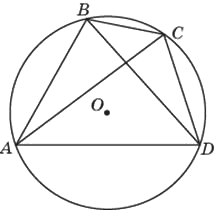
Решение:
Вписанный угол равен половине дуги, на которую он опирается
дуга AD = 106
дуга AB = 776°
дуга BD = 106 + 76 = 182°
`∠BCD = 1/2 * 182 = 91°`
Ответ: 91
mathege, ЕГЭ 2019
Треугольник 𝐴𝐵𝐶 вписан в окружность с центром 𝑂. Угол 𝐵𝐴𝐶 равен 32°. Найдите угол 𝐵𝑂𝐶. Ответ дайте в градусах.
Решение:
Вписанный угол равен половине дуги, на которую он опирается
Центральный угол равен градусной мере дуги, на которую он опирается.
32*2 = 64°
Ответ: 64
Демоверсии ЕГЭ 2015-20
Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии.

Решение:
Признак описанного четырёхугольника – суммы противоположных сторон равны
a+c = b+d
Средняя линия трапеции
-лежит на серединах сторон
- параллельна основаниям
-равна полусумме оснований
42 42
AD + BC = AB + CD
84
`MN = (AB + CD)/2 = 42/2 = 21`
Ответ: 21
mathege
Стороны 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 и 𝐴𝐷 четырёхугольника 𝐴𝐵𝐶𝐷 стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол 𝐴𝐵𝐶. Ответ дайте в градусах.

Решение:
Вписанный угол равен половине дуги, на которую он опирается
Дуга AC = 77 + 106 = 183°
`∠ABC = 1/2 * 183 = 91,5°`
Ответ: 91,5
mathege
Точки 𝐴, 𝐵, 𝐶, 𝐷, расположенные на окружности, делят эту окружность на четыре дуги 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 и 𝐴𝐷, градусные величины которых относятся соответственно как 1:3:15:17. Найдите угол 𝐵𝐴𝐷. Ответ дайте в градусах.

Решение:
Вписанный угол равен половине дуги, на которую он опирается
360 ° = x + 3x + 15x + 17x
360 = 36x
x = 10
Дуга BD = 30 + 150 = 180°
`∠BAD = 1/2 * 180 = 90°`
Ответ: 90
mathege
Точки 𝐴, 𝐵, 𝐶, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как 1:8:9. Найдите больший угол треугольника 𝐴𝐵𝐶. Ответ дайте в градусах.
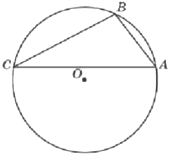
Решение:
x + 8x + 9x = 360 °
18x = 360
x = 20
`1/2 * 180 = 90°`
Ответ: 90
mathege
Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 28.
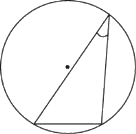
Решение:
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
`(BC)/(sin 30°) = 2*R`
`(BC)/(1/2) = 2 * 28`
`BC = 28`°
Ответ: 28
mathege
Одна сторона треугольника √2, радиус описанной окружности равен 1. Найдите острый угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
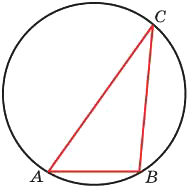
Решение:
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
`(AB)/(sin∠C) = 2*R`
`(sqrt2)/(sin∠C) = 2*1`
`sin∠C = sqrt2/2`
`C = 45`°
Ответ: 45
mathege
Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.

Решение:
Теорема синусов `a/sinα=b/sinβ=c/sinγ=2R`
Обозначим искомый угол α
`(хорда)/(sin α) = 2R`
`(R)/sinα = 2R` |:R
`sinα = 1/2`
α = 30°
Ответ: 30
mathege
Хорда 𝐴𝐵 делит окружность на две дуги, градусные меры которых относятся как 3:5. Под каким углом видна эта хорда из точки 𝐶, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
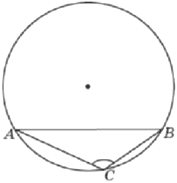
Решение:
5x = 5*45 = 225
(1) Дуга ABмал. = 3x
Дуга ABбол. = 5x
(2) 3x + 5x = 360°
8x = 360
x = 45
(3) `∠ACB = 1/2 * 225 = 112,5°`
Ответ: 112,5
mathege
Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.
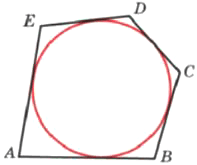
Решение:
Площадь многоугольника S=pr, где p – полупериметр, r – радиус вписанной окружности
(1) P=8 => p = 4
(2) S = 4*1 = 4
Ответ: 4
mathege
Равносторонний шестиугольник
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39?
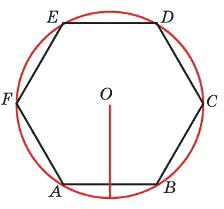
Решение:
Радиус окружности, описанной около равностороннего шестиугольника, равен его стороне
R=a
a = 39
Ответ: 39
mathege
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 10√3.
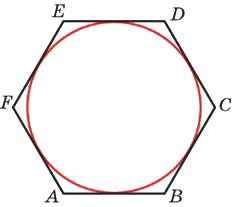
Решение:
Радиус окружности, вписанной в равносторонний шестиугольник
`r = (sqrt3a)/2`
`r = 10sqrt3`
`10sqrt3 = (sqrt3 * a)/2` | : `sqrt3`
`10 = a/2`
`a = 10*2 = 20`
Ответ: 20
mathege
Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Решение:
Радиус окружности, описанной около равностороннего шестиугольника, равен его стороне
R=a
(1) Pшест. = 108 = 6*a
a = 18
(2) d = 2*R = 2 * 18 = 36
Ответ: 36
mathege
Разное
Диагонали четырёхугольника равны 6 и 2. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.
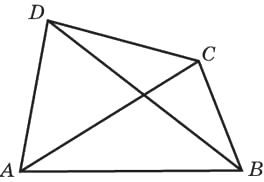
Решение:
Средняя линия треугольника
- лежит на серединах сторон
- параллельна основанию
- равна половине основания
AC = 2
BD = 6
(1) `EK = 1/2 = 1 = PM`
`KM = 1/2 * 6 = 3 = EP`
(2) `P_EKMD = 2*1 + 2*3 = 8`
Ответ: 8
mathege
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.
Решение:
Сумма углов n-угольника = 180(n-2)
n * 168 = 180*(n-2)
168 * n = 180n – 360
360 = 12n
n = 30
Ответ: 30
mathege

