В 17-м задании проверяются знания о четырехугольниках, но не нужно забывать и свойства углов, и свойства треугольников, которые используются в решении практически каждого задания по геометрии. Теорию для вас подобрали специалисты сайта GDZotvet. ru
Параллелограмм
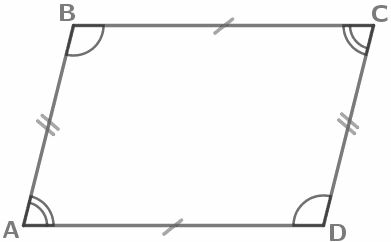 |
В параллелограмме противоположные стороны равны и противоположные углы равны. AB=CD, BC=AD ∠A=∠C, ∠B=∠D |
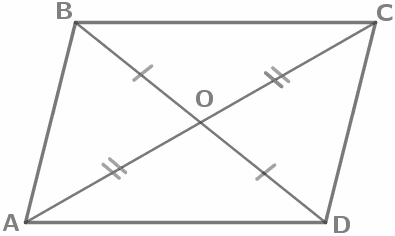 |
Диагонали параллелограмма точкой пересечения делятся пополам. AO=OC, BO=OD |
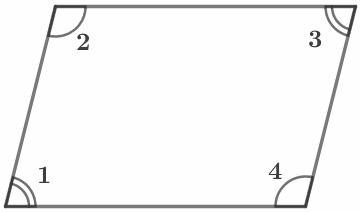 |
Сумма углов, прилегающих к одной стороне параллелограмма, равна 180°. Примеры: ∠1+∠2=180° , ∠2+∠3=180° |
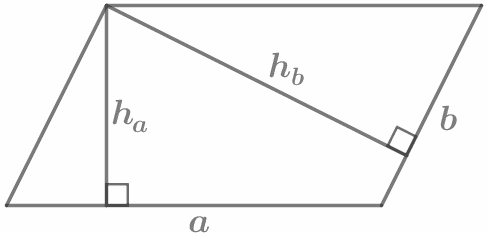 |
Площадь параллелограмма равна произведению его основания на высоту. S = aha = bhb |
Прямоугольник и квадрат
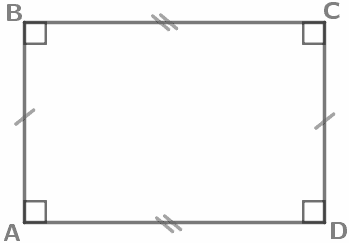 |
Все углы прямоугольника – прямые, а противоположные стороны – равны. ∠A=∠C=∠B=∠D=90° AB=CD, BC=AD |
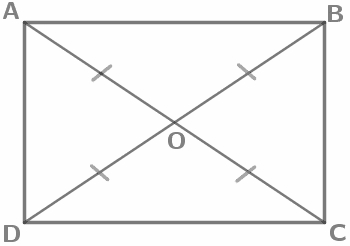 |
Диагонали прямоугольника равны и точкой пересечения делятся пополам. AO=BO=CO=DO |
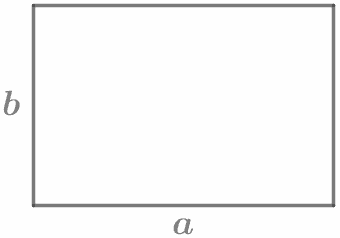 |
Площадь прямоугольника равна произведению длин его смежных сторон. S = ab |
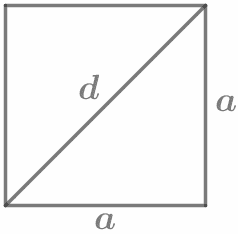 |
Площадь квадрата равна квадрату его стороны. S=a2 Периметр квадрата: P = 4a По теореме Пифагора: d2 = 2a2 |
Трапеция
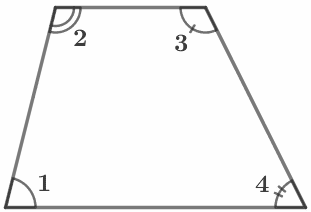 |
Сумма углов, прилегающих к боковой стороне трапеции, равна 180°. ∠1+∠2=180° , ∠3+∠4=180° |
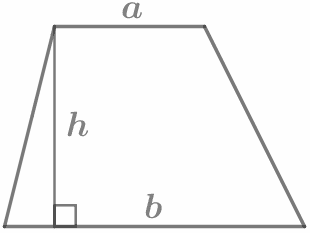 |
Площадь трапеции равна произведению полусуммы ее оснований на высоту. `S=1/2(a+b)h` |
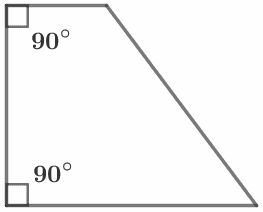 |
У прямоугольной трапеции один из углов прямой. |
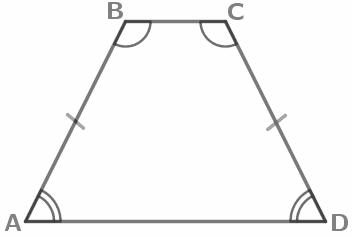 |
Трапеция называется равнобедренной, если её боковые стороны равны. AB=CD В равнобедренной трапеции углы при каждом основании равны. ∠A=∠D, ∠B=∠C |
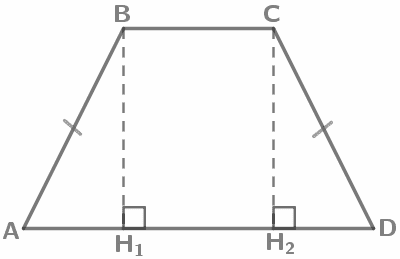 |
`AH_1=H_2D=(AD-BC)/2` |
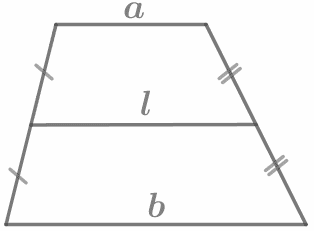 |
Средняя линия трапеции параллельна основаниям и равна их полусумме: l || a, l || b, `l=(a+b)/2` |
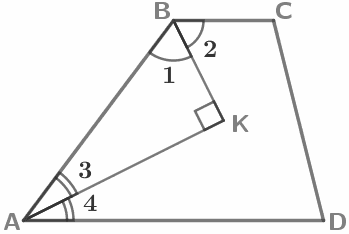 |
BK – биссектриса (∠1=∠2), AK – биссектриса (∠3=∠4 ) ∠AKB=90° |
Ромб
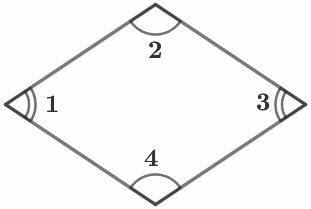 |
В ромбе все стороны равны и противоположные углы равны. ∠1=∠3, ∠2=∠4 Сумма углов, прилегающих к одной стороне ромба, равна 180°. Примеры: ∠1+∠2=180° , ∠2+∠3=180° |
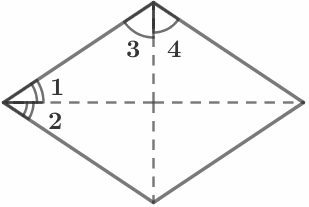 |
Диагонали ромба делят его углы пополам. ∠1=∠2, ∠3=∠4 Периметр ромба: P = 4a |
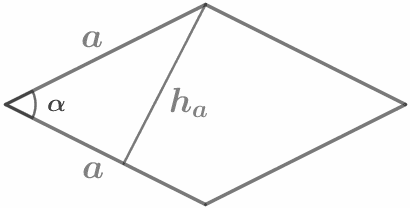 |
Площадь ромба равна… а) произведению его стороны на высоту: S = aha , б) произведению двух его сторон на синус угла между ними: S=a2 sinα |
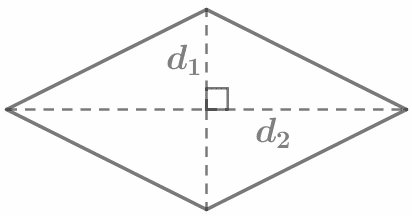 |
Площадь ромба равна половине произведения его диагоналей. `S=1/2d_1d_2` Диагонали ромба взаимно перпендикулярны: d1 ⊥ d2 |
Углы и треугольники (дополнительная информация)
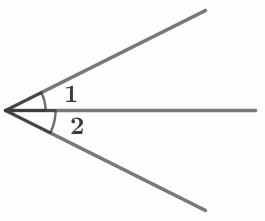 |
Биссектриса делит угол пополам. ∠1= ∠2 |
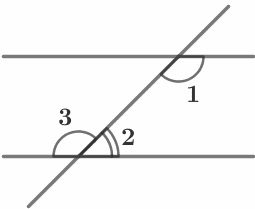 |
Если две параллельные прямые пересечены секущей, то: а) сумма односторонних углов равна 180°: ∠1 + ∠2 =180° ; б) накрест лежащие углы равны: ∠1=∠3 |
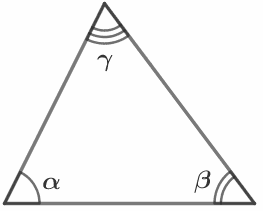 |
Сумма углов треугольника равна 180°: α + β + γ =180°. |
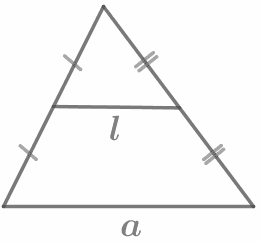 |
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны: l || a, `l=1/2a` |
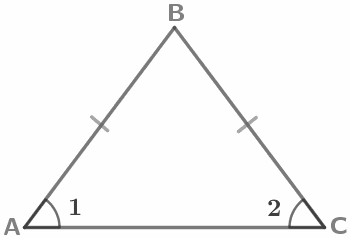 |
В равнобедренном треугольнике углы при основании равны: AB=BC, ∠1=∠2. |
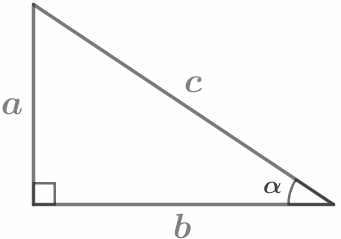 |
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 =a2+b2 |
 |
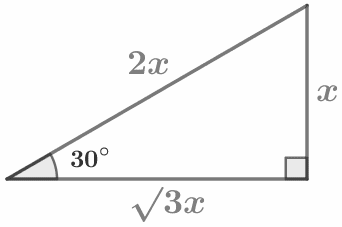
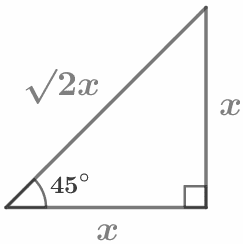
`sinα=a/c=(противолежащий катет)/(гипотенуза)` `cosα=b/c=(прилежащий катет)/(гипотенуза)` `tgα=a/b=(противолежащий катет)/(прилежащий катет)` `sin30°=1/2` |
 |
 |
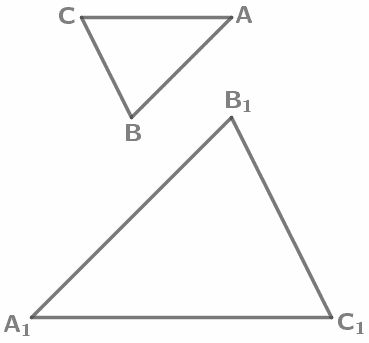 |
Углы подобных треугольников соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого: ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1 `(AB)/(A_1B_1)=(BC)/(B_1C_1)=(CA)/(C_1A_1)` |

