Задание 17 проверяет знания о четырехугольниках, кроме вписанных/описанных. Параллелограммы, ромбы, прямоугольники и другие четырехугольные фигуры.
Типы заданий линейки 17 по ФИПИ
Параллелограмм
1. Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
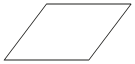
Решение:
Противолежащие углы параллелограмма равны. Так как стороны параллелограмма параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 41° = 139°.
Ответ: 139
2. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
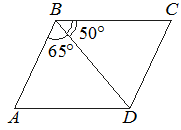
Решение:
В параллелограмме противолежащие углы равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠BAD=∠ВСD — меньший угол параллелограмма.
AD||BC (по определению параллелограмма), следовательно диагональ ВD можно рассматривать как секущую при параллельных прямых,
углы CВD и АDВ равны как накрест лежащие:
∠АDВ = ∠CВD
Рассмотрим треугольник АВD.
Сумма углов треугольника равна 180°. Отсюда:
∠ВАD = 180° - ∠АВD - ∠АDВ = 180° - ∠АВD - ∠CВD = 180° - 65° - 50° = 65°.
Ответ: 65
3. Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 21°. Ответ дайте в градусах.
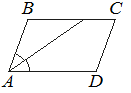
Решение:
Обозначим точку пересечения стороны ВС биссектрисой как Е.
Е
Углы BEA и EAD равны как накрест лежащие углы при параллельных прямых AD и BC.
Поскольку AE — биссектриса угла A,
∠BAD = 2∠BAE = 2∠BEA = 2 * 21 = 42°.
Этот угол является острым углом параллелограмма.
Ответ: 42
4. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=10, BD=22, AB=9. Найдите DO.
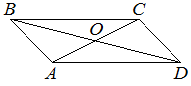
Решение:
В параллелограмме диагонали точкой пересечения делятся пополам. Значит,
DO = ВD/2 = 22/2 = 11
Ответ: 11
Трапеция
5. Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Поскольку трапеция является равнобедренной, углы при основании равны.
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 66° = 114°.
Ответ: 114
6. Сумма двух углов равнобедренной трапеции равна 352°. Найдите меньший угол трапеции. Ответ дайте в градусах.

Решение:
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании.
Поскольку трапеция является равнобедренной, углы при основании равны.
Значит, каждый из них равен
352° / 2 = 176°.
Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен
180° − 176° = 4°.
Ответ: 4
![]() 7. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 17° и 23° соответственно.
7. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 17° и 23° соответственно.
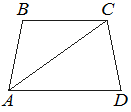
Решение:
В равнобедренной трапеции углы при основаниях равны.
Угол ABC — тупой, а угол BAD — острый, значит, ∠ABC=∠ВСD — больший угол равнобедренной трапеции.
AD||BC (по определению трапеции), следовательно диагональ AС можно рассматривать как секущую,
углы CAD и BCA равны как накрест лежащие.
Сумма углов треугольника равна 180°. Отсюда:
∠ABC= 180 - ∠BCA - ∠BAC = 180° - 17° - 23° = 140°.
Ответ: 140
![]() 8. В трапеции ABCD AB=CD, ∠BDA =38° и ∠BDC=32°. Найдите ∠ABD. Ответ дайте в градусах.
8. В трапеции ABCD AB=CD, ∠BDA =38° и ∠BDC=32°. Найдите ∠ABD. Ответ дайте в градусах.
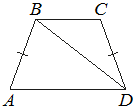
Решение:
∠ADC = ∠BDA + ∠BDC = 38° + 32° = 70°
Трапеция ABCD - равнобедренная (т.к. AB=CD), следовательно, по свойству равнобедренной трапеции,
∠BAD = ∠ADC= 70°
Рассмотрим треугольник ABD.
По теореме о сумме углов треугольника:
∠BAD + ∠ABD + ∠BDA = 180°
∠ABD = 180° - ∠BAD - ∠BDA
∠ABD = 180° - 70° - 38° = 72°
Ответ: 72
9. Один из углов прямоугольной трапеции равен 139°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
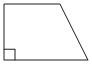
Решение:
Поскольку трапеция является прямоугольной, меньший угол следует искать на другой боковой стороне (которая не образует прямых углов).
Так как сумма односторонних углов трапеции (углы при параллельных прямых и секущей) равна 180°, то больший угол в трапеции
180° - 139° = 41°.
Ответ: 41
Задания про углы с другими числами >>
10. В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.
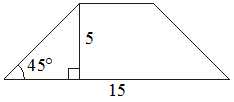
Решение:
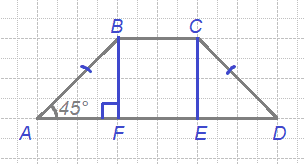
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
ВС = FЕ = АD - (АF + ЕD) = АD - 2АF = 15 - 2 * 5 = 5
Ответ: 5
11. В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.
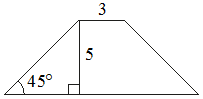
Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 3
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 3 = 13
Ответ: 13
12. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.
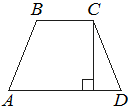
Решение:
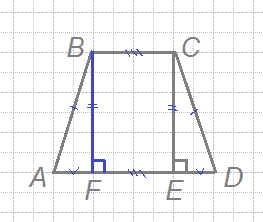
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 15 - 8 = 7
Ответ: 7
Прямоугольник
13. Диагональ прямоугольника образует угол 74° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Решение:
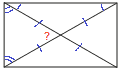
Диагонали прямоугольника точкой пересечения делятся пополам, значит любой треугольник, полученный внутри прямоугольника, равнобедренный, а в равнобедренном треугольнике углы при основании равны.
Сумма углов треугольника равна 180°.
Учитывая вышесказанное, найдем угол между диагоналями прямоугольника:
180° - 2 * 74° = 32° - острый угол
Ответ: 32
14. Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=15 , AB=14. Найдите AC.
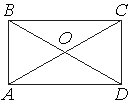
Решение:
Длины диагоналей прямоугольника равны и делятся точкой пересечения пополам. Значит,
AC = ВD = 2 ВО
АС = 2 * 15 = 30
Ответ: 30
Ромб
15. Один из углов ромба равен 62°. Найдите больший угол этого ромба. Ответ дайте в градусах.

Решение:
Противолежащие углы ромба равны. Так как стороны ромба параллельны, любую из них можно рассматривать как секущую к двум другим параллельным друг другу сторонам, а значит сумма односторонних углов параллелограмма равна 180°. Тогда больший угол равен
180° - 62° = 118°.
Ответ: 118
16. В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
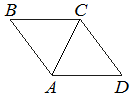
Решение:
Сумма односторонних углов АBС и ВCD равна 180°, отсюда
∠ВCD = 180° - 72° = 108°.
Диагональ ромба AC является биссектрисой угла ВCD, поэтому делит его пополам
∠ACD = 108° / 2 = 54°.
Ответ: 54
2 способ для тех, кто забыл свойства диагонали ромба
По определению ромба все его стороны равны. Тогда треугольник АВС равнобедренный (ВС=ВА), а значит углы при основании равны. Сумма углов треугольника равна 180°. Отсюда
∠ВСА = (180° - ∠ABC) / 2 = (180° - 72°) / 2 = 54°
ВС||АD, а СА - секущая, значит ∠ВСА = ∠САD = 54° как накрест лежащие.
Треугольник АDС так же равнобедренный (СD=АD), значит
∠ACD = ∠САD = 54°
Ответ: 54
17. Сторона ромба равна 34, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 34 * sin30° = 34 * 1/2 = 17
Ответ: 17
Площадь четырехугольника
![]() 18. Сторона квадрата равна 6√2 . Найдите площадь этого квадрата.
18. Сторона квадрата равна 6√2 . Найдите площадь этого квадрата.
☐
Решение:
(6√2)2 = 72
Ответ: 72
![]() 19. Периметр квадрата равен 44. Найдите площадь квадрата.
19. Периметр квадрата равен 44. Найдите площадь квадрата.
☐
Решение:
44:4=11 - сторона квадрата
112 = 121 - площадь
Ответ: 121
20. Найдите площадь параллелограмма, изображённого на рисунке.
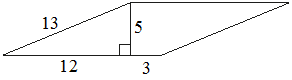
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+3) * 5 = 75
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 75
Задания про параллелограмм с другими числами >>
21. Площадь параллелограмма равна 32, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите большую высоту.
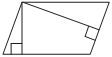
Решение:
Площадь параллелограмма
S=ah, где а - сторона параллелограмма, а h - высота, опущенная к этой стороне.
h=S/a
Тогда первая высота:
h1=32/8=4;
вторая высота:
h2=32/16=2.
Ответ: 4
![]() 22. Площадь параллелограмма ABCD равна 104. Точка E – середина стороны AB. Найдите: а) площадь треугольника CBE; б) площадь трапеции DAEC.
22. Площадь параллелограмма ABCD равна 104. Точка E – середина стороны AB. Найдите: а) площадь треугольника CBE; б) площадь трапеции DAEC.

Решение:
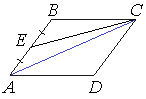
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 104 / 2 = 52.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
а) SCВE = 1/2 SACВ = 52 / 2 = 26
Ответ: 26
б) следовательно,
SAECD = SABCD - SCDE = 104 - 26 = 78.
Ответ: 78
23. Основания трапеции равны 13 и 23, а высота равна 5. Найдите площадь этой трапеции.

Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{13+23}2\ast5=90$
Ответ: 90
24. В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
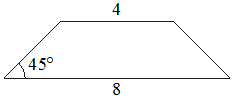
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (8 - 4) / 2 = 2
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (4 + 8) : 2 * 2 = 12
Ответ: 12
![]() 25. Найдите площадь ромба, если его диагонали равны 21 и 6.
25. Найдите площадь ромба, если его диагонали равны 21 и 6.
Решение:
S = (d1 * d2)/2 = 21*6 / 2 = 63
Ответ: 63
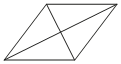
![]() 26. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь ромба.
26. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь ромба.
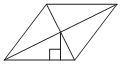
Решение:
S = аh = 12 * 2 * 4 = 96
Ответ: 96
27. Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь ромба.

Решение:
36 : 4 = 9 - длина стороны
S = a²sinα = 92 * sin 30° = 81 * 1/2 = 40,5
Ответ: 40,5
Теорема Пифагора
28. Сторона квадрата равна 11√2 . Найдите диагональ этого квадрата.
Решение:
Диагональ квадрата делит его на 2 прямоугольных треугольника, в которых является гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
с2 = а2 + b2
b = a ⇒ с2 = 2а2
с = √2 * а
с = √2 * 11√2 = 11 * 2 = 22
Ответ: 22
Подобные треугольники
![]() 29. Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38 . Найдите AO.
29. Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38 . Найдите AO.
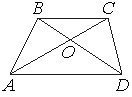
Решение:
Рассмотрим треугольники AOD и BOC. По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда: ∠ BOC = ∠ AOD — вертикальные, ∠ DBC = ∠ BDA — накрест лежащие углы при секущей BD, BC и AD параллельны. Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Из подобия треугольников:
$\frac{АО}{ОС}=\frac{АD}{ВС}=\frac{13}{6}$
значит, точка O делит отрезок AC в отношении 13:6, отсчитывая от вершины А. Это означает, что весь отрезок AC можно разделить на 13+6=19 равных части, 13 из которых составляет АО, а остальное – ОС, то есть:
АО = 38/19 * 13 = 26
Ответ: 26
Ответ:
Средняя линия трапеции
30. Основания трапеции равны 14 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
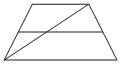
Решение:
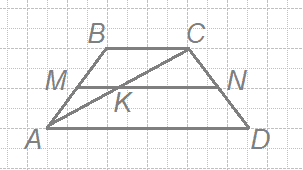
Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC.
AD > ВС, значит КN > МК (как средние линии треугольников)
Рассмотрим треугольник ACD. KN — средняя линия, следовательно,
KN = AD/2 = 19/2 =9,5.
Ответ: 9,5
31. Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
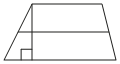
Решение:
Средняя линия трапеции параллельна основаниям и равна их полусумме. Она не зависит от высоты.
(11 + 19) / 2 = 15
Ответ: 15
Еще про среднюю линию трапеции >>
2026 год (9 типов заданий добавлено)
32. В равнобедренной трапеции ABCD угол D равен 68°. Найдите градусную меру угла ACD, если луч AC является биссектрисой угла BAD. (33BD88)
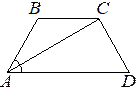
Решение:
∠D=∠BAD=68°, поскольку трапеция равнобедренная
∠CAD=68/2=34° (так как биссектриса делит угол пополам)
Сумма углов треугольника 180°
∠ACD=180-68-34=78°
Ответ: 78
33. В равнобедренной трапеции с основаниями AD и BC угол D равен 74°. Диагональ AC образует со стороной AB угол 21°. Сколько градусов составляет угол между этой диагональю и меньшим основанием трапеции? (66A186)
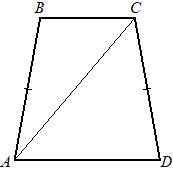
Решение:
∠BCA - ?
∠D=∠BAD=74°, поскольку трапеция равнобедренная
∠CAD=74-21=53°
∠CAD и ∠BCA - внутренние накрест лежащие углы при параллельных прямых и секущей, они равны
∠CAD = ∠BCA = 53°
Ответ: 53
34. Диагональ равнобедренной трапеции образует с её основанием угол 45°. Найдите высоту трапеции, если её основания равны 2 и 7. (829962)
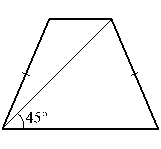
Решение:
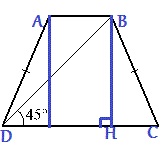
Проведем высоту трапеции BH.
HC=(7-2)/2=2,5 ⇒ DH=7-2,5=4,5
Рассмотрим △DBH. Он прямоугольный (∠H = 90°)
∠D=45°
∠B = 180° – 90° – 45° = 45°, значит боковые стороны равны
DН = BН = 4,5
Ответ: 4,5
35. Высота равнобедренной трапеции, проведённая из конца её меньшего основания, делит большее основание на отрезки длиной 3 и 5. Найдите меньшее основание трапеции. (A74699)
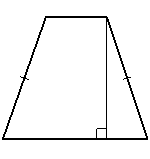
Решение:
Проведем высоту из первого конца верхнего основания. 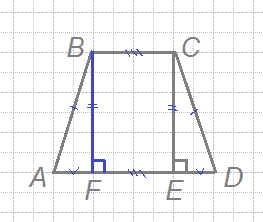
АЕ=5, ЕD=3
Поскольку трапеция равнобедренная, высоты отсекают на нижнем основании от краев одинаковые отрезки длиной 3 каждый.
AF=ЕD=3
FE=BC=5-3=2
Ответ: 2
36. Диагональ равнобедренной трапеции образует с боковыми сторонами углы 26° и 84°. Сколько градусов составляет угол при большем основании трапеции? (7285C7) К слову сказать, этот тип задания уже в начале года был в сборнике Ященко 50 вариантов.

Решение:
Пусть искомый угол α.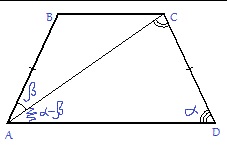
Поскольку в равнобедренной трапеции углы при основании равны, ∠D=∠A
∠CAD = α - 26
Рассмотрим △ACD
Сумма углов треугольника 180°
α - 26 + α + 84 =180
2α = 180 - 84 + 26
2α = 122
α = 61
Ответ: 61
37. Перпендикуляр, проведённый из точки пересечения диагоналей ромба к его стороне, образует с одной из его диагоналей угол 35°. Сколько градусов составляет острый угол ромба? (912787)
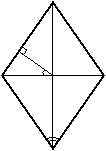
Решение:
В маленьком треугольничке угол 180-35-90=55°
Поскольку диагональ ромба делит угол пополам, то тупой угол ромба 55*2=110°
а острый 180-110=70°
Ответ: 70
38. Один из углов ромба равен 134°. Сколько градусов составляет угол между высотой и большей диагональю ромба? (C23988)
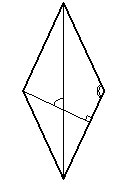
Решение:
Сумма углов ромба, прилежащих к одной стороне, равна 180°.
180-134=46° острый угол ромба
Диагональ делит острый угол пополам
46:2=23° - угол между большей диагональю и стороной ромба
Высота ромба перпендикулярна его стороне (образует угол 90°).
Рассмотрим верхний левый треугольник.
Сумма углов треугольника 180°
180-90-23=67°
Ответ: 67
39. Острый угол ромба равен 52°. Сколько градусов составляет угол между стороной и меньшей диагональю ромба? (AB1B84)
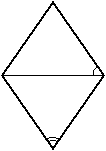
Решение:
Диагональ ромба делит его на 2 равных равнобедренных треугольника ⇒ углы у основания равны.
Сумма углов любого треугольника 180°
(180-52)/2=64
Ответ: 64
40. Диагональ АС ромба АВСD равна 60, а tgBCA=0,4. Найдите площадь ромба. (7B0DD9)
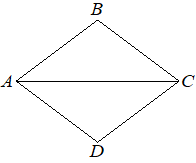
Решение:
AC = 60 ⇒ OC = 30
Проведем вторую диагональ, пусть О - точка пересечения диагоналей. Диагонали делят ромб на 4 прямоугольных треугольника.
∠BCA=∠BCO
tg∠BCO = BO/OC = 0,4 = 4/10 ⇒
BO = 30*4/10 = 12
BD=12*2=24
S=60*24/2=720
Ответ: 720

