Теория к заданию 16 ОГЭ по математике (геометрия). Окружность, круг

Тема 16-го задания "Окружность, круг и их элементы". Выкладываем на ГДЗответ ру всю теорию, которая может пригодиться при решении всех типов заданий из шестнадцатого номера по разделам. Нужны будут знания не только обо всем круглом, вписанном и описанном, но и об углах и многоугольниках.

Окружность

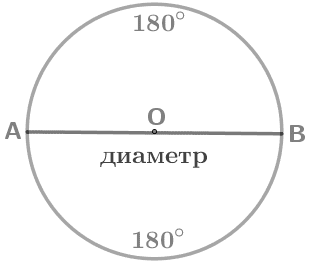	AO, BO – радиусы AO = BO AB – диаметр D=2R Сумма градусных мер двух дуг окружности с общими концами равна 360°. Диаметр делит окружность на две полуокружности. ⋃AB =180°
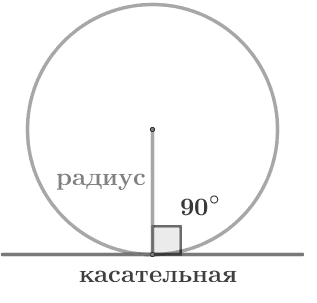	Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. gdzotvet.ru
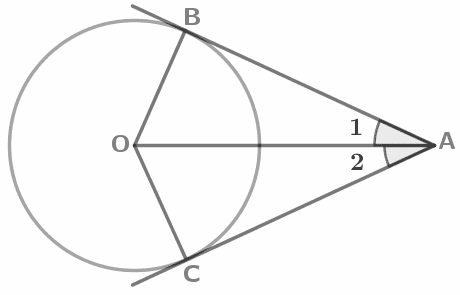	Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности: AB=AC, ∠1= ∠2.
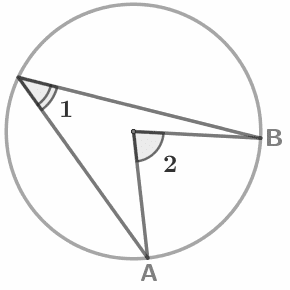	Градусная мера вписанного угла (вершина лежит на окружности) измеряется половиной дуги, на которую он опирается: ∠ 1 = ¹/₂ ⋃AB Градусная мера центрального угла (вершина в центре окружности) равна градусной мере соответствующей дуги окружности: ∠ 2= ⋃AB.
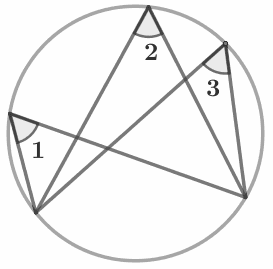	Вписанные углы, опирающиеся на одну и ту же дугу, равны: ∠1 = ∠2 = ∠3 .
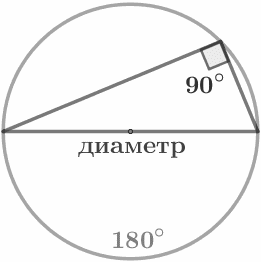	Вписанный угол, опирающийся на полуокружность – прямой (90°).
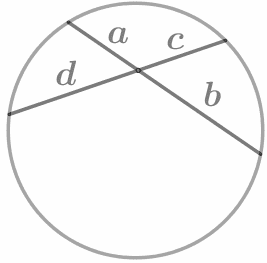	Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды: ab =cd .
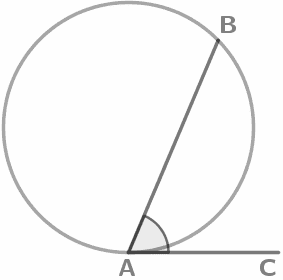	Угол, образованный касательной и хордой измеряется половиной дуги, заключенной между его сторонами: ∠BAC = ¹/₂ ⋃AB
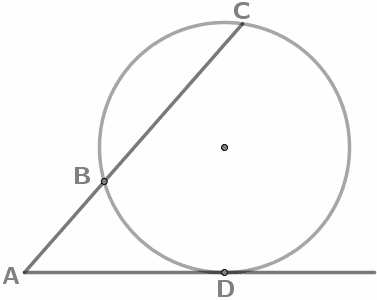	Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть: AD² = AB*AC

Треугольник и четырехугольник

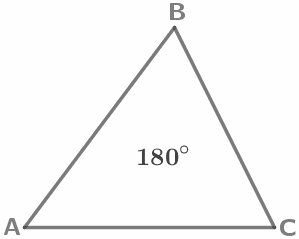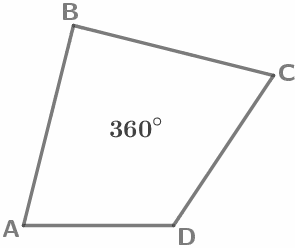
Сумма углов треугольника равна 180°.

Сумма углов выпуклого четырехугольника равна 360°.

Прямоугольный треугольник

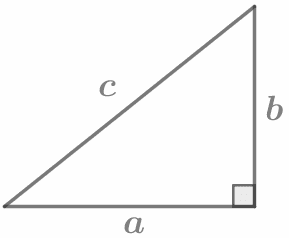Теорема Пифагора:
В прямоугольном треугольнике
квадрат гипотенузы равен сумме
квадратов катетов.
с² = а² + b²

Вписанная и описанная окружность

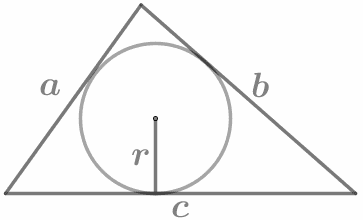S = ¹/₂ Pr

P = a + b + c

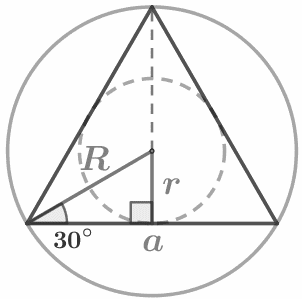	R = 2r h = R + r
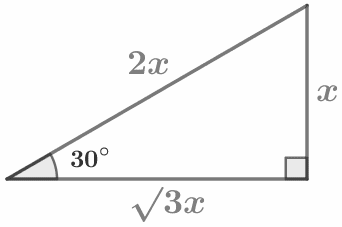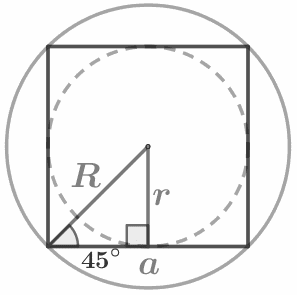	a = 2r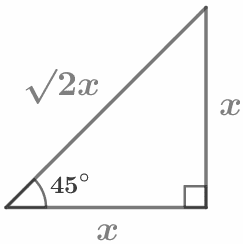

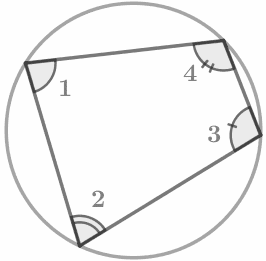	В любом вписанном четырехугольнике сумма противоположных углов равна 180°: ∠1+∠3=∠2+∠4=180°
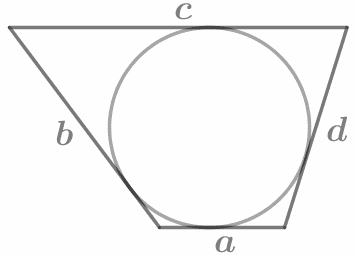	В любом описанном четырехугольнике суммы противоположных сторон равны: a+c=b+d.
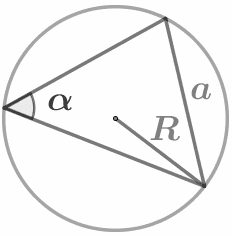	Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла: `2R=a/sinα`

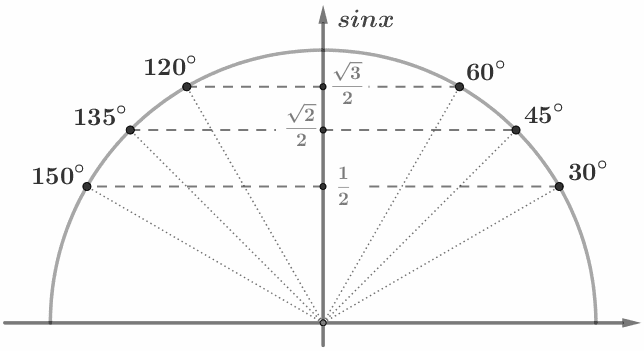
Подобные треугольники

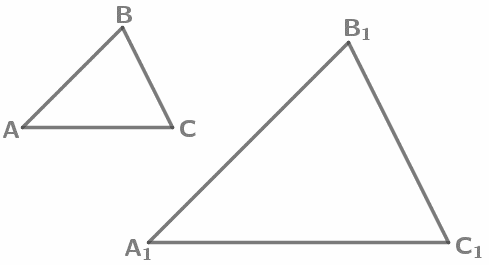Углы подобных треугольников соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого:
∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁
`(AB)/(A_1B_1)=(BC)/(B_1C_1)=(CA)/(C_1A_1)`

Правильные многоугольники

Любой правильный многоугольник можно вписать в окружность.

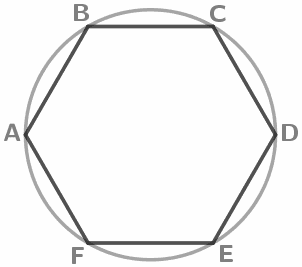У правильного многоугольника все стороны равны.
AB=BC=CD=DE=EF=FA
Равные дуги стягиваются равными хордами.
⋃AB=⋃BC=⋃CD=⋃DE=⋃EF=⋃FA

Все эти нехитрые теоремы могут пригодиться вам на ОГЭ в задании линейки 16.

: Обновлено: 11 октября 2023