В десятом задании могут встретиться задачи на сплавы, растворы, на движение, на совместную работу, трубы, как и было в ОГЭ. Могут дублироваться задания из банка ОГЭ. В ОГЭ они были с развернутым ответом, а на ЕГЭ по профильной математике будут с кратким.
В новом банке ФИПИ содержатся основные типы задач, которые могут выпасть на реальном ЕГЭ. Числа могут отличаться, но алгоритмы решения те же.
Мы собрали ВСЕ задачи из ОБОИХ банков, которые могут попасться на реальном ЕГЭ по профильной математике.
КЭС: Уравнения и неравенства. Тип ответа: Краткий ответ.
Задания линейки 10 ЕГЭ мат профиль из нового банка ФИПИ
Впишите правильный ответ.
Призёрами городской олимпиады по математике стали 6 учеников, что составило 5% от числа участников. Сколько человек участвовало в олимпиаде?
КЭС: 1.1.1 Целые числа 1.1.3 Дроби, проценты, рациональные числа 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
120
100/5=20 часть,
6*20=120 человек
Ответ:120
Номер: 6D1598
Впишите правильный ответ.
Имеется два сплава. Первый сплав содержит 45% меди, второй — 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
Переведем проценты в части, примем за х массу первого сплава и составим уравнение:
0,45х+0,2(х-30)=0,4(х+х-30)
0,45х+0,2х-6=0,8х-12
12-6=0,8х-0,65х
0,15х=6
х=40 кг - масса первого сплава
40-30=10 кг - масса второго
40_10=50 кг - масса третьего
Ответ: 50
ИЛИ
Получается при определенном количестве частей (килограмм) 45% меди и каком-то частей 20% меди получили среднее значение в 40% меди. Если взять массу первого за x кг, то второй x-30. Тогда
`(45x+20(x-30))/(x+x-30) = 40`
`(65x-600)/(2x-30) = 40`
65x-600= (2x-30) * 40`
65x-600= 80x-1200
15x=600
x=40
Находим 3 сплав.
40+(40-30)=50
Ответ:50
Номер: FD5B44
Впишите правильный ответ.
Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа — со скоростью 45 км/ч, а затем два часа — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
55
Берем каждый час за 1 часть и находим среднее для этих частей, тем самым определяя среднюю скорость.
`(115+45*3+ 40*2)/6=330/6=55` км/ч
Ответ: 55
Номер: 081941
Впишите правильный ответ.
Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 2 км/ч, стоянка длится 4 часа, а в пункт отправления теплоход возвращается через 13 часов. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
13-4=9 часов в пути
Пусть x - скорость теплохода по течению, тогда (x-4) - против течения.
Составим уравнение
`(80/(x)+80)/(x-4)=9`
`(80(x-4)+80x)/x(x-4)=9`
`(80x-320+80x)/x(x-4)=9`
160x-320=9x2-36x
9x2-196x+320=0
`D=196^2-4*9*320`=26896
`x=(196+164)/(2*9)=360/18=20`
второй корень будет отрицательный, не имеет смысла
20-2=18 км/ч - скорость теплохода в стоячей воде
Ответ:18
Номер: 06B9F5
Впишите правильный ответ.
Теплоход, скорость которого в неподвижной воде равна 27 км/ч, проходит некоторое расстояние по реке и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 32 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
КЭС: 2.1.2 Рациональные уравнения
Решение:
728
32-5=27 часов в пути
27+1=28 км/ч по течению
27-1=26 км/ч против течения
Получается время потраченное на дорогу туда и обратно будет соизмеримо скоростям теплохода туда и обратно, то есть:
28/26=14/13=1 1/13 столько надо времени теплоходу для того чтобы пройти тоже самое расстояние против течения.
Можно найти среднюю скорость, если взять 1 час где-то на пути туда и обратно
`(28*1+26*1 1/13)/(2 1/13) = (28+364/13)/(27/13)=728/27`
При этом мы знаем, что теплоход плыл 27 часов, значит
`728/27*27`=728
Ответ: 728
Номер: 205CF2
Впишите правильный ответ.
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 200 км — со скоростью 100 км/ч, а затем 160 км — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
90
Берем каждый час за 1 часть и находим среднее для этих частей, тем самым определяя среднюю скорость.
120/60 = 2 части
200/100=2 часа (части)
160/120=1 1/3
`(60*2+100*2+1 1/3*120)/(5 1/3)=480/(5 1/3) = 1440/16`= 90 км/ч Для удобства подсчетов знаменатель и множитель умножили на 3, чтобы избавиться от неправильной дроби.
Ответ: 90
Номер: 5504F2
Впишите правильный ответ.
Заказ на изготовление 198 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 7 деталей больше второго?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
18
Возьмем за x количество деталей за час изготавливаемых первым рабочим.
x-7 изготавливает второй рабочий.
Тогда
198/x столько надо часов чтобы сделать все детали первому рабочему.
198/(x-7) столько надо часов чтобы сделать все детали второму рабочему.
Составим уравнение с поправкой на известное время 7 часов.
`198/x + 7 = 198/(x-7)`
`198/x - 198/(x-7) +7 = 0`
`(198(x-7)-198x)/(x(x-7)) +7 = 0`
`(198x-1386-198x)/(x(x-7)) +7 = 0`
`-1386/(x(x-7)) +7 = 0`
`-1386/(x^2-7x) +7 = 0`
`-1386 = -7(x^2-7x)`
-7x2+49x=-1386
7x2-49x-1386=0
D=2401-4*7*(-1386)=41209
`x=(49+sqrt(41209))/(2*7)=252/14`=18
второй корень отрицательный, не имеет смысла
x=18
Ответ:18
Номер: 444D03
Впишите правильный ответ.
Моторная лодка прошла против течения реки 168 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 13 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
1
x-скорость течения
13+x - скорость по течению
13-x - скорость против течения
Составляем уравнение:
`168/(13+x) + 2 =168/(13-x)`
`168/(13+x) - 168/(13-x) + 2 =0`
`(168(13-x)-168(13+x))/((13+x)(13-x))+2=0`
`(168*13-168x-168x*13-168x)/((13+x)(13-x))+2=0`
`(-336x)/((13+x)(13-x))+2=0`
`(-336x)/(169-13x+13x-x^2)+2=0`
`(-336x)/(169-13x+13x-x^2)=-2`
`-336x=-2(169-x^2)`
`-336х=-338 +2x^2`
2x2+336x-338=0
D=3362-4*2*(-338)=112896+2704=115600
`x= (-336+340)/(2*2) = 4/4` =1
второй корень отрицательный, не имеет смысла
Ответ: 1
Номер: F23E04
Впишите правильный ответ.
Теплоход проходит по течению реки до пункта назначения 468 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 22 км/ч, стоянка длится 3 часа, а в пункт отправления теплоход возвращается через 47 часов. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
4
x-скорость течения
22+x - скорость по течению
22-x - скорость против течения
47-3=44 часа в пути
Составляем уравнение:
`468/(22+x) + 468/(22-x) = 44`
`(468(22-x)+468(22+x))/((22+x)(22-x))=44`
`(468*22-468x+468*22+468x)/((22+x)(22-x))=44`
`20592/(484-22x+22x-x^2)=44`
`468=484-22x+22x-x^2`
`x^2=16`
x=4
Ответ: 4
Номер: 65E80F
Впишите правильный ответ.
Пристани A и B расположены на озере, расстояние между ними равно 264 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась тем же путём обратно со скоростью на 2 км/ч больше прежней, сделав по пути остановку на 1 час. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
КЭС: 2.1 Уравнения 2.2 Неравенства
Решение:
22
x - скорость баржи на пути из A в B
x+2 - скорость баржи на пути из B в A
Составим уравнение
`264/x = 264/(x+2)+1`
`264/(x+2)-264/x+1=0`
`(264x-264x-528)/(x(x+2))+1=0`
`-528/(x^2+2x)+1=0`
`-528/-1 = x^2+2x`
`x^2+2x-528=0`
D=4-4*1*-528=2116
`x=-2+46/(2*1)=22`
Ответ:22
Номер: 8B3972
Впишите правильный ответ.
Теплоход проходит по течению реки до пункта назначения 48 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 10 часов. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
20
Пусть скорость теплохода х км/ч, тогда
48/(х-4) ч - проплыл против течения
48/(х+4) ч - проплыл по течению
Время в пути 10 часов - 5 часов стоянка = 5 часов
Составим уравнение :
`48/(х-4) + 48/(х+4) = 5` (Домножим каждое слагаемое на недостающий знаменатель)
48(х+4) + 48(х-4) = 5(х+4)(х-4)
`48(х+4+х-4) = 5(х^2-16)`
`48*2х = 5(х^2-16)`
`96х = 5x^2 - 80`
`5х^2 - 96х - 80 = 0`
`D = 9216 - 4*5*(-80) = 9216 + 1600 = 10 816 = 104^2`
`х1 = (96+104)/10 = 20`
х2 = 96-104/10 = - 0.8 (не подходит по условию задачи)
Ответ: 20 км/ч
Номер: 4A4AB8
Впишите правильный ответ.
Катер в 10:00 вышел по течению реки из пункта А в пункт В, расположенный в 35 км от А. Пробыв в пункте В 4 часа, катер отправился назад и вернулся в пункт А в 18:00 того же дня. Определите собственную скорость катера (в км/ч), если известно, что скорость течения реки 3 км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
18
Пусть x км/ч — собственная скорость катера. Тогда скорость катера по течению равна x+3 км/ч, против течения — x−3 км/ч. Расстояние между пунктами A и B равно 35 км. Тогда катер потратил на дорогу в одну сторону между пунктами A и B время, равное 35/(x+3), а в другую сторону — 35/(x+3). Время в пути 18-10-4=4 часа был в пути. составим уравнение.
`35/(х-3) + 35/(х+3) = 4` (Домножим каждое слагаемое на недостающий знаменатель)
35(х+3) + 35(х-3) = 4(х+3)(х-3)
`70x = 4(х^2-9)`
`70х = 4x^2 - 36`
`4х^2 - 70х - 36 = 0`
`D = 4900 - 4*4*(-36) = 5476 = 74^2`
`х1 = (70+74)/(2*4) = 18`
Второй корень отрицательный.
Ответ:18
Номер: F017B1
Впишите правильный ответ.
Катер в 10:00 вышел по течению реки из пункта А в пункт В, расположенный в 40 км от А. Пробыв 3 часа в пункте В, катер отправился назад и вернулся в пункт А в 16:00 того же дня. Определите собственную скорость катера (в км/ч), если известно, что скорость течения реки 3 км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
27
Пусть x км/ч — собственная скорость катера. Тогда скорость катера по течению равна x+3 км/ч, против течения — x−3 км/ч. Расстояние между пунктами A и B равно 35 км. Тогда катер потратил на дорогу в одну сторону между пунктами A и B время, равное 35/(x+3), а в другую сторону — 35/(x+3). Время в пути 16-10-3=3 часа был в пути. составим уравнение.
`40/(х-3) + 40/(х+3) = 3` (Домножим каждое слагаемое на недостающий знаменатель)
40(х+3) + 40(х-3) = 3(х+3)(х-3)
`80x = 3(х^2-9)`
`80х = 3x^2 - 27`
`3х^2 - 80х - 27 = 0`
`D = 6400 - 4*3*(-27) = 6724 = 82^2`
`х1 = (80+82)/(2*3) = 27`
Второй корень отрицательный.
Ответ:27
Номер: BCABB7
Впишите правильный ответ.
Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 112 литров она заполняет на 6 минут быстрее, чем первая труба?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
14
I труба х л/мин Заполняет 112 литров за 112/х минут
II труба (х+6) л/мин Заполняет 112 литров за 112/(х+6) минут
Разница 112/х - 112/(х+6) = 6
`112/x - 112/(х+6) = 6`
112(х+6) - 112х = 6х(х+6)
112 ∙ 6 = 6х2 + 6 ∙ 6х
6х2 + 6 ∙ 6х - 112 ∙ 6 = 0 Делим на 6
х2 + 6х - 112 = 0
D = 62 - 4 ∙ 1 ∙ (-112) = 36 + 448 = 484 = 222
x1 = (-6-22)/2 < 0 не удовлетворяет условию задачи, скорость не может быть отрицательной
`x2 = (-6+22)/2 = 16/2` = 8
8+6=14 литров в минуту пропускает вторая труба
Ответ: 14
Номер: 1E4FB8
Впишите правильный ответ.
Имеется два сплава. Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы второго на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
30
в нашем случае 40%-25% = 15% это диапазон изменения процентного соотношения. Мы получили 35%, то есть 40-35 = 5, а 35-25=10.
Получается 40% сплав повлиял на конечную концентрацию в два раза больше, а значит его было в 2 раза больше. Получаем 2 части 40 процентного сплава и 1 часть 35.
Если взять за x одну часть, то
2x=1x+10
x=10
Тогда 40% сплав 10*2=20 кг, а 25% 10*1=10 кг Суммарно 20+10=30 кг
Ответ:30
Номер: 6D55BD
Впишите правильный ответ.
Заказ на изготовление 192 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 4 детали больше?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
12
Возьмем за x количество деталей за час изготавливаемых вторым рабочим.
x+4 изготавливает первый рабочий.
Тогда
192/x столько надо часов чтобы сделать все детали второму рабочему.
198/(x+4) столько надо часов чтобы сделать все детали первому рабочему.
Составим уравнение с поправкой на известное время 4 часа.
`192/x - 192/(x+4) = 4`
`192(x+4) - 192x = 4x(x+4)`
`768 = 4x^2 + 16x`
`4x^2 + 16x -768 = 0`
D=256-4*4*(-768)=12544=1122
`x=(-16+112)/(2*4)=96/8`=12
второй корень отрицательный, не имеет смысла
x=12
Ответ:12
Номер: BB421B
Впишите правильный ответ.
От пристани A к пристани B, расстояние между которыми равно 168 км, отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним со скоростью, на 2 км/ч большей скорости первого, отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
12
Пусть x км/ч — скорость первого теплохода.
x+2 км/ч — скорость второго теплохода.
Тогда составим уравнение
`168/х - 168/(х+2) = 2`
168(х+2) - 168x = 2х(х+2)
`336 = 2х^2+4x`
`2х^2+4x-336 = 0`
`D = 16 - 4*2*(-336) = 2704 = 52^2`
`х1 = (-4+52)/(2*2) = 48/4 =12`
Второй корень отрицательный.
Ответ:12
Номер: 641D12
Впишите правильный ответ.
Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 104 литра она заполняет на 5 минут дольше, чем вторая труба?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
8
x - пропускает в мин первая труба
x+5 - пропускает вторая труба
составим уравнение
`104/х - 104/(х+5) = 5`
104(х+5) - 104x = 5х(х+5)
`520 = 5х^2+25x`
`5х^2+25x-520 = 0`
`D = 625 - 4*5*(-520) = 11025 = 105^2`
`х1 = (-25+105)/(2*5) = 80/10 =8`
Второй корень отрицательный.
Ответ:8
Номер: FAC22B
Впишите правильный ответ.
Два велосипедиста одновременно отправились в 80-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
8
Пусть x км/ч — скорость второго велосипедиста.
x+2 км/ч — скорость первого велосипедиста.
Тогда составим уравнение
`80/х - 80/(х+2) = 2`
80(х+2) - 80x = 2х(х+2)
`160 = 2х^2+4x`
`2х^2+4x-160 = 0`
`D = 16 - 4*2*(-160) = 1296 = 36^2`
`х1 = (-4+36)/(2*2) = 32/4 =8`
Второй корень отрицательный.
Ответ:8
Номер: 591D2E
Впишите правильный ответ.
Моторная лодка прошла против течения реки 117 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
11
Пусть x км/ч — скорость лодки в неподвижной воде.
x+2 км/ч — скорость по течению.
x-2 км/ч — скорость против течения.
Тогда составим уравнение
`117/(х-2) - 117/(х+2) = 4`
117(х+2) - 117(х-2) = 4(х-2)(х+2)
`468 = 4(х^2-4)`
`117 = х^2-4`
`х^2 = 121`
х = 11
Ответ:11
Номер: A08F25
Впишите правильный ответ.
Заказ на изготовление 323 деталей первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 2 детали больше второго?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
19
x - производительность в час первого рабочего
x-2 - производительность в час второго рабочего
Составим уравнение:
`323/(х-2) - 323/х = 2`
323х - 323(х-2) = 2х(х-2)
`646 = 2х^2-4x`
`2х^2-4x -646 = 0`
D = 16-4*2*-646=5184=722
`х = (4+72)/(2*2)=76/4`=19
Второй корень отрицательный.
Ответ:19
Номер: 02F1DB
Впишите правильный ответ.
Теплоход проходит по течению реки до пункта назначения 567 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 54 часа. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
24
x - скорость теплохода в неподвижной воде
x-3 - скорость теплохода против течения
x+3 - скорость теплохода по течению
54-6=48 часов был в пути
Составим уравнение:
`567/(х-3) + 567/(х+3) = 48`
567(х+3) + 567(х-3) = 48(х+3)(х-3)
`1134x = 48(х^2-9)`
`48х^2 - 1134x -432 = 0`
`24х^2 - 567x -216 = 0`
D = 321489-4*24*-216=342225=5852
`х = (567+585)/(2*24)=24
Второй корень отрицательный.
Ответ:24
Номер: 17A0D7
Впишите правильный ответ.
Моторная лодка прошла против течения реки 91 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
10
x - скорость лодки в неподвижной воде
x-3 - скорость лодки против течения
x+3 - скорость лодки по течению
Составим уравнение:
`91/(х-3) - 91/(х+3) = 6`
91(х+3) - 91(х-3) = 6(х+3)(х-3)
`546 = 6(х^2-9)`
`6х^2 = 600`
`х^2 = 100`
х = 10
Ответ:10
Номер: CF56D0
Впишите правильный ответ.
Первые 200 км автомобиль ехал со скоростью 60 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 140 км — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
80
Берем каждый час за 1 часть и находим среднее для этих частей, тем самым определяя среднюю скорость.
200/60 = 3 1/3 части
180/90 = 2 часа (части)
140/120= 7/6
`(60*3 1/3+90*2+7/6*120)/(6,5)=520/(6,5) `= 80 км/ч
Ответ: 80
Номер: 6D24D0
Впишите правильный ответ.
Расстояние между пристанями A и B равно 192 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
20
x - скорость яхты
192/(x+4) + 192/(x-4) - время яхты в пути
92/4 = 23 часа - время в пути плота
23-3=20 время яхты в пути
Составляем уравнение
`192/(x+4) + 192/(x-4)=20`
`192(x-4) + 192(x+4)=20(x+4)(x-4)`
`384x=20(x^2-16)`
`20x^2-384x-320=0`
`10x^2-192x-160=0`
D=36864-4*10*160=43264=2082
`x=(192+208)/2*10`=20
Второй корень отрицательный.
Ответ: 20
Номер: 4BA055
Впишите правильный ответ.
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 35 км/ч. Длина пассажирского поезда равна 250 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского, равно 30 секундам. Ответ дайте в метрах.
КЭС: 2.1 Уравнения 2.2 Неравенства
Решение:
750
85+35=120 км/ч - скорость сближения
По сути пассажирский должен сблизиться с первым вагоном, потом пройти весь поезд, а потом еще 250 метров, то есть свою длину, пока не перестанет условно пересекаться с навстречу идущим.
x - длина скорого поезда
x+250 столько прошел пассажирский поезд.
120:60:2=1 км в пол минуты проходит любой из поездов при их "наложении" друг на друга.
То есть 1000-250=750 м пассажирский поезд.
Ответ:750
Номер: AA1851
Впишите правильный ответ.
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
12
x - скорость лодки в неподвижной воде
x+1 - скорость лодки по течению
x-1 - против течения
`143/(x-1)-143/(x+1)=2`
`143(x+1)-143(x-1)=2(x+1)(x-1)`
`286=2(x^2-1)`
`286=2x^2-2`
`x^2=144`
x=12
Ответ:12
Номер: F2CCA3
Впишите правильный ответ.
Моторная лодка прошла против течения реки 48 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
4
x - скорость течения
8+x - скорость по течению
8-x - скорость против течения
`48/(8-x)-48/(8+x)=8`
`48(8+x)-48(8-x)=8(8-x)(8+x)`
`96x=8(64-x^2)`
`8x^2+96x-512=0`
`x^2+12x-64=0`
D = 144-4*1*-64=400
`x=(-12+20)/(2*1)=4`
второй корень отрицательный
Ответ:4
Номер: 5EB1A5
Впишите правильный ответ.
Катя и Настя, работая вместе, пропалывают грядку за 24 минуты, а одна Настя — за 42 минуты. За сколько минут пропалывает грядку одна Катя?
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
56
Возьмем грядку за условные 100 процентов, тогда
100/24 - столько пропалывают от грядки две девочки за минуту
100/42 - столько пропалывает от грядки Настя за минуту
100/x - столько пропалывает Катя за минуту.
При этом если сложить производительности в минуту Насти и Кати, то получим производительность двух девочек.
`100/24 = 100/42 + 100/x`
`100/24 - 100/42 = 100/x`
`(4200-2400)/1008 = 100/x`
`1800/1008 = 100/x`
`x = (1008*100)/1800 = 56`
* в этой задаче грядку можно взять и за 1 и за 2 и за любое натуральное число, это условность которой не хватает в задачи и которая нужна для определения производительности девочек между собой и для их производительности вместе
Ответ: 56 минут
Номер: AB5ECB
Впишите правильный ответ.
Расстояние между городами A и B равно 500 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
Решение:
1) 500 – 260 = 240 (км) – прошел 2 автомобиль до встречи.
2) 240 : 80 = 3 (ч) – время, затраченное 2 автомобилем до встречи.
3) 3 + 1 = 4 (ч) – время, затраченное 1 автомобилем до встречи.
4) 260 : 4 = 65 (км/ч) – скорость 1 автомобиля.
Ответ: 65
Номер: 2A6A94
Впишите правильный ответ.
Два велосипедиста одновременно отправились в 140-километровый пробег. Первый ехал со скоростью на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
14
x - скорость первого велосипедиста.
x - 4 - скорость второго велосипедиста
`140/(x-4) - 140/x = 4`
`140x - 140(x-4)= 4x(x-4)`
`560= 4x^2-16x`
`4x^2-16x-560=0`
`x^2-4x-140=0`
D=16-4*1*-140=576
`x=(4+24)/(2*1)=28/2=14`
второй корень отрицательный
Ответ:14
Номер: BC64EB
Впишите правильный ответ.
Имеется два сосуда. Первый содержит 40 кг, а второй — 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
КЭС: 1.1.3 Дроби, проценты, рациональные числа 2.1.2 Рациональные уравнения 2.1.8 Простейшие системы уравнений с двумя неизвестными
Решение:
10
Обозначим за х кислотность первого раствора, а за у второго.
Масса кислоты первого будет 40х, а второго 25у, сложив их получим новый раствор (1+2) с массой кислоты 65·0,3.
Если смешать растворы одинаковой массы, возьмём по 25 кг (что бы сократилась переменная y в системе уравнений), то получим раствор (3) с массой кислоты 50·0,36. Составим систему уравнений:
Запишем систему уравнений
| 〈 | 40x+25y=65 25x+25y=50 |
Вычтем из первого уравнения второе:
40х + 25у – 25х – 25у = 65·0,3 – 50·0,36
15х = 65·0,3 – 50·0,36
15х = 1,5
`х=1,5/15`=0.1
Найдём cколько процентов кислоты содержится в первом сосуде: 0,1·100% = 10%
Ответ:10
Номер: ADEDE3
Впишите правильный ответ.
Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 9 км/ч. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
3
x - cкорость течения
9-x - скорость против течения
9+x - скорость по течению
`72/(9-x)-72/(9+x)=6`
`72(9+x)-72(9-x)=6(9+x)(9-x)`
`144x=6(81-x^2)`
`144x=486-6x^2`
`6x^2 + 144x -486= 0`
`x^2 + 24x - 81= 0`
D=576-4*1*-81=900
x=(-24+30)/2=3
второй корень отрицательный
Ответ:3
Номер: 33D8E1
Впишите правильный ответ.
Заказ на изготовление 209 деталей первый рабочий выполняет на 8 часов быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 8 деталей больше?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
11
x - деталей в час производит 2 рабочий
x+8 - деталей в час производит 1 рабочий
`209/x-209/(x+8)=8`
`209(x+8)-209x=8x(x+8)`
`209(x+8)-209x=8x(x+8)`
`1672=8x^2+64x`
`8x^2+64x-209=0`
`x^2+8x-1672=0`
D = 64-4*1*-209=900
`x=(-8+30)/(2*1)=11`
второй корень отрицательный
Ответ:11
Номер: 071261
Впишите правильный ответ.
Первый час автомобиль ехал со скоростью 120 км/ч, следующие три часа — со скоростью 105 км/ч, а затем три часа — со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения
Решение:
90
Берем каждый час за 1 часть и находим среднее для этих частей, тем самым определяя среднюю скорость.
`(120*1+105*3+3*65)/7=630/7 `= 90 км/ч
Ответ: 90
Номер: 0B236A
Впишите правильный ответ.
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 672 литра она заполняет на 4 минуты быстрее, чем первая труба?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
28
Решим задачу при помощи уравнения. Пусть первая труба пропускает х литров в минуту, тогда вторая труба пропускает (х + 4) литров в минуту. Нам известно, что резервуар объемом 672 литра заполняет вторая труба на 4 минуты быстрее, чем первая труба. Составляем уравнение:
`672/х - 672/(х + 4) = 4;`
`(672х + 2 688 - 672х)/(х^2 + 4х) = 4;`
`2 688/(х^ 2+ 4х) = 4;`
`2 688 = 4 * (х^2 + 4х);`
`4х^2 + 16х - 2 688 = 0;`
`х^2 + 4х - 672 = 0;`
`D = b^2 - 4 * а * с = 16 + 2688 = 2 704;`
`х = (-4 + 52)/2` = 24 литра в минуту — пропускает первая труба;
24 + 4 = 28 литров в минуту — пропускает первая труба.
Ответ: 28 литров в минуту.
Номер: 768665
Впишите правильный ответ.
Теплоход проходит по течению реки до пункта назначения 609 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 25 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 51 час. Ответ дайте в км/ч.
КЭС: 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
4
Пусть х - скорость течения
тогда 25 + x - скорость по течению
25 - x - скорость против течения
51-1=50 часов в пути
609 : (25 + x) - время в пути по течению
609 : (25 - x) - время в пути против течения
Составляем уравнение:
`609/(25 + x) + 609/(25 - x) = 50`
Приводим дроби к общему знаменателю, переносим знаменатель в правую часть
609*(25 - x) + 609*(25 + x)= 50(25 + x)(25 - x)
`30450 = 50*(625-x^2)`
`30450 = 31250 - 50x^2`
`50x^2 = 800`
`x^2=16`
x=4
Ответ: 4
Номер: B4C164
Впишите правильный ответ.
Два велосипедиста одновременно отправились в 160-километровый пробег. Первый ехал со скоростью на 6 км/ч большей, чем скорость второго, и прибыл к финишу на 6 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
10
Пусть х - скорость 2-го велосипедиста, тогда
х+6 -скорость 1-го велосипедиста
`t_(медл)-t_(быстр)=6`
`160/х - 160/(х+6) = 6`
`(160х+160*6-160x)/(x^2+6x)=6` |:6
`x^2 + 6x - 160 = 0`
`x_1+x_2=-6`
`x_1*x_2=-160`
`x_1 = 10` км/час
`x_2 = -16` (не удовлетворяет условию)
Ответ: 10
Номер: BAF165
Впишите правильный ответ.
Два велосипедиста одновременно отправились в 220-километровый пробег. Первый ехал со скоростью, на 9 км/ч большей, чем скорость второго, и прибыл к финишу на 9 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
20
х - скорость 1-го велосипедиста
х-9 -скорость 2-го велосипедиста
`220/х = 220/(х-9) - 9`
220 * (х-9) = 220х - 9х * (х-9)
220х - 1980 = 220х - 9х^2 + 81x
`x^2 - 9x - 220 = 0`
D=81-4*1*-220=961=312
`x1 = (9+31)/2 = 20`
x2 = -11 (не удовлетворяет условию)
Ответ: 20 км/час
Номер: 65356D
Впишите правильный ответ.
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 285 литров она заполняет на 4 минуты дольше, чем вторая труба?
КЭС: 2.1.1 Квадратные уравнения 2.1.2 Рациональные уравнения 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Решение:
15
x - первая труба
x+4 - вторая труба
`285/x = 285/(x+4) + 4`
`285/x -285/(x+4) - 4 = 0`
`(285x+1140-285x)/(x(x+4)) - 4 = 0`
`1140/(x^2+4x) - 4 = 0`
`1140/(x^2+4x) = 4`
`1140/4 = x^2+4x`
`x^2+4x-285=0`
D=16-4*1*-285=1156
`x=(-4+34)/(2*1)`
x=15
второй корень отрицательный, смысла не имеет
Ответ:15
Номер: 6ABF35
Задачи из старого банка ФИПИ
КЭС: Уравнения и неравенства
Задачи из старого банка ФИПИ на проценты
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение:
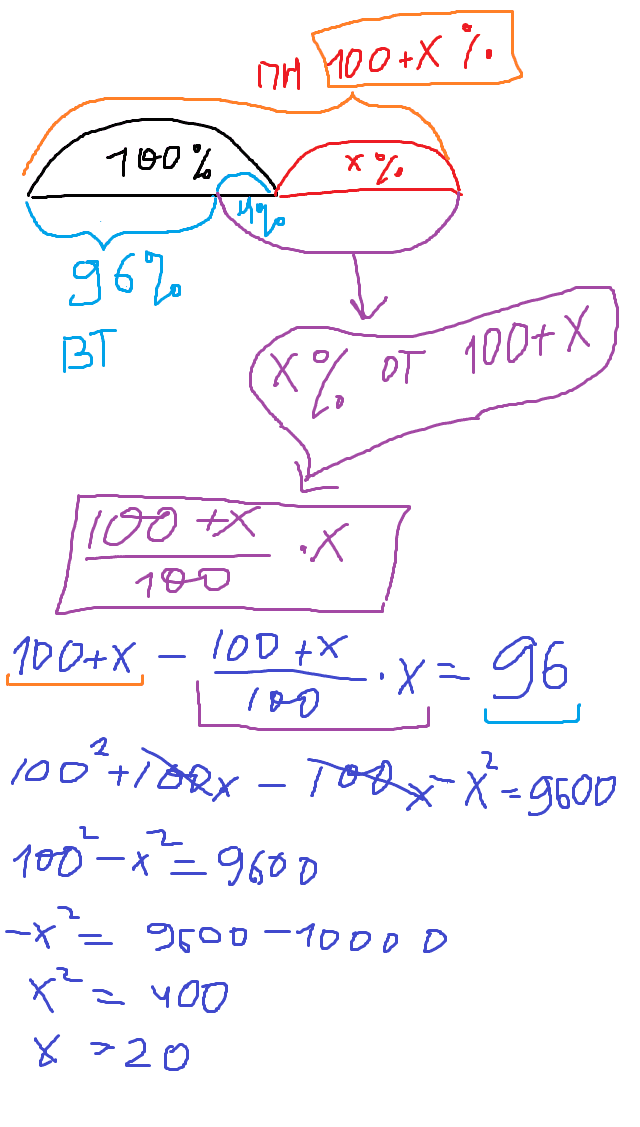
Ответ: 20
Ловите лайфхак. К данным в условии процентам дописываем два нуля и извлекаем корень. Это и будет ответ.
ИЛИ
Пусть S - начальная стоимость акций, х - десятичная запись процентов, на которые дважды происходили изменения стоимости акций. (Десятичная запись процентов - это представление процентов в виде десятичной дроби, например, десятичная запись 55% равна 0,55.)
В понедельник акции подорожали на х процентов, т.е. их стоимость увеличилась на S * х и составила
S+S*x=S(1+x).
Во вторник акции подешевели на х процентов, те. их стоимость уменьшилась на S(1 + х)*х.
Цена акций стала равна
S(1 + х) — S(1 + х) * х = S(1+х)(1 — х),
что составило 100% — 4% = 96% от цены в начале недели (от S). На основании этого составим уравнение:
S(1 + x)(1 - x) = 0,96S
(1 + x)(1 - x) = 0,96
1-x2 = 0,96
x2 = 0,04
Поскольку х > 0,то х = 0,2.
Следовательно, в понедельник и во вторник стоимость акций изменялась на 20%
Ответ: 20
ИЛИ
Обозначим первоначальную стоимость акций за А. Пусть в понедельник акции подорожали на х %, поэтому они стали стоить (100 + х)% от А, то есть
`A⋅(100+x)/100`.
Во вторник они подешевели на х %, поэтому они стали стоить (100 – х) % от `A⋅(100+x)/100`, то есть `A⋅(100+x)/100⋅(100—x)/100`.
В результате акции стали стоить 96% от А:
`A⋅96/100`.
Таким образом, получаем уравнение:
`A⋅(100+x)/100⋅(100—x)/100=A⋅96/100`|:A ⇔ `(100^2—x^2)/100=96` ⇔ `10000—x^2=9600` ⇔
⇔ `x^2=400` ⇔ `x_1=20`; `x_2=—20`.
Так как x>0, то акции подорожали в понедельник на 20%.
Ответ: 20
ИЛИ
Пусть х - десятичная запись количества процентов на которые дорожали и дешевели акции.
100% = 1 – первоначальная стоимость акций;
100 – 4 = 96% = 0,96 – конечная стоимость акций.
Составим уравнение по условию задачи:
1·(1 + х)·(1 – х) = 0,96
1 – х2 = 0,96
–х2 = 0,96 – 1
–х2 = –0,04
х2 = 0,04
х = ±√0,04
х = ±0,2
Количество процентов должно быть положительным, значит акции дорожали и дешевели на 0,2 = 20%.
Ответ: 20
Номер: 716AB2
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
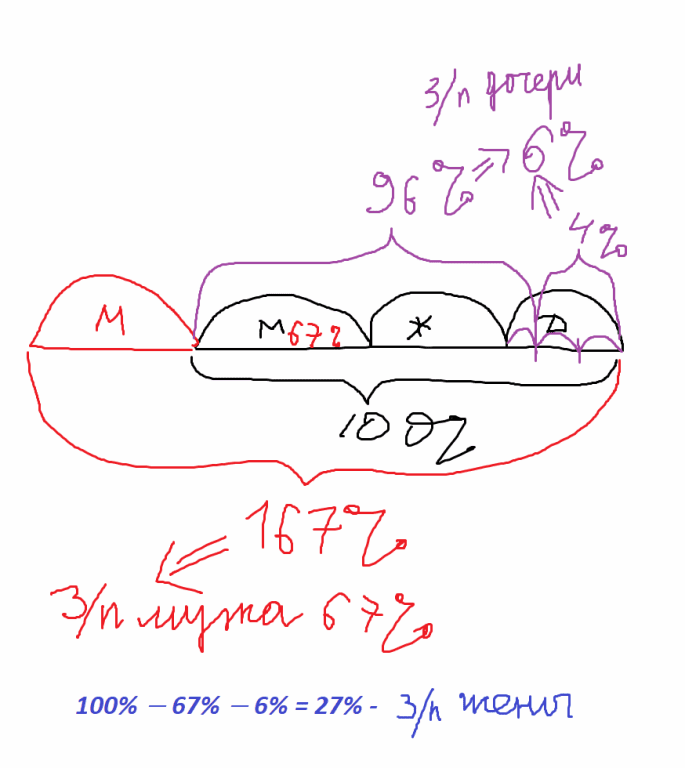
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%, то есть зарплата мужа составляет 67% дохода семьи.
Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%, то есть 2/3 стипендии составляют 4% дохода семьи, а вся стипендия дочери составляет 6% дохода семьи. Таким образом, доход жены составляет
100% − 67% − 6% = 27% дохода семьи.
Ответ: 27
ИЛИ
Пусть доход мужа, жены и дочери составляет x, y и z % соответственно. Тогда первое уравнение: x+y+z=100. Если зарплату мужа увеличить вдвое (зарплата станет 2х), то общий доход увеличиться на 67 %, то есть второе уравнение будет: 2x+y+z=167. Если стипендию дочери уменьшить втрое (стипендия станет z/3), то общий доход уменьшиться на 4 %, то есть третье уравнение будет иметь вид:
`x+y+z/3=96`.
Таким образом, получаем систему уравнений:
`{(x+y+z=100),(2x+y+z=167),(x+y+z/3=96):}`
Вычтем из второго уравнения первое: `2x—x+y—y+z—z=167—100` ⇔ `x=67`.
Вычтем из первого уравнения третье: `x—x+y—y+z—z/3=100—96` ⇔ `(2z)/3=4` ⇔ `z=6`.
Подставляя найденные x и z в первое уравнение, получим: `67+y+6=100` ⇔ `y=27`.
Ответ: 27
Номер: FD8828
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 51%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 3%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
доход мужа - 51 %
доход дочери - 2*3 = 6 %
100−51−6=43 %
Ответ: 43
Номер: 994E2F
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 57%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 1%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
доход мужа - 57 %
доход дочери - 2*1 = 2 %
100−57−2=41 %
Ответ: 41
Номер: 2A50D5
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 66%. Если бы стипендия дочери уменьшилась вчетверо, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
доход мужа - 66 %
доход дочери - 6/3 * 4 = 8 %
100−66−8=26 %
Ответ: 26
Номер: 6624E2
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 38 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*38=30,78 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =30,78
х=30,78:0,18
х=171 кг винограда потребуется для получения 38 килограммов изюма
Ответ: 171
ИЛИ через пропорцию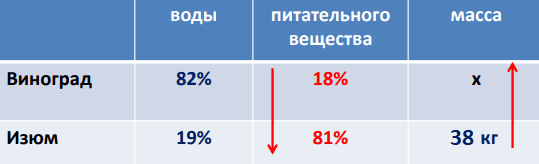
`18/81=38/x`
`x=(81*38)/18`
`x=171`
Ответ: 171
Номер: 40C2A6
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 78 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*78=63,18 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =63,18
х=63,18:0,18
х=351 кг винограда потребуется для получения 78 килограммов изюма
Ответ: 351
Номер: 069345
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 74 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*74=59,94 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =59,94
х=59,94:0,18
х=333 кг винограда потребуется для получения 74 килограммов изюма
Ответ: 333
Номер: 2BEE01
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 8 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*8=6,48 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =6,48
х=6,48:0,18
х=36 кг винограда потребуется для получения 8 килограммов изюма
Ответ: 36
Номер: 549E73
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 46 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*46=37,26 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =37,26
х=37,26:0,18
х=207 кг винограда потребуется для получения 46 килограммов изюма
Ответ: 207
Номер: CC5811
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 98 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*98=79,38 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =79,38
х=79,38:0,18
х=441 кг винограда потребуется для получения 98 килограммов изюма
Ответ: 441
Номер: 61C5A0
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 70 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*70=56,7 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =56,7
х=56,7:0,18
х=315 кг винограда потребуется для получения 70 килограммов изюма
Ответ: 315
Номер: B9E1C5
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 4 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*4=3,24 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =3,24
х=3,24:0,18
х=18 кг винограда потребуется для получения 4 килограммов изюма
Ответ: 18
Номер: F07066
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 60 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*60=48,6 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =48,6
х=48,6:0,18
х=270 кг винограда потребуется для получения 60 килограммов изюма
Ответ: 270
Номер: B09667
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 80 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*80=64,8 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =64,8
х=64,8:0,18
х=360 кг винограда потребуется для получения 80 килограммов изюма
Ответ: 360
Номер: 6DAB67
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 64 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
Виноград содержит 100-82=18% или 0,18 сухого вещества;
изюм содержит 100-19=81% или 0,81 сухого вещества
0,81*64=51,84 кг сухого вещества в изюме, в винограде столько же.
Пусть винограда х кг, тогда 0,18*х - масса сухого вещества в винограде. Составим уравнение
0,18*х =51,84
х=51,84:0,18
х=288 кг винограда потребуется для получения 64 килограммов изюма
Ответ: 288
Номер: 97373B
Десять одинаковых рубашек дешевле куртки на 8%. На сколько процентов пятнадцать таких же рубашек дороже куртки?
Решение:
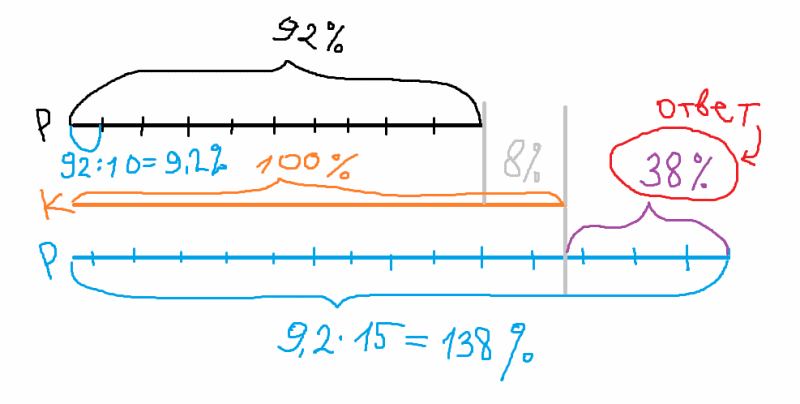
10 рубашек дешевле куртки на 8% означает, что 10 рубашек составляют 100-8=92% от стоимости куртки.
Следовательно, одна рубашка – это 92/10=9,2 % от стоимости куртки, а 15 рубашек 9,2*15=138 %
138 - 100 = 38 %
Ответ: 38
Номер: B656B1
Десять одинаковых рубашек дешевле куртки на 6%. На сколько процентов пятнадцать таких же рубашек дороже куртки?
Решение:
10 рубашек дешевле куртки на 6% означает, что 10 рубашек составляют 100-6=94% от стоимости куртки.
Следовательно, одна рубашка – это 94/10=9,4 % от стоимости куртки, а 15 рубашек 9,4*15=141 %
141 - 100 = 41 %
Ответ: 41
Номер: BC95FD
Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
Решение:
9 рубашек дешевле куртки на 10% означает, что 9 рубашек составляют 100-10=90% от стоимости куртки.
Следовательно, одна рубашка – это 90/9=10 % от стоимости куртки, а 11 рубашек 10*11=110 %
110 - 100 = 10 %
Номер: 2B0545
Семь одинаковых рубашек дешевле куртки на 9%. На сколько процентов девять таких же рубашек дороже куртки?
Решение:
7 рубашек дешевле куртки на 9% означает, что 7 рубашек составляют 100-9=91% от стоимости куртки.
Следовательно, одна рубашка – это 91/7=13 % от стоимости куртки, а 9 рубашек 13*9=117 %
117 - 100 = 17 %
Ответ: 17
Номер: 92E8F0
Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов двенадцать таких же рубашек дороже куртки?
Решение:
9 рубашек дешевле куртки на 10% означает, что 9 рубашек составляют 100-10=90% от стоимости куртки.
Следовательно, одна рубашка – это 90/9=10 % от стоимости куртки, а 12 рубашек 10*12=120 %
120 - 100 = 20 %
Ответ: 20
Номер: 87ECF9
Шесть одинаковых рубашек дешевле куртки на 8%. На сколько процентов девять таких же рубашек дороже куртки?
Решение:
6 рубашек дешевле куртки на 8% означает, что 6 рубашек составляют 100-8=92% от стоимости куртки.
Следовательно, одна рубашка – это 92/6 % от стоимости куртки, а 9 рубашек (92/6)*9 = 46 * 3 = 138 %
138 - 100 = 38 %
Ответ: 38
Номер: DEA5DF
Восемь одинаковых рубашек дешевле куртки на 10%. На сколько процентов двенадцать таких же рубашек дороже куртки?
Решение:
8 рубашек дешевле куртки на 10% означает, что 8 рубашек составляют 100-10=90% от стоимости куртки.
Следовательно, одна рубашка – это 90/8 % от стоимости куртки, а 12 рубашек (90/8)*12 = 45 * 3 = 135 %
135 - 100 = 35 %
Ответ: 35
Номер: 8F1EDC
Восемь одинаковых рубашек дешевле куртки на 4%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
Решение:
8 рубашек дешевле куртки на 4% означает, что 8 рубашек составляют 100-4=96% от стоимости куртки.
Следовательно, одна рубашка – это 96/8 = 12 % от стоимости куртки, а 11 рубашек 12*11 = 132 %
132 - 100 = 32 %
Ответ: 32
Номер: BAFBA3
Шесть одинаковых рубашек дешевле куртки на 1%. На сколько процентов восемь таких же рубашек дороже куртки?
Решение:
6 рубашек дешевле куртки на 1% означает, что 6 рубашек составляют 100-1=99% от стоимости куртки.
Следовательно, одна рубашка – это 99/6% от стоимости куртки, а 8 рубашек (99/6)*8 = 33 * 4 = 132 %
132 - 100 = 32 %
Ответ: 32
Номер: 989DAD
Десять одинаковых рубашек дешевле куртки на 2%. На сколько процентов пятнадцать таких же рубашек дороже куртки?
Решение:
10 рубашек дешевле куртки на 2% означает, что 10 рубашек составляют 100-2=98% от стоимости куртки.
Следовательно, одна рубашка – это 98/10 = 9,8% от стоимости куртки, а 15 рубашек 9,8*15 = 147 %
147 - 100 = 47 %
Ответ: 47
Номер: 309D6A
Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
Решение:
6 рубашек дешевле куртки на 2% означает, что 6 рубашек составляют 100-2=98% от стоимости куртки.
Следовательно, одна рубашка – это 98/6% от стоимости куртки, а 9 рубашек (98/6)*9 = 147 %
147 - 100 = 47 %
Ответ: 47
Номер: 9F4420
Налог на доходы составляет 13% от заработной платы. Заработная плата Андрея Сергеевича равна 13 500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Решение:
За вычетом 13% чел получит 87% или 0,87 часть от зарплаты
0,87*13500=11745 р
Ответ: 11745
ИЛИ
13% - это 0,13 часть от зарплаты
0,13*13500=1755 р составит налог
13500-1755=11745 р получит на руки
Ответ: 11745
Номер: 46BCD0
Налог на доходы составляет 13% от заработной платы. Заработная плата Фёдора Павловича равна 12 000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Решение:
За вычетом 13% человек получит 87% или 0,87 часть от зарплаты
0,87*12000=10 440 р
Ответ: 10440
Номер: E89AFE
Налог на доходы составляет 13% от заработной платы. Заработная плата Ольги Анатольевны равна 9 000 рублей. Какую сумму она получит после вычета налога на доходы? Ответ дайте в рублях.
Решение:
За вычетом 13% человек получит 87% или 0,87 часть от зарплаты
0,87*9000=7 830 р
Ответ: 7830
Номер: 9B07C7
Налог на доходы составляет 13% от заработной платы. Заработная плата Анастасии Владимировны равна 16 500 рублей. Какую сумму она получит после вычета налога на доходы? Ответ дайте в рублях.
Решение:
За вычетом 13% человек получит 87% или 0,87 часть от зарплаты
0,87*16500=14 355 р
Ответ: 14355
Номер: 33B137
Мобильный телефон стоил 9800 рублей. Через некоторое время цену на эту модель снизили до 7546 рублей. На сколько процентов была снижена цена?
Решение:
Начальная цена 9800. Пусть цену снизили на х (в долях), и получили 7546. Составим уравнение:
9800*х=7546
х=7546/9800
х=0,77 или 77% составила стоимость от начальной цены,
значит цена снижена на 100-77=23 %
Ответ: 23
ИЛИ
9800-7546=2254 р скидка
9800*х=2254
х=2254/9800
х=0,23 или 23 % составила скидка
Ответ: 23
ИЛИ сразу в %
Начальная цена 9800. Пусть цену снизили на х %, и получили 7546. Составим уравнение:
9800 : 100 * х = 7546
х=7546 : 98
х=77 % составила стоимость от начальной цены,
значит цена снижена на 100-77=23 %
Ответ: 23
Номер: 9873B7
Мобильный телефон стоил 8400 рублей. Через некоторое время цену на эту модель снизили до 6300 рублей. На сколько процентов была снижена цена?
Решение:
...
Ответ:
Номер: 1F5AAE
Мобильный телефон стоил 3000 рублей. Через некоторое время цену на эту модель снизили до 2220 рублей. На сколько процентов была снижена цена?
Решение:
...
Ответ:
Номер: 03AA6E
Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2660 рублей. На сколько процентов была снижена цена?
Решение:
...
Ответ:
Номер: B4058B
Для приготовления яблочного варенья на 1 кг яблок нужно 1,2 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 26 кг яблок?
Решение:
26*1,2=31,2 кг сахара нужно, но 200 г отдельно не продадут, поэтому покупать придется 32 упаковки по 1 кг.
Ответ: 32
Номер: 7FACF5
Для приготовления вишнёвого варенья на 1 кг вишни нужно 1,5 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 19 кг вишни?
Решение:
19*1,5=28,5 - это 29 килограммовых упаковок
Ответ: 29
Номер: 6DAFD0
Задачи из старого банка ФИПИ на растворы
Смешав 24-процентный и 67-процентный растворы кислоты и добавив 10 кг чистой воды, получили 41-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
Решение:
Нарисуем схему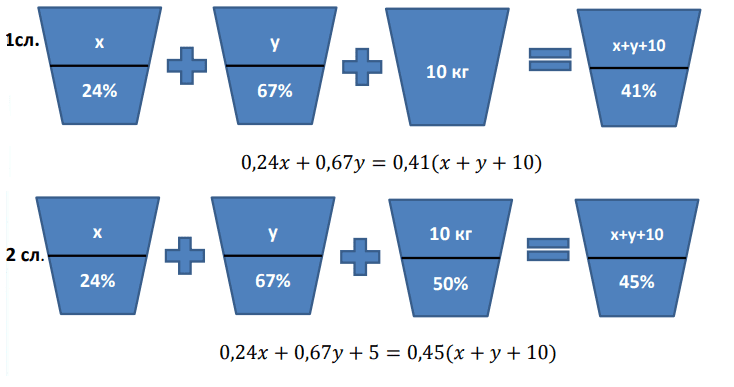
или составим таблицу
| Раствор | % | Масса общая, кг | Масса к-ты, кг |
| 1 | 24 | х | 0,24х |
| 2 | 67 | у | 0,67у |
| 3 | 41 | х+у+10 | 0,24х+0,67у=0,41(х+у+10) |
| 4 | 50 | 10 | 0,5*10=5 |
| 5 | 45 | х+у+10 | 0,24х+0,67у+5=0,45(х+у+10) |
`{(0.24х+0.67у=0.41(х+у+10)),(0.24х+0.67у+5=0.45(х+у+10)):}` |*100
`{(24х+67у=41(х+у+10)),(24х+67у+500=45(х+у+10)):}`
Вычтем из 1 уравнения системы 2 уравнение, выполним преобразования и выразим x:
24х+67у-24х-67у-500=41(х+у+10)-45(х+у+10)
-500=(х+у+10)(41-45)
-500=-4x-4y-40
4x+4y=460
x+y=115
x=115-y
Подставим найденное значение х в первое уравнение системы:
24(115 − 𝑦) + 67𝑦 = 41(115 − 𝑦 + 𝑦 + 10)
y=55.
х=115-55
х=60
ИЛИ
`{(0.24х+0.67у=0.41(х+у+10)),(0.24х+0.67у+5=0.45(х+у+10)):}`
`{(0.17х-0.26у+4.1=0),(0.21х-0.22у-0.5=0):}` |*100
`{(17х-26у+410=0),(21х-22у-50=0):}`
из первого ур-я
`x=(26y-410)/17`
подставляем во второе
`21* (26y-410)/17 - 22у-50=0`
`546y-8610-374y-850=0`
`172y-9460=0`
`у=9460/172`
`у = 55`
`x=(26*55-410)/17`
`х = 60`
Ответ: 60
Номер: 93BF4F
Смешав 43-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 69-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 73-процентный раствор кислоты. Сколько килограммов 43-процентного раствора использовали для получения смеси?
Решение:
...
Ответ:
Номер: 4C502E
Смешав 38-процентный и 52-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?
Решение:
...
Ответ:
Номер: 554D37
Смешав 24-процентный и 67-процентный растворы кислоты и добавив 10 кг чистой воды, получили 41-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
Решение:
...
Ответ:
Номер: F119B4
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
Решение:
...
Ответ:
Номер: 02C0F1
В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 5FDF16
В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 5CD64A
В сосуд, содержащий 10 литров 14-процентного водного раствора некоторого вещества, добавили 4 литра воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: B5FB9B
В сосуд, содержащий 8 литров 15-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: A8E5E3
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 6DEB0C
В сосуд, содержащий 5 литров 10-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 84B5B5
В сосуд, содержащий 8 литров 20-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 6643B5
Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: 0DCA14
Смешали некоторое количество 12-процентного раствора некоторого вещества с таким же количеством 14-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
...
Ответ:
Номер: F3322B
Имеется два сосуда. Первый содержит 60 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде?
Решение:
...
Ответ:
Номер: B968FE
Имеется два сосуда. Первый содержит 40 кг, а второй — 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
Решение:
...
Ответ:
Номер: ADEDE3
Задачи из старого банка ФИПИ на сплавы
Имеется два сплава. Первый сплав содержит 45% меди, второй — 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: FD5B44
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение:
0,1x + 0,35 * (150 – x) = 0,25 * 150
0,1x + 52,5 – 0,35x = 37,5
15 = 0,25х
х = 15/0,25
х =60 кг - масса 1 сплава
150 - 60 = 90 кг - масса 2 сплава
90 - 60 = 30 кг - разница
Ответ: 30
Номер: 5AA449
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение:
...
Ответ:
Номер: 7BD5A9
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: 671196
Имеется два сплава. Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы второго на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: 6D55BD
Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: 72E65F
Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: 8B915C
Первый сплав содержит 5% меди, второй — 11% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: F5899D
Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
...
Ответ:
Номер: E09DE7
Задачи из старого банка ФИПИ на движение
Теплоход, скорость которого в неподвижной воде равна 18 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 39 часов после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
...
Ответ:
Номер: 781081
Теплоход, скорость которого в неподвижной воде равна 17 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 6 часов, а в исходный пункт теплоход возвращается через 40 часов после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
...
Ответ:
Номер: E62B80
Теплоход, скорость которого в неподвижной воде равна 24 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 2 часа, а в исходный пункт теплоход возвращается через 34 часа после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
...
Ответ:
Номер: FE9990
Теплоход, скорость которого в неподвижной воде равна 27 км/ч, проходит некоторое расстояние по реке и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 32 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
Решение:
...
Ответ:
Номер: 205CF2
Теплоход проходит по течению реки до пункта назначения 384 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 48 часов. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 2F20C1
Теплоход проходит по течению реки до пункта назначения 48 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 10 часов. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 4A4AB8
Теплоход проходит по течению реки до пункта назначения 567 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 54 часа. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 17A0D7
Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 2 км/ч, стоянка длится 4 часа, а в пункт отправления теплоход возвращается через 13 часов. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 06B9F5
Теплоход проходит по течению реки до пункта назначения 468 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 22 км/ч, стоянка длится 3 часа, а в пункт отправления теплоход возвращается через 47 часов. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 65E80F
Теплоход проходит по течению реки до пункта назначения 609 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 25 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 51 час. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: B4C164
Расстояние между городами A и B равно 420 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Решение:
...
Ответ:
Номер: 791A06
Расстояние между городами A и B равно 630 км. Из города A в город B выехал первый автомобиль, а через три часа после этого навстречу ему из города B выехал со скоростью 70 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 305DDD
Расстояние между городами A и B равно 390 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 75 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 240 км от города A. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: C824B3
Расстояние между городами A и B равно 500 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 2A6A94
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали мотоциклист и велосипедист. Известно, что за час мотоциклист проезжает на 50 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5 часов позже мотоциклиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: D03826
Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали мотоциклист и велосипедист. Известно, что за час мотоциклист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1,5 часа позже мотоциклиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: D615E9
Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 70 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 10 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: B6C6D1
Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 10 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 317152
Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 80 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 7B8EC8
Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 25 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 50 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: BBDF90
Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 30 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 0AFCE9
Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 20 минут позже автомобилиста. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 4149F8
Байдарка в 10 : 00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки равна 2 км/ч.
Решение:
...
Ответ:
Номер: 5FA179
Байдарка в 10 : 00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки равна 3 км/ч.
Решение:
...
Ответ:
Номер: C08222
Байдарка в 7:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 40 минут, байдарка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость байдарки равна 6 км/ч.
Решение:
...
Ответ:
Номер: 20B3BB
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 4 часа, баржа отправилась назад и вернулась в пункт А в 22:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 8 км/ч.
Решение:
...
Ответ:
Номер: C169EB
Лодка в 8:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 1 час 30 минут, лодка отправилась назад и вернулась в пункт А в 22:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 5 км/ч.
Решение:
...
Ответ:
Номер: BFC9F8
Моторная лодка в 11:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 21:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 9 км/ч.
Решение:
...
Ответ:
Номер: C1BE05
Катер в 10:00 вышел по течению реки из пункта А в пункт В, расположенный в 35 км от А. Пробыв в пункте В 4 часа, катер отправился назад и вернулся в пункт А в 18:00 того же дня. Определите собственную скорость катера (в км/ч), если известно, что скорость течения реки 3 км/ч.
Решение:
...
Ответ:
Номер: F017B1
Катер в 10:00 вышел по течению реки из пункта А в пункт В, расположенный в 40 км от А. Пробыв 3 часа в пункте В, катер отправился назад и вернулся в пункт А в 16:00 того же дня. Определите собственную скорость катера (в км/ч), если известно, что скорость течения реки 3 км/ч.
Решение:
...
Ответ:
Номер: BCABB7
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 200 км — со скоростью 100 км/ч, а затем 160 км — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 5504F2
Первые 200 км автомобиль ехал со скоростью 60 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 140 км — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 6D24D0
Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа — со скоростью 45 км/ч, а затем два часа — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 081941
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 12 часов раньше, чем велосипедист приехал в город А, а встретились они через 2 часа 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: 34F721
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 10 часов раньше, чем велосипедист приехал в город А, а встретились они через 3 часа 45 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: 1720D7
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 2 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 20 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: 002254
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 6 часов раньше, чем велосипедист приехал в город А, а встретились они через 1 час 36 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: 477DEA
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 7 часов раньше, чем велосипедист приехал в город А, а встретились они через 4 часа 40 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: DD428A
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 4 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Решение:
...
Ответ:
Номер: 359317
От пристани A к пристани B, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: E5DDDD
От пристани A к пристани B, расстояние между которыми равно 168 км, отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним со скоростью, на 2 км/ч большей скорости первого, отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 641D12
Моторная лодка прошла против течения реки 187 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 5CD026
Моторная лодка прошла против течения реки 91 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: CF56D0
Моторная лодка прошла против течения реки 165 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: A1799C
Моторная лодка прошла против течения реки 117 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: A08F25
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: F2CCA3
Моторная лодка прошла против течения реки 252 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 2ED701
Моторная лодка прошла против течения реки 168 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 13 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: F23E04
Моторная лодка прошла против течения реки 135 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: CBD866
Моторная лодка прошла против течения реки 48 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 5EB1A5
Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 9 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 33D8E1
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 187 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 936503
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 132 км. На следующий день он отправился обратно со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: DB0573
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 143 км. На следующий день он отправился обратно в А со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: C8D312
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 11C055
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 126 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 02A8A0
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: DDEAA0
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 117 км. На следующий день он отправился обратно в А со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: D170EE
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 168 км. На следующий день он отправился обратно в А со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 7A186A
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 190 км. На следующий день он отправился обратно в А со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 9 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: F1B439
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 150 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: EEDD34
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: AE478C
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 156 км. На следующий день он отправился обратно со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 371585
Два велосипедиста одновременно отправились в 140-километровый пробег. Первый ехал со скоростью на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: BC64EB
Два велосипедиста одновременно отправились в 160-километровый пробег. Первый ехал со скоростью на 6 км/ч большей, чем скорость второго, и прибыл к финишу на 6 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: BAF165
Два велосипедиста одновременно отправились в 80-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 591D2E
Два велосипедиста одновременно отправились в 220-километровый пробег. Первый ехал со скоростью, на 9 км/ч большей, чем скорость второго, и прибыл к финишу на 9 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 65356D
Расстояние между пристанями A и B равно 192 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 4BA055
Пристани A и B расположены на озере, расстояние между ними равно 264 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась тем же путём обратно со скоростью на 2 км/ч больше прежней, сделав по пути остановку на 1 час. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Решение:
...
Ответ:
Номер: 8B3972
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 35 км/ч. Длина пассажирского поезда равна 250 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского, равно 30 секундам. Ответ дайте в метрах.
Решение:
...
Ответ:
Номер: AA1851
Задачи из старого банка ФИПИ на совместную работу
Один мастер может выполнить заказ за 30 часов, а другой — за 15 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Решение:
...Ответ: ...
Номер: 9CCF41
Один мастер может выполнить заказ за 15 часов, а другой — за 10 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Решение:
| Произв | Время | Кол. л | |
| 1 | 1/15 заказа в час | 15 ч | 1 заказ |
| 2 | 1/10 заказа в час | 10 ч | 1 заказ |
| Вместе | 1/6 заказа в час | x | 1 заказ |
1)`1/15+1/10=5/30=1/6`
2) `1:1/6=1*6/1=6`
Ответ: 6
Номер: ...
На изготовление 720 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 840 деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:
...
Ответ:
Номер: 2DE18E
На изготовление 540 деталей первый рабочий затрачивает на 12 часов меньше, чем второй рабочий на изготовление 600 деталей. Известно, что первый рабочий за час делает на 10 деталей больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:
...
Ответ:
Номер: 5A6244
На изготовление 572 деталей первый рабочий затрачивает на 4 часа меньше, чем второй рабочий на изготовление 650 деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:
...
Ответ:
Номер: EEE1CF
На изготовление 696 деталей первый рабочий затрачивает на 5 часов меньше, чем второй рабочий на изготовление 725 деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:
...
Ответ:
Номер: 5CAD74
На изготовление 60 деталей первый рабочий тратит на 4 часа меньше, чем второй рабочий на изготовление 80 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
Решение:
...
Ответ:
Номер: 662145
На изготовление 660 деталей первый рабочий затрачивает на 8 часов меньше, чем второй рабочий на изготовление 780 деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей за час делает первый рабочий?
Решение:
...
Ответ:
Номер: 348B11
На изготовление 77 деталей первый рабочий тратит на 4 часа меньше, чем второй рабочий на изготовление 99 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
Решение:
...
Ответ:
Номер: C98AC4
На изготовление 832 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 928 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей за час делает первый рабочий?
Решение:
...
Ответ:
Номер: 1671E0
Заказ на 88 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 3 детали больше, чем второй?
Решение:
...
Ответ:
Номер: 262AA7
Заказ на 288 деталей первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 2 детали больше, чем второй?
Решение:
...
Ответ:
Номер: 12749F
Заказ на 255 деталей первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 2 детали больше, чем второй?
Решение:
...
Ответ:
Номер: DDF795
Заказ на 72 детали первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше, чем второй?
Решение:
...
Ответ:
Номер: 5979E0
Заказ на 204 детали первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 5 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: 99A1E1
Заказ на 209 деталей первый рабочий выполняет на 8 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 8 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: C9A963
Заказ на 228 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 7 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: D2D832
Заказ на 170 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 7 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: 2E6009
Заказ на 187 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 6 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: AEBC0F
Заказ на 152 детали первый рабочий выполняет на 11 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 11 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: F56BBA
Заказ на 300 деталей первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 5 деталей больше, чем второй?
Решение:
...
Ответ:
Номер: 2C8DB0
Заказ на изготовление 323 деталей первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 2 детали больше второго?
Решение:
...
Ответ:
Номер: 02F1DB
Заказ на изготовление 198 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 7 деталей больше второго?
Решение:
...
Ответ:
Номер: 444D03
Заказ на 300 деталей первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 5 деталей больше?
Решение:
...
Ответ:
Номер: 39A432
Заказ на 380 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Решение:
...
Ответ:
Номер: DF69F6
Заказ на 260 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 7 деталей больше?
Решение:
...
Ответ:
Номер: 62EA0C
Заказ на 247 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 6 деталей больше?
Решение:
...
Ответ:
Номер: 3D6A0C
Заказ на 104 детали первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 5 деталей больше?
Решение:
...
Ответ:
Номер: 732875
Заказ на 140 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 4 детали больше?
Решение:
...
Ответ:
Номер: D6FFD6
Заказ на изготовление 154 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 3 детали больше?
Решение:
...
Ответ:
Номер: 84B86E
Заказ на 270 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 3 детали больше?
Решение:
...
Ответ:
Номер: 96835A
Заказ на 221 деталь первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 4 детали больше?
Решение:
...
Ответ:
Номер: 2D6CBF
Заказ на изготовление 192 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 4 детали больше?
Решение:
...
Ответ:
Номер: BB421B
Заказ на изготовление 209 деталей первый рабочий выполняет на 8 часов быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 8 деталей больше?
Решение:
...
Ответ:
Номер: 071261
Катя и Настя, работая вместе, пропалывают грядку за 24 минуты, а одна Настя — за 42 минуты. За сколько минут пропалывает грядку одна Катя?
Решение:
...
Ответ:
Номер: AB5ECB
Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 104 литра она заполняет на 5 минут дольше, чем вторая труба?
Решение:
...
Ответ:
Номер: FAC22B
Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем вторая труба?
Решение:
...
Ответ:
Номер: BC2088
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 285 литров она заполняет на 4 минуты дольше, чем вторая труба?
Решение:
...
Ответ:
Номер: 6ABF35
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 672 литра она заполняет на 4 минуты быстрее, чем первая труба?
Решение:
...
Ответ:
Номер: 768665
Первая труба наполняет резервуар на 13 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 42 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Решение:
...
Ответ:
Номер: 4E4109
Первая труба наполняет резервуар на 48 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 45 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Решение:
...
Ответ:
Номер: DA0CE3

