КЭС: Функции. Тип ответа: Краткий ответ. Все задания из нового открытого банка ФИПИ к ЕГЭ по профильной математике с графиками функций. Ответы прилагаются.
ВСЕ задания из ОБОИХ банков ФИПИ (в старом только дубли нового).
Задания с Графиками функций №11, новый банк ФИПИ
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax. Найдите значение f(8).
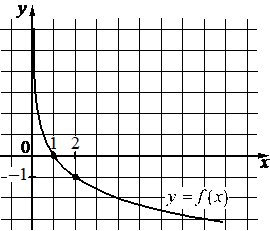
КЭС: 3.3.7 Логарифмическая функция, её график
Решение:
-3
Возьмём точку (2; –1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
f(x) = loga x
`–1 = log_(a)2`
a–1 = 2
`a=1/2`
Значит функция имеет вид:
`f(x) = log_(1/2)x`
Найдём f(8):
`f(8) = log_(1/2)8=log_(2^-1)8=-1 log_(2)8=-1* 3 =-3`
Ответ: –3.
Номер: DA4F4F
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=k/x и g(x)=ax+b, пересекающиеся в точках A и B . Найдите абсциссу точки B .
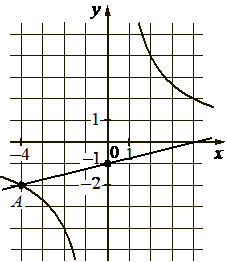
КЭС: 3.3.1 Линейная функция, её график 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
8
`f(x) = k/x`
Подставим координаты точки (–4; –2) найдём k гиперболы:
`–2 = k/(–4)`
k = –2·(–4) = 8
Гипербола имеет вид:
`f(x) = 8/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
`a = tg a =1/4` = 0,25
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –1.
b = –1
Функции прямой имеет вид:
g(x) = 0,25x – 1
Найдём абсциссы точек пересечения функций:
f(x) = g(x)
`8 = (0,25x – 1) * x`
`8 = 0,25x^2 – x`
`0,25x^2 – x – 8 = 0`
D = (–1)2 – 4*0,25*(–8) = 9 = 32
`x_(1)=(1+3)/(2*0.25)=8`
`x_(2)=(1-3)/(2*0.25)=-2/0.5=-4`
У точки А координата х = –4, значит у точки В координата х = 8.
Ответ: 8
Номер: CA314B
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax2+bx+c . Найдите значение f(− 2) .
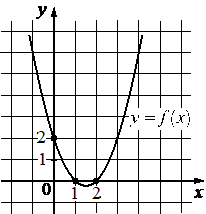
КЭС: 3.3.3 Квадратичная функция, ее график
Решение:
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = 2
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке, заметим, что при возрастании координаты х на 2,5, координата у вырастает на 6,25, т.к. `2,5^2 = 6,25`, значит это обычная парабола с а = +1:
а = +1
Координата х вершины параболы (х = 1,5) находится по формуле:
x=-b/2a
Подставим известные значения и найдём b:
1,5=-b/2
-b=1,5*2=3
b = –3
Функция имеет вид:
f(x) = +1x2 – 3x + 2
Найдём f(–2):
f(–2) = +1*(–2)2 – 3*(–2) + 2 = 4 + 6 + 2 = 12
Ответ: 12.
Номер: BC2802
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax . Найдите значение f(3) .

КЭС: 3.3.6 Показательная функция, ее график
Решение:
Возьмём точку (1; 2) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(3).
f(x) = ax
2 = a1
a = 2
Значит функция имеет вид:
f(x) = 2x
Найдём f(3):
f(3) = 23 = 2·2·2 = 8
Ответ: 8.
Номер: EC397F
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax . Найдите значение f(− 3) .
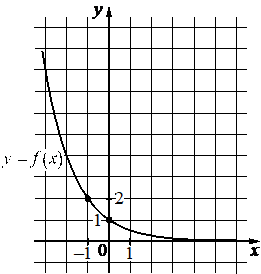
КЭС: 3.3.6 Показательная функция, ее график
Решение:
Возьмём точку (-1; -2) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(-3).
f(x) = ax
`2 = a^(-1)`
1/a = 2
a = 1/2
Значит функция имеет вид:
`f(x) = (1/2)^2`
Найдём f(-3):
`f(-3) = (1/2)^-3 = 1/8^(-1) = 8`
Ответ: 8.
Номер: 783DBA
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=kx+b . Найдите значение f(7) .
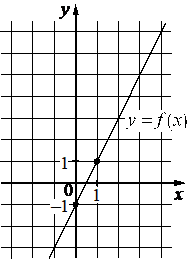
3.3.1 Линейная функция, её график
Решение:
13
График функции проходит через две точки на углах клеток, в которых можно точно определить координаты х и у:
(0; -1)
(1; 1)
На рисунке изображён график функции f(x) = kx + b. Найдите значение х, при котором f(x) = 7.
Функция имеет вид у = kx + b, подставив координаты точек, получим систему из двух уравнений:
-1 = 0k + b
b = -1
Подставим значение b в функцию со второй точкой (1; 1):
1 = k1 -1
k=2
Значит функция имеет вид:
у = 2x -1
Найдём значение х, при котором f(7):
y=2*7-1
y=14-1
y=13
Ответ: 13
Номер: 9CC815
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax . Найдите значение f(8) .
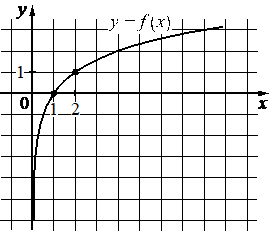
КЭС: 3.3.7 Логарифмическая функция, её график
Решение:
3
Возьмём точку (2; 1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(8).
`f(x) = log_a x`
`1 = log_a 2`
`a^1 = 2`
a = 2
Значит функция имеет вид:
`f(x) = log_2 x`
Найдём f(8):
`f(8) = log_2 x`
x=3
Ответ: 3
Номер: ECB413
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=a√x и g(x)=kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
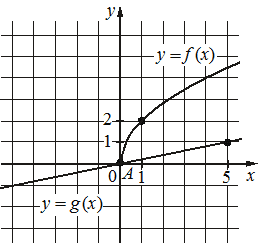
КЭС: 1.1.5 Корень степени n>1 и его свойства 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график
Решение:
100
f(x) кривой проходит через точку (1; 2), подставим значения х и у (это f(x)) в функцию, найдём а:/
f(x) = a√x
2 = a√1
2 = a·1
а = 2
Значит функция имеет вид: f(x) = 2·√x
g(x) прямой проходит через точку (5; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
g(x) = kx
1 = k·5
k=1/5=0,2
Значит функция имеет вид: g(x) = 0,2x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=2sqrt(x)`
`g(x)=0,2x`
`y=2sqrt(x)`
`y=0,2x`
Приравняем через y уравнения:
2√x = 0,2x
Возведём обе части в квадрат:
(2√x)2 = (0,2x)2
4x = 0,04x2
100x = x2
100x – x2 = 0
x*(10 – x) = 0
x1 = 0 (абсцисса точки А)
или
10 – x = 0
х2 = 100 (абсцисса точки В)
Ответ: 100
Номер: 656B14
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=ax2+bx+c и g(x)=kx , пересекающиеся в точках A и B . Найдите абсциссу точки B .
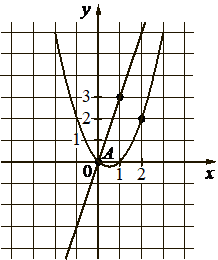
КЭС: 3.3.1 Линейная функция, её график 3.3.3 Квадратичная функция, ее график
Решение:
4
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ax2 + bx + c):
(–1; 2) – в 1-е уравнение значения точки параболы (–1; 2),
(2; 2) – во 2-е уравнение значение точки параболы (2; 2),
и с = 0 в оба уравнения, получим систему из двух уравнений для параболы:
| 〈 | 2 = a(-1)2 + b(-1) + 0 2 = a22 + b * 2 + 0 |
| 〈 | 2 = a – b 2 = 4a + 2b поделим на 2 обе части уравнения |
| 〈 | 2 = a – b 1 = 2a + b |
Cложим уравнения:
2 + 1 = а + 2а – b + b
3 = 3a
a = 3/3 = 1
Подставим а = 1 во первое уравнение системы, найдём b:
2 = 1 – b
2 – 1 = –b
1 = –b
b = –1
Функция параболы имеет вид:
f(x) = 1* x2 – 1* x + 0 = x2 – x
Подставим точку (1; 3) принадлежащую прямой в функцию g(x) = kx и найдём k:
3 = k·1
k = 3
Функция прямой имеет вид:
g(x) = 3x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – x = 3x
x2 – x – 3x = 0
x2 – 4x = 0
x(x – 4) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 4 = 0
х2 = 4 (искомая абсцисса точки В)
Ответ: 4
Номер: 3D9010
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax. Найдите значение f(2).
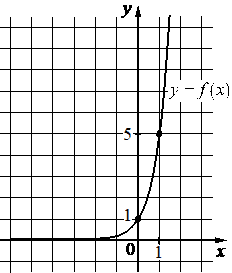
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.6 Показательная функция, ее график
Решение:
25
Возьмём точку (1; 5) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(2).
f(x) = ax
5 = a1
a = 5
Значит функция имеет вид:
f(x) = 5x
Найдём f(2):
f(2) = 52 = 25
Ответ: 25
Номер: 492E2A
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=k/x и g(x)=ax+b, пересекающиеся в точках A и B. Найдите абсциссу точки B.
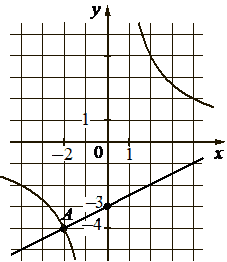
КЭС: 2.1.2 Рациональные уравнения 2.1.8 Простейшие системы уравнений с двумя неизвестными 3.3.1 Линейная функция, её график 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
8
`f(x) = k/x`
Подставим координаты точки (–2; –4) найдём k гиперболы:
`–4 = k/(–2)`
k = –2·(–4) = 8
Гипербола имеет вид:
`f(x) = 8/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
`a = tg a =1/2` = 0,5
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –3.
b = –3
Функции прямой имеет вид:
g(x) = 0,5x – 3
Найдём абсциссы точек пересечения функций:
f(x) = g(x)
`8 = (0,5x – 3) * x`
`8 = 0,5x^2 – 3x`
`0,5x^2 – 3x – 8 = 0`
D = (–3)2 – 4*0,5*(–8) = 25 = 52
`x_(1)=(3+5)/(2*0.5)=8`
`x_(2)=(3-6)/(2*0.5)=-2`
У точки А координата х = –2, значит у точки В координата х = 8.
Ответ: 8
Номер: 6FA927
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax . Найдите значение f(4) .

КЭС: 3.3.6 Показательная функция, ее график
Решение:
16
Возьмём точку (1; 2) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(4).
f(x) = ax
2 = a1
a = 2
Значит функция имеет вид:
f(x) = 2x
Найдём f(4):
f(4) = 24 = 16
Ответ: 16
Номер: 38A32C
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x . Найдите значение f(10) .
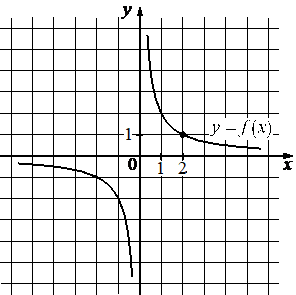
КЭС: 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
0,2
Возьмём точку принадлежащую гиперболе (2; 1) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(10).
1=k/2
k = 1·2 = 2
Функция имеет вид:
f(x)=2/x
Найдём f(10):
f(10)=2/10=0,2
Ответ: 0,2
Номер: 08C3D9
Впишите правильный ответ.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A . Найдите абсциссу точки A .
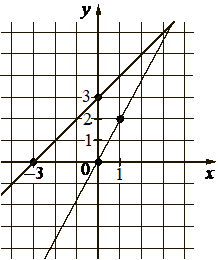
КЭС: 3.3.1 Линейная функция, её график
Решение:
3
На рисунке изображены прямые, линейных функции имеют вид:
y = kx + b
Найдём k и b первой функции:
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
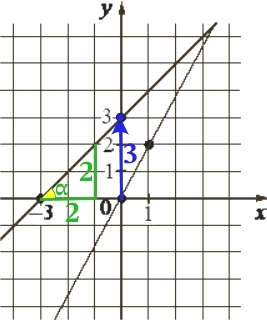
k – тангенс угла (α) наклона прямой, по отношению к оси х. Тангенс – это отношение противолежащего катета, к прилежащему катету. Найдём k:
k = tg α = 2/2 = 1
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 3.
b = 3
Первая функция имеет вид:
y = 1·x + 3 = x + 3
Найдём k и b второй функции:
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
k = tg α = 2/1 = 2
Прямая проходит через начало координат (0; 0), значит b = 0.
Вторая функция имеет вид:
y = 2x + 0 = 2x
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
x + 3 = 2x
3 = 2x – x
3 = x
Ответ: 3
Номер: 7D21DC
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax. Найдите значение f(25).
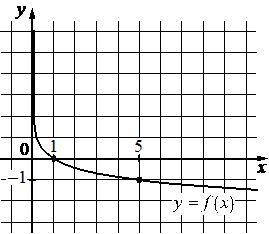
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.7 Логарифмическая функция, её график
Решение:
-2
Возьмём точку (5; –1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
f(x) = loga x
`–1 = log_(a)5`
a–1 = 5
`a=1/5`
Значит функция имеет вид:
`f(x) = log_(1/5)x`
Найдём f(25):
`f(25) = log_(1/5)25=-2`
Ответ: –2.
Номер: A75DDE
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x. Найдите значение f(10).
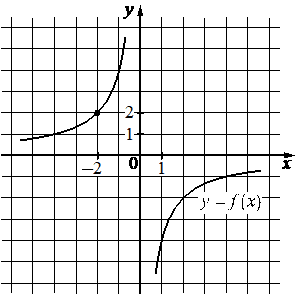
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
-0,4
Возьмём точку принадлежащую гиперболе (-2; 2) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(10).
2=k/-2
k = 2·-2 = -4
Функция имеет вид:
f(x)=-4/x
Найдём f(10):
f(10)=-4/10=-0,4
Ответ: -0,4
Номер: AFF75F
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=k/x и g(x)=ax+b, пересекающиеся в точках A и B. Найдите абсциссу точки B.
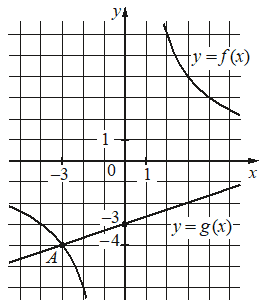
КЭС: 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
12
`f(x) = k/x`
Подставим координаты точки (–3; –4) найдём k гиперболы:
`–4 = k/(–3)`
k = –3·(–4) = 12
Гипербола имеет вид:
`f(x) = 12/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
`a = tg a =1/3`
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –3.
b = –3
Функции прямой имеет вид:
`g(x) = 1/3 x – 3`
Найдём абсциссы точек пересечения функций:
f(x) = g(x)
`12 = (1/3 x – 3) * x`
`12 = 1/3 x^2 – 3x`
`x^2 – 9x – 36 = 0`
D = 81-4*1*-36=225 =152
`x_(1)=(9+15)/(2*1)=12`
`x_(2)=(9-15)/(2*1)=-3`
У точки А координата х = –3, значит у точки В координата х = 12.
Ответ: 12
Номер: 6F2D5E
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x. Найдите значение f(20).
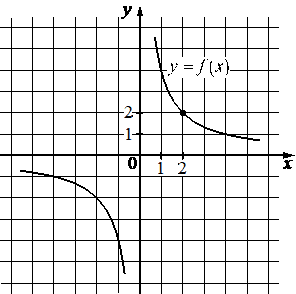
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
0,2
Возьмём точку принадлежащую гиперболе (2; 2) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(20).
2=k/2
k = 2 * 2 = 4
Функция имеет вид:
f(x)=4/x
Найдём f(20):
f(20)=4/20=0,2
Ответ: 0,2
Номер: 30F054
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=ax2+bx+c и g(x)=kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
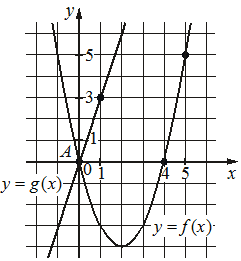
КЭС: 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график 3.3.3 Квадратичная функция, ее график
Решение:
7
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ax2 + bx + c):
(-1;5) – в 1-е уравнение для параболы в точке (-1;5),
(5; 5) – во 2-е уравнение для параболы в точке (5;5),
и с = 0 в оба уравнения, получим систему из двух уравнений:
| 〈 | 5 = a(-1)2 + b(-1) + 0 5 = a(5)2 + b(5) + 0 |
| 〈 | 5 = a - b 5 = 25a + 5b |
упростим второе уравнение в системе, чтобы при сложении сократить b, разделив каждую из частей на 5
| 〈 | 5 = a - b 1 = 5a + b |
Cложим соответствующие части уравнения:
5+1 = 5а + а – b + b
6 = 6a
a = 6/6 = 1
Подставим а = 1 в первое уравнение системы, найдём b:
5 = 1 – b
5 – 1 = –b
4 = –b
b = –4
Функция параболы имеет вид:
f(x) = 1* x2 – 4* x + 0 = x2 – 4 x
Теперь рассмотрим прямую. Подставим точку (1; 3) принадлежащую прямой в функцию g(x) = kx и найдём k:
3 = k·1
k = 3
Функция прямой имеет вид:
g(x) = 3x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – 4x = 3x
x2 – 4x – 3x = 0
x2 – 7x = 0
x(x – 7) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 7 = 0
х2 = 7 (искомая абсцисса точки В)
Ответ: 7
Номер: 82DA5C
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x . Найдите значение f(10) .
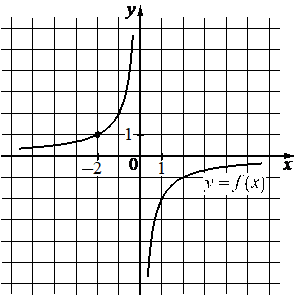
КЭС: 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
-0,2
Возьмём точку принадлежащую гиперболе (-2; 1) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(10).
-2=k/1
k = -2 * 1 = -2
Функция имеет вид:
f(x)=-2/x
Найдём f(10):
f(10)=-2/10=-0,2
Ответ: -0,2
Номер: D6A2A2
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax. Найдите значение f(− 3).
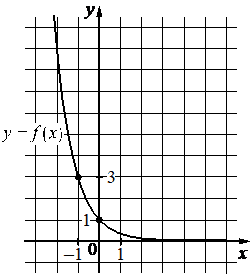
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.6 Показательная функция, ее график
Решение:
27
Возьмём точку (-1; 3) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(-3).
f(x) = ax
`3 = a^(-1)`
a = 1/3
Значит функция имеет вид:
`f(x) = (1/3)^x`
Найдём f(-3):
`f(-3) = (1/3)^-3 = 27`
Ответ: 27
Номер: 91C2AD
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=ax2+bx+c и g(x)=kx , пересекающиеся в точках A и B . Найдите абсциссу точки B .
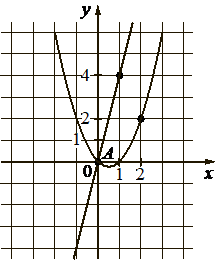
КЭС: 3.3.1 Линейная функция, её график 3.3.3 Квадратичная функция, ее график
Решение:
5
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ax2 + bx + c):
(-1;2) – в 1-е уравнение для параболы в точке (-1;2),
(2; 1) – во 2-е уравнение для параболы в точке (2;2),
и с = 0 в оба уравнения, получим систему из двух уравнений:
| 〈 | 2 = a(-1)2 + b(-1) + 0 2 = a(2)2 + b(2) + 0 |
сокращаем
| 〈 | 2 = a - b 2 = 4a + 2b |
сократим 2 уравнение в системе
| 〈 | 2 = a - b 1 = 2a + b |
Cложим соответствующие части уравнения:
2+1 = 2а + а – b + b
3 = 3a
a = 3/3 = 1
Подставим а = 1 в первое уравнение системы, найдём b:
2 = 1 – b
2 – 1 = –b
1 = –b
b = –1
Функция параболы имеет вид:
f(x) = 1* x2 – 1* x + 0 = x2 – x
Теперь рассмотрим прямую. Подставим точку (1; 4) принадлежащую прямой в функцию g(x) = kx и найдём k:
4 = k·1
k = 4
Функция прямой имеет вид:
g(x) = 4x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – x = 4x
x2 – x – 4x = 0
x2 – 5x = 0
x(x – 5) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 5 = 0
х2 = 5 (искомая абсцисса точки В)
Ответ: 5
Номер: E18EA6
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=k/x и g(x)=ax+b, пересекающиеся в точках A и B. Найдите абсциссу точки B.
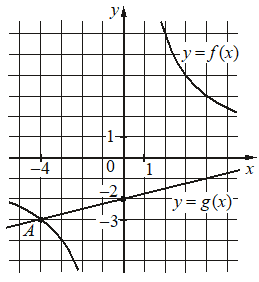
КЭС: 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
12
`f(x) = k/x`
Подставим координаты точки (–4; –3) найдём k гиперболы:
`–3 = k/(–4)`
k = –3·(–4) = 12
Гипербола имеет вид:
`f(x) = 12/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
`a = tg a =1/4`
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –2.
b = –2
Функции прямой имеет вид:
`g(x) = 1/4 x – 2`
Найдём абсциссы точек пересечения функций:
f(x) = g(x)
`12 = (1/4 x – 2) * x`
`12 = 1/4 x^2 – 2x`
`x^2 – 8x – 48 = 0`
D = 64-4*1*-48=256 =162
`x_(1)=(8+16)/(2*1)=12`
`x_(2)=(8-16)/(2*1)=-4`
У точки А координата х = –4, значит у точки В координата х = 12.
Ответ: 12
Номер: 87FAA1
Впишите правильный ответ.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A . Найдите абсциссу точки A .
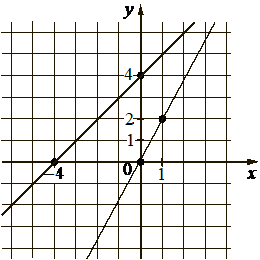
КЭС: 3.3.1 Линейная функция, её график
Решение:
4
На рисунке изображены прямые, линейных функции имеют вид:
y = kx + b
Найдём k и b первой функции:
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
k – тангенс угла (α) наклона прямой, по отношению к оси х. Тангенс – это отношение противолежащего катета, к прилежащему катету. Найдём k:
k = tg α = 4/4 = 1
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 4.
b = 4
Первая функция имеет вид:
y = 1* x + 4 = x + 4
Найдём k и b второй функции:
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
k = tg α = 2/1 = 2
Прямая проходит через начало координат (0; 0), значит b = 0.
Вторая функция имеет вид:
y = 2x + 0 = 2x
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
x + 4 = 2x
4 = 2x – x
4 = x
Ответ: 4
Номер: 1DC3CC
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=ax2+bx+c и g(x)=kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
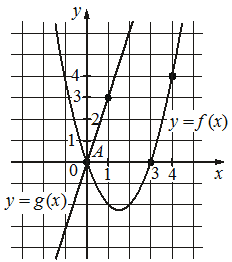
КЭС: 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график 3.3.3 Квадратичная функция, ее график
Решение:
6
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ax2 + bx + c):
(-1;4) – в 1-е уравнение для параболы в точке (-1;4),
(4; 4) – во 2-е уравнение для параболы в точке (4;4),
и с = 0 в оба уравнения, получим систему из двух уравнений:
| 〈 | 4 = a(-1)2 + b(-1) + c 4 = a(4)2 + b(4) + c |
упрощаем
| 〈 | 4 = a - b 4 = 16a + 4b |
сокращаем второе уравнение
| 〈 | 4 = a - b 1 = 4a + b |
Cложим соответствующие части уравнения:
4+1 = 4а + а – b + b
5 = 5a
a = 5/4 = 1
Подставим а = 1 в первое уравнение системы, найдём b:
4 = 1 – b
4 – 1 = –b
3 = –b
b = –3
Функция параболы имеет вид:
f(x) = 1* x2 – 3* x + 0 = x2 – 3x
Теперь рассмотрим прямую. Подставим точку (1; 3) принадлежащую прямой в функцию g(x) = kx и найдём k:
= k·1
k =
Функция прямой имеет вид:
g(x) = 3x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – 3x = 3x
x2 – 3x – 3x = 0
x2 – 6x = 0
x(x – 6) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 6 = 0
х2 = 6 (искомая абсцисса точки В)
Ответ: 6
Номер: 8ADFCC
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=a√x и g(x)=kx , пересекающиеся в точках A и B . Найдите абсциссу точки B .
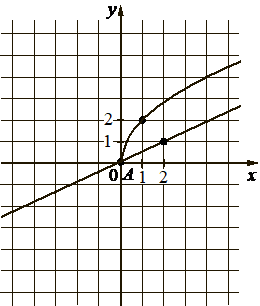
КЭС: 3.3.1 Линейная функция, её график
Решение:
16
f(x) кривой проходит через точку (1; 2), подставим значения х и у (это f(x)) в функцию, найдём а:
f(x) = a√x
2 = a√1
2 = a·1
а = 2
Значит функция имеет вид: f(x) = 2*√x
g(x) проходит через точку (2; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
g(x) = kx
1 = k·2
k=1/2=0,5
Значит функция имеет вид: g(x) = 0,5x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=2sqrt(x)`
`g(x)=0,5x`
`y=2sqrt(x)`
`y=0,5x`
Приравняем через y уравнения:
2√x = 0,5x
Возведём обе части в квадрат:
(2√x)2 = (0,5x)2
4x = 0,25x2
16x = x2
16x – x2 = 0
x*(16 – x) = 0
x1 = 0 (абсцисса точки А)
или
16 – x = 0
х2 = 16 (абсцисса точки В)
Ответ: 16
Номер: 448E90
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=kx+b. Найдите значение f(5).
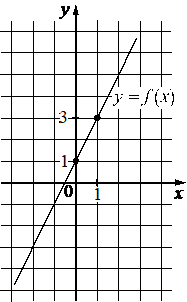
КЭС: 3.3.1 Линейная функция, её график
Решение:
11
График функции проходит через две точки на углах клеток, в которых можно точно определить координаты х и у:
(0; 1)
(1; 3)
На рисунке изображён график функции f(x) = kx + b. Найдите значение х, при котором f(x) = 5.
Функция имеет вид у = kx + b, подставив координаты точек, получим систему из двух уравнений:
1= 0*k + b
3 = 1k + b
Получается b=1, тогда
3 = 1k + b
3 = 1k + 1
2 = k
Значит функция имеет вид:
у = 2x +1
Найдём значение х, при котором f(5):
y = 2*x +1
y = 2*5+1
y=11
Ответ: 11
Номер: 87429D
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x . Найдите значение f(10) .

КЭС: 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
-0,1
Возьмём точку принадлежащую гиперболе (-1; 1) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(10).
-1=k/1
k = -1 * 1 = -1
Функция имеет вид:
f(x)=-1/x
Найдём f(10):
f(10)=-1/10=-0,1
Ответ: -0,1
Номер: 06DEEE
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=kx+b . Найдите значение f(4) .
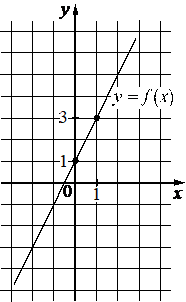
КЭС: 3.3.1 Линейная функция, её график
Решение:
9
График функции проходит через две точки на углах клеток, в которых можно точно определить координаты х и у:
(0; 1)
(1; 3)
На рисунке изображён график функции f(x) = kx + b. Найдите значение х, при котором f(x) = 4.
Функция имеет вид у = kx + b, подставив координаты точек, получим систему из двух уравнений:
1= 0*k + b
3 = 1k + b
Получается b=1, тогда
3 = 1k + b
3 = 1k + 1
2 = k
Значит функция имеет вид:
у = 2x +1
Найдём значение х, при котором f(4):
y = 2*x +1
y = 2*4+1
y=9
Ответ: 9
Номер: CFEAE8
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax . Найдите значение f(16) .
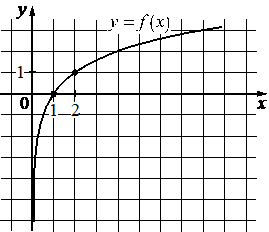
КЭС: 3.3.7 Логарифмическая функция, её график
Решение:
4
Возьмём точку (2; 1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(16).
`f(x) = log_a x`
`1 = log_a 2`
`a^1 = 2`
a = 2
Значит функция имеет вид:
`f(x) = log_2 x`
Найдём f(16):
`f(16) = log_2 x`
x=4
Ответ: 4
Номер: 97C4EA
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=a√x и g(x)=kx , пересекающиеся в точках A и B . Найдите абсциссу точки B .
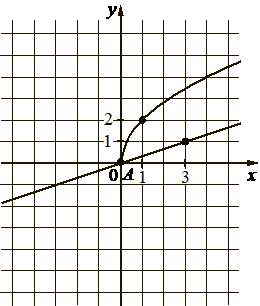
КЭС: 3.3.1 Линейная функция, её график
Решение:
36
f(x) кривой проходит через точку (1; 2), подставим значения х и у (это f(x)) в функцию, найдём а:
f(x) = a√x
2 = a√1
2 = a·1
а = 2
Значит функция имеет вид: f(x) = 2*√x
g(x) проходит через точку (3; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
g(x) = kx
1 = k·3
k=1/3
Значит функция имеет вид: g(x) = 1/3 x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=2sqrt(x)`
`g(x)=1/3 x`
`y=2sqrt(x)`
`y=1/3 x`
Приравняем через y уравнения:
2√x = 1/3 x
Возведём обе части в квадрат:
(2√x)2 = (1/3x)2
4x = 1/9 x2
36x = x2
36x – x2 = 0
x*(36 – x) = 0
x1 = 0 (абсцисса точки А)
или
36 – x = 0
х2 = 36 (абсцисса точки В)
Ответ: 36
Номер: 0B896F
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax2+bx+c . Найдите значение f(− 3) .
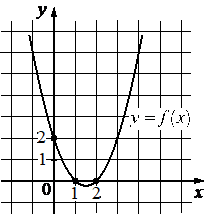
КЭС: 3.3.3 Квадратичная функция, ее график
Решение:
20
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = 2
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке, заметим, что при возрастании координаты х на 2,5, координата у вырастает на 6,25, т.к. 2,52 = 6,25, значит это обычная парабола с а = +1:
а = +1
Координата х вершины параболы (х = 1,5) находится по формуле:
x=-b/2a
Подставим известные значения и найдём b:
1,5=-b/2
-b=1,5*2=3
b = –3
Функция имеет вид:
f(x) = +1x2 – 3x + 2
Найдём f(–3):
f(–3) = +1*(–3)2 – 3*(–3) + 2 = 9 + 9 + 2 = 20
Ответ: 20.
Номер: 12736C
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=kx+b. Найдите значение f(6).
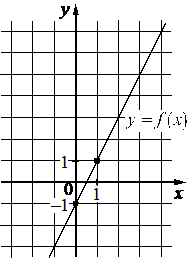
КЭС: 3.3.1 Линейная функция, её график
Решение:
11
График функции проходит через две точки на углах клеток, в которых можно точно определить координаты х и у:
(0; -1)
(1; 1)
На рисунке изображён график функции f(x) = kx + b. Найдите значение х, при котором f(x) = 6.
Функция имеет вид у = kx + b, подставив координаты точек, получим систему из двух уравнений:
-1= 0*k + b
Получается b=-1, тогда при постановке значений второй точки (1; 1)
1 = 1k + b
1 = 1k -1
2 = k
Значит функция имеет вид:
у = 2x - 1
Найдём значение х, при котором f(6):
y = 2*x -1
y = 2*6-1
y=11
Ответ: 11
Номер: 5BF069
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax. Найдите значение f(32).
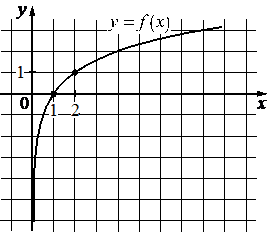
КЭС: 2.1.2 Рациональные уравнения 3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях 3.3.7 Логарифмическая функция, её график
Решение:
5
Возьмём точку (2; 1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(32).
`f(x) = log_a x`
`1 = log_a 2`
`a^1 = 2`
a = 2
Значит функция имеет вид:
`f(x) = log_2 x`
Найдём f(32):
`f(32) = log_2 x`
x=5
Ответ: 5
Номер: ABB360
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=a√x и g(x)=kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
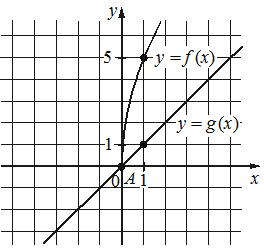
КЭС: 1.1.5 Корень степени n>1 и его свойства 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график
Решение:
25
f(x) кривой проходит через точку (1; 5), подставим значения х и у (это f(x)) в функцию, найдём а:
f(x) = a√x
5 = a√1
5 = a·1
а = 5
Значит функция имеет вид: f(x) = 5*√x
g(x) проходит через точку (3; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
g(x) = kx
1 = k·1
k=1/1
Значит функция имеет вид: g(x) = x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=5sqrt(x)`
`g(x)= x`
`y=5sqrt(x)`
`y= x`
Приравняем через y уравнения:
5√x = x
Возведём обе части в квадрат:
(5√x)2 = (x)2
25x = x2
25x – x2 = 0
x·(25 – x) = 0
x1 = 0 (абсцисса точки А)
или
25 – x = 0
х2 = 25 (абсцисса точки В)
Ответ: 25
Номер: 6E8B6F
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=k/x . Найдите значение f(10) .
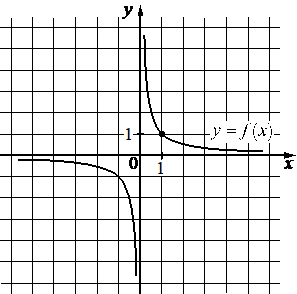
КЭС: 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
0,1
Возьмём точку принадлежащую гиперболе (1; 1) и подставим в функцию, найдём k:
На рисунке изображён график функции вида f(x)=kx. Найдите значение f(10).
1=k/1
k = -1 * 1 = 1
Функция имеет вид:
f(x)=1/x
Найдём f(10):
f(10)=1/10=0,1
Ответ: 0,1
Номер: 31336D
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=ax . Найдите значение f(− 4) .
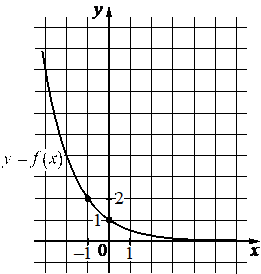
КЭС: 3.3.6 Показательная функция, ее график
Решение:
16
Возьмём точку (-1; 2) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x)= a^x`. Найдите значение f(-4).
f(x) = ax
`2 = a^(-1)`
a = 1/2
Значит функция имеет вид:
`f(x) = (1/2)^x`
Найдём f(-4):
`f(-4) = (1/2)^-4 = 16`
Ответ: 16
Номер: 7C4A3A
Впишите правильный ответ.
На рисунке изображён график функции вида f(x)=logax . Найдите значение f(16) .
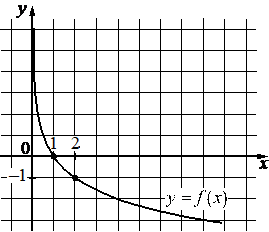
КЭС: 3.3.7 Логарифмическая функция, её график
Решение:
-4
Возьмём точку (2; -1) принадлежащую графику и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(16).
`f(x) = log_a x`
`-1 = log_a 2`
a^-1 = 2
a = 1/2
Значит функция имеет вид:
`f(x) = log_(1/2) x`
Найдём f(16):
`f(16) = log_(1/2) x`
x=-4
Ответ: -4
Номер: 196238
Впишите правильный ответ.
На рисунке изображены графики функций видов f(x)=k/x и g(x)=ax+b, пересекающиеся в точках A и B. Найдите абсциссу точки B.
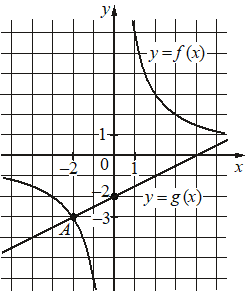
КЭС: 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 3.3.1 Линейная функция, её график 3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
Решение:
6
Подставим координаты точки (–2; –3) найдём k гиперболы:
`–2 = k/(–3)`
k = –2·(–3) = 6
Гипербола имеет вид:
`f(x) = 6/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
`a = tg a =1/2`
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –2.
b = –2
Функции прямой имеет вид:
`g(x) = 1/2 x – 2`
Найдём абсциссы точек пересечения функций:
f(x) = g(x)
`6 = (1/2 x – 2) * x`
`6 = 1/2 x^2 – 2x`
`x^2 – 4x – 12 = 0`
D = 16-4*1*-12=64 =82
`x_(1)=(4+8)/(2*1)=6`
`x_(2)=(4-8)/(2*1)=-2`
У точки А координата х = –2, значит у точки В координата х = 6.
Ответ: 6
Номер: 913A8E

