Задание 5 для 300-х и задание 8 для 100-х вариантов идентичны линейке 13 ОГЭ по математике.
Тип структуры комплекта 300-e варианты. Позиции заданий 5. Или 100-e варианты 8.
Все задания этого типа с ФИПИ для ГВЭ 9
Укажите решение системы неравенств
| { |
− 9+3x<0, |
| 2−3x>− 10. |
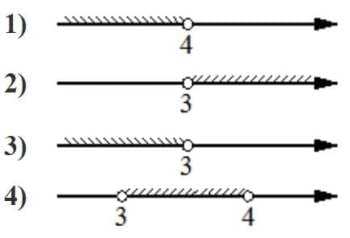
Решение:
− 9+3x<0
3x<9
x<3
2−3x>− 10
3x< 12
x<4
Берем в ответ меньшую область из системы неравенств.
Ответ: 3
Номер: F7F44F
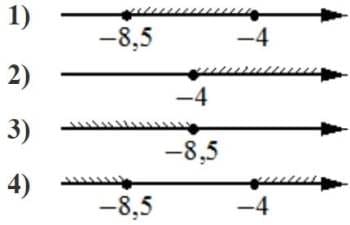
Укажите решение неравенства
6x−x2 >0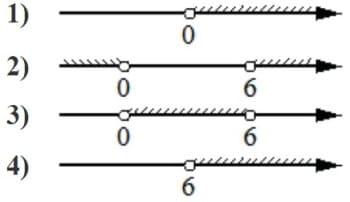
Решение:
6x−x2 >0
x(6-x)>0
x ≠ 0
6-x ≠ 0, значит x ≠ 6
`{(x>0),(6-x>0):}` или `{(x<0),(6-x<0):}`
`{(x>0),(x<6):}` `{(x<0),(x>6):}`
Второе не подходит, так как нет общей области значений.
Значит, условие неравенства будет соблюдаться в диапазоне
0<x<6
по условиям выбираем 3 решение.
Ответ: 3
Номер: F56F41
Укажите решение системы неравенств
| { |
-35+5x<0, |
| 6-3x>-18. |
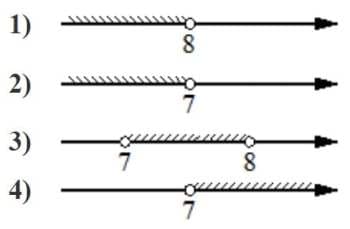
Решение:
-35+5x<0
5x<35
x<7
6-3x>-18
-3x>-24
x<8
берем область с меньшим диапазоном, когда меньшая область включена в большую
Ответ: 2
Номер: F23943
Укажите решение неравенства

1) x2 −49>0
2) x2 −49<0
3) x2 +49<0
4) x2 +49>0
Решение:
1) x2 −49>0
x2 >49
|x| >7
удовлетворяет нашим требованиям, далее не проверяем
2) x2 −49<0
3) x2 +49<0
4) x2 +49>0
Ответ: 1
Номер: BB8B4C
Укажите решение системы неравенств
| { | х+4≥− 4,5, |
| х+4≤0. |
Решение:
Первое
х+4≥− 4,5
х≥− 8,5
Второе
х+4≤0
х≤-4
Область пересечения этих неравенств [-8,5; -4]
Ответ: 1
Номер: A85542
Укажите решение неравенства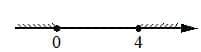
1) x2 −16≤0
2) x2 −4x≤0
3) x2 −4x≥0
4) x2 −16≥0
Решение:
1)
x2 −16≤0
x2 ≤16
|x|≤4
2)
x2 −4x≤0
x(x −4)≤0
0<x<4
3)
x2 −4x≥0
x(x −4)≥0
0>x>4
Дальше не рассматриваем, 3 ответ удовлетворяет условиям.
Ответ: 3
Номер: 9A364B
Укажите решение неравенства
4x-x2<0
1) (− ∞ ; 0)∪(4 ; +∞)
2) (0 ; +∞)
3) (0 ; 4)
4) (4 ; +∞)
Решение:
4x-x2<0
x(4-x)<0
x≠0 x≠4
`{(x>0),(4-x<0):}` или `{(x<0),(4-x>0):}`
`{(x>0),(x>4):}` `{(x<0),(x<4):}`
Область пересечения
x>4 x<0
Ответ: 1
Номер: E2004A
Укажите решение неравенства
(x+5)(x-2)<0
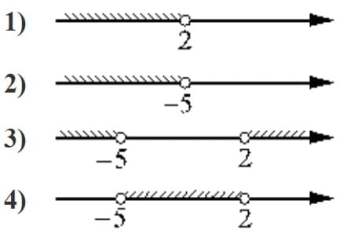
Решение:
(x+5)(x-2)<0
Найдем пределы для скобок
x≠-5
x≠2
`{(x+5<0),(x-2>0):}` или `{(x+5>0),(x-2<0):}`
`{(x<-5),(x>2):}`-нет пересечения `{(x>-5),(x<2):}`
Неравенство будет выполнено для области x (-5 ; 2)
Ответ: 4
Номер: 30ED49
Укажите решение неравенства
(x+2)(x-7)≤0
1) [-2 ; 7]
2) (− ∞ ; -2]∪[7; +∞)
3) (− ∞ ; 7]
4) (− ∞ ; -2]
Решение:
(x+2)(x-7)≤0
пределы
x+2=0
x=-2
x-7=0
x=7
Необходимо, чтобы знаки в скобках были разные при одних значениях х. Это диапазон.
-2<x<7
Ответ: 1
Номер: 89A148
Укажите решение неравенства
x2 >36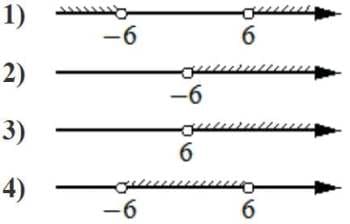
Решение:
x2 >36
|x|>6
Ответ: 1
Номер: 2839F6
Укажите неравенство, решение которого изображено на рисунке.

1) x2 −25>0
2) x2 −25<0
3) x2 +25<0
4) x2 +25>0
Решение:
1) x2 −25>0
|x|>25
далее не рассматриваем, этот вариант подходит
Получаем диапазон (− ∞ ; −5)∪(5 ; +∞)
2) x2 −25<0
3) x2 +25<0
4) x2 +25>0
Ответ: 1
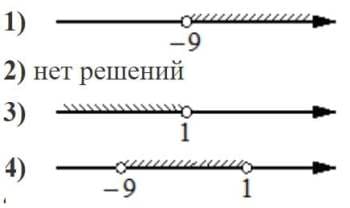
Номер: 4E1607
Укажите решение системы неравенств
| { | -36+4x<0, |
| 5-4x<-3. |
1) (2 ; +∞)
2) нет решений
3) (-∞ ; 9)
4) (2 ; 9)
Решение:
-36+4x<0
-36<-4x
x<9
5-4x<-3
-4x<-8
x>2
Ответ: 4
Номер: 044B01
Укажите решение системы неравенств
| { | -9+3x>0, |
| 2-3x>-10. |
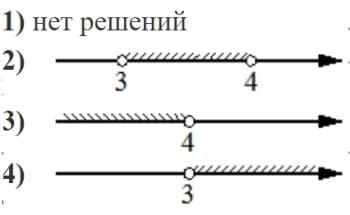
Решение:
-9+3x>0
x>3
2-3x>-10
-3x>-12
x<4
Берем диапазон в котором наши неравенства верные одновременно.
Ответ: 2
Номер: B9AF0F
Укажите решение неравенства
(x+8)(x-3)<0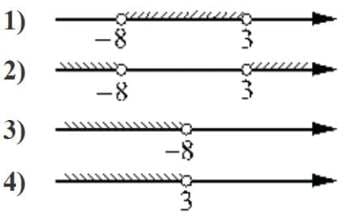
Решение:
(x+8)(x-3)<0
Найдем пределы для скобок
x+8=0
x=-8
x-3=0
x=3
Неравенство будет выполнено для области x (-8 ; 3)
Ответ: 1
Номер: 292A0A
Укажите решение системы неравенств
| { | х+2,7≤0, |
| х+4≥1. |
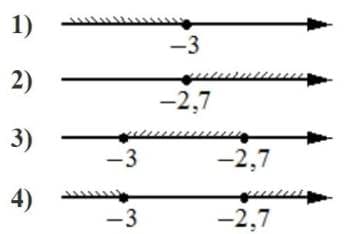
Решение:
Первое неравенство х+2,7≤0
х≤-2,7
Второе неравенство х+4≥1
х≥-3
Области сходятся в диапазоне третьего решения [-3; -2,7].
Ответ: 3
Номер: DCE804
Укажите решение неравенства
5x-x2>0
1) (-∞;-0) ∪ (5;+∞)
2) (0;5)
3) (5;+∞)
4) (0;+∞)
Решение:
5x-x2>0
x(5-x)>0
x ≠ 0
5-x ≠ 0, x ≠ 5
`{(x>0),(5-x>0):}` или `{(x<0),(5-x<0):}`
`{(x>0),(x<5):}` `{(x<0),(x>0):}`-нет пересечения
Условие неравенства будет соблюдаться в диапазоне 0<x<5
Ответ: 2
Номер: DC3106
Укажите решение системы неравенств
| { | -12+3x<0, |
| 9-4x>-23. |
1) (-∞; 8)
2) (-∞; 4)
3) (4; 8)
4) (4; +∞)
Решение:
-12+3x<0
3x<12
x<4
9-4x>-23
-4x>-32
x<8
из двух пределов выберем с меньшей областью, так как в системе должно быть два верных неравенства.
Ответ: 2
Номер: 50DE07
Укажите неравенство, решение которого изображено на рисунке.

1) x2 −64<0
2) x2 −64>0
3) x2 −8x<0
4) x2 −8x>0
Решение:
1) x2 −64<0
|x|<8
2) x2 −64>0
|x|>64
3) x2 −8x<0
x(x-8)<0
Пределы
x=0
x=8
0<x<8
4) x2 −8x>0
x(x-8)>0
Пределы
x=0
x=8
0>x>8
Ответ: 4
Номер: 554902
Укажите решение неравенства
7x-x2≥0
1) [0 ; +∞)
2) [7 ; +∞)
3) (− ∞ ; 0]∪[7 ; +∞)
4) [0; 7]
Решение:
7x-x2≥0
x(7-x)≥0
Рассмотрим пределы для неравенства
х=0
7−x =0
х=7
Область при которых неравенство верное [0; 7]
Ответ: 4
Номер: A3E107
Укажите решение неравенства
x2 −49<0.
1) нет решений
2) (− ∞ ; +∞)
3) (− 7 ; 7)
4) (− ∞ ; −7)∪(7 ; +∞)
Решение:
x2 −49<0
x2 <49
|x|<49
Ответ: 3
Номер: A9B002
Укажите решение неравенства
(x+3)(x-7)≤0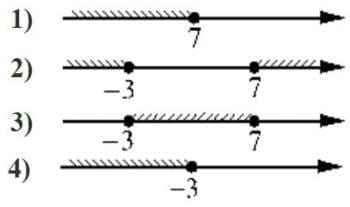
Решение:
У нас должно быть отрицательное произведение или равно 0, то есть одни скобки должны давать - (0),а вторые + (0), тогда будет соблюдаться условие:
(x+3)(x-7)≤0
(x-7)≤0
x-7≤0
x≤7
(x+3)≤0
x+3≤0
x≤-3
Пересечение областей дает решение. (где одна область есть, второй еще нет)
Ответ: 3
Номер: CDA804
Укажите решение неравенства
(x+3)(x-5)≤0
1) (-∞; -3]
2) [-3; 5]
3) (-∞; 5]
4) (-∞; -3] ∪ [5; +∞)
Решение:
(x+3)(x-5)≤0
У нас должно быть отрицательное произведение или равно 0, то есть одни скобки должны давать - (0),а вторые + (0), тогда будет соблюдаться условие:
(x-5)≤0
x≤5
(x+3)≤0
x≤-3
Пересечение областей дает решение. (где одна область есть, второй еще нет)
Ответ: 2
Номер: E17A00
Укажите решение неравенства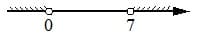
1) x2 −7x<0
2) x2 −49>0
3) x2 −7x>0
4) x2 −49<0
Решение:
1) x2 −7x<0
x(x-7)<0
0<x<7
2) x2 −49>0
x2>49
|x|>49
7<x<-7
не подходит
3) x2 −7x>0
x(x-7)>0
0>x>7
Последнее не рассматриваем, так как 3 решение подходит
4) x2 −49<0
Ответ: 3
Номер: 36A00A
Укажите решение неравенства 7x−x2 >0.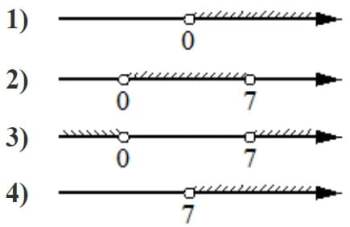
Решение:
7x−x2 >0
x(7-x)>0
Рассмотрим пределы для неравенства
х=0
7−x =0
х=7
Область при которых неравенство верное
0<x<7
Ответ: 2
Номер: 3AC00A
Укажите решение неравенства
(x+4)(x-8)≤0
1) (− ∞ ; 8]
2) (− ∞ ; -4]∪[8 ; +∞)
3) [-4; 8]
4) (− ∞ ; -4]
Решение:
(x+4)(x-8)≤0
Найдем пределы для скобок
x+4=0
x=-4
x-8=0
x=8
Неравенство будет выполнено для области x [-4; 8]
Ответ: 3
Номер: 065C74
Укажите решение системы неравенств
| { | x+4≥-1, |
| x+1,4≥0. |
1) [-5 ; +∞)
2) [-1.4 ; +∞)
3) [-5; -1,4]
4) (− ∞ ; -5]∪[-1.4 ; +∞)
Решение:
x+4≥-1
x≥-5
x+1.4≥0
x≥-1,4
Берем неравенство с меньшей областью.
Ответ: 2
Номер: BDFF71
Укажите решение неравенства
8x - x2 ≤ 0
1) [8;+∞)
2) [0; 8]
3) (-∞;0] ∪ [8;+∞)
4) [0;+∞)
Решение:
8x - x2 ≤ 0
x(8-x) ≤ 0
Первый предел x = 0
Второй предел 8-x = 0
x = 8
При этом для x= условие неравенства будет соблюдаться в диапазоне
8<x<0
Выбираем третье решение.
Ответ: 3
Номер: 25807D
Укажите решение неравенства
x2 −36≥0.
1) (− ∞ ; +∞)
2) нет решений
3) (− ∞ ; −6]∪[6 ; +∞)
4) [− 6 ; 6]
Решение:
x2 −36≥0
x2 ≥36
|x| ≥6
Получаем диапазон (− ∞ ; −6]∪[6 ; +∞)
Ответ: 3
Номер: 53B47A
Укажите решение неравенства
2x-x2≤0
1) (− ∞ ; 0]∪[2 ; +∞)
2) [0 ; +∞)
3) [2 ; +∞)
4) [0;2]
Решение:
2x-x2≤0
x(2-x)≤0
Рассмотрим пределы для неравенства
х=0
2−x =0
х=2
Область при которых неравенство верное
x≤0
x≥7
Ответ: 1
Номер: E0507C
Укажите решение системы неравенств
| { | х−7,4≥0, |
| х+2≥3. |
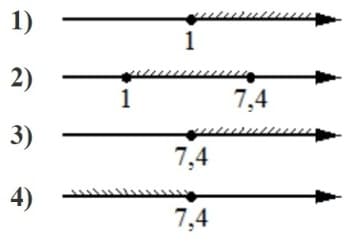
Решение:
Первое условие
х−7,4≥0
х≥7,4
Второе условие
х+2≥3
х≥1
Выбираем накладывающуюся область х≥7,4
Ответ: 3
Номер: 43A0BB
Укажите решение системы неравенств
| { |
x-6,6≥0, |
| x+1≥5. |
1) [4 ; +∞)
2) [4; 6,6]
3) [6,6 ; +∞)
4) (-∞; 4]
Решение:
x-6.6≥0
x≥6,6
x+1≥5
x≥4
Система неравенств будет справедлива для области x [6,6; +∞]
Ответ: 3
Номер: 7012B5
Укажите решение неравенства
(x+2)(x-7)>0;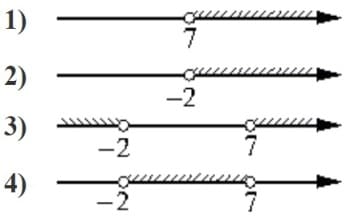
Решение:
(x+2)(x-7)>0
Пределы:
x+2>0
x>-2
и
x-7>0
x>7
x+2<0
x<-2
и
x-7<0
x<7
Ответ: 3
Номер: B2F1B8
Укажите решение неравенства
− 3−3x>7x−9.
1) (0,6 ; +∞)
2) (− ∞ ; 1,2)
3) (1,2 ; +∞)
4) (− ∞ ; 0,6)
Решение:
− 3−3x>7x−9
−10x>-6
x<0,6
Ответ: 4
Номер: 96ABB2
Укажите решение неравенства
| { |
-35+5x<0, |
| 6-3x>-18. |
1) (7;8)
2) (-∞;7)
3) (-∞;8)
4) (7;+∞)
Решение:
-35+5x<0
5x<35
x<7
6-3x>-18
-3x>-24
x<8
Берем область с меньшим диапазоном, чтобы система неравенств выполнялась для обеих неравенств.
Ответ: 2
Номер: E13DB1
Укажите решение системы неравенств
| { |
x-5,2≥0, |
| x+4≤10. |
1) (− ∞ ; 5.2]∪[6 ; +∞)
2) [5.2 ; +∞)
3) [6 ; +∞)
4) [5.2; 6]
Решение:
x-5,2≥0
x≥5,2
x+4≤10
x≤6
5,2<x<6
Ответ: 4
Номер: 8F96B2
Укажите решение неравенства
x2 −64>0.
1) (− ∞ ; +∞)
2) (− 8 ; 8)
3) (− ∞ ; −8)∪(8 ; +∞)
4) нет решений
Решение:
x2 −64>0
x2 >64
|x|>8
x<-8
x>8
Ответ: 3
Номер: 067911
Укажите решение неравенства
81x2 >64.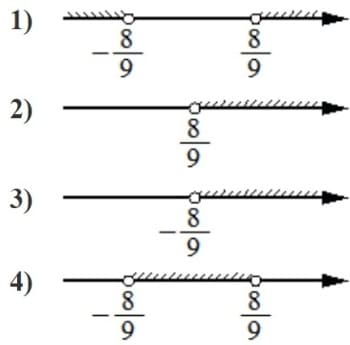
Решение:
81x2 >64
|x| >8/9
Ответ: 1
Номер: 257C17
Укажите решение неравенства
− 3−x≥x−6.
1) (− ∞ ; 1,5]
2) [1,5 ; +∞)
3) (− ∞ ; 4,5]
4) [4,5 ; +∞)
Решение:
− 3−x≥x−6
2x≤3
x≤1,5
Область (− ∞ ; 1,5]
Ответ: 1
Номер: D9FB19
Укажите решение системы неравенств
| { |
х+0,6≤0, |
| х−1≥-4. |
1) (− ∞ ; -3]
2) [-0,6 ; +∞)
3) (− ∞ ; -3]∪[-0,6 ; +∞)
4) [-3; -0,6]
Решение:
х+0,6≤0
х≤-0,6
х−1≥-4
х≥-3
Два неравенства будут действительны в диапазоне [-3; -0,6]
Ответ: 4
Номер: 51B915
Укажите решение неравенства
(x+2)(x-8)≥0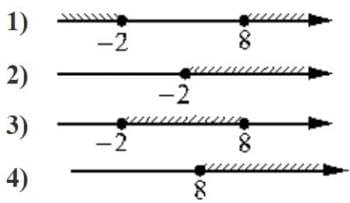
Решение:
(x+2)(x-8)≥0
При положительном значении обоих скобок
x+2≥0
x≥-2
x-8≥0
x≥8
При отрицательном значении обоих скобок
x+2≤0
x≤-2
x-8≤0
x≤8
Объединяем области. Получаем 1 решение.
Ответ: 1
Номер: AFB61B
Укажите решение неравенства

1) x2 −49≤0
2) x2 +49≤0
3) x2 −49≥0
4) x2 +49≥0
Решение:
1) x2 −49≤0
x2≤49
|x|≤7
далее не проверяем, это условие подходит
2) x2 +49≤0
3) x2 −49≥0
4) x2 +49≥0
Ответ: 1
Номер: E29D14
Укажите решение неравенства
(x+5)(x-9)>0
1) (-5 ; +∞)
2) (-5 ; 9)
3) (9 ; +∞)
4) (-∞ ; -5) ∪ (9 ; +∞)
Решение:
(x+5)(x-9)>0
У нас должно быть отрицательное произведение или равно 0, то есть одни скобки должны давать - ,а вторые +, тогда будет соблюдаться условие:
Находим пределы
x-9>0
x>9
x+5>0
x>-5
Пересечение областей дает решение, где каждая из скобок одного знака.
x>9
и
x<-5
Ответ: 4
Номер: 6EE11D
Укажите решение неравенства
x2 <9
Решение:
x2 <9
|x|<√9
|x|<3
Ответ: 1
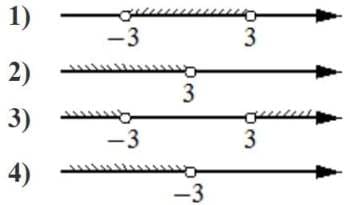
Номер: 3E861E
Укажите решение системы неравенств
| { | -5+5x<0, |
| 4-3x<31. |
Решение:
-5+5x<0
x<1
4-3x<31
-3x<27
x>-9
в системе должно быть два верных неравенства, они возможны только в области
1>x>-9
Ответ: 4
Номер: 4FE427
Укажите решение неравенства
1) x2 −5x≤0
2) x2 −25≤0
3) x2 −5x≥0
4) x2 −25≥0
Решение:
1) x2 −5x≤0
x(x-5)≤0
0<x<5
Подходит. Остальные не рассматриваем.
2) x2 −25≤0
3) x2 −5x≥0
4) x2 −25≥0
Ответ: 1
Номер: 447025
Укажите решение неравенства
49x2 ≥36
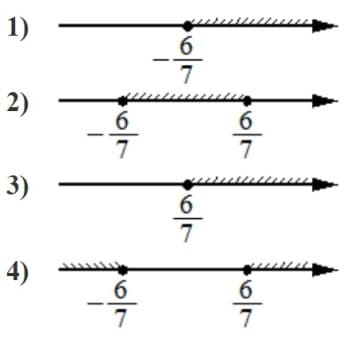
Решение:
49x2 ≥36
x2 ≥36/49
|x|≥6/7
Получили область (− ∞ ; --6/7]∪[6/7 ; +∞)
Ответ: 4
Номер: FCA22E
Укажите решение неравенства
81x2 ≥16.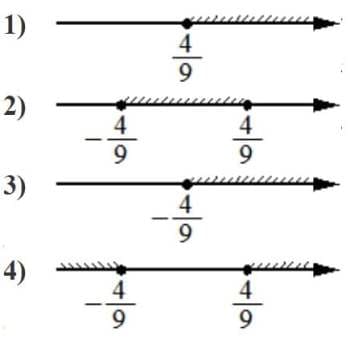
Решение:
81x2 ≥16
x2 ≥16/81
|x|≥4/9
Ответ: 4
Номер: F4C726
Укажите решение неравенства
10x-x2≤0
1) [0; 10]
2) (− ∞ ; 0]∪[10 ; +∞)
3) [10 ; +∞)
4) [0 ; +∞)
Решение:
10x-x2≤0
x(10-x)≤0
Найдем пределы для x и скобок, чтобы неравенство выполнялось
x=0
10-x=0
x=10
Неравенство будет выполнено для области x (− ∞ ; 0]∪[10; +∞)
Ответ: 2
Номер: 0F1123
Укажите решение неравенства
(x+1)(x-6)≤0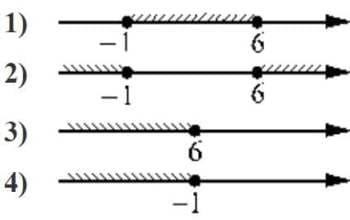
Решение:
(x+1)(x-6)<0
У нас должно быть отрицательное произведение, то есть одни скобки должны давать -,а вторые +, тогда будет соблюдаться условие:
x-6<0
x<6
x+1<0
x<-1
то есть наш диапазон будет от -1 до 6, чтобы знаки у скобок были разные.
Ответ: 1
Номер: BA7D20
Укажите решение неравенства
1) x2 −36≤0
2) x2 +36≥0
3) x2 −36≥0
4) x2 +36≤0
Решение:
1) x2 −36≤0
x2 ≤36
|x|≤6
2) x2 +36≥0
x2 ≥-36
нет решения
3) x2 −36≥0
x2 ≥36
|x|≥6
далее не смотрим
4) x2 +36≤0
Ответ: 3
Номер: BD9920
Укажите решение системы неравенств
| { | -9+3x<0, |
| 2-3x>-10. |
1) (-∞;3)
2) (-∞;4)
3) (3;+∞)
4) (3;4)
Решение:
Первое неравенство -9+3x<0
3х<9
х<3
Второе неравенство 2-3x>-10
-3x>-12
x<4
Области область первого неравенства меньше, его и принимаем за ответ.
Ответ: 1
Номер: 1D8628
Укажите неравенство, решение которого изображено на рисунке.
1) x2 −8x<0
2) x2 −64<0
3) x2 −8x>0
4) x2 −64>0
Решение:
1) x2 −8x<0
x1=0
x2=8
0<x<8
Остальные не смотрим, так как это подходит к нашему графику
2) x2 −64<0
3) x2 −8x>0
4) x2 −64>0
Ответ: 1
Номер: 219B2C
Укажите решение неравенства
x2 −36>0.
1) (-∞; +∞)
2) (-∞;-6) ∪ (6;+∞)
3) (-6;6)
4) нет решений
Решение:
x2 −36>0
x2 >36
|x| >√36
|x| >6
Получаем область (-∞;-6) ∪ (6;+∞)
Ответ: 2
Номер: 52FA27
Укажите неравенство, решение которого изображено на рисунке.

1) x2 −1≥0
2) x2 −x≥0
3) x2 −1≤0
4) x2 −x≤0
Решение:
1) x2 −1≥0
x2 ≥1
|x|≥1
2) x2 −x≥0
x(x −1)≥0
Пределы
x=0
x =1
x≤0
и
x≥1
далее не рассматриваем
3) x2 −1≤0
4) x2 −x≤0
Ответ: 2
Номер: A12922
Укажите решение неравенства
x2 −25<0.
1) (− ∞ ; +∞)
2) нет решений
3) (− 5 ; 5)
4) (− ∞ ; −5)∪(5 ; +∞)
Решение:
x2 −25<0
x2 <25
|x|<5
Получаем диапазон (− ∞ ; −5)∪(5 ; +∞)
Ответ: 3
Номер: A20323
Укажите решение системы неравенств
| { |
− 8+4x>0, |
| 4−3x>− 8. |
1) нет решений
2) (− ∞ ; 4)
3) (2; + ∞)
4) (2; 4)
Решение:
−8+4x>0
4x>8
x>2
4−3x>− 8
4−3x>− 8
−3x>-12
x<4
Пересечение областей (2; 4)
Ответ: 4
Номер: CAEF2C
Укажите решение системы неравенств
| { |
x+2,8≤0, |
| x+0,3≤-1,4. |
1) (− ∞ ; -2.8]
2) (− ∞ ; -2.8]∪[-2.7 ; +∞)
3) [-2.8; -2,7]
4) [-2.7 ; +∞)
Решение:
x+2,8≤0
x≤-2,8
x+0,3≤-1,4
x≤-1,7
берем область с меньшим диапазоном, когда меньшая область включена в большую
Ответ: 1
Номер: 64A625
Укажите решение неравенства
(x+4)(x-8)>0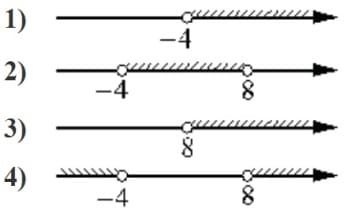
Решение:
(x+4)(x-8)>0
Найдем пределы для скобок
x+4=0
x=-4
x-8=0
x=8
Неравенство будет выполнено для области x (− ∞ ; -4]∪[8 ; +∞)
Ответ: 4
Номер: 356422
Укажите решение неравенства
5x−x2 ≥0.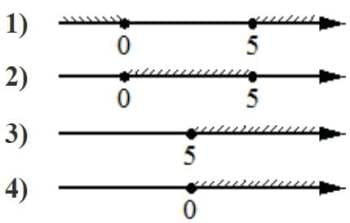
Решение:
5x−x2 ≥0
x(5−x) ≥0
Рассмотрим пределы для неравенства
х=0
5−x =0
х=5
Область при которых неравенство верное
0≤x≤5
Ответ: 2
Номер: 39762E
Укажите решение системы неравенств
| { |
х+0,7≤0, |
| х−1≥− 5. |
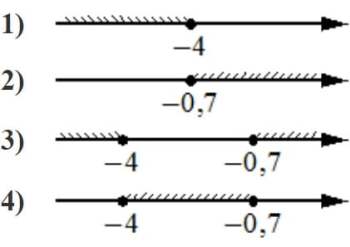
Решение:
х+0,7≤0
х≤-0,7
х−1≥− 5
х≥− 4
-0,7<x<-4
Ответ: 4
Номер: 101EDE
Укажите решение неравенства
6−7x≤3x−7.
1) [0,1 ; +∞)
2) (− ∞ ; 1,3]
3) [1,3 ; +∞)
4) (− ∞ ; 0,1]
Решение:
6−7x≤3x−7
6+7≤3x+7x
13≤10x
x≥1,3
Ответ: 3
Номер: 1027D3
Укажите решение системы неравенств
| { | -27+3x>0, |
| 6-3x<-6. |
1) (4; + ∞)
2) (4 ; 9)
3) (9 ; + ∞)
4) (− ∞ ; -9)
Решение:
-27+3x>0
3x>27
x>9
6-3x<-6
-3x<-12
x>4
Получается берем первое условие, так как у него диапазон меньше.
Ответ: 3
Номер: C64BDA
Укажите решение системы неравенств
| { | х-4≥0, |
| х-0,3≥1. |
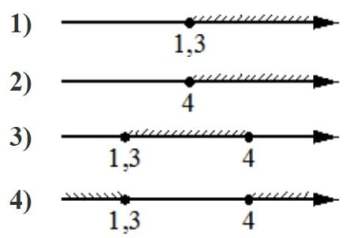
Решение:
Первое неравенство х-4≥0
х≥4
Второе неравенство х-0,3≥1
х≥1,3
Область первого неравенства меньше второго, его и принимаем.
Ответ: 2
Номер: C64BDA
Укажите решение системы неравенств
| { |
х+3,6≤0, |
| х+2≤-1. |
1) (− ∞ ; -3,6]∪[-3 ; +∞)
2) (− ∞ ; -3,6]
3) [-3,6; -3]
4) [-3,6 ; +∞)
Решение:
х+3,6≤0
х≤-3,6
х+2≤-1
х≤-3
Берем в ответ меньшую область из системы неравенств.
Ответ: 2
Номер: 882BD3
Укажите решение неравенства
x2 −36≤0.
1) (− ∞ ; +∞)
2) (− ∞ ; −6]∪[6 ; +∞)
3) [− 6 ; 6]
4) нет решений
Решение:
x2 −36≤0
x2 ≤36
|x|≤6
Ответ: 3
Номер: 237D5D
Укажите решение неравенства

1) x2 +64>0
2) x2 −64>0
3) x2 −64<0
4) x2 +64<0
Решение:
1) x2 +64>0
x2 +64>0
x2 >-64
нет решения
2) x2 −64>0
x2 >64
|x|>8
8<x и x<-8
3) x2 −64<0
x2 <64
|x|<8
8>x и x>-8
наш вариант. далее не проверяем
4) x2 +64<0
Ответ: 3
Номер: D9C655
Укажите решение неравенства
(x+6)(x-1)<0
1) (− ∞ ; 1)
2) (− ∞ ; -6)
3) (− ∞ ; -6) ∪ (1 ; + ∞)
4) (− 6 ; 1)
Решение:
(x+6)(x-1)<0
У нас должно быть отрицательное произведение, то есть одни скобки должны давать -,а вторые +, тогда:
x+6<0
x<-6
x-1<0
x<1
При этом для x= условие неравенства будет соблюдаться в диапазоне x>-6 и x<1.
Ответ: 4
Номер: D7C759
Укажите решение неравенства
1) x2 −36<0
2) x2 −6x<0
3) x2 −6x>0
4) x2 −36>0
Решение:
1) x2 −36<0
x2<36
-6<x<6
2) x2 −6x<0
x2 -6x<0
x(x-6)<0
x≠0
x≠6
При этом для x= условие неравенства будет соблюдаться в диапазоне
0<x<6
подходит это решение, далее не разбираем решения
3) x2 −6x>0
4) x2 −36>0
Ответ: 2
Номер: 5F5E5C
Укажите решение системы неравенств
| { | -48+6x<0, |
| 6-5x<-4. |
1) (2; 8)
2) (-∞; 2)
3) нет решений
4) (8; +∞)
Решение:
-48+6x<0
6x<48
x>8
6-5x<-4
-5x<-10
x<2
Области значений не пересекаются, то есть решения нет.
Ответ: 3
Номер: 6D7357
Укажите решение неравенства
− 3−x>4x+7.
1) (− ∞ ; −0,8)
2) (− ∞ ; −2)
3) (− 2 ; +∞)
4) (− 0,8 ; +∞)
Решение:
− 3−x>4x+7
4x+x<-10
5x<-10
x<-2
Ответ: 2
Номер: 67B05A
Укажите решение неравенства
(x+1)(x-9)>0
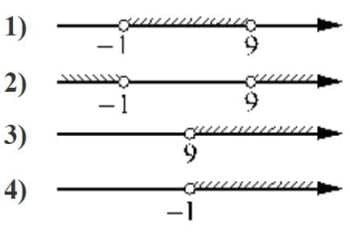
Решение:
(x+1)(x-9)>0
Найдем пределы для скобок
x+1=0
x=-1
x-9=0
x=9
Неравенство будет выполнено для области x (− ∞ ; -1]∪[9 ; +∞)
Ответ: 2
Номер: 346D53
Укажите решение неравенства
81x2 ≤16
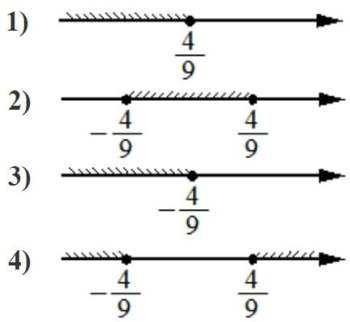
Решение:
81x2 ≤16
x2 ≤16/81
|x|≤4/9
Ответ: 2
Номер: 462FA0
Укажите решение системы неравенств
| { |
х−4,3≥0, |
| х+5≤10. |
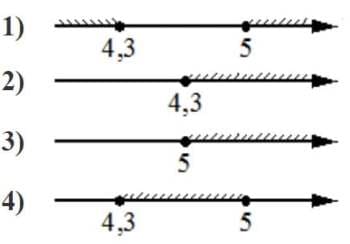
Решение:
х−4,3≥0
х≥4,3
х+5≤10
х≤5
Область при которых система неравенств верная (4,3; 5)
Ответ: 4
Номер: B36CAE
Укажите решение системы неравенств
| { |
-12+3x<0, |
| 9-4x>-23. |
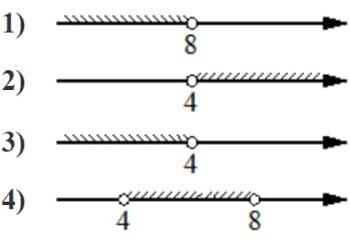
Решение:
-12+3x<0
3x<12
x<4
9-4x>-23
-4x>-32
x<8
берем меньшую область, которая входит в большую, дабы система имела верное решение для обоих неравенств в диапазоне, то есть x<4
Ответ: 3
Номер: 5601A3
Укажите решение неравенства
3x-x2>0
1) (3 ; +∞)
2) (− ∞ ; 0)∪(3 ; +∞)
3) (0 ; +∞)
4) (0 ; 3)
Решение:
3x-x2>0
x(3-x)>0
Рассмотрим пределы для неравенства
х=0
3−x =0
х=3
Область при которых неравенство верное (0; 3)
Ответ: 4
Номер: C9B0AE
Укажите решение системы неравенств
| { | x+3,4≤0, |
| x+5≥1. |
1) (-∞;-4]
2) [-3,4;+∞)
3) [-4; -3,4]
4) (-∞;-4] ∪ [-3,4;+∞)
Решение:
Первое
x+3,4≤0
x≤-3,4
Второе
x+5≥1
x≥-4
Диапазон пересечения неравенств [-4; -3.4]
Ответ: 3
Номер: 3EEAA5
Укажите решение неравенства
x−x2 ≥0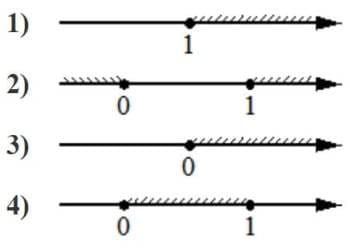
Решение:
x−x2 ≥0
x(1-x)≥0
Пределы
x=0
1-x=0
x=1
Получаем два предела, когда множители x и (1-x) будут иметь одинаковые знак, а значит будут больше или равны 0
0<x<1
Ответ: 4
Номер: 8CB5A9
Укажите неравенство, решение которого изображено на рисунке.

1) x2 +16≥0
2) x2 −16≤0
3) x2 +16≤0
4) x2 −16≥0
Решение:
1) x2 +16≥0
x2 ≥-16
любое значение x
2) x2 −16≤0
x2 ≤16
|x|≤4
-4≤x≤4
остальные можно не смотреть
3) x2 +16≤0
x2 ≤-16
нет решения
4) x2 −16≥0
|x|≥16
-4≥x≥4
Ответ: 2
Номер: 0A23C6
Укажите решение неравенства
6x−x2 ≤0
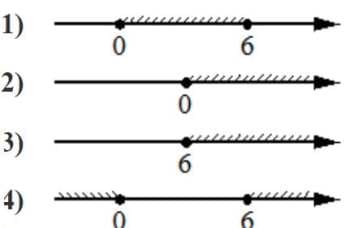
Решение:
6x−x2 ≤0
x(6-x)≤0
Пределы
x=0
6-x=0
x=6
x<0
и
x>6
Ответ: 4
Номер: 2B40CD
Укажите решение неравенства
6x - x2 ≥ 0
1) [0;+∞)
2) (-∞;0] ∪ [6;+∞)
3) [0; 6]
4) [6;+∞)
Решение:
6x - x2 ≥ 0
x(6-x) ≥ 0
Первое
x =0
Второе
6-x=0
x=6
Третье
0≤x≤6
Ответ: 3
Номер: DDC5CA
Укажите решение неравенства
x2 −25>0 .
1) (− ∞ ; −5)∪(5 ; +∞)
2) (− 5 ; 5)
3) нет решений
4) (− ∞ ; +∞)
Решение:
x2 −25>0
x2>25
|x|>25
5<x<-5
Ответ: 1
Номер: 5000CF
Укажите решение системы неравенств
| { |
х+1,8≤0, |
| х+0,5≤− 0,5. |
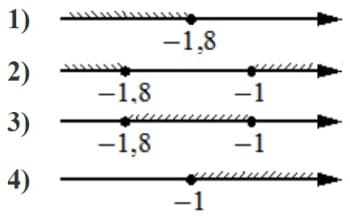
Решение:
х+1,8≤0
х≤-1,8
х+0,5≤− 0,5
х≤− 1
Пересечение областей (-∞; -1,8)
Ответ: 1
Номер: 50ACC8
Укажите решение неравенства
4x−x2 ≤0.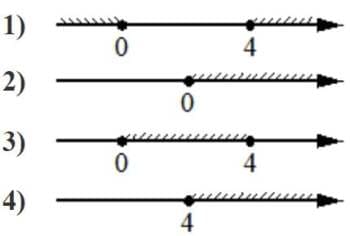
Решение:
4x−x2 ≤0
x(4-x)≤0
Пределы
x=0
4-x=0
x=4
Область при которой множители "x=" будут давать "-" или 0.
0≥x
и
x≤4
Ответ: 1
Номер: 96AFC7
Укажите решение системы неравенств
| { |
х−3,7≤0, |
| х−2≥1. |
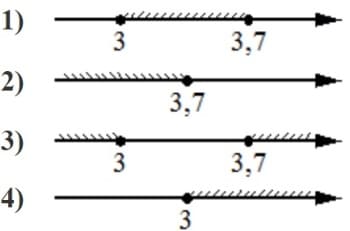
Решение:
х−3,7≤0
х≤3.7
х−2≥1
х≥3
Два неравенства будут действительны в диапазоне [3; 3,7]
Ответ: 1
Номер: 991AC8
Укажите решение системы неравенств
| { |
-9+3x<0, |
| 2-3x<-10. |
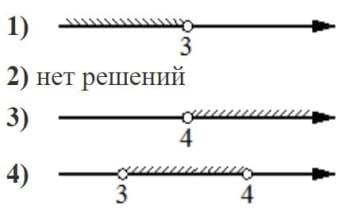
Решение:
-9+3x<0
3x<9
x<3
2-3x<-10
-3x<-12
x>4
области не пересекаются, а значит решений нет
Ответ: 2
Номер: 761893
Укажите решение системы неравенств
| { | -5+5x<0, |
| 4-3x<31. |
1) (-9;1)
2) нет решений
3) (-9;+∞)
4) (-∞;1)
Решение:
Первое неравенство -5+5x<0
5х<5
х<1
Второе неравенство 2-3x>-10
4-3x<31
-3x<27
x>-9
Области пересекаются в первом решении (-9;1) .
Ответ: 1
Номер: 295194
Укажите решение неравенства
− 9−6x>9x+9.
1) (− ∞ ; −1,2)
2) (0 ; +∞)
3) (− 1,2 ; +∞)
4) (− ∞ ; 0)
Решение:
− 9−6x>9x+9
-9>15x+9
15x<-18
x<-18/15
x<-1.2
Ответ: 1
Номер: 20D49B
Укажите решение неравенства
25x2 >49
Решение:
25x2 >49
|x|>49/25
Ответ: 3
Номер: D9E09D
Укажите решение системы неравенств
| { |
-35+5x<0, |
| 6−3x<− 3. |
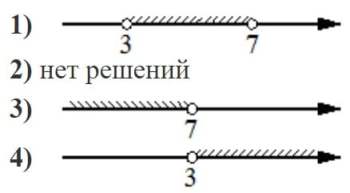
Решение:
-35+5x<0
5x<35
x<7
6−3x<− 3
−3x<− 9
x>3
Получили область (3; 7)
Ответ: 1
Номер: 901498
Укажите решение неравенства
(x+2)(x-10)>0
1) (-2; 10)
2) (-∞;-2) ∪ (10;+∞)
3) (10;+∞)
4) (-2; +∞)
Решение:
(x+2)(x-10)>0
Исключаем случаи, когда в первых или вторых скобках будет 0, то есть левая половина неравенства будет равна 0. Эти значения будут пределами
x+2 ≠0
x ≠ -2
x-10 ≠0
x ≠ 10
Произведение положительно, когда оба множителя одного знака. Рассмотрим 2 случая
`{(x+2>0),(x-10>0):}` или `{(x+2<0),(x-10<0):}`
`{(x>-2),(x>10):}` `{(x<-2),(x<10):}`
Находим области пересечения
x>10 x<-2
Для нашего неравенства верен диапазон (-∞;-2) ∪ (10;+∞).
Ответ: 2
Номер: E8C49D
Укажите решение неравенства
(x +3)(x - 6) > 0
1) (6 ; +∞)
2) (-3 ; +∞)
3) (-3 ; +∞) ∪ (6 ; +∞)
4) (-3 ; 6)
Решение:
(x +3)(x - 6) > 0
Первое
0>x +3>0
-3>x>3
Второе условие
0>x - 6>0
-6>x >6
При положительных значений скобок у нас область больше 3 и больше 6, то есть берем больше x >6.
При отрицательных, меньше -3 и меньше 6, то есть берем x >-3.
Получается 3 решение
Ответ: 3
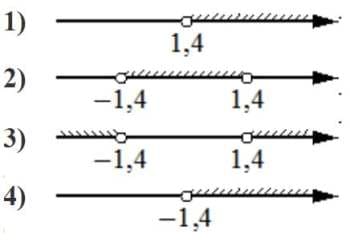
Номер: 416EEB
Укажите решение системы неравенств
`{(х+3.2≤0),(х+1≤− 1):}`
Решение:
`{(х+3,2≤0),(х+1≤− 1):}`
`{(х≤-3,2),(х≤−2):}`
Пересечением является промежуток от минус бесконечности до -3,2
Ответ: 2
Номер: F523E0
Укажите неравенство, решение которого изображено на рисунке.

1) x2 −49<0
2) x2 −7x<0
3) x2 −49>0
4) x2 −7x>0
Решение:
1) x2 −49<0
x2 <49
|x|<7
2) x2 −7x<0
x2 −7x<0
x(x-7)<0
Пределы
x=0
x=7
0<x<7
подходит, остальные не рассматриваем
3) x2 −49>0
4) x2 −7x>0
Ответ: 2
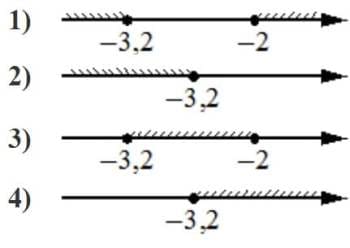
Номер: F674E2
Укажите решение системы неравенств
| { | − 27+3x>0, |
| 6−3x<− 6. |
Решение:
− 27+3x>0
3x>27
x>9
6−3x<− 6
-3x<-12
x>4
Получается диапазон от 9 и больше
Ответ: 4
Номер: 7864E3
Укажите решение неравенства
8x-x2≥0
1) [0 ; +∞)
2) [0; 8]
3) [8 ; +∞)
4) (− ∞ ; 0]∪[8 ; +∞)
Решение:
8x-x2≥0
x(8-x)≥0
Найдем пределы для скобок
x=0
8-x=0
x=8
Неравенство будет выполнено для области x [0; 8]
Ответ: 2
Номер: BEC8EF
Укажите решение системы неравенств
| { | − 12+3x>0, |
| 9−4x>− 3. |
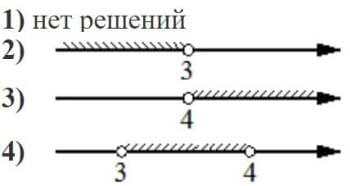
Решение:
− 12+3x>0
3x>12
x>4
9−4x>− 3
−4x>-12
x<3
Области не пересекаются, значит решение нет.
Ответ: 1
Номер: 2CD8E9
Укажите решение неравенства
(x+2)(x-4)≤0
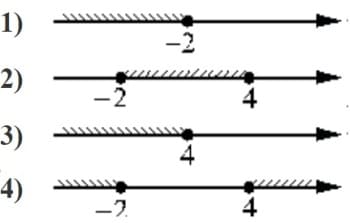
Решение:
(x+2)(x-4)≤0
Пределы для скобок
x+2=0
x=-2
x-4=0
x=4
Нам надо, чтобы у скобок были разные значения знаков. Это будет в диапазоне.
-2<x<4
Ответ: 2
Номер: 5FE2E3
Укажите решение системы неравенств
| { | х+3≥− 2, |
| х+1,1≥0. |
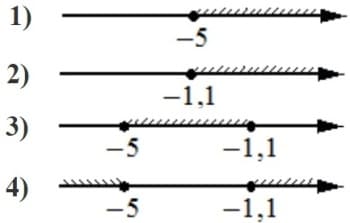
Решение:
Первое неравенство х+3≥− 2
х≥-5
Второе неравенство х+1,1≥0
х≥-1,1
Область второго неравенства меньше первого, его и принимаем.
Ответ: 2
Номер: 963DE2
Укажите решение системы неравенств
| { | х-2,6≤0, |
| х-1≥1. |
1) [2; 2,6]
2) (-∞; 2,6]
3) (-∞; 2,6] ∪ [2,6;+∞)
4) [2;+∞)
Решение:
Первое неравенство х-2,6≤0
х≤2,6
Второе неравенство х-1≥1
х≥2
Области сходятся в диапазоне первого решения [2; 2,6].
Ответ: 1
Номер: 6544EF
Укажите решение неравенства
8x−x2 <0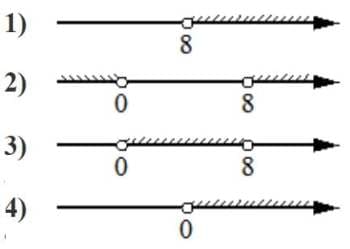
Решение:
8x−x2 <0
x(8-x)<0
8-x<0
x>8
x<0
Получаем два предела, когда множители будут иметь разные знаки при произведении, а значит будут меньше 0
x>8
и
x<0
Ответ: 2
Номер: 64FDED
Укажите решение неравенства
x2 −64≥0.
1) [− 8 ; 8]
2) (− ∞ ; −8]∪[8 ; +∞)
3) нет решений
4) (− ∞ ; +∞)
Решение:
x2 −64≥0
x2 ≥64
|x|≥8
Получаем диапазон (− ∞ ; −8)∪(8 ; +∞)
Ответ: 2
Номер: 357DED
Укажите решение неравенства
− 3−3x<7x−9.
1) (− ∞ ; 0,6)
2) (− ∞ ; 1,2)
3) (0,6 ; +∞)
4) (1,2 ; +∞)
Решение:
− 3−3x<7x−9
10x>6
x>0,6
Ответ: 3
Номер: 0BD565
Укажите решение неравенства
1) x2 +64≥0
2) x2 −64≤0
3) x2 −64≥0
4) x2 +64≤0
Решение:
1) x2 +64≥0
|x|≥-64
будет верно при любом значении x
2) x2 −64≤0
|x|≤64
-8≤x≤8
3) x2 −64≥0
|x|≥64
-8≥x≥8
далее не рассматриваем
4) x2 +64≤0
Ответ: 3
Номер: 7B0064
Укажите решение неравенства
(x+9)(x-4)<0
1) (− 9 ; 4)
2) (− ∞ ; -9) ∪ (4 ; +∞)
3) (− ∞ ; -9)
4) (− ∞ ; 4)
Решение:
(x+9)(x-4)<0
У нас должно быть отрицательное произведение, то есть одни скобки должны давать -,а вторые +, тогда:
x+9<0
x<-9
x-4<0
x<4
При этом для x= условие неравенства будет соблюдаться в диапазоне x>-9 и x<4.
Ответ: 1
Номер: 72FD68
Укажите решение неравенства
x2 −49>0.
1) (− 7 ; 7)
2) нет решений
3) (− ∞ ; +∞)
4) (− ∞ ; −7)∪(7 ; +∞)
Решение:
x2 −49>0
x2>49
|x|>49
7<x<-7
Ответ: 4
Номер: B51C64
Укажите решение неравенства
6x−x2 <0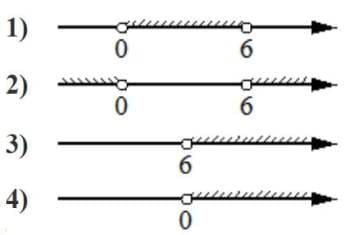
Решение:
6x−x2 <0
x(6-x)<0
Пределы
x=0
x=6
x<0 x>6
Ответ: 2
Номер: 15B864
Укажите решение неравенства
− 3−5x≤x+3 .
1) (− ∞ ; 0]
2) [− 1 ; +∞)
3) [0 ; +∞)
4) (− ∞ ; −1]
Решение:
− 3−5x≤x+3
−6x≤6
x≥-1
Ответ: 2
Номер: 1B676B
Укажите решение неравенства
x2 ≤36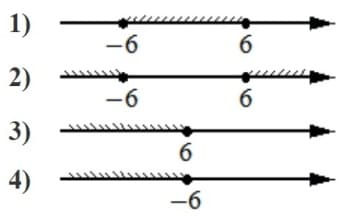
Решение:
x2 ≤36
|x|≤6
Ответ: 1
Номер: 11AD68
Укажите решение системы неравенств
| { |
− 35+5x>0, |
| 6−3x>− 3. |
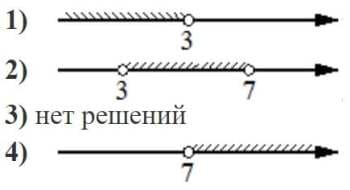
Решение:
− 35+5x>0
5x>35
6−3x>− 3
-3x>− 9
x<3
Области не пересекаются, а значит у системы нет решения.
Ответ: 3
Номер: A71C68
Укажите решение неравенства
1) x2 −36>0
2) x2 +36>0
3) x2 −36<0
4) x2 +36<0
Решение:
1) x2 −36>0
|x|>6
x<-6 и x>6
2) x2 +36>0
x2 >-36
нет решения
3) x2 −36<0
x2 <36
0<x<6
4) x2 +36<0
Ответ: 3
Номер: 951E62
Укажите решение системы неравенств
| { |
-10+2x>0, |
| 7-6x>-5. |
1) нет решений
2) (5; +∞)
3) (2; 5)
4) (-∞; 2)
Решение:
-10+2x>0
2x>10
x>5
7-6x>-5
-6x>-12
x<2
решение неравенств не имеет общей области.
Ответ: 1
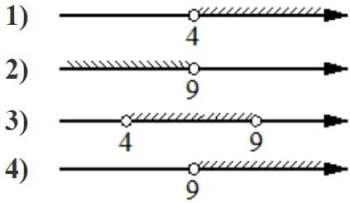
Номер:4 C3830
Укажите неравенство, решение которого изображено на рисунке.

1) x2 +25≤0
2) x2 −25≤0
3) x2 +25≥0
4) x2 −25≥0
Решение:
1) x2 +25≤0
x2 ≤-25
нет решений
2) x2 −25≤0
x2 ≤25
|x|≤5
-5<x<5
далее не проверяем
3) x2 +25≥0
4) x2 −25≥0
Ответ: 2
Номер: 44D733
Укажите решение системы неравенств
| { | x+4≥-3,4, |
| x+5≤0. |
1) [-7,4; -5]
2) [-5; +∞)
3) (-∞; -7,4]
4) (-∞; -7,4] ∪ [-5; +∞)
Решение:
У нас должно быть отрицательное произведение, то есть одни скобки должны давать -,а вторые +, тогда будет соблюдаться условие:
x+4≥-3,4
x≥-7,4
x+5≤0
x≤-5
Ответ: 1
Номер: FF2038
Укажите решение неравенства
3−2x≥8x−1.
1) [− 0,2 ; +∞)
2) (− ∞ ; 0,4]
3) [0,4 ; +∞)
4) (− ∞ ; −0,2]
Решение:
3−2x≥8x−1
-10x≥-4
x≤0,4
Ответ: 2
Номер: 71993C
Укажите решение неравенства
(x+3)(x-8)≥0
1) [-3; 8]
2) (− ∞ ; -3]∪[8 ; +∞)
3) [8 ; +∞)
4) [-3 ; +∞)
Решение:
(x+3)(x-8)≥0
Найдем пределы для скобок
x+3=0
x=-3
x-8=0
x=8
Неравенство будет выполнено для области x (− ∞ ; -3]∪[8 ; +∞)
Ответ: 2
Номер: B5313F
Укажите решение неравенства
x-x2<0
1) (0;1)
2) (0;+∞)
3) (1;+∞)
4) (-∞;0) ∪ (1;+∞)
Решение:
x-x2<0
x(1-x)<0
x≠0
x≠1
Находим пределы
1-x=0
x=1
x=0
Произведение отрицательно, если множители имеют разные знаки.
`{(x<0),(1-x>0):}` или `{(x>0),(1-x<0):}`
`{(x<0),(x<1):}` `{(x>0),(x>1):}`
x<0 x>1
Для x= условие неравенства будет соблюдаться в диапазоне x>1 и x<0.
Ответ: 4
Номер: 217F31
Укажите решение неравенства
1) x2 −9>0
2) x2 +9>0
3) x2 −9<0
4) x2 +9<0
Решение:
1) x2 −9>0
x2>9
|x|>3
далее не рассматриваем
Ответ: 1
Номер: 5ABF32
Укажите решение неравенства
25x2 ≥4
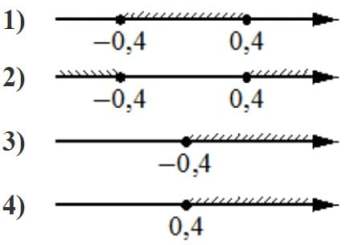
Решение:
25x2 ≥4
x2 ≥4/25
x≥2/5
Получаем диапазон
x<-0,4
x>0,4
Ответ: 2
Номер: A4003B
Укажите решение неравенства
(x+1)(x-7)≥0
1) (− ∞ ; -1]∪[7 ; +∞)
2) [-1 ; +∞)
3) [-1; 7]
4) [7 ; +∞)
Решение:
(x+1)(x-7)≥0
Найдем пределы для скобок
x+1=0
x=-1
x-7=0
x=7
Неравенство будет выполнено для области x (− ∞ ; -1]∪[7 ; +∞)
Ответ: 1
Номер: 903D3F
Укажите решение системы неравенств
| { |
х−3≥0, |
| х−0,2≥2. |
1) [2,2 ; +∞)
2) [3 ; +∞)
3) [2,2; 3]
4) (− ∞ ; 2.2]∪[3 ; +∞)
Решение:
х−3≥0
х≥3
х−0,2≥2
х≥2,2
Два неравенства будут действительны в диапазоне [3; +∞)
Ответ: 2
Номер: 6BBA37
Укажите решение неравенства
− 3−x>4x+7.
1) (− ∞ ; −0,8)
2) (− ∞ ; −2)
3) (− 2 ; +∞)
4) (− 0,8 ; +∞)
Решение:
− 3−x>4x+7
4x+x<-10
5x<-10
x<-2
Ответ: 2
Номер: 60D93E
Укажите решение неравенства
− 9−6x<9x+9.
1) (− ∞ ; −1,2)
2) (− 1,2 ; +∞)
3) (0 ; +∞)
4) (− ∞ ; 0)
Решение:
− 9−6x<9x+9
-15x<18
x>-1,2
Ответ: 2
Номер: 4C8F89
Укажите решение неравенства
8x−x2 >0.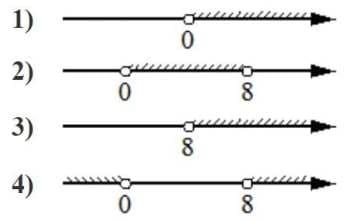
Решение:
8x−x2 >0
x(8-x)>0
Получаем диапазон 0<x<8
Ответ: 2
Номер: F12E88
Укажите решение неравенства
1) x2 −1≤0
2) x2 −x≥0
3) x2 −1≥0
4) x2 −x≤0
Решение:
1) x2 −1≤0
x2 ≤1
|x| ≤1
2) x2 −x≥0
x(x-1)≥0
x≥0 x ≤0
x-1≥0 x -1≤0
x≥1 x ≤1
3) x2 −1≥0
x2 ≥1
|x| ≥1
4) x2 −x≤0
x(x-1)≤0
x ≤0 x≥0
x-1≥0 x-1≤0
x ≥1 x≤1
нет общ. общ от 0 до 1
Ответ: 4
Номер: 141386
Укажите решение неравенства
7x−x2 <0
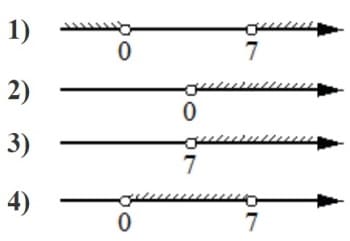
Решение:
7x−x2 <0
x(7−x) <0
Пределы
х=0
х=7
0>x>7
Ответ: 1
Номер: C98B84
Укажите решение неравенства
x2 ≤64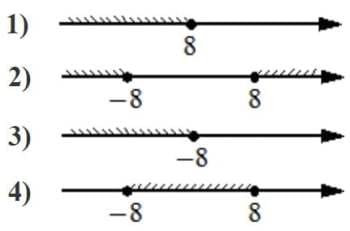
Решение:
x2 ≤64
|x| ≤8
-8≤x≤8
Ответ: 4
Номер: EAF180
Укажите решение системы неравенств
| { |
-12+3x<0, |
| 2-7x<-33. |
1) (-∞; 4)
2) нет решения
3) (4; 5)
4) (5; +∞)
Решение:
-12+3x<0
3x<12
x<4
2-7x<-33
-7x<-35
x>5
области не пересекаются, значит система не имеет решения
Ответ: 2
Номер: E5B887
Укажите решение неравенства
x2 −49≥0.
1) [− 7 ; 7]
2) нет решений
3) (− ∞ ; −7]∪[7 ; +∞)
4) (− ∞ ; +∞)
Решение:
x2 −49≥0
x2 ≥49
|x|≥7
(− ∞ ; −7]∪[7 ; +∞)
Ответ: 3
Номер: EF6A85
Укажите решение неравенства
(x+4)(x-9)≥0
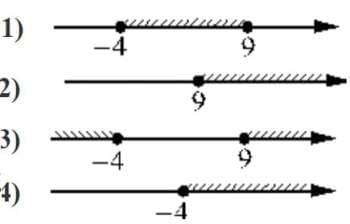
Решение:
(x+4)(x-9)≥0
Пределы
x+4=0
х=-4
x-9=0
х=9
Должны получить разные знаки для скобок, чтобы было больше 0
Ответ: 3
Номер: 6BC38F
Укажите неравенство, решение которого изображено на рисунке

1) x2 −6x<0
2) x2 −6x>0
3) x2 −36<0
4) x2 −36>0
Решение:
1) x2 −6x<0
x(x-6)<0
x<6
x<0
не подходит
2) x2 −6x>0
x(x-6)>0
x>6
x<0
Дальше не рассматриваем, так как это решение подходит.
3) x2 −36<0
4) x2 −36>0
Ответ: 2
Номер: 837085

