Все прототипы заданий из первой части ЕГЭ по профильной математике, в которых нужно найти значения выражений.
Степени
Найдите значение выражения `(5^4)^6:5^22`.
Решение:
`(5^4)^6:5^22=5^24:5^22=5^2=25`
Ответ: 25
Номер: 4EF06F
Найдите значение выражения `4^(1/5)*16^(9/10)`.
Решение:
`4^(1/5)*16^(9/10)=4^(1/5)*(4^2)^(9/10)`
`4^(1/5)*4^(18/10)=4^(20/10)=4^2=16`
Ответ: 16
Номер: C1F1E2 (старый 5152)
Найдите значение выражения `81^(2,6)/9^(3,7)`.
Решение:
`81^(2,6)/9^(3,7)`
`((9^2)^(2,6))/(9^(3,7))=(9^(5,2))/(9^(3,7))=9^(1,5)=(3^2)^(1,5)=3^3=27`
или
`9^(1,5)=9^1*9^(0,5)=9sqrt(9)=9*3=27`
или
`9^(1,5)=sqrt(9^3)=sqrt(729)=27`
Ответ: 27
Номер: CCEA21 (старый 5076)
Найдите значение выражения `(64^9)^3:(16^5)^8`.
Решение:
`(64^9)^3:(16^5)^8`
`((4^3)^9)^3:((4^2)^5)^8`
`4^81:4^80=4^1=4`
Ответ: 4
Номер: 0E5270 (старый 5114)
Найдите значение выражения `3^(sqrt5+10)*3^(−5−sqrt5)`.
Решение:
`3^(sqrt5+10)*3^(−5−sqrt5)`
`3^(sqrt5+10-5-sqrt(5))=3^5=243`
Ответ: 243
Номер: mathege
Найдите значение выражения `7^(2sqrt5−2)*7^(2−3sqrt5):7^(−sqrt5−1)`.
Решение:
`7^(2sqrt5−2+2−3sqrt(5)−(-sqrt5−1))=7^1=7`
Ответ: 7
Номер: mathege
Найдите значение выражения `3^(2sqrt2+1)*9^(2−sqrt2)`.
Решение:
`3^(2sqrt2+1)*9^(2−sqrt2)`
`3^(2sqrt2+1)*(3^2)^(2−sqrt2)`
`3^(2sqrt2+1+4-2sqrt2)=3^5=243`
Ответ: 243
Номер: mathege
Найдите значение выражения `2^(sqrt11+1)/(0,5^(−sqrt11))`.
Решение:
`0,5=5/10=1/2`
`2^(sqrt11+1)/((2^-1)^(−sqrt11))=2^(sqrt11+1)/(2^(sqrt11))=2^(sqrt11+1-sqrt11)=2^1=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `((2^(1/3)*2^(1/4))/(root(12)2))^2`.
Решение:
`((2^(1/3)*2^(1/4))/(root(12)2))^2`
`((2^(1/3))^2*(2^(1/4))^2)/((2^(1/12))^2)`
`(2^(2/3)*2^(2/4))/(2^(2/12))=2^((2*4)/3+(2*3)/4-2/12)=2^((8+6-2)/12)=2^1=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `((5^(3/5)*7^(2/3))^15)/35^9`.
Решение:
`((5^(3/5))^15*(7^(2/3))^15)/(5^9*7^9)`
`(5^9*7^10)/(5^9*7^9)=7^1=7`
Ответ: 7
Номер: 41A772
Найдите значение выражения `(2^(3,2)*6^(6,2))/12^(5,2)`.
Решение:
`(2^(3,2)*6^(6,2))/(2^(5,2)*6^(5,2))=2^-2*6^1=1/2^2*6=6/4=1,5`
Ответ: 1,5
Номер: 901F27
Найдите значение выражения `(5^(sqrt6)*2^(sqrt6))/10^(sqrt6−2)`.
Решение:
`(10^(sqrt6))/10^(sqrt6−2)=10^(sqrt6-(sqrt6-2))=10^(sqrt6-sqrt6+2)=100`
Ответ: 100
Номер: mathege
Найдите значение выражения `4^8*11^10:44^8`.
Решение:
`(4^8*11^10)/(4^8*11^8)=11^2=121`
Ответ: 121
Номер: mathege
Найдите значение выражения `20^(−3,9)*5^(2,9):4^(−4,9)`.
Решение:
`20^(−3,9)*5^(2,9):4^(−4,9)`
`(4^(−3,9)*5^(-3,9)*5^(2,9))/4^(-4,9)=4^(−3,9-(-4,9))*5^(-3,9+2,9)=4^1*5^-1=4/5=(2*4)/(2*5)=8/10=0,8`
Ответ: 0,8
Номер: 8DCF62
Найдите значение выражения `0,75^(1/8)*4^(1/4)*12^(7/8)`.
Решение:
`0,75^(1/8)*4^(1/4)*12^(7/8)`
`(3/4)^(1/8)*4^(2/8)*4^(7/8)*3^(7/8)=(3^(1/8)*4^(2/8)*4^(7/8)*3^(7/8))/4^(1/8)=3^(8/8)*4^(8/8)=3*4=12`
Ответ: 12
Номер: ЕГЭ 2016
Найдите значение выражения `a^(1,72)*a^(0,04)*a^(0,24)` при `a=14`.
Решение:
`a^(1,72)*a^(0,04)*a^(0,24)=a^2`
`a^2=14^2=196`
Ответ: 196
Номер: mathege
Найдите значение выражения `(b^(sqrt2))^(3sqrt2)/b^4` при `b=0,5`.
Решение:
`(b^(sqrt2))^(3sqrt2)/b^4`
`(b^(sqrt2*3sqrt2))/b^4=(b^(3*2))/b^4=b^6/b^4=b^2=0,5^2=0,25`
Ответ: 3
Номер: mathege
Найдите значение выражения `b^(6sqrt2+1)/(b^(sqrt2))^6` при `b=0,5`.
Решение:
`b^(6sqrt2+1)/(b^(sqrt2))^6`
`b^(6sqrt2+1)/(b^(6sqrt2))=b^(6sqrt2+1-6sqrt2)=b^1=0,5`
Ответ: 0,5
Номер: mathege
Найдите значение выражения `(7x^3)^2:7x^6`.
Решение:
`(7x^3)^2:7x^6`
`(49x^6)/(7x^6)=49/7=7`
Ответ: 7
Номер: mathege
Найдите значение выражения `((3x)^2*x^5)/(x^3*10x^4)`.
Решение:
`((3x)^2*x^5)/(x^3*10x^4)`
`(9*x^2*x^5)/(x^3*10*x^4)=(9*x^7)/(10*x^7)=9/10=0,9`
Ответ: 0,9
Номер: mathege
Найдите значение выражения `((2x^3)^4−(x^2)^6):3x^12`.
Решение:
`((2x^3)^4−(x^2)^6):3x^12`
`(16*x^12−x^12)/(3x^12)=(15x^12)/(3x^12)=15/3=5`
Ответ: 5
Номер: mathege
Найдите значение выражения `(4b)^2:b^5*b^3` при `b=128`.
Решение:
`(4b)^2:b^5*b^3`
1)`(16b^2)/(b^5)=16/b^3`
2) `16/b^3 * b^3 =16`
Ответ: 16
Номер: mathege
Найдите значение выражения `b^5:b^4*b^5` при `b=4`.
Решение:
`b^5:b^4*b^5`
`b^1*b^5=b^6=4^6=4^3*4^3=64*64=2^12=4096`
Ответ: 4096
Номер: mathege
Найдите значение выражения `(x^9*x^5)/x^10` при `x=3`.
Решение:
`(x^9*x^5)/x^10`
`x^14/x^10=x^4=3^4=81`
Ответ: 81
Номер: mathege
Найдите значение выражения `32x^6*x^14:(2x^4)^5`.
Решение:
`32x^6*x^14:(2x^4)^5`
`(32x^6*x^14)/(32*x^20)=x^20/x^20=1`
Ответ: 1
Номер: mathege
Найдите значение выражения `(6a)^2:a^7*a^5`.
Решение:
`(6a)^2:a^7*a^5`
1) `(36*a^2)/a^7=36/a^5`
2)`36/a^5*a^5=36`
Ответ: 36
Номер: mathege
Найдите значение выражения `6x*(8x^6)^2:(8x^4)^3` при `x=60`.
Решение:
`6x*(8x^6)^2:(8x^4)^3`
`(6x*64*x^12)/(8*64*x^12)=3/4`
`3/4*x=3/4*60=3*15=45`
Ответ: 45
Номер: mathege
Найдите значение выражения `x*5^(4x−1)*25^(−2x)` при `x=0,1`.
Решение:
`x*5^(4x−1)*25^(−2x)=x*5^(4x−1)*5^(−4x)=x*5^(−1)=x*1/5`
`1/10*1/5=(1*2)/(50*2)=2/100=0,02`
Ответ: 0,02
Номер: mathege
Найдите значение выражения `5^(3x+1):125^x:x` при `x=1/13`.
Решение:
`5^(3x+1):125^x:x`
1)`5^(3x+1)/125^x=5^(3x+1)/((5^3)^x)=5^(3x+1)/5^(3x)=5^1`
2) `5:1/13=5*13/1=65`
Ответ: 65
Номер: mathege
Найдите значение выражения `(11a^6*b^3−(3a^2b)^3):(4a^6b^6)` при `b=2`.
Решение:
`(11a^6*b^3−(3a^2b)^3):(4a^6b^6)`
`(11a^6*b^3−27*a^6*b^3)/(4a^6b^6)=(-16*a^6*b^3)/(4*a^6*b^6)=-4/b^3=-4/8=-0,5`
Ответ: -0,5
Номер: mathege
Найдите значение выражения `a^(3,33)/(a^(2,11)*a^(2,22))` при `a=2/7`.
Решение:
`a^(3,33)/a^(4,33)=a^-1=(2/7)^-1=7/2=3,5`
Ответ: 3,5
Номер: ЕГЭ 2013
Найдите значение выражения `(21(m^5)^6+3(m^3)^10)/(4m^15)^2`.
Решение:
`(21(m^5)^6+3(m^3)^10)/(4m^15)^2`
`(21*m^30+3*m^30)/(16*m^30)=(24*m^30)/(16*m^30)=3/2=1,5`
Ответ: 1,5
Номер: mathege
Найдите значение выражения `((5a^2)^3*(6b)^2)/(30a^3b)^2`.
Решение:
`((5a^2)^3*(6b)^2)/(30a^3b)^2`
`(5^3*a^6*6^2*b^2)/(5^2*6^2*a^6*b^2)=5^1=5`
Ответ: 5
Номер: mathege
Найдите значение выражения `(a^2*b^(−6))/((4a)^3b^(−2))*16/(a^(−1)b^(−4))`.
Решение:
`(a^2*b^(−6))/((4a)^3b^(−2))*16/(a^(−1)b^(−4))`
`(a^2*b^(−6))/(4^3*a^3*b^(−2))*16/(a^(-1)*b^(−4))=1/4=(1*25)/(4*25)=25/100=0,25`
Ответ: 0,25
Номер: mathege
Найдите значение выражения `(6n^(1/3))/(n^(1/12)*n^(1/4))` при `n>0`.
Решение:
`(6n^(1/3))/(n^(1/12)*n^(1/4))`
`(6n^(1/3))/n^(1/12+1/4) = (6n^(1/3))/(n^(4/12))=(6n^(1/3))/(n^(1/3))=6`
Ответ: 6
Номер: mathege
Найдите значение выражения `n^(5/6)/(n^(1/12)*n^(1/4))` при `n=64`.
Решение:
`n^(5/6)/(n^(1/12)*n^(1/4))`
`n^(5/6)/(n^(1/12+1/4))=n^(5/6)/(n^(4/12))=n^(5/6)/(n^(2/6))=n^(3/6)=n^(1/2)=sqrt(n)=sqrt64=8`
Ответ: 8
Номер: mathege
Найдите значение выражения `((9b)^(1,5)*b^(2,7))/b^(4,2)` при `b>0`.
Решение:
`((9b)^(1,5)*b^(2,7))/b^(4,2)`
`(9^(1,5)*b^(4,2))/b^(4,2)=(3^2)^(1,5)=3^3=27`
Ответ: 27
Номер: mathege
Корни
Найдите значение выражения `(sqrt13−sqrt7)(sqrt13+sqrt7)`.
Решение:
`(sqrt13−sqrt7)(sqrt13+sqrt7)`
`sqrt13^2−sqrt7^2=13-7=6`
Ответ: 6
Номер: mathege
Найдите значение выражения `(sqrt12−sqrt75)*sqrt12`.
Решение:
`(sqrt12−sqrt75)*sqrt12`
`12−sqrt900=12-30=-18`
Ответ: -18
Номер: 62754D
Найдите значение выражения `(2sqrt7)^2/14`.
Решение:
`(2sqrt7)^2/14`
`(4*7)/14=(4*7)/(2*7)=4/2=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `(sqrt(1,2)*sqrt(1,4))/sqrt(0,42)`.
Решение:
`(sqrt(1,2)*sqrt(1,4))/sqrt(0,42)`
`sqrt((1,2*1,4*10*10)/(0,42*100))=sqrt((12*14)/42)=sqrt((12*14)/(3*14))=sqrt(12/3)=sqrt4=2`
Ответ: 2
Номер: 391885
Найдите значение выражения `(sqrt7+sqrt5)^2/(60+10sqrt35)`.
Решение:
`(sqrt7+sqrt5)^2/(60+10sqrt35)`
`(sqrt7^2+2sqrt35+sqrt5^2)/(60+10sqrt35)=(12+2sqrt35)/(60+10sqrt35)=(2(6+sqrt35))/(10(6+sqrt35))=0,2`
Ответ: 0,2
Номер: E7C22D
Найдите значение выражения `sqrt(754^2−304^2)`.
Решение:
`sqrt(754^2−304^2)`
`sqrt((754−304)(754+304))=sqrt(450*1058)=sqrt(450*2*529)=sqrt(900*529)=30*23=690`
Ответ: 690
Номер: ЕГЭ 2019
Найдите значение выражения `(sqrt(3 6/7)−sqrt(1 5/7)):sqrt(3/28)`.
Решение:
`(sqrt(3 6/7)−sqrt(1 5/7)):sqrt(3/28)`
1) `(sqrt27/sqrt7)−(sqrt12/sqrt7)=(sqrt93-sqrt(4*3))/sqrt7=(3sqrt3-2sqrt3)/sqrt7=sqrt3/sqrt7`
2) `sqrt3/sqrt7:sqrt3/sqrt28=sqrt3/sqrt7*sqrt28/sqrt3=sqrt4=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `5*root(3)9*root(6)9`.
Решение:
`5*root(3)9*root(6)9`
`5*9^(1/3)*9^(1/6)`
`5*9^(1/3+1/6)`
`5*9^(3/6)=5*9^(1/2)=5*sqrt9=5*3=15`
Ответ: 15
Номер: mathege
Найдите значение выражения `(root(15)5*5*root(10)5)/root(6)5`.
Решение:
`(root(15)5*5*root(10)5)/root(6)5`
`(5^(1/15)*5^1+5^(1/10))/5^(1/6)=5^(1/15+1/1+1/10-1/6)=5^(30/30)=5^1=5`
Ответ: 5
Номер: D818A9
Найдите значение выражения `(root(4)8*root(4)48)/root(4)24`.
Решение:
`(root(4)8*root(4)48)/root(4)24`
`(8^(1/4)*48^(1/4))/24^(1/4)=((8*48)/24)^(1/4)=((8*2)/1)^(1/4)=16^(1/4)=(2^4)^(1/4)=2^1=2`
Ответ: 2
Номер: 334A92
Найдите значение выражения `(12root(9)m*root(18)m)/root(6)m` при `m>0`.
Решение:
`(12root(9)m*root(18)m)/root(6)m`
`(12m^(1/9)*m^(1/18))/m^(1/6)=(12*m^(3/18))/m^(1/6)=12`
Ответ: 12
Номер: mathege
Найдите значение выражения `((sqrt3a)^6sqrt(a^9))/a^(10,5)` при `a>0`.
Решение:
`((sqrt3a)^6sqrt(a^9))/a^(10,5)`
`(sqrt3^6*a^6*a^(9/2))/a^(10,5)`
`((3^(1/2))^6*a^6*a^(4,5))/a^(10,5)`
`(3^3*a^(10,5))/a^(10,5)=3^3=27`
Ответ: 27
Номер: mathege
Найдите значение выражения `(root(3)(22a^2))^6/a^4` при `a≠0`.
Решение:
`(root(3)(22)*root(3)(a^2))^6/a^4=(22^(1/3)*a^(2/3))^6/a^4=(22^2*a^4)/a^4=22^2=484`
Ответ: 484
Номер: mathege
Найдите значение выражения `sqrt(81root(7)b)/root(14)b` при `b>0`.
Решение:
`(sqrt81*sqrt(root(7)b))/root(14)b=(9sqrt(b^(1/7)))/b^(1/14)=(9root(2)((b^(1/7))^1))/b^(1/14)=(9*(b^(1/7))^(1/2))/b^(1/14)=(9*b^(1/14))/b^(1/14)=9`
Ответ: 9
Номер: mathege
Найдите значение выражения `(12root(6)(root(21)a)−4root(7)(root(18)a))/(4root(3)(root(42)a))` при `a>0`.
Решение:
`(12root(6)(root(21)a)−4root(7)(root(18)a))/(4root(3)(root(42)a))`
`(12((a^(1/21))^(1/6)-4*(a^(1/18))^(1/7)))/(4*(a^(1/42))^(1/3))=(12*a^(1/126)-4^(1/126))/(4*a^(1/126))=(8*a^(1/126))/(4*a^(1/126))=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `sqrtm/(root(4)m*root(12)m)` при `m=4096`.
Решение:
`sqrtm/(root(4)m*root(12)m)`
`m^(1/2)/(m^(1/4)*m^(1/12))=m^(1/2)/(m^(3/12+1/12))=m^(1/2)/(m^(1/3))=m^(1/2-1/3)=m^(1/6)=4096^(1/6)=(2^12)^(1/6)=2^2=4`
Ответ: 4
Номер: mathege
Найдите значение выражения `(root(12)a root(24)a)/(aroot(8)a)` при `a=0,5`.
Решение:
`(root(12)a root(24)a)/(aroot(8)a)`
`(a^(1/12)*a^(1/24))/(a*a^(1/8))=(a^(2/24)*a^(1/24))/(a*a^(1/8))=(a^(3/24))/(a*a^(1/8))=a^(1/8)/(a*a^(1/8))=1/a=(1*2)/(0,5*2)=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `(4a)^(3,5)/(a^3sqrta)` при `a>0`.
Решение:
`(4a)^(3,5)/(a^3sqrta)`
`(4^(3,5)*a^(3,5))/(a^3*a^(1/2))=(4^(3,5)*a^(3,5))/(a^(3,5))=4^(3,5)=(2^2)^(3,5)=2^7=128`
Ответ: 128
Номер: mathege
Найдите значение выражения `root(9)(sqrtm)/sqrt(16root(9)m)` при `m>0`.
Решение:
`root(9)(sqrtm)/sqrt(16root(9)m)`
`root(9)(m^(1/2))/sqrt(16*m^(1/9))=root(9)((m^(1/2))^1)/(sqrt16*root(2)((m^(1/9))^1))=((m^(1/2))^(1/9))/(4*(m^(1/9))^(1/2))=(1*m^(1/18))/(4*m^(1/18))=1/4=0,25`
Ответ: 0,25
Номер: mathege
Найдите значение выражения `(8sqrtx−2)/sqrtx+(2sqrtx)/x` при `x>0`.
Решение:
`(8sqrtx−2)/sqrtx+(2sqrtx)/x = (8sqrtx−2)/sqrtx+2/sqrtx=(8sqrtx−2+2)/sqrtx=(8sqrtx)/sqrtx=8`
Ответ: 8
Номер: mathege
Найдите значение выражения `(2sqrtx+3)/sqrtx−(3sqrtx)/x+x+5` при `x=3`.
Решение:
`(2sqrtx+3)/sqrtx−(3sqrtx)/x+x+5`
`(2sqrtx+3)/sqrtx−(3sqrtx)/(sqrtxsqrtx)+x+5`
`(2sqrtx+3-3)/sqrtx+x+5`
`2+x+5`
`7+x=7+3=10`
Ответ: 10
Номер: mathege
Тригонометрия
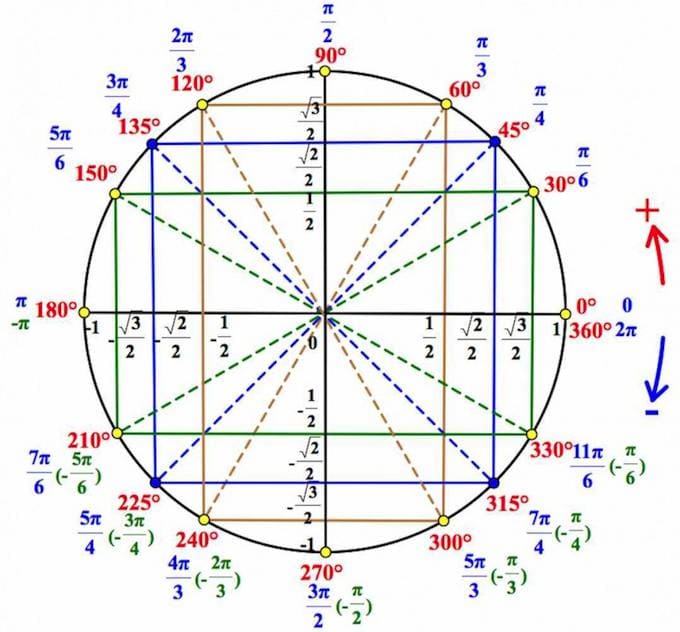
Формулы двойного угла:
`sin2α=2sinα*cosα`
`cos2α=cos^2α-sin^2α`
`cos2α=2cos^2α-1`
`cos2α=1-2sin^2α`
`tg α*ctg α = 1`
Основное тригонометрическое тождество: `sin^2α+cos^2α=1`
Найдите значение выражения `12sin150°*cos120°`.
Решение:
`12*1/2*(-1/2)=-3`
Ответ: -3
Номер: 67D37D
Найдите значение выражения `4sqrt2cos π/4cos (7π)/3`.
Решение:
`(6π)/3 = (2π)` - это полный круг, `(7π)/3` - продолжаем движение против часовой стрелки, это `π/3`
`4sqrt(2)*sqrt2/2*1/2=sqrt4=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `21sqrt6tg π/6sin π/4`.
Решение:
`21sqrt6*(1/2)/(sqrt3/2)*sqrt2/2`
`21sqrt6*(1*2)/(2*sqrt3)*sqrt2/2`
`(21sqrt3*sqrt2*sqrt2)/(sqrt3*2)=21`
Ответ: 21
Номер: ЕГЭ 2018
Найдите значение выражения `8sqrt2cos(−π/3)sin(−π/4)`.
Решение:
`8sqrt2*1/2*(-sqrt2/2)=-2sqrt4=-2*2=-4`
Ответ: -4
Номер: mathege
Найдите значение выражения `12sqrt2cos(−225°)`.
Решение:
`12sqrt2*(-sqrt2/2)=-12*sqrt4/2=-12`
Ответ: -12
Номер: 29144E
Найдите значение выражения `−4sqrt3cos(−750°)`.
Решение:
`-4sqrt3*cos(-750°+360°+360°+360°)=-4sqrt3*cos330°=-4sqrt3*sqrt3/2=-2sqrt3*sqrt3=-2*3=-6`
Ответ: -6
Номер: mathege
Найдите значение выражения `28/(sin(−(25π)/4)cos((23π)/4))`.
Решение:
`28/(sin(-6,25π)*cos(5,75π)) `
`28/(sin((-1π)/4)*cos((7π)/4)) `
`28/(-sqrt2/2*sqrt2/2)=28/(-sqrt4/4)=28/(-1/2)=-28*2=-56`
Ответ: -56
Номер: mathege
Найдите `cosα`, если `sinα=−sqrt51/10` и `α∈(π;(3π)/2)`.
Решение:
`(-sqrt51/10)^2+cos^2∝=1`
`51/100+cos^2∝=1`
`cos^2∝=49/100`
cos∝=0,7 или cos∝=-0,7
Ответ: -0,7
Номер: E418B1
Найдите `3cosα`, если `sinα=−(2sqrt2)/3` и `α∈((3π)/2;2π)`.
Решение:
1)
`((-2sqrt2)/3)^2+cos^2∝=1`
`(4*2)/9+cos^2∝=1`
`cos^2∝=1/9`
`cos∝=1/3` или cos∝=-1/3
2) `3*cos∝=3*1/3=1`
Ответ: 1
Номер: mathege
Найдите `tgα`, если `sinα=−(4sqrt41)/41` и `α∈(π;(3π)/2)`.
Решение:
1)
`((-4sqrt41)/41)^2+cos^2∝=1`
`(16*41)/41^2+cos^2∝=1`
`cos^2∝=25/41`
cos∝=5/√41 или`cos∝=-5/sqrt41`
2)
`tg∝=(-4sqrt41)/41:(-5/sqrt41)=(4sqrt41)/41*sqrt41/5=0,8`
Ответ: 0,8
Номер: BEF0CB
Найдите значение выражения `(16sin98°*cos98°)/(sin196°)`.
Решение:
`(16*sin98°*cos98°)/(2*sin98°*cos98°)=8`
Ответ: 8
Номер: F6B664
Найдите значение выражения `(21(sin^2 66°−cos^2 66°))/(cos132°)`.
Решение:
`(21(sin^2 66°−cos^2 66°))/(cos132°)=(21(sin^2 66°−cos^2 66°))/(cos^2 66°-sin^2 66°)=(-21(cos^2 66°-sin^2 66°))/(cos^2 66°-sin^2 66°)=-21`
Ответ: -21
Номер: 4F534A
Найдите `16cos2α`, если `cosα=0,5`.
Решение:
`cos2α=2cos^2α-1` формула двойного угла
`16(2cos^2α-1)`
`32cos^2α-16`
`32*0,5^2-16`
`32*1/4-16`
`8-16=-8`
Ответ: -8
Номер: 4881FC
Найдите `(3sin6α)/(5cos3α)`, если `sin3α=−0,5`.
Решение:
`(3sin6α)/(5cos3α) = (3sin(2*3α))/(5cos3α) =(3*2sin3α*cos3α)/(5cos3α) = 6/5*(-0,5)=-3/5=-0,6`
Ответ: -0,6
Номер: mathege
Найдите `sin2α`, если `cosα=0,6` и `π<α<2π`.
Решение:
`sin^2α+cos^2α=1` основное тригонометрическое тождество
`sin2α=2sinα*cosα` формула двойного угла
1) `sin^2α+0,6^2=1`
`sin^2α+0,36=1`
`sin^2α=0,64`
sinα=0,8 или sinα=-0,8
2) `sin2α=2*(-0,8)*0,6=-0,96`
Ответ: -0,96
Номер: Демоверсия 2015-2020
Найдите значение выражения `3sqrt2cos^2 (9π)/8−3sqrt2sin^2 (9π)/8`.
Решение:
`cos2α=cos^2α-sin^2α`
`3sqrt2(cos^2 (9π)/8−sin^2 (9π)/8)`
`3sqrt2 cos (2*9π)/8 = 3sqrt2 cos (9π)/4`
`3sqrt2 sqrt2/2 = 3`
Ответ: 3
Номер: A68E99
Найдите значение выражения `sqrt108cos^2 π/12−sqrt27`.
Решение:
`cos2α=2cos^2α-1`
`sqrt108cos^2 π/12−sqrt27`
`sqrt27(sqrt4*cos^2 π/12−1)`
`sqrt27(cos (2π)/12)`
`sqrt27*sqrt3/2=sqrt81/2=9/2=4,5`
Ответ: 4,5
Номер: D78270
Найдите значение выражения `sqrt2−2sqrt2sin^2 (15π)/8`.
Решение:
`cos2α=1-2sin^2α`
`sqrt2(1-2sin^2 (15π)/8)`
`sqrt2 cos (2*15π)/8=sqrt2 cos (15π)/4`
`sqrt2 cos (3,75-2π)`
`sqrt2 cos ((7π)/4)`
`sqrt2 sqrt2/2=sqrt4/2=1`
Ответ: 1
Номер: 0DC0A0
Найдите значение выражения `7sqrt2sin (15π)/8*cos (15π)/8`.
Решение:
`7sqrt2sin (15π)/8*cos (15π)/8`
`3,5 * sqrt2* 2sin (15π)/8*cos (15π)/8`
`3,5 * sqrt2* sin (2*15π)/8=3,5 * sqrt2 sin (15π)/4`
`3,5 * sqrt2* (- (sqrt2)/2)=-3,5`
Ответ: -3,5
Номер: 7C4023
Найдите значение выражения `sqrt2sin (7π)/8*cos (7π)/8`.
Решение:
`(sqrt2*2*sin (7π)/8 * cos (7π)/8)/2`
`sqrt2/2*sin (2*7π)/8 = sqrt2/2*sin (7π)/4`
`sqrt2/2* (-sqrt2/2)=-1/2=-0,5`
Ответ: -0,5
Номер: 11A20A
Найдите `tg(α+π/2)`, если `tgα=0,5`.
Решение:
`tgα*ctgα=1`
1) `tg(α+π/2) = -ctgα`
2) `ctgα=1/(0,5)=2`
3) `-ctgα=-2`
Ответ: -2
Номер: mathege
Найдите значение выражения `5tg(5π−γ)−tg(−γ)`, если `tgγ=7`.
Решение:
`-5tgγ+tgγ=-4tgγ=-4*7=-28`
Ответ: -28
Номер: mathege
Найдите `26cos((3π)/2+α)`, если `cosα=12/13` и `α∈((3π)/2;2π)`.
Решение:
1) `26cos((3π)/2+α)=26sinα`
2) `sin^2α+(12/13)^2=1`
`sin^2α+(144/169)=1`
`sin^2α=25/169`
sinα = 5/13 или `sinα = -5/13`
3) `26*(-5/13)=2*(-5)=-10`
Ответ: -10
Номер: mathege
Найдите значение выражения `(2sin(α−7π)+cos((3π)/2+α))/sin(α+π)`.
Решение:
`(2sin(α−7π)+cos((3π)/2+α))/sin(α+π)`
`(-2sinα+sinα)/(-sinα)=(-sinα)/(-sinα)=1`
Ответ:1
Номер: ЕГЭ 2015
Найдите значение выражения `5sin(α−7π)−11cos((3π)/2+α)`,если `sinα=−0,25`.
Решение:
`-5sinα−11sinα=-16sinα=-16*(-1/4)=4`
Ответ: 4
Номер: mathege
Найдите значение выражения `(−6sin374°)/(sin14°)`.
Решение:
`(−6sin(374°-360°))/(sin14°)=(−6sin14°)/(sin14°)=-6`
Ответ: -6
Номер: 72C72C
Найдите значение выражения `(51cos4°)/(sin86°)+8`.
Решение:
`(51cos4°)/(sin90°-4°)+8`
`(51cos4°)/(cos4°)+8=51+8=59`
Ответ: 59
Номер: AD1B06
Найдите значение выражения `30tg3°*tg87°−43`.
Решение:
`30tg3°*tg87°−43`
`30tg3°*tg(90°-3°)−43`
`90°=π/2`
`30tg3°*ctg3°−43`
`tg α*ctg α = 1`
`30*1-43=-13`
Ответ: -13
Номер: 70CAFA
Найдите значение выражения `(7sin154°)/(cos77°*cos13°)`.
Решение:
`sin2α=2sinα*cosα`
`(7sin154°)/(cos77°*cos(90°-77°))`
`90°=π/2`
1) `cos(90°-77°)=sin77°`
2) `(7*2*sin77°*cos77°)/(cos77°*sin77°)=14`
Ответ: 14
Номер: 5057
Найдите значение выражения `24/(sin^2 127°+4+sin^2 217°)`.
Решение:
`24/(sin^2 (90°+37°)+4+sin^2 (180°+37°))`
`90°=π/2` , `180°=π`
`24/((cos 37°)^2+4+(-sin 37°)^2)`
`24/(sin^2 37°+cos^2 37°+4)`
`24/(1+4)=24/5=4,8`
Ответ: 4,8
Номер: CBCA4A
Найдите `(3cosα−4sinα)/(2sinα−5cosα)`, если `tgα=3`.
Решение:
1) `tgα=3`
`(sinα)/(cosα)=3`
`sinα=3cosα`
2) `(3cosα-4*3cosα)/(2*3cosα-5cosα)=(-9cosα)/(cosα)=-9`
Ответ: -9
Номер: mathege
Найдите `(10cosα+4sinα+15)/(2sinα+5cosα+3)`, если `tgα=−2,5`.
Решение:
1) `(sinα)/(cosα)=2,5`
`sinα=-2,5cosα`
2) `(10cosα+4*2,5cosα+15)/(-2*2,5cosα+5cosα+3)=15/3=5`
Ответ: 5
Номер: mathege
Найдите `tgα`, если `(6sinα−2cosα)/(4sinα−4cosα)=−1`.
Решение:
1) `6sinα-2cosα=-4sinα+4cosα`
`6sinα+4sinα=4cosα+2cosα`
`10sinα=6cosα` |:10
`sinα=0,6cosα`
2) `tgα=(sinα)/(cosα)=(0,6cosα)/(cosα)=0,6`
Ответ: 0,6
Номер: mathege
Найдите `tgα`, если `(3sinα−5cosα+2)/(sinα+3cosα+6)=1/3`.
Решение:
1) `9sinα−15cosα+6=sinα+3cosα+6`
`9sinα−sinα=3cosα+15cos`
`8sinα=18cosα` |:8
`sinα=18/8 cosα=9/4cosα=2,25cosα`
2) `tgα=(sinα)/(cosα)=(2,25cosα)/(cosα)=2,25`
Ответ: 2,25
Номер: mathege
Найдите `tg^2α`, если `5sin^2α+13cos^2α=6`.
Решение:
1) `5sin^2 α+5cos^2 α + 8 cos^2 α = 6`
`5(sin^2 α+cos^2 α) + 8 cos^2 α = 6`
`5*1 + 8 cos^2 α = 6`
`8 cos^2 α = 1`
`cos^2 α = 1/8`
2) `1+tg^2 α = 1/(1/8) `
`1+tg^2 α = 8`
`tg^2 α = 7`
Ответ: 7
Номер: mathege
Логарифмы
`a^(log_a b)=b` основное логарифмическое тождество
`log_a b=1/log_b a`
`log_a b^m=m*log_a b`
`log_a b+log_a c=log_a b*c`
`log_a b-log_a c=log_a b/c`
`log_(a^n) b=1/n log_a b`
`log_a b=(log_c b)/(log_c a)`
Найдите значение выражения `(log_2 16)*(log_6 36)`.
Решение:
`(log_2 16)*(log_6 36)=4*2=8`
Ответ: 8
Номер: mathege
Найдите значение выражения `24/(3^(log_3 2))`.
Решение:
`a^(log_a b)=b`
`24/(3^(log_3 2))=24/2=12`
Ответ: 12
Номер: mathege
Найдите значение выражения `6*7^(log_7 2)`.
Решение:
`a^(log_a b)=b`
`6*7^(log_7 2)=6*2=12`
Ответ: 12
Номер: mathege
Найдите значение выражения `(7^(log_7 5))^(log_5 2)`.
Решение:
`a^(log_a b)=b`
`(7^(log_7 5))^(log_5 2)=5^(log_5 2)=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `(5^(log_3 7))^(log_7 3)`.
Решение:
`log_a b=1/log_b a`
`(5^(log_3 7))^(log_7 3)=5^(log_3 7 * log_7 3)=5^(log_3 7 * 1/(log_3 7)=5^1=5`
Ответ: 5
Номер: mathege
Найдите значение выражения `(5^(log_3 7))^(log_5 3)`.
Решение:
`a^(log_a b)=b`
`(5^(log_3 7))^(log_5 3)=5^(log_3 7 * log_5 3) = 5^(log_5 3 * log_3 7)= (5^(log_5 3))^(log_3 7)=3^(log_3 7)=7`
Ответ: 7
Номер: mathege
Найдите значение выражения `8^(2log_8 3)`.
Решение:
`log_a b^m=m*log_a b`
`a^(log_a b)=b`
`8^(2log_8 3)=8^(log_8 3^2)=8^(log_8 9)=9`
Ответ: 9
Номер: mathege
Найдите значение выражения `5^(3+log_5 2)`.
Решение:
`a^(log_a b)=b`
`5^3*5^(log_5 2)`
`125*2=250`
Ответ: 250
Номер: mathege
Найдите значение выражения `9^(log_3 4)`.
Решение:
`log_a b^m=m*log_a b`
`a^(log_a b)=b`
`9^(log_3 4)`
`3^(2*log_3 4)`
`3^(log_3 16)=16`
Ответ: 16
Номер: mathege
Найдите значение выражения `3^(log_3 7)+49^(log_7 sqrt13)`.
Решение:
`a^(log_a b)=b`
`log_a b^m=m*log_a b`
`3^(log_3 7)+49^(log_7 sqrt13)`
`7+7^(2*log_7 sqrt13)`
`7+7^(log_7 13)`
`7+13=20`
Ответ: 20
Номер: ЕГЭ 2019
Найдите значение выражения `log_4 log_5 25`.
Решение:
`log_4 log_5 25`
1) `log_5 25=2`
2) `log_4 2=1/2=0,5`
Ответ: 0,5
Номер: mathege
Найдите значение выражения `log_7 12,25+log_7 4`.
Решение:
`log_a b+log_a c=log_a b*c`
`log_7 12,25+log_7 4=log_7 (12,25*4)=log_7 49=2`
Ответ: 2
Номер: D27044
Найдите значение выражения `log_2 240−log_2 3,75`.
Решение:
`log_a b-log_a c=log_a b/c`
`log_2 240−log_2 3,75=log_2 240/(3,75)=log_2 64=6`
Ответ: 6
Номер: F6A353
Найдите значение выражения `log_(0,2) 10−log_(0,2) 2`.
Решение:
`log_a b-log_a c=log_a b/c`
`log_(a^n) b=1/n log_a b`
`log_(0,2) 10−log_(0,2) 2= log_(0,2) (10/2) = log_(5^-1) (5^1)=-1log_5 5=-1`
Ответ: -1
Номер: mathege
Найдите значение выражения `(log_2 729)/(log_2 9)`.
Решение:
`log_a b=(log_c b)/(log_c a)`
`(log_2 729)/(log_2 9)=log_9 729=3 `
Ответ: 3
Номер: 84E3EB
Найдите значение выражения `log_4 8`.
Решение:
`log_a b^m=m*log_a b`
`log_(a^n) b=1/n log_a b`
`log_4 8 = log_(2^2) (2^3)=3/2 * log_2 2=3/2*1=1,5`
Ответ: 1,5
Номер: mathege
Найдите значение выражения `(log_6 sqrt13)/(log_6 13)`.
Решение:
`log_a b=(log_c b)/(log_c a)`
`(log_6 sqrt13)/(log_6 13)=log_13 sqrt13=1/2=0,5`
Ответ: 0,5
Номер: mathege
Найдите значение выражения `(log_8 14)/(log_64 14)`.
Решение:
`log_(a^n) b=1/n log_a b`
`(log_8 14)/(log_64 14)=(log_8 14)/(1/2*log_8 14)=1/(1/2)=2`
Ответ: 2
Номер: 7DABAA
Найдите значение выражения `(log_5 2)/(log_5 13)+log_13 0,5`.
Решение:
`log_a b+log_a c=log_a b*c`
`log_a b=(log_c b)/(log_c a)`
`(log_5 2)/(log_5 13)+log_13 0,5 = log_13 2+log_13 (0,5)=log_13 (2*0,5)=log_13 1=0`
Ответ: 0
Номер: 6693B1
Найдите значение выражения `(log_6 180)/(2+log_6 5)`.
Решение:
`log_a b+log_a c=log_a b*c`
`(log_6 180)/(2+log_6 5) = (log_6 (36*5))/(2+log_6 5)=(log_6 36+log_6 5)/(2+log_6 5)=(2+log_6 5)/(2+log_6 5)=1`
Ответ: 1
Номер: mathege
Найдите значение выражения `log_(root(6)13)13`.
Решение:
`log_(a^n) b=1/n log_a b`
`log_(root(6)13)13 =log_(13^(1/6)) 13 = 1/(1/6)*log_13 13 = 6 * 1 = 6`
Ответ: 6
Номер: ЕГЭ 2019
Найдите значение выражения `log_2 7*log_7 4`.
Решение:
`log_a b^m=m*log_a b`
`log_(a^n) b=1/n log_a b`
`log_2 7*log_7 (2^2)`
`2*log_2 7*log_7 2`
`2*log_2 7*1/(log_2 7) =2/1=2`
Ответ: 2
Номер: C63976
Найдите значение выражения `6log_7 root(3)7`.
Решение:
`6log_7 root(3)7`
`6log_7 (7^(1/3))=6*1/3*log_7 7=2*1=2`
Ответ: 2
Номер: ЕГЭ 2019
Найдите значение выражения `log_sqrt11^2 121`.
Решение:
`log_sqrt11^2 121=log_sqrt11 121*log_sqrt11 121=4*4=16`
Ответ: 16
Номер: mathege
Найдите значение выражения `6^(log_12 432)/6^(log_12 3)`.
Решение:
`log_a b-log_a c=log_a b/c`
`6^(log_12 432)/6^(log_12 3)`
`6^(log_12 432-log_12 3)=6^(log_12 (432/3))=6^(log_12 144) = 6^2=36`
Ответ: 36
Номер: mathege
Найдите значение выражения `log_(0,125) 8`.
Решение:
`log_(a^n) b=1/n log_a b`
`log_(0,125) 8=log_(8^-1) 8=1/-1*log_8 8=-1*1=-1`
Ответ: -1
Номер: mathege
Найдите значение выражения `log_(1/13) sqrt13`.
Решение:
`log_a b^m=m*log_a b`
`log_(a^n) b=1/n log_a b`
`log_(1/13) sqrt13`
`log_(13^-1) (13^(1/2))=(1/2)/-1*log_13 13=-0,5*1=-0,5`
Ответ: -0,5
Номер: ЕГЭ 2017
Найдите значение выражения `(1−log_2 12)*(1−log_6 12)`.
Решение:
`log_a b+log_a c=log_a b*c`
`log_a b=1/log_b a`
1) `log_2 12 = log_2 (2*6)=log_2 2+log_2 6=1+log_2 6`
2) `log_6 12 = log_2 (2*6) = log_6 2 + log_6 6 = 1+ log_6 2`
3) `(1-(1+ log_2 6))*(1-(1+ log_6 2))`
`(1-1- log_2 6)*(1-1- log_6 2)`
+ `log_2 6*log_6 2`
`(log_2 6)/(log_2 6)=1`
Ответ: 1
Номер: mathege
Найдите значение выражения `4log_(1,25) 5*log_5 0,8`.
Решение:
`log_a b^m=m*log_a b`
`log_a b=1/log_b a`
`4log_(5/4) 5*log_5 (4/5)`
`4log_(5/4) 5*log_5 ((5/4)^-1)`
`-4log_(5/4) 5*log_5 (5/4)`
`-4log_(5/4) 5*1/(log_(5/4) 5)=-4*1=-4`
Ответ: -4
Номер: 8C4796
Найдите значение выражения `log_a(a^6b^10)`, если `log_a b=8`.
Решение:
`log_a b+log_a c=log_a b*c`
`log_a b^m=m*log_a b`
`log_a(a^6)+log_a(b^10)`
`6*log_a a+10*log_a b`
`6*1+10*8=86`
Ответ: 86
Номер: mathege
Найдите значение выражения `log_a a^4/b^6`, если `log_a b=−14`.
Решение:
`log_a b-log_a c=log_a b/c`
`log_a b^m=m*log_a b`
`log_a a^4 - log_a b^6`
`4 log_a a - 6 log_a b`
`4 *1-6*(-14)=4+84=88`
Ответ: 88
Номер: mathege
Найдите значение выражения `log_a(ab^2)`, если `log_b a=2/11`.
Решение:
`log_a b+log_a c=log_a b*c`
`log_a b^m=m*log_a b`
`log_a b=1/log_b a`
`log_a a + log_a b^2`
`1 + 2 log_a b`
`1 + 2* 1/(log_b a) = 1 + 2 * 1/(2/11)=1+2*11/2=12`
Ответ: 12
Номер: mathege
Модули
Если внутримодульное выражение положительно, просто опускаем скобки; если отрицательное - меняем знаки всех чисел, которые были под модулем.
Свойства модулей:
`|a*b|=|a|*|b|`
`|a/b|=|a|/|b|`
Найдите значение выражения `sqrt((a−3)^2)+sqrt((a−9)^2)` при `3≤a≤9`.
Решение:
`|a-3|+|a-9|`
`a-3-a+9=6`
Ответ: 6
Номер: mathege
Найдите значение выражения `x+sqrt(x^2−4x+4)` при `x≤2`.
Решение:
Формула сокращенного умножения - квадрат разности.
`x+sqrt((x−2)^2)`
`x+|x-2|`
`x-x+2=2`
Ответ: 2
Номер: mathege
Подстановка
Найдите значение выражения `10p(a)−60a−4`, если `p(a)=6a−2`.
Решение:
`10*(6a-2)-60a-4 = 60a-20-60a-4=-24`
Ответ: -24
Номер: mathege
Найдите `2p(x−7)−p(2x)`, если `p(x)=x−3`.
Решение:
1) `p(x-7)=x-7-3=x-10`
2) `p(2x)=2x-3`
3) `2(x-10)-(2x-3)=`
`2x-20-2x+3=-17`
Ответ: -17
Номер: mathege
Найдите значение выражения `q(b−4)−q(b+4)`, если `q(b)=−9b`.
Решение:
1) `q(b-4)=-9*(b-4)=-9b+36`
2) `q(b+4)=-9*(b+4)=-9b-36`
3) `-9b+36-(-9b-36)=`
-9b+36+9b+36=72
Ответ: 72
Номер: mathege
Найдите значение выражения `(g(x−10))/(g(x−11))`, если `g(x)=11^x`.
Решение:
1) `g(x-10)=11^(x-10)`
2) `g(x-11)=11^(x-11)`
3) `(g(x-10))/(g(x-11))=(11^(x-10))/(11^(x-11))=11^(x-10-(x-11))=11^(x-10-x+11)=11`
Ответ: 11
Номер: mathege
Найдите значение выражения `5(p(2x)−2p(x+5))`, если `p(x)=x−10`.
Решение:
1) `p(2x)=2x-10`
2) `p(x+5)=x+5-10=x-5`
3) `5*(2x-10-2(x-5))`
`5*(2x-10-2x-10)`
`5*0=0`
Ответ: 0
Номер: mathege
Найдите `p(x−3)+p(6−x)`, если `p(x)=2x−5`.
Решение:
1) `p(x-3)=2*(x-3)-5=2x-6-5=2x-11`
2) `p(6-x)=2(6-x)-5=12-2x-5=7-2x`
3) `2x-11+7-2x=-4`
Ответ: -4
Номер: mathege
Найдите `(p(b))/(p(1/b))`, если `p(b)=(b+3/b)(3b+1/b)`. При b≠0.
Решение:
1) `p(1/b)=(1/b+3/(1/b))(3*1/b+1/(1/b))=(1/b+3b)(3/b+b)`
2) `(p(b))/(p(1/b))=((b+3/b)(3b+1/b))/((1/b+3b)(3/b+b))=1`
Ответ: 1
Номер: mathege
Найдите `(g(2−x))/(g(2+x))`, если `g(x)=root(3)(x(4−x))` при |x|≠2.
Решение:
1) `g(2-x)=root(3) ((2-x)(4-(2-x)))=root(3) ((2-x)(4-2+x))=root(3) ((2-x)(2+x))`
2) `g(2+x)=root(3) ((2+x)(4-(2+x)))=root(3) ((2+x)(4-2-x))=root(3) ((2+x)(2-x))`
3) `(root(3) ((2-x)(2+x)))/(root(3) ((2-x)(2+x)))=1`
Ответ: 1
Номер: mathege
Найдите `p(x)+p(8−x)`, если `p(x)=(x(8−x))/(x−4)` при x≠4.
Решение:
1)`p(8-x)=((8-x)(8-(8-x)))/(8-x-4)=((8-x)(8-8+x))/(4-x)
=((8-x)*x)/(4-x)`
2) `p(x)+p(8-x)=(x(8-x))/(x-4)+((8-x)x)/(4-x)=(x(8-x))/(x-4)-((8-x)*x)/(x-4)=0`
Ответ: 0
Номер: mathege
Найдите `h(3+x)+h(3−x)`, если `h(x)=root(9)x+root(9)(x−6)`.
Решение:
1) `h(3+x)=root(9) (3+x)+root(9) (3+x-6)= root(9) (3+x)+root(9) (x-3)`
2) `h(3-x)=root(9) (3-x)+root(9) (3-x-6) = root(9) (3-x) + root(9) (-3-x)`
3) `h(3+x)+h(3-x)=root(9) (3+x) + root(9) (x-3) + root(9) (3-x) + root(9) (-3-x)=root(9) (3+x)+root(9) (x-3)-root(9) (x-3)-root(9) (3+x)=0`
Ответ: 0
Номер: mathege
Арифметика
Найдите значение выражения `7 9/13:5/13`.
Решение:
`7 9/13:5/13 = 100/13:5/13=100/13*13/5=100/5=20`
Ответ: 20
Номер: mathege
Найдите значение выражения `(252^2−23^2):275`.
Решение:
`((252−23)(252+23))/275=(229*275)/275=229`
Ответ: 229
Номер: mathege
Найдите значение выражения `(30,9*0,356)/(3,09*35,6)`.
Решение:
`(309*356)/(309*356)=1/10=0,1`
Ответ: 0,1
Номер: mathege
Найдите значение выражения `(3 2/5−2,7)*6 3/7`.
Решение:
`(3 2/5−2,7)*6 3/7=4,5`
1) `17/5−27/10=7/10`
2) `7/10*45/7=4,5`
Ответ: 4,5
Номер: mathege
Найдите значение выражения `(7 3/5−3,5):1/20`.
Решение:
`(7 3/5−3,5):1/20=82`
1)`38/5-35/10=41/10`
2)`41/10 : 1/20=41/10*20/1=82`
Ответ: 82
Номер: mathege
Найдите значение выражения `(3/4+2 3/8)*25,8`.
Решение:
`(3/4+2 3/8)*25,8=80,625`
1) `3/4+19/8=25/8`
2)`25/8 * 25,8 = 25/8*258/10=645/8=80,625`
Ответ: 80,625
Номер: mathege
Найдите значение выражения `(2axy−(−2xya)):4yax`.
Решение:
`(2axy−(−2xya)):4yax = (2axy+2axy)/(4axy)=(4axy)/(4axy)=1`
Ответ: 1
Номер: mathege
Найдите значение выражения `(2x−5)(2x+5)−4x^2`.
Решение:
Формула сокращенного умножения: разность квадратов
`a^2-b^2=(a-b)(a+b)`
`(2x−5)(2x+5)−4x^2 =4x^2-25-4x^2=-25`
Ответ: -25
Номер: mathege
Найдите значение выражения `(9x^2−4)/(3x+2)−3x`.
Решение:
Формула сокращенного умножения: разность квадратов
`a^2-b^2=(a-b)(a+b)`
`(9x^2−4)/(3x+2)−3x = ((3x-2)(3x+2))/(3x+2)-3x=3x-2-3x=-2`
Ответ: -2
Номер: mathege
Найдите значение выражения `((3x+2y)^2−9x^2−4y^2):6xy`.
Решение:
Квадрат суммы `(a+b)^2=a^2+2ab+b^2`
`((3x+2y)^2−9x^2−4y^2):6xy=(9x^2+12xy+4y^2-9x^2-4y^2)/(6xy)=2`
Ответ: 2
Номер: mathege
Найдите значение выражения `(7x−3)(7x+3)−49x^2+6x+22` при `x=80`.
Решение:
Формула сокращенного умножения: разность квадратов
`a^2-b^2=(a-b)(a+b)`
`(7x−3)(7x+3)−49x^2+6x+22`
`49x^2-9−49x^2+6x+22`
`6x+13`
`6*80+13`
`480+13=493`
Ответ: 493
Номер: mathege
Найдите значение выражения `((x−5y)^2−(x+5y)^2):xy`.
Решение:
Квадрат суммы `(a+b)^2=a^2+2ab+b^2`
Квадрат разности `(a-b)^2=a^2-2ab+b^2`
`((x−5y)^2−(x+5y)^2):xy`
`(x^2−10xy+25y^2-(x^2+10xy+25y^2))/(xy)`
`(x^2−10xy+25y^2-x^2-10xy-25y^2)/(xy)`
`(-10xy-10xy)/(xy)`
`(-20xy)/(xy)=-20`
Ответ: -20
Номер: mathege
Найдите значение выражения `(16x^2+9y^2−(4x−3y)^2):(−6xy)`.
Решение:
Квадрат разности `(a-b)^2=a^2-2ab+b^2`
`(16x^2+9y^2−(4x−3y)^2):(−6xy)`
`(16x^2+9y^2−(16x^2-24xy+9y^2))/(−6xy)`
`(24xy)/(−6xy)=-4`
Ответ: -4
Номер: mathege
Найдите значение выражения `((11a)^2−11a)/(11a^2−a)`.
Решение:
`((11a)^2−11a)/(11a^2−a)`
`(121a^2-11a)/(11a^2−a)=(11a(11a-1))/(a(11a-1))=11`
Ответ: 11
Номер: mathege
Найдите значение выражения `(25a^2−16)*(1/(5a+4)−1/(5a−4))`.
Решение:
Разность квадратов `a^2-b^2=(a-b)(a+b)`
`(25a^2−16)*(1/(5a+4)−1/(5a−4))`
`(5a−4)*(5a+4)*(5a−4-5a-4)/((5a+4)(5a-4))=-8`
Ответ: -8
Номер: mathege
Найдите значение выражения `(49b^2−36)*(1/(7b−6)−1/(7b+6))−2b+15` при `b=65`.
Решение:
Разность квадратов `a^2-b^2=(a-b)(a+b)`
`(49b^2−36)*(1/(7b−6)−1/(7b+6))−2b+15`
`(7b−6)*(7b+6)*(7b+6-7b+6)/((7b-6)(7b+6))-2b+15`
`12-2b+15`
`27-2*65=27-130=-103`
Ответ: -103
Номер: mathege
Найдите значение выражения `a(81a^2−64)(1/(9a+8)−1/(9a−8))` при `a=22,8`.
Решение:
Разность квадратов `a^2-b^2=(a-b)(a+b)`
`a(81a^2−64)(1/(9a+8)−1/(9a−8))`
`a(9a−8)(9a+8)*(9a−8-9a-8)/((9a+8)(9a-8))`
`a*(-16)`
`-22,8*16=-364,8`
Ответ: -364,8
Номер: mathege
Найдите `a/b`, если `(2a+5b)/(5a+2b)=1`.
Решение:
`(2a+5b)/(5a+2b)=1`
1) 2a+5b=5a+2b
5b-2b=5a-2a
3b=3a |:3
a=b
2) `a/b=b/b=1`
Ответ: 1
Номер: mathege
Найдите `(a+9b+16)/(a+3b+8)`, если `a/b=3`.
Решение:
`(a+9b+16)/(a+3b+8)`
1) a=3b
2) `(3b+9b+16)/(3b+3b+8)=(12b+16)/(6b+8)=(4(3b+4))/(2(3b+4))=2`
Ответ: 2
Номер: mathege
Найдите `21a−14b−20`,если `(3a−4b+2)/(4a−3b+2)=6`.
Решение:
`(3a−4b+2)/(4a−3b+2)=6`
1) 6(4a-3b+2)=1(3a-4b+2)
24a-18b+12-3a+4b-2=0
21a-14b=-10
2) (21a-14b)-20=-10-20=-30
Ответ: -30
Номер: mathege
Найдите значение выражения `2x+y+6z`, если `4x+y=5`, `12z+y=7`.
Решение:
`{(4x+y=5), (12z+y=7):}`
4x+2y+12z=12
2x+y+6z=6
Ответ: 6
Номер: mathege

