Все прототипы заданий из первой части ЕГЭ по профильной математике, в которых нужно уметь работать с графиками производной и первообразной функции.
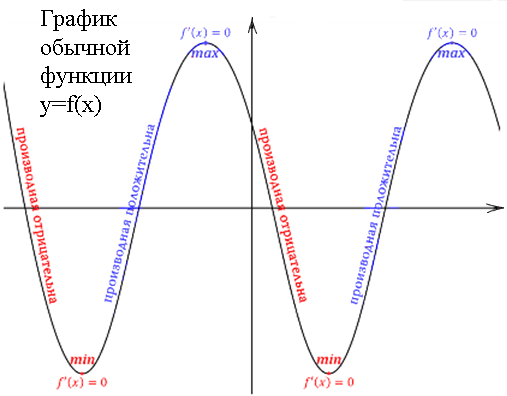

Внимательно к заданию, на каком отрезке надо найти точки, бывает, не совпадает с целым графиком!
Дана обычная функция
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек производная функции f(x) положительна?
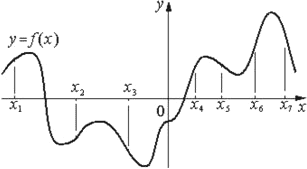
Ответ:
Производная положительная на тех промежутках функции, где функция имеет положительный прирост, проще говоря на возрастании функции.
То есть нам надо найти точки х, в которых функция растет:
х1, х2, х4, х6 в 4 точках
Ответ: 4
Номер: A5894A
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
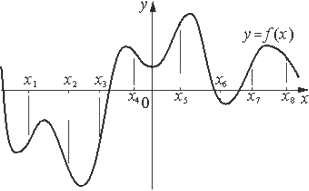
Ответ:
Производная отрицательна на тех промежутках функции, где она имеет убывание, проще говоря, где есть отрицательная динамика.
То есть нам надо найти точки х, в которых функция убывает:
х2, х4, х6, х8 в 4 точках
Ответ: 4
Номер: 20047E A2CAD3
На рисунке изображён график функции y=f(x), определённой на интервале (−9;5). Найдите количество точек, в которых производная функции f(x) равна 0.
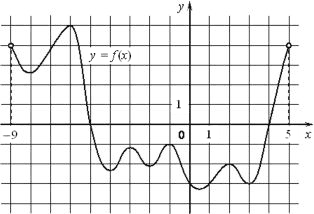
Ответ:
Производная равна нулю на участке функции, где она меняет свое направление с возрастания на убывание или наоборот.
У нас таких участков 9
Ответ: 9
Номер: 8E93FF
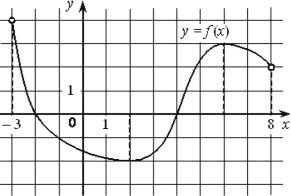
На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (−3;8). Найдите точку из отрезка [−2;5], в которой производная функции f(x) равна 0.
Ответ:
Производная равна нулю на участке функции, где она меняет свое направление с возрастания на убывание или наоборот.
На отрезке [−2;5] это точка 2, где есть условный "перелом" изменение направления функции, значит в ней производная равна 0
Ответ: 2
Номер: 55F759
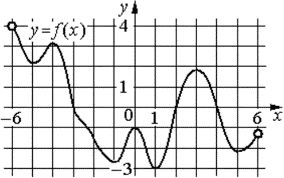
На рисунке изображён график функции y=f(x), определённой на интервале (−6;6). Найдите количество решений уравнения f´(x)=0 на отрезке [−4,5;2,5].
Ответ:
То есть нам надо найти точки, где производная функции равна нулю.
Производная равна нулю на участке функции, где она меняет свое направление с возрастания на убывание или наоборот.
На отрезке [−4,5;2,5] это 4 участка.
Ответ: 4
Номер: 9933A1
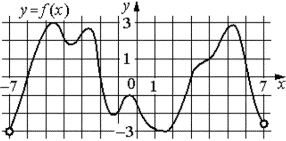
На рисунке изображён график функции y=f(x), определённой на интервале (−7;7). Определите количество целых точек, в которых производная функции положительна.
Ответ:
Производная положительная на тех промежутках функции, где она имеет прирост, проще говоря, на возрастании функции.
Причем, нас просят найти целые точки, то есть это значения, где номинал является целым числом, в нашем случае это:
| Участок возрастания | Целые точки |
| -7; -5,5 | -6, -5 |
| -4,5; -3 | -3 |
| -1,2; -0,5 | -1 |
| 1,8 5,2 | 2, 3, 4, 5 |
Всего 8 точек
Ответ: 8
Номер: 2E361B
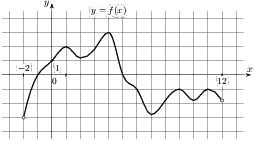
На рисунке изображен график функции y=f(x), определенной на интервале (−2;12). Найдите сумму точек экстремума функции f(x).
Ответ:
Экстремумы функции - это когда производная равна 0 или точки, где функция меняет свое направление.
Это точки: 1, 2, 4, 7, 9, 10, 11
Сумма точек 1+2+4+7+9+10+11=44
Ответ: 44
Номер: mathege
Дан график производной
На рисунке изображён график y=f´(x)− производной функции f(x). На оси абсцисс отмечены шесть точек: x1, x2, x3, x4, x5, x6. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
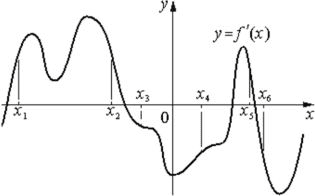
Ответ:
Возрастание функции наблюдается при положительной производной, то есть когда прирост функции больше нуля, что собственно и характеризует производная.
Положительное значение берется для y, получается положительный у в точках:
х1, х2, х5
Ответ: 3 точки
Номер: A9FB0A
На рисунке изображён график y=f´(x)− производной функции f(x). На оси абсцисс отмечены девять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9. Сколько из этих точек лежит на промежутках убывания функции f(x)?
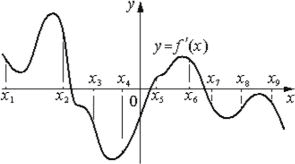
Ответ:
Убывание функции наблюдается при отрицательной производной, то есть когда прирост функции меньше нуля, что собственно и характеризует производная.
У нас отрицательные значения берется для y, в точках:
х3, х4, х7, х8, х9
Ответ: 5
Номер: 8FD3A4
На рисунке изображён график y=f´(x) — производной функции f(x), определенной на интервале (−19;3). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−17;−4].
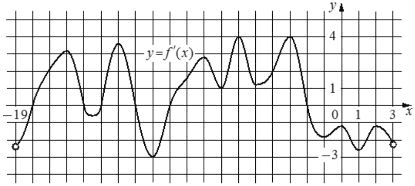
Ответ:
Рассмотрим график производной y=f´(x) на отрезке [− 17; − 4], проанализируем. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или, наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, точки экстремума функции будут там, где производная равна 0.
| Области | [− 17; − 15) | -15 | (-15;-14) | -14 | (-14;12) | -12 | (-12;-10) | -10 | (-10; -4) |
| Значение производной (динамика функции) |
+ | 0 | - | 0 | + | 0 | - | 0 | + |
| Что с функцией? | растет↑ | макс | убывает↓ | мин | растет↑ | макс | убывает↓ | мин | растет↑ |
Получается 4 точки где производная равна 0 и меняет свой знак, а значит функция имеет "горбы" максимум или минимум - точек экстремума.
Универсальное правило: корни производной являются точками экстремума для самой функции!
Ответ: 4
Номер: 0ED279
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−9;8). Найдите точку экстремума функции f(x) на отрезке [−3;3].
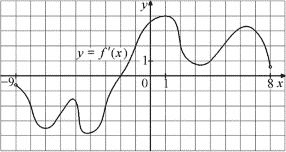
Ответ:
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, точки экстремума функции будут там, где производная равна 0.
Универсальное правило: корни производной являются точками экстремума для самой функции!
Это только точка -2
Ответ: -2
Номер: 720371
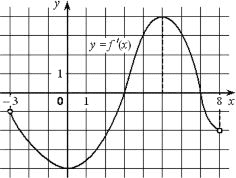
На рисунке изображён график функции y=f´(x)− производной функции f(x), определённой на интервале (−3;8). Найдите точку максимума функции f(x).
Ответ:
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или, наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, точки экстремума функции будут там, где производная равна 0. Причем нас интересует 0, где до него была производная положительная, а потом отрицательная, так как это будет максимум функции, где она росла, а потом стала уменьшаться. Это точка 7
Ответ: 7
Номер: FFD023
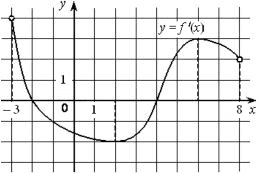
На рисунке изображён график функции y=f´(x)− производной функции f(x), определённой на интервале (−3;8). Найдите точку минимума функции f(x).
Ответ:
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или, наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x.
Делаем вывод, точки экстремума функции будут там, где производная равна 0. Причем нас интересует 0, где до него была производная отрицательная, а потом положительная, так как это будет минимум функции, где она убывала, а потом стала расти. Это точка 4
Ответ: 4
Номер: 453C87
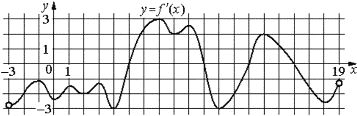
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−3;19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−2;15].
Ответ:
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или, наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, точки экстремума функции будут там, где производная равна 0. Причем нас интересует 0, где до него была производная положительная, а потом отрицательная, так как это будет максимум функции, где она росла, а потом стала уменьшаться, на отрезке [−2;15]. Это точки 10 и 16, но берем до 15, то есть всего 1 точка.
Ответ: 1
Номер: 25CE62
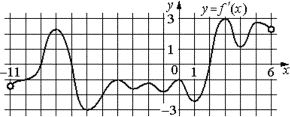
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−11;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−6;4].
Ответ:
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x.
Делаем вывод, точки экстремума функции будут там, где производная равна 0. Причем нас интересует 0, где до него была производная отрицательная, а потом положительная, так как это будет минимум функции, где она убывала, а потом стала расти принадлежащих отрезку [−6;4]. Это одна точка 2.
Ответ: 1
Номер: 7D7A50
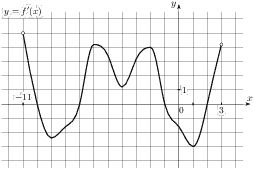
На рисунке изображен график y=f´(x) — производной функции f(x), определенной на интервале (−11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Ответ:
Промежутки возрастания функции соответствуют положительному значению производной.
Наибольший от -7 до -1 по оси х равен 6
7 - 1 =6
Ответ: 6
Номер: mathege
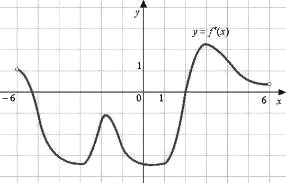
На рисунке изображен график y=f´(x) — производной функции f(x), определенной на интервале (−6;6). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ:
Промежутки возрастания функции соответствуют положительному значению производной. У нас производная положительна на участке от 2 до 6, где в точке в точке 2 равна 0, тогда сумма целых будет равна:
2+3+4+5= 14
6 не берем, так как она не включена в отрезок. -6 тоже, и -5 не берем, до нее график не достает.
2 берем, хотя по сути это точка экстремума, где функция ни туда ни сюда... по хорошему составителям график надо было хоть немного сместить левее точки 2
Ответ:14
Номер: mathege 6429
Эскиз обычной функции
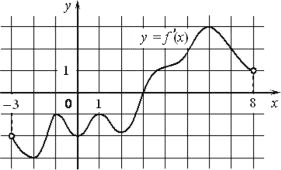
На рисунке изображён график y=f´(x) производной функции f(x), определённой на интервале (−3;8). В какой точке отрезка [−2;3] функция f(x) принимает наименьшее значение?
Ответ:
Необходимо, по сути, найти точку минимума, она будет в точке экстремума функции, если таковая есть на этом участке, когда производная меняет свой знак с минуса на плюс. Точка, удовлетворяющая нашим условиям по отрезкам, это точка 3.
Ответ: 3
Номер: 16B2FF
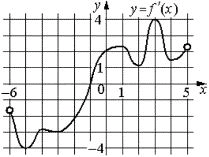
На рисунке изображен график y=f´(x) — производной функции f(x), определенной на интервале (−6;5). В какой точке отрезка [−5;−1] функция f(x) принимает наибольшее значение?
Ответ:
Необходимо по сути найти точку максимума, она будет в точке экстремума функции, если таковая есть на участке, когда производная меняет свой знак с плюса на минус. У нас такого экстремума нет, но есть минусовые значения производной на участке [−5;−1]. И так как это минус, то получается функция убывала на всем участке, а наибольшее значение значит имела вначале участка. Точка, удовлетворяющая нашим условиям, точка -5.
Ответ: -5
Номер: 4478
На рисунке изображён график y=f´(x) — производной функции f(x), определенной на интервале (−9;2). В какой точке отрезка [−8;−4] функция f(x) принимает наибольшее значение?
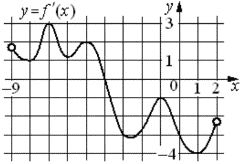
Ответ:
Необходимо по сути найти точку максимума, она будет в точке экстремума функции, если таковая есть на участке.
У нас это точка - 4
Ответ: -4
Номер: 4499
На рисунке изображён график y=f´(x) производной функции f(x), определённой на интервале (−2;9). В какой точке отрезка [2;8] функция f(x) принимает наименьшее значение?
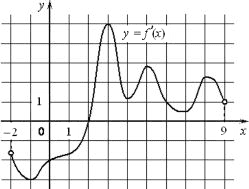
Ответ:
Необходимо по сути найти точку минимума, она будет в точке экстремума функции, если таковая есть на участке. При этом на отрезке [2;8] у нас экстремум именно в точке 2, где отрицательные значения меняются на положительные, то есть точка минимума.
Ответ: 2
Номер: 12659F
Геометрический смысл производной
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
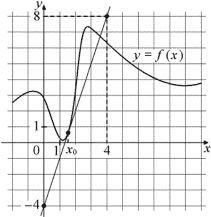
Ответ:
Геометрический смысл производной: f(x0)=k=tg α
По факту нам надо найти крутизну касательной, которая как раз и будет определять значение производной.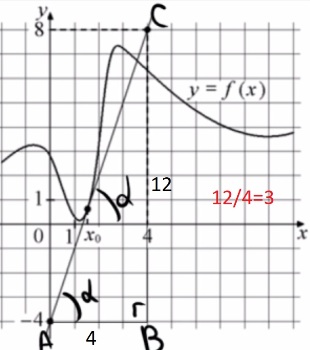
1) Построим прямоугольный треугольник с углом α = ∠CAB. α - угол между касательной и осью x
2) tgα = 12/4=3
3) f´(x) = 3
Ответ: 3
Номер: 56F47A
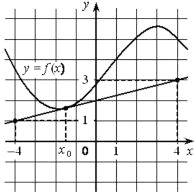
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ:
Геометрический смысл производной: f(x0)=k=tg α
1) Построим прямоугольный треугольник с углом α (гипотенуза это касательная, а вершины (-4;1) и (0;2), α - угол между касательной и осью x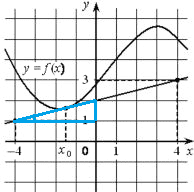
2) `tgα = 1/4=0,25`
3) f`(x) = 0,25
Ответ: 0,25
Номер: C70016
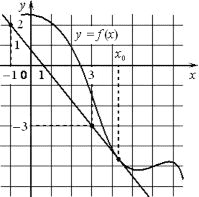
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ:
Геометрический смысл производной: f(x0)=k=tg α
1) Построим прямоугольный треугольник с углом α (гипотенуза это касательная, а вершины (-1;2), (3; -3) α - угол между касательной и осью x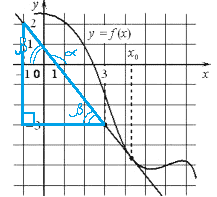
Но α получился тупым углом, значит невозможно построить прямоугольный треугольник.
`tgα=-tgβ`, где β - смежный угол
2) `tgβ = 5/4=1,25`
3) f`(x) = -1,25 так как касательная направлена вниз, то производная имеет отрицательный знак
Ответ: -1,25
Номер: 5D7FC4
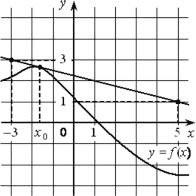
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ:
Геометрический смысл производной: f(x0)=k=tg α
1) Построим прямоугольный треугольник с углом α (гипотенуза это касательная, а вершины (-3; 3), (5; 1) α - угол между касательной и осью x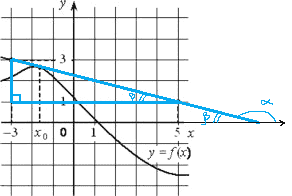
2) tgα = 2/8=0,25
3) f`(x) = - 0,25 так как касательная направлена вниз, то производная имеет отрицательный знак
Ответ: -0,25
Номер: E0C82C
Физический смысл производной
`S´(t)=v(t)`
`v´(t)=a(t)`
Производные:
`C´=0`
`x´=1`
`(Cx)´=C`
`(x^n)´=n*x^(n-1)`
Материальная точка движется прямолинейно по закону `x(t)=1/2t^2+4t+27`, где x – расстояние от точки отсчёта в метрах, t− время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=2 с.
Ответ:
`C´=0`
`(Cx)´=C`
`(x^n)´=n*x^(n-1)`
`x(t)=1/2t^2+4t+27`
`x´(t)=v(t)=1/2*2t+4+0`
`v(2)=1/2*2*2+4=6`
Ответ: 6
Номер: 8EAF19
Материальная точка движется прямолинейно по закону `x(t)=1/6t^3−2t^2+6t+250`, где x− расстояние от точки отсчёта в метрах, t− время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 96 м/с?
Ответ:
`C´=0`
`(Cx)´=C`
`(x^n)´=n*x^(n-1)`
`x(t)=1/6t^3−2t^2+6t+250`
`x´(t)=v(t)=1/6*3*t^2−2*2*t+6=96`
`v(t)=1/2*t^2−4t+6=96`
`1/2*t^2−4t+6=96`
`t^2/2−4t-90=0`
`t^2−8t-180=0`
`t_1=18`
`t_2=-10` - отрицательное значение не принимаем во внимание
Ответ: 18
Номер: D14B5E
Сравнение значений тангенсов
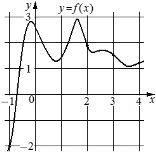
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки −1, 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ:
В точках -1 и 4 производная положительна (график растет). Причем, чем выше рост функции (чем ближе линия к вертикальной), тем больше производная, тогда это точка x= -1.
Ответ: -1
Для понимания: в точке 4 угол графика с осью х примерно 30°, `tg30°=1/sqrt3`; в точке -1 угол наклона графика около 60°, `tg60°=sqrt3`, что больше, чем tg30°, значит и производная больше.
Номер: 56EA1A
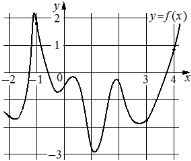
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки −2, −1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ:
Производная отрицательна в точках -2 и -1.
Производная максимально отрицательная при максимальном убывании функции (линия графика ближе к вертикальной), это точка -1
Ответ: -1
Для понимания: в точке -1 угол графика с осью х примерно 120°, `tg120°=-sqrt3`; в точке -2 угол наклона графика около 150°, `tg150°=-1/sqrt3`, что меньше, чем tg120°, значит и производная больше.
Номер: 099555
Касательная параллельна или совпадает
На рисунке изображён график функции y=f(x), определённой на интервале (−4;13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14.
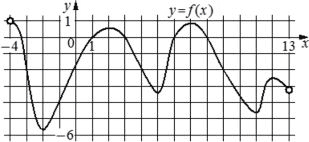
Ответ:
Прямая y=14 не включает в себя значения x, то есть она параллельна оси x, не важно какое у него значение, но y всегда равен 14.
При этом нам надо найти касательные, параллельные ей. По факту, это будут точки экстремума, когда касательные горизонтальны. У нас таких 6 "горбов и впадин", то есть 6 точек.
Ответ: 6
Не всегда данная в условии прямая параллельна оси х. Поэтому, универсальный способ решения:
1. y=kx+b
У прямой y=14 k=0.
2. Условия параллельности двух прямых: k одинаковые, а b разные. ⇒ k касательной = 0
3. `k=f´(x_0)` - геометрический смысл производной
f´(x_0)=0, а производная равна нулю там, где у обычной функции вершины и впадины.
Номер: 935729
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−4;6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней.
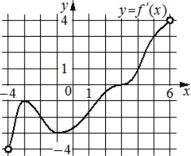
Ответ:
1) Итак, у нас прямая y=3x, то условно можно сказать так, отношение оси ординат y в три раза меньше, чем абсцисс x. Угол такой касательной нетрудно посчитать через tg.
tgα=3/1=3 это примерно 72 градуса к оси x. По сути нам интересен коэффициент возрастания К по оси у при увеличении x.
К = 3.
2) Причем если нам надо найти касательную к функции, то она как раз и будет отражать динамику производной, то есть имеющийся график. Так вот, на имеющемся графике ищем такие точки, где наша условная касательная будет проведена к графику и при этом соответствовать
К = 3
3) И здесь, вспоминая вычисление производной, найдем ее для y=3x
y´ = 3
При этом x = 5. (видно из графика пересечение y=3 только в одной точке (5;3))
Ответ: 5
Второй вариант объяснения:
1. y=3x ⇒ k=3
2. Условия параллельности двух прямых: k одинаковые, а b разные. ⇒ k касательной = 3
3. `k=f´(x_0)` - геометрический смысл производной
`f´(x_0)=3=y`
Ищем по графику точку, в которой y=3. Это точка (5;3). x = 5
Ответ: 5
Номер: 345AAE
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−4;13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=−2x−10 или совпадает с ней.
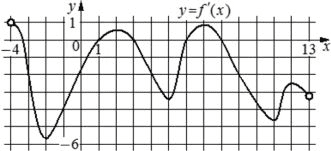
Ответ:
1) Итак, у нас прямая y=−2x−10, то условно можно сказать так, отношение оси ординат y в 2 раза меньше, чем абсцисс x. Угол такой касательной нетрудно посчитать через tg. tgα=-2/1=-2. По сути нам интересен коэффициент возрастания К по оси у при увеличении x. К = -2.
2) Причем если нам надо найти касательную к функции, то она как раз и будет отражать динамику производной, то есть имеющийся график. Так вот на имеющемся графике ищем такие точки, где наша условная касательная будет проведена к графику и при этом соответствовать
К = -2
3) И здесь вспоминая вычисление производной найдем ее для y=−2x−10
y´ = -2
В итоге нам получается надо найти точки пересечения этого графика с y = -2
Получается так: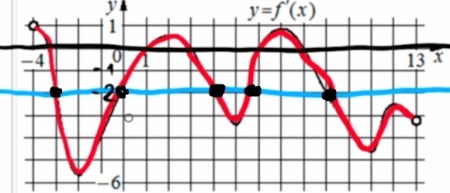
Пересечение y = -2 с графиком в 5 точках.
Ответ: 5 точек
Второй вариант объяснения:
1. y=−2x−10 ⇒ k=-2
2. Условие параллельности или совпадения двух прямых: k одинаковые. ⇒ k касательной = -2
3. `k=f´(x_0)` - геометрический смысл производной
`f´(x_0)=-2=y`
Ищем по графику точки, в которых y=-2. Таких точек 5.
Ответ: 5
Номер: ADB310
На рисунке изображён график y=f´(x)− производной функции f(x), определённой на интервале (−2;11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.
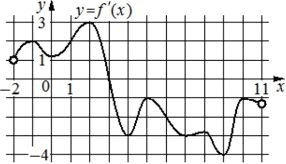
Ответ:
1) Итак, у нас прямая y=f(x), то можно сказать, изменение у прямо пропорционально изменению х.
2) Коэффициент касательной равен производной от функции
К = 0
В итоге, нам надо найти точки пересечения этого графика с y = 0
Это одна точка 3
Ответ: 3
Второе объяснение:
1. Ось абсцисс - это ось ох. Ее уравнение y=0.
y=kx+b, k=0
2. Условие параллельности или совпадения двух прямых: k одинаковые. ⇒ k касательной = 0
3. `k=f´(x_0)` - геометрический смысл производной
`f´(x_0)=0=y`
Проводим горизонтальную прямую через y=0 (то есть совпадающую с осью ох).
Абсцисса точки пересечения этой прямой с графиком производной и будет ответом.
х = 3
Ответ: 3
Номер: 7C42F8
Прямая `y=7x−5` параллельна касательной к графику функции `y=x^2+6x−8`. Найдите абсциссу точки касания.
Ответ:
1) Итак, у нас прямая `y=7x−5`, то можно найти коэффициент возрастания или уменьшения найдя производную.
y´=7, К = 7
2) Коэффициент касательной равен коэффициенту функции К = 7
В итоге нам получается надо найти точки пересечения этого графика с y = 7
Приравниваем нашу производную функции к y=7
`y=x^2+6x−8`
`y´=2x+6`
`7=2x+6`
`2x=1`
`x=1/2=0,5`
Ответ: 0,5
Второе объяснение:
1. Прямая `y=7x−5`, а y=kx+b ⇒ k прямой=7
2. Условия параллельности двух прямых: k одинаковые, а b разные. ⇒ k касательной = 7
3. `k=f´(x_0)` - геометрический смысл производной
`f´(x_0)=7`
Найдем производную для параболы `y=x^2+6x−8`
`C´=0`
`(Cx)´=C`
`(x^n)´=n*x^(n-1)`
`y´=2x_0+6`
`7=2x_0+6`
`2x_0=1`
`x_0=1/2=0,5`
Ответ: 0,5
Номер: mathege
Условие касания
Прямая `y=−4x−11` является касательной к графику функции `y=x^3+7x^2+7x−6`. Найдите абсциссу точки касания.
Ответ:
Составим два уравнения, причем в первом случае производную прямой приравняем к производной функции, так как динамика той и другой в точке касания будет одинаковой.
А во второй приравняем прямую к функции. Это все условия касания функции и прямой.
`{(-4=3x^2+7*2x+7),(-4x-11=x^3+7x^2+7x-6):}`
Получаем:
`-4=3x^2+7*2x+7`
`3x^2+14x+11=0`
`D=196-132=8^2`
`x=(-14±8)/6`
`x_1=-1`
`x_2=-11/3`
подставим во 2 уравнение, получаем
при
`x_1=-1`
`-4x-11=x^3+7x^2+7x-6`
`-4*-1-11=-1^3+7*-1^2+7*-1)-6`
`4-11=-1+7-7-6`
`-7=-7`
`x_2=-11/3` это уравнение не решается, не получаем нужное нам равенство, значит его исключаем. (можете проверить, но поверьте это так!)
Ответ: -1
Номер: ЕГЭ 2016
Прямая `y=−3x−8` является касательной к графику функции `ax^2+27x+7`. Найдите a.
Ответ:
Составим два уравнения, причем в первом случае производную прямой приравняем к производной функции, так как динамика той и другой в точке касания будет одинаковой.
А во второй приравняем прямую к функции
`{(-3=2ax+27),(−3x−8=ax^2+27x+7):}`
Из верхнего уравнения найдем a
`-30=2xa`
`a = (-30)/(2x)=(-15)/x`
Подставим в нижнее
`-3x-8=(-15)/x*x^2+27+7`
`-3x-8=12x+7`
`-15=15x`
`x=-1`
`a = -15/-1=15`
Ответ: 15
Номер: mathege
Прямая `y=9x+5` является касательной к графику функции `18x^2+bx+7`. Найдите b, учитывая, что абсцисса точки касания меньше 0.
Ответ:
Составим два уравнения, причем в первом случае производную прямой приравняем к производной функции, так как динамика той и другой в точке касания будет одинаковой.
А во второй приравняем прямую к функции
`{(9=18*2x+b),(9x+5=18x^2+bx+7):}`
Из верхнего уравнения найдем a
`b=9-36x`
Подставим в нижнее
`9x+5=18x^2+(9-36x)*x+7`
`9x+5=18x^2+9x-36x^2+7`
`18x^2=2`
`x^2=1/9`
x1=1/3 (не принимаем во внимание, так как по условию надо выбрать абсциссу точки касания меньше 0)
`x_2=-1/3`
`b=9-36(-1/3)=21`
Ответ: 21
Номер: mathege
Прямая `y=−3x−5` является касательной к графику функции `y=x^2+7x+c`. Найдите c.
Ответ:
Составим два уравнения, причем в первом случае производную прямой приравняем к производной функции, так как динамика той и другой в точке касания будет одинаковой.
А во второй приравняем прямую к функции
`{(-3=2x+7),(-3x-5=x^2+7x+c):}`
Из верхнего
`-10=2x`
`x=-5`
Подставляем в нижнее
`-3*(-5)-5=(-5)^2+7*(-5)+c`
`15-5=25-35+c`
`c = 20`
Ответ: 20
Номер: 7B24D9
Первообразная
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек функция f(x) положительна?
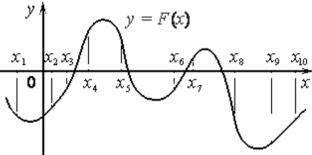
Ответ:
Если взять производную от первообразной, то получится обычная функция. По сути, это противоположность производной.
Если посмотреть на график обычной функции, тут первообразную F(x)можно считать за обычную функцию, а обычную функцию f(x) за производную. Все закономерности те же самые, что для графика обычной функции.
И вот значит для функции, те участки где есть возрастание первообразной будут положительные, а где убывание, будут отрицательные.
У нас рост первообразной наблюдается в точках:
x2, x3, x4, x6, x7, x9, x10 - 7 точек
Ответ: 7
Номер: 42A509
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек функция f(x) отрицательна?
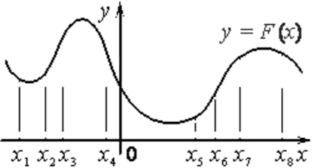
Ответ:
Если взять производную от первообразной, то получится обычная функция. По сути, первообразная - это противоположность производной.
Если посмотреть на график обычной функции, тут первообразную F(x)можно считать за обычную функцию, а обычную функцию f(x) за производную. Все закономерности те же самые, что для графика обычной функции.
И вот значит для функции, те участки где есть возрастание первообразной будут положительные, а где убывание, будут отрицательные.
У нас убывание первообразной наблюдается в точках:
x1, x4, x8 - 3 точки
Ответ: 3
Номер: DD57EB
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (−7;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−5;2].
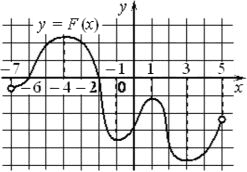
Ответ:
Если взять производную от первообразной, то получится обычная функция. По сути, первообразная - это противоположность производной.
Если посмотреть на график обычной функции, тут первообразную F(x)можно считать за обычную функцию, а обычную функцию f(x) за производную. Все закономерности те же самые, что для графика обычной функции.
И вот значит для функции, те участки, где есть возрастание, будут положительные, а где убывание, будут отрицательные.
То есть у нашей функции будет 0 тогда, когда у первообразной были экстремумы, тогда был переход у функции с плюса в минус или наоборот. У первообразной 4 экстремума, значит 4 точки (-4, -1, 1, 3) пересечения оси х. С учетом отрезка [−5;2] остается три точки.
Ответ: 3
Номер: 1E2DFC
На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(−1)−F(−8), где F(x)− одна из первообразных функции f(x).
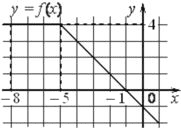
Ответ:
Если взять производную от первообразной, то получится обычная функция. По сути, первообразная - это противоположность производной.
И вот значит для функции, те участки где есть возрастание первообразной будут положительные, а где убывание, будут отрицательные.
У нас на участке -8 до - 5 не было изменения функции, которая является производной для первообразной при этом y=f(-8)=4. Это говорит возрастающей первообразной.
И для точки -1 будет так y=f(-1)=0.
То есть здесь можно говорить условно о линейном росте первообразной с последующим замедлением роста и выходом в экстремум.
Если скажем перевести это все в жизненные реалии, то это примерно так. Первоначально тело двигалось 3 секунды со скоростью 4 м/с, а потом каждую секунду началось сокращение скорости на 1 м/с, то есть появилось отрицательное ускорение, пока тело не остановилось в точке -1.
Так вот если соотнести F(−1)−F(−8) то это по факту прикинуть какой путь прошло тело. 4*3+4+3+2+1 то есть за первые 4 секунда 12 метров, потом за 5 , 4 метра, потом 3 и т.д.
Еще проще, можно просто посчитать площадь фигуры под графиком функции и до оси х. Это площадь трапеции.
`S = (3+7)/2 * 4 = 20`
Ответ: 20
Номер: ЕГЭ 2013, 2014
На рисунке изображён график некоторой функции y=f(x).
Функция `F(x)=1/2x^3−9/2x^2+14x−10`− одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
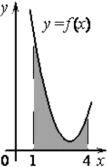
Ответ:
Площадь фигуры будет равна разности значений функции в ее крайних точках 1 и 4 по оси х. Используем формулу Ньютона-Лейбница.
`S = F(4)-F(1)`
`F(x)=1/2x^3−9/2x^2+14x−10`
`F(4)=1/2*4^3−9/2*4^2+14*4−10=1/2*64−9/2*16+14*4−10`
`F(1)=1/2*1−9/2*1+14*1−10`
`F(4)-F(1)=1/2*64−9/2*16+14*4−10-1/2*1−9/2*1+14*1−10=31,5-67,5+42=6`
Ответ: 6
Номер: ЕГЭ 2013
На рисунке изображён график некоторой функции y=f(x).
Функция `F(x)=−4/9x^3−34/3x^2−280/3x−18/5` — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
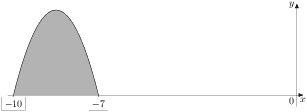
Ответ:
Площадь фигуры будет равна разности значений функции в ее крайних точках -10 и -7 по оси х. Используем формулу Ньютона-Лейбница.
`S = F(-7)-F(-10)`
`F(x)=−4/9x^3−34/3x^2−280/3x−18/5`
`F(-7)=−4/9*343−34/3*49−280/3*7−18/5`
`F(-10)=−4/9*1000−34/3*100−280/3*10−18/5`
`S = F(-7)-F(-10) = -657*4/9+51*34/3-3*280/3=-292+578-280=578-572=6`
Ответ: 6
Номер: ЕГЭ 2013

