Задание 16 в ОГЭ по математике - геометрия. Проверяется знание материала, касающегося окружности, кругов и их элементов. Задание с кратким ответом, в ответ идет число. Если посчитали правильно - получите 1 балл.
Типы заданий линейки 16 по ФИПИ
Касательная к окружности
![]() (скорее всего будет в этом году, в демо есть, в банке пока нет) 1. Касательные в точках A и B к окружности с центром O пересекаются под углом 58°. Найдите угол ABO. Ответ дайте в градусах.
(скорее всего будет в этом году, в демо есть, в банке пока нет) 1. Касательные в точках A и B к окружности с центром O пересекаются под углом 58°. Найдите угол ABO. Ответ дайте в градусах.
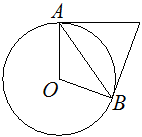
Решение:
 С
С
Обозначим точку пересечения касательных как С. ∠С по условию 58°
Касательные, проведённые к окружности из одной точки, равны, поэтому
AC=BC,
следовательно, треугольник ABC — равнобедренный.
Отсюда
∠CAB = ∠CBA = (180 - ∠ACB) / 2 = (180° - 58°) / 2 = 61°
Касательные перпендикулярны радиусу, проведенному в точку касания, следовательно
∠CBO = 90°
∠ABO = ∠CBO - ∠CBA = 90° - 61° = 29°
Ответ: 29
Еще вариант решения:
∠С по условию 58°
OA и OB - радиусы, значит △OAB равнобедренный и ∠OAB=∠OBA
Сумма углов четырехугольника 360°. 2 угла прямые (так как СА и СВ - касательные, а они всегда под прямым углом к радиусу) и дают в сумме 180°.
∠AOB = 180° - 58° = 122°
Сумма углов треугольника 180°
∠OAB=∠OBA=(180° - 122°)/2 = 58/2 = 29°
Ответ: 29
![]() 2. В угол C величиной 87° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
2. В угол C величиной 87° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.
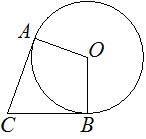
Решение:
∠AOB = 180° - 87° = 93°
Ответ: 93
Центральные и вписанные углы
3. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 64°. Ответ дайте в градусах.
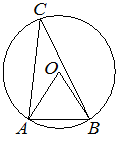
Решение:
Угол AOB является центральным углом, ∠ACB — вписанным.
Оба угла опираются на одну и ту же дугу, следовательно, ∠ACB в два раза меньше ∠AOB.
∠ACB = ∠AOB / 2 = 64° / 2 = 32°.
Ответ: 32
4. В окружности с центром в точке O отрезки AC и BD – диаметры. Угол AOD равен 72°. Найдите угол ACB. Ответ дайте в градусах.
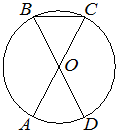
Ответ:
Углы АОD и ВОС - вертикальные, значит ∠АОD = ∠ВОС = 72°
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
Сумма углов треугольника равна 180°.
∠АСВ = ∠ОСВ = (180° - 72°) / 2 = 108° / 2 = 54°
Ответ: 54
5. Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 25°. Найдите угол AOD. Ответ дайте в градусах.
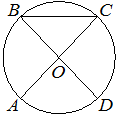
Ответ:
Поскольку АС и ВD - диаметры, ВО = ОС, то есть треугольник ВОС - равнобедренный, значит его углы при основании равны.
∠АСВ = ∠ОСВ = ∠ОВС = 25°
Сумма углов треугольника равна 180°.
∠ВОС = 180° - 2*25° = 130°
Углы АОD и ВОС - вертикальные, значит они равны:
∠АОD = ∠ВОС = 130°
Ответ: 130
6. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=55° . Найдите ∠NMB. Ответ дайте в градусах.
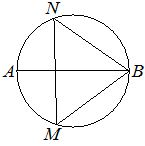
Ответ:
Угол NBA — вписанный, поэтому он равен половине дуги, на которую он опирается.
Следовательно, дуга AN = 2∠NBA = 2 · 55° = 110°
Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°,
откуда дуга NB = 180° − 110° = 70°
Угол NMB — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен
70°/2 = 35°
Ответ: 35
![]() 7. Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=49° и ∠OAB=34°. Найдите ∠BCO. Ответ дайте в градусах.
7. Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=49° и ∠OAB=34°. Найдите ∠BCO. Ответ дайте в градусах.
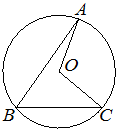
Ответ:
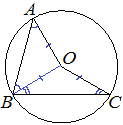 Проведём радиус OB.
Проведём радиус OB.
Рассмотрим треугольник AOB:
AO = OB, следовательно, углы при основании равнобедренного треугольника
∠OAB = ∠ABO = 34°.
Рассмотрим треугольник BOC:
BO = OC, следовательно,
∠BCO = ∠OBC = ∠ABC − ∠ABO = 49° −34° = 15°.
Ответ: 15
![]() 8. На окружности отмечены точки A и B так, что меньшая дуга AB равна 136°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна 136°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
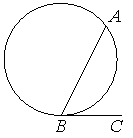
Ответ:
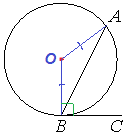 Проведем отрезки из центра окружности к точкам А и В.
Проведем отрезки из центра окружности к точкам А и В.
∠AOB - центральный, следовательно равен градусной мере дуги,
т.е. ∠AOB=136°.
Рассмотрим треугольник AОB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник равнобедренный. Следовательно,
∠OAB=∠OBA (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠OBA = 180°
∠OAB = ∠OBA = (180-136) : 2 = 44 : 2 = 22°
∠OBC = 90° (по свойству касательной он перпендикулярен радиусу).
∠ABC = ∠OBC - ∠OBA
∠ABC = 90° - 22°= 68°
Ответ: 68
Еще варианты заданий такого типа с ФИПИ >>
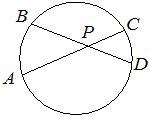
![]() 9. Хорды AC и BD окружности пересекаются в точке P, BP =20, CP =30, DP =24. Найдите AP.
9. Хорды AC и BD окружности пересекаются в точке P, BP =20, CP =30, DP =24. Найдите AP.
Ответ:
PC = DP
BP АР
АР = BP*DP
PC
AP = (20*24)/30=480/30=16
Ответ: 16
Еще задания того же типа с ФИПИ >>
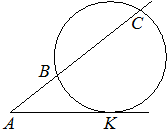
![]() 10. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=7, AC=28. Найдите AK.
10. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=7, AC=28. Найдите AK.
Ответ:
По теореме о касательной и секущей:
AK2=AB*AC
AK2=7*28
AK2=196
AK=√196=14
Ответ: 14
![]() 11. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, BC=18 . Найдите AK.
11. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, BC=18 . Найдите AK.

Ответ:
По теореме о касательной и секущей:
AK2=AB*AC
АС=АВ+ВС=6+18=24
AK2=6*24
AK2=144
AK=√144=12
Ответ: 12
Еще задания такого типа от ФИПИ>>
Вписанная окружность
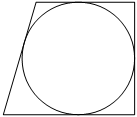
12. Радиус окружности, вписанной в прямоугольную трапецию, равен 38. Найдите высоту этой трапеции.
Ответ:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*38=76
Ответ: 76
13. Сторона квадрата равна 46. Найдите радиус окружности, вписанной в этот квадрат.

Ответ:
Если провести линию через центр окружности, параллельно стороне квадрата, она окажется диаметром окружности. Значит, ее радиус равен половине стороны квадрата.
46/2 = 23
Ответ: 23
14. Найдите площадь квадрата, описанного вокруг окружности радиуса 11.

Ответ:
Так как радиус 11, значит диаметр 22, и он равен длине стороны квадрата.
Sкв.= 222 = 484
Ответ: 484
15. Радиус вписанной в квадрат окружности равен 10√2 . Найдите диагональ этого квадрата.
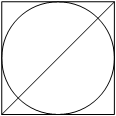
Ответ:
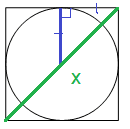
Запишем равенство, используя теорему Пифагора
х=2√((10√2)2+(10√2)2)=2√(100*2+100*2)=2*20=40
Ответ: 40
Типовые задания с другими числами >>
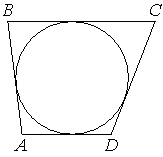
16. Четырёхугольник ABCD описан около окружности, AB=14, BC=15, CD=23. Найдите AD.
Ответ:
По второму свойству вписанной в четырехугольник окружности: если в четырехугольник можно вписать окружность, то суммы его противолежащих сторон равны.
AB+CD=BC+AD
AD=AB+CD-ВС
AD= 14 + 23 - 15 = 22
Ответ: 22
17. Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5. Найдите площадь этого треугольника.
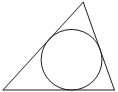
Ответ:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 56/2 * 5 = 140
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 140
![]() 18. Радиус окружности, вписанной в равносторонний треугольник, равен 11. Найдите высоту этого треугольника.
18. Радиус окружности, вписанной в равносторонний треугольник, равен 11. Найдите высоту этого треугольника.
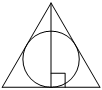
Ответ:
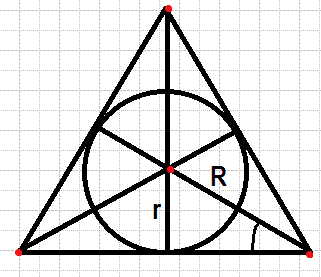
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
11*3=33
Ответ: 33
19. Радиус окружности, вписанной в равносторонний треугольник, равен 11√3 . Найдите длину стороны этого треугольника.

Решение:

Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(11\surd3\right)^2=\left(11\surd3\right)^2+x^2\\x^2=\;3\left(11\surd3\right)^2\\х^2=3\ast121\ast3\\х=\sqrt{1089}\\х=33$
33*2=66
Ответ: 66
20. Сторона равностороннего треугольника равна 4√3 . Найдите радиус окружности, вписанной в этот треугольник.

Ответ:
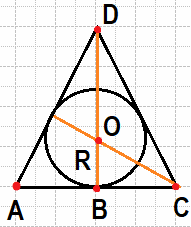
Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.
$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}$
Подставляем в формулу значение и считаем.
R=AC/2√ 3=4√ 3/2√ 3=2
Ответ: 2
Описанная окружность
21. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 38°, угол CAD равен 54°. Найдите угол ABC. Ответ дайте в градусах.
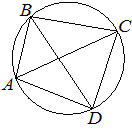
Ответ:
Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 54°
∠ABC = ∠ABD + ∠CBD = 38° + 54° = 92°
Ответ: 92
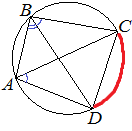
22. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132°, угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.
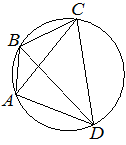
Ответ:

Угол CAD и угол CBD — вписанные углы, опирающиеся на одну дугу, а значит, они равны:
∠CBD = ∠CAD = 80°
∠ABC = ∠ABD + ∠CBD, отсюда
∠ABD = ∠ABC - ∠CBD
∠ABD = 132° - 80° = 52°
Ответ: 52
![]() 23. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
23. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
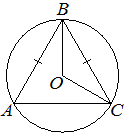
Ответ:
Сумма углов треугольника равна 180°.
Треугольник ABC — равнобедренный, следовательно
∠BAC = ∠BCA = (180° - ∠ABC) / 2
Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается.
Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается.
Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
∠BOC = 2∠BAC = 2 * (180° - ∠ABC) / 2 = 180° - ∠ABC
∠BOC = 180° - 57° = 123 °.
Ответ: 123
24. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах.
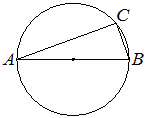
Ответ:
Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол ACB равен 90°.
Сумма углов треугольника равна 180°, значит
∠ABC = 180° - 90° - 9° = 81°
Ответ: 81
25. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 12,5. Найдите AC, если BC=24.
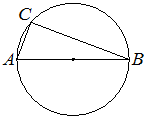
Ответ:
Если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.
AB = 12,5*2 = 25
По теореме Пифагора
AB2 = АС2 + ВС2
АС2 = AB2 - ВС2
АС2 = 252 - 242
АС2 = 49
АС = 7
Ответ: 7
26. Угол A четырёхугольника ABCD, вписанного в окружность, равен 62°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
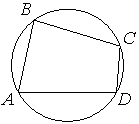
Ответ:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 62° = 118°
Ответ: 118
27. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 111°. Найдите угол C этой трапеции. Ответ дайте в градусах.
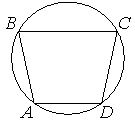
Ответ:
Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°:
∠A + ∠C = 180°, отсюда
∠C = 180 - ∠A = 180° - 111° = 69°
Ответ: 69
28. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 76°. Найдите угол B этой трапеции. Ответ дайте в градусах.

Ответ:
Посмотрим на основания трапеции как на параллельные прямые, а на боковую сторону AB как на секущую.
Тогда углы A и B - внутренние односторонние, а сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°, значит:
∠A + ∠B = 180°
∠B = 180° - ∠A
∠B = 180° - 76° = 104°
Ответ: 104
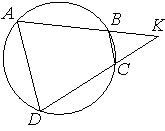
![]() 29. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
29. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Ответ:
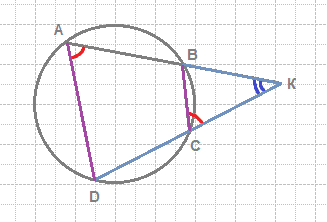
По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.
Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD (это мы определили ранее)
Следовательно, данные треугольники подобны (по первому признаку подобия).
Тогда:
BK = BC
DK AD
AD = DK*BC
BK
AD = 12*6
8
AD = 9
Ответ: 9
30. Сторона квадрата равна 14√2 . Найдите радиус окружности, описанной около этого квадрата.

Ответ:
Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.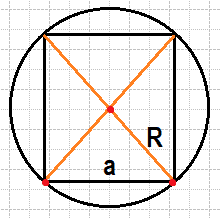
Получаем:
a2=R2+R2
a2=2R2
R=a/√ 2
Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.
R=a/√ 2=14√ 2/√ 2=14
Ответ: 14
![]() 31. Радиус вписанной в квадрат окружности равен 20√2 . Найдите радиус окружности, описанной около этого квадрата.
31. Радиус вписанной в квадрат окружности равен 20√2 . Найдите радиус окружности, описанной около этого квадрата.
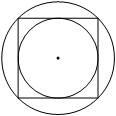
Ответ:
Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.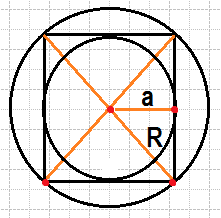
Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√ 2
Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.
R=20√ 2*√ 2=20*2=40
Ответ: 40
![]() 32. Радиус окружности, описанной около квадрата, равен 6√2 . Найдите радиус окружности, вписанной в этот квадрат.
32. Радиус окружности, описанной около квадрата, равен 6√2 . Найдите радиус окружности, вписанной в этот квадрат.

Ответ:

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$
Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.
a=R/√ 2=6√ 2/√ 2=6
Ответ: 6
33. Радиус окружности, описанной около квадрата, равен 32√2 . Найдите длину стороны этого квадрата.

Ответ:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны, используя теорему Пифагора. Записываем.
$\left(2\ast32\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast32\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast32\surd2\right)^2}2}\\х=\frac{2\ast32\surd2}{\sqrt2}=64$
Ответ: 64
![]() 34. Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
34. Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
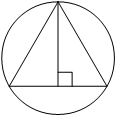
Ответ:
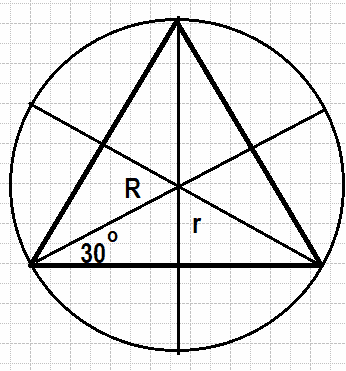
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
16*1.5=24
Ответ: 24
35. Сторона равностороннего треугольника равна 18√3 . Найдите радиус окружности, описанной около этого треугольника.

Ответ:
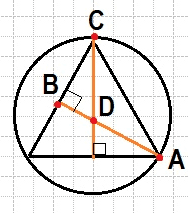
Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.
$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}$
Подставляем значение и вычисляем.
R = 18√ 3/√ 3=18
Ответ: 18
36. Радиус окружности, описанной около равностороннего треугольника, равен 11√3 . Найдите длину стороны этого треугольника.

Ответ:

Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(11\surd3\right)^2=\left(\frac{11\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(11\surd3\right)^2}4-\frac{\left(11\surd3\right)}4^2\\х^2=\frac{3\left(11\surd3\right)^2}4\\х=\sqrt{\frac{3\ast121\ast3}4}\\х=\sqrt{\frac{1089}4}=\frac{33}2=16.5$
16.5*2=33
Ответ: 33
Расширенная теорема синусов
37 (2025). В треугольнике ABC угол C равен 45°, AB=8√2. Найдите радиус окружности, описанной около этого треугольника.
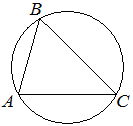
Ответ:
Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}$
sin45°=√ 2/2
Подставляем в формулу значение:
R=AB/2sin∠C=
= 8√ 2 *2
2√ 2 = 8
Ответ: 8
38 (2025). В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
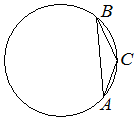
Ответ:
Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}$
Подставляем в формулу значение:
R=AB/2sin∠C=
= 14√ 2 *2
2√ 2 = 14
Ответ: 14
Длина окружности и площадь круга
![]() 39. На окружности с центром O отмечены точки A и B так, что ∠AOB=120°. Длина меньшей дуги AB равна 67. Найдите длину большей дуги.
39. На окружности с центром O отмечены точки A и B так, что ∠AOB=120°. Длина меньшей дуги AB равна 67. Найдите длину большей дуги.
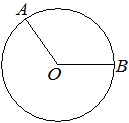
Ответ:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 120°.
Значит градусная мера большей дуги равна
360° - 120° = 240°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
120° - 67
240° - х
120 = 67
240 х
x = 240*67
120
x = 16080
120
х = 134
Ответ: 134
![]() 40. Площадь круга равна 123. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
40. Площадь круга равна 123. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
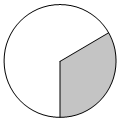
Ответ:
Круг составляет 360°, его площадь равна 123.
Пусть х - площадь сектора, центральный угол которого равен 120°. Составим пропорцию.
угол площадь
360° - 123
120° - х
360/120 = 123/x
х = (123 * 120) / 360 = 14760 / 360 = 41
Значит, площадь сектора равна 41 кв. единица.
Ответ: 41
Еще про площадь сектора круга >>
Неразобранное
2025 41. Точка 𝑂 является серединой стороны 𝐶𝐷 квадрата 𝐴𝐵𝐶𝐷. Радиус окружности с центром в точке 𝑂, проходящей через вершину 𝐴, равен 2. Найдите площадь квадрата 𝐴𝐵𝐶𝐷.
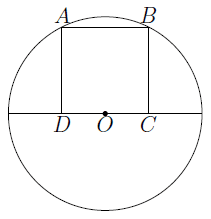
Ответ:
Проведем отрезок ОА, он же радиус.
Так как DO - половина стороны DC, а все стороны квадрата равны, значит DO - также половина любой другой стороны, в частности: DO-половина AD.
Рассмотри треугольник AOD: он- прямоугольный, DO-половина AD, AO=2 (по условию). Пусть DO=x, тогда AD=2x.
По теореме Пифагора: `AD^2+DO^2=AO^2`
Тогда: `(2x)^2+x^2=2^2`
`4x^2+x^2=4`
`5x^2=4`
`x^2=4/5`
`x=2/sqrt5`
Тогда `AD=2*2/sqrt5=4/sqrt5`
Тогда площадь квадрата= `4/sqrt5*4/sqrt5=3,2`
Ответ: 3,2
Лайфхак: умножь число в условии на себя, полученное умножь на 0,8.
Номер: 85B940
2026 42. В окружность с центром в точке О вписан равносторонний треугольник. Расстояние от точки О до сторон треугольника равно `5sqrt3`. Найдите сторону треугольника.
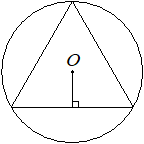
Решение:
Для равностороннего треугольника со стороной a, радиусом вписанной окружности r и радиусом описанной окружности R имеют место соотношения:
`h=sqrt3/2 a=1,5R=3r`
`h=3r=3*5sqrt3=15sqrt3`
`a=(2h)/sqrt3`=30
Ответ: 30
2026 43. Синус угла между стороной и диагональю прямоугольника равен 0,6. Диаметр описанной около него окружности равен 10. Найдите площадь прямоугольника.
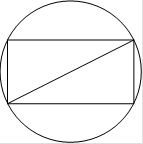
Решение:
Для любого прямоугольника диаметр описанной около него окружности равен его диагонали:
d=10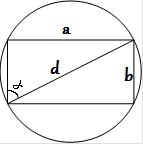
Синус угла в прямоугольном треугольнике - это отношение противолежащего катета к гипотенузе:
`sinα=a/d`
`a=d*sinα=10*0,6=6`
По теореме Пифагора `d^2=a^2+b^2`
`b^2=d^2-a^2=100-36=64`
`b=8`
Площадь S=6*8=48
Ответ: 48
2026 44. Диагональ АС ромба АВСD равна 48, а `tgBCA=7/24`. Найдите радиус окружности, вписанной в ромб.
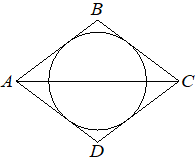
Решение:
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Рассмотрим прямоугольный треугольник BOC (O — точка пересечения диагоналей).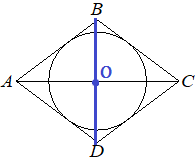
Дано:
AC = 48 ⇒ OC = 24
`∠BCA = ∠BCO`
`tg∠BCO = (BO)/(OC) = 7/24` ⇒
`BO = 24*7/24 = 7`
Сторона ромба: \( BC = \sqrt{OC^2 + BO^2} = \sqrt{24^2 + 7^2} = \sqrt{576 + 49} = \sqrt{625} = 25 \).
Площадь ромба: \( S = \dfrac{AC \cdot BD}{2} = \dfrac{48 \cdot (2 \cdot 7)}{2} = \dfrac{48 \cdot 14}{2} = 336 \).
Площадь также равна полупроизведению периметра на радиус вписанной окружности: \( S = \dfrac{1}{2} P r \), где \( P = 4 \cdot 25 = 100 \).
\( 336 = \dfrac{1}{2} \cdot 100 \cdot r \Rightarrow 336 = 50r \Rightarrow r = \dfrac{336}{50} = \dfrac{168}{25}=6,72 \).
Ответ: 6,72
Типы заданий по СтатГраду с краткими ответами
Касательная, хорда, секущая, радиус
1. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, BC = 72. Найдите AK .

Ответ:
15
2. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 8, BC = 24. Найдите AK .

Ответ:
16
3. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 5, BC =15. Найдите AK.

Ответ:
10
4. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, BC =16. Найдите AK.

Ответ:
6
5. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.
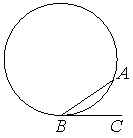
Ответ:
36
6. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
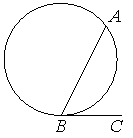
Ответ:
46
7. На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.
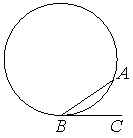
Ответ:
28
8. На окружности отмечены точки A и B так, что меньшая дуга AB равна 152° . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
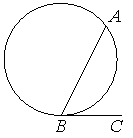
Ответ:
76
Центральные и вписанные углы
9. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 113°. Ответ дайте в градусах.
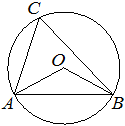
Ответ:
56,5
10. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.
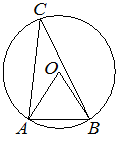
Ответ:
29,5
11. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 167°. Ответ дайте в градусах.
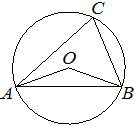
Ответ:
83,5
12. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах.
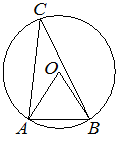
Ответ:
23,5
13. В угол C величиной 157° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
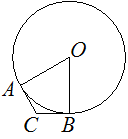
Ответ:
23
14. В угол C величиной 18° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
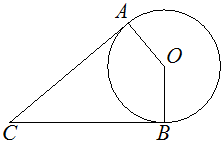
Ответ:
162
15. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
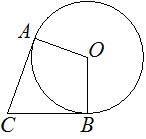
Ответ:
97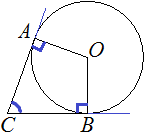
16. В угол C величиной 133° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
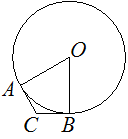
Ответ:
47
Окружность, описанная вокруг многоугольника
17. Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.

Ответ:
9
18. Радиус окружности, описанной около равностороннего треугольника, равен 18. Найдите высоту этого треугольника.

Ответ:
27
19. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:
148
20. Угол A трапеции ABCD с основаниями AD и BC , вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.

Ответ:
99
21. Радиус окружности, описанной около квадрата, равен 16√2 . Найдите длину стороны этого квадрата.

Ответ:
32
22. Радиус окружности, описанной около квадрата, равен 28√2 . Найдите длину стороны этого квадрата.

Ответ:
56
23. Угол A четырёхугольника ABCD, вписанного в окружность, равен 112° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
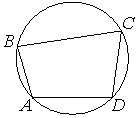
Ответ:
68
24. Угол A четырёхугольника ABCD, вписанного в окружность, равен 56° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

Ответ:
124
25. Четырёхугольник ABCD описан около окружности, AB =12, BC = 6, CD =13. Найдите AD.
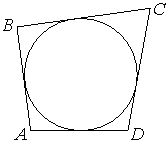
Ответ:
19
26. Четырёхугольник ABCD описан около окружности, AB =11, BC = 7, CD =12. Найдите AD.

Ответ:
16
27. Угол A четырёхугольника ABCD , вписанного в окружность, равен 37° . Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
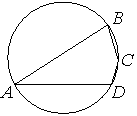
Ответ:
143

