Задание 6 300-е варианты и задание 9 100-е варианты - это геометрия, задачи про треугольники и четырехугольники. Для вас собрали все задания этой линейки из открытого банка заданий ФИПИ.
Тип структуры комплекта 300-e варианты. Позиции заданий 6. Или 100-e варианты 9. Со справочные материалами к приведенным далее заданиям можно ознакомиться ЗДЕСЬ.
Все задания этого типа с ФИПИ для ГВЭ 9
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11. Найдите длину основания BC.
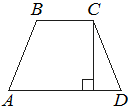
Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 10 и 11, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
11-10=1
Ответ:1
Номер: 43BF45
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 42, сторона BC равна 44, сторона AC равна 62. Найдите MN.
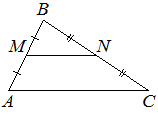
Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=62/2=31`
Ответ:31
Номер: F1CC42
Впишите правильный ответ.
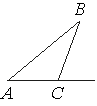
В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-133°=47°
Ответ:47
Номер: 087849
Впишите правильный ответ.
Диагональ прямоугольника образует угол 86° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
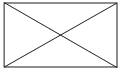
Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*86°=8° это и будет острый угол между диагоналями.
Ответ:8
Номер: 71FA4B
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(4*9)/2=18`
Ответ:18
Номер: B19742
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=86° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
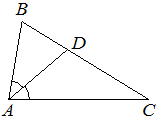
Решение:
Биссектриса делит угол на два равных, тогда 86°:2=43°
Ответ:43
Номер: 17B640
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 108°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*108)/2=72`°
Ответ:72
Номер: 1BAC40
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 11 и 14. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 14 и 11, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
14-11=3
Ответ:
Номер: 1B2B45
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=82° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 82°:2=41°
Ответ:41
Номер: 23E24A
Впишите правильный ответ.

Сторона ромба равна 28, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 28/2=14
Ответ:14
Номер: 29A549
Впишите правильный ответ.
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(19*16)/2=152
Ответ:152
Номер: DFD347
Впишите правильный ответ.
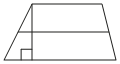
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(11+19)/2=15`
Ответ:15
Номер: D2E245
Впишите правильный ответ.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
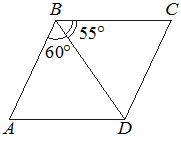
Решение:
Все углы равны 360º, половина углов в состав которой будет входить меньший равна 180º, а меньший:
180º-(60º+55º)=65º
Ответ:65
Номер: 55E444
Впишите правильный ответ.
В треугольнике два угла равны 57° и 86°. Найдите его третий угол. Ответ дайте в градусах.
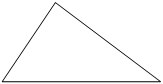
Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(57º+86º)=37º
Ответ:37
Номер: ACF14E
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=24° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 24°:2=12°
Ответ:
Номер: A2DD46
Впишите правильный ответ.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
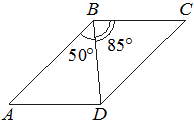
Решение:
Все углы равны 360º, половина углов в состав которой будет входить меньший равна 180º, а меньший:
180º-(50º+85º)=45º
Ответ:
Номер: C08249
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 9 и 41 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`41^2=9^2+x^2`
`x^2=41^2-9^2`
`x=sqrt(1600)`
Ответ:40
Номер: C2A246
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 55°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*55)/2=125`°
Ответ:
Номер: 96084A
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=128°. Найдите угол BCA. Ответ дайте в градусах.
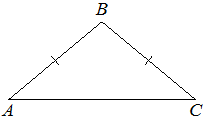
Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-128)/2=26º
Ответ:26
Номер: 33CF44
Впишите правильный ответ.
Сторона треугольника равна 8, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(8*31)/2=124
Ответ:
Номер: 386846
Впишите правильный ответ.

Основания трапеции равны 4 и 12, а высота равна 6. Найдите площадь этой трапеции.
Решение:
`(6*(4+12))/2 = 48`
Ответ:48
Номер: 838A48
Впишите правильный ответ.
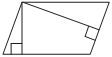
Площадь параллелограмма равна 54, а две его стороны равны 9 и 18. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
9*h1=54
h1=6
18*h2=54
h2=3
Ответ:3
Номер: F4D8F4
Впишите правильный ответ.
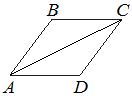
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
(180-146)/2=17
Ответ:17
Номер: F6F9FB
Впишите правильный ответ.
Диагональ прямоугольника образует угол 70° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*70°=40° это и будет острый угол между диагоналями.
Ответ:
Номер: F293FE
Впишите правильный ответ.

Основания трапеции равны 7 и 21, а высота равна 6. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(7+21)/2=14`
Ответ:
Номер: 00A9FF
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=124°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-124)/2=28º
Ответ:28
Номер: 0A9FFB
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух острых углов, то есть тупой угол будет вычисляться так:
180º-50º/2=155º
Ответ:155
Номер: 0CE2F2
Впишите правильный ответ.

Основания трапеции равны 5 и 11, а высота равна 7. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(11+5)/2=8`
Ответ:
Номер: 720EFB
Впишите правильный ответ.
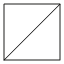
Сторона квадрата равна 7`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(7sqrt2)^2+(7sqrt2)^2`
`x^2=2(7sqrt2)^2`
`x^2=2*49*2`
`x=sqrt196`
х=14
Ответ:14
Номер: B8F7FD
Впишите правильный ответ.

Один из углов ромба равен 24°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-24°=156°
Ответ:156
Номер: 10A5FF
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 36°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+36°)=54°
Ответ:54
Номер: 14E2F1
Впишите правильный ответ.
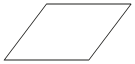
Один из углов параллелограмма равен 111°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-111°=69°
Ответ:69
Номер: 1581FD
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , sinB=712 , AB=48. Найдите AC.
Решение:
Синус это отношение противолежащего катета к гипотенузе, тогда
AC/AB=sinB
AC=sinB*AC
AC=48*7/12=28
Ответ:28
Номер: DE8CF4
Впишите правильный ответ.
В треугольнике ABC известно, что AC=54 , BM — медиана, BM=43. Найдите AM.
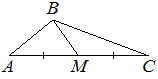
Решение:
Медиана делит сторону на два равных отрезка.
54/2=27
Ответ:27
Номер: DC9FFB
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*66)/2=114`°
Ответ:
Номер: 5861FC
Впишите правильный ответ.
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(14*23)/2=161
Ответ:
Номер: AAF8FF
Впишите правильный ответ.

Сторона ромба равна 22, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 22/2=11
Ответ:
Номер: A322F0
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 14 и 19. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 14 и 19, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
19-14=5
Ответ:
Номер: CCE8F8
Впишите правильный ответ.

Основания трапеции равны 1 и 5, а высота равна 3. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(1+5)/2=3`
Ответ:
Номер: EED3F4
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.

Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+7)*4=40
Ответ:40
Номер: E792F5
Впишите правильный ответ.

Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-114°=66°
Ответ:66
Номер: 6602F4
Впишите правильный ответ.

В треугольнике ABC угол C равен 177°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-177°=3°
Ответ:
Номер: 6C18F3
Впишите правильный ответ.
В треугольнике два угла равны 28° и 93°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(28º+93º)=59º
Ответ:
Номер: 3C0FF5
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 74°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*74)/2=106`°
Ответ:
Номер: 313DF9
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=62° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 62°:2=31°
Ответ:
Номер: 8A1FF0
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+34°)=56°
Ответ:56
Номер: 8961FD
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 1 и 11. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 1 и 11, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
11-1=10
Ответ:
Номер: FE010A
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 9 и 15 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`15^2=9^2+x^2`
`x^2=15^2-9^2`
`x=sqrt(144)`
Ответ:12
Номер: FF1408
Впишите правильный ответ.
В треугольнике ABC известно, что AC=38 , BM — медиана, BM=17. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
38/2=19
Ответ:19
Номер: 001507
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 131°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*131)/2=49`°
Ответ:
Номер: B8520B
Впишите правильный ответ.
Биссектриса равностороннего треугольника равна 13`sqrt3`. Найдите сторону этого треугольника.
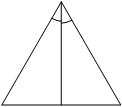
Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(13sqrt3)^2+(1/2x)^2=x^2`
`169*3=x^2-(1/2x)^2`
`169*3=x^2 - 1/4x^2`
`169*3=3/4x^2`
`169*4=x^2`
`x=sqrt676`
x=26
Ответ:26
Номер: BD5205
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=84° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 84°:2=42°
Ответ:
Номер: BFA103
Впишите правильный ответ.

Основания трапеции равны 8 и 14, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(8+14)/2*5=112/2*5=55`
Ответ:55
Номер: 1BF00E
Впишите правильный ответ.
Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(19*24)/2=228
Номер: 2AB907
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 20 и 25 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`25^2=20^2+x^2`
`x^2=25^2-20^2`
`x=sqrt(225)`
Ответ:15
Номер: 286207
Впишите правильный ответ.

Основания трапеции равны 4 и 6, а высота равна 4. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(4+6)/2=5`
Ответ:
Номер: 208C07
Впишите правильный ответ.
В треугольнике ABC известно, что AC=56 , BM — медиана, BM=48. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
56/2=28
Ответ:28
Номер: 217305
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(14*5)/2=35`
Ответ:
Номер: D5E30C
Впишите правильный ответ.

Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-41°=139°
Ответ:139
Номер: D56908
Впишите правильный ответ.
В треугольнике ABC известно, что AC=40 , BC=30 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`40^2+30^2=AB^2`
`1600+900=AB^2`
`AB=sqrt(2500)`
AB=50 - диаметр.
R=AB/2=25
Ответ:25
Номер: 5ED50C
Впишите правильный ответ.
Медиана равностороннего треугольника равна 13`sqrt3`. Найдите сторону этого треугольника.
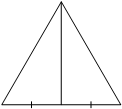
Решение:
Медиана в равностороннем треугольнике является в том числе и высотой. По теореме Пифагора, если принять сторону за x, тогда:
`(13sqrt3)^2+(1/2x)^2=x^2`
`169*3=x^2-(1/2x)^2`
`169*3=x^2 - 1/4x^2`
`169*3=3/4x^2`
`169*4=x^2`
`x=sqrt676`
x=26
Ответ:26
Номер: 58F20E
Впишите правильный ответ.
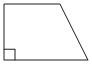
Один из углов прямоугольной трапеции равен 72°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-72°=108°
Ответ:108
Номер: AE0504
Впишите правильный ответ.
Сторона равностороннего треугольника равна 14`sqrt3`. Найдите медиану этого треугольника.

Решение:
Медиана в равностороннем треугольнике является в том числе и высотой. По теореме Пифагора, если известна гипотенуза, тогда:
`(14sqrt3)^2=(1/2*14sqrt3)^2+x^2`
`196*3=(196*3)/4+x^2`
`196*3-(196*3)/4=x^2`
`x^2=588-147`
`x^2=441`
x=21
Ответ:21
Номер: 931301
Впишите правильный ответ.
Сторона равностороннего треугольника равна 14`sqrt3`. Найдите высоту этого треугольника.
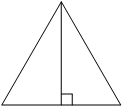
Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(14sqrt3)^2=(1/2*14sqrt3)^2+x^2`
`196*3=(196*3)/4+x^2`
`196*3-(196*3)/4=x^2`
`x^2=588-147`
`x^2=441`
x=21
Ответ:21
Номер: EB4A00
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`41^2=40^2+x^2`
`x^2=41^2-40^2`
`x=sqrt(81)`
Ответ:9
Номер: EBCF0C
Впишите правильный ответ.

В треугольнике ABC угол C равен 97°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-97°=83°
Ответ:
Номер: EBAD08
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 11 и 6. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(11*6)/2=33`
Ответ:
Номер: 67C901
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
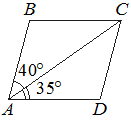
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(40°+35°)=105°
Ответ:105
Номер: 643E01
Впишите правильный ответ.
Периметр ромба равен 56, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 56:4=14
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=14/2=7
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=7*14=98
Ответ:98
Номер: 68A60E
Впишите правильный ответ.

В треугольнике ABC угол C равен 142°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-142°=38°
Ответ:
Номер: 38680C
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=144°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-144)/2=18º
Ответ:
Номер: 81270B
Впишите правильный ответ.

Сторона ромба равна 54, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 54/2=27
Ответ:
Номер: 8E9B0E
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=46° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 46°:2=23°
Ответ:
Номер: 4EC57D
Впишите правильный ответ.

Сторона квадрата равна 2`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(2sqrt2)^2+(2sqrt2)^2`
`x^2=2(2sqrt2)^2`
`x^2=2*4*2`
`x=sqrt16`
х=4
Ответ:4
Номер: 44977D
Впишите правильный ответ.

Один из углов параллелограмма равен 61°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-61°=119°
Ответ:119
Номер: F4D87F
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 94°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух острых углов, то есть тупой угол будет вычисляться так:
180º-94º/2=133º
Ответ:133
Номер: FC3177
Впишите правильный ответ.

Площадь параллелограмма равна 45, а две его стороны равны 5 и 15. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
Площадь параллелограмма равна произведению основания на высоту.
45=5*h1
h1=45/5=9
45=15*h1
h1=45/15=3
Ответ:9
Номер: FD0375
Впишите правильный ответ.
Медиана равностороннего треугольника равна 12`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(12sqrt3)^2+(1/2x)^2=x^2`
`144*3=x^2-(1/2x)^2`
`144*3=x^2 - 1/4x^2`
`144*3=3/4x^2`
`144*4=x^2`
`x=sqrt576`
x=24
Ответ:24
Номер: F8BE76
Впишите правильный ответ.

Сторона ромба равна 46, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 46/2=23
Ответ:
Номер: F02E73
Впишите правильный ответ.
В треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(27º+79º)=74º
Ответ:74
Номер: 7A457D
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
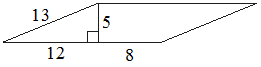
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(12+8)*5=100
Ответ:100
Номер: 791778
Впишите правильный ответ.
Сторона равностороннего треугольника равна 12`sqrt3`. Найдите высоту этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(12sqrt3)^2=(1/2*12sqrt3)^2+x^2`
`144*3=(144*3)/4+x^2`
`144*3-(144*3)/4=x^2`
`x^2=432-108`
`x^2=324`
x=18
Ответ:18
Номер: 28CE77
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 8 и 17. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 8 и 17, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
17-8=9
Ответ:
Номер: 29017C
Впишите правильный ответ.

Один из углов параллелограмма равен 128°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-128°=52°
Ответ:52
Номер: 267079
Впишите правильный ответ.

Сторона квадрата равна 5`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(5sqrt2)^2+(5sqrt2)^2`
`x^2=2(5sqrt2)^2`
`x^2=2*25*2`
`x=sqrt100`
х=10
Ответ:10
Номер: D02B71
Впишите правильный ответ.
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(72º+42º)=66º
Ответ:66
Номер: A7F27D
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 94°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*94)/2=86`°
Ответ:
Номер: A10875
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 51°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-51°=129°
Ответ:129
Номер: AC7373
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 10 и 24. Найдите гипотенузу этого треугольника.

Решение:
102+242=x2
x2=100+576
`x=sqrt(676)=26`
Ответ:26
Номер: CC9E7D
Впишите правильный ответ.

Сторона квадрата равна 11`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(11sqrt2)^2+(11sqrt2)^2`
`x^2=2(11sqrt2)^2`
`x^2=2*121*2`
`x=sqrt484`
х=22
Ответ:22
Номер: C0567E
Впишите правильный ответ.
Высота равностороннего треугольника равна 12`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(12sqrt3)^2+(1/2x)^2=x^2`
`144*3=x^2-(1/2x)^2`
`144*3=x^2 - 1/4x^2`
`144*3=3/4x^2`
`144*4=x^2`
`x=sqrt576`
x=24
Ответ:24
Номер: 98A274
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 3 и 11. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 3 и 11, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
11-3=8
Ответ:
Номер: 9F017F
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=50/2=25`
Ответ:
Номер: 983E79
Впишите правильный ответ.
В треугольнике два угла равны 47° и 64°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(47º+64º)=69º
Ответ:69
Номер: E57E70
Впишите правильный ответ.
В треугольнике ABC известно, что AC=20 , BC=21 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`20^2+21^2=AB^2`
`400+441=AB^2`
`AB=sqrt(841)`
AB=29 - диаметр.
R=AB/2=14,5
Ответ:14,5
Номер: EC207D
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
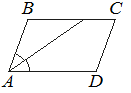
Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*15º=30º
Ответ:30
Номер: 66ED77
Впишите правильный ответ.
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
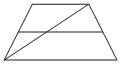
Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
11/2=5,5
Ответ:5,5
Номер: 6B3778
Впишите правильный ответ.
В треугольнике ABC известно, что AC=14 , BM — медиана, BM=10. Найдите AM.
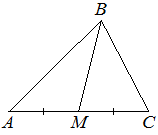
Решение:
Медиана делит сторону на два равных отрезка.
14/2=7
Ответ:7
Номер: 312475
Впишите правильный ответ.

Основания трапеции равны 2 и 12, а высота равна 6. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(2+12)/2=7`
Ответ:
Номер: 8BF372
Впишите правильный ответ.
Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
19/2=9,5
Ответ:9,5
Номер: 89DE7C
Впишите правильный ответ.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
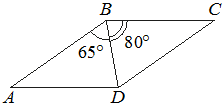
Решение:
Все углы равны 360º, половина углов в состав которой будет входить меньший равна 180º, а меньший:
180º-(65º+80º)=35º
Ответ:
Номер: 4201B5
Впишите правильный ответ.
Сторона равностороннего треугольника равна 12`sqrt3`. Найдите биссектрису этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(12sqrt3)^2=(1/2*12sqrt3)^2+x^2`
`144*3=(144*3)/4+x^2`
`144*3-(144*3)/4=x^2`
`x^2=432-108`
`x^2=324`
x=18
Ответ:18
Номер: 20C1B4
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 8 и 18. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 8 и 18, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
18-8=10
Ответ:
Номер: D7F2B4
Впишите правильный ответ.

Основания трапеции равны 8 и 18, а высота равна 5. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(8+18)/2=13`
Ответ:
Номер: 5717B9
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 12°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*12º=24º
Ответ:24
Номер: C6FEB7
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=148°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-148)/2=16º
Ответ:
Номер: C20ABB
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*33º=66º
Ответ:66
Номер: CBD1B1
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 17 и 19. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 17 и 19, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
19-17=2
Ответ:
Номер: C014BE
Впишите правильный ответ.

Площадь параллелограмма равна 28, а две его стороны равны 14 и 7. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
28=14*h1
h1=28/14=2
28=7*h1
h1=28/7=4
Ответ:4
Номер: CDECB3
Впишите правильный ответ.

Один из углов ромба равен 104°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-104°=76°
Ответ:
Номер: 902DB6
Впишите правильный ответ.
В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(38º+89º)=83º
Ответ:83
Номер: 9EDEB6
Впишите правильный ответ.
Основания трапеции равны 1 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
11/2=5,5
Ответ:5,5
Номер: 9390B3
Впишите правильный ответ.
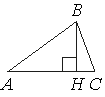
В остроугольном треугольнике ABC проведена высота BH , ∠BAC=19°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
Высота образует прямоугольный треугольник. ∠BAC=9° ∠BHA=90°, тогда
∠ABH=180°-(90°+19°)=71°
Ответ:71
Номер: E0AAB0
Впишите правильный ответ.

Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
48=8*h1
h1=48/8=6
45=15*h1
h1=48/16=3
Ответ:3
Номер: E185BD
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 24, сторона BC равна 13, сторона AC равна 26. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=25/2=13`
Ответ:
Номер: 6B7AB7
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-102)/2=39º
Ответ:
Номер: 65ABB2
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=108°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-108)/2=36º
Ответ:
Номер: 628BBA
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=142°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-142)/2=19º
Ответ:
Номер: 6C10B6
Впишите правильный ответ.

Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 4/2=2
Ответ:
Номер: 642DB8
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+21°)=69°
Ответ:69
Номер: 3430B9
Впишите правильный ответ.
В треугольнике ABC известно, что AC=30 , BC=16 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Медиана делит сторону на два равных отрезка.
30/2=15
Ответ:15
Номер: 8CCBB2
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 53°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+53°)=37°
Ответ:37
Номер: 8E34B5
Впишите правильный ответ.

Один из углов ромба равен 76°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-76°=104°
Ответ:104
Номер: 4CF910
Впишите правильный ответ.

Сторона квадрата равна 6`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(6sqrt2)^2+(6sqrt2)^2`
`x^2=2(6sqrt2)^2`
`x^2=2*36*2`
`x=sqrt144`
х=12
Ответ:12
Номер: 4E8510
Впишите правильный ответ.
Диагональ прямоугольника образует угол 44° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол меньший. 90°-44°=46° будет больший.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*46°=88° это и будет острый угол между диагоналями.
Ответ:
Номер: F8931E
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=64/2=32`
Ответ:
Номер: FE6718
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 12 и 20 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`20^2=12^2+x^2`
`x^2=20^2-12^2`
`x=sqrt(256)`
Ответ:16
Номер: 0E8814
Впишите правильный ответ.
Медиана равностороннего треугольника равна 9`sqrt3`. Найдите сторону этого треугольника.

Решение:
Медиана в равностороннем треугольнике является в том числе и высотой. По теореме Пифагора, если принять сторону за x, тогда:
`(9sqrt3)^2+(1/2x)^2=x^2`
`81*3=x^2-(1/2x)^2`
`81*3=x^2 - 1/4x^2`
`81*3=3/4x^2`
`81*4=x^2`
`x=sqrt324`
x=18
Ответ:18
Номер: 028C16
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 12 и 5. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(12*5)/2=30`
Ответ:
Номер: B18014
Впишите правильный ответ.

Сторона квадрата равна 8`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(8sqrt2)^2+(8sqrt2)^2`
`x^2=2(8sqrt2)^2`
`x^2=2*64*2`
`x=sqrt256`
х=16
Ответ:16
Номер: B0F219
Впишите правильный ответ.
В треугольнике ABC известно, что AC=32 , BM — медиана, BM=23. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
32/2=16
Ответ:16
Номер: B0541E
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(4*11)/2=22`
Ответ:
Номер: 192B1F
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 102°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-102°)/2=39°
Ответ:39
Номер: 17C619
Впишите правильный ответ.
Периметр ромба равен 72, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 72:4=18
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=18/2=9
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=9*18=162
Ответ:162
Номер: 1C9D13
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 44°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*44º=88º
Ответ:88
Номер: 2CB417
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 68°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+68°)=22°
Ответ:22
Номер: 23F11D
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 43°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*43)/2=137`°
Ответ:
Номер: D0CC19
Впишите правильный ответ.
Периметр ромба равен 88, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 88:4=22
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=22/2=11
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=22*11=242
Ответ:242
Номер: 5FBA1E
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 156°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-156°)/2=12°
Ответ:12
Номер: CCA619
Впишите правильный ответ.
Сторона равностороннего треугольника равна 12`sqrt3`. Найдите медиану этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(12sqrt3)^2=(1/2*12sqrt3)^2+x^2`
`144*3=(144*3)/4+x^2`
`144*3-(144*3)/4=x^2`
`x^2=432-108`
`x^2=324`
x=18
Ответ:18
Номер: C3CC16
Впишите правильный ответ.
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(18*22)/2=198
Ответ:
Номер: 961117
Впишите правильный ответ.

В треугольнике ABC угол C равен 159°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-159°=21°
Ответ:
Номер: 9F701B
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(7*12)/2=42`
Ответ:
Номер: 947718
Впишите правильный ответ.
В треугольнике ABC известно, что AC=10 , BC=24 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`10^2+24^2=AB^2`
`100+576=AB^2`
`AB=sqrt(676)`
AB=26 - диаметр.
R=AB/2=13
Ответ:13
Номер: EB2011
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+57°)=33°
Ответ:33
Номер: ED2416
Впишите правильный ответ.
Основания трапеции равны 1 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
19/2=9,5
Ответ:9,5
Номер: E32313
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
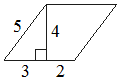
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+2)*4=20
Ответ:20
Номер: 6E1610
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=146°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-146)/2=17º
Ответ:
Номер: 673017
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 21°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*21º=42º
Ответ:42
Номер: 342519
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
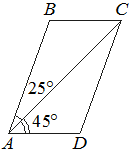
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(45°+25°)=110°
Ответ:110
Номер: 303816
Впишите правильный ответ.
Основания трапеции равны 14 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
19/2=9,5
Ответ:9,5
Номер: 85731F
Впишите правильный ответ.
Диагональ прямоугольника образует угол 63° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*63°=54° это и будет острый угол между диагоналями.
Ответ:
Номер: 4B652C
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 26, сторона BC равна 39, сторона AC равна 48. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=48/2=24`
Ответ:
Номер: FB9322
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 36°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*36º=72º
Ответ:72
Номер: 785E24
Впишите правильный ответ.
В треугольнике ABC известно, что AC=12 , BC=5 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`12^2+5^2=AB^2`
`144+25=AB^2`
`AB=sqrt(169)`
AB=13 - диаметр.
R=AB/2=6,5
Ответ:6,5
Номер: 71B029
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*113)/2=67`°
Ответ:
Номер: 7DE329
Впишите правильный ответ.

Сторона ромба равна 14, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 14/2=7
Ответ:
Номер: B7602D
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(18*7)/2=63`
Ответ:
Номер: 579C24
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=42° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 42°:2=21°
Ответ:
Номер: 553221
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 20 и 15. Найдите гипотенузу этого треугольника.

Решение:
202+152=x2
x2=400+225
`x=sqrt(625)=25`
Ответ:25
Номер: C87A27
Впишите правильный ответ.
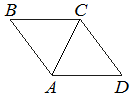
В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-40°)/2=70°
Ответ:70
Номер: CDA627
Впишите правильный ответ.

Основания трапеции равны 13 и 23, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(13+23)/2*5=36/2*5=90`
Ответ:90
Номер: C92821
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 9 и 6. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(6*9)/2=27`
Ответ:
Номер: 313421
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.

Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+8)*4=44
Ответ:44
Номер: 32F22D
Впишите правильный ответ.

Сторона квадрата равна 4`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(4sqrt2)^2+(4sqrt2)^2`
`x^2=2(4sqrt2)^2`
`x^2=2*16*2`
`x=sqrt64`
х=8
Ответ:
Номер: 309D29
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 8 и 17 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`17^2=8^2+x^2`
`x^2=17^2-8^2`
`x=sqrt(225)`
Ответ:15
Номер: 8D0625
Впишите правильный ответ.
Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 36:4=9
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=9/2=4,5
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=9*4,5=40,5
Ответ:40,5
Номер: 4547D7
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-113°=67°
Ответ:67
Номер: 4D3FD7
Впишите правильный ответ.

Сторона ромба равна 18, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 18/2=9
Ответ:
Номер: 4015D9
Впишите правильный ответ.
Сторона равностороннего треугольника равна 10`sqrt3`. Найдите медиану этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(10sqrt3)^2=(1/2*10sqrt3)^2+x^2`
`100*3=(100*3)/4+x^2`
`100*3-(100*3)/4=x^2`
`x^2=300-75`
`x^2=225`
x=15
Ответ:15
Номер: F836D4
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-64°=116°
Ответ:116
Номер: F38CDA
Впишите правильный ответ.

В треугольнике ABC угол C равен 115°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-115°=65°
Ответ:
Номер: 0E8FD4
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 26°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+26°)=64°
Ответ:64
Номер: 0BADD3
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 48°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-48°)/2=66°
Ответ:66
Номер: 057AD8
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 9°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*9º=18º
Ответ:18
Номер: 7AC3D4
Впишите правильный ответ.
Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 24:4=6
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=6/2=3
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=3*6=18
Ответ:18
Номер: 7126D1
Впишите правильный ответ.

Сторона квадрата равна 10`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(10sqrt2)^2+(10sqrt2)^2`
`x^2=2(10sqrt2)^2`
`x^2=2*100*2`
`x=sqrt400`
х=20
Ответ:20
Номер: 75C2DE
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 56°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-56°)/2=62°
Ответ:62
Номер: B266D3
Впишите правильный ответ.
Сторона равностороннего треугольника равна 16`sqrt3`. Найдите высоту этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(16sqrt3)^2=(1/2*16sqrt3)^2+x^2`
`256*3=(256*3)/4+x^2`
`256*3-(256*3)/4=x^2`
`x^2=768-192`
`x^2=576`
x=24
Ответ:24
Номер: 1F86DB
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 99°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*99)/2=81`°
Ответ:
Номер: 268BD0
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+48°)=42°
Ответ:42
Номер: 24A8D7
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*41º=82º
Ответ:82
Номер: 2722D1
Впишите правильный ответ.
Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
17/2=8,5
Ответ:8,5
Номер: 273FD5
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 218°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух тупых углов, то есть меньший угол будет вычисляться так:
180º-218º/2=71º
Ответ:71
Номер: 5632D0
Впишите правильный ответ.
В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(36º+73º)=71º
Ответ:71
Номер: 5112D5
Впишите правильный ответ.

Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(3+9)/2=6`
Ответ:
Номер: 5592DA
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
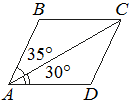
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(30°+35°)=115°
Ответ:115
Номер: AC15D1
Впишите правильный ответ.
В треугольнике ABC известно, что AC=34 , BM — медиана, BM=26. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
34/2=17
Ответ:17
Номер: ABB0D2
Впишите правильный ответ.
Периметр ромба равен 48, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 48:4=12
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=12/2=6
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=6*12=72
Ответ:72
Номер: E296DA
Впишите правильный ответ.

Основания трапеции равны 4 и 14, а высота равна 8. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(14+4)/2=9`
Ответ:
Номер: E52BDC
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.

Решение:
72+242=x2
x2=49+576
`x=sqrt(625)=25`
Ответ:25
Номер: 375ED9
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 6 и 13. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(6*13)/2=39`
Ответ:
Номер: 3192DE
Впишите правильный ответ.

Сторона квадрата равна 9`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(9sqrt2)^2+(9sqrt2)^2`
`x^2=2(9sqrt2)^2`
`x^2=2*81*2`
`x=sqrt324`
х=18
Ответ:18
Номер: 84EFDE
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
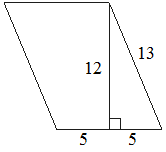
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(5+5)*12=120
Ответ:120
Номер: 46CE52
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-84°)/2=48°
Ответ:48
Номер: 4C3959
Впишите правильный ответ.
В треугольнике ABC известно, что AC=52 , BM — медиана, BM=36. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
52/2=26
Ответ:26
Номер: FBE55F
Впишите правильный ответ.
Периметр ромба равен 28, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 28:4=7
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=7/2=3,5
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=7*3,5=24,5
Ответ:24,5
Номер: 7B1650
Впишите правильный ответ.
Биссектриса равностороннего треугольника равна 11`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(11sqrt3)^2+(1/2x)^2=x^2`
`121*3=x^2-(1/2x)^2`
`121*3=x^2 - 1/4x^2`
`121*3=3/4x^2`
`121*4=x^2`
`x=sqrt484`
x=22
Ответ:22
Номер: 78D35A
Впишите правильный ответ.
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(14*31)/2=217
Ответ:
Номер: BB8A5E
Впишите правильный ответ.

Один из углов параллелограмма равен 26°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-26°=154°
Ответ:154
Номер: 12B054
Впишите правильный ответ.
В треугольнике ABC известно, что AC=7 , BC=24 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`7^2+24^2=AB^2`
`49+576=AB^2`
`AB=sqrt(625)`
AB=25 - диаметр.
R=AB/2=12,5
Ответ:12,5
Номер: 134A57
Впишите правильный ответ.
Сторона равностороннего треугольника равна 10`sqrt3`. Найдите высоту этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(10sqrt3)^2=(1/2*10sqrt3)^2+x^2`
`100*3=(100*3)/4+x^2`
`100*3-(100*3)/4=x^2`
`x^2=300-75`
`x^2=225`
x=15
Ответ:15
Номер: 122557
Впишите правильный ответ.
Сторона равностороннего треугольника равна 16`sqrt3`. Найдите медиану этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(16sqrt3)^2=(1/2*16sqrt3)^2+x^2`
`256*3=(256*3)/4+x^2`
`256*3-(256*3)/4=x^2`
`x^2=768-192`
`x^2=576`
x=24
Ответ:24
Номер: 506B50
Впишите правильный ответ.
Диагональ прямоугольника образует угол 74° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*74°=32° это и будет острый угол между диагоналями.
Ответ:
Номер: AB1A51
Впишите правильный ответ.
В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(54º+58º)=68º
Ответ:68
Номер: A6615D
Впишите правильный ответ.

Один из углов параллелограмма равен 74°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-74°=106°
Ответ:106
Номер: 9E8B53
Впишите правильный ответ.
В треугольнике ABC известно, что AC=58 , BM — медиана, BM=37. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
58/2=29
Ответ:29
Номер: E2275D
Впишите правильный ответ.

Основания трапеции равны 6 и 14, а высота равна 8. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(6+14)/2*5=20/2*5=50`
Ответ:50
Номер: 6ADF52
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 46°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух острых углов, то есть тупой угол будет вычисляться так:
180º-46º/2=157º
Ответ:157
Номер: 354354
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 95, сторона BC равна 80, сторона AC равна 128. Найдите MN.
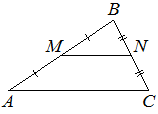
Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=128/2=64`
Ответ:
Номер: 37BA59
Впишите правильный ответ.

Площадь параллелограмма равна 56, а две его стороны равны 7 и 28. Найдите его высоты. В ответе укажите меньшую высоту.
Решение:
56=7*h1
h1=56/7=8
56=28*h1
h1=56/28=2
Ответ:2
Номер: 81BF5F
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=26° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
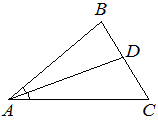
Решение:
Биссектриса делит угол на два равных, тогда 26°:2=13°
Ответ:
Номер: 82D357
Впишите правильный ответ.
Периметр ромба равен 20, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 20:4=5
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=5/2=2,5
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=5*2,5=12,5
Ответ:12,5
Номер: 8F9E5B
Впишите правильный ответ.

В треугольнике ABC угол C равен 106°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-106°=74°
Ответ:
Номер: 80F452
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`50^2=40^2+x^2`
`x^2=50^2-40^2`
`x=sqrt(900)`
Ответ:30
Номер: F2EAA0
Впишите правильный ответ.

Один из углов параллелограмма равен 102°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-102°=78°
Ответ:78
Номер: FA5CAD
Впишите правильный ответ.
Сторона равностороннего треугольника равна 14`sqrt3`. Найдите биссектрису этого треугольника.

Решение:
Медиана в равностороннем треугольнике является в том числе и высотой. По теореме Пифагора, если известна гипотенуза, тогда:
`(14sqrt3)^2=(1/2*14sqrt3)^2+x^2`
`196*3=(196*3)/4+x^2`
`196*3-(196*3)/4=x^2`
`x^2=588-147`
`x^2=441`
x=21
Ответ:21
Номер: 04D0AA
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

Решение:
82+152=x2
x2=64+225
`x=sqrt(289)=17`
Ответ:17
Номер: 027BA6
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 82°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-82°=98°
Ответ:98
Номер: 0AD8A6
Впишите правильный ответ.
Основания трапеции равны 2 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
9/2=4,5
Ответ:4,5
Номер: 1B2FAF
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 12 и 5. Найдите гипотенузу этого треугольника.

Решение:
122+52=x2
x2=144+25
`x=sqrt(169)=13`
Ответ:13
Номер: 2877A2
Впишите правильный ответ.

Один из углов равнобедренной трапеции равен 29°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
У равнобедренной трапеции два острых угла и два тупых, причем углы у оснований одинаковые. Получается острый угол можно найти так:
`(360-2*29)/2=151`°
Ответ:
Номер: 2BFFA8
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=126°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-126)/2=28º
Ответ:
Номер: 5D3CA9
Впишите правильный ответ.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*50°=80° это и будет острый угол между диагоналями.
Ответ:
Номер: C0BDA7
Впишите правильный ответ.
Высота равностороннего треугольника равна 9`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(9sqrt3)^2+(1/2x)^2=x^2`
`81*3=x^2-(1/2x)^2`
`81*3=x^2 - 1/4x^2`
`81*3=3/4x^2`
`81*4=x^2`
`x=sqrt324`
x=18
Ответ:18
Номер: E898A0
Впишите правильный ответ.
Биссектриса равностороннего треугольника равна 12`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(12sqrt3)^2+(1/2x)^2=x^2`
`144*3=x^2-(1/2x)^2`
`144*3=x^2 - 1/4x^2`
`144*3=3/4x^2`
`144*4=x^2`
`x=sqrt576`
x=24
Ответ:24
Номер: 6F01AB
Впишите правильный ответ.

Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 38/2=19
Ответ:
Номер: 6540AD
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 107°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-107°=73°
Ответ:73
Номер: 8C6BAA
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=104/2=52`
Ответ:
Номер: 8A24A8
Впишите правильный ответ.

Один из углов параллелограмма равен 91°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-91°=89°
Ответ:89
Номер: 497DC2
Впишите правильный ответ.
В треугольнике ABC известно, что AC=16 , BM — медиана, BM=12. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
16/2=8
Ответ:8
Номер: F5BBC0
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
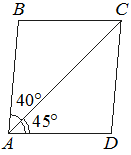
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(40°+45°)=95°
Ответ:95
Номер: F41BC1
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=68° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 68°:2=34°
Ответ:
Номер: 0B16C1
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 139°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-139°=41°
Ответ:41
Номер: 7D0FC4
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 102°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух острых углов, то есть тупой угол будет вычисляться так:
180º-102º/2=129º
Ответ:129
Номер: B4A2C0
Впишите правильный ответ.

Основания трапеции равны 3 и 5, а высота равна 9. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(3+5)/2*5=40/2*5=100`
Ответ:100
Номер: 1E26CA
Впишите правильный ответ.
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(12*33)/2=198
Ответ:
Номер: 1CFEC6
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 18 и 24. Найдите гипотенузу этого треугольника.

Решение:
182+242=x2
x2=324+576
`x=sqrt(900)=30`
Ответ:30
Номер: 21E8C1
Впишите правильный ответ.
Высота равностороннего треугольника равна 13`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(13sqrt3)^2+(1/2x)^2=x^2`
`169*3=x^2-(1/2x)^2`
`169*3=x^2 - 1/4x^2`
`169*3=3/4x^2`
`169*4=x^2`
`x=sqrt676`
x=26
Ответ:
Номер: 2607CE
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+63°)=27°
Ответ:27
Номер: D4F8C0
Впишите правильный ответ.

Один из углов ромба равен 93°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-93°=87°
Ответ:87
Номер: D0C6C9
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 102°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-102°=78°
Ответ:78
Номер: D427CE
Впишите правильный ответ.
В треугольнике ABC известно, что AC=18 , BM — медиана, BM=14. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
18/2=9
Ответ:9
Номер: 5EE1CC
Впишите правильный ответ.

Основания трапеции равны 7 и 11, а высота равна 7. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(7+11)/2*7=18/2*7=63`
Ответ:63
Номер: A927C2
Впишите правильный ответ.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите бо́льшую высоту.

Решение:
60=4*h1
h1=60/4=15
45=15*h1
h1=60/20=3
Ответ:15
Номер: A187CC
Впишите правильный ответ.

Сторона ромба равна 24, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 24/2=12
Ответ:
Номер: C3FCCC
Впишите правильный ответ.
Медиана равностороннего треугольника равна 11`sqrt3`. Найдите сторону этого треугольника.

Решение:
Медиана в равностороннем треугольнике является в том числе и высотой. По теореме Пифагора, если принять сторону за x, тогда:
`(11sqrt3)^2+(1/2x)^2=x^2`
`121*3=x^2-(1/2x)^2`
`121*3=x^2 - 1/4x^2`
`121*3=3/4x^2`
`121*4=x^2`
`x=sqrt484`
x=22
Ответ:22
Номер: 9C06CA
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+23°)=67°
Ответ:67
Номер: 9EECCA
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 15 и 8, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
15-8=7
Ответ:
Номер: E5F7CA
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 9 и 12. Найдите гипотенузу этого треугольника.

Решение:
92+122=x2
x2=81+144
`x=sqrt(225)=15`
Ответ:15
Номер: 604AC1
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 21, сторона BC равна 22, сторона AC равна 28. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=28/2=14`
Ответ:
Номер: 63AEC1
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 30 и 50 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`50^2=30^2+x^2`
`x^2=50^2-30^2`
`x=sqrt(1600)`
Ответ:40
Номер: 60E4C2
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(4*10)/2=20`
Ответ:
Номер: 36BBCF
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 268°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух тупых углов, то есть меньший угол будет вычисляться так:
180º-268º/2=46º
Ответ:46
Номер: 4F7697
Впишите правильный ответ.

Один из углов параллелограмма равен 96°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-96°=84°
Ответ:84
Номер: 084E97
Впишите правильный ответ.
Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 60:4=15
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=15/2=7,5
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=15*7,5=112,5
Ответ:112,5
Номер: 06F396
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=28° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 28°:2=14°
Ответ:
Номер: 1E729A
Впишите правильный ответ.
В треугольнике ABC известно, что AC=16 , BC=12 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`16^2+12^2=AB^2`
`256+144=AB^2`
`AB=sqrt(400)`
AB=20 - диаметр.
R=AB/2=10
Ответ:10
Номер: 24749F
Впишите правильный ответ.
Площадь параллелограмма равна 30, а две его стороны равны 6 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.

Решение:
30=6*h1
h1=30/6=5
30=10*h1
h1=30/10=3
Ответ:5
Номер: 279F96
Впишите правильный ответ.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
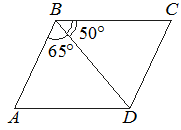
Решение:
Все углы равны 360º, половина углов в состав которой будет входить меньший равна 180º, а меньший:
180º-(65º+50º)=65º
Ответ:65
Номер: D29E94
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=64° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 64°:2=32°
Ответ:
Номер: 52BC97
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
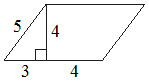
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+4)*4=56
Ответ:56
Номер: CBFF9F
Впишите правильный ответ.

Площадь параллелограмма равна 36, а две его стороны равны 6 и 12. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
36=6*h1
h1=36/6=12
36=12*h1
h1=36/12=3
Ответ:12
Номер: C9F797
Впишите правильный ответ.
В треугольнике ABC известно, что AC=40 , BC=9 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`40^2+9^2=AB^2`
`1600+81=AB^2`
`AB=sqrt(1681)`
AB=41 - диаметр.
R=AB/2=20,5
Ответ:20,5
Номер: 92F597
Впишите правильный ответ.
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(29*12)/2=174
Ответ:
Номер: 962796
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`20^2=16^2+x^2`
`x^2=20^2-16^2`
`x=sqrt(144)`
Ответ:12
Номер: EC029B
Впишите правильный ответ.
Диагональ прямоугольника образует угол 61° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*61°=58° это и будет острый угол между диагоналями.
Ответ:
Номер: EC579C
Впишите правильный ответ.
Диагональ прямоугольника образует угол 65° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*65°=50° это и будет острый угол между диагоналями.
Ответ:
Номер: 69C097
Впишите правильный ответ.

Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите большую высоту.
Решение:
40=5*h1
h1=40/5=9
40=10*h1
h1=40/10=4
Ответ:9
Номер: 3B1F90
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-121°=59°
Ответ:59
Номер: 351F95
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 8°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*8º=16º
Ответ:16
Номер: 328099
Впишите правильный ответ.
В треугольнике ABC известно, что AC=36 , BM — медиана, BM=13. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
36/2=18
Ответ:18
Номер: 4140E2
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 82°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-82°)/2=49°
Ответ:49
Номер: 4CBEEC
Впишите правильный ответ.

В треугольнике ABC угол C равен 124°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-124°=56°
Ответ:
Номер: 4F1AE3
Впишите правильный ответ.
В треугольнике ABC известно, что ∠BAC=48° , AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Решение:
Биссектриса делит угол на два равных, тогда 48°:2=24°
Ответ:
Номер: F7F6E7
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 13 и 4. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(4*13)/2=26`
Ответ:
Номер: FBB6E7
Впишите правильный ответ.

Сторона квадрата равна 3`sqrt2`. Найдите диагональ этого квадрата.
Решение:
По теореме Пифагора
`x^2=(3sqrt2)^2+(3sqrt2)^2`
`x^2=2(3sqrt2)^2`
`x^2=2*9*2`
`x=sqrt36`
х=6
Ответ:6
Номер: 0D7EEE
Впишите правильный ответ.
Высота равнобедренной трапеции, проведённая из вершины C , делит основание AD на отрезки длиной 16 и 17. Найдите длину основания BC.

Решение:
В равнобедренной трапеции проекции боковых сторон на основание равные, то есть блина основания это проекция на нее двух проекций сторон и проекции верхнего основания.
Так как получившиеся отрезки равны 17 и 16, то в большем отрезке как раз проекция одной стороны и верхнего основания. Но так как основания параллельны, то можно утверждать, что при вычитании проекции стороны мы получим реальную величину верхнего основания.
17-16=1
Ответ:
Номер: 7BC7E6
Впишите правильный ответ.

В треугольнике ABC угол C равен 168°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-168°=12°
Ответ:
Номер: 2ABFE8
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 60 и 80. Найдите гипотенузу этого треугольника.

Решение:
602+802=x2
x2=3600+6400
`x=sqrt(10000)=100`
Ответ:100
Номер: D5CFE5
Впишите правильный ответ.

Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Решение:
Средняя линия находится как сумма оснований разделенная на два, тогда
`(2+6)/2=4`
Ответ:
Номер: D8A6E6
Впишите правильный ответ.

Один из углов ромба равен 43°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-43°=137°
Ответ:137
Номер: A840E0
Впишите правильный ответ.

Один из углов ромба равен 99°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-99°=81°
Ответ:81
Номер: CD44EA
Впишите правильный ответ.
В треугольнике два угла равны 31° и 94°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(31º+94º)=55º
Ответ:55
Номер: C2F1EC
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.

Решение:
302+402=x2
x2=900+1600
`x=sqrt(2500)=50`
Ответ:50
Номер: C017E3
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=72/2=36`
Ответ:
Номер: 952CEB
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*40º=80º
Ответ:80
Номер: 9458ED
Впишите правильный ответ.

Основания трапеции равны 4 и 10, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(4+10)/2*5=14/2*5=35`
Ответ:35
Номер: EE5CEF
Впишите правильный ответ.
Основания трапеции равны 3 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
11/2=5,5
Ответ:5,5
Номер: E6AFE5
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+43°)=47°
Ответ:47
Номер: E690E5
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=74/2=37`
Ответ:
Номер: 81EFE0
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 178°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух острых углов, то есть тупой угол будет вычисляться так:
180º-178º/2=91º
Ответ:91
Номер: 8D7AEA
Впишите правильный ответ.
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(46º+78º)=56º
Ответ:56
Номер: 43376B
Впишите правильный ответ.

Один из углов ромба равен 35°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-35°=145°
Ответ:145
Номер: 49F569
Впишите правильный ответ.
В треугольнике два угла равны 48° и 65°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(48º+65º)=67º
Ответ:67
Номер: F27664
Впишите правильный ответ.
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.

Решение:
Так как сумма углов в треугольнике равна 180, то:
180º-(43º+88º)=49º
Ответ:49
Номер: FE9E6C
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
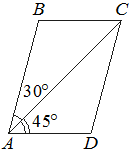
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(45°+30°)=105°
Ответ:105
Номер: FAC266
Впишите правильный ответ.
Биссектриса равностороннего треугольника равна 9`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(9sqrt3)^2+(1/2x)^2=x^2`
`81*3=x^2-(1/2x)^2`
`81*3=x^2 - 1/4x^2`
`81*3=3/4x^2`
`81*4=x^2`
`x=sqrt324`
x=18
Ответ:18
Номер: 70CA68
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

Решение:
162+302=x2
x2=256+900
`x=sqrt(1156)=34`
Ответ:34
Номер: BDF56F
Впишите правильный ответ.

Сторона ромба равна 34, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
У ромба два тупых угла и два острых. Тупой как раз угол 150°, а острый равен 180-150=30°. Получается у нас есть прямоугольный треугольник с углом в 30 градусов. При этом в прямоугольном треугольнике катет лежащий против такого угла равен половине гипотенузы. Тогда высота, которая является как раз таким катетом равна: 34/2=17
Ответ:
Номер: B71163
Впишите правильный ответ.

Один из углов ромба равен 62°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-62°=118°
Ответ:118
Номер: 115B67
Впишите правильный ответ.
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(27*16)/2=216
Номер: 2C9E6C
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=34/2=17`
Ответ:
Номер: 254969
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 196°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух тупых углов, то есть острый угол будет вычисляться так:
180º-196º/2=82º
Ответ:82
Номер: DF3C63
Впишите правильный ответ.
Сторона равностороннего треугольника равна 10`sqrt3`. Найдите биссектрису этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(10sqrt3)^2=(1/2*10sqrt3)^2+x^2`
`100*3=(100*3)/4+x^2`
`100*3-(100*3)/4=x^2`
`x^2=300-75`
`x^2=225`
x=15
Ответ:15
Номер: DEF868
Впишите правильный ответ.
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 17. Найдите площадь этого треугольника.

Решение:
По формуле площади треугольника она равна основание умноженное на высоту и поделить пополам.
S=(18*17)/2=153
Ответ:
Номер: C22763
Впишите правильный ответ.

Один из углов прямоугольной трапеции равен 37°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение:
Два смежных угла в четырехугольнике равны 180 градусам, тогда:
180°-37°=143°
Ответ:143
Номер: 628961
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.

Решение:
122+162=x2
x2=144+256
`x=sqrt(400)=20`
Ответ:20
Номер: 67156A
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух тупых углов, то есть меньший угол будет вычисляться так:
180º-220º/2=70º
Ответ:70
Номер: 384467
Впишите правильный ответ.
Один из острых углов прямоугольного треугольника равен 18°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Второй угол можно найти из условия, что один угол известен, и один угол 90 градусов, тогда:
180°-(90°+18°)=72°
Ответ:72
Номер: 48CD30
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`25^2=7^2+x^2`
`x^2=25^2-7^2`
`x=sqrt(576)`
Ответ:24
Номер: 418831
Впишите правильный ответ.
Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.

Решение:
Если треугольник прямоугольный, то его катеты можно представить как основание и высота. Из формулы площади треугольника:
`S=(a*h)/2`, где a - основание, h - высота можно вычислить площадь треугольника.
`S=(6*7)/2=21`
Ответ:
Номер: F65330
Впишите правильный ответ.

Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(5+13)/2*9=18/2*9=81`
Ответ:81
Номер: 7BF730
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-122)/2=29º
Ответ:
Номер: 71513D
Впишите правильный ответ.
Точки M и N являются серединами сторон AB и BC треугольника ABC , сторона AB равна 31, сторона BC равна 27, сторона AC равна 40. Найдите MN.

Решение:
МN по всем признакам является средней линией, так как ее точки M и N являются серединами сторон AB и BC, а значит к ней применима формула:
`MN=(AC)/2=40/2=20`
Ответ:
Номер: 73C63E
Впишите правильный ответ.
Найдите острый угол параллелограмма ABCD , если биссектриса угла A образует со стороной BC угол, равный 34°. Ответ дайте в градусах.

Решение:
В параллелограмме стороны параллельны, поэтому угол со стороной ВС равен углу со стороной АD как накрест лежащие.
Тогда острый угол 2*34º=68º
Ответ:68
Номер: 7D4C36
Впишите правильный ответ.
Основания трапеции равны 8 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
17/2=8,5
Ответ:8,5
Номер: B9613D
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=104°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-104)/2=38º
Ответ:
Номер: BBF435
Впишите правильный ответ.
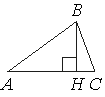
В остроугольном треугольнике ABC проведена высота BH , ∠BAC=9°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
Высота образует прямоугольный треугольник. ∠BAC=9° ∠BHA=90°, тогда
∠ABH=180°-(90°+9°)=81°
Ответ:81
Номер: 161334
Впишите правильный ответ.
В треугольнике ABC известно, что AC=12 , BM — медиана, BM=11. Найдите AM.

Решение:
Медиана делит сторону на два равных отрезка.
12/2=6
Ответ:6
Номер: D74030
Впишите правильный ответ.
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*51°=78° это и будет острый угол между диагоналями.
Ответ:
Номер: DDE935
Впишите правильный ответ.
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение:
Искомый острый угол между диагоналями является вершиной равнобедренного треугольника с наибольшими у основания углами. Наибольшие углы в данном случае это те углы, которые в прямом угле прямоугольника имеют большее значение со смежным углом. Скажем 90 градусов сам угол прямоугольника, а наибольший угол значит более 45 градусов, то есть известный нам угол.
С условием, что в треугольнике все углы 180 градусов, следует что вершина такого треугольника равна 180°-2*47°=86° это и будет острый угол между диагоналями.
Ответ:
Номер: D6FA33
Впишите правильный ответ.
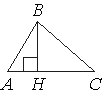
В остроугольном треугольнике ABC проведена высота BH , ∠BAC=48°. Найдите угол ABH. Ответ дайте в градусах.
Решение:
Высота образует прямоугольный треугольник. ∠BAC=9° ∠BHA=90°, тогда
∠ABH=180°-(90°+48°)=42°
Ответ:42
Номер: 54DA37
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
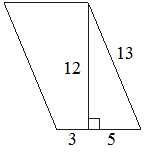
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+5)*12=96
Ответ:96
Номер: A50631
Впишите правильный ответ.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
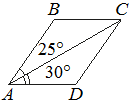
Решение:
Больший угол можно найти из условия, что смежные углы в четырехугольнике равны 180 градусов:
180°-(30°+25°)=125°
Ответ:125
Номер: A97035
Впишите правильный ответ.

Основания трапеции равны 2 и 4, а высота равна 11. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(2+4)/2*11=6/2*11=33`
Ответ:33
Номер: 9B803A
Впишите правильный ответ.

Основания трапеции равны 7 и 19, а высота равна 6. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна сумма оснований разделить на два и умножить на высоту.
`(7+19)/2*6=26/2*6=78`
Ответ:78
Номер: E4B83D
Впишите правильный ответ.

Площадь параллелограмма равна 32, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите бо́льшую высоту.
Решение:
32=8*h1
h1=32/8=4
32=16*h1
h1=32/16=2
Ответ:4
Номер: E39038
Впишите правильный ответ.
Сумма двух углов равнобедренной трапеции равна 352°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Решение:
Имеем сумму двух больших углов, то есть острый угол будет вычисляться так:
180º-352º/2=4º
Ответ:4
Номер: 6B2831
Впишите правильный ответ.
Высота равностороннего треугольника равна 11`sqrt3`. Найдите сторону этого треугольника.

Решение:
По формуле Пифагора, если принять сторону за x, тогда:
`(11sqrt3)^2+(1/2x)^2=x^2`
`121*3=x^2-(1/2x)^2`
`121*3=x^2 - 1/4x^2`
`121*3=3/4x^2`
`121*4=x^2`
`x=sqrt484`
x=22
Ответ:22
Номер: 397439
Впишите правильный ответ.
Найдите площадь параллелограмма, изображённого на рисунке.
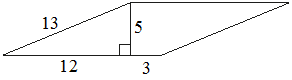
Решение:
Площадь параллелограмма равна произведение высоты на основание.
(3+12)*5=75
Ответ:75
Номер: 365439
Впишите правильный ответ.
Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение:
Больший из отрезков, на которые делит среднюю линию трапеции одна из её диагоналей, равен половине большего основания трапеции, так как этот больший отрезок является по факту средней линией треугольника с этим основанием.
17/2=8,5
Ответ:8,5
Номер: 441D89
Впишите правильный ответ.
В треугольнике ABC известно, что AC=8 , BC=15 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`8^2+15^2=AB^2`
`64+225=AB^2`
`AB=sqrt(289)`
AB=17 - диаметр.
R=AB/2=8,5
Ответ:8,5
Номер: F00986
Впишите правильный ответ.
Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь этого ромба.

Решение:
Сторона ромба равна 12:4=3
При этом высота равна половине стороны, так как высота образует прямоугольный треугольник, где она является катетом против угла в 30 градусов у которого гипотенуза равна стороне.
h=3/2=1,5
В итоге площадь ромба можно найти как произведение основания (стороны), на высоту.
S=3*1,5=4,5
Ответ:4,5
Номер: 7DB985
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`34^2=16^2+x^2`
`x^2=34^2-16^2`
`x=sqrt(900)`
Ответ:30
Номер: 22EA84
Впишите правильный ответ.
Катеты прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.

Решение:
202+212=x2
x2=400+441
`x=sqrt(841)=29`
Ответ:29
Номер: DF9E81
Впишите правильный ответ.

В треугольнике ABC угол C равен 151°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол будет равен 180°-151°=29°
Ответ:
Номер: D8D182
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , tgB=4/7 , BC=35. Найдите AC.
Решение:
Тангенс это отношение противолежащего катета к прилежащему, тогда
AC/BС=tgB
AC=tgB*BC
AC=35*4/7=20
Ответ:20
Номер: D02489
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 134°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-134°)/2=23°
Ответ:23
Номер: A54182
Впишите правильный ответ.
В треугольнике ABC известно, что AB=BC , ∠ABC=106°. Найдите угол BCA. Ответ дайте в градусах.

Решение:
В равностороннем треугольники углы у основания равны, тогда:
(180-106)/2=37º
Ответ:
Номер: A08F8E
Впишите правильный ответ.

Один из углов ромба равен 127°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-127°=53°
Ответ:53
Номер: CBC28C
Впишите правильный ответ.

В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Решение:
CA является диагональю и делит BCD на два равных угла, тогда ACD равен:
(180°-72°)/2=54°
Ответ:54
Номер: CF5988
Впишите правильный ответ.
В треугольнике ABC известно, что AC=6 , BC=8 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Тогда по теореме Пифагора диаметр равен AB=D:
`AC^2+BC^2=AB^2`
`6^2+8^2=AB^2`
`36+64=AB^2`
`AB=sqrt(100)`
AB=10 - диаметр.
R=AB/2=5
Ответ:5
Номер: 951C84
Впишите правильный ответ.
В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора:
`13^2=5^2+x^2`
`x^2=13^2-5^2`
`x=sqrt(144)`
Ответ:12
Номер: E96385
Впишите правильный ответ.

Один из углов параллелограмма равен 33°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение:
Искомый угол находим вычитая из 180 градусов известный. Так как в четырехугольнике два смежных угла равны 180 градусам.
180°-33°=147°
Ответ:147
Номер: EA2B8E
Впишите правильный ответ.
Сторона равностороннего треугольника равна 16`sqrt3`. Найдите биссектрису этого треугольника.

Решение:
Высота в равностороннем треугольнике перпендикулярна основанию. По теореме Пифагора, если известна гипотенуза (сторона), тогда:
`(16sqrt3)^2=(1/2*16sqrt3)^2+x^2`
`256*3=(256*3)/4+x^2`
`256*3-(256*3)/4=x^2`
`x^2=768-192`
`x^2=576`
x=24
Ответ:24
Номер: 65EF81

