Первое задание ЕГЭ по математике профильного уровня - из раздела геометрии. Базовый уровень сложности, краткий ответ.
В новом банке ФИПИ заданий по геометрии для ЕГЭ профильного уровня 37 штук. В старом помимо них еще хрЕнова гора, плюс задания с масегэ, и это все задания, которые могут выпасть вам на реальном профильном ЕГЭ по математике.
Мы собрали для вас ВСЕ задания из ОБОИХ банков ФИПИ. Без дублей.
Задания линейки 1 ЕГЭ мат профиль, новый банк ФИПИ
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=10 , BC=√19. Найдите cosA.
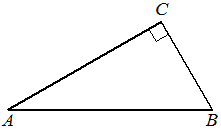
КЭС: 5.1.1 Треугольник
Решение:
0,9
Находим неизвестный катет по теореме Пифагора.
`10^2=sqrt(19)^2+x^2`
`x^2=10^2-sqrt(19)^2`
`x^2 = 81`
`х=9`
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
`cosA=9/10=0,9`
Ответ: 0,9
Номер: A33A46
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 41°. Найдите величину угла AOD. Ответ дайте в градусах.
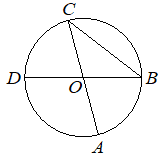
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
98
CO=OB из условия, так как это половина диаметра, то есть радиус. Значит треугольник OCB равнобедренный, а углы у основания равны.
Тогда угол вершины этого треугольника равен ∠COB = 180-2*41= 98º
При этом ∠AOD=∠COB = 98º
Ответ: 98
Номер: 80A34C
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=10 , AC=√51. Найдите sinA .
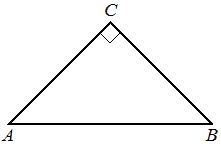
КЭС: 5.1.1 Треугольник
Решение:
0,7
Вначале найдем неизвестный катет
`10^2=sqrt(51)^2+x^2`
`x^2 = 10^2-sqrt(51)^2`
`x^2 = 49`
`x = 7`
Cинус угла равен отношению противоположного катета к гипотенузе.
`sinA=7/10=0,7`
Ответ: 0,7
Номер: 7FA4FB
Впишите правильный ответ.
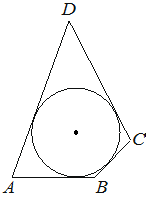
Найдите величину угла ACO, если его сторона CA касается окружности с центром O, отрезок CO пересекает окружность в точке B (см. рисунок), а дуга AB окружности, заключённая внутри этого угла, равна 66°. Ответ дайте в градусах.
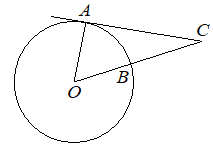
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
24
АС-касательная, тогда ∠СAO=90º Градусная мера дуги указывает на то, что ∠AOB=66º, тогда
∠ACO=180º-90º-66º=24º
Ответ: 24
Номер: 84E9F2
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=10, AC=√91. Найдите sinA.

КЭС: 5.1.1 Треугольник
Решение:
0,3
Вначале найдем неизвестный катет
`10^2=sqrt(91)^2+x^2`
`x^2 = 10^2-sqrt(91)^2`
`x^2 = 100-91=9`
`x=3`
Cинус угла равен отношению противоположного катета к гипотенузе.
`sinA=3/10=0,3`
Ответ: 0,3
Номер: FFBD0F
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 61° , угол CAD равен 37°. Найдите угол ABC . Ответ дайте в градусах.
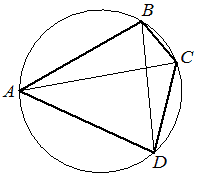
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
98
Вписанные в окружность углы опирающиеся на одну и ту же дугу равны, тогда
∠CAD=∠CBD=37°
тогда
∠ABD+∠CBD=37°+61°=98°
Ответ: 98
Номер: 3CF402
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=5 , BC=4. Найдите cosA .
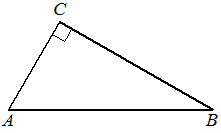
КЭС: 5.1.1 Треугольник
Решение:
0,6
Находим неизвестный катет по теореме Пифагора.
52 = 42+x2
x2 = 52-42
x2 = 25-16
x2 =9
х = 3
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
`cosA = 3/5=0,6`
Ответ: 0,6
Номер: 847B0B
Впишите правильный ответ.
В треугольнике ABC сторона AB равна `3sqrt2`, угол C равен 135°. Найдите радиус описанной около этого треугольника окружности.
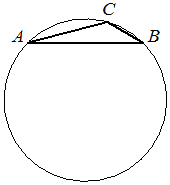
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
3
По теореме синусов:
`(AB)/(sinC)=2R`
`(3sqrt2)/(sqrt2/2)=2R`
2R =6
R=3
Ответ: 3
Номер: 1DD37A
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 16°. Найдите вписанный угол ACB. Ответ дайте в градусах.
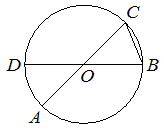
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
82
∠DOA=∠COB=16° как углы накрест лежащие
`(180°-16°)/2=82°` углы у основания равны, так как треугольник равнобедренный
Ответ: 82
Номер: BC72B9
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 98°, угол CAD равен 44°. Найдите угол ABD. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
54
Вписанные в окружность углы опирающиеся на одну и ту же дугу равны, тогда
∠CAD=∠CBD=44°
тогда
∠ABС-∠CBD=∠ABD=98°-44°=54°
Ответ: 54
Номер: 9C6FBB
Впишите правильный ответ.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AD. Найдите площадь трапеции BCDE .
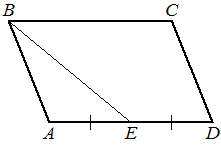
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
21
Площадь параллелограмма равна
S=AD*h
Площадь трапеции
S=`(AD+ED)/2*h=(1,5AD)/2 * h` = 0,75h
То есть 0,75 от площади параллелограмма равна площадь трапеции
28*0,75=21
Ответ:21
Номер: F12D1C
Впишите правильный ответ.
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB . Найдите площадь трапеции ABED.
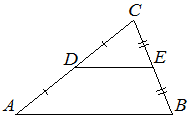
КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
18
Средняя линия равна половине основания, а высота половине высоты, при этом исходя из формулы площади
`S_(ABC)=1/2*AB*h`
`S_(DCE)=1/2*1/2 AB*1/2 h=1/2*1/4*AB*h`
То есть площадь меньше в 4 раза. То есть площадь трапеции равна `3/4=0,75` от площади треугольника
24*0,75=18
Ответ: 18
Номер: 5B3F1A
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 136°. Найдите угол BCD. Ответ дайте в градусах.
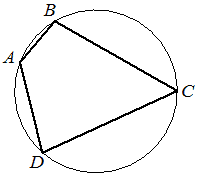
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
44
В четырехугольнике вписанном в окружность противоположные углы равны в сумме 180º, тогда
180º-136º=44º
Ответ: 44
Номер: CE4D1D
Впишите правильный ответ.
Площадь параллелограмма ABCD равна 24. Точка E — середина стороны AD. Найдите площадь трапеции BCDE.

КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
18
Площадь параллелограмма равна
S=AD*h
Площадь трапеции
`S= (AD+ED)/2*h=(1,5AD)/2 * h` = 0,75h
То есть 0,75 от площади параллелограмма равна площадь трапеции
24*0,75=18
Ответ:18
Номер: 282EDC
Впишите правильный ответ.
Острый угол B прямоугольного треугольника ABC равен 21°. Найдите величину угла между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла C. Ответ дайте в градусах.
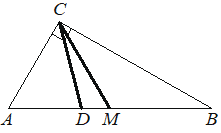
КЭС: 5.1.1 Треугольник 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
24
Медиана СМ является половиной гипотенузы, значит ∠MCB = ∠MBC = 21° так как CMB равнобедренный треугольник. Значит ∠CMB = 180º-2*21º=138º.
При этом ∠AMC = 180-138=42º, а ∠BCD = 45º, тогда ∠CDM = 180°-21°-45°=114°. Значит угол ∠DCM = 180°-114°-42°=24°
Ответ: 24
Номер: B54D55
Впишите правильный ответ.
Найдите центральный угол, если он на 28° больше острого вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.
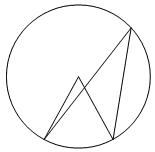
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
56
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*28°=56°
Ответ: 56
Номер: 907C53
Впишите правильный ответ.
Две стороны треугольника равны 15 и 18. Высота, опущенная на большую из этих сторон, равна 10. Найдите длину высоты, опущенной на меньшую из этих сторон треугольника.
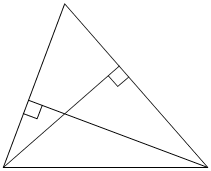
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
12
Соотношение высот можно найти из формулы площади треугольника.
`S=1/2*18*10`
`S=1/2*15*h`
`1/2*18*10=1/2*15*h`
`h=180/15=12`
Ответ: 12
Номер: 3B5E5D
Впишите правильный ответ.
Две стороны треугольника равны 21 и 28. Высота, опущенная на бо́льшую из этих сторон, равна 15. Найдите высоту, опущенную на меньшую из этих сторон треугольника.

КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
20
Соотношение высот можно найти из формулы площади треугольника.
`S=1/2*28*15`
`S=1/2*21*h`
`1/2*28*15=1/2*21*h`
`h=280/21=20`
Ответ: 20
Номер: CA58AE
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 32°. Найдите угол AOD. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
116
∠COB = 180°-2*32°=116° углы у основания равны, так как треугольник равнобедренный
∠DOA=∠COB=116° как углы накрест лежащие
Ответ: 116
Номер: FDDACE
Впишите правильный ответ.
Два угла вписанного в окружность четырёхугольника равны 99 и 117. Найдите бо́льший из оставшихся углов. Ответ дайте в градусах.
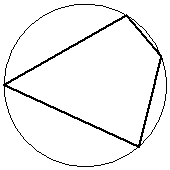
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
81
Во вписанной четырехугольнике противоположные углы равны 180 градусам, значит
180-99=81º
Ответ: 81
Номер: A9DCC5
Впишите правильный ответ.
Стороны параллелограмма равны 18 и 20. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите длину высоты, опущенной на большую сторону параллелограмма.
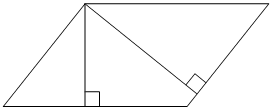
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
9
Исходя из площади нахождения параллелограмма:
S=18*10
S=20*h
составим уравнение
18*10=20*h
`h=180/20=9`
Ответ: 9
Номер: 697AC9
Впишите правильный ответ.
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
6
Средняя линия равна половине основания, а высота половине высоты, при этом исходя из формулы площади
`S_(ABC)=1/2*AB*h`
`S_(DCE)=1/2*1/2AB*1/2h=1/2*1/4*AB*h`
То есть площадь меньше в 4 раза.
24/4=6
Ответ: 6
Номер: F34697
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 61°. Найдите угол AOD. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
58
∠COB = 180°-2*61°=58° углы у основания равны, так как треугольник равнобедренный
∠DOA=∠COB=58° как углы накрест лежащие
Ответ: 58
Номер: FFE399
Впишите правильный ответ.
Угол ACO равен 57°. Его сторона CA касается окружности с центром в точке O. Отрезок CO пересекает окружность в точке B (см. рисунок). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
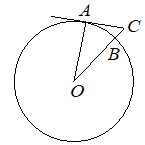
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
33
АС-касательная, тогда ∠СAO=90º Градусная мера дуги равна ∠AOB, тогда
∠AOB=180º-90º-57º=33º
Ответ: 33
Номер: CC7A9E
Впишите правильный ответ.
Найдите угол ACO, если его сторона CA касается окружности с центром O, отрезок CO пересекает окружность в точке B (см. рис.), а дуга AB окружности, заключённая внутри этого угла, равна 17° . Ответ дайте в градусах.
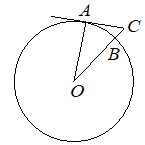
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
73
АС-касательная, тогда ∠СAO=90º Градусная мера дуги равна равна ∠AOB = 17°, тогда
∠AСB=180º-90º-17º=73º
Ответ: 73
Номер: 0005E9
Впишите правильный ответ.
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.

КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
16
Исходя из площади нахождения параллелограмма:
S=24*18
S=27*h
составим уравнение
18*24=27*h
`h=432/27=16`
Ответ: 16
Номер: DF24E0
Впишите правильный ответ.
Центральный угол на 32° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
32
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*32°=64°, то есть центральный как раз 32
Ответ: 32
Номер: 30B4E7
Впишите правильный ответ.
Найдите величину центрального угла, если он на 69° больше острого вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.
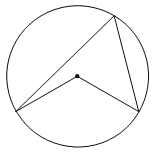
КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
138
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*69°=138°
Ответ: 138
Номер: 01BE6F
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
33
∠DOA=∠COB=114° как углы накрест лежащие
`∠COB = (180°-114°)/2=33°` углы у основания равны, так как треугольник равнобедренный
Ответ: 33
Номер: AD5F64
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
25
∠DOA=∠COB=130° как углы накрест лежащие
`∠COB = (180°-130°)/2=25°` углы у основания равны, так как треугольник равнобедренный
Ответ: 25
Номер: 9B7E69
Впишите правильный ответ.
Центральный угол на 29° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите величину вписанного угла. Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
29
Вписанный угол измеряется половиной дуги, на которую он опирается. Так как полный угол для дуги в градусах берется относительно центра, то центральный угол будет соответственно в два раза больше.
2*29°, а вот вписанный будет равен как раз 29°
Ответ: 29
Номер: 3D4E60
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 58° , угол CAD равен 39° . Найдите угол ABC . Ответ дайте в градусах.

КЭС: 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
97
∠CBD=∠CAD = 39°
тогда ∠ABC=39°+58°=97°
Ответ: 97
Номер: D7423F
Впишите правильный ответ.
Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AD. Найдите площадь треугольника ABE.

КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
15
Площадь параллелограмма равна
S=AD*h
Площадь трапеции
S=`(ЕD)/2*h=(0,5AD)/2 * h` = 0,25h
То есть 0,25 от площади параллелограмма равна площадь треугольника
24*0,25=15
Ответ: 15
Номер: B3E586
Впишите правильный ответ.
Угол ACO равен 62°. Его сторона CA касается окружности с центром в точке O. Отрезок CO пересекает окружность в точке B (см. рис.). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
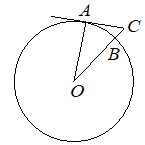
КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Решение:
28
АС-касательная, тогда ∠СAO=90º Градусная мера дуги равна ∠AOB, тогда
∠AOB=180º-90º-62º=28º
Ответ: 28
Номер: 21628C
Впишите правильный ответ.
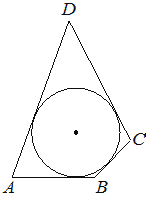
В четырёхугольник ABCD вписана окружность, AB=10, CD=17. Найдите периметр четырёхугольника ABCD.
КЭС: 5.1.4 Окружность и круг 5.1.6 Многоугольник. Сумма углов выпуклого многоугольника 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
54
К свойствам описанного четырехугольника относится свойство, - суммы длин противоположных сторон равны, тогда
(10+17)*2=54 периметр четырехугольника
Ответ: 54
Номер: 59978F
Впишите правильный ответ.
Площадь треугольника ABC равна 60, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
45
Средняя линия равна половине основания, а высота половине высоты, при этом исходя из формулы площади
`S_(ABC)=1/2*AB*h`
`S_(DCE)=1/2*1/2AB*1/2h=1/2*1/4*AB*h`
То есть площадь меньше в 4 раза. То есть площадь трапеции равна 3/4=0,75 от площади треугольника
60*0,75=45
Ответ:45
Номер: EE7C83
Впишите правильный ответ.
В треугольнике ABC сторона AB равна 2√3, угол C равен 120°. Найдите радиус описанной около этого треугольника окружности.

КЭС: 5.1.1 Треугольник 5.1.4 Окружность и круг 5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
2
По теореме синусов:
`(AB)/(sinC)=2R`
`(2sqrt3)/(sqrt3/2)=2R`
2R =4
R=2
Ответ: 2
Номер: 8D3587
Задания из старого банка ФИПИ
Периметр прямоугольной трапеции, описанной около окружности, равен 40, её большая боковая сторона равна 11. Найдите радиус окружности.

Решение:
Признак описанного четырёхугольника – суммы противоположных сторон равны
a+c = b+d
P = AB + CD + AD + BC = 40 => AB + CD = 20
AB = 20 – 11 = 9
`R = 9/2 = 4,5`
Ответ: 4,5
Номер: 47EA41
Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.

Решение:
...
Ответ:
Номер: C9FC03
Периметр прямоугольной трапеции, описанной около окружности, равен 24, её большая боковая сторона равна 7. Найдите радиус окружности.

Решение:
...
Ответ:
Номер: 07965E
Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.

Решение:
...
Ответ:
Номер: ECF938
Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.

Решение:
Признаком описанного четырехугольника является свойство, когда сумма противоположных сторон равна.
AB +CD = BC + DA
Средняя линия трапеции равна половине суммы оснований.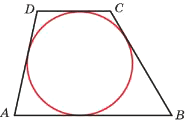
1) AB+CD=15+22=BC+AD
BC+AD=37
2) Ср. линия = `(BC+AD)/2=37/2=18,5`
Ответ: 18,5
Номер: F6F40C
Боковые стороны трапеции, описанной около окружности, равны 9 и 12. Найдите среднюю линию трапеции.

Решение:
...
Ответ:
Номер: 1F11DD
Боковые стороны трапеции, описанной около окружности, равны 12 и 15. Найдите среднюю линию трапеции.

Решение:
...
Ответ:
Номер: 1E11A7
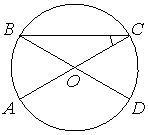
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Решение:
∠BOC = 114°
△BOC – р/б
`∠OCB = (180-114)/2 = 33°`
Ответ: 33
Номер: 29D9FB
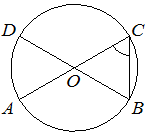
Отрезки AC и BD — диаметры окружности с центром O . Угол AOD равен 68° . Найдите вписанный угол ACB. Ответ дайте в градусах.
Решение:
...
Ответ:
Номер: 87911B
Отрезки AC и BD — диаметры окружности с центром O . Угол AOD равен 130° . Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 9B7E69
Отрезки AC и BD — диаметры окружности с центром O . Угол AOD равен 16° . Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: BC72B9
Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: AD5F64
Отрезки AC и BD — диаметры окружности с центром O . Угол ACB равен 56° . Найдите угол AOD. Ответ дайте в градусах.
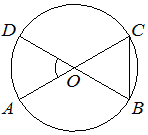
Решение:
...
Ответ:
Номер: CE2813
Отрезки AC и BD — диаметры окружности с центром O . Угол ACB равен 32° . Найдите угол AOD. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: FDDACE
Отрезки AC и BD — диаметры окружности с центром O . Угол ACB равен 61°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: FFE399
Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности. Ответ дайте в градусах.
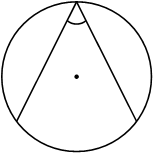
Решение:
Вписанный угол равен половине дуги, на которую он опирается
Дуга `BC = 1/5 * 360 = 72 °`
`∠d = 72 * 1/2 = 36°`
Ответ: 36
Номер: 343A64
Найдите вписанный угол, опирающийся на дугу, равную 7/18 окружности. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: EB2CDC
Найдите вписанный угол, опирающийся на дугу, равную 5/12 окружности. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 25C9F9
Найдите вписанный угол, опирающийся на дугу, равную 13/36 окружности. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 0745B2
На окружности отмечены точки A, B и C. Дуга окружности AC, не содержащая точку B, составляет 200°. Дуга окружности BC, не содержащая точку A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.
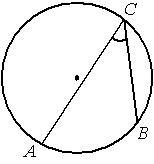
Решение:
Вписанный угол равен половине дуги, на которую он опирается
Дуга AB = 360 -200 -80 = 80°
`∠ACB = 80/2 = 40°`
Ответ: 40
Номер: 65729E
На окружности отмечены точки A , B и C . Дуга окружности AC , не содержащая точку B , составляет 120° . Дуга окружности BC , не содержащая точку A , составляет 82° . Найдите вписанный угол ACB . Ответ дайте в градусах.
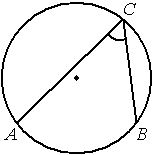
Решение:
...
Ответ:
Номер: 03E351
На окружности отмечены точки A , B и C . Дуга окружности AC , не содержащая точку B , составляет 105° . Дуга окружности BC , не содержащая точку A , составляет 91° . Найдите вписанный угол ACB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 8F88EA
На окружности отмечены точки A , B и C . Дуга окружности AC , не содержащая точку B , составляет 125° . Дуга окружности BC , не содержащая точку A , составляет 79° . Найдите вписанный угол ACB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: FF92F2
На окружности отмечены точки A , B и C . Дуга окружности AC , не содержащая точку B , составляет 165° . Дуга окружности BC , не содержащая точку A , составляет 55° . Найдите вписанный угол ACB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 35FBFB
На окружности отмечены точки A , B и C . Дуга окружности AC , не содержащая точку B, составляет 110° . Дуга окружности BC , не содержащая точку A , составляет 88° . Найдите вписанный угол ACB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 8A3DB9
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 58° , угол CAD равен 39° . Найдите угол ABC . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: D7423F
Два угла вписанного в окружность четырёхугольника равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
Решение:
Признак вписанного четырехугольника
∠A + ∠C = 180°
∠B + ∠D = 180°
∠C = 180 – 56 = 124°
∠D = 180 – 77 = 103°
Ответ: 103
Номер: C3174D
Два угла вписанного в окружность четырёхугольника равны 59° и 83°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
Решение:
...
Ответ:
Номер: F24900
Два угла вписанного в окружность четырёхугольника равны 63° и 76° . Найдите меньший из оставшихся углов. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: EB4D59
Два угла вписанного в окружность четырёхугольника равны 78° и 113° . Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 51281C
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 82°, угол ABD равен 47°. Найдите угол CAD. Ответ дайте в градусах.
Решение:
Вписанный угол равен половине дуги, на которую он опирается
∠CBD = 82 – 47 = 35°
Дуга CD = 2 * 35 = 70°
`∠ CAD = 1/2 * 70 = 35°`
Ответ: 35
Номер: F62324
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 136° . Найдите угол BCD . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: CE4D1D
Угол ACO равен 27°, где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B (см. рис.). Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.

Решение:
Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Центральный угол равен градусной мере дуги, на которую он опирается.
∠AOC = 180 – 90 – 27 = 63°
Дуга AB = 63°
Ответ: 63
Номер: A6532B
Угол ACO равен 28°. Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.
Решение:
∠AOC = 180 – 90 – 28 = 62°
∠AOD = 180 – 62 = 118°
Дуга AD = 118°
Ответ: 118
Номер: 292C86
Угол ACB равен 54° . Градусная мера дуги AB окружности, не содержащей точек D и E , равна 138°. Найдите угол DAE. Ответ дайте в градусах.
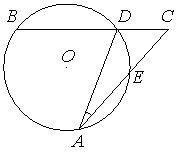
Решение:
Вписанный угол равен половине дуги, на которую он опирается
`∠BDA = 1/2 * 138 = 69°`
∠ADC = 180 – 69 = 111°
∠DAC = 180 – 111 – 54 = 15°
Ответ: 15
Номер: 6328DF
Угол ACO равен 57°. Его сторона CA касается окружности с центром в точке O. Отрезок CO пересекает окружность в точке B (см. рисунок). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
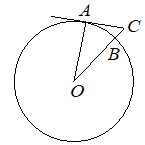
Решение:
...
Ответ:
Номер: CC7A9E
Найдите угол ACO , если его сторона CA касается окружности с центром O , отрезок CO пересекает окружность в точке B (см. рис.), а дуга AB окружности, заключённая внутри этого угла, равна 17° . Ответ дайте в градусах.
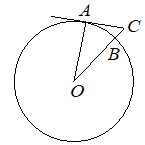
Решение:
...
Ответ:
Номер: 0005E9
Угол ACO равен 62° . Его сторона CA касается окружности с центром в точке O . Отрезок CO пересекает окружность в точке B (см. рис.). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
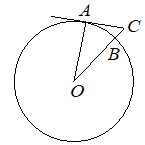
Решение:
...
Ответ:
Номер: 21628C
Через концы A и B дуги окружности с центром O проведены касательные AC и BC . Меньшая дуга AB равна 58° . Найдите угол ACB . Ответ дайте в градусах.
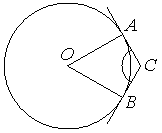
Решение:
Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Центральный угол равен градусной мере дуги, на которую он опирается.
Сумма углов четырехугольника 360°
∠AOB = 58°
∠ACB = 360 – 90 – 90 – 58 = 122°
Ответ: 122
Номер: 0EB251
Найдите величину центрального угла, если он на 69° больше острого вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 01BE6F
Центральный угол на 32° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 30B4E7
Центральный угол на 29° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите величину вписанного угла. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 3D4E60
В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 5°. Найдите угол B. Ответ дайте в градусах.
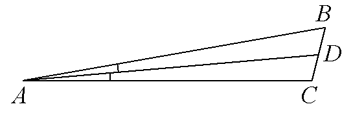
Решение:
∠A=10°
∠B=180-104-10=66°
Ответ: 66
Номер: 1A845D
В треугольнике ABC AD — биссектриса, угол C равен 105°, угол CAD равен 7°. Найдите угол B. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: C08947
В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 6°. Найдите угол B . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 8A79D6
В треугольнике ABC AD — биссектриса, угол C равен 103° , угол CAD равен 7°. Найдите угол B. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: C04782
В треугольнике ABC AD — биссектриса, угол Cравен 103°, угол CADравен 4°. Найдите угол B. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: F66398
В треугольнике ABC AD — биссектриса, угол C равен 102° , угол CAD равен 2°. Найдите угол B. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 17C2E0
В треугольнике ABC CD — медиана, угол C равен 90° , угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.
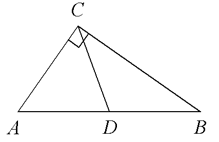
Решение:
Свойство медианы. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы
1) ∠BCD = 35°
2) ∠ACD = 90 - 35 = 55°
Ответ: 55
Номер: 5B17F7
В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14° . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
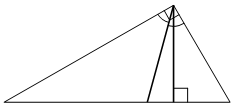
Решение:
1) ∠BCH=45-14=31º
2) ΔBCH: ∠B = 180-90-31=59º
3) ΔABC: ∠A = 180-90-59=31º
Ответ: 31
Номер: 70BEF2
Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14° . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
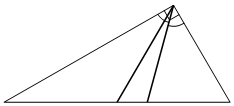
Решение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
1) ∠BCK=45º
2) ∠ACM=90-45-14=31º
3) ∠A = 31º так как ΔACM равнобедренный.
Ответ: 31
Номер: CAC0BA
Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 19°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 6948D5
Острый угол B прямоугольного треугольника ABC равен 210 . Найдите величину угла между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: B54D55
Острые углы прямоугольного треугольника равны 84° и 6° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
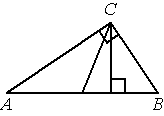
Решение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
1) ΔBCH: ∠BCH=180-90-84=6º
2) ∠ACM =6 так как ΔACM равнобедренный
3) ∠MСH = 90-6-6=78º
Ответ: 78
Номер: F1150D
Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 15650E
Острые углы прямоугольного треугольника равны 87° и 3° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 891BD1
Острые углы прямоугольного треугольника равны 62° и 28° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 4C1DAE
В остроугольном треугольнике ABC угол A равен 78°, BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE. Ответ дайте в градусах.
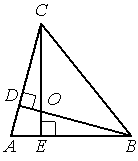
Решение:
...
Ответ:
Номер: 5B0518
В остроугольном треугольнике ABC угол A равен 72° , BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE . Ответ дайте в градусах.
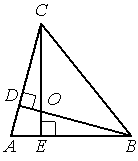
Решение:
...
Ответ:
Номер: C053C7
В остроугольном треугольнике ABC угол A равен 69° , BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE . Ответ дайте в градусах.
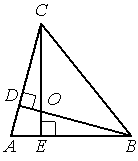
Решение:
...
Ответ:
Номер: 0DE16C
В остроугольном треугольнике ABC угол A равен 87° , BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE . Ответ дайте в градусах.
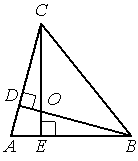
Решение:
...
Ответ:
Номер: B10C80
Один угол параллелограмма больше другого на 40° . Найдите меньший угол. Ответ дайте в градусах.
Решение:
В параллелограмме сумма углов, прилегающих к любой стороне, равна 180 градусам.
∝+∝+40=180
2∝ = 140
∝ =70°
Ответ: 70
Номер: 2E0A28
Один угол параллелограмма больше другого на 52° . Найдите больший угол. Ответ дайте в градусах.

Решение:
В параллелограмме сумма углов прилегающих к любой стороне равна 180 градусам.
∝+∝-52=180
2∝ = 232
∝ = 116
Ответ: 116
Номер: 3C09A9
В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
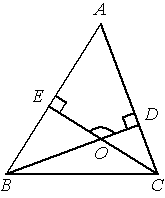
Решение:
Рассмотрим четырехугольник ADOE.
∠DOE=360-90-90-56=124°
Ответ: 124
Номер: A4D931
В треугольнике ABC угол A равен 68°, углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.
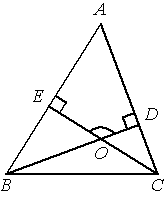
Решение:
...
Ответ:
Номер: FBB82D
В треугольнике ABC угол A равен 44°, углы B и C — острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 9B7123
В треугольнике ABC угол A равен 46° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 4E8056
В треугольнике ABC угол A равен 58° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 75A457
В треугольнике ABC угол A равен 50° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 119550
В треугольнике ABC угол A равен 64° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 4739A4
В треугольнике ABC угол A равен 49° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 02E0A6
В треугольнике ABC угол A равен 47° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 7209AE
В треугольнике ABC угол A равен 53° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: DDC3A1
В треугольнике ABC угол A равен 61° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 735091
В треугольнике ABC угол A равен 62° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 284E9A
В треугольнике ABC угол A равен 67° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 8CD291
В треугольнике ABC угол A равен 70° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 532BE8
В треугольнике ABC угол A равен 52° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 952E99
В треугольнике ABC угол A равен 43° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 64D50B
В треугольнике ABC угол A равен 65° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 80FA73
В треугольнике ABC угол A равен 41° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 5930B0
В треугольнике ABC угол A равен 40° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: BCBD13
В треугольнике ABC угол A равен 59° , углы B и C — острые, высоты BD и CE пересекаются в точке O . Найдите угол DOE . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 0687B6
В треугольнике ABC угол C равен 58° , биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.
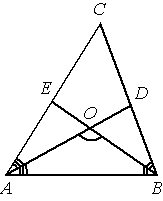
Решение:
∠A+∠B=180-58=122°
`1/2∠A+1/2∠B=122/2=61`°
∠AOB=180-61=119°
Ответ: 119
Номер: 540F92
В треугольнике ABC угол C равен 66° , биссектрисы AD и BE пересекаются в точке O . Найдите угол AOB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: ADDBA5
В треугольнике ABC угол C равен 78° , биссектрисы AD и BE пересекаются в точке O . Найдите угол AOB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 88C3A9
В треугольнике ABC угол C равен 74° , биссектрисы AD и BE пересекаются в точке O . Найдите угол AOB . Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 7A406A
В треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 32°. Найдите угол B. Ответ дайте в градусах.
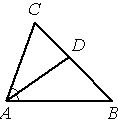
Решение:
...
Ответ:
Номер: AF2E4F
В треугольнике ABC AD — биссектриса, угол Cравен 62°, угол CADравен 31°. Найдите угол B. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 50EE9E
В ромбе ABCD угол CDA равен 78°. Найдите угол ACB. Ответ дайте в градусах.
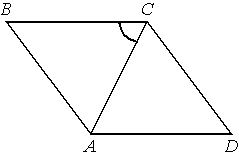
Решение:
1) ∠B = 78
2) AB=BC
⇒ ΔABC равнобедренный
3) `∠ACB =(180-78)/2=51`
Ответ: 51
Номер: 257EE0
В ромбе ABCD угол DAB равен 148°. Найдите угол BDC. Ответ дайте в градусах.
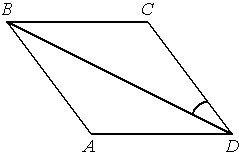
Решение:
...
Ответ:
Номер: 71BD8E
В ромбе ABCD угол BCD равен 48° . Найдите угол DBA . Ответ дайте в градусах.
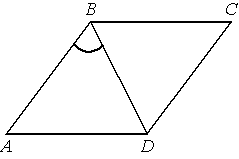
Решение:
...
Ответ:
Номер: 175BFE
В ромбе ABCD угол ABC равен 150° . Найдите угол ACD . Ответ дайте в градусах.
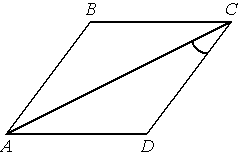
Решение:
...
Ответ:
Номер: 778FB3
В треугольнике ABC угол A равен 37°, стороны AC и BC равны. Найдите угол C. Ответ дайте в градусах.
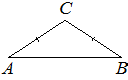
Решение:
∠C=180-37-37=106°
Ответ: 106
Номер: 8286C4
В треугольнике ABC угол C равен 102° , стороны AC и BC равны. Найдите угол A . Ответ дайте в градусах.

Решение:
∠A=(180-102)/2=39°
Ответ: 39
Номер: 7AFD6F
В треугольнике ABC AB=BC, AC=14, высота CH равна 7. Найдите синус угла ACB.
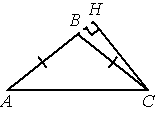
Решение:
1) ΔAHC
`sin∠A = 7/14 = 1/2 = 0,5`
2) sin∠ACB = 0,5
Ответ: 0,5
Номер: 387739
В треугольнике ABC AB=BC , AC=16 , высота CH равна 4. Найдите синус угла ACB .

Решение:
...
Ответ:
Номер: 1397F6
В треугольнике ABC AB=BC , AC=2 , высота CH равна 1. Найдите синус угла ACB .

Решение:
...
Ответ:
Номер: D53519
В треугольнике ABC AB=BC , AC=15 , высота CH равна 6. Найдите синус угла ACB .

Решение:
...
Ответ:
Номер: 1F01DD
В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC.
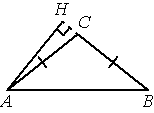
Решение:
1) ΔABH
`sin∠B = 8/20 = 4/10 = 0,4`
2) sin∠BAC = 0,4
Ответ: 0,4
Номер: B26F8E
В треугольнике ABC AC=BC , AB=10 , высота AH равна 3. Найдите синус угла BAC .

Решение:
...
Ответ:
Номер: 87AB89
В треугольнике ABC AB=BC , AC=30 , высота CH равна 27. Найдите синус угла ACB .
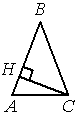
Решение:
...
Ответ:
Номер: 6D9CBC
В треугольнике ABC AB=BC , AC=20 , высота CH равна 16. Найдите синус угла ACB .

Решение:
...
Ответ:
Номер: 6E360C
В треугольнике ABC AB=BC , AC=24 , высота CH равна 18. Найдите синус угла ACB .

Решение:
...
Ответ:
Номер: A78362
В треугольнике ABC AC=BC , AB=10 , высота AH равна 9. Найдите синус угла BAC .
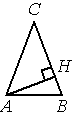
Решение:
...
Ответ:
Номер: 2EBC0B
В треугольнике ABC AC=BC , AB=30 , высота AH равна 24. Найдите синус угла BAC .

Решение:
...
Ответ:
Номер: DAFA32
В треугольнике ABC AC=BC , AB=5 , высота AH равна 4. Найдите синус угла BAC .

Решение:
...
Ответ:
Номер: B7BA85
В треугольнике ABC AC=BC, AB=14, AH — высота, BH=7. Найдите косинус угла BAC.
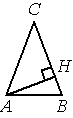
Решение:
...
Ответ:
Номер: 7BCA6B
В треугольнике ABC AC=BC, AB=15, AH — высота, BH=6. Найдите косинус угла BAC.

Решение:
1) ∠A =∠B
2) ΔABH
`сos∠B = 6/15 = 2/15 = 0,4`
2) cos∠BAC = 0,4
Ответ: 0,4
Номер: C18485
В треугольнике ABC AC=BC , AB=12 , AH — высота, BH=3 . Найдите косинус угла BAC .

Решение:
...
Ответ:
Номер: 4BDC28
В треугольнике ABC AC=BC , AB=10 , AH — высота, BH=5 . Найдите косинус угла BAC .

Решение:
...
Ответ:
Номер: 89B5EE
В треугольнике ABC AC=BC , AB=8 , AH — высота, BH=2 . Найдите косинус угла BAC .

Решение:
...
Ответ:
Номер: 711164
В треугольнике ABC AC=BC , AB=12 , AH — высота, BH=6 . Найдите косинус угла BAC .

Решение:
...
Ответ:
Номер: F1733B
В треугольнике ABC угол C равен 90°, BC=6, AB=10. Найдите sinB.
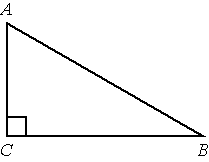
Решение:
1) `10^2=6^2+AC^2`
`100=36+AC^2`
`AC^2 =64`
AC =8
2) `sinB=8/10=0,8`
Ответ: 0,8
Номер: 27BB40
В треугольнике ABC угол C равен 90°, BC=12√3, AB=24. Найдите sinB.

Решение:
...
Ответ:
Номер: F227D1
В треугольнике ABC угол C равен 90° , BC=8√6 , AB=20 . Найдите sinB .

Решение:
...
Ответ:
Номер: 0A6FEF
В треугольнике ABC угол C равен 90° , BC=3√21 , AB=15 . Найдите sinB .

Решение:
...
Ответ:
Номер: 817F41
В треугольнике ABC угол C равен 90° , sinA=0,8. Найдите sinB .

Решение:
`sin^2B+cos^2B=1`
`sin^2B+0,64=1`
`sin^2B=0,36`
`sinB=0,6`
Ответ: 0,6
Номер: CD84BB
В треугольнике ABC угол C равен 90° , AB=10 , AC=√91 . Найдите sinA .

Решение:
...
Ответ:
Номер: FFBD0F
В треугольнике ABC угол C равен 90° , AB=40 , AC=4√51 . Найдите sinA .

Решение:
...
Ответ:
Номер: F538A3
В треугольнике ABC угол C равен 90° , AB=30 , AC=3√19 . Найдите sinA .

Решение:
...
Ответ:
Номер: ACE58C
В треугольнике ABC угол Cравен 90°, AB=15, BC=9. Найдите cosA.

Решение:
...
Ответ:
Номер: BA38D8
В треугольнике ABC угол Cравен 90°, AB=25, BC=24. Найдите cosA.

Решение:
...
Ответ:
Номер: 6C25D6
В треугольнике ABC угол C равен 90° , AB=5 , BC=√21 . Найдите cosA .

Решение:
...
Ответ:
Номер: 7C0AAE
В треугольнике ABC угол C равен 90° , AB=10 , BC=8 . Найдите cosA .

Решение:
...
Ответ:
Номер: CB6791
В треугольнике ABC угол C равен 90° , AB=10 , BC=√19 . Найдите cosA .

Решение:
...
Ответ:
Номер: C76503
В треугольнике ABC угол C равен 90° , AB=6 , BC=3√3 . Найдите cosA .

Решение:
...
Ответ:
Номер: 631EB2
В треугольнике ABC угол C равен 90° , AB=5 , BC=4 . Найдите cosA .

Решение:
...
Ответ:
Номер: 847B0B
В треугольнике ABC AC=BC=20 , AB=28 . Найдите cosA .
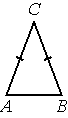
Решение:
`cosA = (AH)/(AC)=14/20=7/10=0,7`
Ответ: 0,7
Номер: 565E4B
В треугольнике ABC AC=BC=20 , AB=18 . Найдите cosA .

Решение:
...
Ответ:
Номер: 935C7B
В треугольнике ABC AC=BC=12 , AB=6 . Найдите cosA .

Решение:
...
Ответ:
Номер: 47932B
В треугольнике ABC AC=BC=16 , AB=8 . Найдите cosA .

Решение:
...
Ответ:
Номер: 755A91
В треугольнике ABC AC=BC=20 , AB=8 . Найдите cosA .

Решение:
...
Ответ:
Номер: 2DB39E
В треугольнике ABC AC=BC=20 , AB=12 . Найдите cosA .

Решение:
...
Ответ:
Номер: E9A23E
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.

Решение:
`S_(△ABC)=1/2*11*11*sin30°=1/2*11*11*1/2=30,25`
Ответ: 30,25
Номер: 21470A
Площадь параллелограмма ABCD равна 132. Точка G — середина стороны CD. Найдите площадь трапеции ABGD.
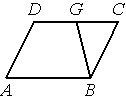
Решение:
Если из середины G провести параллельную прямую стороне CB, то она также будет делить АB пополам.
Площадь такого параллелограмма будет равна `132/2=66`
При этом GB будет диагональю правой половины и делит ее тоже пополам.
Тогда:
`S_(ABGD) = 66+33=99`
Ответ: 99
Номер: 2695F1
Площадь параллелограмма ABCD равна 20. Точка F — середина стороны BC . Найдите площадь трапеции AFCD .
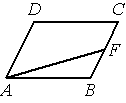
Решение:
...
Ответ:
Номер: E183B6
Площадь параллелограмма ABCD равна 3. Точка H — середина стороны AD . Найдите площадь трапеции AHCB .
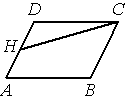
Решение:
...
Ответ:
Номер: 918418
Площадь параллелограмма ABCD равна 142. Точка H — середина стороны AD . Найдите площадь трапеции BHDC .

Решение:
...
Ответ:
Номер: 5AEAC4
Площадь параллелограмма ABCD равна 126. Точка E — середина стороны AB . Найдите площадь трапеции BCDE .
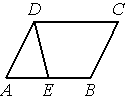
Решение:
...
Ответ:
Номер: 6266DF
Площадь параллелограмма ABCD равна 92. Точка F — середина стороны BC . Найдите площадь трапеции ADFB .
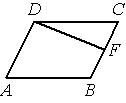
Решение:
...
Ответ:
Номер: AE853D
В равностороннем треугольнике ABC высота CH равна 45√3 . Найдите AB .
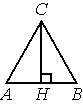
Решение:
`45sqrt3=(sqrt3*AB)/2`| :3
`AB=45*2=90`
Ответ: 90
Номер: 7CD17A
В равностороннем треугольнике ABC высота CH равна 47√3 . Найдите AB .

Решение:
...
Ответ:
Номер: FE9018
В равностороннем треугольнике ABC высота CH равна 27√3 . Найдите AB .

Решение:
...
Ответ:
Номер: 2EEDCC
В равностороннем треугольнике ABC высота CH равна 24√3 . Найдите AB .

Решение:
...
Ответ:
Номер: 4B763D
В треугольнике ABC AC=BC , высота CH равна 19,2, cosA=7/25 . Найдите AC .
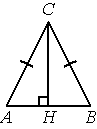
Решение:
1) `sin^2α + (7/25)^2=1`
`sin^2A + (49/625)^2=1`
`sin^2A = 576/625`
`sinA = 24/25`
2) `sinA = 24/25=(19,2)/(AC)`
`AC = (25*19,2*0,8)/24 =20`
Ответ: 20
Номер: 244628
В треугольнике ABC AC=BC , высота CH равна 7,2, cosA=45 . Найдите AC .

Решение:
...
Ответ:
Номер: 757ADF
В треугольнике ABC AC=BC , высота CH равна 16, cosA=0,6 . Найдите AC .

Решение:
...
Ответ:
Номер: 0B56CC
В треугольнике ABC AC=BC , высота CH равна 1, cosA=2√6/5 . Найдите AC .

Решение:
...
Ответ:
Номер: C79D98
В треугольнике ABC AC=BC , высота CH равна 9,6, cosA=7/25 . Найдите AC .

Решение:
...
Ответ:
Номер: 97CF97
В треугольнике ABC AC=BC , высота CH равна 2√6 , cosA=0,2 . Найдите AC .

Решение:
...
Ответ:
Номер: 6E33E1
В треугольнике ABC угол C равен 90° , AC=6 , tgA=√5/2 . Найдите AB .

Решение:
`1+tg^2α=1/(cos^2α)`
1) `1/9+5/4=1/(cos^2A)`
`9/4=1/(cos^2A)`
`cos^2A =4/9`
`cosA = 2/3`
2) `cosA = 2/3 =6/(AB)`
`AB = 9`
Ответ: 9
Номер: 58D926
В треугольнике ABC угол C равен 90° , AC=16 , tgA=9/40 . Найдите AB .

Решение:
...
Ответ:
Номер: 2D53A3
В треугольнике ABC угол C равен 90° , AC=6 , tgA=5/12 . Найдите AB .

Решение:
...
Ответ:
Номер: 6B509C
В треугольнике ABC угол C равен 90° , BC=12 , cosB=3/5 . Найдите AB .

Решение:
`cosB = 3/5 = 12/(AB)`
`AB=(5*12)/3=20`
Ответ: 20
Номер: D74EE5
В треугольнике ABC угол C равен 90° , AC=5 , tgA=125 . Найдите AB .

Решение:
...
Ответ:
Номер: 0F1E66
В треугольнике ABC угол C равен 90° , AC=7 , tgA=√3 . Найдите AB .

Решение:
...
Ответ:
Номер: 525760
В треугольнике ABC угол C равен 90° , AC=2 , tgA=158 . Найдите AB .

Решение:
...
Ответ:
Номер: 573480
В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC .
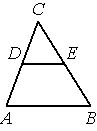
Решение:
DE — средняя линия, значит k=2
`S_(△ABC)/S_(△CDE)=2^2`
`S_(△ABC)=24*4=96`
Ответ: 96
Номер: 509E9A
В треугольнике ABC EF — средняя линия. Площадь треугольника BEF равна 4. Найдите площадь треугольника ABC .
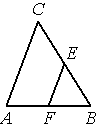
Решение:
...
Ответ:
Номер: C7EDE0
В треугольнике ABC DF — средняя линия. Площадь треугольника ADF равна 40. Найдите площадь треугольника ABC .
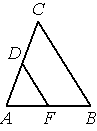
Решение:
...
Ответ:
Номер: C3A5EC
В треугольнике ABC EF — средняя линия. Площадь треугольника BEF равна 6. Найдите площадь треугольника ABC .

Решение:
...
Ответ:
Номер: 54CC33
Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.

Решение:
Площадь параллелограмма равна произведению основания на высоту.
`S = 5*3=15`
`S = 10*h_(10)=15`
`h_(10) = 15/10=1,5`
Ответ: 1,5
Номер: D254F2
Стороны параллелограмма равны 9 и 15. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите высоту, опущенную на большую сторону параллелограмма.

Решение:
...
Ответ:
Номер: 6127BC
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.

Решение:
...
Ответ:
Номер: DF24E0
Стороны параллелограмма равны 18 и 20. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Решение:
...
Ответ:
Номер: 697AC9
В четырёхугольник ABCD вписана окружность, AB=19 , BC=7 и CD=10 . Найдите четвёртую сторону четырёхугольника.
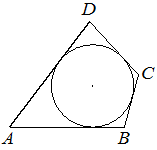
Решение:
...
Ответ:
Номер: 9623DC
В четырёхугольник ABCD вписана окружность, AB=22 , CD=17. Найдите периметр четырёхугольника ABCD.

Решение:
Признаком описанного четырехугольника является свойство, когда суммы противоположных сторон равны.
AB +CD = BC + DA
1) BC+AD=22+17=39
2) BC + DA = AB +CD = 22 + 17 =39
`P_(ABCD) = AB +CD + BC + DA = 39+39=78`
Ответ: 78
Номер: CB8C97
В четырёхугольник ABCD вписана окружность, AB=23 , BC=7 и CD=5 . Найдите четвёртую сторону четырёхугольника.
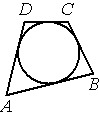
Решение:
...
Ответ:
Номер: 46ABC6
В четырёхугольник 𝐴𝐵𝐶𝐷 вписана окружность, 𝐴𝐵=13, 𝐵𝐶=7 и 𝐴𝐷=11. Найдите четвёртую сторону четырёхугольника.
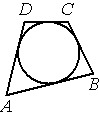
Решение:
Признаком описанного четырехугольника является свойство, когда суммы противоположных сторон равны.
AB +CD = BC + DA
11+7=13+CD
18=13+CD
CD =5
Ответ: 5
Номер: 31765C
В четырёхугольник ABCD вписана окружность, AB=10, CD=17. Найдите периметр четырёхугольника ABCD.
Решение:
...
Ответ:
Номер: 59978F
Две стороны треугольника равны 15 и 18. Высота, опущенная на большую из этих сторон, равна 10. Найдите длину высоты, опущенной на меньшую из этих сторон треугольника.

Решение:
...
Ответ:
Номер: 3B5E5D
В треугольнике ABC сторона AB равна 2√3, угол C равен 120°. Найдите радиус описанной около этого треугольника окружности.

Решение:
...
Ответ:
Номер: 8D3587
Площадь треугольника ABC равна 60, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение:
...
Ответ:
Номер: EE7C83
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AD . Найдите площадь трапеции BCDE .

Решение:
Площадь параллелограмма равна
S=AD*h
Площадь трапеции
S=`(AD+ED)/2*h=(1,5AD)/2 * h` = 0,75h
То есть 0,75 от площади параллелограмма равна площадь трапеции
28*0,75=21
Ответ: 21
Номер: F12D1C
Площадь параллелограмма ABCD равна 24. Точка E — середина стороны AD. Найдите площадь трапеции BCDE.

Решение:
...
Ответ:
Номер: 282EDC
Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AD. Найдите площадь треугольника ABE.

Решение:
...
Ответ:
Номер: B3E586
Устаревшие задания с развернутым ответом
Это более сложные задания, промежуточные между нынешними 1 и 17, такого формата сейчас на ЕГЭ нет. Возможно, задачки немного переформулируют и раскидают по планиметрии.
В треугольнике ABC известны стороны: AB=7 , BC=9, AC=10. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Решение:
...
Ответ:
Номер: 7C44EF
В треугольнике ABC известны стороны: AB=7 , BC=10 , AC=8 . Окружность, проходящая через точки A и C , пересекает прямые BA и BC соответственно в точках K и L , отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC . Найдите длину отрезка KL .
Решение:
...
Ответ:
Номер: FDE265
В треугольнике ABC известны стороны: AB=4 , BC=6 , AC=5 . Окружность, проходящая через точки A и C , пересекает прямые BA и BC соответственно в точках K и L , отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC . Найдите длину отрезка KL .
Решение:
...
Ответ:
Номер: 38798C
В треугольнике ABC известны стороны: AB=5 , BC=6 , AC=7 . Окружность, проходящая через точки A и C , пересекает прямые BA и BC соответственно в точках K и L , отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC . Найдите длину отрезка KL .
Решение:
...
Ответ:
Номер: 8A7988
В треугольнике ABC известны стороны: AB=5 , BC=7 , AC=8 . Окружность, проходящая через точки A и C , пересекает прямые BA и BC соответственно в точках K и L , отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC . Найдите длину отрезка KL .
Решение:
...
Ответ:
Номер: 802202
В треугольнике ABC известны стороны: AB=7 , BC=8 , AC=9 . Окружность, проходящая через точки A и C , пересекает прямые BA и BC соответственно в точках K и L , отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC . Найдите длину отрезка KL .
Решение:
...
Ответ:
Номер: 894F03
Окружности радиусов 2 и 3 с центрами O1 и O2 соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую — в точке C. Найдите площадь треугольника BCO2, если ∠ABO1=30°.
Решение:
...
Ответ:
Номер: C513A9
Окружности радиусов 5 и 8 с центрами O1 и O2 соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую — в точке C. Найдите площадь треугольника BCO2, если ∠ABO1=15°.
Решение:
...
Ответ:
Номер: 8A316A
Окружности радиусов 3 и 9 с центрами O1 и O2 соответственно касаются в точке A . Прямая, проходящая через точку A , вторично пересекает меньшую окружность в точке B , а большую — в точке C . Найдите площадь треугольника BCO2 , если ∠ABO1=30° .
Решение:
...
Ответ:
Номер: 75C747
Окружности радиусов 1 и 7 с центрами O1 и O2 соответственно касаются в точке A . Прямая, проходящая через точку A , вторично пересекает меньшую окружность в точке B , а большую — в точке C . Найдите площадь треугольника BCO2 , если ∠ABO1=22,5° .
Решение:
...
Ответ:
Номер: 43DB17
Окружности радиусов 3 и 5 с центрами O1 и O2 соответственно касаются в точке A . Прямая, проходящая через точку A , вторично пересекает меньшую окружность в точке B , а большую — в точке C . Найдите площадь треугольника BCO2 , если ∠ABO1=15° .
Решение:
...
Ответ:
Номер: 20722F
Окружности радиусов 2 и 10 с центрами O1 и O2 соответственно касаются в точке A . Прямая, проходящая через точку A , вторично пересекает меньшую окружность в точке B , а большую — в точке C . Найдите площадь треугольника BCO2 , если ∠ABO1=22,5° .
Решение:
...
Ответ:
Номер: C57587
Окружности радиусов 4 и 13 с центрами O1 и O2 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке K, а большую — в точке M. Найдите площадь треугольника KMO1, если ∠LMO2=22,5°.
Решение:
...
Ответ:
Номер: 3207C1
Окружности радиусов 9 и 15 с центрами O1 и O2 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке K, а большую — в точке M. Найдите площадь треугольника KMO1, если ∠LMO2=15°.
Решение:
...
Ответ:
Номер: F9CE82
Окружности радиусов 5√3 и 7√3 с центрами O1 и O2 соответственно касаются в точке L . Прямая, проходящая через точку L , вторично пересекает меньшую окружность в точке K , а большую — в точке M . Найдите площадь треугольника KMO1 , если ∠LMO2=30° .
Решение:
...
Ответ:
Номер: 1BBB26
Окружности радиусов 5 и 9 с центрами O1 и O2 соответственно касаются в точке L . Прямая, проходящая через точку L , вторично пересекает меньшую окружность в точке K , а большую — в точке M . Найдите площадь треугольника KMO1 , если ∠LMO2=15° .
Решение:
...
Ответ:
Номер: 777D99
Окружности радиусов 2 и 9 с центрами O1 и O2 соответственно касаются в точке L . Прямая, проходящая через точку L , вторично пересекает меньшую окружность в точке K , а большую — в точке M . Найдите площадь треугольника KMO1 , если ∠LMO2=15° .
Решение:
...
Ответ:
Номер: 55E390
Окружности радиусов 5√2 и 8√2 с центрами O1 и O2 соответственно касаются в точке L . Прямая, проходящая через точку L , вторично пересекает меньшую окружность в точке K , а большую — в точке M . Найдите площадь треугольника KMO1 , если ∠LMO2=22,5° .
Решение:
...
Ответ:
Номер: 9B7F8D
Окружности радиусов 13 и 20 с центрами O1 и O2 соответственно касаются внешним образом в точке C, AO1 и BO2 — параллельные радиусы этих окружностей, причём ∠AO1O2=60°. Найдите AB.
Решение:
...
Ответ:
Номер: 549C41
Окружности радиусов 13 и 35 с центрами O1 и O2 соответственно касаются внешним образом в точке C, AO1 и BO2 — параллельные радиусы этих окружностей, причём ∠AO1O2=60°. Найдите AB.
Решение:
...
Ответ:
Номер: 34BE41
Окружности радиусов 11 и 21 с центрами O1 и O2 соответственно касаются внешним образом в точке C , AO1 и BO2 — параллельные радиусы этих окружностей, причём ∠AO1O2=60° . Найдите AB .
Решение:
...
Ответ:
Номер: B48527
Окружности радиусов 1 и 4 с центрами O1 и O2 соответственно касаются внешним образом в точке C , AO1 и BO2 — параллельные радиусы этих окружностей, причём ∠AO1O2=60° . Найдите AB .
Решение:
...
Ответ:
Номер: F40456
Окружности радиусов 11 и 21 с центрами O1 и O2 соответственно касаются внутренним образом в точке K , MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120° . Найдите MN .
Решение:
...
Ответ:
Номер: 84178E
Окружности радиусов 13 и 35 с центрами O1 и O2 соответственно касаются внутренним образом в точке K , MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120° . Найдите MN .
Решение:
...
Ответ:
Номер: 261E88
Окружности радиусов 11 и 24 с центрами O1 и O2 соответственно касаются внутренним образом в точке K , MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120° . Найдите MN .
Решение:
...
Ответ:
Номер: A2FB54
Окружности радиусов 13 и 20 с центрами O1 и O2 соответственно касаются внутренним образом в точке K , MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120°. Найдите MN.
Решение:
...
Ответ:
Номер: D8C8F4
Окружности радиусов 1 и 15 с центрами O1 и O2 соответственно касаются внутренним образом в точке K, MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120°. Найдите MN.
Решение:
...
Ответ:
Номер: 886909
Окружности радиусов 1 и 4 с центрами O1 и O2 соответственно касаются внутренним образом в точке K , MO1 и NO2 — параллельные радиусы этих окружностей, причём ∠MO1O2=120° . Найдите MN .
Решение:
...
Ответ:
Номер: A6AF30
Окружности радиусов 3 и 5 с центрами O1 и O2 соответственно касаются в точке A . Прямая, проходящая через точку A , вторично пересекает меньшую окружность в точке B , а большую — в точке C . Найдите площадь выпуклого четырёхугольника, вершинами которого являются точки O1 , O2 , B и C , если ∠ABO1=15° .
Решение:
...
Ответ:
Номер: FCD808
Окружность вписана в равнобедренную трапецию, основания которой равны 18 и 50. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Решение:
...
Ответ:
Номер: 5405B4
Периметр равнобедренной трапеции равен 136. Известно, что в эту трапецию можно вписать окружность, причём боковая сторона делится точкой касания в отношении 9 : 25. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Решение:
...
Ответ:
Номер: 815E72
Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
Решение:
...
Ответ:
Номер: 52F0CC
Боковые стороны KL и MN трапеции KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A . Найдите радиус окружности, вписанной в треугольник ALM .
Решение:
...
Ответ:
Номер: CDD1F3
Точки M , K и N лежат на сторонах соответственно AB , BC и AC треугольника ABC, причём AMKN— параллелограмм, площадь которого составляет 4/9 площади треугольника ABC. Найдите диагональ MN параллелограмма, если известно, что AB = 21 , AC = 12 и ∠BAC = 120°.
Решение:
...
Ответ:
Номер: 5036B5
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
Решение:
...
Ответ:
Номер: 824C9A
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 4, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC .
Решение:
...
Ответ:
Номер: 91D67D
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 18, а боковые рёбра равны 15. Точка R принадлежит ребру MB, причём MR:RB=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки C и R параллельно прямой BD.
Решение:
...
Ответ:
Номер: 580A5F
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 12, а боковые рёбра равны 24. Точка G принадлежит ребру MA, причём MG:GA=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и G параллельно прямой AC.
Решение:
...
Ответ:
Номер: B04B20
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 10, а отношение катетов треугольника равно 5/12.
Решение:
...
Ответ:
Номер: 0CB8B8
Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 24, а синус угла при основании равен 4/5.
Решение:
...
Ответ:
Номер: 627502
Дан треугольник со сторонами 30, 30 и 36. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: C24E52
Дан треугольник со сторонами 80, 80 и 96. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: C11B5D
В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 1/5 ?
Решение:
...
Ответ:
Номер: F343A9
В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 2/7 ?
Решение:
...
Ответ:
Номер: 664444
В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон, в 7 раз больше радиуса вписанной окружности?
Решение:
...
Ответ:
Номер: 86DCBB
В окружности проведены хорды PQ и CD , причём PQ=PD=CD=10 , CQ=6 . Найдите CP .
Решение:
...
Ответ:
Номер: E41141
В окружности проведены хорды PQ и CD , причём PQ=PD=CD=12 , CQ=4 . Найдите CP .
Решение:
...
Ответ:
Номер: CE197C
В окружности проведены хорды PQ и CD , причём PQ=PD=CD=14 , CQ=10 . Найдите CP .
Решение:
...
Ответ:
Номер: 3D59BD
В окружности проведены хорды PQ и CD , причём PQ=PD=CD=8 , CQ=6 . Найдите CP .
Решение:
...
Ответ:
Номер: 297181
Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CDпересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
Решение:
...
Ответ:
Номер: 925C29
Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12,5, средняя линия трапеции равна 27,5. Прямые AB и CD пересекаются в точке M . Найдите радиус окружности, вписанной в треугольник BMC .
Решение:
...
Ответ:
Номер: 8D5AAC
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что DB : DC = 2 : 3 . Найдите угол A .
Решение:
...
Ответ:
Номер: A4755C
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что DB:DC=1:3 . Найдите угол A .
Решение:
...
Ответ:
Номер: 2474C1
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что DB:DC=2:5 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 2EB266
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что DB:DC=1:2 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 75967B
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=2:3 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: C82C45
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:5 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 2697F6
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:4 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: D147FF
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:4 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 5B3676
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=3:5 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 2A3CBB
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:2 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: E2A7BF
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=5:6 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 0D9A1C
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=3:4 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: B8982B
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:3 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 40019C
Угол C треугольника ABC равен 30° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:6 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: D1589A
Угол C треугольника ABC равен 60° , D — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC=1:2 . Найдите синус угла A .
Решение:
...
Ответ:
Номер: 4D4A8C
Точка O — центр правильного шестиугольника ABCDEF со стороной 14√3 . Найдите радиус окружности, касающейся окружностей, описанных около треугольников AOB , COD и EOF .
Решение:
...
Ответ:
Номер: 02BCC3
Точка O — центр правильного шестиугольника ABCDEF , в котором AC=10,5 . Найдите радиус окружности, касающейся окружностей, описанных около треугольников AOB , COD и EOF .
Решение:
...
Ответ:
Номер: C2CCCF
Точка O — центр правильного шестиугольника ABCDEF со стороной 7. Найдите радиус окружности, касающейся окружностей, описанных около треугольников BOD , DOF и BOF .
Решение:
...
Ответ:
Номер: FAD1F0
Точка O — центр правильного шестиугольника ABCDEF , в котором AC=14√3 . Найдите радиус окружности, касающейся окружностей, описанных около треугольников BOD , DOF и BOF .
Решение:
...
Ответ:
Номер: 809CB5
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 8 и 17.
Решение:
...
Ответ:
Номер: 3AEF5A
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 3 и 5.
Решение:
...
Ответ:
Номер: 9D89CE
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 5 и 13.
Решение:
...
Ответ:
Номер: 45133B
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 4 и 5.
Решение:
...
Ответ:
Номер: D07570
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 20 и 29.
Решение:
...
Ответ:
Номер: 7B2915
Отрезки AP , BN и CM — биссектрисы внутренних углов треугольника ABC . Один из углов треугольника равен 120° . Найдите площадь треугольника PNM , если две стороны этого треугольника равны 12 и 13.
Решение:
...
Ответ:
Номер: 3F401F
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F , отличной от A . Найдите радиус окружности, описанной около треугольника ABC , если AC=8 , AF=3 , угол BAC равен 45° .
Решение:
...
Ответ:
Номер: 9775A3
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F , отличной от A . Найдите радиус окружности, описанной около треугольника ABC , если AC=4 , AF=2 , угол BAC равен 60∘ .
Решение:
...
Ответ:
Номер: 9E17EA
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F , отличной от A . Найдите радиус окружности, описанной около треугольника ABC , если AC=7 , AF=2 , угол BAC равен 60° .
Решение:
...
Ответ:
Номер: D71465
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F , отличной от A . Найдите радиус окружности, описанной около треугольника ABC , если AC=5 , AF=1 , угол BAC равен 30° .
Решение:
...
Ответ:
Номер: CDD2F5
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F , отличной от A . Найдите радиус окружности, описанной около треугольника ABC , если AC=8 , AF=2 , угол BAC равен 30° .
Решение:
...
Ответ:
Номер: 376405
Продолжение биссектрисы CD неравнобедренного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке E . Окружность, описанная около треугольника ADE , пересекает прямую AC в точке F, отличной от A. Найдите радиус окружности, описанной около треугольника ABC, если AC=6, AF=3, угол BAC равен 45°.
Решение:
...
Ответ:
Номер: 1EF358
Окружность радиуса 6√2 вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 8. Найдите MN .
Решение:
...
Ответ:
Номер: DAEEF2
Окружность радиуса 12 вписана в угол, равный 60° . Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 8. Найдите MN .
Решение:
...
Ответ:
Номер: 202405
Окружность радиуса 6 вписана в угол, равный 60° . Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 4. Найдите MN .
Решение:
...
Ответ:
Номер: 770921
Окружность радиуса 12√2 вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 16. Найдите MN .
Решение:
...
Ответ:
Номер: 24A6AF
Окружность радиуса 8√2 вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 12. Найдите MN .
Решение:
...
Ответ:
Номер: 9BBF60
Окружность радиуса 10√2 вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M и N . Известно, что расстояние между центрами окружностей равно 12. Найдите MN .
Решение:
...
Ответ:
Номер: A65130
Дан равнобедренный прямоугольный треугольник с боковой стороной 2. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: BF5567
Дан равнобедренный треугольник с боковой стороной 4 и углом 120° . Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: A2EA44
Найдите угол при основании равнобедренного треугольника, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 2/5 .
Решение:
...
Ответ:
Номер: E834ED
Найдите угол при основании равнобедренного треугольника, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны и продолжений двух других сторон треугольника, равно 1/4 .
Решение:
...
Ответ:
Номер: 9A5C4E
Радиусы окружностей с центрами O1 и O2 равны соответственно 2 и 9. Найдите радиус третьей окружности, которая касается двух данных и прямой O1O2 , если O1O2=21 .
Решение:
...
Ответ:
Номер: DCD471
Радиусы окружностей с центрами O1 и O2 равны соответственно 1 и 3. Найдите радиус третьей окружности, которая касается двух данных и прямой O1O2 , если O1O2=14 .
Решение:
...
Ответ:
Номер: 69EFA9
Радиусы окружностей с центрами O1 и O2 равны соответственно 1 и 8. Найдите радиус третьей окружности, которая касается двух данных и прямой O1O2 , если O1O2=21 .
Решение:
...
Ответ:
Номер: 162D4C
Основание равнобедренного треугольника равно 80, а высота, опущенная на боковую сторону равна 64. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: B320B2
Основание равнобедренного треугольника равно 40, а высота, опущенная на боковую сторону равна 24. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: C60B58
Косинус угла при основании равнобедренного треугольника равен 5/13 , а боковая сторона равна 39. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 33659E
Косинус угла при вершине равнобедренного треугольника равен − 7/25 , а основание равно 16. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 1B40F0
Косинус угла, противолежащего основанию равнобедренного треугольника, равен 7/25 , а боковая сторона равна 15. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 02DAF3
Найдите косинус угла при основании равнобедренного треугольника, если известно, что радиус его вписанной окружности в 6 раз меньше радиуса окружности, касающейся стороны и продолжений двух других сторон треугольника.
Решение:
...
Ответ:
Номер: 17AB7E
На прямой, содержащей биссектрису AD прямоугольного треугольника ABC с прямым углом C , взята точка E , удалённая от вершины A на расстояние, равное √10 . Найдите площадь треугольника BCE , если BC=3 , AC=4 .
Решение:
...
Ответ:
Номер: 8DDF97
На прямой, содержащей медиану AD прямоугольного треугольника ABC с прямым углом C , взята точка E , удалённая от вершины A на расстояние, равное 4 . Найдите площадь треугольника BCE , если BC=6 , AC=4 .
Решение:
...
Ответ:
Номер: 7B1531
На прямой, содержащей биссектрису AD прямоугольного треугольника ABC с прямым углом C, взята точка E, удалённая от вершины A на расстояние, равное √26. Найдите площадь треугольника BCE, если BC=5, AC=12.
Решение:
...
Ответ:
Номер: E41156
Синус угла при основании равнобедренного треугольника равен 817 , а основание равно 60. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 843233
Дан треугольник со сторонами 26, 26 и 20. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 875E8C
Дан треугольник со сторонами 115, 115 и 184. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение:
...
Ответ:
Номер: 7EE5DE

