КЭС 1.4.1 Преобразования выражений, включающих арифметические операции 1.4.2 Преобразования выражений, включающих операцию возведения в степен 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учёт реальных ограничений 2.2.2 Рациональные неравенства Тип ответа: краткий ответ.
В банке заданий ФИПИ есть следующие задачи на смекалку к 21-й линейке. Любое из них может вам попасться на реальном ЕГЭ базового уровня сложности по математике.
Задачи на смекалку ЕГЭ база по математике, задание 21
Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 9 м. За сколько дней улитка впервые доползёт до вершины дерева?
Решение:
(9-2):(2-1)=7 дней до 7 метров
7+2=9 это на следующий день,
тогда 7+1=8 дней
Ответ:8
Номер: 0D274E
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева от его основания?
Решение:
(10-4):(4-3)=6 дней до 6 метров
6+4=10 это на следующий день,
тогда 6+1=7 дней
Ответ:7
Номер: A167BF
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 12 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Решение:
(12-4):(4-2)=4 дня до 8 метров
8+4=12 это на следующий день,
тогда 4+1=5 дней
Ответ:5
Номер: C84D54 93F33E
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Решение:
(13-4):(4-1)=3 дня до 9 метров
9+4=13 это на следующий день,
тогда 3+1=4 дня
Ответ:
Номер: 5297EA 218383
Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 2 м. Высота дерева 10 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Решение:
(10-3):(3-2)=7 дней до 7 метров
7+3=10 это на следующий день,
тогда 7+1=8 дней
Ответ:8
Номер: C0D9A6
Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 1 м. Высота дерева 11 м. За сколько дней улитка впервые доползёт до вершины дерева от его основания?
Решение:
(11-3):(3-1)=4 дня до 9 метров
9+3=11 это на следующий день,
тогда 4+1=5 дней
Ответ:5
Номер: 62D3E6
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?
Решение:
7
Номер: CF0E2F
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 12 прыжков?
Решение:
13
Номер: CA72B7
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 11 прыжков?
Решение:
12
Номер: 7AC4A4
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 8 прыжков?
Решение:
9
Номер: 740DFA
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 7 прыжков?
Решение:
8
Номер: 357FF8
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 10 прыжков?
Решение:
11
Номер: 8B2FB1
В корзине лежит 27 грибов: рыжики и грузди. Известно, что среди любых 19 грибов имеется хотя бы один рыжик, а среди любых 10 грибов — хотя бы один груздь. Сколько груздей в корзине?
Решение:
18
Номер: 16ADFA
В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
Решение:
24
Номер: 9A27F4 FC10C0
В корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов — хотя бы один груздь. Сколько рыжиков в корзине?
Решение:
19
Номер: 34DB25
В корзине лежит 34 гриба: рыжики и грузди. Известно, что среди любых 20 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько груздей в корзине?
Решение:
19
Номер: 5B5CD4
В корзине лежит 37 грибов: рыжики и грузди. Известно, что среди любых 22 грибов имеется хотя бы один рыжик, а среди любых 17 грибов хотя бы один груздь. Сколько груздей в корзине?
Решение:
21
Номер: 295059
В корзине лежит 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов — хотя бы один груздь. Сколько рыжиков в корзине?
Решение:
15
Номер: 49A39A
На прилавке цветочного магазина стоят 3 вазы с розами: голубая, зелёная и жёлтая. Слева от зелёной вазы 27 роз, справа от голубой вазы 23 розы. Всего в вазах 42 розы. Сколько роз в жёлтой вазе?
Решение:
8
(27+23)-42=8
Номер: F4590E
На прилавке цветочного магазина стоят 3 вазы с розами: синяя, белая и фиолетовая. Слева от фиолетовой вазы 21 роза, справа от белой вазы 12 роз. Всего в вазах 26 роз. Сколько роз в синей вазе?
Решение:
7
(21+12)-26=7
Номер: A62B7B
На прилавке цветочного магазина стоят 3 вазы с розами: чёрная, зелёная и оранжевая. Слева от чёрной вазы 32 розы, справа от оранжевой вазы 9 роз. Всего в вазах 37 роз. Сколько роз в зелёной вазе?
Решение:
4
(32+9)-37=4
Номер: FB4A14
На прилавке цветочного магазина стоят 3 вазы с розами: жёлтая, зелёная и красная. Слева от зелёной вазы 21 роза, справа от жёлтой вазы 31 роза. Всего в вазах 40 роз. Сколько роз в красной вазе?
Решение:
12
(21+31)-40=12
Номер: FB7411
На прилавке цветочного магазина стоят 3 вазы с розами: чёрная, синяя и жёлтая. Слева от чёрной вазы 17 роз, справа от жёлтой вазы 16 роз. Всего в вазах 24 розы. Сколько роз в синей вазе?
Решение:
9
(17+16)-24=9
Номер: 88241F
На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от синей вазы 15 роз, справа от белой вазы 11 роз. Всего в вазах 23 розы. Сколько роз в оранжевой вазе?
Решение:
3
(11+25)-23=3
Номер: 5A0C58
Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 9 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Решение:
45
9+8+7+6+5+4+3+2+1=45
Номер: 498C45
Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Решение:
40
10*8=80 связей. При этом реальных в два раза меньше, так как на два столба одна связь, тогда 80/2=40
Номер: F36D25
Девять столбов соединены между собой проводами так, что от каждого столба отходит ровно 6 проводов. Сколько всего проводов протянуто между этими девятью столбами?
Решение:
27
От каждого столба отходит ровно 6 проводов, получается, что всего 9⋅6 = 54 соединения. При подсчете соединений, каждый провод между двумя столбами был подсчитан два раза, так как соединение между столбами 1 и 2 и соединение между столбами 2 и 1 — это один и тот же провод. Значит, что всего между девятью столбами будет протянуто проводов в два раза меньше, чем соединений, то есть 54:2 = 27 проводов.
Номер: 7FE143
Семь столбов соединены между собой проводами так, что от каждого столба отходит ровно 6 проводов. Сколько всего проводов протянуто между этими семью столбами?
Решение:
21
7*6=42 связей. При этом реальных в два раза меньше, так как на два столба одна связь, тогда 42/2=21
Номер: E0E840
Восемь столбов соединены между собой проводами так, что от каждого столба отходит ровно 6 проводов. Сколько всего проводов протянуто между этими восемью столбами?
Решение:
24
8*6=48 связей. При этом реальных в два раза меньше, так как на два столба одна связь, тогда 48/2=24
Номер: 442B2C
Восемь столбов соединены между собой проводами так, что от каждого столба отходит ровно 5 проводов. Сколько всего проводов протянуто между этими шестью столбами?
Решение:
20
8*5=40 связей. При этом реальных в два раза меньше, так как на два столба одна связь, тогда 40/2=20
Номер: 9EA11B
Из десяти стран две подписали договор о дружбе ровно с шестью другими странами, а каждая из оставшихся восьми — ровно с пятью. Сколько всего было подписано договоров?
Решение:
26
2*6:2+8*5:2=6+20=26
Номер: F72034 70789A
Из десяти стран четыре подписали договор о дружбе ровно с четырьмя другими странами, а каждая из оставшихся шести — ровно с тремя. Сколько всего было подписано договоров?
Решение:
17
4*4:2+6*3:2=8+9=17
Номер: DBBC7E
Из десяти стран четыре подписали договор о дружбе ровно с четырьмя другими странами, а каждая из оставшихся шести — ровно с пятью. Сколько всего было подписано договоров?
Решение:
23
4*4:2+6*5:2=8+15=23
Номер: D68550
Из десяти стран четыре подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся шести — ровно с двумя. Сколько всего было подписано договоров?
Решение:
16
4*5:2+6*2:2=10+6=16
Номер: B9E01B
Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров?
Решение:
21
(7*3+3*7):2=21
Номер: 2B4A25
Из десяти стран семь подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров?
Решение:
28
Номер: B23CA0
На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
432
18*24=432
Номер: DF9541
На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
350
14*25=350
Номер: E4E62F CAA7C9
На поверхности глобуса фломастером проведены 14 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
330
15*22=330
Номер: 969E0A
На поверхности глобуса фломастером проведены 16 параллелей и 20 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
340
17*20=340
Номер: 918D7F
На поверхности глобуса фломастером проведены 24 параллели и 17 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
425
25*17=425
Номер: 3BC2F1 47B8CE
На поверхности глобуса фломастером проведены 15 параллелей и 20 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение:
320
16*20=315
Номер: A2F525 33E0E9
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 49, во втором — 97, в третьем — 146, а сумма чисел в каждой строке больше 18, но меньше 21. Сколько всего строк в таблице?
Решение:
15
Значение в каждой строке или 19 или 20
49+97+146=292
Ищем минимальное значение строк и максимальное
292/19=14,6
292/20=15,4
Но так как количество строк это натуральное число, то получается 15
Номер: E532F1
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, чтобы сумма всех чисел в первом столбце была равна 119, во втором — 125, в третьем — 133, а сумма чисел в каждой строке была больше 15, но меньше 18. Сколько всего строк в таблице?
Решение:
23
Значение в каждой строке или 16 или 17
119+125+133=377
Ищем минимальное значение строк и максимальное
377/16=23,6
377/17=22,2
Но так как количество строк это натуральное число, то получается 23
Номер: 120CB6
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 85, во втором — 77, в третьем — 71, а сумма чисел в каждой строке больше 12, но меньше 15. Сколько всего строк в таблице?
Решение:
17
Значение в каждой строке или 13 или 14
85+77+71=233
Ищем минимальное значение строк и максимальное
233/13=17,9
233/14=16,7
Но так как количество строк это натуральное число, то получается 17
Номер: BD6455
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, чтобы сумма всех чисел в первом столбце была равна 127, во втором — 136, в третьем — 146, а сумма чисел в каждой строке была больше 17, но меньше 20. Сколько всего строк в таблице?
Решение:
17
Значение в каждой строке или 13 или 14
85+77+71=233
Ищем минимальное значение строк и максимальное
233/13=17,9
233/14=16,7
Но так как количество строк это натуральное число, то получается 17
Номер: 6E5B75
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, чтобы сумма всех чисел в первом столбце была равна 224, во втором — 193, в третьем — 162, а сумма чисел в каждой строке была больше 20, но меньше 23. Сколько всего строк в таблице?
Решение:
27
Значение в каждой строке или 21 или 22
224+193+162=579
Ищем минимальное значение строк и максимальное
579/21=27,6
579/22=26,31
Но так как количество строк это натуральное число, то получается 27
Номер: 20375B
В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 93, во втором — 107, в третьем — 123, а сумма чисел в каждой строке больше 19, но меньше 22. Сколько всего строк в таблице?
Решение:
16
Значение в каждой строке или 20 или 21
93+107+123=323
Ищем минимальное значение строк и максимальное
323/20=16,2
323/21=15,4
Но так как количество строк это натуральное число, то получается 16
Номер: 526AAA
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 2230. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
3
подбираем что делится без остатков
2230:5=446
446:2=223
отметки
5*2*223
среднее
14/5=2,8, округляем до целого
Номер: 15B142
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3495. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
3
подбираем что делится без остатков
3495:5=699
699:3=223
отметки
5*3*223
среднее
15/5=3
Номер: D2F545
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 7845. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
4
подбираем что делится без остатков
7845:5=1569
1569:3=523
отметки
5*3*523
среднее
18/5=3,6
Номер: E29140
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3530. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
4
подбираем что делится без остатков
3530:5=706
706:2=353
отметки
5*2*353
среднее
18/5=3,6
Номер: E73042
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3177. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
3
подбираем что делится без остатков
3177:3=1059
1059:3=353
отметки
3*3*353
среднее
17/5=3,4
Номер: 89FE4D
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 2097. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение:
3
подбираем что делится без остатков
2097:3=699
699:3=233
отметки
3*3*233
среднее
14/5=2,8
Номер: 75D904
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Решение:
117700
`Sn=(n(2a1+(n-1)d))/2=(11(2*4200+10*1300))/2`=117700
Номер: F98942 BE457F
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
Решение:
77200
`Sn=(n(2a1+(n-1)d))/2=(8(2*3700+7*1700))/2`=77200
Номер: 6C4E28 D69CDE
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4000 рублей, а за каждый следующий метр будет платить на 1600 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 7 метров?
Решение:
61600
`Sn=(n(2a1+(n-1)d))/2=(7(2*4000+6*1600))/2`=61600
Номер: 20C64C FA3BB3
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3600 рублей, а за каждый следующий метр — на 1400 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
Решение:
68000
`Sn=(n(2a1+(n-1)d))/2=(8(2*3600+7*1400))/2`=68000
Номер: AB244E
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3900 рублей, а за каждый следующий метр будет платить на 1200 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 6 метров?
Решение:
41400
`Sn=(n(2a1+(n-1)d))/2=(6(2*3900+5*1200))/2`=41400
Номер: ADC9F0 C78A0D
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4100 рублей, а за каждый следующий метр будет платить на 1700 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 7 метров?
Решение:
64400
`Sn=(n(2a1+(n-1)d))/2=(7(2*4100+6*1700))/2`=64400
Номер: CB54BA
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 9 партий, а Коля – 19. Сколько партий сыграл Лёша?
Решение:
10
Номер: 3924B6 330BA6
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 11 партий, а Коля – 23. Сколько партий сыграл Лёша?
Решение:
12
Номер: AF6EB8 45A72A
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 10 партий, а Коля — 21. Сколько партий сыграл Лёша?
Решение:
11
Номер: 0F3E5E
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 13 партий, а Коля – 27. Сколько партий сыграл Лёша?
Решение:
14
Номер: 555FE3 DC5C3E
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 12 партий, а Коля – 25. Сколько партий сыграл Лёша?
Решение:
13
Номер: 3B8719
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 254, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
85
254 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
7, 9, 1, 3, 5 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 425. Получаем диапазон страниц
(424-254)/2=85
Номер: E1A247
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 326, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
148
326 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
9, 1, 3, 5, 7 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 623. Получаем диапазон страниц
(622-326)/2=148
Номер: 77CB01
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 298, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
265
298 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
1, 3, 5, 7, 9 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 829. Получаем диапазон страниц
(828-298)/2=265
Номер: 4DC474
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 276, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
175
276 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
9, 1, 3, 5, 7 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 627. Получаем диапазон страниц
(626-276)/2=175
Номер: 7F1575
из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
85
352 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
5, 7, 9, 1, 3 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 523. Получаем диапазон страниц
(522-352)/2=85
Номер: 6DB474
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 274, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Решение:
76
274 последняя страница и может прибавляться только по 2 стр., то есть 1 лист, тогда получим ряд с возможными числами:
7, 9, 1, 3, 5 то есть на эти числа должна начинаться следующая страница после вырванного блока. Это будет 427. Получаем диапазон страниц
(426-274)/2=76
Номер: 7EC2BB
На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 5 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 15 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
10
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 5 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 15 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 5
z+x - y = 15
складываем половины неравенств
y + x - z + z + x - y = 5 + 15
2x=20
x=10
Номер: 6E0103
На ленте по разные стороны от её середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 25 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 5 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
15
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 25 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 55 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 25
z+x - y = 5
складываем половины неравенств
y + x - z + z + x - y = 25 + 5
2x=30
x=15
Номер: 06A5B2
На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 35 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 5 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
20
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 35 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 5 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 35
z+x - y = 5
складываем половины неравенств
y + x - z + z + x - y = 35 + 5
2x=40
x=20
Номер: 7E1F5E
На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 15 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 75 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
45
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 15 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 75 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 15
z+x - y = 75
складываем половины неравенств
y + x - z + z + x - y = 15 + 75
2x=90
x=45
Номер: 26347D
На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 35 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 75 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
55
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 35 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 75 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 35
z+x - y = 75
складываем половины неравенств
y + x - z + z + x - y = 35 + 75
2x=110
x=55
Номер: D09DA9
На ленте по разные стороны от середины отмечены тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 30 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 50 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.
Решение:
40
| y I x I z |
1) разрезав ленту по красной полоске, часть y + x будет длиннее части z на 30 см;
2) разрезав ленту по синей полоске, часть z + x будет длиннее части y на 50 см.
Таким образом, мы имеем систему из двух уравнений:
y+x - z = 30
z+x - y = 50
складываем половины неравенств
y + x - z + z + x - y = 30 + 50
2x=80
x=40
Номер: A06570
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым – 7 кусков, а если по зелёным – 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
21
___ |____|____|____|___ – 4 линии, 4 распила и 5 кусков.
Если распилить палку по красным линиям, получится 5 кусков, значит распилов 4, красных линий – 4
Если распилить палку по жёлтым — 7 кусков, значит распилов 6, 6 желтых линий.
Если распилить палку по зелёным — 11 кусков, значит распилов 10, 10 зеленых линий
4+6+10=20 цветных линий.
Если сделать распилы по этим 20–ти линиям получится 21 кусок.
Номер: 38B0FE
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 10 кусков, если по жёлтым — 8 кусков, а если по зелёным — также 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
24
_|__|__|__|__|__|__|__|__|___ – 9 линий, 9 распилов и 10 кусков.
Если распилить палку по красным линиям, получится 10 кусков, значит распилов 9, красных линий – 9
Если распилить палку по жёлтым — 8 кусков, значит распилов 7, 7 желтых линий.
Если распилить палку по зелёным — 8 кусков, значит распилов 7, 7 зеленых линий
9+7+7=23 цветных линий.
Если сделать распилы по этим 23–ем линиям получится 24 куска.
Номер: D6FB0C
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым – 12 кусков, а если по зелёным – 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
27
_|__|__|__|__|__|__|__|__ – 8 линий, 8 распилов и 9 кусков.
Если распилить палку по красным линиям, получится 9 кусков, значит распилов 8, красных линий – 8
Если распилить палку по жёлтым — 12 кусков, значит распилов 11, 11 желтых линий.
Если распилить палку по зелёным — 8 кусков, значит распилов 7, 7 зеленых линий
8+11+7=26 цветных линий.
Если сделать распилы по этим 26–ти линиям получится 27 кусков.
Номер: 694B19
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 7 кусков, если по жёлтым — 13 кусков, а если по зелёным — 5 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
23
_|__|__|__|__|__|__ – 6 линий, 6 распилов и 8 кусков.
Если распилить палку по красным линиям, получится 7 кусков, значит распилов 6, красных линий – 6
Если распилить палку по жёлтым — 13 кусков, значит распилов 12, 12 желтых линий.
Если распилить палку по зелёным — 5 кусков, значит распилов 4, 4 зеленых линий
6+12+4=22 цветные линий.
Если сделать распилы по этим 22–м линиям получится 23 куска.
Номер: C23627
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым – 7 кусков, а если по зелёным – 6 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
20
_|__|__|__|__|__|__|__|__ – 8 линий, 8 распилов и 9 кусков.
Если распилить палку по красным линиям, получится 9 кусков, значит распилов 8, красных линий – 8
Если распилить палку по жёлтым — 7 кусков, значит распилов 6, 6 желтых линий.
Если распилить палку по зелёным — 6 кусков, значит распилов 5, 5 зеленых линий
8+6+5=19 цветных линий.
Если сделать распилы по этим 19 линиям получится 20 кусков.
Номер: BBD953
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым – 5 кусков, а если по зелёным – 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение:
25
_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ – 14 линий, 14 распилов и 15 кусков.
Если распилить палку по красным линиям, получится 15 кусков, значит распилов 14, красных линий – 14
Если распилить палку по жёлтым — 5 кусков, значит распилов 4, 4 желтых линий.
Если распилить палку по зелёным — 7 кусков, значит распилов 6, 6 зеленых линий
14+4+6=24 цветных линий.
Если сделать распилы по этим 24 линиям получится 25 кусков.
Номер: 1864F9 235527
Взяли несколько досок и распилили их. Всего сделали 13 поперечных распилов, в итоге получилось 18 кусков. Сколько досок взяли?
Решение:
5
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
18-13=5
Номер: FC884B
Взяли несколько досок и распилили их. Всего сделали 8 поперечных распилов, в итоге получилось 19 кусков. Сколько досок взяли?
Решение:
11
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
19-8=11
Номер: 41E3FA
Взяли несколько досок и распилили их. Всего сделали 9 поперечных распилов, в итоге получилось 17 кусков. Сколько досок взяли?
Решение:
8
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
17-9=8
Номер: 03B204
Взяли несколько досок и распилили их. Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли?
Решение:
5
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
16-11=5
Номер: E6C10C
Взяли несколько досок и распилили их. Всего сделали 5 поперечных распилов, в итоге получилось 23 куска. Сколько досок взяли?
Решение:
18
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
23-5=18
Номер: FA817E
Взяли несколько досок и распилили их. Всего сделали 8 поперечных распилов, в итоге получился 21 кусок. Сколько досок взяли?
Решение:
13
Для примера: Если распиливаем доску в 2 местах, то получается 3 куска, если в 3, то 4, то есть у нас на 1 кусок больше, чем резов. Делаем вывод, что разность резов и кусков и будет указывать на количество досок.
21-8=13
Номер: DA9073
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 50 км, между А и В — 40 км, между В и Г — 25 км, между Г и А — 35 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
10
Между Б и В = 50-40=10
Номер: 0A4EBE
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 50 км, между А и В — 30 км, между В и Г — 25 км, между Г и А — 45 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
20
Между Б и В = 50-30=20
Номер: 0384F6
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 55 км, между А и В — 50 км, между В и Г — 40 км, между Г и А — 20 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
5
Между Б и В = 55-50=5
Номер: C382FD
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 75 км, между А и В — 50 км, между В и Г — 40 км, между Г и А — 60 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
25
Между Б и В = 75-50=25
Номер: 9A0DB6 C81957
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 60 км, между А и В — 45 км, между В и Г — 40 км, между Г и А — 35 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
15
Между Б и В = 60-45=15
Номер: AEB619 01B9A2
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 35 км, между А и В — 15 км, между В и Г — 25 км, между Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Решение:
20
Между Б и В = 35-15=20
Номер: 3B425F
Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 165. Какое число было загадано?
Решение:
33
7-5=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=165, тогда из условия выше получаем
163≤x*A≤167
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
164:7=23,8
Номер: 2751B2
Про натуральные числа A, B и С известно, что каждое из них больше 5, но меньше 9. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 164. Какое число было загадано?
Решение:
27
8-6=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=164, тогда из условия выше получаем
162≤x*A≤166
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
162:6=27
Номер: F7C3D0
Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано?
Решение:
23
9-7=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=186, тогда из условия выше получаем
184≤x*A≤188
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
184:8=23
Номер: 4FC2F9
Про натуральные числа A, B и С известно, что каждое из них больше 5, но меньше 9. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 172. Какое число было загадано?
Решение:
29
8-6=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=172, тогда из условия выше получаем
170≤x*A≤174
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
174:6=29
Номер: 22FB33
Про натуральные числа A, B и С известно, что каждое из них больше 5, но меньше 9. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 249. Какое число было загадано?
Решение:
31
8-6=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=249, тогда из условия выше получаем
247≤x*A≤251
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
248:8=31
Номер: EC2990
Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 195. Какое число было загадано?
Решение:
31
9-7=2 возможный максимальный диапазон между числами A, B и С
x*A+B-C=195, тогда из условия выше получаем
193≤x*A≤197
Перебираем варианты, с условием что загаданное число должно быть натуральным, отбрасываем варианты где делитель явно не дает целого числа...
248:8=31
Номер: 171362
Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 3. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 5?
Решение:
35
Пусть x и y наши множители, тогда из условия задачи
(x+1)*(y+1)=xy+3
xy+x+y+1=xy+3
x+y=2
Теперь рассмотрим случай, когда мы их увеличим на 5
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 5 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+5)*(y+5)=xy+z
xy+5x+5y+25=xy+z
5x+5y+25=z
x+y=z/5-5
вот тут самое время избавиться от x и y, зная что x+y=2, тогда
z/5-5=2
z/5=7
z=35
Номер: FFF22F A5935A
Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 11. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 2?
Решение:
24
Пусть x и y наши множители, тогда из условия задачи
(x+1)*(y+1)=xy+11
xy+x+y+1=xy+11
x+y=10
Теперь рассмотрим случай, когда мы их увеличим на 2
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 2 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+2)*(y+2)=xy+z
xy+2x+2y+4=xy+z
2x+2y+4=z
x+y=z/2-2
вот тут самое время избавиться от x и y, зная что x+y=10, тогда
z/2-2=10
z/2=12
z=24
Номер: A4E749
Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 8. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3?
Решение:
30
Пусть x и y наши множители, тогда из условия задачи
(x+1)*(y+1)=xy+8
xy+x+y+1=xy+8
x+y=7
Теперь рассмотрим случай, когда мы их увеличим на 3
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 3 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+3)*(y+3)=xy+z
xy+3x+3y+9=xy+z
3x+3y+9=z
x+y=z/3-3
вот тут самое время избавиться от x и y, зная что x+y=7, тогда
z/3-3=7
z/3=10
z=30
Номер: A8C118
Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 12. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 4?
Решение:
60
Пусть x и y наши множители, тогда из условия задачи
(x+1)*(y+1)=xy+12
xy+x+y+1=xy+12
x+y=11
Теперь рассмотрим случай, когда мы их увеличим на 4
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 4 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+4)*(y+4)=xy+z
xy+4x+4y+16=xy+z
4x+4y+16=z
x+y=z/4-4
вот тут самое время избавиться от x и y, зная что x+y=11, тогда
z/4-4=11
z/4=15
z=60
Номер: 4408A2
Если бы каждый из двух множителей увеличили на 2, то их произведение увеличилось бы на 12. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3?
Решение:
21
Пусть x и y наши множители, тогда из условия задачи
(x+2)*(y+2)=xy+12
xy+2x+2y+4=xy+12
2x+2y=8
x+y=4
Теперь рассмотрим случай, когда мы их увеличим на 3
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 3 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+3)*(y+3)=xy+z
xy+3x+3y+9=xy+z
3x+3y+9=z
x+y=z/3-3
вот тут самое время избавиться от x и y, зная что x+y=4, тогда
z/3-3=4
z/3=7
z=21
Номер: 61A794
Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 11. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 2?
Решение:
24
Пусть x и y наши множители, тогда из условия задачи
(x+1)*(y+1)=xy+11
xy+x+y+1=xy+11
x+y=10
Теперь рассмотрим случай, когда мы их увеличим на 2
...получается, что нам надо найти разницу, которую примем за Z между множителями увеличенными на 2 по отношению к их произведению без этих прибавлений, записываем уравнение
(x+2)*(y+2)=xy+z
xy+2x+2y+4=xy+z
2x+2y+4=z
x+y=z/2-2
вот тут самое время избавиться от x и y, зная что x+y=10, тогда
z/2-2=10
z/2=12
z=24
Номер: 6D7263
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Решение:
22
70 очков это 10 правильных ответов, остается 33-10=23 ответа было еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 7 и 12, это получается 84. То есть 12 правильных и 7 неправильных.
12+7=19, все другие были ответы пропущены, так как невозможно их свести между собой за 33-29=4 ответа (по баллам).
Верные 10+12=22 ответа
Номер: 5E004B
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 13 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 56 очков, если известно, что по крайней мере один раз он ошибся?
Решение:
21
56 очков это 8 правильных ответов, остается 33-8=25 ответа было еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 7 и 13, это получается 91. То есть 13 правильных и 7 неправильных.
13+7=20, все другие были ответы пропущены, так как невозможно их свести между собой за 33-28=5 ответов (по баллам).
Верные 8+13=21 ответ
Номер: 03871E
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?
Решение:
16
42 очка это 6 правильных ответов, остается 25-6=19 ответа было еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 7 и 10, это получается 70. То есть 10 правильных и 7 неправильных.
10+7=17, все другие были ответы пропущены, так как невозможно их свести между собой за 25-23=2 ответа (по баллам).
Верные 6+10=16 ответов
Номер: 041C0F
Список заданий викторины состоял из 50 вопросов. За каждый правильный ответ участник получал 9 очков, за неправильный ответ с него списывали 16 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал участник, набравший 171 очко, если известно, что по крайней мере один раз он ошибся?
Решение:
35
171 очко это 19 правильных ответов, остается 50-19=31 ответ был еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 9 и 16, это получается 144. То есть 16 правильных и 9 неправильных.
16+9=25, все другие были ответы пропущены, так как невозможно их свести между собой за 50-44=6 ответов (по баллам).
Верные 19+16=35 ответов
Номер: 64F608
Список заданий викторины состоял из 50 вопросов. За каждый правильный ответ участник получал 9 очков, за неправильный ответ с него списывали 13 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал участник, набравший 225 очков, если известно, что по крайней мере один раз он ошибся?
Решение:
38
225 очко это 25 правильных ответов, остается 50-25=25 ответ был еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 9 и 13, это получается 117. То есть 13 правильных и 9 неправильных.
13+9=22, все другие были ответы пропущены, так как невозможно их свести между собой за 50-47=3 ответа (по баллам).
Верные 25+13=38 ответов
Номер: E2AD2C
Список заданий викторины состоял из 40 вопросов. За каждый правильный ответ участник получал 9 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал участник, набравший 171 очко, если известно, что по крайней мере один раз он ошибся?
Решение:
30
171 очко это 19 правильных ответов, остается 50-19=31 ответ был еще. При этом если была ошибка, то ее надо компенсировать правильными ответами в 0. Находим общее делимое для 9 и 11, это получается 99. То есть 11 правильных и 9 неправильных.
11+9=20, все другие были ответы пропущены, так как невозможно их свести между собой за 40-20+19=1 ответ (по баллам).
Верные 19+11=30 ответов
Номер: 4B5758
Клетки таблицы 4×5 раскрашены в чёрный и белый цвета так, что получилось 15 пар соседних клеток разного цвета и 11 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Решение:
5
В таблице 4x5 имеется 4 строки и 5 столбцов. В каждой строке возможны 4 пары соседних клеток.
Например,
(1,2), (2,3), (3,4), (4,5)
В каждом столбце возможны 3 пары соседних клеток.
Например,
(1,6), (6,11), (11,16).
Всего имеется 4·4+5·3 = 16+15 = 31 соседних клеток.
В них входят соседние пары черных клеток, соседние пары белых клеток и соседние пары разных цветов.
Обозначим искомое число соседних пар белых клеток через x.
По условию
31 = 15+11+x
31=26+ x
х = 31–26 = 5.
Имеется 5 пар соседних клеток белого цвета.
Ответ: 5.
Номер: 270CDC
Клетки таблицы 6×5 раскрашены в чёрный и белый цвета так, что получилось 26 пар соседних клеток разного цвета и 6 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Решение:
17
В таблице 6 строки и 5 столбцов. Т.к. клетки считаются соседними только если у них есть одна общая сторона, то получается, что в каждой строке 4 пары соседних клеток. А в каждом столбце 5 пар соседних клеток.
Значит, всего соседних клеток в строках 6⋅4=24 и в столбцах 5⋅5=25. Общее количество получается равно 24+25=49.
Пусть x – соседние пары клеток белого цвета. Т. к. по условию 26 пар соседних клеток разного цвета и 6 пар соседних клеток черного цвета, то можно составить уравнение:
49=26+6+x (всего пар соседних клеток и черного, и белого и разных цветов)
x=17.
Получилось, что 17 пар соседних клеток белого цвета.
Ответ: 17.
Номер: 205E02
Клетки таблицы 7×5 раскрашены в чёрный и белый цвета так, что получилось 27 пар соседних клеток разного цвета и 21 пара соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько получилось пар соседних клеток белого цвета?
Решение:
10
Ниже на рисунке представлена таблица 7х5 клеток с отмеченными характерными клетками.
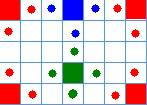
Из рисунка видно, что угловые клетки (красные) имеют по 2 соседа, а всего таких клеток 4, то есть, получаем число пар, равное 2∙4 = 8. Боковые клетки (синие) имеют по 3 пары и таких клеток в таблице 16, а пар 16∙3 = 48. Наконец, все остальные клетки (зеленые) имеют по 4 пары. Таких клеток 15, а пар 15∙4 = 60. Таким образом, имеем всего
8+48+60 = 116 пар.
В приведенных расчетах все пары взяты дважды (так как мы брали все клетки подряд). На рисунке ниже для одной зеленой клетки показана пара, взятая дважды (см. черный кружок и зеленый не закрашенный квадрат).

Поэтому, число уникальных пар, равно
116:2 = 58.
По условию задания пар соседних клеток разного цвета 27, а пар соседних клеток чёрного цвета 21, следовательно, пар соседних клеток белого цвета, ровно
58-27-21 = 10.
Ответ: 10.
Номер: 0C46FB FCF9B5
Клетки таблицы 5×5 раскрашены в чёрный и белый цвета так, что получилось 14 пар соседних клеток разного цвета и 11 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько получилось пар соседних клеток белого цвета?
Решение:
15
Всего имеется 4·5+5·4 = 20+20 = 40 соседних клеток.
В них входят соседние пары черных клеток, соседние пары белых клеток и соседние пары разных цветов.
Обозначим искомое число соседних пар белых клеток через x.
По условию
40 = 14+11+x
40=25+ x
х = 15.
Имеется 15 пар соседних клеток белого цвета.
Ответ: 15
Номер: 010901 A6F514
Клетки таблицы 4×8 раскрашены в чёрный и белый цвета так, что получилось 22 пары соседних клеток разного цвета и 19 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Решение:
11
Всего границ между клетками 3*8 + 4*7 = 24 + 28 = 52. У нас 22 границы черно-белые и 19 границ черно-черные.
Остальные 52 - 22 - 19 = 11 границ бело-белые. (равно парам)
Номер: FEB942
Клетки таблицы 3×7 раскрашены в чёрный и белый цвета так, что получилось 17 пар соседних клеток разного цвета и 11 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Решение:
4
Всего границ между клетками 2*7 + 3*6 = 14 + 18 = 32. У нас 17 границы черно-белые и 11 границ черно-черные.
Остальные 32 - 17 - 11 = 4 границ бело-белые. (равно парам)
Номер: 7D637B
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 13, 14 и 12. Найдите периметр четвёртого прямоугольника.
| 13 | 14 |
| ? | 12 |
Решение:
11
(14-12)/2=1 настолько длиннее сторона прямоугольника с периметром 14 в отличии от прямоугольника с периметром 12.
Так как у них ширина одинаковая, а длина больше за счет стороны которая длиннее и ее надо поделить на 2, так как этих стороны "работающих на удлинение" две.
(14-13)/2=0,5 настолько длиннее сторона прямоугольника с периметром 14 в отличии от прямоугольника с периметром 13.
В итоге получается у неизвестного прямоугольника стороны складываются из условий, что одна короче на 1 сантиметр, а вторая на 0,5 см чем стороны прямоугольника с периметром 14, тогда:
14-(1+0,5)*2=11
Номер: 9BCE1D
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
| 24 | 28 |
| ? | 16 |
Решение:
12
(28-16)/2=6 настолько длиннее сторона прямоугольника с периметром 28 в отличии от прямоугольника с периметром 16.
Так как у них ширина одинаковая, а длина больше за счет стороны которая длиннее и ее надо поделить на 2, так как этих стороны "работающих на удлинение" две.
(28-24)/2=2 настолько длиннее сторона прямоугольника с периметром 28 в отличии от прямоугольника с периметром 24.
В итоге получается у неизвестного прямоугольника стороны складываются из условий, что одна короче на 6 сантиметр, а вторая на 2 см чем стороны прямоугольника с периметром 28, тогда:
28-(6+2)*2=12
Номер: F8D8D7
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 17, 15 и 18. Найдите периметр четвёртого прямоугольника.
| 17 | 15 |
| ? | 18 |
Решение:
20
(18-15)/2=1,5 настолько длиннее сторона прямоугольника с периметром 18 в отличии от прямоугольника с периметром 15.
Так как у них ширина одинаковая, а длина больше за счет стороны которая длиннее и ее надо поделить на 2, так как этих стороны "работающих на удлинение" две.
(17-15)/2=1 настолько длиннее сторона прямоугольника с периметром 17 в отличии от прямоугольника с периметром 15.
В итоге получается у неизвестного прямоугольника стороны складываются из условий, что одна длиннее на 1,5 сантиметр, а вторая на 1 см чем стороны прямоугольника с периметром 15, тогда:
15+(1+1,5)*2=20
Номер: BAC3CE
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 18, 15 и 20. Найдите площадь четвёртого прямоугольника.
| 18 | 15 |
| ? | 20 |
Решение:
24
18-15=3 это разность площадей верхних прямоугольников. При этом прямоугольник 18, по факту является тем же прямоугольником с площадью 15 плюс маленький прямоугольник с площадью 3. Одна сторона у них одинаковая. можно записать так (х - высота, y - длина прямоугольника 15, z - длина прямоугольника 3)
x*y=15, x=15/y
x*z=3, x=3/z, тогда
15/y=3/z
15z=3y
5z=y, то есть z это 1/5 часть от длины прямоугольника 15
Тоже самое для прямоугольников справа.
20-15=5 это разность площадей прямоугольников справа.
можно записать так (х - ширина, y - высота прямоугольника 15, z - высота прямоугольника 5)
x*y=15, x=15/y
x*z=5, x=5/z, тогда
15/y=5/z
15z=5y
3z=y, то есть z это 1/3 часть от длины прямоугольника 15
Получается неизвестный прямоугольник на 3 часть шире и на 5 часть выше чем прямоугольник с площадью 15
То есть можно действовать поступательно. Вначале узнаем насколько увеличилась площадь, если увеличить ширину на 3 часть.
15+15*1/3=20
а теперь, получившийся прямоугольник надо увеличить на высоту в 1/5 часть
20+20*1/5=24
Это и будет площадь искомого прямоугольника
Ответ: 24
2 способ (намного проще):
Отношение площадей для прямоугольников сверху и снизу будет одинаковым, тогда
15/20=18/x
x=(18*20)/15
x=24
Номер: 10983C
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.
| 12 | 18 |
| ? | 30 |
Решение:
20
Отношение площадей для прямоугольников сверху и снизу будет одинаковым, тогда
18/30=12/x
x=(30*12)/18
x=20
Номер: A9F6B4
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 15, 12 и 24. Найдите площадь четвёртого прямоугольника.
| 15 | 12 |
| ? | 24 |
Решение:
30
Отношение площадей для прямоугольников сверху и снизу будет одинаковым, тогда
12/24=15/x
x=(24*15)/12
x=30
Ответ:30
Номер: 3D0CBD
В доме, в котором живёт Яна, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Яна живёт в квартире № 53. В каком подъезде живёт Яна?
Решение:
2
3*9=27 квартир в подъезде
53/27=1,96 то есть 2 подъезд
Номер: 5CA0FB
В доме, в котором живёт Галя, 9 этажей и несколько подъездов. На каждом этаже находится по 5 квартир. Галя живёт в квартире № 54. В каком подъезде живёт Галя?
Решение:
2
9*5=45 квартир в подъезде
54/45=1,2 то есть 2 подъезд
Ответ:2
Номер: 47940C
В доме, в котором живёт Дина, 5 этажей и несколько подъездов. На каждом этаже находится по 5 квартир. Дина живёт в квартире № 51. В каком подъезде живёт Дина?
Решение:
3
5*5=25 квартир в подъезде
51/25=2,04 то есть 3 подъезд
Ответ:3
Номер: 034607
В доме, в котором живёт Соня, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Соня живёт в квартире № 84. В каком подъезде живёт Соня?
Решение:
4
9*3=27 квартир в подъезде
84/27=3,111 то есть 4 подъезд
Ответ:4
Номер: 990D01
В доме, в котором живёт Петя, 5 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Петя живёт в квартире № 62. В каком подъезде живёт Петя?
Решение:
5
5*3=15 квартир в подъезде
62/15=4,133 то есть 5 подъезд
Ответ:5
Номер: EFC00C
В доме, в котором живёт Ася, 17 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Ася живёт в квартире № 56. В каком подъезде живёт Ася?
Решение:
2
17*3=51 квартир в подъезде
56/51=1,09 то есть 2 подъезд
Ответ:2
Номер: B1127B
В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире № 49. На каком этаже живёт Петя?
Решение:
9
49/6=8,2 то есть на 9 этаже
Ответ: 9
Номер: C50C5B A1010A
В доме, в котором живёт Петя, один подъезд. На каждом этаже по пять квартир. Петя живёт в квартире № 32. На каком этаже живёт Петя?
Решение:
7
32/5=6,4 то есть на 7 этаже
Ответ: 7
Номер: B92D79 361660
В доме, в котором живёт Петя, один подъезд. На каждом этаже по семь квартир. Петя живёт в квартире № 52. На каком этаже живёт Петя?
Решение:
8
52/7=7,42 то есть на 8 этаже
Ответ: 8
Номер: A40039 92D815
В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире № 50. На каком этаже живёт Петя?
Решение:
9
50/6=8,33 то есть на 9 этаже
Ответ: 9
Номер: C9E2F0 3668F3
В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире № 69. На каком этаже живёт Петя?
Решение:
12
69/6=11,5 то есть на 12 этаже
Ответ: 12
Номер: 85CCC9
В доме, в котором живёт Петя, один подъезд. На каждом этаже по семь квартир. Петя живёт в квартире № 67. На каком этаже живёт Петя?
Решение:
10
67/7=9,57 то есть на 10 этаже
Ответ: 10
Номер: F74D92
Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
Решение:
10
12*8=96 - условных этажей
468/96=4,9 не меньше чем столько квартир должно быть на площадке.
Если их 5 на этаже, то квартир в 7 подъездах будет 12*5*7=420
Если их 6, то в 7 подъездах будет 12*6*7=504, чего не может быть, так как у Пети квартира с меньшим номером в следующем подъезде.
Тогда 468-420=48
48/5=9,6 получается 10 этаж
Номер: 688BFE E48CEC
Саша пригласил Петю в гости, сказав, что живёт в двенадцатом подъезде в квартире № 465, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом пятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
Решение:
4
12*5=60 - условных этажей в 12 подъездах
465/60=7,75 не меньше чем столько квартир должно быть на площадке.
Допустим их 8 на этаже, то квартир в 12 подъездах будет 60*8=480, тогда 480/12=40 квартир в каждом подъезде, что сходится с условием задачи.
Если взять 9 квартир, то будет 540/12=45,
540-45=495 это квартира с которой должен начинаться 12 подъезд, чего не может быть.
Тогда 480-465=15
15/8=1,875
5-1=4 этаж
Номер: DCA5C3 4A7B82
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, нумерация квартир в доме начинается с единицы.)
Решение:
5
7*7=49 - условных этажей в 7 подъездах 7 этажного дома
462/49=9,42 не меньше чем столько квартир должно быть на площадке.
Допустим их 10 на этаже, то квартир в 7 подъездах будет 10*7*7=490, тогда 490/10=49 квартир в каждом подъезде, что сходится с условием задачи.
Если взять 11 квартир, то будет 11*7*7=539
539-77=462, то есть 462 будет уже в 6 подъезде, что не сходится.
Тогда 490-462=28
28/10=2,8
7-2=5 этаж
Номер: 8EACC7 0C7B30
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, нумерация квартир в доме начинается с единицы.)
Решение:
3
9*10=90 - условных этажей в 10 подъездах 9 этажного дома
333/90=3,7 не меньше чем столько квартир должно быть на площадке.
Допустим их 4 на этаже, то квартир в 10 подъездах будет 10*4*9=360, тогда 360/10=36 квартир в каждом подъезде, что сходится с условием задачи.
Если взять 5 квартир, то будет 10*5*9=450 (450/10=45)
450-45=405, то есть с 405 кв будет начинаться 10 подъезд, что не сходится.
Тогда 360-333=27
27/4=6,75
9-6=3 этаж
Номер: 8A8382
В доме всего десять квартир, их номера от 1 до 10. В каждой квартире живёт не меньше одного и не больше трёх человек. В квартирах с 1-й по 8-ю включительно живёт суммарно 10 человек, и в квартирах с 7-й по 10-ю включительно живёт суммарно 10 человек. Сколько всего человек живёт в этом доме?
Решение:
16
Решение
Пусть в квартирах №7 и №8 живут суммарно x человек. Определим, чему может быть равно x.
С одной стороны, в квартирах №1–№6 живут не менее 6 человек, значит, поскольку в квартирах №1–№8 живут 10 человек, то x ≤ 10 - 6 = 4
С другой стороны, в квартирах №9 и №10 живут не более 6 человек, значит, поскольку в квартирах №7–№10 живут 10 человек, то x ≥ 10 - 6 = 4
x ≤ 4 и x ≥ 4, поэтому x = 4. Тогда в квартирах №1–№6 живут 10 - 4 = 6 человек, в квартирах №9–10 – 10 - 4 = 6 человек, а всего в доме 6 + 4 + 6 = 16 жителей.
Ответ:16
Номер: 5A87A0
В доме всего восемнадцать квартир, их номера от 1 до 18. В каждой квартире живёт не меньше одного и не больше трёх человек. В квартирах с 1-й по 13-ю включительно живёт суммарно 15 человек, а в квартирах с 11-й по 18-ю включительно живёт суммарно 20 человек. Сколько всего человек живёт в этом доме?
Решение:
30
Пусть в квартирах 11,12,13 живут суммарно x человек. Определим, чему может быть равно x.
С 1 по 13 живет не менее 13 человек
С 11 по 18 - 20 человек, то есть практически все квартиры под завязку, кроме одной.
Значит чтобы получить 15 человек в первых 13 квартирах, надо их взять из 20 человек, тогда в 11,12,13 будет 1, 2, 2 человека итого 5
Получаем: 10 чел с 1 по 10 + 15 человек с 14 по 18 + 5 с 11 по 13
10+5+15=30
Ответ:30
Номер: 26BEB3 549A5A
В доме всего пятнадцать квартир с номерами от 1 до 15. В каждой квартире живёт не меньше одного и не больше трёх человек. В квартирах с 1-й по 12-ю включительно живёт суммарно 14 человек, а в квартирах с 11-й по 15-ю включительно живёт суммарно 13 человек. Сколько всего человек живёт в этом доме?
Решение:
23
Графически получается наиболее наглядно, что других вариантов нет
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| * | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| * | * | * | * | * | ||||||||||
| * | * | * |
Ответ:23
Номер: 910216
В доме всего четырнадцать квартир с номерами от 1 до 14. В каждой квартире живёт не менее одного и не более трёх человек. В квартирах с 1-й по 10-ю включительно живёт суммарно 12 человек, а в квартирах с 7-й по 14-ю включительно живёт суммарно 18 человек. Сколько всего человек живёт в этом доме?
Решение:
24
Графически получается наиболее наглядно, что других вариантов нет
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| ** | * | * | * | * | |||||||||
| * | * | * | * | ||||||||||
Ответ:24
Номер: C131B8
В доме всего четырнадцать квартир с номерами от 1 до 14. В каждой квартире живёт не менее одного и не более трёх человек. В квартирах с 1-й по 9-ю включительно живёт суммарно 12 человек, а в квартирах с 6-й по 14-ю включительно живёт суммарно 22 человека. Сколько всего человек живёт в этом доме?
Решение:
27
Графически получается наиболее наглядно, что других вариантов нет
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| * | * | * | * | * | * | * | * | * | * | * | * | * | * |
| *** | * | * | * | * | * | ||||||||
| * | * | * | * | * | |||||||||
Ответ:27
Номер: 1E3E63
В доме всего десять квартир с номерами от 1 до 10. В каждой квартире живёт не меньше одного и не больше четырёх человек. В квартирах с 1-й по 6-ю включительно живёт суммарно 9 человек, а в квартирах с 4-й по 10-ю включительно живёт суммарно 22 человека. Сколько всего человек живёт в этом доме?
Решение:
25
Графически получается наиболее наглядно, что других вариантов нет
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| * | * | * | * | * | * | * | * | * | * |
| * | * | * | * | * | * | * | |||
| * | * | * | * | ||||||
| * | * | * | * |
Ответ:25
Номер: 9F1269
Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?
Решение:
11
Пусть число подъездов x > 1. Тогда квартир y > x, а число этажей z > y. Число 110 должно быть составлено из чисел x, y и z:
110=xyz
В то же время, число 110 можно разложить на простые множители так:
110=2*5*11
Значит, x=2, y=5, z=11. То есть, в доме 11 этажей.
Ответ:11
Номер: 57A800 83DCE6
Во всех подъездах дома одинаковое число этажей, а на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 455 квартир?
Решение:
13
Пусть число подъездов x > 1. Тогда квартир y > x, а число этажей z > y. Число 455 должно быть составлено из чисел x, y и z:
455=xyz
В то же время, число 455 надо разложить на простые множители:
455=5*7*13
Значит, в доме 13 этажей.
Ответ:13
Номер: 56784E 96E04C
Во всех подъездах дома одинаковое число этажей, а на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 114 квартир?
Решение:
19
Пусть число подъездов x > 1. Тогда квартир y > x, а число этажей z > y. Число 455 должно быть составлено из чисел x, y и z:
114=xyz
В то же время, число 114 надо разложить на простые множители:
114=2*3*19
Значит, в доме 13 этажей.
Ответ:19
Номер: BD43C7 7DC8ED
Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 357 квартир?
Решение:
17
Пусть число подъездов x > 1. Тогда квартир y > x, а число этажей z > y. Число 455 должно быть составлено из чисел x, y и z:
357=xyz
В то же время, число 357 надо разложить на простые множители:
357=3*7*17
Значит, в доме 13 этажей.
Ответ:17
Номер: 56D012 5C4906
Во всех подъездах дома одинаковое число этажей, а на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 105 квартир?
Решение:
17
Пусть число подъездов x > 1. Тогда квартир y > x, а число этажей z > y. Число 455 должно быть составлено из чисел x, y и z:
357=xyz
В то же время, число 357 надо разложить на простые множители:
357=3*7*17
Значит, в доме 13 этажей.
Ответ:17
Номер: 8B6B93
Петя меняет маленькие фишки на большие. За один обмен он получает 1 большую фишку, отдав 10 маленьких. До обменов у Пети было 150 фишек (среди них были и большие, и маленькие), а после стало 60. Сколько обменов он совершил?
Решение:
10
Петя отдает 10 маленьких, а получает 1 большую, то есть за каждый раз отдает 9 фишек. Тогда (150-60)/9=10
Ответ:10
Номер: C2CABE
Петя меняет маленькие фишки на большие. За один обмен он получает 4 больших фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 64. Сколько обменов он совершил?
Решение:
6
Петя отдает 10, а получает 4, то есть за каждый раз отдает 6 фишек. Тогда (100-64)/6=6
Ответ:6
Номер: E12630
Петя меняет маленькие фишки на большие. За один обмен он получает 7 больших фишек, отдав 11 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 68. Сколько обменов он совершил?
Решение:
8
Петя отдает 11, а получает 7, то есть за каждый раз отдает 4 фишек. Тогда (100-68)/4=8
Ответ:8
Номер: 7A5A50
Петя меняет маленькие фишки на большие. За один обмен он получает 5 больших фишек, отдав 13 маленьких. До обменов у Пети было 50 фишек (среди них были и большие, и маленькие), а после стало 26. Сколько обменов он совершил?
Решение:
3
Петя отдает 13, а получает 5, то есть за каждый раз отдает 8 фишек. Тогда (50-26)/8=3
Ответ:3
Номер: 4D1C22
Петя меняет маленькие фишки на большие. За один обмен он получает 4 большие фишки, отдав 11 маленьких. До обменов у Пети было 150 фишек (среди них были и большие, и маленькие), а после стало 73. Сколько обменов он совершил?
Решение:
11
Петя отдает 11, а получает 4, то есть за каждый раз отдает 7 фишек. Тогда (150-73)/7=11
Ответ:11
Номер: ED5722
Петя меняет маленькие фишки на большие. За один обмен он получает 3 большие фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 65. Сколько обменов он совершил?
Решение:
5
Петя отдает 10, а получает 3, то есть за каждый раз отдает 7 фишек. Тогда (100-65)/7=5
Ответ:5
Номер: FEF4DB
Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
48
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 4 раза дольше Маши и к тому же ел их в 4 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 4∙4=16 печений, съеденных Медведем. В сумме эти печенья составляют 1+16=17 и таких сумм в 51 печеньях ровно 51:17 = 3. Значит, Маша съела 3 печенья, а Медведь 3∙16=48.
Ответ: 48
Номер: 2E1F09 8610B7
Маша и Медведь съели 85 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
80
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 4 раза дольше Маши и к тому же ел их в 4 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 4∙4=16 печений, съеденных Медведем. В сумме эти печенья составляют 1+16=17 и таких сумм в 85 печеньях ровно 85:17 = 5. Значит, Маша съела 5 печений, а Медведь 5∙16=80.
Ответ: 80
Номер: AEA031
Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
90
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем. В сумме эти печенья составляют 1+9=10 и таких сумм в 100 печеньях ровно 100:10 = 10. Значит, Маша съела 10 печений, а Медведь 10∙9=90.
Ответ: 90
Номер: 3C3441 EE453D
Маша и Медведь съели 110 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
99
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем. В сумме эти печенья составляют 1+9=10 и таких сумм в 110 печеньях ровно 110:10 = 11. Значит, Маша съела 10 печений, а Медведь 11∙9=99.
Ответ: 99
Номер: 9691FF 584F1E
Маша и Медведь съели 140 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
126
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем. В сумме эти печенья составляют 1+9=10 и таких сумм в 140 печеньях ровно 140:10 = 14. Значит, Маша съела 10 печений, а Медведь 14∙9=126.
Ответ: 126
Номер: 33D9AB
Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Решение:
144
Так как варенье и Маша и Медведь съели поровну и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину). Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем. В сумме эти печенья составляют 1+9=10 и таких сумм в 160 печеньях ровно 160:10 = 16. Значит, Маша съела 10 печений, а Медведь 16∙9=144.
Ответ: 144
Номер: F0E454
В обменном пункте можно совершить одну из двух операций:
• за 4 золотые монеты получить 5 серебряных и одну медную;
• за 7 серебряных монет получить 5 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
15
Решение 1
Условно обозначим через a – число золотых монет, через b – число серебряных монет, а через c – число медных монет. В этих обозначениях обменные операции можно записать так:
4а=5b+c
7b=5a+c
По итогам обменных операций Николай должен иметь: , а серебряных b меньше первоначальной величины. Так как изначально у Николая есть только серебряные монеты, то первая обменная операция будет
7b=5a+c,
в результате которой появится 5 золотых и одна серебряная монета. Можно заметить, что если провести 4 таких операции подряд, то число серебряных монет уменьшится на 7∙4=28, золотых станет 5∙4=20 и медных 4. Но теперь мы можем совершить 5 первых операций и избавиться от всех золотых монет. В результате у Николая прибавится: 5∙5=25 серебряных и 5 медных. В результате 4+5=9 таких обменных операций Николай уменьшит число серебряных монет на 28-25 = 3, медных станет 5+4=9, а золотых не будет совсем. Результат удовлетворяет условию задания. И чтобы получилось 45 медных монет необходимо сделать 45:9 = 5 таких групп операций. Учитывая, что при каждой группе операций у Николая число серебряных монет уменьшается на 3, то за 5 таких групп число серебряных уменьшится на 3∙5 = 15.
Решение 2
4 зол. = 5 сер. + 1 мед., отсюда 1 мед. = 4 зол. - 5 сер.
7 сер. = 5 зол. + 1 мед., отсюда 1 мед. = 7 сер. - 5 зол.
Значит, 4 зол. - 5 сер. = 7 сер. - 5 зол.
4 зол. + 5 зол. = 7 сер. + 5 сер.
9 зол. = 12 сер.
3 зол. = 4 сер.
Поскольку У Николая не появилось золотых монет, нас интересует только серебро.
1 мед. = 4 зол. - 5 сер.
3 мед. = 12 зол. - 15 сер.
3 мед. = 16 сер. - 15 сер.
3 мед. = 1 сереб.
Николай получил с каждой серебряной монеты 3 медных, а всего 45 медных монет, тогда 45 : 3 = 15 серебра он потратил.
Решение 3
Чтобы осталось только серебро, в результате операции №2 надо получить число золотых монет, кратное 4 и 5, это 20, а затем обменять их в операции №1 на серебро.
Меняем серебро на золото (операция 2) 4 раза, получаем 20 золота и 4 меди, тратим при этом 7*4=28 серебра.
Затем меняем полученное золото на серебро (операция 1) 5 раз, получаем 25 серебра и 5 меди.
Из потраченных 28 серебра вернулось 25, то есть на 28 - 25 = 3 серебра получили 4 + 5 = 9 меди.
Значит, если надо получить 45 меди, разница будет больше в 45 : 9 = 5 раз.
На 3 * 5 = 15 уменьшилось количество серебряных монет.
Номер: 83557D 54BC1F
В обменном пункте можно совершить одну из двух операций:
• за 4 золотых монеты получить 5 серебряных и одну медную;
• за 8 серебряных монет получить 5 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
35
Надо найти общий "знаменатель" для 5 и 4, это 20, то есть вторую операцию надо совершить 4 раза, чтобы без остатка совершить 5 раз первую операцию
В итоге получим 4 меди со второй операции и с первой 25 серебряных и 5 медных. То есть с двух операций 9 медных. При этом надо 45/9=5 раз повторить этот цикл. При этом на цикл тратим 8*4=32 серебра, а получаем на выходе 25. То есть затрата на цикл 32-25=7 серебра.
В итоге 5 циклов по 7 монет =35
Ответ: 35
Номер: C6C2F5 4368DA
В обменном пункте можно совершить одну из двух операций:
• за 5 золотых монет получить 7 серебряных и одну медную;
• за 10 серебряных монет получить 7 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 60 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
5
Надо найти общий "знаменатель" для 5 и 7, это 35, то есть вторую операцию надо совершить 5 раз, чтобы без остатка совершить 7 раз первую операцию
В итоге получим 5 меди со второй операции и с первой 49 серебряных и 7 медных. То есть с двух операций 12 медных. При этом надо 60/12=5 раз повторить этот цикл. При этом на цикл тратим 10*5=50 серебра, а получаем на выходе 49. То есть затрата на цикл 50-49=1 серебра.
В итоге 5 циклов по 1 монете =5
Ответ: 5
Номер: E6AE09 A79011
В обменном пункте можно совершить одну из двух операций:
• за 5 золотых монет получить 6 серебряных и одну медную;
• за 8 серебряных монет получить 6 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 55 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
20
Надо найти общий "знаменатель" для 5 и 6, это 30, то есть вторую операцию надо совершить 5 раз, чтобы без остатка совершить 6 раз первую операцию.
В итоге получим 5 меди со второй операции и с первой 36 серебряных и 6 медных. То есть с двух операций 11 медных. При этом надо 55/11=5 раз повторить этот цикл. При этом на цикл тратим 8*5=40 серебра, а получаем на выходе 6*6=36. То есть затрата на цикл 40-36=4 серебра.
В итоге 5 циклов по 4 монете =20
Ответ: 20
Номер: A94F22
В обменном пункте можно совершить одну из двух операций:
• за 3 золотых монеты получить 4 серебряных и одну медную;
• за 6 серебряных монет получить 4 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых
не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
10
Надо найти общий "знаменатель" для 4 и 3, это 12, то есть вторую операцию надо совершить 3 раза, чтобы без остатка совершить 4 раза первую операцию.
В итоге получим 3 меди со второй операции и с первой 16 серебряных и 4 медных. То есть с двух операций 7 медных. При этом надо получить 35, тогда 35/7=5 раз повторить этот цикл из двух операций. При этом на цикл тратим 6*3=18 серебра, а получаем на выходе 4*4=16. То есть затрата на цикл 18-16=2 серебра.
В итоге 5 циклов по 2 монеты =10
Ответ: 10
Номер: 5E07A3
В обменном пункте можно совершить одну из двух операций:
• за 2 золотые монеты получить 3 серебряные и одну медную;
• за 5 серебряных монет получить 3 золотые и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых
не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
10
Надо найти общий "знаменатель" для 3 и 2, это 6, то есть вторую операцию надо совершить 2 раза, чтобы без остатка совершить 3 раза первую операцию.
В итоге получим 2 меди со второй операции и с первой 9 серебряных и 3 медных. То есть с двух операций 5 медных. При этом надо получить 50, тогда 50/5=10 раз повторить этот цикл из двух операций. При этом на цикл тратим 5*2=10 серебра, а получаем на выходе 3*3=9. То есть затрата на цикл 10-9=1 серебра.
В итоге 10 циклов по 1 монете =10
Ответ: 10
Номер: 56BB9F
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
17
если взять за x меньший угол, то составим уравнение:
3x+y=360, при условии y > x, где y - средний угол,
Возьмем предел, где x = y, тогда 360/4=90, но этот предел по условиям (y > x) должен быть меньше 90, то есть здесь есть стремление к уменьшению x.
Мы можем уменьшать х от 89 и меньше до тех пор, пока y < 2x, возьмем крайний предел, когда y = 2x, тогда получаем 2x+2x+x=360
х=360/5=72, то есть нельзя уменьшать x ниже этого значения, так как это повлечет невыполнение y < 2x. В итоге получаем диапазон
от 90 включительно и до 72 не включительно. 90-73=17.
Номер: 6B9D46
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 5 раз больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
19
Больший и меньший угол составляют 6 частей, так как соотносятся (1:5), а также + средний 1 часть, в случае если он будет максимальный.
Больший и меньший угол составляют 6 частей, так как соотносятся (1:5), а также + средний 5 частей, в случае если он будет минимальный.
Тогда:
6+1=7 частей
360/7=51,42
тогда меньший угол 51 градус
6+5=11 частей
360/11=32,72
тогда меньший угол 33 градуса
При этом каждое изменение значения меньшего угла повлечет за собой изменение показания и среднего и большого. Количество изменений будет кратно изменению меньшего угла.
Тогда 51-33=19 значений будет у 1,2,3 угла (изменение меньшего угла на 1 автоматически уменьшает на 5 единиц больший угол)
Ответ: 19
Номер: 796E7E
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 4 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
19
Больший и меньший угол составляют 5 частей, так как соотносятся (1:4), а также + средний 1 часть, в случае если он будет максимальный.
Больший и меньший угол составляют 5 частей, так как соотносятся (1:4), а также + средний 4 частей, в случае если он будет минимальный.
Тогда:
5+1=6 частей
360/6=60
тогда меньший угол 60 градусов
5+4=9 частей
360/9=40
тогда меньший угол 41 градусов
При этом каждое изменение значения меньшего угла повлечет за собой изменение показания и среднего и большого. Количество изменений будет кратно изменению меньшего угла.
Тогда 60-41=19 значений будет у 1,2,3 угла
Ответ: 19
Номер: 1CA79C
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 6 раз больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
17
Больший и меньший угол составляют 7 частей, так как соотносятся (1:6), а также + средний 1 часть, в случае если он будет максимальный.
Больший и меньший угол составляют 7 частей, так как соотносятся (1:6), а также + средний 6 частей, в случае если он будет минимальный.
Тогда:
7+1=8 частей
360/8=45
тогда меньший угол 45 градусов
7+6=13 частей
360/13=27,7
тогда меньший угол 28 градусов
При этом каждое изменение значения меньшего угла повлечет за собой изменение показания и среднего и большого. Количество изменений будет кратно изменению меньшего угла.
Тогда 45-28=17 значений будет у 1,2,3 угла
Ответ: 17
Номер: 158B67
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 7 раз больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
15
Больший и меньший угол составляют 8 частей, так как соотносятся (1:7), а также + средний 1 часть, в случае если он будет максимальный.
Больший и меньший угол составляют 8 частей, так как соотносятся (1:7), а также + средний 7 частей, в случае если он будет минимальный.
Тогда:
8+1=9 частей
360/8=45
тогда меньший угол 40 градусов
7+8=15 частей
360/15=24
тогда меньший угол 25 градусов
При этом каждое изменение значения меньшего угла повлечет за собой изменение показания и среднего и большого. Количество изменений будет кратно изменению меньшего угла.
Тогда 40-25=15 значений будет у 1,2,3 угла
Ответ: 15
Номер: 6D2080
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение:
20
Больший и меньший угол составляют 4 частей, так как соотносятся (1:3), а также + средний 1 часть, в случае если он будет максимальный.
Больший и меньший угол составляют 4 частей, так как соотносятся (1:3), а также + средний 3 частей, в случае если он будет минимальный.
Тогда:
4+1=5 частей
360/5=72
тогда меньший угол 72 градусов
4+3=7 частей
360/7=51,4
тогда меньший угол 52 градусов
При этом каждое изменение значения меньшего угла повлечет за собой изменение показания и среднего и большого. Количество изменений будет кратно изменению меньшего угла.
Тогда 72-52=20 значений будет у 1,2,3 угла
Ответ: 20
Номер: 90B62F

