В 2024 году в ЕГЭ по профильной математике ввели новое задание - линейка 2, манипуляции с векторами. Примеры заданий перед вами.
Для решение задач данной группы вам потребуется знание 4 основных теорем.
1. При отходе от целочисленных координат необходимо: из координат его конца, отнимаем координаты его начала.
2. Складывание/вычитание векторов производится путем сложения/вычитания соответствующих координат первого и второго вектора.
3. Скалярное произведение векторов аb равно произведению модулей векторов, умноженному на косинус угла между ними: AC*AB = |AC|*|AB| * cos a и та же формула в другой интерпретации, - умножение векторов производим по формуле: a*b = x1*x2 + y1*y2
Задания про векторы ЕГЭ мат профиль, ФИПИ
КЭС: 7.5 Координаты и векторы
Впишите правильный ответ.
Даны векторы `veca`(− 13 ; 4) и `vecb`(− 6 ; 1). Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
82
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(-13;4) и b(-6;1).
По формуле находим:
a·b=(-13)·(-6)+4·1=82
Номер: 0A394E
Впишите правильный ответ.
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите длину вектора `veca` +4`vecb`.
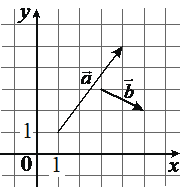
Ответ:
11
`veca`(4-1;5-1)=(3;4)
`vecb`(5-3;2-3) , 4`vecb`(8;-4)
Координаты искомого вектора будут равны сумме соответствующих координат:
`veca` +4`vecb`(x1+x2; y1+y2) = `veca` +4`vecb`(3+8; 4-4) = `veca` +4`vecb`(11; 0)
А теперь находим его длину
|`veca` +4`vecb`|=`sqrt(11^2+0^2)`=11
Номер: 579B74
Впишите правильный ответ.
Даны векторы `veca`( 14; − 2) и `vecb`(5 ; − 8). Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
86
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(14;-2) и b(5;-8).
По формуле находим:
a·b=14·5+(-2)·(-8)=86
Номер: E68A17
Впишите правильный ответ.
Даны векторы `veca`(− 3 ; 5) и `vecb`(1 ; 13). Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
62
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(-3;5) и b(1;13).
По формуле находим:
a·b=-3·1+5·13=62
Номер: FFBFD7
Впишите правильный ответ.
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите длину вектора `veca` +3`vecb`.
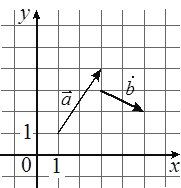
Ответ:
8
Номер: B515D1
Впишите правильный ответ.
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите скалярное произведение `veca`⋅`vecb`.
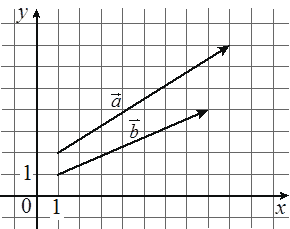
Ответ:
71
`veca`(5;8) `vecb`(3;7)
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(5;8) и b(3;7).
По формуле находим:
a·b=5·3+8·7=71
Номер: E5399A
Впишите правильный ответ.
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите скалярное произведение `veca`⋅`vecb`.
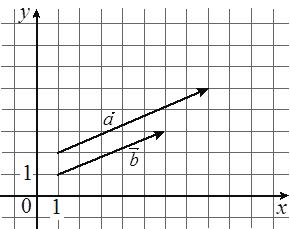
Ответ:
41
`veca`(3;7) `vecb`(2;5)
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(3;7) и b(2;5).
По формуле находим:
a·b=3·2+7·5=41
Номер: 0432E9
Впишите правильный ответ.
Даны векторы `veca`(5; −7) и `vecb`(14 ; 1). Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
63
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2.
Найдем скалярное произведение векторов a=(5;-7) и b(14;1).
По формуле находим:
a·b=5·14-7·1=63
Номер: 71AC6C
Впишите правильный ответ.
Длины векторов `veca` и `vecb` равны 3 и 5, а угол между ними равен 60°. Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
7,5
|3|*|5|*cos60°=15*1/2=7,5
Номер: 238861
Впишите правильный ответ.
Длины векторов `veca` и `vecb` равны 3 и 7, а угол между ними равен 60°. Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
10,5
|3|*|7|*cos60°=21*1/2=10,5
Номер: 028837
Впишите правильный ответ.
Даны векторы `veca`(25; 0) и `vecb`(1; −5). Найдите длину вектора `veca`−4`vecb`.
Ответ:
29
Длина вектора: если `veca(x;y)`, то `|veca|=sqrt(x^2+y^2)`
Сложение векторов: если `veca(x_1;y_1)` и `vecb(x_2;y_2)`, то `veca+vecb=(x_1+x_2;y_1+y_2)`
`4vecb (4; −20)`
`veca−4 vecb (25-4;0+20)=(21;20)`
`|veca−4vecb|=sqrt(21^2+20^2)=sqrt841=29`
Ответ: 29
Номер: 40B442
Впишите правильный ответ.
Даны векторы `veca`(1; 1) и `vecb` (0; 7). Найдите длину вектора 8`veca`+`vecb`.
Ответ:
17
Длина вектора: если `veca(x;y)`, то `|veca|=sqrt(x^2+y^2)`
Сложение векторов: если `veca(x_1;y_1)` и `vecb(x_2;y_2)`, то `veca+vecb=(x_1+x_2;y_1+y_2)`
Номер: D891F7
Впишите правильный ответ.
Даны векторы `veca`(5; 3) и `vecb` (4; −6). Найдите скалярное произведение `veca`⋅`vecb`.
Ответ:
2
Скалярное произведение в координатах: если `veca(x_1;y_1)` и `vecb(x_2;y_2)`, то `veca*vecb=x_1*x_2 + y_1*y_2`
По формуле находим:
`veca*vecb=5·4+3·(-6)=20-18=2`
Ответ: 2
Номер: FC0F78
Впишите правильный ответ.
Даны векторы `veca`(31; 0) и `vecb` (1; −1). Найдите длину вектора `veca`−24`vecb`.
Ответ:
25
Длина вектора: если `veca(x;y)`, то `|veca|=sqrt(x^2+y^2)`
Сложение векторов: если `veca(x_1;y_1)` и `vecb(x_2;y_2)`, то `veca+vecb=(x_1+x_2;y_1+y_2)`
`24vecb (24;-24)`
`veca-24vecb=(31-24;0+24)=(7;24)`
`|veca-24vecb|=sqrt(7^2+24^2)=sqrt625=25`
Ответ: 25
Номер: C9EE7C
Впишите правильный ответ.
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите скалярное произведение `veca`⋅`vecb`.

Ответ:
1
Номер: A288A1
Впишите правильный ответ.
Даны векторы `veca`(2; 0) и `vecb` (1; 4). Найдите длину вектора `veca`+3`vecb`.
Ответ:
13
Номер: D331CB
Задания про векторы с Масегэ с ответами
1. Найдите длину вектора `veca`(6;8).
Ответ:
10
`|\veca|=\sqrt{6^{2}+8^{2}}=\sqrt{36+64}=\sqrt{100}=10`
2. Найдите квадрат длины вектора `vec(AB)`.
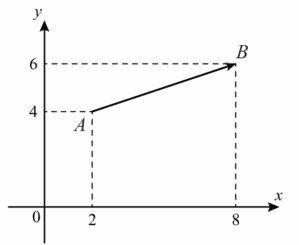
Ответ:
40
Координаты вектора `vec(AB)`(8-2;6-4)=(6;2)
Длина вектора `|vec(AB)|=sqrt(36+4)=sqrt(40)`
`vec(AB)`2 = 40
3. Найдите квадрат длины вектора `veca+vecb`
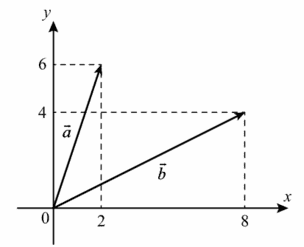
Ответ:
200
`veca`(2;6) + `vecb`(8;4) = `vecc`(10;10)
c2=102 +102
c2=200
4. Найдите скалярное произведение векторов `veca` и `vecb`
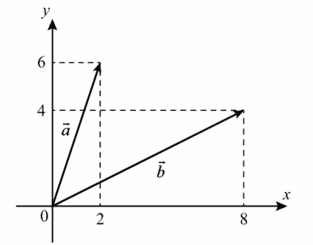
Ответ:
40
При скалярном произведении векторов получается число, не зависящее от системы координат, в которых находятся исходные вектора. Результат является характеристикой длин векторов, составляющих произведение, и угла между ними.
Существует еще векторное произведение, представляющее собой результирующий вектор.
Как вычислить скалярное произведение векторов
Скалярное произведение векторов аb равно произведению модулей векторов, умноженному на косинус угла между ними:
аb = |а|*|b| * cos a
В случае плоскостного расположения векторов (а (х1; у1) и b (у1; у2) их скалярное произведение аb будет иметь вид:
аb = х1х2 + у1у2.
`veca`(2;6)`*vecb`(8;4) = 2*8+6*4=16+24=40
5. Найдите квадрат длины вектора `veca+vecb`
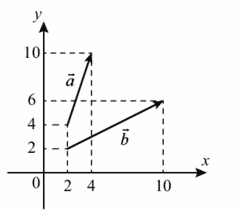
Ответ:
200
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(4-2;10-4) а(2;6)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(10-2;6-2) b(8;4)
Квадрат длины вектора a+b равен сумме квадратов его координат, то есть
`veca`(2;6) + `vecb`(8;4) = `vecc`(10;10)
c2=102 +102
c2=200
Ответ: 200
6. Найдите квадрат длины вектора `veca-vecb`
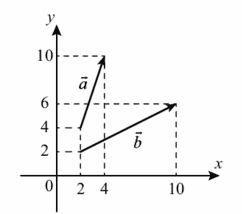
Ответ:
40
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(4-2;10-4) а(2;6)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(10-2;6-2) b(8;4)
Найдем координаты вектора a-b, - найдем разность соответствующих координат
a-b(2-8;6-4)=(-6;2)
Длина вектора a-b=√(-6)2+22=√40
Квадрат из корня равен числу под корнем
Ответ: 40
7. Найдите скалярное произведение векторов `veca` и `vecb`

Ответ:
40
Найдём скалярное произведение по формуле:
ab=a1*b1+a2*b2
Чтобы найти координаты вектора необходимо из координат конца вектора вычесть соответствующие координаты его начала, значит
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(4-2;10-4) а(2;6)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(10-2;6-2) b(8;4)
Вычисляем скалярное произведение: a*b = x1*x2 + y1*y2
ab=2*8+6*4=40
Ответ: 40
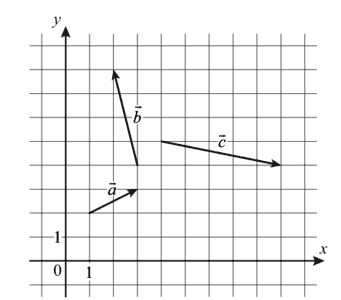
8. На координатной плоскости изображены векторы `veca`, `vecb` и `vecc`. Найдите длину вектора `veca`+ `vecb` + `vecc`.
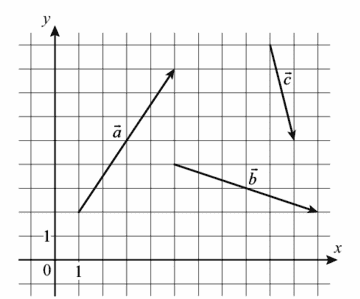
Ответ:
11
У нас есть векторы с целочисленными координатами, теперь переходим к координатам каждого из векторов по следующему алгоритму:
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(5-1;8-2) а(4;6)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(11-5;2-4) b(6;-2)
Находим координаты вектора c, из координат его конца, отнимаем координаты его начала, тогда
c(10-9;5-9) c(1;-4)
Координаты искомого вектора будут равны сумме соответствующих координат:
a+b+c(x1+x2+x3; y1+y2+y3) = a+b+c (4+6+1; 6-2-4) = a+b+c (11; 0)
А теперь находим его длину
/a+b+c/=`sqrt(11^2+0^2)`=11
Ответ: 11
9. На координатной плоскости изображены векторы `veca`и `vecb`. Найдите скалярное произведение `veca*vecb`.
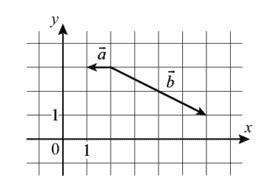
Ответ:
-4
Найдём скалярное произведение по формуле:
a*b = x1*x2 + y1*y2
Однако прежде необходимо найти координаты векторов по целочисленным координатам.
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(1-2;3-3) а(-1;0)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(6-2;1-3) b(4;-2)
ab=-1*4+0*-2 = -4
Ответ: -4
10. Даны векторы `veca`(1;3) и `vecb`(-4;2). Найдите скалярное произведение `veca*vecb`
Ответ:
2
Найдём скалярное произведение по формуле:
a*b = x1*x2 + y1*y2, при этом у векторов уже есть свой координаты, то есть они не с целочисленными координатами.
ab=1*-4+3*2=-4+6=2
Ответ: 2
11. На координатной плоскости изображены векторы `veca`и `vecb`. Найдите скалярное произведение `veca*vecb`.
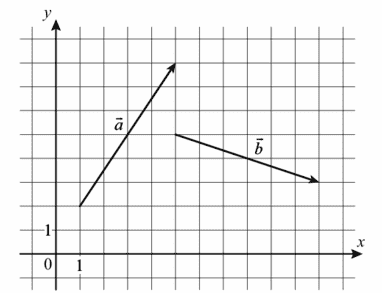
Ответ:
12
Найдём скалярное произведение по формуле:
a*b = x1*x2 + y1*y2
Однако прежде необходимо найти координаты векторов по целочисленным координатам.
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(5-1;8-2) а(4;6)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(11-5;3-5) b(6;-2)
ab=4*6+6*-2=24-12=12
Ответ: 12
12. Даны векторы `veca`(0;3), `vecb`(-2;4) и `vecc`(4;-1). Найдите длину вектора `veca`+ 2`vecb` + `vecc`.
Ответ:
10
Сложение векторов производим складывая соответствующие координаты между собой
a+2b+c(0+2*-2+4; 3+2*4-1)=a+2b+c(0;10)
Получается вектор идет по оси ординат и значит его длина равна значению по этой оси 10
Ответ: 10
13. Даны векторы `veca`(1;2), `vecb`(3;-6) и `vecc`(4;-3). Найдите значение выражения `(veca+vecb)*vecc`.
Ответ:
28
Сложение векторов производим складывая соответствующие координаты между собой
a+b=a+b(1+3; 2-6)=a+b(4;-4)
Умножение векторов производим по формуле: a*b = x1*x2 + y1*y2, где берем сумму произведений соответствующих координат
(a+b)*с=4*4+4*3=16+12=28
Ответ: 28
14. На координатной плоскости изображены векторы `veca`, `vecb` и `vecc`. Найдите значение выражения `(veca-vecb)*vecc`
Ответ:
18
Вычитание векторов производим вычитая соответствующие координаты между собой. Так как векторы имеют целочисленные координаты найдем их упрощенные координаты.
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(3-1;3-2) а(2;1)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(2-3;8-4) b(-1;4)
Находим координаты вектора c, из координат его конца, отнимаем координаты его начала, тогда
c(9-4;4-5) c(5;-1)
a-b =a-b(2+1;1-4)=a-b(3;-3)
Умножение векторов производим по формуле: a*b = x1*x2 + y1*y2, где берем сумму произведений соответствующих координат
(a-b)*с=(a-b)*с(3*5+3*1)=15+3=18
Ответ: 18
15. Даны векторы `veca`(0;3), `vecb`(-2;4) и `vecc`(4;-1). Найдите длину вектора `veca- 2vecb+vecc`.
Ответ:
10
Вычитание векторов производим вычитая соответствующие координаты между собой, а сложение складывая эти координаты
a-2b+c=a-2b+c(0-2*(-2)+4; 3-2*4+(-1))=c=a-2b+c(8; -6)
Теперь находим длину.
/a-2b+c/=`sqrt(8^2+-6^2)`=10
Ответ: 10
16. На координатной плоскости изображены векторы `veca`и `vecb`. Найдите длину вектора `2veca-vecb`.
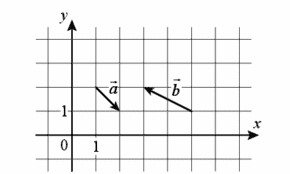
Ответ:
1
Вычитание векторов производим вычитая соответствующие координаты между собой
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(2-1;1-2) а(-1;1)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(3-5;2-1) b(-2;1)
Производим вычитание векторов
a-b=a-b(-1-(-2); 1-1)=a-b(1;0)
Теперь находим длину.
/a-b/=`sqrt(1^2+0^2)`=1
Ответ: 1
17. Длины векторов `veca`и `vecb` равны `2sqrt3` и 5, а угол между ними равен 150°. Найдите скалярное произведение `veca*vecb`.
Ответ:
-15
Скалярное произведение векторов аb равно произведению модулей векторов, умноженному на косинус угла между ними: аb = |а|*|b| * cos a
При этом cos 150 = -√3/2, можно посмотреть в табличных значениях, тогда
аb = 2√3* 5 * cos 150 = 2√3 * -√3/2 * 5 = -3*5=-15
Ответ: -15
18. Даны векторы `veca`(3;4) и`vecb`(-4;-3). Найдите косинус угла между ними.
Ответ:
-0.96
Формула вычисления угла между векторами
cosα = `(ab)/(|а|*|b|)`
Произведение векторов находим по формуле a*b = x1*x2 + y1*y2
ab = 3*-4+4*-3=-12-12=-24
Найдем модули векторов, то есть их длины:
Если построить вектор а на оси координат, то можно увидеть, что по оси x = 3, по y = 4 при этом длина вектора |a| = `sqrt(3^2+4^2)` = √25 = 5
Если построить вектор b на оси координат, то можно увидеть, что по оси x = -4, по y = -3 при этом длина вектора |b| = `sqrt(-4^2+(-3)^2)` = √25 = 5
cosα = `-24/(5*5) =-24/25`= -0.96
Ответ: -0,96
19. На координатной плоскости изображены векторы `veca`и `vecb`. Найдите косинус угла между ними.
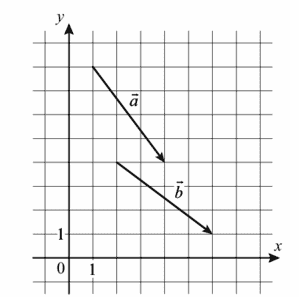
Ответ:
0.96
Формула вычисления угла между векторами
cosα = `(ab)/(|а|*|b|)`
Находим координаты вектора а, из координат его конца, отнимаем координаты его начала, тогда
а(4-1;4-8) а(3;-4)
Находим координаты вектора b, из координат его конца, отнимаем координаты его начала, тогда
b(6-2;1-4) b(4;-3)
Произведение векторов находим по формуле a*b = x1*x2 + y1*y2
ab = 3*4+(-4)*-3=12+12=24
Найдем модули векторов, то есть их длины:
Если построить вектор а на оси координат, то можно увидеть, что по оси x = 3, по y = -4 при этом длина вектора |a| = `sqrt(3^2+(-4)^2)` = √25 = 5
Если построить вектор b на оси координат, то можно увидеть, что по оси x = 4, по y = -3 при этом длина вектора |b| = `sqrt(4^2+(-3)^2)` = √25 = 5
cosα = `24/(5*5) =24/25`= 0.96
20. Длина вектора `veca` равна `2sqrt2`, угол между векторами `veca` и `vecb` равен 45°, а скалярное произведение `veca*vecb` равно 12. Найдите длину вектора `vecb`.
Ответ:
6
Формула вычисления угла между векторами
cosα = `(ab)/(|а|*|b|)` при этом известно, что ab = 12 и |а| = 2√2. Также смотрим табличное значение cos45º= √2/2
√2/2 = `12/(2sqrt2*|b|)` отсюда |b|
|b| = `(12*2)/(sqrt2*2sqrt2)` = 24/4 = 6
Ответ: 6
21. На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найдите скалярное произведение `vec(AB)*vec(AC)`.
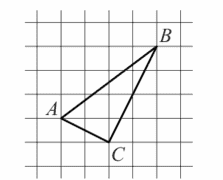
Ответ:
5
Условно примем за начало координат точку А, тогда можно будет уйти от целочисленных координат векторов и получаем значения
АВ(4;3)
АС(2;-1)
Умножение векторов производим по формуле: a*b = x1*x2 + y1*y2, где берем сумму произведений соответствующих координат
ab=4*2+3*(-1)=8-3=5
Ответ: 5
22. В прямоугольном треугольнике ABC катет AC равен `sqrt3`. Найдите скалярное произведение `vec(AB)*vec(AC)`.
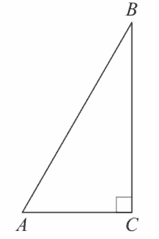
Ответ:
3
Так как треугольник прямоугольный, то проекция АВ на ось абсцисс является фактически катетом АС, то есть АС=AB*cosα,
cosα = AC/AB
Скалярное произведение векторов аb равно произведению модулей векторов, умноженному на косинус угла между ними:
AC*AB = |AC|*|AB| * cos a = |AC|*|AB|*`AC/AB`=|AC|2=√32=3
Ответ: 3
23. Даны векторы `vec a`(3;-2) и `vec b`(0;1). Найдите скалярное произведение `veca*vecb`.
Ответ:
-2
Умножение векторов производим по формуле: a*b = x1*x2 + y1*y2, где берем сумму произведений соответствующих координат
ab=a1*b1+a2*b2=3*0+(-2)*1=-2
Ответ: -2

