Тип структуры комплекта 300-e варианты. Позиции заданий 7. 100-e варианты 10. Снова геометрия, на этот раз все, что касается окружности, в том числе вписанной и описанной из открытого банка заданий ФИПИ
Все задания ФИПИ ГВЭ-9 по математике
Впишите правильный ответ.
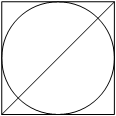
Радиус вписанной в квадрат окружности равен 18`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`18sqrt2^2+18sqrt2^2=x^2`
`x^2=324*2+324*2`
`x^2=1296`
`x=sqrt(1296)`
x=36
36*2=72
Ответ:72
Номер: 419544
Впишите правильный ответ.
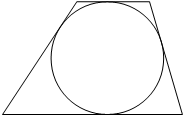
Радиус окружности, вписанной в трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
36*2=72
Ответ:72
Номер: 484E42
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Противоположные углы составляют 180 градусов.
180º-32º=148º
Ответ:148
Номер: 40134C
Впишите правильный ответ.

Сторона квадрата равна 22. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
22/2=11
Ответ:11
Номер: 4F584E
Впишите правильный ответ.
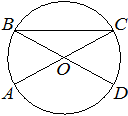
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 148°. Найдите угол ACB. Ответ дайте в градусах.
Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-148º)/2=16º
Ответ:16
Номер: 443C4E
Впишите правильный ответ.

Сторона равностороннего треугольника равна 16`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(16sqrt3sqrt3)/6=(16*3)/6=8`
Ответ:8
Номер: 05A445
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 68°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
Внутренние односторонние углы составляют 180 градусов.
180º-68º=112º
Ответ:112
Номер: 0A4143
Впишите правильный ответ.
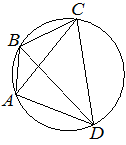
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132°, угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
∠CAD=∠CBD=80° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 132°
∠ABD = ∠ABC - ∠CBD = 132°-80°=52°
Ответ:52
Номер: 7C9148
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 2`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`2sqrt2^2+2sqrt2^2=x^2`
`x^2=4*2+4*2`
`x^2=16`
`x=sqrt(16)`
x=4
4*2=8
Ответ:8
Номер: B85F47
Впишите правильный ответ.
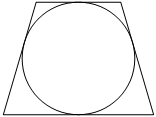
Радиус окружности, вписанной в равнобедренную трапецию, равен 44. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
44*2=88
Ответ:88
Номер: 13F94A
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 4`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу и высоту, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы найдем половину стороны квадрата.
`4sqrt2^2=x^2+x^2`
`2x^2=16*2`
`x^2=16`
`x=sqrt(16)`
x=4
4*2=8
Ответ:8
Номер: 261242
Впишите правильный ответ.

Сторона равностороннего треугольника равна 4`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(4sqrt3sqrt3)/6=(4*3)/6=2`
Ответ:2
Номер: 513E4F
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
18*2=36
Ответ:36
Номер: 509B4B
Впишите правильный ответ.

Сторона квадрата равна 4`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((4sqrt2)/2)^2+((4sqrt2)/2)^2=x^2`
`x^2=(2sqrt2)^2+(2sqrt2)^2`
`x^2=4*2+4*2`
`x^2=16`
`x=sqrt(16)`
x=4
Ответ:4
Номер: E0AB4F
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 62°. Найдите угол AOD. Ответ дайте в градусах.
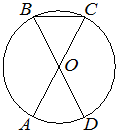
Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(62º*2)=56º
Ответ:56
Номер: ECD94D
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 8`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*8sqrt3)/(sqrt3)=24`
Ответ:24
Номер: 61E94B
Впишите правильный ответ.

Сторона квадрата равна 32`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((32sqrt2)/2)^2+((32sqrt2)/2)^2=x^2`
`x^2=(16sqrt2)^2+(16sqrt2)^2`
`x^2=256*2+256*2`
`x^2=1024`
`x=sqrt(1024)`
x=32
Ответ:32
Номер: 364542
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 19.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(19*2)^2=1444`
Ответ:1444
Номер: 35234E
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 69°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Противоположные углы составляют 180 градусов.
180º-69º=111º
Ответ:111
Номер: 3E3243
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 14.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(14*2)^2=784`
Ответ:784
Номер: 89B044
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 5`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*5sqrt3)/(sqrt3)=15`
Ответ:15
Номер: 80F241
Впишите правильный ответ.

Сторона равностороннего треугольника равна 10`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(10sqrt3sqrt3)/3=(10*3)/3=10`
Ответ:10
Номер: 88034D
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 17°. Ответ дайте в градусах.
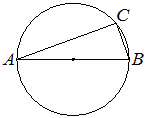
Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-17°=73°
Ответ:73
Номер: 4885F2
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 78°, угол CAD равен 40°. Найдите угол ABC. Ответ дайте в градусах.
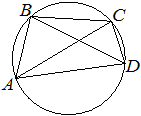
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=78°+40°=118°
Ответ:118
Номер: F2C3FD
Впишите правильный ответ.

Сторона квадрата равна 8`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((8sqrt2)/2)^2+((8sqrt2)/2)^2=x^2`
`x^2=(4sqrt2)^2+(4sqrt2)^2`
`x^2=16*2+16*2`
`x^2=64`
`x=sqrt(64)`
x=8
Ответ:8
Номер: 092DF0
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 36`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`36sqrt2^2=x^2+x^2`
`2x^2=1296*2`
`x^2=1296`
`x=sqrt(1296)`
x=36
36*2=72
Ответ:72
Номер: 06CAF0
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(78º*2)=24º
Ответ:24
Номер: 0DB9F3
Впишите правильный ответ.
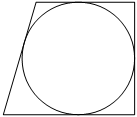
Радиус окружности, вписанной в прямоугольную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
32*2=64
Ответ:64
Номер: 04E4F8
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 16`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`16sqrt2^2=x^2+x^2`
`2x^2=256*2`
`x^2=256`
`x=sqrt(256)`
x=16
16*2=32
Ответ:32
Номер: B1B0F1
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 92°. Найдите угол ACB. Ответ дайте в градусах.
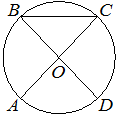
Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-92º)/2=44º
Ответ:44
Номер: B438FC
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
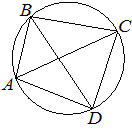
Решение:
∠CAD=∠CBD=60° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 92°
∠ABD = ∠ABC - ∠CBD = 92°-60°=32°
Ответ:32
Номер: 1400F1
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 33°. Ответ дайте в градусах.
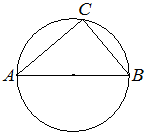
Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-33°=57°
Ответ:57
Номер: 1646F3
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 120°, угол CAD равен 74°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=74° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 120°
∠ABD = ∠ABC - ∠CBD = 120°-74°=46°
Ответ:46
Номер: 2BD0F1
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-9°=81°
Ответ:81
Номер: 208FF3
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 9`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*9*sqrt3)/(sqrt3)=54`
Ответ:54
Номер: D610F2
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
42*2=84
Ответ:84
Номер: 5FCEFB
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20,5. Найдите BC, если AC=9.
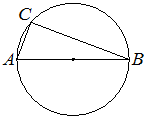
Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(20,5*2)2 = 92+ВС2
BC2=412 - 92
BC2=1600
`BC^2=1600`
`BC=sqrt(1600)`
BC=40
Ответ:40
Номер: C12AFF
Впишите правильный ответ.

Сторона квадрата равна 62. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
62/2=31
Ответ:31
Номер: CB73F0
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 59°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-59º=121º
Ответ:121
Номер: CB64F0
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 18.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(18*2)^2=1296`
Ответ:1296
Номер: E214F2
Впишите правильный ответ.
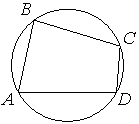
Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-82°=98°
Ответ:98
Номер: 0F3F05
Впишите правильный ответ.
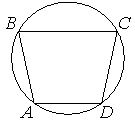
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 111°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Противоположные углы составляют 180 градусов.
180º-111º=69º
Ответ:69
Номер: 27810B
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.
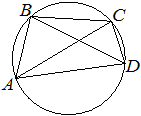
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=39°+55°=94°
Ответ:94
Номер: 2CBE0A
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 112°, угол CAD равен 70°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=70° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 112°
∠ABD = ∠ABC - ∠CBD = 112°-70°=42°
Ответ:42
Номер: 2A7A03
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 6`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*6sqrt3)/(sqrt3)=18`
Ответ:18
Номер: D28E09
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 38°, угол CAD равен 54°. Найдите угол ABC. Ответ дайте в градусах.
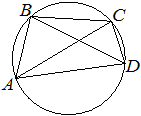
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=38°+54°=92°
Ответ:92
Номер: C62204
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-52º=128º
Ответ:128
Номер: 35FA03
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-50º)/2=65º
Ответ:65
Номер: 329E08
Впишите правильный ответ.

Сторона равностороннего треугольника равна 10`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(10sqrt3sqrt3)/6=(10*3)/6=5`
Ответ:5
Номер: 8B7C03
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 14. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
14*2=28
Ответ:28
Номер: FACD75
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 11`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*11sqrt3)/(sqrt3)=33`
Ответ:33
Номер: 1C4C75
Впишите правильный ответ.

Сторона квадрата равна 26. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
26/2=13
Ответ:13
Номер: 12787A
Впишите правильный ответ.

Сторона равностороннего треугольника равна 20`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(20sqrt3sqrt3)/3=(20*3)/3=20`
Ответ:20
Номер: 1D8D73
Впишите правильный ответ.

Сторона равностороннего треугольника равна 16`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(16sqrt3sqrt3)/3=(16*3)/3=16`
Ответ:16
Номер: 212079
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 3`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*3sqrt3)/(sqrt3)=9`
Ответ:9
Номер: 534C72
Впишите правильный ответ.
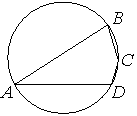
Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-37°=143°
Ответ:143
Номер: A57D71
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 38. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
38*2=76
Ответ:76
Номер: C19C7F
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
28*2=56
Ответ:56
Номер: 4849B0
Впишите правильный ответ.
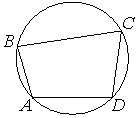
Угол A четырёхугольника ABCD, вписанного в окружность, равен 112°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-112°=68°
Ответ:68
Номер: 4B9BB6
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(25*2)2 = 482+ВС2
BC2=502 - 482
BC2=2500-2304
`BC^2=196`
`BC=sqrt(196)`
BC=14
Ответ:14
Номер: 0023B2
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
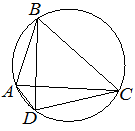
Решение:
∠CAD=∠CBD=49° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 70°
∠ABD = ∠ABC - ∠CBD = 70°-49°=21°
Ответ:21
Номер: 704CB0
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
30*2=60
Ответ:60
Номер: 7B9DB9
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 18`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`18sqrt2^2=x^2+x^2`
`2x^2=324*2`
`x^2=324`
`x=sqrt(324)`
x=18
18*2=36
Ответ:36
Номер: D32DBB
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 2`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*2*sqrt3)/(sqrt3)=12`
Ответ:12
Номер: 9C6CB9
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 6`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`6sqrt2^2+6sqrt2^2=x^2`
`x^2=36*2+36*2`
`x^2=144`
`x=sqrt(144)`
x=12
12*2=24
Ответ:24
Номер: 650DBC
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 76°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-76º=104º
Ответ:104
Номер: 6150BC
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(15*2)2 = 242+ВС2
BC2=302 - 242
`BC^2=324`
`BC=sqrt(324)`
BC=18
Ответ:18
Номер: 4F9111
Впишите правильный ответ.

Сторона равностороннего треугольника равна 12`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(12sqrt3sqrt3)/6=(12*3)/6=6`
Ответ:6
Номер: F3911C
Впишите правильный ответ.

Сторона равностороннего треугольника равна 20`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(20sqrt3sqrt3)/6=(20*3)/6=10`
Ответ:10
Номер: 016810
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 6`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*6*sqrt3)/(sqrt3)=36`
Ответ:36
Номер: B52D12
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 7`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*7sqrt3)/(sqrt3)=21`
Ответ:21
Номер: 1CF91F
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 7`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*7*sqrt3)/(sqrt3)=42`
Ответ:42
Номер: 272812
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 14`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`14sqrt2^2+14sqrt2^2=x^2`
`x^2=196*2+196*2`
`x^2=784`
`x=sqrt(784)`
x=28
28*2=56
Ответ:56
Номер: 2E1C19
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 54°, угол CAD равен 41°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=41° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 54°
∠ABD = ∠ABC - ∠CBD = 54°-41°=13°
Ответ:13
Номер: 2D4016
Впишите правильный ответ.

Сторона равностороннего треугольника равна 18`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(18sqrt3sqrt3)/3=(18*3)/3=18`
Ответ:18
Номер: AAAC1C
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 40.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(40*2)^2=6400`
Ответ:6400
Номер: C12B11
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 23°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(23º*2)=134º
Ответ:134
Номер: 9A9610
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 88°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-88º)/2=46º
Ответ:46
Номер: 9D1317
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
26*2=52
Ответ:52
Номер: 941C12
Впишите правильный ответ.

Сторона квадрата равна 34. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
34/2=17
Ответ:17
Номер: 9CE213
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
26*2=52
Ответ:52
Номер: 3D1114
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
12*2=24
Ответ:24
Номер: 380116
Впишите правильный ответ.

Сторона равностороннего треугольника равна 6`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(6sqrt3sqrt3)/3=(6*3)/3=6`
Ответ:6
Номер: 4AE124
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-114º)/2=33º
Ответ:33
Номер: 49D72A
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 56°, угол CAD равен 42°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=42° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 56°
∠ABD = ∠ABC - ∠CBD = 56°-42°=14°
Ответ:14
Номер: 081E2A
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
18*2=36
Ответ:36
Номер: 058C28
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 77°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Противоположные углы составляют 180 градусов.
180º-77º=103º
Ответ:103
Номер: 74502C
Впишите правильный ответ.

Сторона квадрата равна 18`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((18sqrt2)/2)^2+((18sqrt2)/2)^2=x^2`
`x^2=(9sqrt2)^2+(9sqrt2)^2`
`x^2=81*2+81*2`
`x^2=324`
`x=sqrt(324)`
x=18
Ответ:18
Номер: 77C42E
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
36*2=72
Ответ:72
Номер: 5DD722
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 77°, угол CAD равен 43°. Найдите угол ABC. Ответ дайте в градусах.
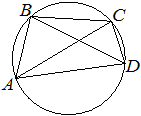
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=77°+43°=120°
Ответ:120
Номер: 93F924
Впишите правильный ответ.

Сторона квадрата равна 46. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
46/2=23
Ответ:23
Номер: 92532C
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 53°. Ответ дайте в градусах.
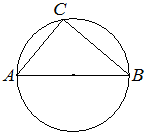
Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-53°=37°
Ответ:37
Номер: EAF121
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 78°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-78°=102°
Ответ:102
Номер: 8BDC29
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(59º*2)=62º
Ответ:62
Номер: 888126
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(74º*2)=32º
Ответ:32
Номер: 1B0CD1
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 10`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`10sqrt2^2+10sqrt2^2=x^2`
`x^2=100*2+100*2`
`x^2=400`
`x=sqrt(400)`
x=20
20*2=40
Ответ:40
Номер: 205DD2
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(54º*2)=72º
Ответ:72
Номер: D9A3DF
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 8,5. Найдите BC, если AC=8.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(8,5*2)2 = 82+ВС2
BC2=172 - 82
BC2=289-64
`BC^2=225`
`BC=sqrt(225)`
BC=15
Ответ:15
Номер: 5D76D9
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 4`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*4sqrt3)/(sqrt3)=12`
Ответ:12
Номер: 539DD6
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 54°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-54°=126°
Ответ:126
Номер: A3E6DA
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
30*2=60
Ответ:60
Номер: A9A0DE
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 28`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`28sqrt2^2=x^2+x^2`
`2x^2=784*2`
`x^2=784`
`x=sqrt(784)`
x=28
28*2=56
Ответ:56
Номер: 67BBDA
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-124º)/2=28º
Ответ:28
Номер: 3102D1
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 108°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-108º)/2=36º
Ответ:36
Номер: 35CADA
Впишите правильный ответ.

Сторона квадрата равна 14`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((14sqrt2)/2)^2+((14sqrt2)/2)^2=x^2`
`x^2=(7sqrt2)^2+(7sqrt2)^2`
`x^2=49*2+49*2`
`x^2=196`
`x=sqrt(196)`
x=14
Ответ:14
Номер: 38F1D3
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(10*2)2 = 162+ВС2
BC2=202 - 162
BC2=400-256
`BC^2=144`
`BC=sqrt(144)`
BC=12
Ответ:12
Номер: 8020DB
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 82°, угол CAD равен 28°. Найдите угол ABC. Ответ дайте в градусах.
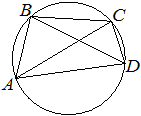
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=82°+28°=110°
Ответ:110
Номер: 439250
Впишите правильный ответ.

Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
6/2=3
Ответ:3
Номер: 03A95F
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 10`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*10sqrt3)/(sqrt3)=30`
Ответ:30
Номер: 05AB58
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах.
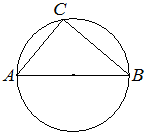
Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-48°=42°
Ответ:42
Номер: 768452
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
34*2=68
Ответ:68
Номер: 1B765F
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
48*2=96
Ответ:96
Номер: 17FD5D
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 14,5. Найдите AC, если BC=21.
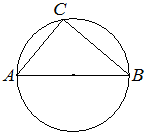
Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(14,5*2)2 = 212+ВС2
BC2=292 - 212
BC2=841-441
`BC^2=400`
`BC=sqrt(400)`
BC=20
Ответ:20
Номер: 28115B
Впишите правильный ответ.

Сторона равностороннего треугольника равна 14`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(14sqrt3sqrt3)/3=(14*3)/3=14`
Ответ:14
Номер: 513E55
Впишите правильный ответ.

Сторона равностороннего треугольника равна 8`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(8sqrt3sqrt3)/6=(8*3)/6=4`
Ответ:4
Номер: C87452
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 34`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`34sqrt2^2=x^2+x^2`
`2x^2=1156*2`
`x^2=1156`
`x=sqrt(1156)`
x=34
34*2=68
Ответ:68
Номер: 9E795E
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 16`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`16sqrt2^2+16sqrt2^2=x^2`
`x^2=256*2+256*2`
`x^2=1024`
`x=sqrt(1024)`
x=32
32*2=64
Ответ:64
Номер: E99E56
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 10. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
10*2=20
Ответ:20
Номер: 4800A2
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 24`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`24sqrt2^2+24sqrt2^2=x^2`
`x^2=576*2+576*2`
`x^2=2304`
`x=sqrt(2304)`
x=48
48*2=96
Ответ:96
Номер: 4756A8
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 25°, угол CAD равен 41°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=25°+41°=66°
Ответ:66
Номер: 0FD1A9
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 46°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-46º=134º
Ответ:134
Номер: 1780AD
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 61°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
Противоположные углы составляют 180 градусов.
180º-61º=119º
Ответ:119
Номер: 29C0A8
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 8`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*8*sqrt3)/(sqrt3)=48`
Ответ:48
Номер: D106A5
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 10`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*10*sqrt3)/(sqrt3)=60`
Ответ:60
Номер: DFCEAC
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 13. Найдите AC, если BC=24.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(13*2)2 = 242+ВС2
BC2=262 - 242
BC2=676-576
`BC^2=100`
`BC=sqrt(100)`
BC=10
Ответ:10
Номер: EC27A6
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(79º*2)=22º
Ответ:22
Номер: 8609AF
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол ABC. Ответ дайте в градусах.
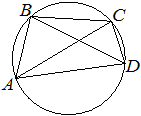
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=80°+34°=114°
Ответ:114
Номер: 8C11AB
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 71°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-71°=109°
Ответ:109
Номер: 863CA5
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 48°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-48°=132°
Ответ:132
Номер: 85C6AC
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 16°, угол CAD равен 32°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=16°+32°=48°
Ответ:48
Номер: 41A4C0
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
32*2=64
Ответ:64
Номер: 490EC2
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 62°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-62°=118°
Ответ:118
Номер: FF47CC
Впишите правильный ответ.
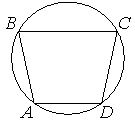
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-108º=72º
Ответ:72
Номер: FEB6CE
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=83° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 138°
∠ABD = ∠ABC - ∠CBD = 138°-83°=55°
Ответ:55
Номер: FAC7C3
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(20*2)2 = 322+ВС2
BC2=402 - 322
BC2=1600-1024
`BC^2=576`
`BC=sqrt(576)`
BC=24
Ответ:24
Номер: DB36C9
Впишите правильный ответ.
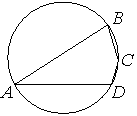
Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-33°=147°
Ответ:147
Номер: 561AC3
Впишите правильный ответ.

Сторона квадрата равна 24`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((24sqrt2)/2)^2+((24sqrt2)/2)^2=x^2`
`x^2=(12sqrt2)^2+(12sqrt2)^2`
`x^2=144*2+144*2`
`x^2=576`
`x=sqrt(576)`
x=24
Ответ:24
Номер: 5069C8
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 44°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-44º)/2=68º
Ответ:68
Номер: A732C7
Впишите правильный ответ.

Сторона квадрата равна 16`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((16sqrt2)/2)^2+((16sqrt2)/2)^2=x^2`
`x^2=(8sqrt2)^2+(8sqrt2)^2`
`x^2=64*2+64*2`
`x^2=256`
`x=sqrt(256)`
x=16
Ответ:16
Номер: A874CC
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 14`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`14sqrt2^2=x^2+x^2`
`2x^2=196*2`
`x^2=196`
`x=sqrt(196)`
x=14
14*2=28
Ответ:28
Номер: C7B4C4
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-24°=66°
Ответ:66
Номер: 99ECCD
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-30°=60°
Ответ:60
Номер: 9A9CCE
Впишите правильный ответ.

Сторона равностороннего треугольника равна 2`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(2sqrt3sqrt3)/3=(2*3)/3=2`
Ответ:2
Номер: E26CCD
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 36°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
180º-36º=144º
Ответ:144
Номер: EB67C6
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
24*2=48
Ответ:48
Номер: 64AFC2
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 86°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-86º)/2=47º
Ответ:47
Номер: 8A73C6
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
180º-81º=99º
Ответ:99
Номер: 45BC91
Впишите правильный ответ.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 74°. Найдите угол ACB. Ответ дайте в градусах.

Решение:
Угол ACB является углом у основания равнобедренного треугольника, где вершина угла равна углу AOD как накрест лежащему.
(180º-74º)/2=53º
Ответ:53
Номер: FC6A90
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 17. Найдите AC, если BC=30.
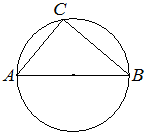
Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(17*2)2 = 302+ВС2
BC2=342 - 302
BC2=1156-900
`BC^2=256`
`BC=sqrt(256)`
BC=16
Ответ:16
Номер: FA289E
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 26`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`26sqrt2^2=x^2+x^2`
`2x^2=676*2`
`x^2=676`
`x=sqrt(676)`
x=26
26*2=52
Ответ:52
Номер: 0E2A96
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 79°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-79º=101º
Ответ:101
Номер: 19F992
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
16*2=32
Ответ:32
Номер: 267F92
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
20*2=40
Ответ:40
Номер: D5B794
Впишите правильный ответ.

Сторона квадрата равна 48. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
48/2=24
Ответ:24
Номер: DA219F
Впишите правильный ответ.

Сторона квадрата равна 38`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((38sqrt2)/2)^2+((38sqrt2)/2)^2=x^2`
`x^2=(19sqrt2)^2+(19sqrt2)^2`
`x^2=361*2+361*2`
`x^2=1444`
`x=sqrt(1444)`
x=38
Ответ:38
Номер: D0CF93
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 38°, угол CAD равен 33°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=33° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 38°
∠ABD = ∠ABC - ∠CBD = 38°-33°=5°
Ответ:5
Номер: A7A29B
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 4`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*4*sqrt3)/(sqrt3)=24`
Ответ:24
Номер: E8249B
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 25.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(25*2)^2=2500`
Ответ:2500
Номер: 4EEDE4
Впишите правильный ответ.

Сторона равностороннего треугольника равна 6`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(6sqrt3sqrt3)/6=(6*3)/6=3`
Ответ:3
Номер: 0856EE
Впишите правильный ответ.

Сторона равностороннего треугольника равна 4`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(4sqrt3sqrt3)/3=(4*3)/3=4`
Ответ:4
Номер: 0C86E3
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
32*2=64
Ответ:64
Номер: B1B4E7
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 4`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`4sqrt2^2+4sqrt2^2=x^2`
`x^2=16*2+16*2`
`x^2=64`
`x=sqrt(64)`
x=8
8*2=16
Ответ:16
Номер: 1D68E2
Впишите правильный ответ.

Сторона равностороннего треугольника равна 12`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(12sqrt3sqrt3)/3=(12*3)/3=12`
Ответ:12
Номер: 1040EE
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 44°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-44°=46°
Ответ:46
Номер: 27C1ED
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 32`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`32sqrt2^2=x^2+x^2`
`2x^2=1024*2`
`x^2=1024`
`x=sqrt(1024)`
x=32
32*2=64
Ответ:64
Номер: 242BE8
Впишите правильный ответ.

Сторона равностороннего треугольника равна 18`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(18sqrt3sqrt3)/6=(18*3)/6=9`
Ответ:9
Номер: CAD6E4
Впишите правильный ответ.

Сторона квадрата равна 40`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((40sqrt2)/2)^2+((40sqrt2)/2)^2=x^2`
`x^2=(20sqrt2)^2+(20sqrt2)^2`
`x^2=400*2+400*2`
`x^2=1600`
`x=sqrt(1600)`
x=40
Ответ:40
Номер: 985BE7
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 19°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(19º*2)=142º
Ответ:142
Номер: 99BAEC
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 3`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*3*sqrt3)/(sqrt3)=18`
Ответ:18
Номер: 99D2EE
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
42*2=84
Ответ:84
Номер: 6B27EC
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если BC=12.

Решение:
В нашем случае так как угол С опирается на радиус, то треугольник прямоугольный, значит используя теорему Пифагора:
(6,5*2)2 = 122+ВС2
BC2=132 - 122
BC2=169-144
`BC^2=25`
`BC=sqrt(25)`
BC=5
Ответ:5
Номер: 8445E4
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
12*2=24
Ответ:24
Номер: 406C61
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.

Решение:
∠CAD=∠CBD=81° как углы опирающиеся на одну секущую и вписанные в окружность.
Соответственно ∠ABD является частью угла ∠ABC = 134°
∠ABD = ∠ABC - ∠CBD = 134°-81°=53°
Ответ:53
Номер: 0B1561
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 47°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
180º-47º=133º
Ответ:133
Номер: 045E65
Впишите правильный ответ.

Сторона равностороннего треугольника равна 14`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(14sqrt3sqrt3)/6=(14*3)/6=7`
Ответ:7
Номер: BD6E6B
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 35°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-35º=145º
Ответ:145
Номер: 1C5067
Впишите правильный ответ.

Угол A четырёхугольника ABCD, вписанного в окружность, равен 56°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Решение:
Противоположные углы вместе образуют 180 (четырехугольник во вписанной окружности)
180°-56°=124°
Ответ:124
Номер: 2A6B6D
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 85°, угол CAD равен 19°. Найдите угол ABC. Ответ дайте в градусах.
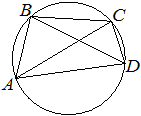
Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=85°+19°=104°
Ответ:104
Номер: D0DD6F
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 32.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(32*2)^2=4096`
Ответ:4096
Номер: A12165
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 9.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(9*2)^2=324`
Ответ:324
Номер: C43163
Впишите правильный ответ.

Сторона равностороннего треугольника равна 2`sqrt3`. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
Если достроить радиусы окружности идущие перпендикулярно к сторонам, то получим радиусы, между которыми 120 градусов, так как 360/3=120.
Далее строим основание треугольника с вершиной в центре окружности, с двумя равнобедренными сторонам в виде тех же радиусов построенных ранее и основанием - секущей, идущей от одного радиуса к другому. При этом также получаем еще один равносторонний треугольник, у которого стороны в два раза меньше реальных сторон нашего треугольника. Проводим высоту равнобедренном треугольнике и делаем заключение, что гипотенуза, которая является также радиусом относится к высоте как 1:2, так как высота лежит напротив угла в 30 градусов в прямоугольном треугольнике. В итоге получается, известный катет этого прямоугольного треугольника, равный 4 части от стороны и гипотенуза и катет с известной зависимость 1:2. Можно по теореме Пифагора посчитать радиус.
...или берем формулу из справочных материалов): `R =(asqrt3)/6` где а сторона треугольника.
`R =(2sqrt3sqrt3)/6=(2*3)/6=1`
Ответ:1
Номер: EEA961
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 53°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(53º*2)=74º
Ответ:74
Номер: EFE261
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
28*2=56
Ответ:56
Номер: 660864
Впишите правильный ответ.

Сторона квадрата равна 16. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
16/2=8
Ответ:8
Номер: 657D69
Впишите правильный ответ.

Сторона равностороннего треугольника равна 8`sqrt3`. Найдите радиус окружности, описанной около этого треугольника.
Решение:
...берем формулу из справочных материалов): `R =(asqrt3)/3` где а сторона треугольника.
`R =(8sqrt3sqrt3)/3=(8*3)/3=8`
Ответ:8
Номер: 3E0467
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 54°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-54º=126º
Ответ:126
Номер: 3F6663
Впишите правильный ответ.

Радиус окружности, вписанной в равнобедренную трапецию, равен 22. Найдите высоту этой трапеции.
Решение:
Высота трапеции равна диаметру окружности:
22*2=44
Ответ:44
Номер: 805A65
Впишите правильный ответ.

Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
56/2=28
Ответ:28
Номер: 4AA037
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 2`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*2sqrt3)/(sqrt3)=6`
Ответ:6
Номер: 4D3B32
Впишите правильный ответ.

Радиус окружности, вписанной в прямоугольную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Два радиуса равны высоте трапеции.
20*2=40
Ответ:40
Номер: 4D2039
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 55°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
180º-55º=125º
Ответ:125
Номер: B3D034
Впишите правильный ответ.
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 16°. Найдите угол AOD. Ответ дайте в градусах.

Решение:
Если провести прямую AD, то получим два равных равнобедренных треугольника, так как у них стороны равны, являются радиусами, и углы у вершин также равны, как накрест лежащие. Зная угол у основания, можно найти угол у вершины.
180º-(16º*2)=148º
Ответ:148
Номер: BC183C
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 11`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*11*sqrt3)/(sqrt3)=66`
Ответ:66
Номер: 18EB3F
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 8`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`8sqrt2^2+8sqrt2^2=x^2`
`x^2=64*2+64*2`
`x^2=256`
`x=sqrt(256)`
x=16
16*2=32
Ответ:32
Номер: 1C933B
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 51°, угол CAD равен 42°. Найдите угол ABC. Ответ дайте в градусах.

Решение:
∠ABD =∠AСD=78°
∠CAD =∠DBC=40°
так как эти углы опираются на одну секущую и вписаны в окружность по одну ее сторону.
∠ABС = ∠ABD + ∠DBC=51°+42°=93°
Ответ:93
Номер: D34E3F
Впишите правильный ответ.

Сторона квадрата равна 12`sqrt2`. Найдите радиус окружности, описанной около этого квадрата.
Решение:
По теореме Пифагора:
`((12sqrt2)/2)^2+((12sqrt2)/2)^2=x^2`
`x^2=(6sqrt2)^2+(6sqrt2)^2`
`x^2=36*2+36*2`
`x^2=144`
`x=sqrt(144)`
x=12
Ответ:12
Номер: A31132
Впишите правильный ответ.

Сторона квадрата равна 24. Найдите радиус окружности, вписанной в этот квадрат.
Решение:
Сторона квадрата равна диаметру, а радиусу равна половина стороны.
24/2=12
Ответ:12
Номер: 687E3E
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 7.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(7*2)^2=196`
Ответ:196
Номер: 6EDC36
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 53°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Решение:
180º-53º=127º
Ответ:127
Номер: 39B031
Впишите правильный ответ.

Радиус вписанной в квадрат окружности равен 22`sqrt2`. Найдите диагональ этого квадрата.
Решение:
Если провести радиус окружности перпендикулярно стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна половине диагонали квадрата.
`18sqrt2^2+18sqrt2^2=x^2`
`x^2=484*2+484*2`
`x^2=1936`
`x=sqrt(1936)`
x=44
44*2=88
Ответ:88
Номер: 37B433
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 75°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-75°=15°
Ответ:15
Номер: 82113B
Впишите правильный ответ.

Радиус окружности, описанной около квадрата, равен 22`sqrt2`. Найдите длину стороны этого квадрата.
Решение:
Если провести радиус окружности к углу квадрата и высоту к его стороне, то получим равнобедренный прямоугольный треугольник. Его гипотенуза будет равна радиусу, а мы сможем найти половину стороны квадрата.
`22sqrt2^2=x^2+x^2`
`2x^2=484*2`
`x^2=484`
`x=sqrt(484)`
x=22
22*2=44
Ответ:44
Номер: 8F8331
Впишите правильный ответ.

Радиус окружности, описанной около равностороннего треугольника, равен 9`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Из справочных материалов `R=(asqrt3)/3`, тогда a:
`a=(3R)/(sqrt3)=(3*9sqrt3)/(sqrt3)=27`
Ответ:27
Номер: 4F8F8A
Впишите правильный ответ.

Радиус окружности, вписанной в равносторонний треугольник, равен 5`sqrt3`. Найдите длину стороны этого треугольника.
Решение:
Берем формулу из справочных материалов: `R =(asqrt3)/6` где а сторона треугольника.
`a =(6R)/(sqrt3) =(6*5*sqrt3)/(sqrt3)=30`
Ответ:30
Номер: 46578E
Впишите правильный ответ.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 74°. Ответ дайте в градусах.

Решение:
Вписанный угол в окружность и опирающийся на секущую диаметра является прямым, то есть у нас прямоугольный треугольник. Тогда:
180°-90°-74°=16°
Ответ:16
Номер: 166A8C
Впишите правильный ответ.

Радиус окружности, вписанной в трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Диаметр вписанной в трапецию окружности равен ее высоте, тогда:
34*2=68
Ответ:68
Номер: 5EA080
Впишите правильный ответ.
Найдите площадь квадрата, описанного около окружности радиуса 4.

Решение:
Площадь квадрата будет равна произведению его диаметров.
`(4*2)^2=64`
Ответ:64
Номер: 56AD8B
Впишите правильный ответ.

Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Решение:
180º-31º=149º
Ответ:149
Номер: 391A8C

