Задания первой линейки ЕГЭ по физике, согласно спецификации, охватывают КЭС 1.1.5 Равномерное прямолинейное движение. 1.1.6 Равноускоренное прямолинейное движение. Других КЭС по этой линейке в спецификации нет, но задания из них в №1 есть, то есть на практике в первом номере встречаются и другие разделы кинематики 1.1. Обычно дан график, по нему нужно дать ответ в виде числа, но бывает и просто задача.
С 2024 года из линейки 1 убрали относительность движения и движение по окружности. Свободного падения и баллистики в этой линейке тоже нет.
Путь S - это расстояние, пройденное телом вдоль траектории движения. S=vt - путь при равномерном прямол. движении - площадь фигуры внутри графика.
Проекция перемещения (не путать с путем) - это расстояние от начала до конца пути. Может совпадать с путем, если движение в одном направлении, может нет - при движении туда/сюда.
`S = v_0*t + (at^2)/2`- путь при равноускоренном прямол. движении.
Ускорение a=Δv/Δt
Скорость v=ΔS/Δt или v=Δx/Δt
В задании может потребоваться найти как саму величину (знак имеет значение), так и ее модуль (всегда положительна).
Тут ФИПИ - весь банк + прототипы Демидовой без повторов, в общем, всё, что может попасться на реальном ЕГЭ по физике в линейке 1. На ЕГЭ будут другие числа, алгоритмы решения останутся те же.
Все задания линейки №1 ЕГЭ по физике
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости υx от времени t для тела, движущегося прямолинейно вдоль оси Ox. Определите проекцию ax ускорения тела.
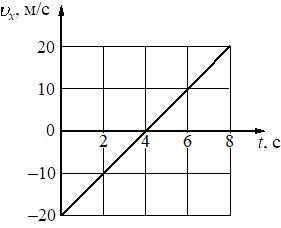
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_2 – v_0)/(t_2-t_0) = (0 + 20)/(4-0) = 20/4 = 5`
Номер: E01406
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
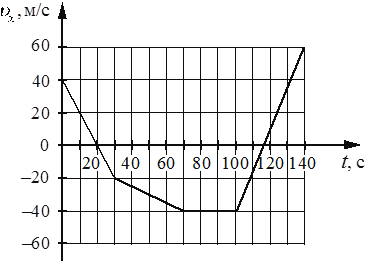
Определите проекцию ax ускорения этого тела в интервале времени от 40 до 60 с. Ответ запишите с учётом знака проекции.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
-0,5
Так как ускорение было линейное на интервале от 30 до 70 секунды, то можно взять для вычислений этот интервал, как наиболее удобный для расчетов. Величина ускорения равна:
`a_x = (v_(70)-v_(30))/(t_(70)-t_(30)) = (-40-(-20))/(70-30)=-20/40=-0.5`
Номер: 7FDF75
Впишите правильный ответ.
На рисунке приведён график зависимости проекции ux скорости тела от времени t.
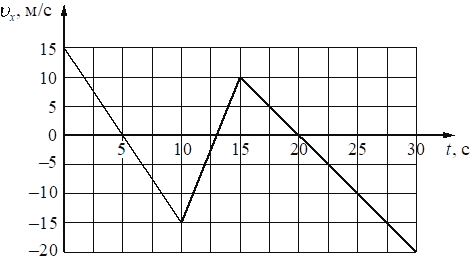
Определите проекцию ax ускорения этого тела в интервале времени от 20 до 30 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-2
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(30)-v_(15))/(t_(30)-t_(15)) = (-20-10)/(30-15)=-30/15=-2`
Номер: 371718
Впишите правильный ответ.
Тело движется по прямой, параллельной оси Ox. На графике представлена зависимость проекции υx его скорости от времени t.
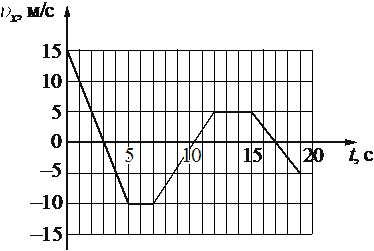
Определите проекцию ax ускорения тела в интервале времени от 0 до 5 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(5)-v_(0))/(t_(5)-t_(0)) = (-10-15)/(5-0)=-25/5=-5`
Номер: EA992E
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
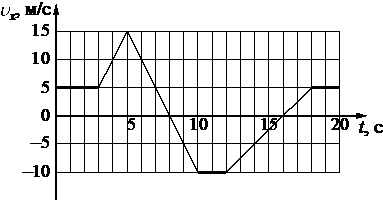
Определите проекцию ax ускорения этого тела в интервале времени от 8 до 10 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(10)-v_(8))/(t_(10)-t_(8)) = (-10-0)/(10-8)=-10/2=-5`
Номер: 4DDEDB
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
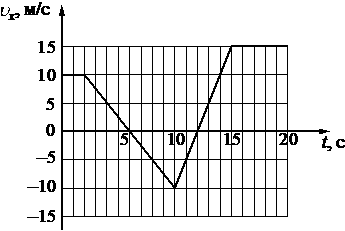
Определите проекцию ax ускорения этого тела в интервале времени от 10 до 15 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(15)-v_(10))/(t_(15)-t_(10)) = (15-(-10))/(15-10)=25/5=5`
Номер: AA3BD8
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
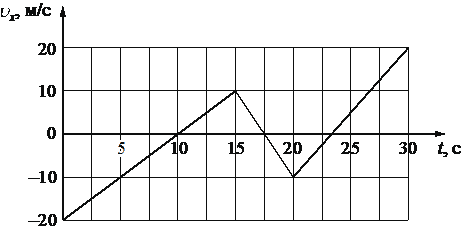
Определите проекцию ax ускорения этого тела в интервале времени от 20 до 30 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
3
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(30)-v_(20))/(t_(30)-t_(20)) = (20-(-10))/(30-20)=30/10=3`
Номер: 788CAE
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости υx от времени t для тела, движущегося прямолинейно вдоль оси Оx. Определите проекцию ax ускорения тела.
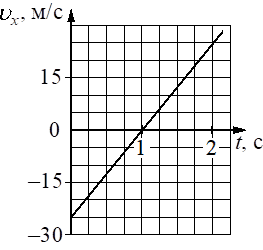
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
25
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки (скажем 0 и 2 секунды) на прямой следующим образом:
`a_x = (v_2 – v_0)/(t_2-t_0) = (25 - (-25))/(2-0) = 50/2 = 25`
Номер: 0E7CCE
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
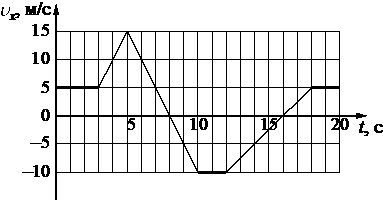
Определите проекцию ax ускорения этого тела в интервале времени от 5 до 8 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(8)-v_(5))/(t_(8)-t_(5)) = (0-15))/(8-5)=-15/3=-5`
Номер: F9D994
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
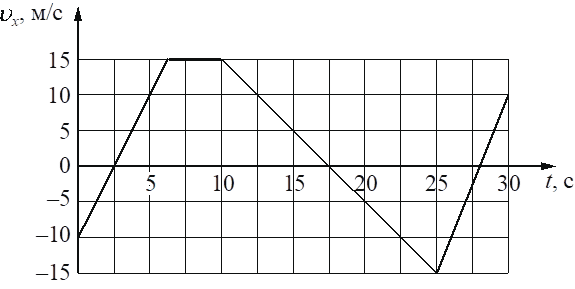
Определите проекцию ax ускорения этого тела в интервале времени от 0 до 5 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
4
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(5)-v_(0))/(t_(5)-t_(0)) = (10-(-10)))/(5-0)=20/5=4`
Номер: 535663
Впишите правильный ответ.
На рисунке показан график зависимости от времени для проекции υx скорости тела. Какова проекция ax ускорения этого тела в интервале времени от 4 до 8 c?
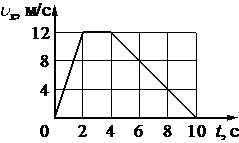
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-2
Ускорение тела равно: `a_x=(∆v_x)/t`
Где `∆v_x = 4-12= -8` м/с – изменение скорости
Тогда
`a_x = -8/4 = -2` м/с²
Номер: 259807
Впишите правильный ответ.
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 3 до 4 c?
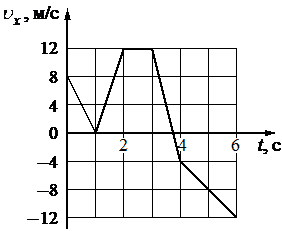
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-16
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_4 – v_3)/(t_4-t_3) = (-4 -12)/(4-3) = -16/1 = -16`
Номер: C013BD
Впишите правильный ответ.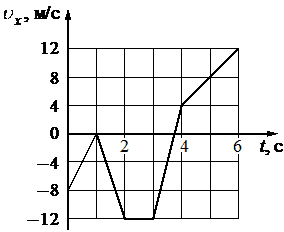
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 4 до 6 c?
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
4
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_6 – v_4)/(t_6-t_4) = (12 - 4)/(6-4) = 8/2 = 4`
Номер: C5B0B3
Впишите правильный ответ.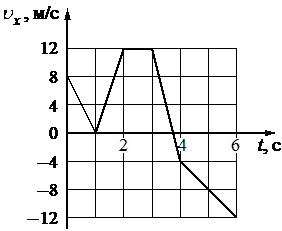
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 1 до 2 c?
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
12
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_2 – v_1)/(t_2-t_1) = (12 - 0)/(2-1) = 12/1 = 12`
Номер: DA7AD2
Впишите правильный ответ.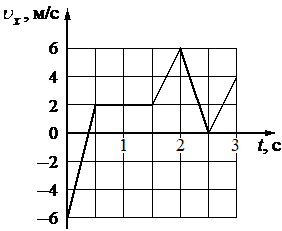
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 1,5 до 2 c?
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
8
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки (скажем на 0 и 2 секунде) на прямой следующим образом:
`a_x = (v_2 – v_(1.5))/(t_2-t_(1.5)) = (6 - 2)/(2-1.5) = 4/(0.5) = 8`
Номер: 09B5CD
Впишите правильный ответ.
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 1 до 1,5 c?
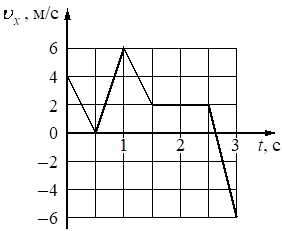
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-8
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(1.5) – v_1)/(t_(1.5)-t_1) = (2 - 6)/(1.5-1) = -4/(0.5) = -8`
Номер: 87FF90
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости тела υx от времени t.
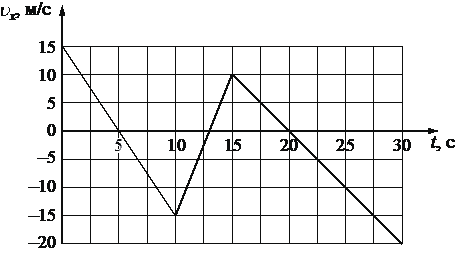
Определите проекцию ускорения этого тела ax в интервале времени от 10 до 15 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки (скажем на 0 и 2 секунде) на прямой следующим образом:
`a_x = (v_(15) – v_(10))/(t_(15)-t_(10)) = (10 - (-15))/(15-10) = 25/5 = 5`
Номер: FCB3C2
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости тела υx от времени.
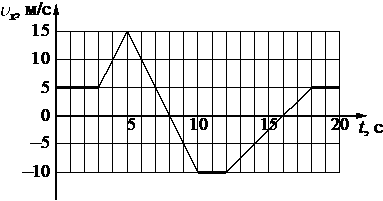
Определите проекцию ускорения этого тела ax в интервале времени от 3 до 5 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки (скажем на 0 и 2 секунде) на прямой следующим образом:
`a_x = (v_5 – v_3)/(t_5-t_3) = (15 - 5)/(5-3) = 10/2 = 5`
Номер: D5639B
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости υx от времени t для тела, движущегося прямолинейно по оси x. Определите проекцию ускорения тела ax.
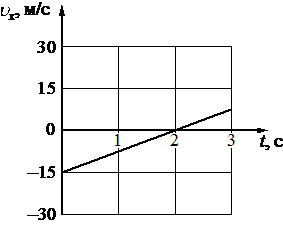
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
7,5
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки (скажем на 0 и 2 секунде) на прямой следующим образом:
`a_x = (v_2 – v_0)/(t_2-t_0) = (0 - (-15))/(2-0) = 15/2 = 7,5`
Номер: C85E34
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости тела υx от времени.
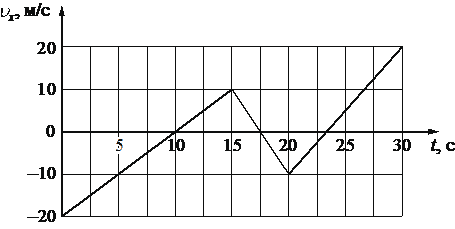
Определите проекцию ускорения этого тела ax в интервале времени от 15 до 20 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-4
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(20) – v_(15))/(t_(20)-t_(15)) = (-10 - 10))/(20-15) = -20/5 = -4`
Номер: 873033
Впишите правильный ответ.
Автомобиль движется по прямой улице, параллельной оси Ox. На графике представлена зависимость проекции его скорости υx от времени t.
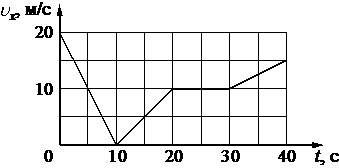
Определите проекцию ускорения автомобиля ax в интервале времени от 0 до 10 с.
м/с2
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
-2
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_10 – v_0)/(t_10-t_0) = (0 - 20)/(10-0) = -20/10 = -2`
Номер: E0C5B4
Автомобиль движется по прямой улице. На графике представлена зависимость его скорости от времени.

Определите проекцию ускорения автомобиля ax в интервале времени от 20 до 30 с.
Ответ:
0
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_10 – v_0)/(t_10-t_0)`
Демидова
На рисунке приведён график зависимости проекции vx скорости тела от времени t.
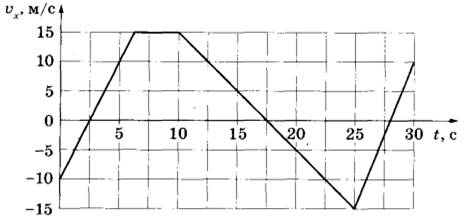
Определите проекцию аx ускорения этого тела в момент времени 15 секунд.
Ответ:
-2
При t = 15 сек скорость линейно уменьшается, значит, тело движется с постоянным отрицательным ускорением. Величину этого ускорения можно найти по формуле:
`a_x = (Δv)/(Δt)=(5-15)/(15-10)--10/5=-2` м/с2
Демидова
Впишите правильный ответ. 2024
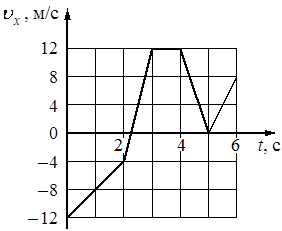
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 0 до 2 c? Ответ запишите с учётом знака проекции.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Тип ответа: Краткий ответ
Ответ:
4
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_2 – v_1)/(t_2-t_1) = (- 4 - (- 12))/(2-0) = 8/2 = 4`м/с2
Номер: 2A0F1F
Впишите правильный ответ. 2024
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
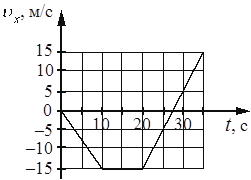
Определите проекцию ax ускорения этого тела в интервале времени от 20 до 25 с. Ответ запишите с учётом знака проекции.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Тип ответа: Краткий ответ
Ответ:
2
График скорости имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_x = (v_(25)-v_(20))/(t_(25)-t_(20)) = (-5-(-15))/(25-20)=10/5=2`
Номер: B9A0DF
Впишите правильный ответ. 2024
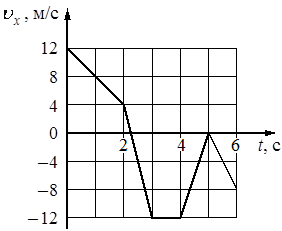
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в интервале времени от 4 до 5 c? Ответ запишите с учётом знака проекции.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Тип ответа: Краткий ответ
Ответ:
12
Применим формулу, для того чтобы узнать ускорение:
`a = (v-v_0)/(t_0-t)`
Возьмем 4 и 5 секунду и видим:
`a = (v - v_0)/(t_0-t) = (0-(-12))/(5-4) = 12/1 = 12` м/с2
Номер: 58C03A
Впишите правильный ответ. 2024
На рисунке показан график зависимости проекции υx скорости тела от времени t. Какова проекция ax ускорения этого тела в момент времени 2 c?
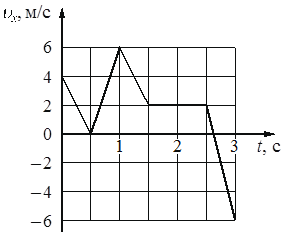
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Тип ответа: Краткий ответ
Ответ:
0
Применим формулу, для того чтобы узнать ускорение:
`v_x = v_0x+a_xt`
Возьмем 2 и 3 секунду и видим, что `v_x = v_0x`, то есть `a_xt = 0`, значит ускорение равно 0, так как время не равно 0.
Номер: 277542
На рисунке показан график зависимости проекции vx скорости тела от времени t. Какова проекция ax ускорения этого тела в момент времени 2 с?
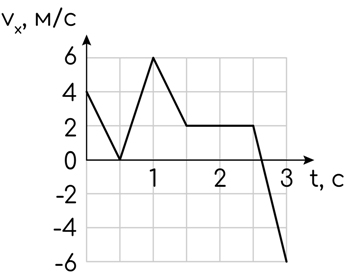
Ответ:
0
Участок горизонтален ⇒ движение равномерное ⇒ ускорение равно 0
Демидова
Впишите правильный ответ.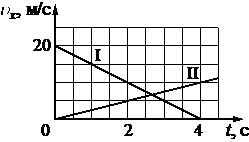
На рисунке приведены графики зависимости проекции скорости от времени для легкового автомобиля (I) и микроавтобуса (II), движущихся по прямой дороге, вдоль которой и направлена ось Ох. Определите отношение модулей ускорений aI/aII.
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
2
График скоростей имеет линейную зависимость от времени. Это означает, что скорость менялась с постоянным ускорением. Для вычисления ускорения достаточно взять две точки на прямой следующим образом:
`a_I = (v_2 – v_0)/(t_2-t_0) = (0-20)/(4-0) = -20/4 = -5`
`a_(II) = (v_2 – v_0)/(t_2-t_0) = (10-0)/(4-0) = 10/4 = 2,5`
5/2,5=2
Номер: 081272 ЕГЭ 2024
Впишите правильный ответ.
На рисунке представлен график зависимости модуля скорости u прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.
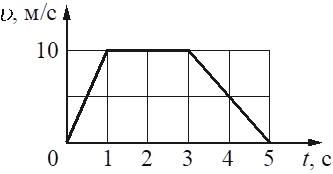
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
30
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 1 до 5 секунды, площадь представляется треугольником и прямоугольником над осью абсцисс: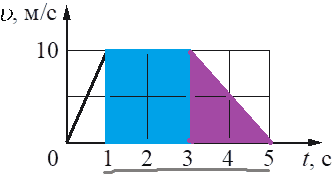
Следовательно, путь: S = 1/2 * 2 * 10 + 2 * 10 = 20+10=30 метров
Номер: BD0C23
Впишите правильный ответ.
На рисунке представлен график зависимости скорости υ прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 0 до 3 с после начала движения.
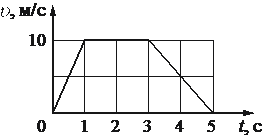
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
25
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 0 до 3 секунды, площадь представляется прямоугольным треугольником и прямоугольником над осью абсцисс:
Следовательно, путь равен: S = 1/2 * 1 * 10 + 2 * 10= 5+20=25 метров
Номер: CC405D
Впишите правильный ответ.
На рисунке представлен график зависимости скорости υ тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 0 до 1 с после начала движения.
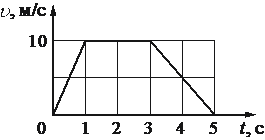
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
5
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 0 до 1 секунды, площадь представляется прямоугольным треугольником над осью абсцисс:
Следовательно, путь равен: S = 1/2 * 1 * 10 = 5 метров
Номер: 06B062
Впишите правильный ответ. 2024
На рисунке представлен график зависимости модуля скорости υ тела от времени t. Найдите путь, пройденный телом за время от 0 до 12 с.
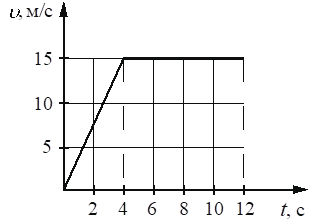
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Тип ответа: Краткий ответ
Ответ:
150
До 4 с движение было равноускоренное, причем ускорение составило за 15 м/с2 за 4 с, а дальше равномерное, без ускорения.
До 4 с:
`S = v_0*t + (at^2)/2`
`S = (15/4*16)/2 = 30` м
С 4 с:
S= V*t =15 * 8 = 120
Складываем 120+30 = 150 метров
Номер: 6EC247
Впишите правильный ответ.
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50с.
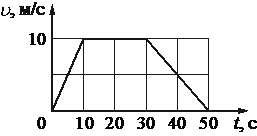
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
200
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 20 до 50 секунды, площадь представляется прямоугольным треугольникам и прямоугольником над осью абсцисс:
Следовательно, путь равен: S = 1/2 * 20 * 10 + 10 * 10 = 200 метров
Номер: D109D1
Впишите правильный ответ.
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 40 с после начала движения.
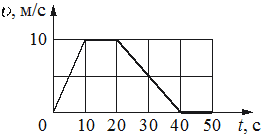
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
250
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 0 до 40 секунды, площадь представляется двумя прямоугольными треугольниками и прямоугольником над осью абсцисс:
Следовательно, путь равен: S = 1/2 * 10 * 10 + 10 * 10 + 1/2 * 10 * 20= 50+100+100=250 метров
Номер: 6ADAD4
Впишите правильный ответ.
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=10 с до t2=50 от начала движения.
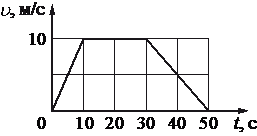
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
300
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 10 до 50 секунды, площадь представляется прямоугольным треугольником и прямоугольником над осью абсцисс:
Следовательно, путь равен: S = 20 * 10 + 1/2 * 10 * 20= 200+100=300 метров
Номер: A24553
Впишите правильный ответ.
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем за время от 30 до 50 с.
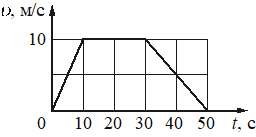
м
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
100
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 30 до 50 секунды, площадь представляется прямоугольным треугольником над осью абсцисс:
Следовательно, путь равен: S = 1/2 * 20 * 10 =100 метров
Номер: D359AA
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
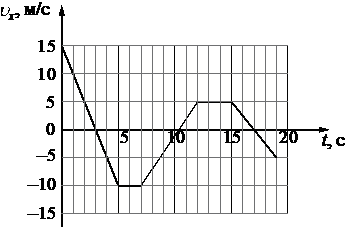
Определите путь, пройденный телом в интервале времени от 15 до 19 с.
м
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
10
Путь, пройденный телом, можно вычислить как площадь под графиком зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 15 до 19 секунд, площадь представляется двумя прямоугольными треугольниками над и под осью абсцисс:
Следовательно, путь равен: S = 1/2 * 2 * 5 + 1/2 * 2 * 5 = 10 метров
Номер: D5307D
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
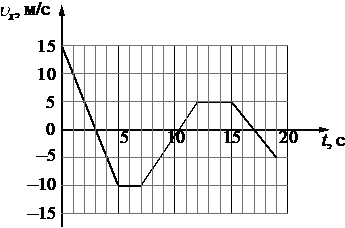
Определите путь, пройденный телом в интервале времени от 0 до 5 с.
м
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
32,5
Путь, пройденный телом, можно вычислить как площадь под графиком зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 0 до 5 секунд, площадь представляется двумя прямоугольными треугольниками: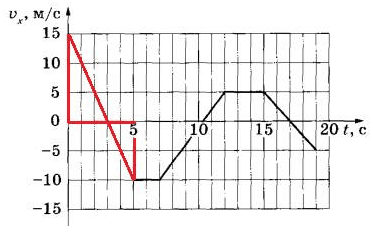
Следовательно, путь равен: S = 1/2 * 15 * 3 + 1/2 * 2 * 10 = 32,5 метров
Номер: 41FCF3
Впишите правильный ответ.
На рисунке приведён график зависимости проекции υx скорости тела от времени t.
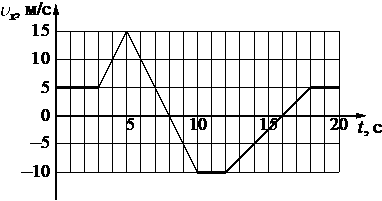
Определите путь, пройденный телом в интервале времени от 5 до 10 с.
м
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
32,5
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 5 до 10 секунды, площадь представляется двумя прямоугольными треугольниками над и под осью абсцисс:
Следовательно, путь равен: S = 1/2 * 2 * 10 + 1/2 * 3 * 15 = 10+22,5=32,5 метров
Номер: DAA0DF
Впишите правильный ответ.
Тело движется вдоль оси Ox. На рисунке приведён график зависимости проекции ux скорости тела от времени t.
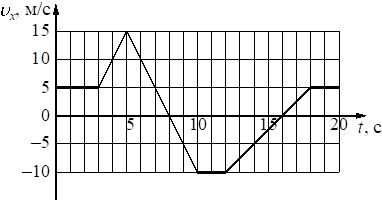
Определите путь, пройденный телом в интервале времени от 12 до 18 с.
м
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
25
Путь, пройденный телом, можно вычислить как площадь внутри графика зависимости скорости от времени, так как S = vt. Из рисунка видно, что на интервале от 12 до 18 секунды, площадь представляется двумя прямоугольным треугольником над и под осью абсцисс:
Следовательно, путь равен: S = 1/2 * 4 * 10 + 1/2 * 5 * 2 = 20 + 5 = 25 метров
Номер: 3F1CCC
Впишите правильный ответ.
На рисунке приведён график зависимости проекции скорости тела υx от времени t.
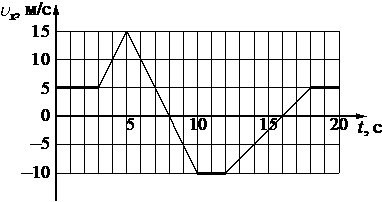
Определите путь тела за первые 5 секунд движения.
м
КЭС: 1.1.4 Ускорение материальной точки
Ответ:
35
первые 3 сек - 15 м, в последние 2 сек скорость увеличивалась равномерно, за 2 с пройдено 10 м
15 + 10 = 35
Номер: 008243
Впишите правильный ответ.
Тело движется вдоль оси Оx. По графику зависимости проекции скорости тела υx от времени t установите модуль перемещения тела за время от t1 = 6 c до t2 = 10 c.
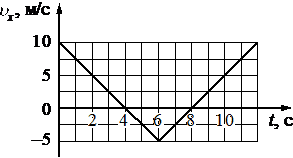
м
КЭС: 1.1.3 Скорость материальной точки
Ответ:
0
Скорость меняется с отрицательной на положительную, то есть имеем два участка с перемещением в разных направлениях. Путь равен площади от графика до оси абсцисс, так как S=vt. В итоге модуль перемещения будет равен разности площадей.
Находим S
S = 1/2*2*5-1/2*2*5=0 м
Номер: 715DD2
Впишите правильный ответ.
Тело движется вдоль оси Оx. По графику зависимости проекции скорости тела υx от времени t установите модуль перемещения тела за время от t1 = 2 c до t2 = 6 c.
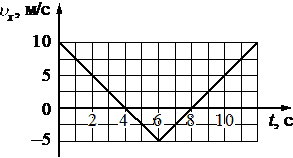
м
КЭС: 1.1.3 Скорость материальной точки
Ответ:
0
Скорость меняется с положительной на отрицательную, то есть имеем два участка с перемещением в разных направлениях. Путь равен площади от графика до оси абсцисс, так как S=vt. В итоге модуль перемещения будет равен разности площадей.
Находим S
S = 1/2*2*5-1/2*2*5=0 м
Номер: C297D4
На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику проекцию перемещения тела в интервале времени от 0 до 5 с. Ответ выразите в м.
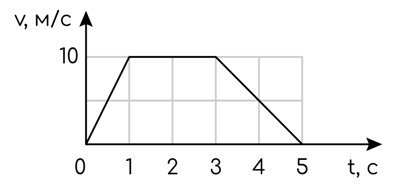
Ответ:
35
Когда дана зависимость скорости от времени, перемещение можно найти как площадь фигуры под графиком (ВАЖНО учитывать проекции, движения в обратном направлении тут нет, значит проекция = путь).
Фигура представляет из себя трапецию с основаниями 2 и 5, высотой равной 10. Площадь находим по формуле площади трапеции (полусумма оснований * на высоту)
`S=(5+2)/2*10=35` м
Демидова
Тело движется вдоль оси Ох. На рисунке приведен график зависимости проекции vx скорости тела от времени t.
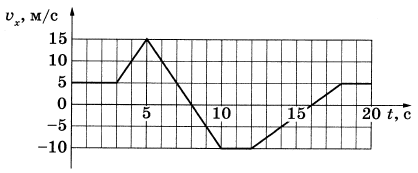
Определите проекцию перемещения тела Sx в интервале времени от 5 до 10 с.
Ответ:
12,5
Перемещение - расстояние от начальной до конечной точки. Раз скорость переходит в отрицательную, то тело движется туда и обратно. Путь можно вычислить как площадь внутри графика. В одном направлении - прямоугольный треугольник над осью t, в другом - под осью. Чтобы узнать перемещение, вычтем из первого второе.
`(15*3)/2-(10*2)/2=45/2-20/2=25/2=12,5` м
Демидова 2024
По графику зависимости модуля скорости тела от времени (см. рисунок) определите ускорение прямолинейно движущегося тела в момент времени 2 с.
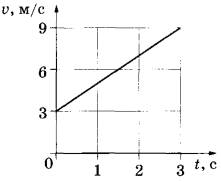
м/с2
Ответ:
2
В промежутке времени от 0 до 3 секунд тело линейно набирает скорость, то есть движется равноускоренно ⇒ ускорение одинаково хоть в 2 с, хоть в 3. Удобнее по графику взять 3 с. Ускорение на этом промежутке времени можно найти как
`a=(Δv)/(Δt)=(9-3)/3=6/3=2`м/с2
Демидова
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите ускорение тела.
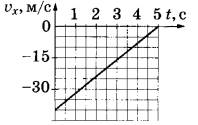
м/с2
Ответ:
8
Так как скорость линейно возрастает со временем, то ускорение можно вычислить как a=Δv/Δt.
Из рисунка видно, что при Δt=5 с изменение скорости равно 0-(-40) м/с и ускорение равно 40/5=8 м/с2
Демидова
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
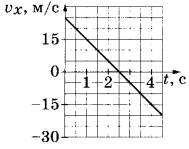
м/с2
Ответ:
10
На графике показано линейное изменение скорости от времени, то есть тело движется равнозамедленно (скорость постепенно уменьшается, ускорение не изменяется). В этом случае ускорение тела можно найти как a=Δv/Δt.
Из графика видно, что при Δt=1 с, изменение скорости Δv составляет 25-15=10 м/с. Следовательно, ускорение тела a равно 10/1=10 м/с2
Модуль равен 10
Демидова
Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени.
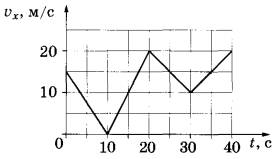
Определите модуль минимального ускорения автомобиля за время наблюдения.
м/с2
Ответ:
1
При минимальном ускорении изменение скорости автомобиля также будет наименьшим. Другими словами нужно выбрать участок прямой с наименьшим наклоном к оси времени. Этому соответствует участок времени от 20 до 30 секунд, на котором ускорение равно
a=Δv/Δt=(10-20)/(30-20)=-1 м/с2
|a|=1 м/с2
или участок от 30 до 40 с тем же модулем ускорения.
Вопрос может звучать как определите модуль максимального ускорения автомобиля за время наблюдения. При максимальном ускорении скорость автомобиля меняется на большую величину за единицу времени. Следовательно, на графике нужно выбрать линию с наибольшим наклоном к оси времени. Этому соответствует участок при t=10-20 секунд. Ускорение на нем равно 2 м/с2.
Демидова
На рисунке представлен график зависимости скорости v тела от времени t. Определите среднюю скорость тела в интервале времени от 1 до 5 с после начала движения.
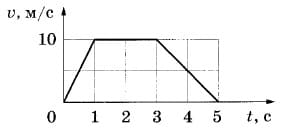
Ответ:
7,5
Среднюю скорость можно найти по формуле v=S/t, где S - путь, пройденный телом за время t = 5 c.
Путь S можно найти как площадь под графиком скорости (площадь прямоугольной трапеции с основаниями a=2, b=4 и высотой h=10), имеем:
`S=(2+4)/2*10=30` м
Средняя скорость `v=30/(5-1)=30/4=7,5` м/с
Демидова
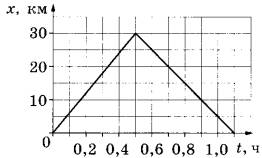
На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х = 0, а пункт Б — в точке х = 30 км. Чему равна скорость автобуса на пути из Б в А?
км/ч
Ответ:
50
Так как точка Б соответствует x=30 км, а точка А x=0 км, то путь, пройденный из Б в А, это второй линейный сегмент на графике, начиная с t=0,5 ч и заканчивая t=1,1 ч.
Так как координата x меняется линейно со времен, то скорость автобуса на данном участке была постоянной, следовательно, ее можно найти по формуле
v=Δx/Δt=(30-0)/(1,1-0,5)=30/0,6=50 км/ч
Вопрос может звучать как Чему равна скорость автобуса на пути из А в Б? Тогда ответ 60 км/ч.
Демидова
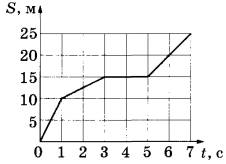
На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите максимальную скорость точки за время наблюдения.
м/с
Ответ:
10
Чем больше скорость, тем быстрее меняется путь S со временем, то есть для определения максимальной скорости нужно выбрать быстровозрастающий линейный сегмент. Из рисунка видно, что это первый линейный сегмент, на котором скорость была равна
v=ΔS/t=10/1=10 м/с
В задании может требоваться найти скорость точки на любом участке или найти минимальную скорость точки за время наблюдения. Минимальная скорость - прямой горизонтальный участок (путь не меняется со временем, то есть тело покоится, скорость = 0)
Демидова
На рисунке приведён график зависимости координаты тела х от времени t при прямолинейном движении тела вдоль оси Ох. Определите проекцию перемещения этого тела на ось Ох в промежутке времени от 0 до 14 с.
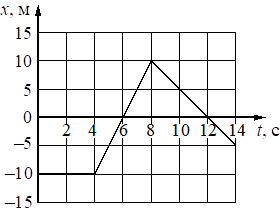
Ответ:
5
Проекция перемещения (не путать с путем) - это вектор от начала до конца пути.
Исходная точка х=-10, конечная -5, передвинулись на 5 в положительном направлении, ответ 5
Демидова
На рисунке приведён график зависимости координаты тела х от времени t при его прямолинейном движении вдоль оси Ох. Определите проекцию перемещения этого тела на ось Ох в промежутке времени от 8 до 14 с.
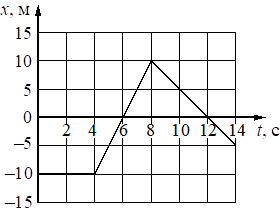
Ответ:
-15
В интервале времени от 8 до 14 с тело линейно меняет свое положение от 10 м до -5 м, то есть, начальная х=10, конечная -5, тело передвинулось на -15
ЕГЭ 2022
Впишите правильный ответ.
На рисунке приведён график зависимости координаты тела x от времени t при прямолинейном движении тела вдоль оси Ox. Определите проекцию скорости этого тела на ось Ox в промежутке времени от 8 до 12 с.
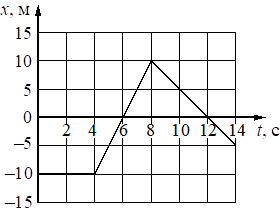
м/с
КЭС: 1.1.3 Скорость материальной точки
Ответ:
-2,5
За 2 секунды тело проходило 5 метров. В итоге за 4 секунды 10, тогда 10/4=2,5 м/с.
Но так как график идет на снижение, то скорость берем со знаком -
ИЛИ
`v=ΔS/Δt=-10/(12-8)=-10/4=-2,5`
Номер: 89DC6C
Впишите правильный ответ.
На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении вдоль оси Ox. Определите проекцию скорости этого тела на ось Ox в промежутке времени от 4 до 6 с.
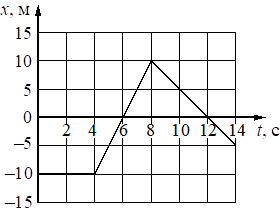
м/с
КЭС: 1.1.3 Скорость материальной точки
Ответ:
5
v=ΔS/Δt
За 2 с тело прошло 10 м, значит за одну 10:2= 5 м ⇒ скорость 5 м/с
В задании может потребоваться узнать модуль скорости.
Номер: B51AF2
Впишите правильный ответ.
На рисунке представлен график зависимости координаты x велосипедиста от времени t. Определите модуль скорости велосипедиста в промежутке времени от 0 до 10 с.
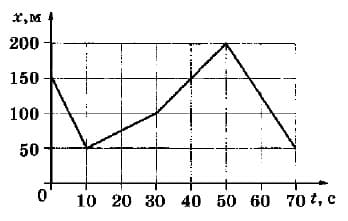
м/с
Ответ:
10
v=Δх/Δt=(50-150)/(10-0)=-100/10=-10, модуль равен 10
Ответ: 10
Демидова
Впишите правильный ответ.
Координата x тела меняется с течением времени t согласно закону x=23+5t−2t2 , где все величины выражены в СИ. Определите проекцию аx ускорения этого тела.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
-4
Ускорение – это вторая производная от координаты x(t). Вычислим вторую производную от x(t), получим:
v=x'= 5 - 4t
a=x'= - 4
Ответ: - 4
Еще способ:
Запишем закон изменения координаты тела x:
`x(t)=x_0+v_0*t+(at^2)/2`
Соотнося эту формулу с выражением x=23+5t−2t2 , видно, что ускорение тела a=-4
, так как `(at^2)/2=−2t^2=-(4t^2)/2`.
Номер: 3CF615
Координата тела меняется с течением времени согласно закону x = 4 - 2t, где все величины выражены в СИ. Определите проекцию скорости vx этого тела.
Ответ:
-2
Скорость тела – это производная пути по времени, то есть `v_x=x_t^'=-2` м/с
Таким образом, проекция скорости будет представлять собой прямую линию параллельную оси t на уровне -2 по оси vx.
Демидова
Впишите правильный ответ.
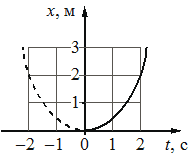
Материальная точка движется прямолинейно с постоянным ускорением вдоль оси Ох. График зависимости её координаты от времени x=x(t) изображён на рисунке. Определите проекцию ах ускорения этого тела.
м/с2
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
1
За первую секунду было пройдено 0,5 метра, за вторую 1,5 метра.
`a_x =x_0+v_0 * t + (a_x*t^2)/2 `
где x0 – начальная координата (в данном случае равна 0), v0 – начальная скорость (тоже равна 0, так как тангенс угла наклона равен 90∘ в точке (0,0)). Возьмем точку (2,2) для определения ускорения
`a_x = (2x)/(t^2)` = 2⋅2/4 = 1 м/с2
Номер: 7CFB3E
Впишите правильный ответ.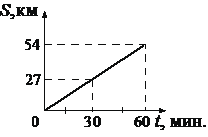
Из населённого пункта одновременно в одном направлении выезжают грузовой автомобиль и бульдозер и движутся по дороге с постоянными скоростями. На графике показана зависимость расстояния между грузовиком и бульдозером от времени. Скорость грузовика равна 25 м/с, а скорость бульдозера меньше. С какой скоростью движется бульдозер?
м/с
КЭС: 1.1.5 Равномерное прямолинейное движение
Ответ:
10
Пусть x м/с – скорость бульдозера, тогда они отдаляются со скоростью 25 - x м/с. Из графика видно, удаление за час составило S=54 км = 54000 м за t=60 минут = 3600 секунд, то есть,
`25 - x = S/t`
`x = 25 - S/t `
`x = 25 – 54000/3600 = 25-15=10` м/с
Номер: 424A13
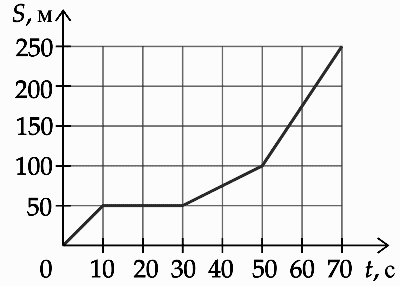
На рисунке представлен график зависимости пути S велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 50 до 70 с. Ответ дайте в м/с.
Ответ:
7,5
При равномерном движении путь определяется по формуле: S=vt, где v - скорость, t - время.
Значит, графиком равномерного движения будет прямая, что подходит под наш случай. При этом путь равен:
S = 250-100=150 м
Движение равномерное, скорость вычисляется по формуле:
v=S/t=150/20=7,5 м/с
Ответ: 7,5 м/с
Демо 2017
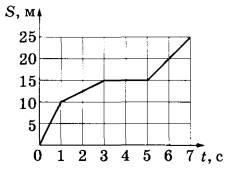
На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите скорость тела в интервале времени от 1 до 3 с.
Ответ:
2,5
При равномерном движении путь определяется по формуле: S=vt, где v - скорость, t - время.
Значит, графиком равномерного движения будет прямая, что подходит под наш случай.
При этом скорость равна:
`v=S/t=(15-10)/2=5/2=2,5` м/с
Демидова
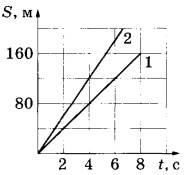
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела v2 больше скорости первого тела v1.
Ответ:
1,5
На графике представлены линейные зависимости пути S от времени t, следовательно, тела двигались с постоянной скоростью. Скорость тел можно найти по формуле v=ΔS/Δt.
Для первого тела примем Δt=8 с, которому соответствует ΔS=160 м, и скорость равна 160/8=20 м/с.
Для второго тела выберем Δt=4 с, которому соответствует ΔS=120 м, и скорость 120/4=30 м/с.
Получаем отношение v2/v1=30/20=1,5 ,то есть скорость второго тела в 1,5 раза больше скорости первого тела.
Демидова
Впишите правильный ответ.
Расстояние между пунктами А и В равно 30 км. Из пункта А в направлении пункта В выезжает мотоциклист со скоростью 50 км/ч. Одновременно из пункта В в том же направлении, что и мотоциклист, выезжает трактор со скоростью 20 км/ч. На каком расстоянии от пункта А мотоциклист догонит трактор?
км
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
50
Между А и В - 30 км.
мотоциклист - 50 км/ч
трактор - 20 км/ч
50+20=70 км/ч скорость сближения.
x - время через которое автомобиль догонит трактор.
Составляем уравнение:
20x + 30 = 50x
30=30x
x = 1
То есть через час транспортные средства сравняются, тогда 50*1=50 км, такое расстояние проедет автомобиль.
Номер: 5E532C
Впишите правильный ответ.
Начальная скорость движения тела равна 5 м/с. Сколько потребуется времени, чтобы увеличить его скорость в 3 раза при равноускоренном движении по прямой в одном направлении на пути в 20 м?
с
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
2
То есть на расстоянии 20 м от первоначального, скорость тела должна быть равна 15 м/с
То есть нам за 20 метров надо изменить скорость на 10 м/с
Запишем формулу при равноускоренном движении:
`S = (v^2 - v_0^2)/(2a)`
При этом у нас `v = 3v_0`;
`a = (v^2 - v_0^2)/(2S) = (9v_0^2 - v_0^2)/(2S)=(8v_0^2)/(2S)=(4v_0^2)/S=(4*5*5)/20=5` м/с
Находим время
`t = (v - (v_0))/a = (15 - 5)/5 = 2` cекунды
Номер: B5F7C7
Впишите правильный ответ.
Какой путь пройдет тело за 2 с, двигаясь по прямой в одном направлении, если его скорость за это время уменьшается в 3 раза? Модуль ускорения тела равен 5 м/с2.
м
КЭС: 1.1.6 Равноускоренное прямолинейное движение
Ответ:
20
При этом у нас `v = v_0/3`;
`a = 5 = (v - v_0)/t = (v_0/3 - v_0)/t = (v_0 - 3v_0)/(3t) = -(2v_0)/(3t)` м/с
Поскольку скорость тела уменьшается, значит проекция ускорения на ось, направленную вдоль начальной скорости, отрицательна
`v_0= -(3at)/2 = (3*5*2)/2 = 15` м/c
Находим путь.
`S = v_0*t + (at^2)/2 = 15*2-(5*2^2)/2 = 20` метров
Номер: A32BC5
Движение двух велосипедистов задано уравнениями x1 = 3t (м) и x2 =12−t (м). Велосипедисты двигаются вдоль одной прямой. Найдите координату x места встречи велосипедистов. (Ответ дайте в метрах)
Ответ:
9
Велосипедисты встретятся, если совпадут их координаты, отсюда:
x1 = x2
Подставим уравнения:
3t= 12 − t
4t= 12
Отсюда время, в которое встретятся велосипедисты:
t= 3 c
Найдем координату x места встречи велосипедистов, для этого подставим время t в оба уравнения:
x1 = 3⋅3 = 9 м
x2 = 12−3 = 9 м
Графический способ:
Изобразим движение велосипедистов на графике: 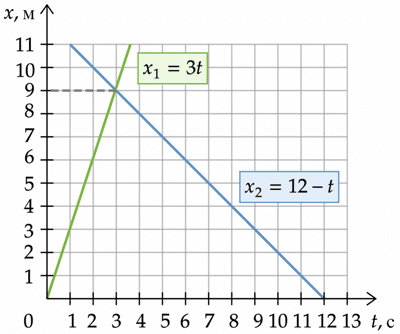
Найдем пересечение графиков и опустим перпендикуляр к оси Oy.
Ответ: 9 м
Демо 2017
Устаревшие задания ФИПИ из линейки 1
По идее, их в ЕГЭ теперь быть не должно, но мало ли... В Демидовой 2024 года издания они есть.
Впишите правильный ответ.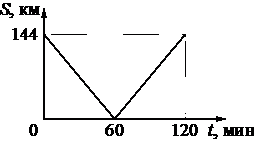
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля 15 м/с. С какой скоростью движется второй автомобиль?
м/с
КЭС: 1.1.1 Механическое движение. Относительность механического движения. Система отсчёта
Ответ:
25
Пусть x м/с – скорость второго автомобиля, тогда они сближаются со скоростью x+15 м/с. Из графика видно, что они оба прошли S=144 км = 144000 м за t=60 минут = 3600 секунд, то есть,
`х + 15 = S/t`
`х = S/t – 15 = 144000/3600 – 15 = 25` м/с
Номер: 61A437 Демидова 2024
Впишите правильный ответ.
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. С какой скоростью едет по дороге второй автомобиль, если скорость первого автомобиля равна 15 м/с?
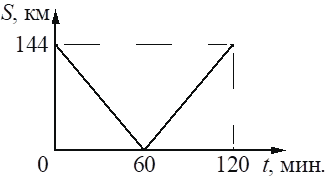
м/с
КЭС: 1.1.3 Скорость материальной точки
Ответ:
25
Пусть x м/с – скорость второго автомобиля, тогда они сближаются со скоростью x+15 м/с. Из графика видно, что они оба прошли S=144 км = 144000 м за t=60 минут = 3600 секунд, то есть,
`х + 15 = S/t`
`х = S/t – 15 = 144000/3600 – 15 = 25` м/с
Номер: 38F045
Впишите правильный ответ.
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Какова скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
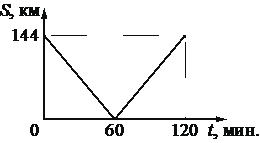
м/с
КЭС: 1.1.3 Скорость материальной точки
Ответ:
40
Из графика видно, что они оба прошли S=144 км = 144000 м за t=60 минут = 3600 секунд, то есть,
`V = S/t = 144000/3600 = 40` м/с скорость сближения.
Номер: 65EA74
Впишите правильный ответ.
Материальная точка равномерно движется по окружности радиусом 2 м с центростремительным ускорением, равным 2 м/с2. Определите скорость точки.
м/с
КЭС: 1.1.8 Движение материальной точки по окружности
Ответ:
2
Дано: R = 2 м; aц = 2 м/с2
Найти: v - ?
Решение:
`v = sqrt(a_цR)`
`v = sqrt(2*2) = 2` м/с
Номер: 8A3445
Впишите правильный ответ.
Материальная точка равномерно движется по окружности радиусом R со скоростью v. Во сколько раз нужно увеличить скорость её движения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
в___раз(а)
КЭС: 1.1.8 Движение материальной точки по окружности
Ответ:
2
Дано: R; v; R2 = 4R; а1 = а2
Найти: v2/v - ?
Решение:
`a_1 = v^2/R` (1)
`a_2 = v_2^2/R_2` (2)
`a_1 = a_2` (3)
Подставим (1) и (2) в (3):
`v^2/R = v_2^2/R_2` (4)
`v^2/R = v_2^2/(4R)` (5)
`v_2 = sqrt((4Rv^2)/R) = 2v` (6)
Номер: 913207
Впишите правильный ответ.
Шарик движется по окружности радиусом R с угловой скоростью ω. Во сколько раз уменьшится центростремительное ускорение шарика, если радиус окружности увеличить в 2 раза, а угловую скорость уменьшить в 2 раза?
в___(раз)а
КЭС: 1.1.8 Движение материальной точки по окружности
Ответ:
2
`a_n=ω^2∗R`
R увеличить в 2 раза - ускорение увеличится в 2 раза
ω уменьшить в 2 раза - ускорение уменьшится в 4 раза, так как ω в квадрате
Если увеличить в 2 раза, а затем уменьшить в 4 раза, то итого уменьшится в 2 раза
Номер: B5CFF9
Мяч брошен вертикально вверх с начальной скоростью 20 м/с. Чему равно перемещение мяча за 3 с, считая от момента броска? Сопротивлением воздуха пренебречь. Ответ выразите в м.
Ответ:
15
Ответ: 15 м
Демо 2016
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 36 раз меньше, чем для второй. Каково отношение R1/R2 радиусов орбит первой и второй планет?
Ответ:
6
Демидова
Две планеты обращаются по круговым орбитам вокруг звезды. Масса первой планеты в 4 раза меньше массы второй, а отношение R1/R2 радиусов орбит первой и второй планет равно 2,5. Каково отношение сил притяжения первой и второй планет к звезде F1/F2?
Ответ:
0,04
Демидова
К пружине школьного динамометра подвесили груз массой 0,1 кг. Пружина при этом упруго удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза уменьшится вдвое?
Ответ:
1,25
Демидова
Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н? см
Ответ:
16
Демидова
Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,8 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них m/2, а расстояние между их центрами 2r?
Ответ:
0,05
Демидова
Расстояние от искусственного спутника до поверхности Земли равно радиусу Земли. Во сколько раз уменьшится сила притяжения спутника к Земле, если расстояние от него до поверхности Земли станет равным трём радиусам Земли?
Ответ:
4
Демидова
В инерциальной системе отсчёта сила 50 Н сообщает телу массой 5 кг некоторое ускорение. Какая сила сообщает такое же ускорение телу массой 3 кг?
Ответ:
30
Демидова
Материальная точка движется по окружности радиусом R с постоянной по модулю скоростью v. Во сколько раз уменьшится центростремительное ускорение точки, если скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить??
Ответ:
8
Демидова
Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2 . Чему равна скорость автомобиля?
Ответ:
10
`a_w=v^2/R`
Демидова
Материальная точка движется по окружности радиусом R с частотой обращения v. Во сколько раз нужно уменьшить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
Ответ:
2
Демидова 2024

