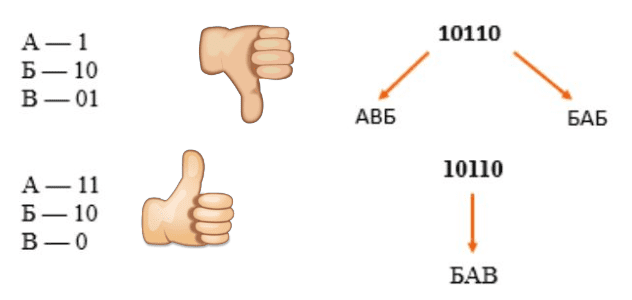
Ручное решение
Условие Фано:
«Никакое кодовое слово не может быть началом другого кодового слова» Условие Фано позволяет декодировать сообщение единственным образом.
Алгоритм построения дерева по кодовым словам
В любом прототипе задания №4 построение бинарного дерева - это наш первый шаг.
- Количество уровней дерева = длина максимального кодового слова (последовательности цифр). Нарисовать линии.
- Корень дерева — над 1 уровнем.
- Нарисовать ветки 0 и 1 для свободной вершины.
- Если последовательность 0 и 1 от корня в ветке составляет существующее кодовое слово, то ветка обрезается крестиком.
- Повторить шаги 3–4 до тех пор, пока не будут отмечены все существующие кодовые слова.
Прототипы с ЕГЭ
Задача №1 Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Например, пара кодовых слов 11 и 111 не выполняют условие Фано, потому что 111 является началом 11. А вот 100 и 110 уже выполняют условие Фано.
Мы знаем кодовые слова некоторых букв:
Л - 00
М - 01
Н - 11
П - ?
Р - ?
Отмечаем известные кодовые слова, которые кодируют буквы Л,М,Н. Где буквы уже есть, там следующим этажом бинарное поставить нельзя, так как не будет выполняться условие Фано. На 10 буквы нет, это может быть началом другого слова. Но саму десятку брать нельзя, потому что нам надо закодировать 2 буквы (если ее займем, то вторую невозможно будет закодировать).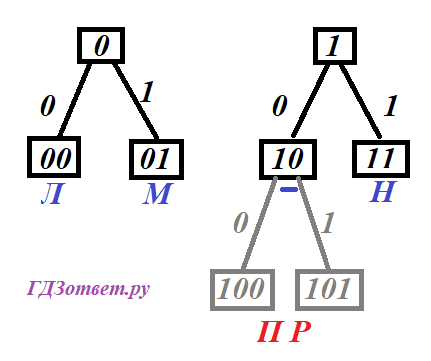
Нам нужно найти коды еще для двух букв. Мы видим, что таких кода два - это 100 и 101. В таком случае по условию нам нужно выбрать код с наименьшим числовым значением.
100 = 410, 101 = 510.
На бинарном дереве все наглядно, чем левее число на этаже, тем меньше его числовое значение. Если уровни разные, меньшее короче (выше).
Ответ: 100
Задача №2 Для кодирования растрового рисунка, напечатанного с использованием шести красок, применили неравномерный двоичный код. Для кодирования цветов используются кодовые слова. Белый — 0, Зелёный — 11111, Фиолетовый — 11110, Красный — 1110, Чёрный — 10. Укажите кратчайшее кодовое слово для кодирования синего цвета, при котором код допускает однозначное декодирование.
Решение:
Рисуем бинарное дерево, у существующих ветвей пишем цвет. 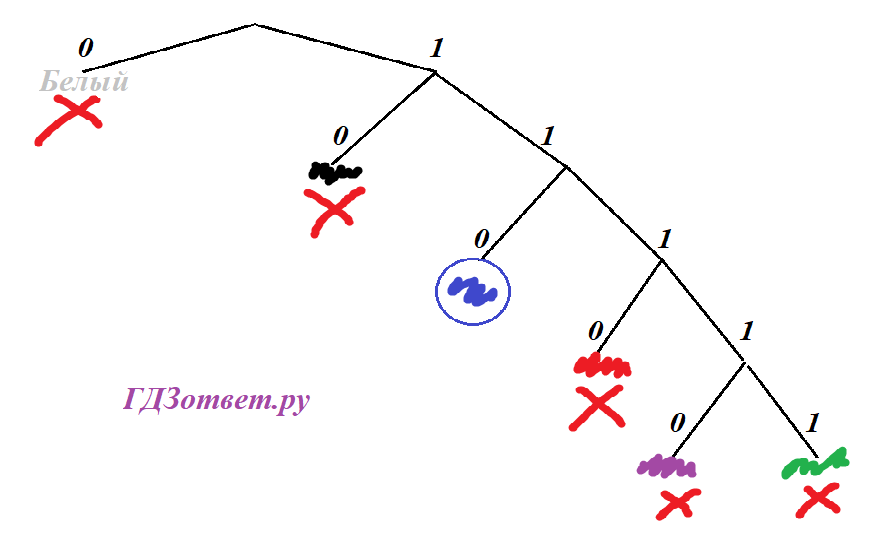
Свободна только ветка 110, там и будет синий.
Ответ: 110
Задача №3 По каналу связи передаются сообщения, содержащие только десять букв: А, Б, В, Г, Д, Е, И, К, Л, М. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово | Буква | Кодовое слово | |
| А | 00 | Е | 011 | |
| Б | 111 | И | 1011 | |
| В | 010 | К | 1000 | |
| Г | 1100 | Л | ||
| Д | 1010 | М | 1001 |
Укажите кратчайшее кодовое слово для буквы Л. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание: условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Рисуем бинарное дерево в 4 уровня, подписываем буквы, ищем свободную ветку.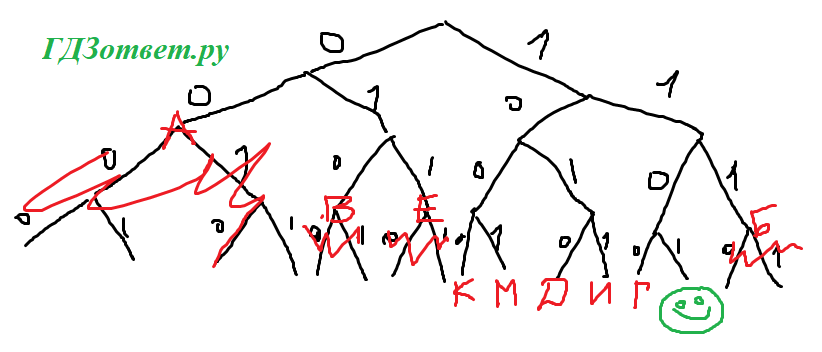
Ответ: 1101
Задача №4 Для кодирования некоторой последовательности, состоящей из букв N, P, R, Q, X, W, Z, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв Q и R использовали кодовые слова 11 и 100 соответственно. Определите наименьшую возможную сумму длин всех семи кодовых слов, учитывая, что кодовые слова оставшихся букв имеют одинаковую длину.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
Рисуем бинарное дерево в 3 уровня, отмечаем буквы Q и R.
Осталось 5 свободных веток, а у нас как раз еще 5 букв, которые и будут на этих ветках.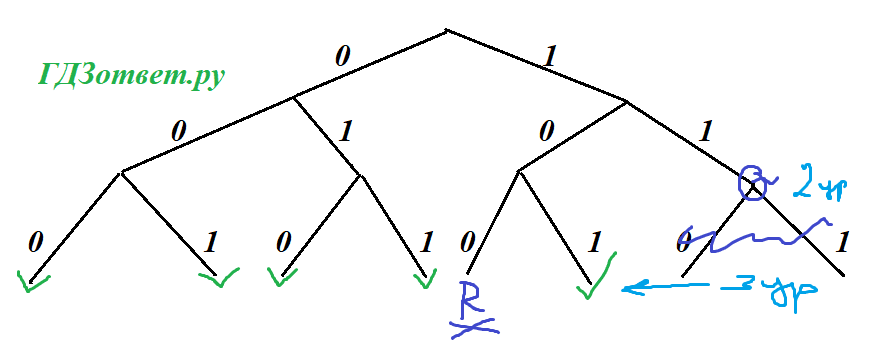
Q на втором уровне - длина 2 символа.
R и остальные на 3 уровне, длина 3 символа.
2 + 6*3 = 20 символов
Если бы другие ветки были заняты, из свободных выбирали бы те, что выше, чтобы обеспечить наименьшую сумму длин.
Ответ: 20
Задача №5 По каналу связи передаются сообщения, содержащие только буквы из набора: А, К, Л, Н, О. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: О - 100, К - 111. Для трёх оставшихся букв А, Л и Н кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЛАНКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Решение:
Строим бинарное дерево, отмечаем буквы О, К. Для свободных мест возможно 2 варианта. 1: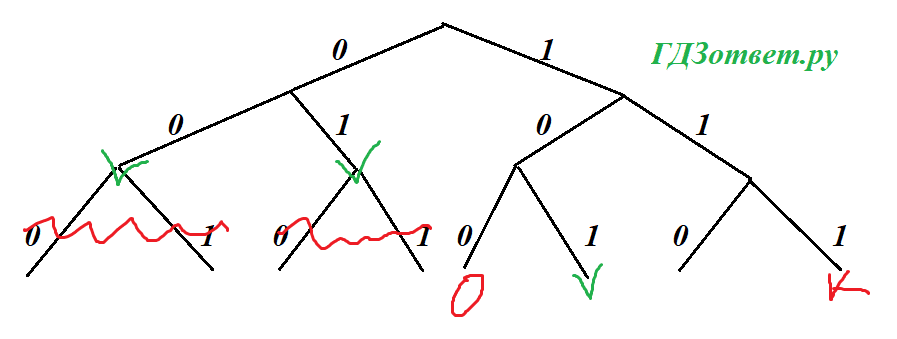
Свободно 2 двузначных места и 1 трехзначное.
Для А берем длину поменьше, так как буква чаще остальных повторяется.
К А Л А Н К А
3 2 2 2 3 3 2 = 17
Просчитываем 2й вариант: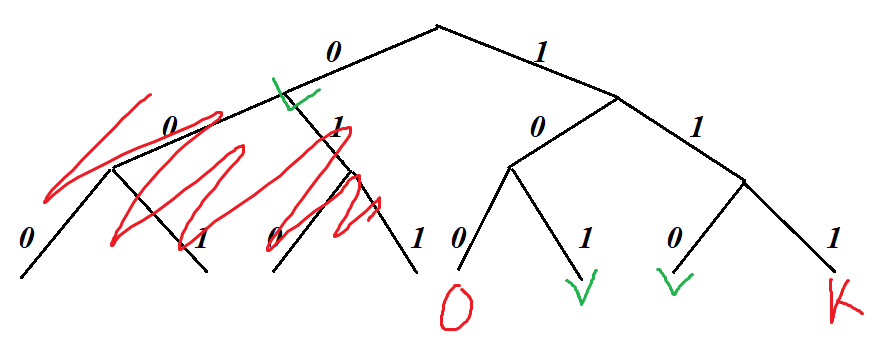
Снова для А берем меньшую - теперь уже длиной 1 знак, но на Л и Н остаются трехзначные.
К А Л А Н К А
3 1 3 1 3 3 1 = 15
15 меньше 17-ти, идет в ответ.
Ответ: 15
Задача №6 По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Решение:
Строим бинарное дерево в 4 уровня (потому что Н – 1111 – это 4 знака). По аналогии с предыдущим заданием ставим на места Н и З, отмечаем свободные ветки.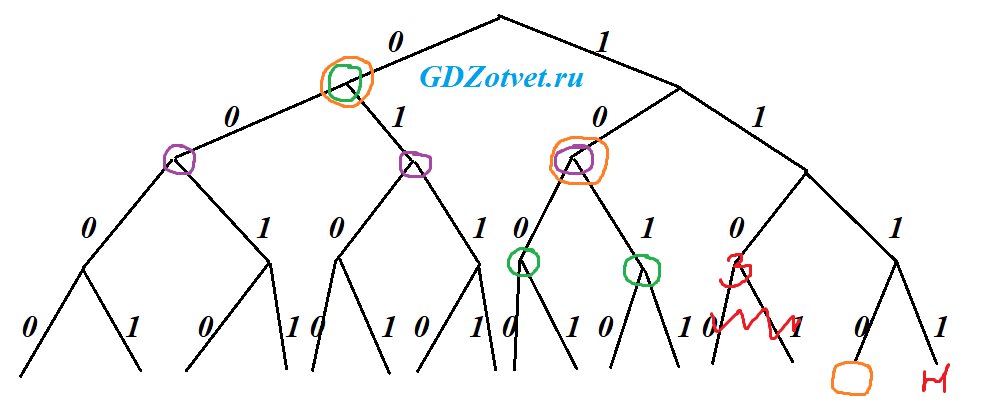
Н – 1111, З – 110 заняты.
Для буквы А выбираем самую меньшую длину, так как буква повторяется чаще всех, для К тоже поменьше.
Рассматриваем все варианты:
1) А - 1 знак, З, К и Ч по 3 знака, КАЗАЧКА = 15
2) З - 3 знака по условию, А, К и Ч по 2 знака, КАЗАЧКА = 15
3) З - 3 знака по условию, А - 1 знак, К - 2 знака, Ч - 4 знака, КАЗАЧКА = 14 - меньшее
Ответ: 14
Задания уровня ЕГЭ
Задача №1 Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: И – 0001, Н – 1110, Ф – 1111, О – 1000, Р – 001, М – 110, А – 0000, Т – 101, К – 01 Укажите возможный код минимальной длины для буквы Ю. Если таких кодов несколько, укажите минимальное числовое значение.
Решение:
Строим бинарное дерево на 4 уровня (максимальное количество знаков в коде букв). Отмечаем известные буквы. 9 мест они займут. Только 1 ветка остается свободной. Но на нее надо повесить весь оставшийся алфавит - многа букафф, и чтобы начало кода не повторялось (правило Фано). Так что занимать это место буквой нельзя. 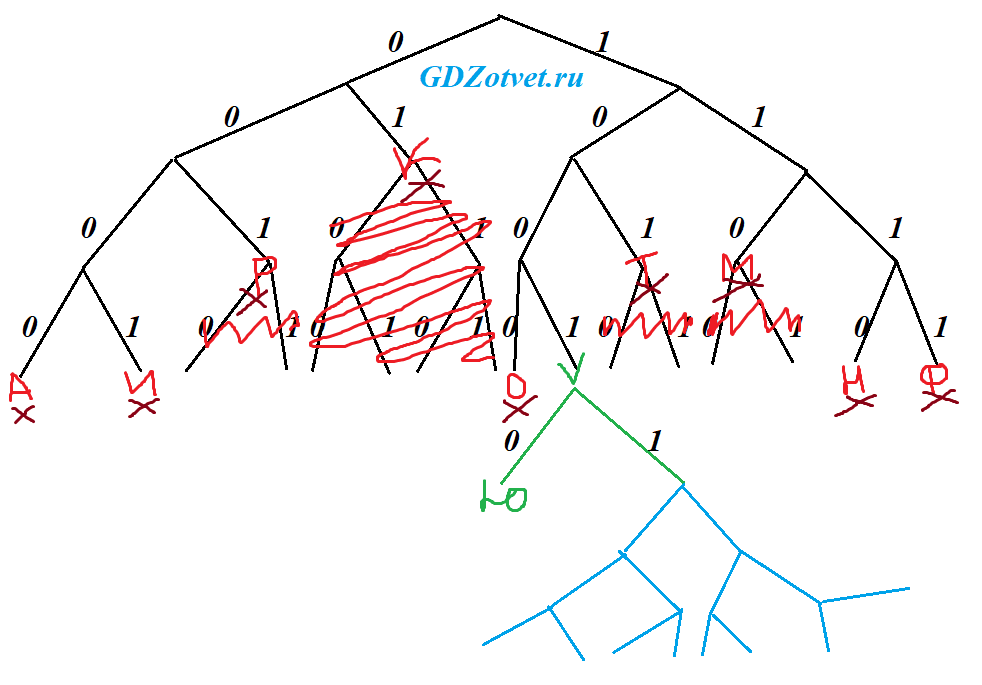
Строим отсюда еще развилку (зеленым на рисунке). Первая ветка пойдет под букву Ю (потому что нам надо минимальное числовое значение), к тому же с нулем, потому что опять же минимальное, а во второй пусть размещают весь свой оставшийся алфавит.
Ответ: 10010
Задача №2 Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: К – 00, О – 010, Д – 011, Ф – 100, А – 11. Укажите возможный код минимальной длины для буквы Н. Если таких кодов несколько, укажите тот из них, который имеет минимальное числовое значение.
Решение:
Рисуем бинарное дерево в 3 уровня, вставляем на свои места известные буквы.
Свободна линия 101, но туда мы не можем поставить букву Н, поскольку надо оставить место и для остальных букв алфавита. Строим отсюда еще развилку, на 0 повесим Н.
Ответ: 1010
Задача №3 Известно, что слово КАШКА закодировали с помощью последовательности 1110110011101. При этом код удовлетворяет условию Фано. Найдите минимальную длину кодовой последовательности для слова ПАМПУШКА? Известно, что другие буквы в кодируемой последовательности встретиться не могут.
Решение:
В слове КАШКА сочетание КА повторяется, это последовательность 11101, в середине осталась Ш - 100. К 1 не может быть (Фано против), и А 1 тоже. (К 11, А 101) или (К111, А 01).
Второй выигрышнее, потому что в ПАМПУШКА две А, они должны быть короче, его и проверим.
Свободное место для П - 00 (повторяется 2 раза, нужно покороче)
М - 101, У - 110, или поменять М с У, не принципиально.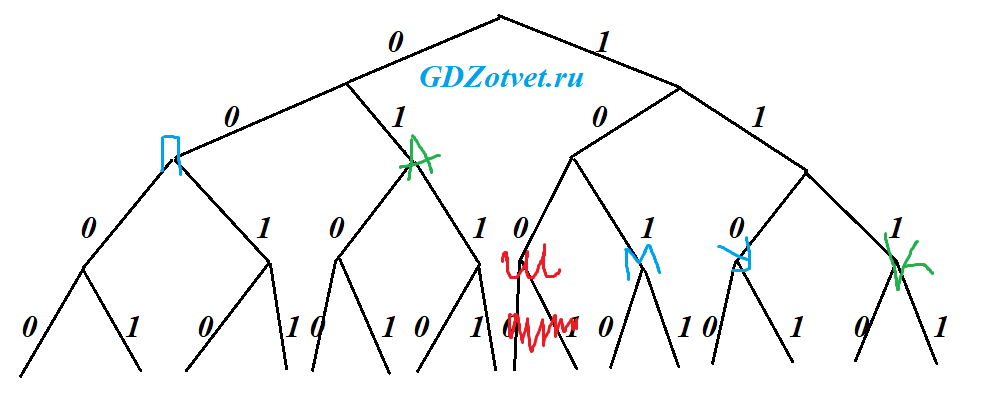
П А М П У Ш К А
2 2 3 2 3 3 3 2 = 20
Можно (и нужно) проверить и альтернативный вариант, но этот короче.
Ответ: 20
Задача №4 Для кодирования букв Ч, И, Т, А, Й, В, С, Ё, использован неравномерный двоичный код. Для букв А, В, И, Й, Ё, использовали кодовые слова 10, 101, 100, 111, 1101. Какова минимальная общая длина кодовых слов для букв Ч, Т, С, при которых код не будет удовлетворять условию Фано? Известно, что ни одно кодовое слово не совпадает с уже используемыми и длина любого кодового слова более одного символа. Примечание. Условие Фано означает, что соблюдается одно из двух условий. Либо никакое кодовое слово не является началом другого кодового слова, либо никакое кодовое слово не является окончанием другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
Строим бинарное дерево в 4 уровня, расставляем известные буквы. Оставшиеся можно расставить в свободные места, начиная со второго уровня (по условию длина любого кодового слова более одного символа, значит 0 или 1 нельзя). Условие Фано НЕ выполняем.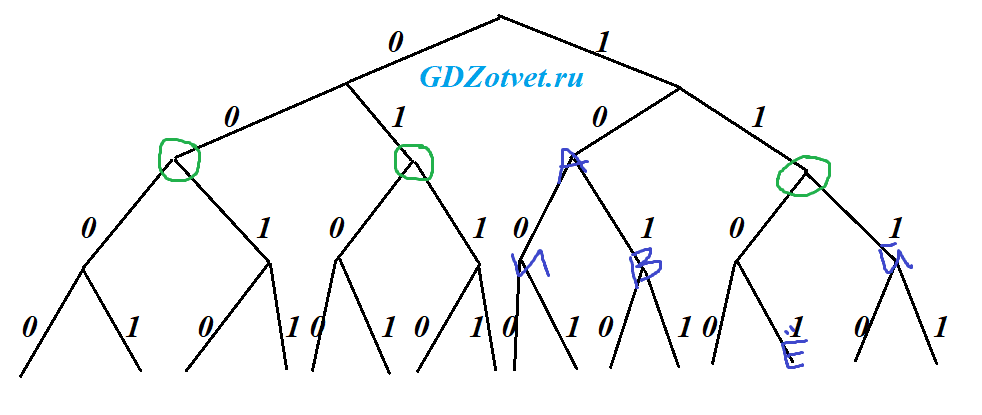
На втором уровне как раз 3 свободных места: 00, 01, 11 - 6 символов
Ответ: 6
Задача №5 По каналу связи передаются сообщения, содержащие только заглавные буквы русского алфавита. Для передачи используется двоичный код, удовлетворяющий условию Фано. Укажите минимальную возможную длину закодированной последовательности АТТЕСТАТ. Примечание: условие Фано выполняется, когда либо ни одно кодовое слово не является началом другого кодового слова, либо ни одно кодовое слово не является окончанием другого кодового слова.
Решение:
Строим бинарное дерево.
Буква Т (4 шт. ⇒ выбираем самый короткий код в 1 цифру), буквы А, Е, С на 3 уровне. АТТЕСТАТ = 16
Второй вариант - Т, А, Е на 2 ур, С на 3 уровне. АТТЕСТАТ = 17
Третий вариант - Т на первом, А на втором, Е на третьем, С на 4. АТТЕСТАТ = 15 - меньший
Не забывайте при подборе свободную ветку оставлять под остальной алфавит.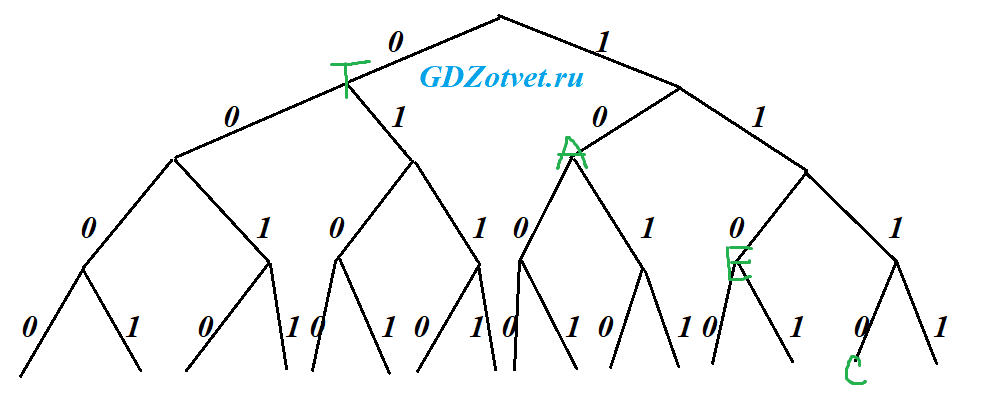
Ответ: 15

