Почти ручное решение
Основные формулы
Изображение:
V=m∙n∙i
V – Объем памяти для хранения растрового изображения, бит
m ∙ n – размер изображения, пиксели
i – глубина кодирования, бит
Максимальное количество цветов в изображении (K) вычисляется формулой:
K=2i,
где i – глубина кодирования.
Звук:
V=(количество каналов)∙ N∙i∙t
N частота дискретизации, Герц,
i – глубина звука, бит
t – время звучания, секунды
Монозапись – 1 канал
Стерео – 2 канала
Квадро – 4 канала
Передача информации:
V=q∙t
V – Объем передаваемого файла, бит
q – пропускная способность (скорость передачи информации), бит/с
t – время передачи, с
Дополнительные условия
Сжатие данных:
`V=(V_(сж.)*100)/(100-p)`
Vсж. – объем сжатого файла , p – количество процентов, на который уменьшается объем , V – полный объем файла
Но это все зависит от того, что нужно принимать за 100%.
Дополнительные биты при кодировании изображения:
i = iцв + iдоп =цв+доп
i – глубина кодирования, бит
iцв цв – биты на хранение цвета, бит
iдоп доп – биты на хранение дополнительной информации, бит
Единицы измерения
1 бит Наименьшая единица измерения информации
1 байт 8 бит 23 бит
1 Кбайт 1024 байт 213 бит
1 Мбайт 1024 Кбайт 223 бит
1 Гбайт 1024 Мбайт 233 бит
Внимательно, где просто берем целое, а где округляем, это разные вещи.
Прототипы с ЕГЭ
Задача №1 Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 40 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Решение:
Известен размер изображения 128×320 пикселей, его объем 40 Кбайт
V=m∙n∙i, где V – Объем памяти для хранения растрового изображения, бит
m ∙ n – размер изображения, пиксели
i – глубина кодирования, бит
Из этой формулы мы можем найти глубину цвета, т.е. объем одного пикселя в битах. Для этого мы общий объем изображения должны поделить на количество пикселей.
`i=V/(m*n)`
128х320 - это и есть количество пикселей.
Обратите внимание, что объем изображения в условии дан в Кбайтах. Мы Кбайты умножаем на 1024 (или `2^10`) - получаем байты. А чтобы получить биты, нужно умножить еще на 8 (или `2^3`).
`i=(40*2^10*2^3)/(128*320)=(10*2^2* 2^10*2^3)/(2^7*2^5*10)=2^15/2^12=2^3=8` бит - это глубина цвета
Кол-во цветов `K=2^i=2^8=256`
Ответ: 256
Задача №2.1 Для хранения произвольного сжатого растрового изображения размером 486x720 пикселей отведено 80 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. После сохранения информации о пикселях изображение сжимается. Размер итогового файла после сжатия на 15% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Решение:
Размер итогового файла после сжатия на 15% меньше исходного. Исходный 100%, наш 100-15=85% ⇒
исходный 80*100/85≈94 Кбайт.
Кбайт переводим в биты и находим глубину цвета
`i=V/(m*n)=(94*2^10*2^3)/(486*720)=2,2...` - округляем в меньшую сторону, так как отведено ограниченное кол-во памяти, i= 2
Кол-во цветов `K=2^i=2^2=4`
Ответ: 4
Задача №2.2 Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кбайт памяти без учёта размера заголовка файла. Исходный файл изображения больше, чем сжатый, на 35% (считая размер сжатого файла за 100%). Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Решение:
Задача отличается от предыдущей тем, что берется за 100%
170 Кбайт - 100%, исходный файл - 135 % = 229,5 Кбайт
i = 229,5*1024*8/640*256=11,475 , округляем в меньшую сторону, так как отведено ограниченное кол-во памяти, i= 11
`K =2^11=2048`
Ответ: 2048
Задача №3 Для хранения произвольного растрового изображения размером 1024 на 120 пикселей отведено 210 Кбайт памяти без учёта размера заголовка файла. При кодировании каждого пикселя используется 7 бит для определения степени прозрачности и одинаковое количество бит для указания его цвета. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов (без учета степени прозрачности) можно использовать в изображении?
Решение:
Здесь говорится о степени прозрачности изображения и определенном количестве бит, отведенных для её определения. Поскольку изображения бывают многослойными (накладываются друг на друга), заходит речь о степени прозрачности их пикселей. Тогда глубина кодирования включает в себя дополнительный канал на кодирование определенного количества уровней прозрачности каждого пикселя.
В задаче требуется найти количество цветов в изображении, для чего необходимо знать глубину кодирования цвета. Поскольку имеется дополнительная информация об отведенных битах для определения степени прозрачности, становится понятно, что глубина кодирования здесь является составной и состоит из двух частей - глубины кодирования цвета и определенном количество битов, отведенных под определение степени прозрачности. Тогда, решая, получаем:
i = 210*1024*8/(1024*120) = 14.
Поскольку i = i1 + i2, где i1 - глубина кодирования цвета, i2 - количество бит, отведенных под степень прозрачности, соответственно, а из условия задачи i2 = 7, тогда i1 = i - i2 = 14 - 7 = 7 бит. Тогда количество цветов = 2^7 = 128.
Ответ: 128
Задача №4 Для хранения произвольного растрового изображения размером 1024 на 120 пикселей отведено 210 Кбайт памяти без учёта размера заголовка файла. К коду каждого пикселя дописывается 1 бит четности. Полученные таким образом коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Решение:
Тоже имеем дело с составной глубиной кодирования, где помимо глубины кодирования цвета к коду каждого пикселя дописывается ещё и вторая часть - биты чётности. Биты чётности обычно используются для контроля и проверки того, что передаваемая информация была доставлена точно. Они устанавливаются для каждого кода таким образом, чтобы все коды содержали в себе нечётное или чётное число единиц.
i = 210*1024*8/(1024*120) = 14.
Помним, что i = i1 + i2, где i2 - бит чётности, он по условию = 1.
Отсюда глубина кодирования цвета = i - i2 = 14 - 1 = 13.
А количество цветов = 2^13 = 8192.
Ответ: 8192
Задача №5 Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 640×320 пикселей при условии, что в изображении могут использоваться 64 различных цвета? Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Искомый объём не учитывает размера заголовка файла. В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
K=2i,
i=log264=6
V=m∙n∙i=640*320*6=1228800 бит, а надо в Кбайт
1228800 :8 :1024=150 Кбайт
Ответ: 150
Задача №6 Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×768 пикселей, используя палитру из 4096 цветов. Для передачи снимки группируются в пакеты по 256 штук. Определите максимальный размер одного пакета фотографий в Мбайт. В ответе запишите только число.
Решение:
4096 - это 2 в 12й степени, i=12
V=12*1024×768=9437184 бит = 1152 Кбайт - 1 штука, а по условию 256 штук в пакете
1152 * 256 = 294 912 Кбайт, а надо в Мбайтах
294 912 : 1024 = 288 Мбайт
Ответ: 288
Задача №7 Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1280×1024 пикселей, используя палитру из 16 384 цветов. Снимки сохраняются в памяти камеры, группируются в пакеты по несколько штук, а затем передаются в центр обработки информации со скоростью передачи данных 94 371 840 бит/с. Каково максимально возможное число снимков в одном пакете, если на передачу одного пакета отводится не более 128 секунд?
В ответе запишите целое число.
Решение:
Зная разрешение и палитру, можем найти объем 1 фотографии.
Сначала из палитры найдем глубину кодирования:
16384 цветов = `2^i` ⇒ `i =14`
Затем объем 1 снимка в битах:
1280*1024*14=18 350 080 бит
Скорость передачи данных 94 371 840 бит/с, 128 секунд на 1 пакет ⇒ можем найти, сколько данных передадим за эти 128 с:
94371840*128=12 079 595 520 бит - это 1 пакет
Знаем сколько данных в пакете, знаем объем 1 снимка, найдем количество снимков в пакете:
12079595520 : 18 350 080 = 658,28... по условию берем целое 658
Ответ: 658
Задача №8 Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×960 пикселей, используя палитру из 8192 цветов. Снимки сохраняются в памяти камеры, группируются в пакеты по 160 шт., затем передаются в центр обработки информации со скоростью передачи данных 14 680 064 бит/с. Сколько секунд требуется для передачи одного пакета фотографий?
В ответе запишите целую часть полученного числа.
Решение:
`8192 = 2^13`, i = 13 глубина кодирования
1024*960*13=12 779 520 разрешение изображения
12 779 520*160/14 680 064= 139,3 секунд требуется для передачи одного пакета фотографий
целая часть полученного числа 139
Ответ: 139
Задача №9 Пользователь записал голосовое сообщение. Сообщение представляет собой стерео аудиофайл со следующими параметрами: глубина кодирования – 24 бит, частота дискретизации 16000 отсчётов в секунду, время записи – 90 с. Данное сообщение было отправлено по Сети со скоростью 64 000 бит/c. Сколько секунд будет передаваться голосовое сообщение?
Решение:
Выпишем условия задачи:
Глубина кодирования i = 24 бит.
Частота дискретизации 16000 отсчётов в секунду.
Время записи t = 90 секунд.
Количество каналов записи 2 (стерео).
Скорость передачи данных 64000 бит/с.
Находим объём данных для голосового сообщения, используя формулу для объёма информации звукового файла: V=(количество каналов)∙ N∙i∙t
Подставляем значения:
2*16000*24*90=69120000 бит
Вычисляем время передачи голосового сообщения, используя формулу для времени передачи:
V=q∙t ⇒
t = V/q = 69120000/64000=1080 секунд
Ответ: 1080
Задача №10 Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объём не учитывает размера заголовка файла.
Решение:
12 Мбайт - первый файл, 4 канала.
Второй файл - 1 канал (в 4 раза меньше первого), разрешение в 2 раза выше, частота дискретизации в 1,5 раза меньше:
12 :4 *2 :1,5 = 4 Мбайт
Ответ: 4
Задача №11 Голосовое сообщение продолжительностью 90 с было записано в формате стерео и оцифровано с глубиной кодирования 16 бит и частотой дискретизации 48 000 измерений в секунду. Сжатие данных не использовалось. Файл с оцифрованным голосовым сообщением был передан по каналу связи, пропускная способность которого 3200 бит/с. Сколько секунд длилась передача файла? В ответе запишите целое число, единицу измерения указывать не нужно.
Решение:
V=(количество каналов)∙ N∙i∙t=2*48000*16*90=138 240 000 бит
138 240 000:3200 =43200 с
Ответ: 43200
Задача №12 Производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 96 кГц и 24-битным разрешением. В результате был получен файл размером 792 Мбайт, без учёта размера заголовка и без сжатия данных. Определите длительность звукозаписи (в минутах). В качестве ответа укажите ближайшее к полученному времени записи целое число.
Решение:
792 Мбайт = `792 *2^23` бит
96 кГц = 96000 Гц
`t=(792 *2^23)/(4*96000*24)= 720,896` сек = 12,01... мин
по условию в ответ идет ближайшее к полученному времени записи целое число, то есть округляем до 12
Ответ: 12
Задача №13 Сколько секунд потребуется обычному модему, передающему сообщения со скоростью 28 800 бит/с, чтобы передать цветное растровое изображение размером 640 на 480 пикселей, при условии, что цвет каждого пикселя кодируется 3 байтами?
Решение:
3 байт = 3*8 = 24 бит - глубина цвета i
Объем изображения 640 * 480 * 24 = 7372800 бит
7372800 : 28800 = 256 с
Ответ: 256
Задача №14 Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 256 Кбит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Фактически нужно определить, сколько времени будет передаваться файл объемом 5 Мбайт по каналу со скоростью передачи данных 32 Кбит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 256 Кбит/с).
В первую очередь важно выразить все в единых единицах измерения. Чтобы не ошибиться, можно всегда переводить в биты, но по логике хватит и просто одних и тех же единиц. Пропускная способность в килобитах в с, так что переводим размеры файлов тоже в килобиты
512 Кбайт * 8 = 4096 Кбит - должен скачать Вася, чтобы началась передача Пете
4096 : 256 = 16 с - через 16 секунд компьютер Васи начнет ретрансляцию
5 Мбайт * 1024 * 8 = 40960 Кбит - передается Пете
40960 : 32 = 1280 с - надо для передачи данных Пете
1280 + 16 = 1296 с
Ответ: 1296
Задача №15 (самый частый прототип) Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами.
А. Сжать архиватором, передать архив по каналу связи, распаковать.
Б. Передать по каналу связи без использования архиватора. Какой способ быстрее и насколько, если:
- средняя скорость передачи данных по каналу связи составляет `2^20` бит в секунду;
- объём сжатого архиватором документа равен 20% исходного;
- время, требуемое на сжатие документа, – 5 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Единиц измерения «секунд», «сек.», «с.» к ответу добавлять не нужно.
Решение:
А. Определим сколько времени потратим, если будем передавать сжатый файл по каналу связи. Сжатый файл имеет объём 20% от 20 Мбайт.
20 Мбайт - 100%
х - 20 %
20*20:100=4 Мбайт = `4 * 2^10 * 2^10 * 2^3 = 2^25` бит - объем сжатого файла
Передаваться он будет `2^25 : 2^20 = 2^5` c + 5 с на сжатие, + 1 сек на с на распаковку = 38 c
Б. Определим, сколько потратим времени на целый файл.
20 Мбайт = `20 * 2^10 * 2^10 * 2^3 = 20 * 2^23`бит - несжатый файл
`20 * 2^23 : 2^20 = 20 * 2^3` = 160 с
Сжатый быстрее на 160-38=122 с
Ответ: А122
Задача №16 Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 50 секунд.
Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. Размер упакованного документа составляет 20% размера исходного документа.
Сколько всего времени ушло на упаковку и распаковку данных, если считать, что время передачи файла пропорционально его размеру? Ответ запишите в секундах без указания размерности.
Решение:
...
Ответ:
Номер: 0F4A18
Задания уровня ЕГЭ
Задача №1 Для хранения сжатого изображения отведено 3 МБайта памяти без учёта размера заголовка файла. Известно, что изображение имеет размер 1600х1200 пикселей и содержит не более 1024 цветов. При этом цвет каждого пикселя кодируется с помощью минимального и одинакового для всех пикселей количества бит. К каждому пикселю добавлено одинаковое количество бит, отвечающих за его прозрачность. После кодирования изображение сжимается, при этом объем дискового пространства, требуемый для хранения файла с несжатым изображением, на 20 % больше, чем объем дискового пространства, требуемый для хранения сжатого изображения. Какое максимальное количество уровней прозрачности может быть у пикселя?
Решение:
1024 цвета, 1024=2^10 ⇒ i=10 глубина кодирования без учета прозрачности, то есть 10 бит на пиксель выделяются под цвет.
Узнаем фактическую глубину прозрачности из размера файла. Сжатое 3 МБайта, нам над несжатое.
3 МБайта - 100%
х - 120 %
х = 3,6 МБайт = (3,6 * 2^23) бит - размер несжатого файла
отсюда i = (3,6 * 2^23)/1600х1200 = 15,7... бит на 1 пиксель
Дальше надо выяснить, в какую сторону округлять! до 15 или до 16?
Мы должны вписаться в (3,6 * 2^23) = 30 198 988,8 бит!
1600х1200*16=30 720 000 бит, не влазит, значит округляем в меньшую сторону. Запомните, что если надо вписаться в указанный объем, то округляем всегда в меньшую.
i = 15 бит. Из них 10 выделяется под цвет
15 - 10 = 5 - под прозрачность.
Тогда уровней прозрачностей может быть максимум `2^5=32`
Ответ: 32
Задача №2 Музыкальный фрагмент записали в формате стерео. Размер полученного файла составил 18 Мбайт. После чего музыкальный фрагмент перевели в формат квадро, при этом уменьшив частоту дискретизации вдвое и увеличив скорость произведения в 1.5 раза. Полученный фрагмент также сохранили в виде файла. Методы сжатия в обоих случаях не применялись. Найдите размер полученного после преобразования файла.
Решение:
Было 18 Мбайт файл стерео. Стало квадро. ↓ частоту дискретизации в 2 р, ↑ скорость произведения в 1.5 раза.
V=(количество каналов)∙ N∙i∙t
В формате квадро каналов в два раза больше, чем в в стерео. Увеличивая скорость в 1,5 раза, уменьшают время воспроизведение во столько же раз. Получаем, что финальный размер файла
`(18 * 2)/(2 : 1,5) = 12` Мбайт
Ответ: 12
Задача №3 Растровое изображение размером 192 на 960 пикселей сохраняют в памяти компьютера. Каждый пиксель в изображении может иметь один из 2048 цветов. Все цвета представлены с помощью битовых последовательностей одинаковой длины, при этом длина этих последовательностей минимальна.
На сколько процентов необходимо уменьшить полученный файл, чтобы сжатое изображение можно было сохранить в отведенные для хранения 180 Кбайт памяти?
В качестве ответа приведите минимальное целое подходящее число.
Решение:
K=2i=2048 ⇒ i = 11
V=m∙n∙i=192*960*11=2027520 бит = : 8 :1024 = 247,5 Кбайт
Нам надо, чтобы влезло 180 Кбайт
247,5 Кбайт - 100%
180 Кбайт - х %
х = 180 *100 / 247,5 = 72,7... берем целое 72
100 - 72 = 28 %
Ответ: 28
Задача №4 Для хранения сжатого аудио файла отведено 25 Мбайт памяти. Известно, что фрагмент кодируется в формате стерео, частотой дискретизации 50 кГц и глубиной кодирования 16 бит. После кодирования звуковых дорожек фрагмент сжимается. Сжатый размер закодированного фрагмента меньше исходного на 25%. К сжатому фрагменту дописывается информация о заголовке и дополнительная информация, суммарно занимающая 40 Кбайт. Укажите максимальную длительность в минутах фрагмента, который сохраняется по приведенному алгоритму?
В ответе запишите только число – целую часть полученного числа.
Решение:
Было 25 Мбайт файл стерео, частота дискретизации 50 кГц и глубина кодирования 16 бит. Файл сжался на 25%, дописывается информация, занимающая 40 Кбайт.
Переводим в си
25 Мбайт = 25 * 1024 * 1024 * 8 = 209715200 бит
40 Кбайт = 40 * 1024 * 8 = 327680 бит
50 кГц = 50000 Гц
209715200 - 327680 = 209387520 бит - занимает сжатая запись без доп. информации
100-25=75%=0,75
209387520/0,75=279183360 бит - занимает не сжатая запись без доп. информации
V=(количество каналов)∙N∙i∙t
t=V/(количество каналов∙N∙i)=279183360/2*50000*16=174,4896 с
174,4896 с : 60 = 2,90816 мин то есть 2 минуты (целая часть полученного числа, указано в условии)
Ответ: 2
Задача №5 Стоит задача передать файл размером 500 Мбайт между компьютерами в одной локальной сети. При этом есть два способа:
А) записать файл на USB-накопитель, перенести физически накопитель до приемника, выгрузить файл,
Б) передать по локальной сети со скоростью 10 Мбит/сек.
Известно, что скорость записи и чтения файла через USB составляет 100 Мбит/сек. На перемещение USB-накопителя понадобится 40 секунд.
Какой способ быстрее и на сколько? В ответе запишите сначала букву А или Б – вариант, с помощью которого файл получится передать быстрее, и число – разницу в секундах между этими двумя способами. Разделители между буквой и числом указывать не нужно.
Решение:
А. 100 Мбит/сек : 8 = 12,5 Мбайт/с
500 : 12,5 = 40 с будет записываться на USB-накопитель
+ 40 с на перенос + 40 с на выгрузку = 120 с
Б. 10 Мбит/сек : 8 = 1,25 Мбайт/с
500/1,25 = 400 с
400-120=280
Ответ: А280
Задача №6 Геннадий создает мультипликационный ролик, где каждый кадр – отдельно отрисованная картинка.
Известно, что каждая картинка имеет разрешение 640х480 пикселей и цветовую палитру в 216 = 65536 цветов. Каждый пиксель кодируется с помощью минимально возможного и одинакового для всех пикселей количества бит. Картинки записываются одна за другой без разделителей и заголовков файла. Частота смены кадров в конечном ролике – 24 кадра/сек. В качестве звукового сопровождения выбран формат стерео с глубиной кодирования 10 бит и частотой дискретизации 40 кГц.
Найдите размер мультфильма в МБайтах, если известно, что его длительность 5 минут. В качестве ответа укажите число – минимальное целое количество Мбайт достаточное для хранения такого файла.
Решение:
Изображение:
K=2i
i = 16
V=m∙n∙i=640*480*16=4915200 бит на 1 кадр, а у нас 24 кадра в с
4915200*24 =117964800 бит в с, а у нас 5 минут
117964800*60*5=35389440000 бит все картинки мультика
Звук:
V=(количество каналов)∙N∙i∙t= 2*40000*10*5*60= 240000000 бит
Целиком:
`(35389440000+240000000)/(8*1024*1024)=4247,36...` Мбайт
Или в одну строку:
`((640*480*16*24+2*10*40000)*5*60)/(8*2^20)=4247,36...` Мбайт
Минимальное целое количество Мбайт достаточное для хранения такого файла 4248 Мбайт
Ответ: 4248
Задача №7 20 изображений разрешением 1600х1200 пикселей отправили по каналу связи со средней пропускной способностью 223 бит/секунду. Все изображения были приняты приемником не более, чем 10 секунд. Известно, что изображение кодируется как набор пикселей, каждый из которых закодирован с помощью одинакового и минимально возможного количества бит. Изображения в целях ускорения передачи записаны в памяти подряд, без разделителей и заголовков. Какое максимальное число цветов может быть в палитре?
Решение:
Чтобы найти максимальное количество цветов, надо найти сначала i.
Объем переданной информации V=q∙t=223*10
20 изображений, значит одно `(2^23*10)/20=2^22`
V=m∙n∙i
`i=2^22/(1600х1200)=2^22/(1600х1200)=2,18...` то есть 2
K=2i, 22=4
Ответ: 4
Прототипы с решением на Python
Задача №1 Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×768 пикселей, используя палитру из 4096 цветов. Для передачи снимки группируются в пакеты по 256 штук. Определите максимальный размер одного пакета фотографий в Мбайт.
В ответе запишите только число.
Решение:
(1024*768*12*256) / 8 / 1024/ 1024 = 288
from math import *
K=1024*768
N=4096
i=ceil(log2(N))
I=K*i
n256=I*256
print(n256/8/1024/1024)Ответ: 288
Задача 2. Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1440×900 пикселей. Используется палитра из 2048 цветов, причём каждый пиксель кодируется одинаковым минимально возможным количеством бит. Для передачи снимки группируются в пакеты по 256 штук, а после передаются по каналу связи, пропускная способность которого равна 21600 Кбайт/с. Определите, сколько минут потребуется для передачи 32 таких пакетов. В ответе запишите только число.
Решение:
from math import *
K=1440*900
N=2048
i=ceil(log2(N))
I=K*i
packet=I*256/8/1024
skorost=21600
t=packet/skorost
print((t*32)/60)Ответ: 11
Задача 3. Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла — 324 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно (одноканальная запись) и оцифрован с разрешением в 4 раза выше, темп воспроизведения при этом увеличен в 12 раз. Сжатие данных не производилось. Получившийся аудиофайл передали по каналу связи, пропуская способность которого равна 4 Мбит/с.
Решение:
from math import *
V=324
x=V/2*4/12
t=(x*1024*1024*8)/(4*1024*1024)
print(t)Ответ: 108
Определите, сколько секунд ушло на передачу файла. В ответе укажите только число.
Задача 4. Голосовое сообщение длительностью 90 секунд было закодировано в формате стерео с частотой дискретизации 48000 измерений в секунду и передано по каналу связи, пропускная способность которого равна 1600 бит/с, за 86400 секунд.
Определите максимальное количество уровней громкости цифрового звука, которое может использоваться в этом голосовом сообщении. В ответе запишите только целое число.
Решение:
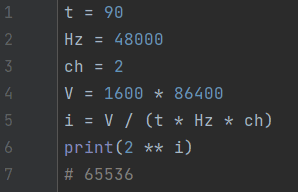
Ответ: 65536
Задача 5. Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1440×900 пикселей. Для передачи снимки группируются в пакеты по 128 штук. Известно, что один пакет занимает не более 100 Мбайт.
Определите максимальное количество цветов, которое может быть использовано в данных изображениях. В ответе запишите только число.
Решение:
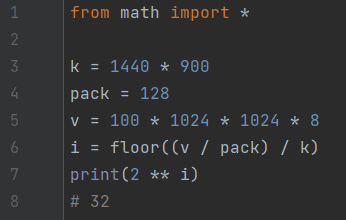
Ответ: 32
Задача 6. Голосовое сообщение длительностью 2 минуты было закодировано в формате квадро с разрешением 16 бит и частотой дискретизации 48000 измерений в секунду и передано по каналу связи за 12800 секунд.
Определите пропускную способность канала связи в бит/с. В ответе запишите только целое число.
Решение:
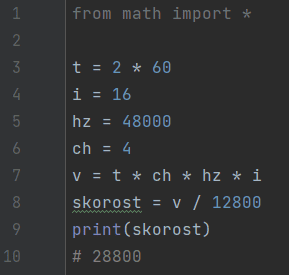
Ответ: 28800
Задача 7. Автоматическая фотокамера каждые 10 секунд создаёт растровое изображение. Размер изображения — 1536×1024 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Все изображения, полученные за 1 минуту, занимают 9 Мбайт. Найдите максимально возможное количество цветов в палитре изображения.
Решение:
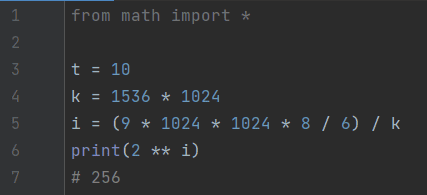
Ответ: 256
Задача 8. Модему, передающему сообщения со скоростью 65536 бит/с, чтобы передать цветное растровое изображение размером 1024 на 768 пикселей, потребовалось 288 секунд.
Определите, какое максимальное количество цветов может быть использовано в таком изображении. В ответе запишите только число.
Решение:
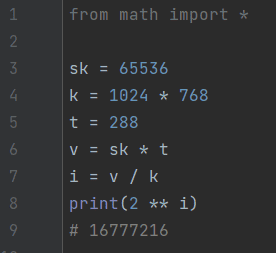
Ответ: 16777216
Задача 9. Цветное растровое изображение размером 1200 на 1800 пикселей, в котором цвет каждого пикселя кодируется 2 байтами, было передано по каналу связи ровно за 6 минут.
Определите пропускную способность канала связи в бит/с. В ответе запишите только число.
Решение:
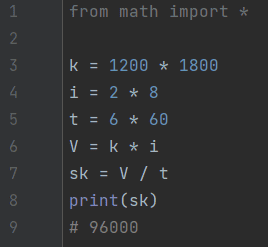
Ответ: 96000
Задача 10. Растровые изображения размером 1600 на 900 пикселей с палитрой из 2048 цветов группируются в пакеты по 16 штук и передаются по каналу связи. Известно, что время передачи одного такого пакета занимает ровно 5 минут.
Определите, чему равна пропускная способность канала связи в бит/с. В ответе запишите только число.
Решение:
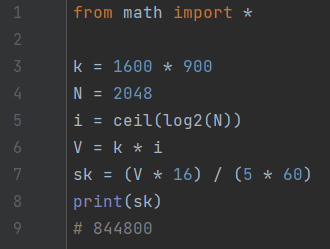
Ответ: 844800
Задача 11. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Размер полученного файла составил 30 Мбайт. Получившийся файл был передан в город А по каналу связи за 15 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза меньше и частотой дискретизации в 3 раза выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 5 секунд.
Определите среднюю скорость передачи в пункт Б в Мбайт/сек.
Решение:

Ответ: 9
Задача 12. Музыкальный фрагмент записали в формате моно и отправили по каналу передачи в город А. Процесс передачи файла занял 90 секунд. Затем тот же музыкальный фрагмент записали в формате стерео с разрешением вдвое больше и частотой дискретизации в 1.5 раза меньше. Данный файл отправили по каналу связи в город Б. Процесс передачи занял 120 секунд.
Определите во сколько раз средняя скорость передачи в пункт Б больше средней скорости передачи в город А.
Решение:

Ответ: 2
Задача 13. Сколько секунд потребуется обычному модему, передающему сообщения со скоростью 65536 бит/с, чтобы передать цветное растровое изображение размером 1024 на 768 пикселей, при условии, что в палитре 24 цвета?
Решение:
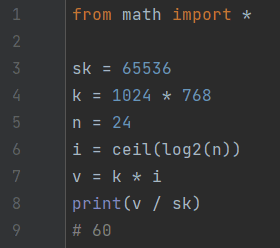
Ответ: 60
Задача 14. Сколько минут потребуется обычному модему, передающему сообщения со скоростью 65536 бит/с, чтобы передать цветное растровое изображение размером 1024 на 768 пикселей, при условии, что в палитре 28 цветов?
Решение:
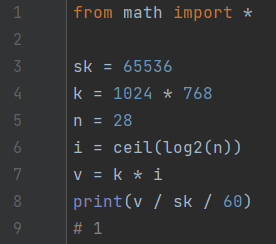
Ответ: 1
Задача 15. Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 120 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) будет на 20 секунд меньше. Размер упакованного документа составляет 15% от размера исходного документа. Сколько всего времени ушло на упаковку и распаковку данных, если считать, что время передачи файла пропорционально его размеру? Ответ запишите в секундах без указания единиц измерения.
Решение:

Ответ: 82
Задача 16. Растровое изображение в разрешении 300 ppi сохранили в палитре, содержащей 2¹⁶ = 65536 цветов. Размер полученного изображения составил 20 Мбайт. После чего, для экономии места, было решено использовать палитру, содержащую 256 цветов, и уменьшить разрешение до 150 ppi. Известно, что цвет каждого пикселя кодируется минимально возможным количеством бит, общим для всех пикселей. Определите размер полученного после преобразования файла в Кбайт. В ответе запишите только число.
Решение:
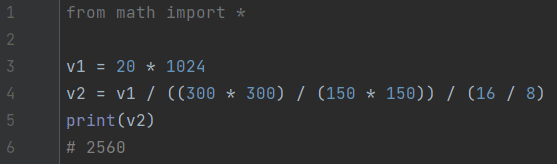
Ответ: 2560
Задача 17. Растровое изображение сохранили в палитре, содержащей 2²⁴ = 16777216 цветов. Размер полученного изображения составил 50 Мбайт. После чего, для экономии места, было решено использовать палитру, содержащую 4096 цветов, и уменьшить количество пикселей в 5 раз. Известно, что цвет каждого пикселя кодируется минимально возможным количеством бит, общим для всех пикселей. Определите размер полученного после преобразования файла в Мбайт. В ответе запишите только число.
Решение:
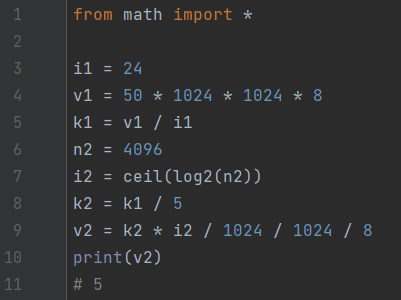
Ответ: 5
Задача 18. Фотографии сканируют с разрешением 300 dpi. При сканировании используют 2²⁴ цветов. Под хранение файла отведено 13 Мб. Какую максимальную площадь (в квадратных дюймах) может иметь фотография? В ответе запишите целую часть числа.
Решение:
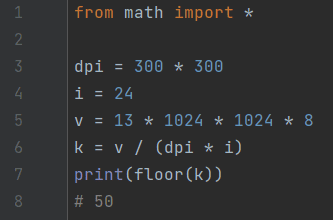
Ответ: 50
Задача 19. При кодировании произвольного сжатого растрового изображения размером 1280×1024 пикселей используется палитра из 2³² цветов. Коды пикселей записываются в файл один за другим без промежутков. После сохранения информации о пикселях изображение сжимается. Размер итогового файла после сжатия на 40% меньше исходного. Определите, какой минимальный объем памяти в Мегабайтах необходимо выделить для хранения такого изображения.
Решение:
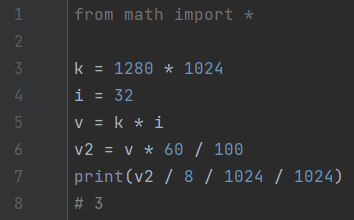
Ответ: 3
Задача 20. Музыкальный фрагмент записали в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла — 48 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 1.5 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Размер полученного файла без учёта размера заголовка файла — 6 Мбайт. При повторной оцифровке использовалось сжатие. Определите коэффициент сжатия (отношение размеров несжатого и сжатого файла).
Решение:

Ответ: 2
Задача 21. Музыкальный фрагмент записали в формате стерео. Размер полученного файла составил 18 Мбайт. После чего музыкальный фрагмент перевели в формат квадро, при этом уменьшив частоту дискретизации вдвое и увеличив скорость произведения в 1.5 раза. Полученный фрагмент также сохранили в виде файла. Методы сжатия в обоих случаях не применялись.
Найдите размер полученного после преобразования файла в МБайтах.
Решение:

Ответ: 12
Задача 22. Голосовое сообщение было записано в формате моно и оцифровано с глубиной кодирования 16 бит и частотой дискретизации 32000 измерений в секунду. Сжатие данных не использовалось. Файл с оцифрованным голосовым сообщением был передан по каналу связи, пропускная способность которого 1024000 бит/с в течение 5 секунд. Какова продолжительность голосового сообщения в секундах? В ответе запишите целое число, единицу измерения указывать не нужно.
Решение:
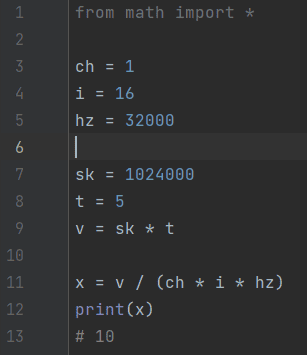
Ответ: 10
Задача 23. Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранен в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла — 45 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате квадро, оцифрован с разрешением в 3 раза ниже и частотой дискретизации в 2 раза выше, чем в первый раз. Сжатие данных не производилось.
Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объем не учитывает размера заголовка файла.
Решение:

Ответ: 60
Задача 24. Голосовое сообщение длительностью 3 минуты было закодировано в формате квадро с разрешением 16 бит и частотой дискретизации 48000 измерений в секунду и передано по каналу связи. Сжатия данных не производилось. Пропускная способность канала связи равна 3200 бит/с. Определите, сколько часов необходимо для передачи голосового сообщения. В ответе запишите только целое число.
Решение:

Ответ: 48

