КЭС 4.1 Анализ данных. Основные задачи анализа данных: прогнозирование, классификация, кластеризация, анализ отклонений. Последовательность решения задач анализа данных: сбор первичных данных, очистка и оценка качества данных, выбор и/или построение модели, преобразование данных, визуализация данных, интерпретация результатов. Программные средства и интернет-сервисы для обработки и представления данных. Большие данные. Машинное обучение

Все задания 27 ФИПИ к ЕГЭ по информатике

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

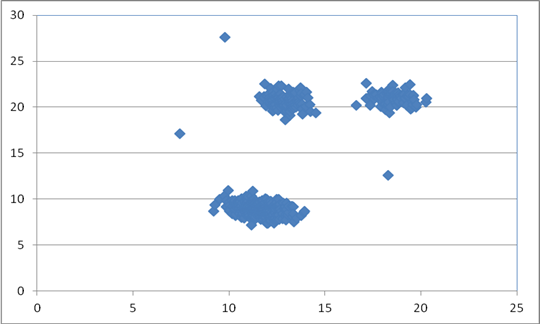
В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек
не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Qx – сумму абсцисс центров кластеров с минимальным и максимальным количеством точек, и Qy – сумму ординат центров кластеров с минимальным и максимальным количеством точек.

Гарантируется, что во всех кластерах количество точек различно.

В ответе запишите четыре числа: в первой строке – сначала абсолютную величину целой части произведения Px × 10 000, затем абсолютную величину целой части произведения Py × 10 000; во второй строке – сначала абсолютную величину целой части произведения Qx × 10 000, затем абсолютную величину целой части произведения Qy × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла

Файл с данными

Номер: 9c8c86

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек
не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – максимальную из абсцисс центров кластеров, и Py – максимальную из ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Qx – разность абсцисс центров кластеров с минимальным и максимальным количеством точек, и Qy – разность ординат центров кластеров с минимальным и максимальным количеством точек. Гарантируется, что во всех кластерах количество точек различно.

В ответе запишите четыре числа: в первой строке – сначала целую часть абсолютного значения произведения Px × 10 000, затем целую часть абсолютного значения произведения Py × 10 000; во второй строке – сначала целую часть абсолютного значения произведения Qx × 10 000, затем целую часть абсолютного значения произведения Qy × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: 82e6AD

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – минимальную из абсцисс центров кластеров и Py – минимальную из ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Q1 – расстояние между центрами кластеров с минимальным и максимальным количеством точек и Q2 – максимальное расстояние от центра кластера до точки этого же кластера среди всех кластеров. Гарантируется, что во всех кластерах количество точек различно.

В ответе запишите четыре числа: в первой строке – сначала абсолютную величину целой части произведения Px × 10 000, затем абсолютную величину целой части произведения Py × 10 000; во второй строке – сначала целую часть произведения Q1 × 10 000, затем целую часть произведения Q2 × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: AeB8BB

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек не превышает 10 000. Структура хранения информации в файле Б аналогична в структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – сумму абсцисс центров кластеров и Py – сумму ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Q1 – минимальное расстояние между центрами различных кластеров и Q2 – максимальное расстояние между центрами кластеров.

В ответе запишите четыре числа: в первой строке – сначала абсолютную величину целой части произведения Px × 10 000, затем абсолютную величину целой части произведения Py × 10 000; во второй строке – сначала абсолютную величину целой части произведения Q1 × 10 000, затем абсолютную величину целой части произведения Q2 × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: 76B8BD

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек
не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – сумму абсцисс центров кластеров и Py – сумму ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Q1 – минимальное расстояние между центрами различных кластеров и Q2 – максимальное расстояние между центрами кластеров.

В ответе запишите четыре числа: в первой строке – сначала абсолютную величину целой части произведения Px × 10 000, затем абсолютную величину целой части произведения Py × 10 000; во второй строке – сначала абсолютную величину целой части произведения Q1 × 10 000, затем абсолютную величину целой части произведения Q2 × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: B5FB72

20.10.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6 и W = 4,5 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

В файле Б хранятся координаты точек трёх кластеров, где H = 6, W = 5 для каждого кластера. Известно, что количество точек
не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.

Для файла А определите координаты центра каждого кластера, затем найдите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров.

Для файла Б определите координаты центра каждого кластера, затем найдите два числа: Qx – сумму абсцисс центров кластеров с минимальным и максимальным количеством точек, и Qy – сумму ординат центров кластеров с минимальным и максимальным количеством точек.

Гарантируется, что во всех кластерах количество точек различно.

В ответе запишите четыре числа: в первой строке – сначала абсолютную величину целой части произведения Px × 10 000,
затем абсолютную величину целой части произведения Py × 10 000; во второй строке – сначала абсолютную величину целой части произведения Qx × 10 000, затем абсолютную величину целой части произведения Qy × 10 000.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: c22345

20.05.2025
Задание выполняется с использованием прилагаемых файлов.

Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на N непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной H и W, причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.

Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости A(x1, y1) и B(x2, y2) вычисляется по формуле:

`d(A,B)=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

В файле A хранятся координаты точек двух кластеров, где H = 6, W = 6 для каждого кластера. В каждой строке записана информация о расположении на карте одной точки: сначала координата x, затем координата y. Известно, что количество точек не превышает 1000.

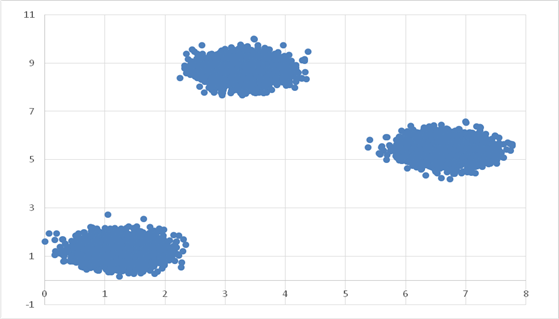
В файле Б хранятся координаты точек трёх кластеров, где H = 8, W = 8 для каждого кластера. Известно, что количество точек не превышает 10 000. Структура хранения информации в файле Б аналогична структуре в файле А.

Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров.

В ответе запишите четыре числа: в первой строке – сначала абсолютное значение целой части произведения Px × 10 000, затем абсолютное значение целой части произведения Py × 10 000 для файла А; во второй строке – аналогичные данные для файла Б.

Возможные данные одного из файлов проиллюстрированы графиком.

Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Файл с данными

Номер: AAB9D2

===================== 

22.10.2024
Задание выполняется с использованием прилагаемых файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим Si, Sj, Sk три элемента последовательности S, где i < j < k.

Определите в последовательности S три таких числа Si, Sj, Sk, что Si > Sj, Sk > Sj и значение выражения (Si – Sj) + (Sk – Sj) максимально. В ответе укажите найденное максимальное значение выражения (Si – Sj) + (Sk – Sj). Гарантируется, что в последовательности есть три числа Si, Sj, Sk, удовлетворяющие условию задачи.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

9

6

9

7

5

8

6

10

–5

–6

При таких входных данных искомую максимальную сумму разностей образуют второй, четвёртый и седьмой элементы данной последовательности. Значение этой суммы разностей равно (9 – 5) + (10 – 5) = 9. Для седьмого, восьмого и девятого элементов последовательности искомая величина равна 14, но девятый элемент меньше восьмого, что не удовлетворяет условию задачи. Ответом является число 9.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий искомую величину для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 3169CC

22.10.2024
Задание выполняется с использованием прилагаемых файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим S(L, R) подпоследовательность, состоящую из идущих подряд элементов, входящих в S, начиная с элемента с номером L и заканчивая элементом с номером R включительно.

Требуется найти такую подпоследовательность S(L, R) максимальной длины, что сумма её элементов отрицательна и нечётна. Гарантируется, что хотя бы одна подпоследовательность требуемого вида существует.

В ответе укажите длину искомой подпоследовательности.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000. В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

6

20

2

–8

4

–5

3

При таких входных данных L = 2, R = 5. Сумма подпоследовательности равна (2 + (–8) + 4 + (–5)) = –7. Ответом является длина этой подпоследовательности, равная 4.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: A47CA1

22.10.2024 23:09:52
Задание выполняется с использованием прилагаемых файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим S(L, R) подпоследовательность, состоящую из идущих подряд элементов, входящих в S, начиная с элемента с номером L и заканчивая элементом с номером R.

Требуется найти такие значения номеров элементов L, M, R, где
0 < L < M < R – 1 (т.е. между элементами с номерами M и R есть ещё как минимум один элемент), чтобы разность суммы элементов подпоследовательности S(M + 1, R) и суммы элементов подпоследовательности S(L, M) была максимальна.

В ответе укажите максимальное значение разности подобных сумм.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

7

20

4

–2

13

–1

2

–10

При таких входных данных L = 2, M = 3, R = 6. Искомая максимальная разность равна (13 + (–1) + 2) – (4 + (–2)) = 12. Подпоследовательность «–2 13 –1» разбить на две подпоследовательности требуемого вида невозможно.

Ответом является число 12.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий разность для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 519CA0

22.10.2024
Задание выполняется с использованием прилагаемых файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим S(L, R) подпоследовательность, состоящую из идущих подряд элементов, входящих в S, начиная с элемента с номером L и заканчивая элементом с номером R.

Требуется найти такие значения номеров элементов L, M, R, где
0 < L < M < R – 1 (т.е. между элементами с номерами M и R есть ещё как минимум один элемент), чтобы разность суммы элементов подпоследовательности S(L, M) и суммы элементов подпоследовательности S(M + 1, R) была максимальна.

В ответе укажите максимальное значение разности подобных сумм.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

7

–20

3

–1

8

4

–2

10

При таких входных данных L = 2, M = 4, R = 6. Искомая максимальная разность равна (3 + (–1) + 8) – (4 + (–2)) = 8. Подпоследовательность «8 4 –2» разбить на две подпоследовательности требуемого вида невозможно.

Ответом является число 8.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий разность для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: BDD715

22.10.2024
Задание выполняется с использованием прилагаемых файлов.

Для участников велогонки на каждом километре кольцевой трассы с двусторонним движением установлены пункты питания. Длина кольцевой трассы равна N километров. Нулевой и N-й километры трассы находятся в одной точке. Известно количество комплектов питания в каждом из пунктов на трассе. В каждый пункт комплекты питания доставляет отдельный электрокар. Стоимость доставки питания вычисляется как произведение количества комплектов питания на расстояние от мобильного цеха их подготовки до пункта питания спортсменов на трассе. Мобильный цех подготовки комплектов расположен в одном из пунктов питания на трассе таким образом, что общая стоимость доставки из цеха во все пункты минимальна.

Определите минимальную суммарную стоимость доставки питания для спортсменов из цеха его подготовки в пункты питания на трассе.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов питания на кольцевой трассе. В каждой из следующих
N строк находится число – количество комплектов питания на пункте (все числа натуральные, количество комплектов питания на каждом пункте не превышает 1000). Числа указаны в порядке расположения пунктов питания спортсменов на трассе, начиная
с первого километра.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

6

8

20

5

13

7

19

При таких исходных данных, если пункты питания установлены на каждом километре трассы, необходимо открыть мобильный цех подготовки комплектов питания для спортсменов в пункте 6.
В этом случае сумма транспортных затрат составит:

1 ∙ 7 + 0 ∙ 19 + 1 ∙ 8 + 2 ∙ 20 + 3 ∙ 5 + 2 ∙ 13.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 69BBBF

22.10.2024

Задание выполняется с использованием прилагаемых
файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим Si, Sj, Sk три элемента последовательности S, где i < j < k.

Определите в последовательности S три таких числа Si, Sj, Sk, что Si > Sj, Sk > Sj и значение выражения (Si – Sj) + (Sk – Sj) максимально. В ответе укажите найденное максимальное значение выражения (Si – Sj) + (Sk – Sj). Гарантируется, что в последовательности есть три числа Si, Sj, Sk, удовлетворяющие условию задачи.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

9

6

9

7

5

8

6

10

–5

–6

При таких входных данных искомую максимальную сумму разностей образуют второй, четвёртый и седьмой элементы данной последовательности. Значение этой суммы разностей равно (9 – 5) + (10 – 5) = 9. Для седьмого, восьмого и девятого элементов последовательности искомая величина равна 14, но девятый элемент меньше восьмого, что не удовлетворяет условию задачи. Ответом является число 9.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий искомую величину для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 38414E

22.10.2024

Задание выполняется с использованием прилагаемых
файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим S(L, R) подпоследовательность, состоящую из идущих подряд элементов, входящих в S, начиная
с элемента с номером L и заканчивая элементом с номером R включительно.

Требуется найти такую подпоследовательность S(L, R) максимальной длины, что сумма её элементов положительна
и чётна. Гарантируется, что хотя бы одна подпоследовательность требуемого вида существует.

В ответе укажите длину искомой подпоследовательности.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000. В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

6

–20

–3

8

–4

5

–10

При таких входных данных L = 2, R = 5. Сумма подпоследовательности равна ((–3) + 8 + (–4) + 5) = 6. Ответом является длина этой подпоследовательности, равная 4.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 952F46

22.10.2024

Задание выполняется с использованием прилагаемых
файлов.

Пусть S – последовательность из N целых чисел, пронумерованных подряд начиная с 1. Обозначим Si, Sj, Sk три элемента последовательности S, где i < j < k.

Определите в последовательности S три таких числа Si, Sj, Sk, что Si < Sj, Sk < Sj и значение выражения (Sj – Si) + (Sj – Sk) максимально. В ответе укажите найденное максимальное значение выражения (Sj – Si) + (Sj – Sk). Гарантируется, что в последовательности есть три числа Si, Sj, Sk, удовлетворяющие условию задачи.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (5 ≤ N ≤ 10 000 000) – количество целых чисел. Каждая из следующих N строк содержит одно целое число, значение которого по модулю не превышает 1000.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

9

30

3

7

8

2

6

1

20

21

При таких входных данных искомую максимальную сумму разностей образуют второй, четвёртый и седьмой элементы данной последовательности. Значение этой суммы разностей равно (8 – 3) + (8 – 1) = 12. Для седьмого, восьмого и девятого элементов последовательности искомая величина равна 18, но девятый элемент больше восьмого, что не удовлетворяет условию задачи. Ответом является число 12.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: A6A247

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность натуральных чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин., а произведение этих трёх чисел было максимально возможным. Запишите в ответе найденное произведение.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно натуральное число, не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

5

7

3

1

3

9

При таких исходных данных искомая величина равна 135 – это произведение значений, зафиксированных на первой, третьей и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий произведение для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: EF3033

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность целых чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин., а сумма этих трёх чисел была максимально возможной. Запишите в ответе найденную сумму.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно целое число, по модулю не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

150

–150

20

–200

–300

0

При таких исходных данных искомая величина равна 170 – это сумма значений, зафиксированных на первой, третьей и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: DD9960

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность натуральных чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин.,
а произведение этих трёх чисел было максимально возможным. Запишите в ответе найденное произведение.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно натуральное число, не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

5

7

3

1

3

9

При таких исходных данных искомая величина равна 135 – это произведение значений, зафиксированных на первой, третьей
и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий произведение для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 522BD9

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность натуральных чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин.,
а произведение этих трёх чисел было максимально возможным. Запишите в ответе найденное произведение.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно натуральное число, не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

5

7

3

1

3

9

При таких исходных данных искомая величина равна 135 – это произведение значений, зафиксированных на первой, третьей
и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий произведение для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: F13E1D

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность целых чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин., а сумма этих трёх чисел была максимально возможной. Запишите в ответе найденную сумму.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно целое число, по модулю не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

150

–150

20

–200

–300

0

При таких исходных данных искомая величина равна 170 – это сумма значений, зафиксированных на первой, третьей и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: E8867C

16.04.2024

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность целых чисел – показания прибора. В течение N мин. (N – натуральное число) прибор ежеминутно регистрирует значение силы тока (в условных единицах) в электрической сети и передаёт его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин., а сумма этих трёх чисел была минимально возможной. Запишите в ответе найденную сумму.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих
N строк находится одно натуральное число, не превышающее 10 000 000, которое обозначает значение силы тока в соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

2

6

15

14

20

23

21

10

При таких исходных данных искомая величина равна 45 – это сумма значений, зафиксированных на первой, третьей и шестой минутах измерений.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: C2D70A

28.05.2023

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят
в специальных транспортировочных контейнерах вместимостью не более 44 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.

Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) –– количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6

1 100

2 200

5 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 * 2 + 3 * 1 + 5 * 1 + 6 * 1 + 8 * 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 327EB5

04.05.2023

Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность целых неотрицательных чисел – показания прибора, полученные
с интервалом в 1 мин. в течение T мин. (T – целое число). Прибор измеряет количество атмосферных осадков, полученное регистратором за минуту, предшествующую моменту регистрации,
и передаёт это значение в условных единицах измерения.

Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее K мин., а их сумма была максимально возможной. Укажите найденное суммарное количество осадков.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – количество минут, которое должно пройти между двумя передачами показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000,
N > K). В каждой из следующих N строк находится одно целое неотрицательное число, не превышающее 100 000, обозначающее количество осадков за соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

3

5

15

10

200

0

30

При таких исходных данных максимально возможное суммарное количество осадков равно 45 – это сумма осадков, выпавших на первой и пятой минутах.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 5ABB91

04.05.2023
Задание выполняется с использованием прилагаемых
файлов.

По каналу связи передаётся последовательность целых неотрицательных чисел – показания прибора, полученные
с интервалом в 1 мин. в течение T мин. (T – целое число). Прибор измеряет количество атмосферных осадков, полученное регистратором за минуту, предшествующую моменту регистрации,
и передаёт это значение в условных единицах измерения.

Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее K мин., а их сумма была максимально возможной. Укажите найденное суммарное количество осадков.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит натуральное число K – количество минут, которое должно пройти между двумя передачами показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000,
N > K). В каждой из следующих N строк находится одно целое неотрицательное число, не превышающее 100 000, обозначающее количество осадков за соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

3

5

15

10

200

0

30

При таких исходных данных максимально возможное суммарное количество осадков равно 45 – это сумма осадков, выпавших на первой и пятой минутах.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 6E6BDD

04.05.2023
Задание выполняется с использованием прилагаемых файлов.

По каналу связи передаётся последовательность целых неотрицательных чисел – показания прибора, полученные с интервалом в 1 мин. в течение T мин. (T – целое число). Прибор измеряет количество атмосферных осадков, полученное регистратором за минуту, предшествующую моменту регистрации, и передаёт это значение в условных единицах измерения.

Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее K мин., а их сумма была максимально возможной. Укажите найденное суммарное количество осадков.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых в первой строке содержит натуральное число K – количество минут, которое должно пройти между двумя передачами показаний, а во второй – количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих N строк находится одно целое неотрицательное число, не превышающее 100 000, обозначающее количество осадков за соответствующую минуту.

Запишите в ответе два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

3

5

15

10

200

0

30

При таких исходных данных максимально возможное суммарное количество осадков равно 45 – это сумма осадков, выпавших на первой и пятой минутах.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 13F17F

 28.03.2023

Задание выполняется с использованием прилагаемых
к заданию файлов.

Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не делилась на k = 109 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно.

Программа должна напечатать одно число –– максимально возможную сумму, соответствующую условиям задачи.

Входные данные.

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество троек N (1 ≤ N ≤ 1 000 000). Каждая из следующих N строк содержит три натуральных числа, не превышающих 12 000.

Пример организации исходных данных во входном файле:

6

1 3 7

5 12 6

6 9 11

5 4 8

3 5 4

1 1 1

Для указанных входных данных, в случае, если k = 5, значением искомой суммы является число 44.

В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 549B82

28.03.2023
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго, i и j –
–
порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 114. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.

Пример входных данных:

6

60

128

61

100

282

53

Пример выходных данных для приведённого выше примера входных данных:

128 100

Пояснение. Из шести заданных чисел можно составить 3 пары, сумма элементов которых делится на m=114: 60+282, 128+100, 61+53. Во второй
и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.

Требуется написать эффективную по времени и памяти программу для решения описанной задачи.

Программа считается эффективной по времени, если при одновременном увеличении количества элементов последовательности n и параметра m
в k раз, время работы программы увеличивается не более чем в k раз. Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 4 килобайта и не увеличивается с ростом n.

Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, –
–
4 балла.

Максимальная оценка за правильную программу, возможно, неэффективную по памяти или время выполнения которой существенно зависит от
величины m, –
–
3 балла.

Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, –
–
2 балла.

Вы можете сдать одну программу или две программы решения задачи (например, одна из программ может быть менее эффективна). Если Вы сдадите две программы, то каждая из них будет оцениваться независимо от другой, итоговой станет большая из двух оценок.

Перед текстом программы обязательно кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.

Файл с данными >>

Номер: F6FBF6

28.03.2023
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго, i и j –
–
порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 117. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.

Пример входных данных:

6

60

134

61

100

291

56

Пример выходных данных для приведённого выше примера входных данных:

134 100

Пояснение. Из шести заданных чисел можно составить 3 пары, сумма элементов которых делится на m=117: 60+291, 134+100, 61+56. Во второй
и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.

Требуется написать эффективную по времени и памяти программу для решения описанной задачи.

Программа считается эффективной по времени, если при одновременном увеличении количества элементов последовательности n и параметра m
в k раз, время работы программы увеличивается не более чем в k раз. Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 4 килобайта и не увеличивается с ростом n.

Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, –
–
4 балла.

Максимальная оценка за правильную программу, возможно, неэффективную по памяти или время выполнения которой существенно зависит от
величины m, –
–
3 балла.

Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, –
–
2 балла.

Вы можете сдать одну программу или две программы решения задачи (например, одна из программ может быть менее эффективна). Если Вы сдадите две программы, то каждая из них будет оцениваться независимо от другой, итоговой станет боьшая из двух оценок.

Перед текстом программы обязательно кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.

Файл с данными >>

Номер: ECAE49

28.03.2023
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго, i и j –
–
порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 107. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.

Пример входных данных:

6

60

114

61

100

261

46

Пример выходных данных для приведённого выше примера входных данных:

114 100

Пояснение. Из шести заданных чисел можно составить 3 пары, сумма элементов которых делится на 107: 60+261, 114+100, 61+46. Во второй
и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.

Требуется написать эффективную по времени и памяти программу для решения описанной задачи.

Программа считается эффективной по времени, если при одновременном увеличении количества элементов последовательности n и параметра m
в k раз, время работы программы увеличивается не более чем в k раз. Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 4 килобайта и не увеличивается с ростом n.

Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, –
–
4 балла.

Максимальная оценка за правильную программу, возможно, неэффективную по памяти или время выполнения которой существенно зависит от
величины m, –
–
3 балла.

Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, –
–
2 балла.

Вы можете сдать одну программу или две программы решения задачи (например, одна из программ может быть менее эффективна). Если Вы сдадите две программы, то каждая из них будет оцениваться независимо от другой, итоговой станет бо�
�
ьшая из двух оценок.

Перед текстом программы обязательно кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.

Файл с данными >>

Номер: AAEE69

28.03.2023
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго, i и j –
–
порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 109. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.

Пример входных данных:

6

60

118

61

100

267

48

Пример выходных данных для приведённого выше примера входных данных:

118 100

Пояснение. Из шести заданных чисел можно составить 3 пары, сумма элементов которых делится на m=109: 60+267, 118+100, 61+48. Во второй
и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.

Требуется написать эффективную по времени и памяти программу для решения описанной задачи.

Программа считается эффективной по времени, если при одновременном увеличении количества элементов последовательности n и параметра m
в k раз, время работы программы увеличивается не более чем в k раз. Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 4 килобайта и не увеличивается с ростом n.

Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, –
–
4 балла.

Максимальная оценка за правильную программу, возможно, неэффективную по памяти или время выполнения которой существенно зависит от
величины m, –
–
3 балла.

Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, –
–
2 балла.

Вы можете сдать одну программу или две программы решения задачи (например, одна из программ может быть менее эффективна). Если Вы сдадите две программы, то каждая из них будет оцениваться независимо от другой, итоговой станет бо�
�
ьшая из двух оценок.

Перед текстом программы обязательно кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.

Файл с данными >>

Номер: DBA49E

28.03.2023
На вход программы поступает последовательность из n целых положительных чисел. Рассматриваются все пары элементов последовательности ai и aj, такие что i < j и ai > aj (первый элемент пары больше второго, i и j –
–
порядковые номера чисел в последовательности входных данных). Среди пар, удовлетворяющих этому условию, необходимо найти и напечатать пару с максимальной суммой элементов, которая делится на m = 111. Если среди найденных пар максимальную сумму имеют несколько, то можно напечатать любую из них.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел n (2 ≤ n ≤ 12 000). В каждой из последующих n строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать элементы искомой пары. Если таких пар несколько, можно вывести любую из них. Гарантируется, что хотя бы одна такая пара в последовательности есть.

Пример входных данных:

6

60

122

61

100

273

50

Пример выходных данных для приведённого выше примера входных данных:

122 100

Пояснение. Из шести заданных чисел можно составить 3 пары, сумма элементов которых делится на m=111: 60+273, 122+100, 61+50. Во второй
и третьей из этих пар первый элемент больше второго, но во второй паре сумма больше.

Требуется написать эффективную по времени и памяти программу для решения описанной задачи.

Программа считается эффективной по времени, если при одновременном увеличении количества элементов последовательности n и параметра m
в k раз, время работы программы увеличивается не более чем в k раз. Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 4 килобайта и не увеличивается с ростом n.

Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, –
–
4 балла.

Максимальная оценка за правильную программу, возможно, неэффективную по памяти или время выполнения которой существенно зависит от
величины m, –
–
3 балла.

Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, –
–
2 балла.

Вы можете сдать одну программу или две программы решения задачи (например, одна из программ может быть менее эффективна). Если Вы сдадите две программы, то каждая из них будет оцениваться независимо от другой, итоговой станет боьшая из двух оценок.

Перед текстом программы обязательно кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.

Файл с данными >>

Номер: 357E1D

28.03.2023

Задание выполняется с использованием прилагаемых к заданию файлов.

Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не делилась на k = 109 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно.

Программа должна напечатать одно число –– максимально возможную сумму, соответствующую условиям задачи.

Входные данные.

Даны два входных файла (файл A и файл B), каждый из которых содержит
в первой строке количество троек N (1 ≤ N ≤ 1 000 000). Каждая из следующих N строк содержит три натуральных числа, не превышающих
12 000.

Пример организации исходных данных во входном файле:

6

1 3 7

5 12 6

6 9 11

5 4 8

3 5 4

1 1 1

Для указанных входных данных, в случае, если k = 5, значением искомой суммы является число 44.

В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Ответ:

Файл с данными >>

Номер: 028200

20.01.2023

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят
в специальных транспортировочных контейнерах вместимостью не более 40 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.

Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров
с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (1 ≤ N ≤ 10 000 000) –– количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6

1 100

2 200

5 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ** 2 + 3 ** 1 + 5 ** 1 + 6 ** 1 + 8 ** 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 494D7D

20.01.2023

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят
в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.

Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров
с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (1 ≤ N ≤ 10 000 000) –– количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6

1 100

2 200

5 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ** 2 + 3 ** 1 + 5 ** 1 + 6 ** 1 + 8 ** 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 0348F9

20.01.2023

Задание выполняется с использованием прилагаемых
файлов.

На каждом 3-м километре кольцевой автодороги с двусторонним движением установлены контейнеры для мусора. Длина кольцевой автодороги равна 3N километров. Нулевой километр и 3N-й километр автодороги находятся в одной точке. Известно количество мусора, которое накапливается ежедневно в каждом из контейнеров. Из каждого пункта мусор вывозит отдельный мусоровоз. Стоимость доставки мусора вычисляется как произведение количества мусора на расстояние от пункта до центра переработки. Центр переработки отходов расположен в одном из пунктов сбора мусора таким образом, что общая стоимость доставки мусора из всех пунктов минимальна.

Определите минимальную суммарную стоимость доставки мусора из всех пунктов сбора в центр переработки отходов.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) –– количество пунктов сбора мусора на кольцевой автодороге. В каждой из следующих N строк находится число –– количество мусора в контейнере (все числа натуральные, количество мусора в каждом пункте не превышает 1000). Числа указаны в порядке расположения контейнеров на автомагистрали, начиная с первого километра.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6

8

20

5

13

7

19

При таких исходных данных, если контейнеры установлены на каждом километре автодороги, необходимо открыть центр переработки в пункте 6. В этом случае сумма транспортных затрат составит:

1 ** 7 + 0 ** 19 + 1 ** 8 + 2 ** 20 + 3 ** 5 + 2 ** 13.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: BED6E1

20.01.2023

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят
в специальных транспортировочных контейнерах вместимостью не более 46 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.

Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров
с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых
в первой строке содержит число N (1 ≤ N ≤ 10 000 000) –– количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6

1 100

2 200

5 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ** 2 + 3 ** 1 + 5 ** 1 + 6 ** 1 + 8 ** 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 2E1A79

20.01.2023

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов.

Компания планирует открыть лабораторию в одном из имеющихся пунктов. Перевозить биоматериалы разрешается на расстояние не более M. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 12 штук. Каждый транспортировочный контейнер используется для доставки пробирок только из одного пункта приёма, при этом из каждого пункта приёма может быть доставлено не более одного контейнера
с неполной загрузкой. Пункт для лаборатории выбрали таким образом, чтобы количество доставляемых туда контейнеров
с пробирками было максимальным. Определите необходимое количество контейнеров для доставки пробирок в эту лабораторию.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит два числа N и M (1 ≤ N ≤ 10 000 000, 1 ≤ M ≤ 10 000 000) –– количество пунктов приёма биоматериалов
и максимальное расстояние, на которое разрешено перевозить биоматериалы. В каждой из следующих N строк находятся два числа: номер пункта и количество пробирок, принимаемых на этом пункте за сутки (все числа натуральные, количество пробирок
в каждом пункте не превышает 1000). Пункты перечислены
в порядке их расположения вдоль автомагистрали, считая от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем –– для файла B.

Типовой пример организации данных во входном файле

6 3

1 100

3 200

6 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 3. В этом случае количество контейнеров в ней составит: 2 + 3 + 1.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 12C4CF

25.10.2022

Задание выполняется с использованием прилагаемых
файлов.

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов.

Компания планирует открыть лабораторию в одном из имеющихся пунктов. Перевозить биоматериалы разрешается на расстояние не более M. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 30 штук. Каждый транспортировочный контейнер используется для доставки пробирок только из одного пункта приёма, при этом из каждого пункта приёма может быть доставлено не более одного контейнера с неполной загрузкой. Пункт для лаборатории выбрали таким образом, чтобы количество доставляемых туда контейнеров
с пробирками было максимальным. Определите необходимое количество контейнеров для доставки пробирок в эту лабораторию.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых
в первой строке содержит два числа N и M (1 ≤ N ≤ 10 000 000, 1 ≤ M ≤ 10 000 000) –– количество пунктов приёма биоматериалов и максимальное расстояние, на которое разрешено перевозить биоматериалы. В каждой из следующих N строк находятся два числа: номер пункта и количество пробирок, принимаемых на этом пункте за сутки (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль автомагистрали, считая от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Типовой пример организации данных во входном файле

6 3

1 100

3 200

6 4

7 3

8 2

10 195

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 3. В этом случае количество контейнеров в ней составит: 2 + 3 + 1.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 30C294

 06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 97. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

93

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 48B0C6

06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 61. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

93

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 1D695E

06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 71. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

93

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 072D53

06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 79. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

93

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 9F4BD8

06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

93

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: F291D4

06.03.2022

Задание выполняется с использованием прилагаемых
к заданию файлов.

Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 53. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько,
в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число,
не превышающее 10 000.

Пример организации исходных данных во входном файле:

7

1

3

4

43

8

5

95

Для указанных входных данных при k = 50 искомая длина последовательности равна 2.

В ответе укажите два числа: значение длины искомой подпоследовательности сначала для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Файл с данными >>

Номер: 377100

06.08.2021
По каналу связи передаётся последовательность положительных целых чисел, все числа не превышают 1000. Количество чисел известно, но может быть очень велико. Затем передаётся контрольное значение последовательности –
–
наименьшее число R, удовлетворяющее следующим условиям:

1) R является произведением двух различных переданных элементов последовательности («различные» означает, что не рассматриваются квадраты переданных чисел, произведения различных элементов последовательности, равных по величине, допускаются);

2) R кратно 14.

Если такого числа R нет, то контрольное значение полагается равным 0.

В результате помех при передаче как сами числа, так и контрольное значение могут быть искажены.

Напишите эффективную, в том числе по используемой памяти, программу (укажите используемую версию языка программирования, например, Borland Pascal 7.0), которая будет проверять правильность контрольного значения. Программа должна напечатать отчёт по следующей форме:

Вычисленное контрольное значение: …

Контроль пройден (или –
–
Контроль не пройден)

Перед текстом программы кратко опишите используемый Вами алгоритм решения.

На вход программе в первой строке подаётся количество чисел N;
в программе можно считать, что 2 ≤ N ≤ 10 000. В каждой из последующих
N строк записано одно натуральное число, не превышающее 1000.
В последней строке записано контрольное значение –
–
натуральное число,
не превышающее 1 000 000.

Пример входных данных:

6

70

14

3

7

4

300

28

Пример выходных данных для приведённого выше примера входных данных:

Вычисленное контрольное значение: 28

Контроль пройден

Файл с данными >>

Номер: C4454B