Задания 27 ЕГЭ из разных источников
ЕГЭ 2026. Статград. 16.12.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Диаметром кластера назовём максимальное расстояние между двумя точками в кластере. Для каждого кластера гарантируется, что диаметр образует единственная пара точек. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле А хранятся данные о звёздах двух кластеров, где \(H = 3,\) \(W = 4\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле Б хранятся данные о звёздах трёх кластеров, где \(H = 6,\) \(W = 5\) для каждого кластера. Известно, что количество звёзд не превышает \(10000.\) Структура хранения информации о звёздах в файле Б аналогична файлу А.
Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла А найдите пары точек, которые образуют диаметр каждого кластера. Затем вычислите два числа: \(P_x\) – минимальную из сумм абсцисс этих точек для всех кластеров и \(P_y\) – минимальную из сумм ординат этих точек для всех кластеров. Для файла Б найдите два числа: \(Q_1\) – диаметр кластера с минимальным количеством точек и \(Q_2\) – максимальное расстояние от точки, образующей диаметр одного кластера, до точки, образующей диаметр другого кластера.
Гарантируется, что во всех кластерах количество точек различно.
В ответе запишите четыре числа: в первой строке – сначала целую часть абсолютного значения произведения \(P_x \times 10000,\) затем целую часть абсолютного значения произведения \(P_y \times 10000;\) во второй строке – сначала целую часть произведения \(Q_1\times 10000,\) затем целую часть произведения \(Q_2 \times 10000.\)
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.
Решение:
Python
from math import dist
base = ''
files = ['27A.txt', '27B.txt']
eps = 1
for t in (0, 1):
data = [tuple(map(float, line.split())) for line in open(base + files[t])]
clusters = []
while data:
clusters.append([data.pop(0)])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
clusters = [cl for cl in clusters if len(cl) > 1]
clusters.sort(key=lambda cl: len(cl))
#print(len(clusters), [len(cl) for cl in clusters])
diameters = []
for cl in clusters:
dmax = 0
pair = None
for i in range(len(cl) - 1):
for j in range(i + 1, len(cl)):
d = dist(cl[i], cl[j])
if d > dmax:
dmax = d
pair = (cl[i], cl[j])
diameters.append((pair, dmax))
#print(diameters)
if t == 0:
px = min(pt[0][0] + pt[1][0] for pt, d in diameters)
py = min(pt[0][1] + pt[1][1] for pt, d in diameters)
print(int(px * 10000), int(py * 10000))
else:
q1 = diameters[0][1]
q2 = 0
for i in range(len(diameters) - 1):
for j in range(i + 1, len(diameters)):
d1 = dist(diameters[i][0][0], diameters[j][0][0])
d2 = dist(diameters[i][0][0], diameters[j][0][1])
d3 = dist(diameters[i][0][1], diameters[j][0][0])
d4 = dist(diameters[i][0][1], diameters[j][0][1])
q2 = max(q2, d1, d2, d3, d4)
print(int(q1 * 10_000), int(q2 * 10_000))
Ответ:
\(145015 \,\, 313020\)
\(29254 \,\, 488624\)
ЕГЭ 2026. ЕГКР. 13.12.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2) \) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} .$$ В файле А хранятся данные о звёздах двух кластеров, где \(H=6{,}5,\) \(W=4{,}5\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле B хранятся данные о звёздах трёх кластеров, где \(H=6{,}5,\) \(W=5\) для каждого кластера. Известно, что количество звёзд не превышает \(1000.\) Структура хранения информации о звездах в файле B аналогична файлу A.
Для файла A определите координаты центра каждого кластера, затем найдите два числа: \(P_1\) — минимальное расстояние от точки с координатами \((1{,}0; \, 1{,}0)\) до центра кластера, и \(P_2\) — максимальное расстояние от этой же точки до центра кластера.
Для файла B определите координаты центра каждого кластера, затем найдите два числа: \(Q_1\) — в кластере с наибольшим количеством точек число таких точек, которые находятся на расстоянии не более \(1{,}2\) от центра кластера, и \(Q_2\) — в кластере с наибольшим количеством точек число таких точек, которые находятся на расстоянии не более \(0{,}75\) от центра кластера.
Гарантируется, что во всех кластерах количество точек различно.
В ответе запишите четыре числа: в первой строке — сначала целую часть произведения \(P_1 \times 10~000,\) затем целую часть произведения \(P_2 \times 10~000;\) во второй строке — сначала \(Q_1 ,\) затем \(Q_2 .\)
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Решение:
Python
from math import dist
base = ''
files = ['27_A.txt', '27_B.txt']
eps = 1
for t in (0, 1):
data = [tuple(map(float, line.replace(',', '.').split())) for line in open(base + files[t])]
clusters = []
while data:
clusters.append([data.pop(0)])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
clusters.sort(key=lambda cl: len(cl))
#print(len(clusters), [len(cl) for cl in clusters])
centers = []
for cl in clusters:
dmin = float('inf')
c = cl[0]
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
if t == 0:
p12 = [dist(p, (1.0, 1.)) for p in centers]
print(int(min(p12) * 10_000), int(max(p12) * 10_000))
else:
q12 = (len([p for p in clusters[-1] if dist(p, centers[-1]) < 1.2]),
len([p for p in clusters[-1] if dist(p, centers[-1]) < 0.75]))
print(q12[0], q12[1])
Ответ:
\(58605 \,\, 128643\)
\(358 \,\, 203\)
Задание 27. Информатика. ЕГЭ 2026. Статград. 23.10.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть антицентром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера максимальна. Для каждого кластера гарантируется единственность его антицентра. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B (x_2, \, y_2)\) на плоскости вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ В файле А хранятся координаты точек двух кластеров, где \(H=8,\) \(W=4\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество точек не превышает \(1000.\)
В файле Б хранятся координаты точек трёх кластеров, где \(H=6,\) \(W=7\) для каждого кластера. Известно, что количество точек не превышает \(10~000.\) Структура хранения информации о звёздах в файле Б аналогична структуре в файле А. Известно, что в файле Б имеются координаты ровно трёх «лишних» точек, представляющих аномалии, которые возникли в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла А определите координаты антицентра каждого кластера, затем вычислите два числа: \(P_1\) – сумма абсциссы и ординаты антицентра кластера с наименьшим количеством точек, и \(P_2\) – сумма абсциссы и ординаты антицентра кластера с наибольшим количеством точек. Гарантируется, что во всех кластерах количество точек различно.
Для файла Б определите координаты антицентра каждого кластера, затем вычислите два числа: \(Q_x\) – абсциссу наиболее отдалённого антицентра кластера от начала координат, и \(Q_y\) – ординату ближайшего антицентра кластера к началу координат.
В ответе запишите четыре числа: в первой строке – сначала целую часть абсолютного значения произведения \(P_1 \times 10~000,\) затем целую часть абсолютного значения произведения \(P_2 \times 10~000;\) во второй строке – сначала целую часть абсолютного значения произведения \(Q_x \times 10~000,\) затем целую часть абсолютного значения произведения \(Q_y \times 10 000.\)
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.

Решение:
Python
from math import dist
files = ['27_A.txt', '27_B.txt']
path = ''
eps = 1
for t in (0, 1):
data = [tuple(map(float, line.replace(',','.').split())) for line in open(path + files[t])]
clusters = []
while data:
clusters.append([data.pop(0)])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
clusters = [cl for cl in clusters if len(cl) > 1]
#print(len(clusters), [len(c) for c in clusters])
if t == 0:
clusters.sort(key=lambda c: len(c))
ac = []
for cl in clusters:
dmax = 0
apt = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d > dmax:
dmax = d
apt = p
ac.append(apt)
if t == 0:
P1 = sum(ac[0])
P2 = sum(ac[1])
print(int(abs(P1)*10_000), int(abs(P2)*10_000))
else:
ac.sort(key=lambda a: dist(a, (0, 0)))
print(int(abs(ac[-1][0]) * 10_000), int(abs(ac[0][1]) * 10_000))
Ответ:
\(1126711 \,\, 1517181\)
\(213883 \,\, 264132\)
Основная волна. Пересдача. 03.07.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле A хранятся данные о звёздах двух кластеров, где \(H=6,\) \(W=4{,}5\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле B хранятся данные о звёздах трёх кластеров, где \(H=6,\) \(W = 5\) для каждого кластера. Известно, что количество звёзд не превышает \(1000.\) Структура хранения информации о звездах в файле B аналогична файлу A.
Известно, что в файле B имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла A определите координаты центра каждого кластера, затем найдите два числа: \(P_x\) — сумму абсцисс центров кластеров, и \(P_y\) — сумму ординат центров кластеров. Для файла B найдите два числа: \(Q_1\) — минимальное расстояние между точками, принадлежащими двум различным кластерам, и \(Q_2\) — максимальное расстояние между точками, принадлежащими двум различным кластерам.
В ответе запишите четыре числа: в первой строке — сначала абсолютную величину целой части произведения \(P_x \times 10~000,\) затем абсолютную величину целой части произведения \(P_y \times 10~000;\) во второй строке — сначала целую часть произведения \(Q_1 \times 10~000,\) затем целую часть произведения \(Q_2 \times 10~000.\)
Возможные данные одного из файлов иллюстрированы графиком. Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
Python
from math import dist
base = ''
files = ['27A.txt', '27B.txt']
eps = 1
for t in [0, 1]:
data = [tuple(map(float, line.replace(',', '.').split())) for line in open(base + files[t])]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
clusters = [cl for cl in clusters if len(cl) > 1]
#print(len(clusters), [len(cl) for cl in clusters])
if t == 0:
centers = []
for cl in clusters:
dmin = 10 ** 100
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
c = p
dmin = d
centers.append(c)
px = sum(x for x, y in centers)
py = sum(y for x, y in centers)
print(int(abs(px * 10_000)), int(abs(py * 10_000)))
else:
q1 = 10**100
q2 = 0
for i in range(2):
for j in range(i+1, 3):
q1 = min(q1, min(dist(p1, p2) for p1 in clusters[i] for p2 in clusters[j]))
q2 = max(q2, max(dist(p1, p2) for p1 in clusters[i] for p2 in clusters[j]))
print(int(q1 * 10_000), int(q2 * 10_000))
Ответ:
\(92256 \,\, 258611\)
\(33863 \,\, 170816\)
Основная волна. Резерв. 23.06.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ Аномалиями назовём звёзды, находящиеся на расстоянии более пяти условных единиц от звёзд кластеров. При расчётах аномалии учитывать не нужно.
В файле A хранятся данные о звёздах двух кластеров, где \(H=16,\) \(W=16\) для каждого кластера. В каждой строке записана информация о расположение на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество точек не превышает \(1000.\)
В файле B хранятся данные о звёздах трёх кластеров, где \(H=12,\) \(W=12\) для каждого кластера. Известно, что количество точек не превышает \(10~000.\) Структура хранения информации о звездах в файле B аналогична файлу A. Известно, что в файле B имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла A определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — сумма абсцисс центров кластеров, и \(P_y\) — сумма ординат центров кластеров.
Для файла B определите координаты центра каждого кластера, затем вычислите два числа: \(Q_1\) — минимальное расстояние от центра до начала координат. \(Q_2\) — максимальное расстояние от центра до начала координат.
Гарантируется, что во всех кластерах количество точек различно.
В ответе запишите четыре числа: в первой строке — сначала целую часть абсолютного значения произведения \(P_x \times 10~000,\) затем целую часть абсолютного значения произведения \(P_y \times 10~000;\) во второй строке — сначала целую часть абсолютного значения произведения \(Q_1 \times 10~000,\) затем целую часть абсолютного значения произведения \(Q_2 \times 10~000.\)
Возможные данные одного из файлов иллюстрированы графиком. Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.

Решение:
Python
from math import dist
base = ''
files = ['27A.txt', '27B.txt']
eps = 5
for t in [0, 1]:
data = [tuple(map(float, line.replace(',', '.').split())) for line in open(base + files[t])]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
clusters = [cl for cl in clusters if len(cl) > 1]
#print(len(clusters), [len(cl) for cl in clusters])
centers = []
for cl in clusters:
dmin = 10**100
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
c = p
dmin = d
centers.append(c)
if t == 0:
px = sum(x for x, y in centers)
py = sum(y for x, y in centers)
print(int(abs(px * 10_000)), int(abs(py * 10_000)))
else:
q1 = min(dist(p, (0, 0)) for p in centers)
q2 = max(dist(p, (0, 0)) for p in centers)
print(int(q1 * 10_000), int(q2 * 10_000))
Ответ:
\(404241 \,\, 1013671\)
\(349898 \,\, 471860\)
Основная волна. Резерв. 19.06.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле А хранятся данные о звёздах двух кластеров, где \(H=6,\) \(W=4{,}5\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле В хранятся данные о звёздах трёх кластеров, где \(H=6,\) \(W=5\) для каждого кластера. Известно, что количество звёзд не превышает \(1000.\) Структура хранения информации о звездах в файле В аналогична файлу А.
Известно, что в файле B имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла А определите координаты центра каждого кластера, затем найдите два числа: \(P_x\) — сумму абсцисс центров кластеров, и \(P_y\) — сумму ординат центров кластеров. Для файла B определите координаты центра каждого кластера, затем найдите два числа: \(Q_1\) — минимальное расстояние от центра кластера до начала координат, и \(Q_2\) — максимальное расстояние от центра кластера до начала координат.
В ответе запишите четыре числа: в первой строке — сначала абсолютную величину целой части произведения \(P_x \times 10~000,\) затем абсолютную величину целой части произведения \(P_y \times 10~000;\) во второй строке — сначала целую часть произведения \(Q_1 \times 10~000,\) затем целую часть произведения \(Q_2 \times 10~000.\)
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
Python
from math import dist
base = ''
files = ['27_A_23384.txt', '27_B_23384.txt']
eps = 1.1
for task in (0, 1):
fp = open(base + files[task])
fp.readline()
data = [tuple(map(float, line.replace(',', '.').split())) for line in fp]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(cl) for cl in clusters])
clusters = [cl for cl in clusters if len(cl) > 1]
centers = []
for cl in clusters:
dmin = float('inf')
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
if task == 0:
px = sum(c[0] for c in centers)
py = sum(c[1] for c in centers)
print(abs(int(px * 10000)), abs(int(py * 10000)))
else:
q1 = float('inf')
q2 = 0
orig = (0, 0)
for c in centers:
d = dist(c, orig)
q1 = min(q1, d)
q2 = max(q2, d)
print(abs(int(q1 * 10000)), abs(int(q2 * 10000)))
Ответ:
\(110156 \,\, 196632\)
\(224871 \,\, 273226\)
Задание 27. Информатика. ЕГЭ. Основная волна. 11.06.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле A хранятся координаты точек двух кластеров, где \(H=6\) и \(W = 4{,}5\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Известно, что количество точек не превышает \(1000.\)
В файле B хранятся координаты точек трёх кластеров, где \(H=6,\) \(W=5\) для каждого кластера. Известно, что количество точек не превышает \(10000.\) Структура хранения информации в файле B аналогична в структуре в файле A.
Известно, что в файле B имеются координаты ровно трёх «лишних» точек, являющихся аномалиями, возникшими в результате помех при передаче данных. Эти три точки не относятся ни к одному из кластеров, их учитывать не нужно.
Для файла A определите координаты центра каждого кластера, затем найдите два числа: \(P_x\) — сумму абсцисс центров кластеров и \(P_y\) — сумму ординат центров кластеров.
Для файла B определите координаты центра каждого кластера, затем найдите два числа: \(Q_1\) — минимальное расстояние между центрами различных кластеров и \(Q_2\) — максимальное расстояние между центрами кластеров.
В ответе запишите четыре числа: в первой строке — сначала абсолютную величину целой части произведения \(P_x \times 10~000,\) затем абсолютную величину целой части произведения \(P_y \times 10~000;\) во второй строке — сначала абсолютную величину целой части произведения \(Q_1 \times 10~000,\) затем абсолютную величину целой части произведения \(Q_2 \times 10~000.\)
Возможные данные одного из файлов проиллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
Python
from math import dist
base = ''
files = ['27_A_23284.txt', '27_B_23284.txt']
eps = 1.1
for task in (0, 1):
fp = open(base + files[task])
fp.readline()
data = [tuple(map(float, line.replace(',', '.').split())) for line in fp]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(cl) for cl in clusters])
clusters = [cl for cl in clusters if len(cl) > 1]
centers = []
for cl in clusters:
dmin = float('inf')
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
if task == 0:
px = sum(c[0] for c in centers)
py = sum(c[1] for c in centers)
print(abs(int(px * 10000)), abs(int(py * 10000)))
else:
q1 = float('inf')
q2 = 0
for a in range(2):
for b in range(a+1, 3):
d = dist(centers[a], centers[b])
q1 = min(q1, d)
q2 = max(q2, d)
print(abs(int(q1 * 10000)), abs(int(q2 * 10000)))
Ответ:
\(107002 \,\, 323741\)
\(58778 \,\, 151839\)
Апробация. 14.05.2025-1
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ В файле А хранятся данные о звёздах двух кластеров, где \(H=6, \, W=6\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\) В файле Б хранятся данные о звёздах трёх кластеров, где \(H=9, W=9\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала абсолютное значение целой части произведения \(P_x \times 10~000,\) затем абсолютное значение целой части произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
Python
from math import dist
files = ['27_A.txt', '27_B.txt']
tasks = [0, 1]
eps = [2, 2.5]
for t in tasks:
fd = open(files[t])
fd.readline()
data = [tuple(map(float, line.replace(',', '.').split())) for line in fd]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps[t]]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(c) for c in clusters])
centers = []
for cl in clusters:
dmin = 10**100
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
px = sum(c[0] for c in centers) / len(centers)
py = sum(c[1] for c in centers) / len(centers)
print(abs(int(px * 10_000)), abs(int(py * 10_000)))
Ответ:
\(71942 \,\, 23058\)
\(75268 \,\, 114280\)
ЕГКР. 19.04.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле A хранятся данные о звёздах двух кластеров, где \(H=11, \, W=11\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле B хранятся данные о звёздах трёх кластеров, где \(H=13, \, W=13\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле B аналогична файлу A.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(P_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала абсолютное значение целой части произведения \(P_x \times 10000,\) затем абсолютное значение целой части произведения \(P_y \times 10000\) для файла A, во второй строке — аналогичные данные для файла B. Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
Python
from math import dist
files = ['27_A.txt', '27_B.txt']
for task in (0, 1):
data = []
fd = open(files[task])
fd.readline()
for line in fd:
x, y = map(float, line.replace(',', '.').split())
data.append((x, y))
clusters = []
eps = [2, 2]
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh= [pt for pt in data if dist(p, pt) < eps[task]]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(cl) for cl in clusters])
centers = []
for cl in clusters:
dmin = float('inf')
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
px = sum(c[0] for c in centers) / len(centers)
py = sum(c[1] for c in centers) / len(centers)
print(abs(int(10_000 * px)), abs(int(10_000 * py)))
Ответ:
\(32540 \,\, 13646\)
\(47031 \,\, 25263\)
Досрочный экзамен. 08.04.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ В файле А хранятся данные о звёздах двух кластеров, где \(H=11, \, W=11\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\) В файле Б хранятся данные о звёздах трёх кластеров, где \(H=13, W=13\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала абсолютное значение целой части произведения \(P_x \times 10~000,\) затем абсолютное значение целой части произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.

Решение:
Python
from math import dist
base = ''
files = ['27_A.txt', '27_B.txt']
tasks = [0, 1]
eps = [2, 2.5]
for t in tasks:
data = [tuple(map(float, line.replace(',', '.').split())) for line in open(base + files[t])]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps[t]]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(c) for c in clusters])
centers = []
for cl in clusters:
dmin = 10**100
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
px = sum(c[0] for c in centers) / len(centers)
py = sum(c[1] for c in centers) / len(centers)
print(abs(int(px * 10_000)), abs(int(py * 10_000)))
Ответ:
\(167990 \,\, 73043\)
\(122627 \,\, 29105\)
Апробация. 05.03.2025
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников. Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} .$$ В файле А хранятся данные о звёздах двух кластеров, где \(H=7, \, W=7\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\) В файле Б хранятся данные о звёздах трёх кластеров, где \(H=8, \, W=8\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(P_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(|P_x| \times 10~000,\) затем целую часть произведения \(|P_y| \times 10~000\) для файла А, во второй строке — аналогичные данные для файла Б. Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.

Решение:
Python
from math import dist
base = ''
files = ['27_A.txt', '27_B.txt']
for task in (0, 1):
eps = 1.6
fd = open(base + files[task])
fd.readline()
data = [tuple(map(float, line.replace(',', '.').split())) for line in fd]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(c) for c in clusters])
centers = []
for cl in clusters:
d_min = float('inf')
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < d_min:
d_min = d
c = p
centers.append(c)
px = sum(p[0] for p in centers) / len(centers)
py = sum(p[1] for p in centers) / len(centers)
#print(centers)
print(int(abs(px) * 10_000), int(abs(py) * 10_000))
Ответ:
\(28603 \,\, 10294\)
\(61260 \,\, 11206\)
Шастин. 7.6.2025
(Д. Бахтиев) Во время геофизического исследования был построен план подземного участка местности. На карте, спроецированной на плоскость с декартовой системой координат, отмечены сигналы, полученные от различных объектов. Каждая точка на карте соответствует зарегистрированному сигналу с координатами \(x\) и \(y\) (в условных единицах).
Учёный решил провести кластеризацию этих сигналов, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров). Гарантируется, что такое разбиение существует и единственно.
Будем называть центром кластера такую его точку, сумма расстояний от которой до всех остальных точек кластера минимальна. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ В процессе анализа выяснилось, что среди сигналов присутствуют аномальные шумы. Это — ложные сигналы, вызванные помехами. Известно следующее:
Учёный не знает координат аномалий заранее;
Однако он знает, что:
Аномалии не принадлежат ни одному кластеру
Для любой пары настоящих точек одного кластера можно найти последовательность \(A = P_1, \, P_2, \, \ldots , P_k = B,\) где расстояние между соседними сигналами \(P_i\) и \(P_{i+1}\) меньше \(1.\)
В единичной окрестности любой настоящей точки нет ни одной аномальной;
В любом кластере более \(5\) точек;
Количество аномалий не более \(20\) для каждого из файлов.
Входные данные задаются в двух файлах: файл A и файл B. В каждой строке файлов записана информация о расположении на карте одного сигнала или аномалии: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество записей не превышает \(1000\) для файла A и \(10000\) для файла B.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(P_y\) — среднее арифметическое ординат центров кластеров.
В ответе запишите четыре числа: в первой строке сначала целую часть абсолютно значения произведения \(P_x \times 10000,\) затем целую часть абсолютного значения произведения \(P_y \times 10000\) для файла A, во второй строке — аналогичные данные для файла B.
Решение:
Python
from math import dist
files = ['27A_22624.txt', '27B_22624.txt']
eps = 1
for task in (0, 1):
data = [tuple(map(float, line.split())) for line in open(files[task])]
clusters = []
while data:
clusters.append([data.pop()])
for p in clusters[-1]:
neigh = [pt for pt in data if dist(p, pt) < eps]
clusters[-1] += neigh
for pt in neigh:
data.remove(pt)
#print(len(clusters), [len(cl) for cl in clusters])
clusters = [cl for cl in clusters if len(cl) > 5]
#print(len(clusters), [len(cl) for cl in clusters])
centers = []
for cl in clusters:
dmin = float('inf')
c = None
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
px = sum(c[0] for c in centers) / len(centers)
py = sum(c[1] for c in centers) / len(centers)
print(abs(int(px * 10_000)), abs(int(py * 10_000)))
Ответ:
\(132357 \,\, 174676\)
\(64525 \,\, 71672\)
Задание 27. Информатика. ЕГЭ. Шастин. 5.6.2025
(Л. Шастин) Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть ядром кластера точку этого кластера, сумма расстояний от которой до \(K=10\) самых удалённых от неё и до \(V=5\) самых близких к ней точек этого же кластера минимальна. Для каждого кластера гарантируется единственность его ядра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ В файле A хранятся данные о звёздах двух кластеров, где \(H=6,\) \(W=6\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле B хранятся данные о звёздах трёх кластеров, где \(H=5,\) \(W=5\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле B аналогична файлу A.
Для каждого файла определите координаты ядра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс ядер кластеров, и \(P_y\) — среднее арифметическое ординат ядер кластеров.
В ответе запишите четыре числа: в первой строке сначала целая часть абсолютного значения произведения \(P_x \times 10000,\) затем целая часть абсолютного значения произведения \(P_y \times 10000\) для файла A, во второй строке — аналогичные данные для файла B.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Решение:
...
Ответ:
Шастин. 3.6.2025
(Д. Бахтиев) Учёный наблюдает проекцию звёздного скопления на плоскость с декартовой системой координат. Полученные точки (звёзды) необходимо разбить на \(N\) непересекающихся непустых кластеров. Каждый кластер размещается внутри прямоугольника размером \(H \times W,\) при этом прямоугольники не перекрываются. Стороны прямоугольников не обязаны быть параллельны осям координат. Гарантируется, что такое разбиение единственно для заданных размеров прямоугольников. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ A(x_1, \, y_1) = \sqrt{(x_2 - y_1)^2 + (y_2 - y_1)^2} $$ Центром кластера будем называть точку кластера, сумма расстояний от которой до остальных точек этого кластера минимальна. Антицентром кластера будем называть точку кластера, сумма расстояний от которой до остальных точек этого кластера максимальна.
Входные данные
Файл A: содержит координаты звёзд, расположенных в \(2\) кластерах, размеры кластеров \(H = 5,\) \(W = 4,\) не более \(1000\) точек.
Файл В: содержит координаты звёзд в \(3\) кластерах, размеры кластеров \(H = 4,\) \(W =5,\) не более \(10~000\) точек.
Каждая строка файлов A и B содержит два числа — координаты звезды: сначала по оси \(x,\) затем по оси \(y.\)
Для каждого файла определите координаты центра и антицентра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(S_y\) — среднее арифметическое ординат антицентров кластеров.
В ответе запишите четыре числа: в первой строке сначала целую часть абсолютного значения произведения \(P_x \times 10000,\) затем целую часть абсолютного значения произведения \(S_y \times 10000\) для файла A, во второй строке — аналогичные данные для файла B.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Решение:
...
Ответ:
Шастин. 1.6.2025
(Д. Бахтиев) Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества находятся внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём прямоугольники не пересекаются между собой. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера такую его точку, сумма расстояний от которой до всех остальных точек кластера минимальна, а плотностью кластера — отношение числа звёзд в нём к площади прямоугольника (в у.е.), внутри которого этот кластер находится. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2.}$$ В файле A хранятся данные о звёздах трёх кластеров, где \(H = 4,\) \(W = 4\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле B хранятся данные о звёздах пяти кластеров, где \(H = 4,\) \(W = 4\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звездах в файле В аналогична файлу A.
Для каждого файла определите \(P_s\) — среднее арифметическое плотности всех кластеров, а также \(S_p\) — расстояние между центрами кластеров с наибольшей и наименьшей плотностью.
В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_s \cdot 1000,\) затем целую часть произведения \(S_p \cdot 1000\) для файла A, во второй строке — аналогичные данные для файла В.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию.
Для выполнения задания используйте данные из прилагаемого файла.

Решение:
...
Ответ:
Статград. Профиль. 12.05.2025-1
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров так, что каждая точка попадает ровно в один кластер, при этом ближайшие точки разных кластеров отстоят друг от друга не менее, чем на единичное расстояние.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо в каждом кластере определить экспериментальную точку, вокруг которой расположено максимальное количество других точек на расстоянии не более одной единицы. Если таких точек несколько, то выбирается точка с наибольшей координатой \(X.\) По данному протоколу надо определить минимальное расстояние между найденными экспериментальными точками двух различных кластеров.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе запишите два числа: сначала минимальное расстояние между двумя найденными точками для файла A, затем для файла B. В качестве значения указывайте целую часть от умножения найденного числового значения на \(10~000.\)
Решение:
...
Ответ:
Задание 27. Информатика. ЕГЭ Статград. База. 12.05.2025
Океанограф проводит анализ множества островов по их расположению на карте. Каждый остров задаётся своими координатами \((x, \, y).\) Два острова считаются соседними, если расстояние между ними по формуле Евклида $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 -y_1)^2}$$ строго меньше \(1\) условной единицы. При этом используется следующее определение архипелага и одиночного острова: острова принадлежат одному и тому же архипелагу, если между ними существует цепочка соседних островов (то есть, для любой пары островов \(A\) и \(B\) в архипелаге можно найти последовательность \(A = P_1, \, P_2, \, \ldots , \, P_k = B,\) где расстояние между соседними островами \(P_i\) и \(P_{i+1}\) меньше \(1).\) Архипелагом считается только такое объединение островов, в котором общее количество островов не менее \(20.\) Если какая-либо группа островов, связанная по вышеописанному принципу, содержит менее \(20\) островов, она не рассматривается как архипелаг, а все входящие в неё острова считаются одиночными и не учитываются в дальнейшем анализе.
Антицентроидом архипелага называется такой остров, принадлежащий архипелагу, для которого сумма расстояний до всех остальных островов этого архипелага максимальна. При условии, что одиночные острова при расчётах игнорируются, требуется определить координаты \(M_x\) и \(M_y\) антицентроида с наибольшей суммой расстояний до других островов своего архипелага.
Входные данные задаются в двух файлах: файл A и файл B. В каждой строке файлов содержатся координаты островов: сначала по оси \(x,\) затем по оси \(y.\) Количество островов не превышает \(1000\) для файла A и не превышает \(11~000\) для файла B.
В ответе запишите четыре числа: в первой строке – целые части абсолютных значений произведений \(M_x \times 10~000\) и \(M_y \times 10~000\) для файла A. Во второй строке – целые части абсолютных значений произведений \(M_x \times 10~000\) и \(M_y \times 10~000\) для файла B.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
...
Ответ:
Демо-2025
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд(точек) на графике, лежащий внутри прямоугольника высотой \(H\) и шириной \(W\). Каждая звезда обязательно принадлежит только одному из кластеров.
Истинный центр кластера или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Под расстоянием понимается расстояние Евклида между двумя точками \(A \,(x_1, \, y_1)\) и \(B \, (x_2, \, y_2)\) на плоскости, которое вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ В файле A хранятся данные о звёздах двух кластеров, где \(H=3\), \(W=3\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\). Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле Б хранятся данные о звёздах трёх кластеров, где \(H=3\), \(W=3\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\) , затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
...
Ответ:
Задание 27. Информатика. ЕГЭ. Шастин. 7.05.2025
(Д. Бахтиев) Компания «СвязьЛес» разрабатывает проект по обеспечению бесперебойной связи в двух труднодоступных лесных массивах. Для этого необходимо установить по одному мощному ретранслятору сигнала в каждом из районов, в местах, где их воздействие будет максимальным. Каждый район состоит из множества лесных участков, представленных в виде геопозиций — точек на плоскости (в декартовой системе координат). Известно, что участки можно разделить на группы лесных кварталов, при этом каждая геопозиция квартала удалена от всех точек других кварталов не менее чем на \(R\) условных единиц.
Компания «СвязьЛес» проводит анализ каждой группы (лесного квартала) и выбирает в ней антицентроид — такую геопозицию, сумма расстояний от которой до всех других точек этого квартала максимальна. После этого, опираясь на данные о расположении всех антицентроидов, выбирается финальная точка установки ретранслятора — такая геопозиция, сумма расстояний от которой до всех антицентроидов максимальна. Именно здесь устанавливается ретранслятор.
Расстояние между двумя точками вычисляется по формуле Евклида: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.\)
В файле А хранятся данные обо всех геопозициях первого района. В первой строке записано значение \(R\) для этого района. В каждой из следующих строк записана информация о расположении в районе одной геопозиции: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах, которые представлены вещественными числами. Известно, что количество геопозиций не превышает \(2000.\) В файле Б хранятся данные обо всех геопозициях второго района. В первой строке записано значение \(R\) для этого района. Известно, что количество геопозиций не превышает \(10~000.\) Структура хранения информации в файле Б аналогична файлу А.
Для каждого файла выведите координаты точки установки ретранслятора. В ответе запишите четыре числа: в первой строке сначала целую часть модуля произведения координаты \(x\) этой геопозиции на \(10000,\) затем целую часть модуля произведения координаты \(y\) этой геопозиции на \(10000\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
...
Ответ:
ЕГКР. 21.12.2024
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри прямоугольника со сторонами длиной \(H\) и \(W,\) причём эти прямоугольники между собой не пересекаются. Стороны прямоугольников не обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для заданных размеров прямоугольников.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
В файле А хранятся координаты точек двух кластеров, где \(H = 6, \, W = 6\) для каждого кластера. В каждой строке записана информация о расположении на карте одной точки: сначала координата \(x,\) затем координата \(y.\) Известно, что количество точек не превышает \(1000.\)
В файле Б хранятся координаты точек трёх кластеров, где \(H = 5, \, W = 5\) для каждого кластера. Известно, что количество точек не превышает \(10~000.\) Структура хранения информации в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(P_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала абсолютное значение целой части произведения \(P_x \times 10~000,\) затем абсолютное значение целой части произведения \(P_y \times 10~000\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
...
Ответ:
Статград. 01.04.2025-1
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров) так, что они будут лежать внутри сектора окружности радиуса \(R = 50\) с центральным углом \(20^\circ .\) Гарантируется, что такое разбиение существует и единственно. Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками на плоскости \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} .$$ В файле А хранятся данные о звёздах трёх кластеров, для которых центром окружности является точка \(C (5, \, -9).\) В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x,\) затем координата \(y.\) Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\)
В файле Б хранятся данные о звёздах шести кластеров, для которых центром окружности является точка \(C (-10, \, -7).\) Известно, что количество звёзд не превышает \(10~000.\) Структура хранения информации о звёздах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) — среднее арифметическое абсцисс центров кластеров, и \(P_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(|P_x | \times 10~000,\) затем целую часть произведения \(|P_y | \times 10~000\) для файла А, во второй строке — аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющий отношения к заданию. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
...
Ответ:
Статград. 04.03.2025
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров — кругов радиуса не более \(2\) единиц так, что каждая точка попадает ровно в один кластер. Центром кластера считается та из входящих в него точек, для которой минимально максимальное из расстояний до всех остальных точек кластера. При этом расстояние вычисляется по стандартной формуле расстояния между точками на евклидовой плоскости.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить минимальное расстояние между центрами двух различных кластеров.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе запишите два числа: сначала минимальное расстояние между центрами кластеров для файла A, затем для файла B. В качестве значения указывайте целую часть от умножения найденного числового значения на \(10~000.\)
Решение:
...
Ответ:
Статград. 28.01.2025-1
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям. По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – кругов радиуса не более \(3\) единиц – так, что каждая точка попадает ровно в один кластер. Центром кластера считается та из входящих в него точек, для которой минимально среднее расстояние до всех остальных точек кластера. При этом расстояние вычисляется по стандартной формуле расстояния между точками на евклидовой плоскости. Радиусом кластера считается максимальное из расстояний от центра до остальных точек кластера.
Обработка результатов эксперимента включает следующие шаги:
кластер, содержащий наименьшее число точек, исключается;
определяются центры и радиусы всех оставшихся кластеров;
вычисляется средний радиус оставшихся кластеров.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить средний радиус всех кластеров за исключением содержащего наименьшее число точек. Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите средний радиус по описанным выше правилам. В ответе запишите два числа: сначала средний радиус для файла A, затем для файла B. В качестве значения указывайте целую часть от умножения найденного числового значения на \(10~000.\)
Решение:
...
Ответ:
Статград. 17.12.2024
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – кругов радиуса не более \(3\) единиц так, что каждая точка попадает ровно в один кластер. Центром кластера считается та из входящих в него точек, для которой минимально максимальное из расстояний до всех остальных точек кластера. При этом расстояние вычисляется по стандартной формуле расстояния между точками на евклидовой плоскости. Радиусом кластера считается максимальное из расстояний от центра до остальных точек кластера.
Обработка результатов эксперимента включает следующие шаги:
кластер, содержащий наименьшее число точек, исключается;
определяются центры и радиусы всех оставшихся кластеров;
вычисляется средний радиус оставшихся кластеров.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить средний радиус всех кластеров за исключением содержащего наименьшее число точек.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите средний радиус по описанным выше правилам. В ответе запишите два числа: сначала средний радиус для файла A, затем для файла B. В качестве значения указывайте целую часть от умножения найденного числового значения на \(10~000.\)
Решение:
...
Ответ:
Задание 27. Информатика. ЕГЭ. Статград. 24.10.2024-2
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – прямоугольников размером \(3 \times 3\) так, что каждая точка попадает ровно в один кластер.
Центроидом кластера называется та из входящих в него точек, для которой минимальна сумма расстояний до всех остальных точек кластера. Обработка результатов эксперимента включает следующие шаги:
кластер, содержащий наибольшее число точек, исключается;
определяются центроиды всех оставшихся кластеров;
для найденных центроидов вычисляется средняя точка. Средней для группы точек называется точка (не обязательно входящая в группу), координаты которой определяются как средние арифметические значения координат всех точек группы.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить среднюю точку центроидов всех кластеров за исключением содержащего наибольшее число точек.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите координаты средней точки по описанным выше правилам. В ответе запишите четыре числа: сначала (в первой строке) координаты \(X\) и \(Y\) средней точки для файла A, затем (во второй строке) координаты \(X\) и \(Y\) средней точки для файла B. В качестве значения координаты указывайте целую часть от умножения числового значения координаты на \(10~000.\)
Решение:
...
Ответ:
Статград. 24.10.2024-1
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – прямоугольников размером \(3 \times 3\) так, что каждая точка попадает ровно в один кластер.
Центроидом кластера называется та из входящих в него точек, для которой минимальна сумма расстояний до всех остальных точек кластера. Обработка результатов эксперимента включает следующие шаги:
кластер, содержащий наименьшее число точек, исключается;
определяются центроиды всех оставшихся кластеров;
для найденных центроидов вычисляется средняя точка. Средней для группы точек называется точка (не обязательно входящая в группу), координаты которой определяются как средние арифметические значения координат всех точек группы.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить среднюю точку центроидов всех кластеров за исключением содержащего наименьшее число точек.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите координаты средней точки по описанным выше правилам. В ответе запишите четыре числа: сначала (в первой строке) координаты \(X\) и \(Y\) средней точки для файла A, затем (во второй строке) координаты \(X\) и \(Y\) средней точки для файла B. В качестве значения координаты указывайте целую часть от умножения числового значения координаты на \(10~000.\)
Решение:
...
Ответ:
Шастин. 9.2.2025
(Д. Бахтиев) Учёный решил провести кластеризацию множества звёзд по их расположению на карте звёздного неба. Каждая звезда задаётся своими координатами \((x, \, y).\) Две звезды считаются соседними, если расстояние между ними по формуле Евклида $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ строго меньше \(1\) условной единицы.
При этом используется следующее определение кластера и аномалии: звезды принадлежат одному и тому же кластеру, если между ними существует цепочка соседних звёзд (то есть, для любой пары звёзд \(A\) и \(B\) в кластере можно найти последовательность $$ A = P_1, \, P_2, \, \ldots , P_k = B, $$ где расстояние между соседними звёздами \(P_i\) и \(P_{i+1}\) меньше \(1\)). При этом кластером считается только такое объединение звёзд, в котором общее число точек не менее \(20.\) Если какая-либо группа звёзд, связанная по вышеописанному принципу, содержит менее \(20\) точек, она не рассматривается как кластер, а все входящие в неё звёзды считаются аномалиями.
Входные данные задаются в двух файлах: файл \(A\) и файл \(B.\) В каждой строке файлов содержатся координаты звёзд: сначала по оси \(x,\) затем по оси \(y.\) При условии, что аномалии при расчётах игнорируются, требуется определить координаты центроида самого маленького (по числу звёзд) кластера. Центроид кластера определяется как звезда, принадлежащая кластеру, для которой сумма расстояний до всех остальных звёзд этого кластера минимальна. Гарантируется, что такой кластер определяется однозначно. В ответе запишите четыре числа: в первой строке для файла \(A\) результаты произведений \(C_x \cdot 10000\) и \(C_y \cdot 10000,\) где \(C_x\) и \(C_y\) — координаты центроида кластера по осям \(x\) и \(y\) соответственно, а во второй строке аналогичные данные для файла \(B.\)
Решение:
...
Ответ:
Шастин. 19.01.2025
(Д. Бахтиев) Компания «Энергосеть» занимается оптимизацией энергоснабжения в нескольких регионах. Для этого нужно определить местоположение главных трансформаторных узлов, которые обеспечат минимальные потери при распределении энергии. В каждом регионе имеются несколько подрегионов, каждый из которых характеризуется тем, что расстояние от любой точки в подрегионе до точки из другого подрегиона не менее \(R\) условных единиц. Необходимо определить место для трансформаторного узла, которое находится за два шага: сначала для каждого подрегиона нужно найти его центр нагрузки — такую точку в регионе, от которой суммарное расстояние до всех остальных точек подрегиона минимально. Затем, учитывая данные о центрах нагрузки всех подрегионов, найти центральный трансформаторный узел — такая точка в одном из регионов, от которой суммарное расстояние до всех центров нагрузки минимально. Расстояние между двумя точками \((x_1, \, y_1)\) и \((x_2, \, y_2)\) на плоскости вычисляется по формуле Евклида: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Файл 27_A.txt содержит данные о точках двух регионов. Файл 27_B.txt содержат данные о точках трёх регионов. В первой строке каждого файла записано значения \(R.\) В каждой из следующих строк записаны координаты \(x\) и \(y\) очередной точки. Количество точек в файле 27_A.txt не превышает \(1000,\) в 27_B.txtне превышает \(10000.\)
Для каждого региона определить координаты центрального трансформаторного узла. В ответе укажите четыре целых числа. В первой строке: ближайшие целые числа значений произведения \(x\)-координаты узла на \(10000\) и \(y\)-координаты узла на \(10000\) для региона А. Во второй строке: аналогичные данные для региона В.
Решение:
...
Ответ:
Шастин. 18.12.2024
(Л. Шастин, В. Лашин) В администрации резиденции Деда Мороза проводится активное обсуждение вопроса эффективности перевозки мириад подарков в канун волшебного Нового Года. Снегурочка настаивает на немедленном внедрении передовых технологий: «Старый мешок с письмами никуда не годится — в этой куче адресов невозможно разобраться, да и Дед уже не тот, даже таблетки не помогают. Если мы срочно не решим эту проблему, наш дорогой Дед Мороз скоро превратится в Санта Клауса! Министерство культуры РФ такое точно не одобрит». В сказочной резиденции с женщинами спорить не принято, тем более с такими молодыми и горячими, как прелестная Снегурочка. Да и аргументы в этот раз звучат убедительно...
Отдел аналитики данных возложил решение обозначенной ранее проблемы на могучие плечи СнегПрогов (снеговиков-программистов). СнегПроги предложили простую концепцию: разделить письма на группы (города) по характеристике места жительства (геопозиции) их отправителей. Благодаря этому гениальному подходу Деду Морозу не придется по сто раз перемещаться между Москвой и Владивостоком, ведь он сможет переходить к доставке подарков по Москве только после того, как развезет все подарки владивостокцам. И Декабрь, Январь и Февраль точно останутся благодарны своему хозяину. К тому же получится сэкономить на бензине, что в наше время совсем не дурно!
Одним городом СнегПроги решили считать такую группу геопозиций (точек, определенных по двум координатам \(x\) и \(y\)), в которой любая из геопозиций удалена от геопозиции из другой группы хотя бы на \(E = 20\) у.е. (условных единиц). А метрикой расстояния между двумя точками (геопозициями) уже традиционно стала формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$
Помогите СнегПрогам найти оптимальные геопозиции в каждом городе для открытия в них новых филиалов резиденции. Лучшим местом будет считаться такая геопозиция, суммарное расстояние от которой до всех других геопозиций в этом же городе минимально. Если у вас все получится, СнегПроги получат в подарок от Деда Мороза новые чудо-компьютеры, сделанные из льдинок высочайшего качества. А вам в таком случае полагается хорошее настроение =)
В файле А хранятся записи об адресах первой партии полученных писем, образующих 2 города. В каждой строке записана информация о двух показателях геопозиции конкретного письма: сначала координата \(x,\) затем координата \(y.\) Известно, что количество записей не превышает \(2200.\) В файле Б хранятся записи об адресах второй партии полученных писем, образующих \(3\) города. Известно, что количество записей не превышает \(15~500.\) Структура хранения информации в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты новых филиалов резиденции для всех городов, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс этих филиалов, и \(S_y\) — среднее арифметическое их ординат. В ответе запишите четыре числа: в первой строке сначала целую часть значения \(S_x,\) затем целую часть значения \(S_y\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
...
Ответ:
Шастин. 30.11.2024
(Л. Шастин) Ведущие специалисты отдела бизнес-аналитики торгового маркетплейса «Ozonyol» собирают статистику и изучают предпочтения покупателей за период летних и осенних продаж. Перед ними стоит задача — проанализировать рынок и сделать выводы об уровне спроса на товары различных категорий для выделения наиболее перспективных траекторий развития площадки с привлечением инвестиционных средств. По итогам сбора информации имеется набор данных, включающих записи о товарах, каждый из которых содержит три показателя — номер сегмента товара, характеризующий его расположение на сайте, коэффициент успешных конверсий и уровень заинтересованности поуапателей, выраженный в коэффициенте их активности. Общий спрос на товар вычисляется как среднее арифметическое второго и третьего показателей. На основании полученной информации строится графический отчёт, отражающий общий спрос на товар в зависимости от его номера сегмента, в котором записи, лежащие в области окружности с радиусом \(R\), выделяются в отдельные кластеры. В итоге решено привлекать средства на продвижение товаров только из кластеров, содержащих хотя бы \(K\) записей, причем первые вложения направить в товары-медоиды. Медоидом (центром) кластера называется такая запись о товаре, суммарное расстояние от которой до других записей в кластере минимально. Метрикой расстояния между двумя записями \(A(x_1, \, x_2)\) и \(B(x_2, \, y_2)\) является формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ Примечание. Гарантируется, что товар принадлежит только одному из кластеров.
В файле A в первой строке записаны числа \(R\) и \(K.\) В остальных строках хранятся записи о товарах за период летних продаж, образующих \(3\) кластера. В каждой строке записана информация о трёх показателях конкретного товара: сначала номер сегмента, затем коэффициент успешных конверсий и коэффициент активности. Известно, что количество записей не превышает \(1100.\) В файле Б хранятся записи о товарах за период осенних продаж, образующих \(6\) кластеров, и соответствующие осенним продажам числа \(R\) и \(K.\) Известно, что количество записей не превышает \(11~000.\) Структура хранения информации о товарах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты медоидов (центров) всех кластеров, для продвижения которых будут привлечены инвестиционные средства, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс центров кластеров, и \(S_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(S_x \times 100~000,\) затем целую часть произведения \(S_y \times 100~000\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
...
Ответ:
Задание 27. Информатика. ЕГЭ. Шастин. 19.09.2024
(Л. Шастин) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд(точек) на графике, лежащий внутри прямоугольника высотой \(H\) и шириной \(W\). Каждая звезда обязательно принадлежит только одному из кластеров. Под расстоянием между двумя кластерами понимается минимальное расстояние между двумя звёздами этих кластеров, а расстояние между двумя точками \(A \,(x_1, \, y_1)\) и \(B \, (x_2, \, y_2)\) на плоскости вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ В файле A хранятся данные о звёздах двух кластеров, где \(H=3\), \(W=3\) для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\). Значения даны в условных единицах. Известно, что количество звёзд не превышает \(1000.\) В файле Б хранятся данные о звёздах трёх кластеров, где \(H=2\), \(W=2\) для каждого кластера. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите два кластера, расстояние между которыми минимально, и затем вычислите два числа: \(S_x\) — сумму координат абсцисс точек, образующих минимальное расстояние между этими кластерами, и \(S_y\) — сумму ординат этих точек.
В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(S_x \times 1000\), затем целую часть произведения \(S_y \times 1000\) для файла А, во второй строке — аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.

Решение:
...
Ответ:
Поляков-7738
(А. Кабанов) Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри сектора круга радиусом \(R\) и центральным углом \(H\) градусов, причём эти сектора между собой не пересекаются. Гарантируется, что такое разбиение существует и единственно. Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах трёх кластеров с параметрами \(R=5\) и \(H=30.\) В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает \(1000.\) В файле Б такой же структуры хранятся данные о звёздах пяти кластеров с параметрами \(R=10\) и \(H=45.\) Известно, что количество звёзд не превышает \(10~000.\) Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000,\) затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7737
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7736
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7735
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7734
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7733
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7732
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7731
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7730
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7729
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7728
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7717
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7716
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7715
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7714
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7713
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7712
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7711
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7710
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7709
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7708
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7707
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7706
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7705
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7704
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7703
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор не менее чем из 30 соседних звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7702
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7701
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7700
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7699
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7698
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7660
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7659
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7658
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7657
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7656
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7655
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7654
(М. Крючков) В лесу выделено несколько мест (кластеров), где растёт много деревьев, предназначенных для вырубки. После спиливания дерева его нужно доставить в точку сбора, которая совпадает с одним из деревьев кластера. Стоимость доставки определяется как расстояние от дерева до точки сбора, умноженное на высоту дерева. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ В каждом кластере нужно найти оптимальную точку сбора (центр), такую что суммарная стоимость доставки в это место всех спиленных деревьев данного кластера минимальна. Аномалиями назовём совокупности из не более чем \(10\) точек, каждая из которых находится на расстоянии более \(30\) м от точек кластеров. Аномалии в расчётах не учитываются. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о двух кластерах. Каждый кластер имеет форму прямоугольника размером \(100 \times 100\) м. Каждая строка файла содержит три характеристики одного дерева: координату \(x\), затем координату \(y\) и затем высоту дерева. Количество деревьев в каждом кластере не превышает \(1000\). В файле Б той же структуры хранятся данные о трёх кластерах, каждый из которых имеет вид прямоугольника размером не более \(100 \times 200\) м. Количество точек в каждом кластере не превышает \(10~000\). Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7653
(В. Ланская, Р. Ягафаров) В городе X тестируется проект по оптимизации размещения кранов на складах. Оптимальное местоположение для крана (или центроид) будет таким, при котором сумма расстояний Чебышева от этого места до всех других точек на складе была минимальной. Расстояние Чебышева между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \max (|x_2 - x_1|, \, |y_2 - y_1|) $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о двух складских комплексах (кластерах). Каждый комплекс имеет форму прямоугольника размером \(H = 3\) и \(W = 5\). Каждая строка файла содержит координаты одной точки на складе: сначала \(x\), затем \(y\). Количество точек в каждом комплексе не превышает \(1000\). В файле Б той же структуры хранятся данные о трёх кластерах, каждый из которых имеет вид прямоугольника размером \(H = 6\) и \(W = 8\). Количество точек в каждом комплексе не превышает \(10~000\).
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7652
(В. Ланская, Р. Ягафаров) Шёл 2077 год. Ученому необходимо провести кластеризацию населенных пунктов двух больших районов на картах планет Информатикус и Алгоритмикус. Район (кластер) – это групп населенных пунктов, которые находятся внутри прямоугольника высотой \(H\) и шириной \(W\). Каждый населенный пункт обязательно принадлежит только одному району. Столица района (или центроид) – это такой населенный пункт, сумма манхэттенских расстояний от которого до всех других населённых пунктов в кластере минимальна. Манхэттенское расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = | x_2 - x_1| + |y_2 - y_1| $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о точках двух кластеров. В каждой строке записана информация о расположении одной точки: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество точек не превышает \(1000\). В файле Б той же структуры хранятся данные о точках трёх кластеров. Известно, что количество точек не превышает \(10~000\). Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7651
(В. Ланская, Р. Ягафаров) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах четырёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
...
Ответ:
Поляков-7644
(В. Шубинкин) В ходе эксперимента были зафиксированы очаги радиации. Чтобы изучить данное явление, решили провести кластеризацию источников излучения. Кластер – это набор источников (точек) на графике, лежащий внутри прямоугольника высотой \(H\) и шириной \(W\). Каждая точка обязательно принадлежит только одному из кластеров. Истинный центр кластера, или центроид, – это одна из точек на графике, сумма расстояний от которой до всех остальных точек кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём совокупности из не более чем \(10\) точек, каждая из которых находится на расстоянии более одной условной единицы от точек кластеров. Аномалии в расчётах не учитываются. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о точках двух кластеров. В каждой строке записана информация о расположении одной точки: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество точек не превышает \(1000\). В файле Б той же структуры хранятся данные о трёх кластерах. Известно, что количество точек не превышает \(10~000\). Структура хранения информации о точках в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7612
(В. Шубинкин) При проведении эксперимента заряженные частицы попадают на чувствительный экран размером \(12\) на \(9\) условных единиц. При попадании каждой частицы на экран в протоколе фиксируются координаты попадания в условных единицах. При анализе результатов выделяют кластеры – группы точек на экране, в которые попали частицы. Каждая точка принадлежит только одному кластеру. Минимальное (максимальное) расстояние между кластерами – это минимальное (максимальное) расстояние между двумя точками, одна из которых принадлежит одному кластеру, а вторая – другому. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Аномалиями назовём совокупности из не более чем \(10\) точек, каждая из которых находится на расстоянии более одной условной единицы от точек кластеров. Аномалии в расчётах не учитываются. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о частицах двух кластеров. В каждой строке записана информация о расположении на карте одной точки: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество точек не превышает \(1000\). В файле Б хранятся данные о трёх кластерах. Известно, что количество точек не превышает \(10~000\). Структура хранения информации о точках в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите минимальное \(d_{min}\) и максимальное \(d_{max}\) расстояния между двумя кластерами. В ответ запишите \(4\) числа: в первой строке целую часть произведения \(d_{min} \times 10~000\), затем целую часть произведения \(d_{max} \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.
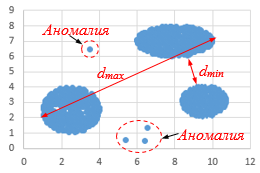
Решение:
...
Ответ:
Поляков-7601
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7600
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7599
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7598
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7597
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7596
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7595
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7594
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7593
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7592
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7591
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7590
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7589
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7588
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7587
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7586
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7585
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7584
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7583
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-7582
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 10~000\), затем целую часть произведения \(P_y \times 10~000\) для файла А, во второй строке – аналогичные данные для файла Б.

Решение:
...
Ответ:
Поляков-2677
(А. Жуков) Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \((a_i, \, a_j)\) этого набора, в которых \(1 \leqslant i+5 \leqslant j \leqslant N\), сумма элементов нечётна, а произведение делится на \(13\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) \((1 \leqslant N \leqslant 100000)\). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(7\)
\(4\)
\(14\)
\(27\)
\(39\)
\(7\)
\(2\)
\(13\)
Для указанных входных данных количество подходящих пар должно быть равно \(2\). В приведённом наборе имеются две пары \((4, \, 13)\) и \((14, \, 13)\), сумма элементов которых нечётна, произведение кратно \(13\) и индексы элементов последовательности отличаются не менее, чем на \(5\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2676
(А. Жуков) Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \((a_i, \, a_j)\) этого набора, в которых \(1 \leqslant i < j \leqslant N\), сумма элементов нечётна, а произведение делится на \(13\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) \((1 \leqslant N \leqslant 100000)\). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(5\)
\(4\)
\(13\)
\(27\)
\(39\)
\(7\)
Для указанных входных данных количество подходящих пар должно быть равно \(2\). В приведённом наборе имеются две пары \((4, \, 13)\) и \((4, \, 39)\), сумма элементов которых нечётна, и произведение кратно \(13\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2675
Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \((a_i, \, a_j)\) этого набора, в которых \(1 \leqslant i+5 \leqslant j \leqslant N\) и сумма элементов кратна \(14\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) \((1 \leqslant N \leqslant 100000)\). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(8\)
\(7\)
\(5\)
\(6\)
\(12\)
\(24\)
\(7\)
\(9\)
\(12\)
Для указанных входных данных количество подходящих пар должно быть равно \(2\). В приведённом наборе имеются две пары \((7, \, 7)\) и \((5, \, 9)\), сумма элементов которых кратна \(14\) и индексы в последовательности отличаются не менее, чем на \(5\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2674
(Д.В. Богданов) Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \((a_i, \, a_j)\) этого набора, в которых \(1 \leqslant i < j \leqslant N\) и сумма элементов кратна \(12\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) \((1 \leqslant N \leqslant 100000)\). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(5\)
\(7\)
\(5\)
\(6\)
\(12\)
\(24\)
Для указанных входных данных количество подходящих пар должно быть равно \(2\). В приведённом наборе имеются две пары \((7, \, 5)\) и \((12, \, 24)\), сумма элементов которых кратна \(12\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2673
Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \((a_i, \, a_j)\) этого набора, в которых \(1 \leqslant i + 7 \leqslant j \leqslant N\) и произведение элементов кратно \(14\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) \((1 \leqslant N \leqslant 100000)\). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(9\)
\(7\)
\(5\)
\(6\)
\(12\)
\(5\)
\(11\)
\(8\)
\(16\)
\(14\)
Для указанных входных данных количество подходящих пар должно быть равно \(3\). В приведённом наборе имеются три подходящие пары \((7, \, 16)\), \((7, \, 14)\), \((5, \, 14)\), произведение элементов которых кратно \(14\), а индексы элементов последовательности различаются не меньше, чем на \(7\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2672
(Д.В. Богданов) Имеется набор данных, состоящий из положительных целых чисел. Необходимо определить количество пар элементов \( (a_i, \, a_j) \) этого набора, в которых \(1 \leqslant i < j \leqslant N\) и произведение элементов кратно \(6\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) (\( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(4\)
\(7\)
\(5\)
\(6\)
\(12\)
Для указанных входных данных количество подходящих пар должно быть равно \(5\). В приведённом наборе из \(4\) чисел имеются пять пар \((7, \, 6)\), \((5, \, 6)\), \((7, \, 12)\), \((5, \, 12)\), \((6, \, 12)\), произведение элементов которых кратно \(6\).
В ответе укажите два числа: сначала количество подходящих пар для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2671
Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел делилась на \(8\) и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество троек \(N\) (\( 1 \leqslant N \leqslant 100000 \)). Каждая из следующих \(N\) строк содержит три натуральных числа, не превышающих \(10~000\).
Пример входного файла:
\(6\)
\(8 \,\, 3 \,\, 4\)
\(4 \,\, 8 \,\, 12\)
\(9 \,\, 5 \,\, 6\)
\(2 \,\, 8 \,\, 3\)
\(12 \,\, 3 \,\, 5\)
\(1 \,\, 4 \,\, 12\)
Для указанных входных данных значением искомой суммы должно быть число \(56\).
В ответе укажите два числа: сначала искомое значение для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2670
(Д.Ф. Муфаззалов) Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не делилась на \(4\) и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество троек \(N\) (\(1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит три натуральных числа, не превышающих \(10~000\).
Пример входного файла:
\(6\)
\(1 \,\, 3 \,\, 2\)
\(5 \,\, 12 \,\, 12\)
\(6 \,\, 8 \,\, 12\)
\(5 \,\, 4 \,\, 12\)
\(3 \,\, 3 \,\, 12\)
\(1 \,\, 1 \,\, 13\)
Для указанных входных данных значением искомой суммы должно быть число \(63\).
В ответе укажите два числа: сначала значение искомой суммы для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2669
На спутнике «Восход» установлен прибор, предназначенный для измерения солнечной активности. Каждую минуту прибор передаёт по каналу связи неотрицательное целое число – количество энергии солнечного излучения, полученной за последнюю минуту, измеренное в условных единицах. Временем, в течение которого происходит передача, можно пренебречь. Необходимо найти в заданной серии показаний прибора минимальное нечётное произведение двух показаний, между моментами передачи которых прошло не менее \(6\) минут. Если получить такое произведение не удаётся, ответ считается равным «\(-1\)».
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) (\(1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(11\)
\(12\)
\(45\)
\(5\)
\(3\)
\(17\)
\(23\)
\(21\)
\(20\)
\(19\)
\(12\)
\(26\)
Для указанных входных данных искомое контрольное значение равно \(95\).
В ответе укажите два числа: сначала контрольное значение для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2668
Имеется набор данных, состоящий из положительных целых чисел, каждое из которых не превышает \(1000\). Они представляют собой результаты измерений, выполняемых прибором с интервалом \(1\) минута. Требуется найти для этой последовательности контрольное значение — наименьшую сумму квадратов двух результатов измерений, выполненных с интервалом не менее, чем в \(5\) минут.
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) (\( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(9\)
\(12\)
\(45\)
\(5\)
\(4\)
\(21\)
\(20\)
\(10\)
\(12\)
\(26\)
Для указанных входных данных искомое контрольное значение равно \(169\).
В ответе укажите два числа: сначала контрольное значение для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2667
Имеется набор данных, состоящий из положительных целых чисел, каждое из которых не превышает \(1000\). Требуется найти для этой последовательности контрольное значение — наибольшее число \(R\), удовлетворяющее следующим условиям:
— \(R\) — произведение двух различных переданных элементов последовательности («различные» означает, что не рассматриваются квадраты переданных чисел, произведения различных, но равных по величине элементов допускаются);
— \(R\) делится на \(7\) и не делится на \(49\).
Если такое произведение получить невозможно, считается, что контрольное значение \(R = 1\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) (\(1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(6\)
\(60\)
\(17\)
\(3\)
\(7\)
\(9\)
\(60\)
Для указанных входных данных искомое контрольное значение равно \(420\).
В ответе укажите два числа: сначала контрольное значение для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2666
Имеется набор данных, состоящий из положительных целых чисел, каждое из которых не превышает \(1000\). Требуется найти для этой последовательности контрольное значение — наибольшее число \(R\), удовлетворяющее следующим условиям:
— \(R\) — произведение двух различных переданных элементов последовательности («различные» означает, что не рассматриваются квадраты переданных чисел, произведения различных, но равных по величине элементов допускаются);
— \(R\) делится на \(6\).
Входные данные. Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых содержит в первой строке количество чисел \(N\) (\(1 \leqslant N \leqslant 100000\)). Каждая из следующих \(N\) строк содержит одно натуральное число, не превышающее \(10~000\).
Пример входного файла:
\(6\)
\(60\)
\(17\)
\(3\)
\(7\)
\(9\)
\(60\)
Для указанных входных данных искомое контрольное значение равно \(3600\).
В ответе укажите два числа: сначала контрольное значение для файла \(А\), затем для файла \(B\).
Решение:
...
Ответ:
Поляков-2665
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел делилась на \(3\) и при этом была минимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — минимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 11\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \(20\).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Решение:
...
Ответ:
Поляков-2664
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел делилась на \(5\) и при этом была максимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 11\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \(30\).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Решение:
...
Ответ:
Поляков-2663
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел делилась на \(3\) и при этом была минимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — минимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 11\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \(21\).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Решение:
...
Ответ:
Поляков-2662
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел делилась на \(3\) и при этом была максимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 11\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \(30\).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Решение:
...
Ответ:
Поляков-2661
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на \(3\) и при этом была минимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — минимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 12\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \(20\).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Предупреждение: для обработки файла \( B \) не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение:
...
Ответ:
Поляков-2660
(Демовариант 2021). Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на \(3\) и при этом была максимально возможной. Гарантируется, что искомую сумму чисел получить можно.
Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл \( A \) и файл \( B\)), каждый из которых содержит в первой строке количество пар \(N\) ( \( 1 \leqslant N \leqslant 100000\)). Каждая из следующих \( N \) строк содержит два натуральных числа, не превышающих \( 10\, 000\).
Пример организации исходных данных во входном файле:
\(6\)
\(1\,\, 3\)
\(5\,\, 12\)
\(6\,\, 9\)
\(5\,\, 4\)
\(3\,\, 3\)
\(1\,\, 1\)
Для указанных входных данных значением искомой суммы должно быть число \( 32 \).
В ответе укажите два числа: сначала значение искомой суммы для файла \( A \), затем для файла \( B\).
Предупреждение: для обработки файла \( B \) не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение:
...
Ответ:
ЕГЭ 2024. Крылов-1
По каналу связи ежедневно раз в день в течение \(N\) дней (\(N\) — натуральное число) передаётся последовательность натуральных чисел — сумма выручки в некотором отделении банка за день.
Определите три таких переданных числа, чтобы между моментами передачи любых из двух из них прошло не менее \(K\) дней, а сумма этих трёх чисел была минимально возможной. Запишите в ответе найденную сумму.
Входные данные
Даны два входных файла (файл \(A\) и файл \(B\)), каждый из которых в первой строке содержит натуральное число \(K\) — минимальное количество дней, которое должно пройти между моментами передачи сумм выручки, а во второй — количество переданных значений \(N\) ( \(1 \leqslant N \leqslant 10~000~000\), \(N>K\)). В каждой из следующих \(N\) строк находится одно натуральное число, не превышающее \(10~000~000\), которое обозначает сумму выручки в отделении банка за соответствующий день.
Запишите в ответе два числа: сначала значение искомой величины для файла \(A\), затем — для файла \(B\).
Типовой пример организации данных во входном файле
\(2\)
\(6\)
\(15\)
\(26\)
\(30\)
\(23\)
\(22\)
\(20\)
При таких исходных данных искомая величина равна \(65\) — это сумма значений выручки, полученной в первый, третий и шестой дни.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла \(B\) не следует использовать переборный алгоритм, вычисляющий сумму для всех всевозможных вариантов, поскольку по такому алгоритму программа будет выполняться слишком долго.
Решение:
...
Ответ:
ЕГЭ-2022. 1 вариант
У медицинской компании есть \(N\) пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более \(36\) штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла (файл \(A\) и файл \(B\)), каждый из которых в первой строке содержит число \(N\) (\(1 \leq N \leq 10~000~000\)) – количество пунктов приёма биоматериалов. В каждой из следующих \(N\) строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает \(1~000\)). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. В ответе укажите два числа: сначала значение искомой величины для файла \(A\), затем – для файла \(B\).
Типовой пример организации данных во входном файле
\(6\)
\(1\) \(100\)
\(2\) \(200\)
\(5\) \(4\)
\(7\) \(3\)
\(8\) \(2\)
\(10\) \(190\)
При таких исходных данных и вместимости транспортировочного контейнера, составляющей \(96\) пробирок, компании выгодно открыть лабораторию в пункте \(2\). В этом случае сумма транспортных затрат составит: \(1 \cdot 2 + 3 \cdot 1 + 5 \cdot 1 + 6 \cdot 1 + 8 \cdot 2 = 32\).
Решение:
...
Ответ:

