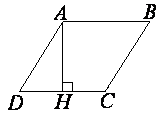Площадь ромба вычисляется тремя путями:
1) по формуле S=аh, где а-длина стороны, h - высота. Высота ромба представляет собой перпендикуляр, который опущен из одного из его углов на сторону, противоположную данному углу.
2) по формуле для параллелограмма S = a * b * sinα (a и b - смежные стороны параллелограмма, α - угол между ними); a и b в случае ромба будут равны друг другу. То есть для ромба можно записать площадь как
S = a²sinα
3) площадь ромба равна половине произведения диагоналей.
S = (d1 x d2)/2, где S - площадь, d1, d2 - диагонали ромба.
У ФИПИ есть задания для ОГЭ из раздела "геометрия" на все три формулы и их сочетание.
Варианты заданий с ФИПИ
Найти площадь ромба по стороне и перпендикуляру
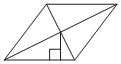
В данном варианте задачи высота не дана, а известно только расстояние от точки пересечения диагоналей ромба до стороны.
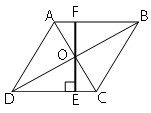Обозначим ключевые точки, как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F.
EF - высота ромба (т.к. EF перпендикулярна CD).
Рассмотрим треугольники DOE и BOF.
DO=OB (по второму свойству ромба: диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.)
∠DOE=∠BOF (т.к. они вертикальные)
∠EDO=∠FBO (т.к. это внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по второму признаку.
Тогда OE=OF => EF=2*OE
Sромба=EF*CD=2*OE*CD
Так же можно доказать, что треугольники DОС и АОВ равны по трем сторонам, а значит и их высоты ОЕ и ОF равны, значит EF=2*OE.
Доказав, что высота равна удвоенному перпендикуляру от точки пересечения диагоналей к стороне, можно переходить к расчетам (они приведены под каждой задачей под кнопкой "Решение").
Задания
Сторона ромба равна 5, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Решение:
S = аh = 5 * 2 * 2 = 20
Ответ: 20
67B0F9
Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Решение:
S = аh = 12 * 2 * 1 = 24
Ответ: 24
042AD2
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Решение:
S = аh = 8 * 2 * 2 = 32
Ответ: 32
74C240
Сторона ромба равна 7, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба.
Решение:
S = аh = 7 * 2 * 3 = 42
Ответ: 42
FC6CC0
Сторона ромба равна 9, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Решение:
S = аh = 9 * 2 * 1 = 18
Ответ: 18
5D6B72
Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба.
Решение:
S = аh = 10 * 2 * 3 = 60
Ответ: 60
857D14
Сторона ромба равна 7, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Решение:
S = аh = 7 * 2 * 1 = 14
Ответ: 14
C3B85D
Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Решение:
S = аh = 12 * 2 * 2 = 48
Ответ: 48
AB55BC
Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь этого ромба.
Решение:
S = аh = 12 * 2 * 4 = 96
Ответ: 96
D286A2
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Решение:
S = аh = 4 * 2 * 1 = 8
Ответ: 8
7C9C93
Найти площадь ромба по периметру и углу
Площадь параллелограмма вычисляется по формуле
S = a * b * sinα (a и b - смежные стороны параллелограмма, α - угол между ними)
То есть для ромба можно записать
S = a²sinα
Ромб - параллелограмм, в котором все стороны равны между собой; a и b в случае ромба будут равны друг другу. Поделив периметр на 4, найдем длину стороны.
Далее подставляем числа в формулу и вычисляем площадь.
Синусы на экзамене смотрим по таблице, которая будет у вас напечатана на бланке ОГЭ.
Задания
Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
24 : 4 = 6 - длина стороны
S = a²sinα = 62 * sin 30° = 36 * 1/2 = 18
Ответ: 18
4647CD
Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
36 : 4 = 9 - длина стороны
S = a²sinα = 92 * sin 30° = 81 * 1/2 = 40,5
Ответ: 40,5
4CAF07
Периметр ромба равен 72, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
72 : 4 = 18 - длина стороны
S = a²sinα = 182 * sin 30° = 324 * 1/2 = 162
Ответ: 162
AA4DCC
Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
60 : 4 = 15 - длина стороны
S = a²sinα = 152 * sin 30° = 225 * 1/2 = 112,5
Ответ: 112,5
EDC29B
Периметр ромба равен 48, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
48 : 4 = 12 - длина стороны
S = a²sinα = 122 * sin 30° = 144 * 1/2 = 72
Ответ: 72
148EC1
Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
12 : 4 = 3 - длина стороны
S = a²sinα = 32 * sin 30° = 9 * 1/2 = 4,5
Ответ: 4,5
5E113B
Периметр ромба равен 88, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
88 : 4 = 22 - длина стороны
S = a²sinα = 222 * sin 30° = 484 * 1/2 = 242
Ответ: 242
895412
Периметр ромба равен 56, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
56 : 4 = 14 - длина стороны
S = a²sinα = 142 * sin 30° = 196 * 1/2 = 98
Ответ: 98
C6D6F9
Периметр ромба равен 28, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
28 : 4 = 7 - длина стороны
S = a²sinα = 72 * sin 30° = 49 * 1/2 = 24,5
Ответ: 24,5
D6F8CF
Периметр ромба равен 20, а один из углов равен 30°. Найдите площадь этого ромба.
Решение:
20 : 4 = 5 - длина стороны
S = a²sinα = 52 * sin 30° = 25 * 1/2 = 12,5
Ответ: 12,5
8F0AD7
Найти высоту ромба
Следующее задание - продолжение расчетов предыдущего. Высота ромба находится, когда знаешь площадь и сторону ромба.
Площадь можно вычислить по формуле S = a * b * sinα (a и b - смежные стороны параллелограмма, у ромба они равны; α - угол между ними).
То есть для ромба можно записать S = a²sinα Если дан тупой угол, переводим в острый. Острый угол ромба: 180° - 150° = 30°.
Так же площадь вычисляется по формуле S=аh, где а - длина стороны ромба, h - высота. Выражаем и находим высоту:
h=S/а
Можно найти площадь по первой формуле и подставить ее во вторую, а можно выразить высоту как
h= S/а=a²sinα/а=a sinα и уже в нее подставлять известные значения.
Задания
Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 4 * sin30° = 4 * 1/2 = 2
Ответ: 2
7C9123
Сторона ромба равна 14, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 14 * sin30° = 14 * 1/2 = 7
Ответ: 7
74C966
Сторона ромба равна 18, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 18 * sin30° = 18 * 1/2 = 9
Ответ: 9
4912B6
Сторона ромба равна 22, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 22 * sin30° = 22 * 1/2 = 11
Ответ: 11
157535
Сторона ромба равна 24, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 24 * sin30° = 24 * 1/2 = 12
Ответ: 12
BABF20
Сторона ромба равна 34, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 34 * sin30° = 34 * 1/2 = 17
Ответ: 17
12BC49
Сторона ромба равна 46, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 46 * sin30° = 46 * 1/2 = 23
Ответ: 23
F07A0E
Сторона ромба равна 28, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 28 * sin30° = 28 * 1/2 = 14
Ответ: 14
F0772B
Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 38 * sin30° = 38 * 1/2 = 19
Ответ: 19
B04913
Сторона ромба равна 54, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Решение:
Острый угол ромба: 180° - 150° = 30°.
Площадь ромба равна S = a*h, с другой стороны S = a²sinα. Приравниваем площади, получаем:
a * h = a²sinα
h = a sinα = 54 * sin30° = 54 * 1/2 = 27
Ответ: 27
BD132F
Найти площадь ромба по диагоналям
Площадь ромба равна половине произведения диагоналей.
S = (d1 * d2)/2, где S - площадь, d1, d2 - диагонали ромба.
Задания
Найдите площадь ромба, если его диагонали равны 14 и 6.
Решение:
S = (d1 * d2)/2 = 14*6 / 2 = 42
Ответ: 42
DAFCE7
Найдите площадь ромба, если его диагонали равны 4 и 6.
Решение:
S = (d1 * d2)/2 = 4*6 / 2 = 12
Ответ: 12
901A43
Найдите площадь ромба, если его диагонали равны 19 и 6.
Решение:
S = (d1 * d2)/2 = 19*6 / 2 = 57
Ответ: 57
658489
Найдите площадь ромба, если его диагонали равны 10 и 6.
Решение:
S = (d1 * d2)/2 = 10*6 / 2 = 30
Ответ: 30
2A6166
Найдите площадь ромба, если его диагонали равны 5 и 6.
Решение:
S = (d1 * d2)/2 = 5*6 / 2 = 15
Ответ: 15
908C40
Найдите площадь ромба, если его диагонали равны 8 и 6.
Решение:
S = (d1 * d2)/2 = 8*6 / 2 = 24
Ответ: 24
1E2D36
Найдите площадь ромба, если его диагонали равны 21 и 6.
Решение:
S = (d1 * d2)/2 = 21*6 / 2 = 63
Ответ: 63
6EB401
Найдите площадь ромба, если его диагонали равны 32 и 4.
Решение:
S = (d1 * d2)/2 = 32*4 / 2 = 64
Ответ: 64
162D63
Найдите площадь ромба, если его диагонали равны 20 и 6.
Решение:
S = (d1 * d2)/2 = 20*6 / 2 = 60
Ответ: 60
3443A9
Найдите площадь ромба, если его диагонали равны 34 и 4.
Решение:
S = (d1 * d2)/2 = 34*4 / 2 = 68
Ответ: 68
2EA574
Задания ко второй части ОГЭ с развернутым ответом
Это задачи с развернутым ответом к второй части ОГЭ по математике.
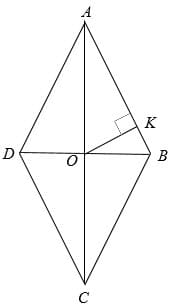
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 60.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 15
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 60/2 = 30.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
D9E6CA
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 40.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 10
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 40/2 = 20.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
987228
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 44.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 11
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 44/2 = 22.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
40D431
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 48.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 12
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 48/2 = 24.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EBA29F
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 52.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 13
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 52/2 = 26.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
D01FBF
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 56.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 14
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 56/2 = 28.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EFC57B
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 64.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 16
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 64/2 = 32.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
9C2D65
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 68.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 17
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 68/2 = 34.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
0247D6
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 18, а одна из диагоналей ромба равна 72. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 72.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 18
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 72/2 = 36.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
2FCCDB
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Решение:
Cделаем рисунок: ромб ABCD
Пусть AC = 76.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 19
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 76/2 = 38.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EEF3FC
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH=8+2=10 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2=AH2+DH2
AH2=AD2-DH2
AH2=102-82
AH2=100-64
AH2=36
AH=6
Ответ: AH=6
DAF765
Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=1. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 12 + 1 = 13 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 132 - 122
AH2 = 169 - 144
AH2 = 25
AH = 5
Ответ: AH = 5
C5C26D
Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=3. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 12 + 3 = 15 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 152 - 122
AH2 = 225 - 144
AH2 = 81
AH = 9
Ответ: AH = 9
F69509
Высота AH ромба ABCD делит сторону CD на отрезки DH=15 и CH=2. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 15 + 2 = 17 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 172 - 152
AH2 = 289 - 225
AH2 = 64
AH = 8
Ответ: AH = 8
F47774
Высота AH ромба ABCD делит сторону CD на отрезки DH=16 и CH=4. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 16 + 4 = 20 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 202 - 162
AH2 = 400 - 256
AH2 = 144
AH = 12
Ответ: AH = 12
8E9764
Высота AH ромба ABCD делит сторону CD на отрезки DH=20 и CH=5. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 20 + 5 = 25 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 252 - 202
AH2 = 625 - 400
AH2 = 225
AH = 15
Ответ: AH = 15
F80C88
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=1. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 24 + 1 = 25 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 252 - 242
AH2 = 625 - 576
AH2 = 49
AH = 7
Ответ: AH = 7
FDB483
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 24 + 2 = 26 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 262 - 242
AH2 = 676 - 576
AH2 = 100
AH = 10
Ответ: AH = 10
745683
Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH=21+8=29 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2=AH2+DH2
292=AH2+212
841=AH2+441
AH2=400
AH=20
Ответ: AH=20
B5384B
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=6. Найдите высоту ромба.
Решение:
AB=BC=CD=AD=DH+CH= 24 + 6 = 30 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 302 - 242
AH2 = 900 - 576
AH2 = 324
AH = 18
Ответ: AH = 18
8C5FB4
