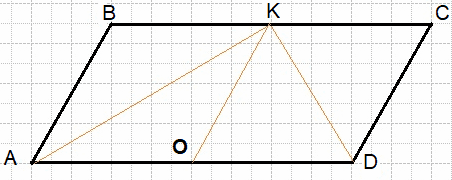Номер 24 в ОГЭ по математике относится к геометрии. Это задание с расширенным ответом. Нужно доказать какое-либо утверждение. Давайте разберемся, какие задания к этому номеру есть в открытом банке ФИПИ и как их решать. 15 типов задач.
Реальные задания по геометрии из банка ФИПИ
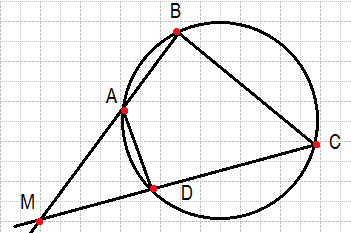
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Решение:
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180°, поэтому ∠DAB +∠ BCD=180º. Углы MAD и DAB образуют развёрнутый угол, значит, ∠MAD+∠DAB=180º. Из приведённых равенств получаем, что ∠BCD=∠MAD. Рассмотри треугольники MBC и MDA, угол M — общий, углы BCD и MAD равны, следовательно, треугольники подобны.
9B683D
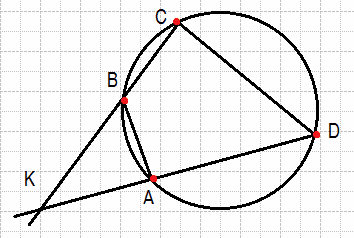
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Решение:
Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°. Следовательно, ∠KDC =180° − ∠ADC = ∠ABC.
Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.
B81A7C
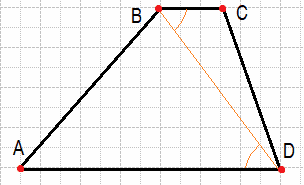
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
5 = 10
10 20
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
A810F6
Основания BC и AD трапеции ABCD равны соответственно 4,5 и 18, BD=9. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
4.5 = 9
9 18
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
E7E298
Основания BC и AD трапеции ABCD равны соответственно 3 и 12, BD=6. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
3 = 6
6 12
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
BE34E8
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
4 = 16
16 64
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:4 и в другом треугольнике 4:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
BE9A49
Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
5 = 15
15 45
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:3 и в другом треугольнике 3:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
9D9F45
Основания BC и AD трапеции ABCD равны соответственно 6 и 24, BD=12. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
6 = 12
12 24
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
D294F5
Основания BC и AD трапеции ABCD равны соответственно 7 и 28, BD=14. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
7 = 14
14 28
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
7487CE
Основания BC и AD трапеции ABCD равны соответственно 8 и 32, BD=16. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
8 = 16
16 32
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
25581B
Основания BC и AD трапеции ABCD равны соответственно 9 и 36, BD=18. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
9 = 18
18 36
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:2 и в другом треугольнике 2:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
F149FA
Основания BC и AD трапеции ABCD равны соответственно 2 и 32, BD=8. Докажите, что треугольники CBD и BDA подобны.
Решение:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. Заметим, что соотношения в треугольниках CBD и ADB:
BC = BD
BD AD
2 = 8
8 32
, следовательно, эти треугольники подобны по двум парам пропорциональных сторон (BD общая сторона, которая имеет прилежащий равный угол (∠CBD=∠BDA) и отношение со смежной стороной 1:4 и в другом треугольнике 4:1). То есть соотношение сторон сохраняется и есть одинаковый угол между ними.
Примечание.
Здесь важно заметить, что несмотря на то, что треугольники подобные, они при своем подобии фактически подменяют символьный порядок вершин, так как стороны при соотношении, если можно выразиться меняются местами, большая сторона в одном треугольнике становится меньшей стороной в другом.
9F76F4
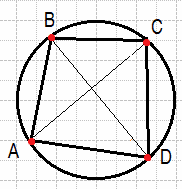
В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
Решение:
Воспользуемся теоремой: если отрезок АВ виден из точек С и D, лежащих по одну сторону от прямой АВ, под одним и тем же углом, то точки А, В, С, D лежат на одной окружности (см. рис.). А тогда ∠ABD = ∠ACD как вписанные углы, опирающиеся на одну дугу AD. Что и требовалось доказать.
367109
В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
Решение:
Поскольку ABCD выпуклый и ∠ABD = ∠ACD, получаем, что около четырёхугольника ABCD можно описать окружность. А тогда ∠DAC = ∠DBC как вписанные углы, опирающиеся на одну дугу CD.
3AA429
В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.
Решение:
Поскольку четырехугольник ABCD выпуклый и ∠DAC=∠DBC, около четырехугольника ABCD можно описать окружность. Значит, ∠CDB=∠CAB как вписанные углы, опирающиеся на одну дугу ВС.
1F1A22
В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA и BDA также равны.
Решение:
Поскольку четырехугольник ABCD выпуклый и ∠CDB=∠CAB, около четырехугольника ABCD можно описать окружность. Значит, ∠BCA=∠BDA как вписанные углы, опирающиеся на одну дугу ВA.
613B4F
Дайте развернутый ответ. 2025
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
Решение:
Дубль номера F57F67
Номер: E85022
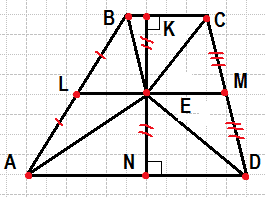
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
Решение:
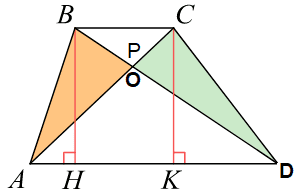
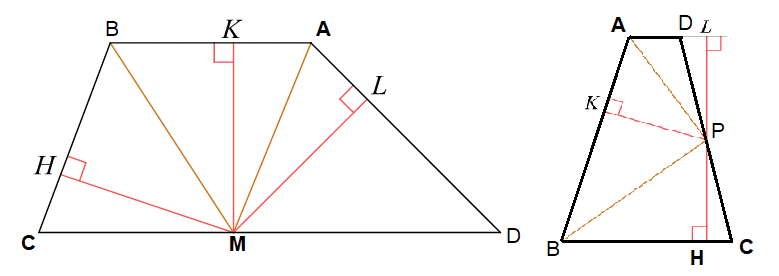
Введём обозначения, как показано на рисунке. Проведём высоту EN через точку K. Поскольку LM — средняя линия, LM параллельно AD и параллельно BC. Отрезки AL и BL равны, следовательно, по теореме Фалеса, EK=EN.
SΔBCE = 1/2 * BC * EK.
SΔAED = 1/2 * AD * KN.
Найдём сумму площадей этих треугольников и сравним с площадью трапеции по формуле, где площадь равна половине суммы оснований умноженная на высоту:
SΔAED+SΔBCE=
=$\frac12\ast BC\ast EK+\;\frac12\ast AD\ast NE=\;\frac12\ast BC\ast NE+\;\frac12\ast AD\ast NE=\\=\frac12\ast NE\;(BC+AD)=\frac12\ast\frac{KN}2\;(BC+AD)$
отсюда как раз и видно, что сумма площадей треугольников равна половине площади трапеции.
F57F67
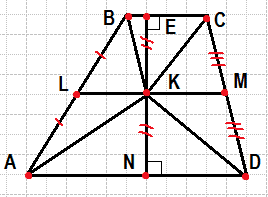
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
Решение:
Введём обозначения, как показано на рисунке. Проведём высоту EN через точку K. Поскольку LM — средняя линия, LM параллельно AD и параллельно BC. Отрезки AL и BL равны, следовательно, по теореме Фалеса, EK=KN.
SΔBCK = 1/2 * BC * EK.
SΔAKD = 1/2 * AD * KN.
Найдём сумму площадей этих треугольников и сравним с площадью трапеции по формуле, где площадь равна половине суммы оснований умноженная на высоту:
SΔAKD+SΔBCK=
=$\frac12\ast BC\ast EK+\;\frac12\ast AD\ast KN=\;\frac12\ast BC\ast KN+\;\frac12\ast AD\ast KN=\\=\frac12\ast KN\;(BC+AD)=\frac12\ast\frac{EN}2\;(BC+AD)$
отсюда как раз и видно, что сумма площадей треугольников равна половине площади трапеции.
8A0155
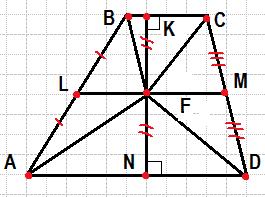
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
Решение:
Введём обозначения, как показано на рисунке. Проведём высоту EN через точку K. Поскольку LM — средняя линия, LM параллельно AD и параллельно BC. Отрезки AL и BL равны, следовательно, по теореме Фалеса, FK=FN.
SΔBCF = 1/2 * BC * FK.
SΔAFD = 1/2 * AD * FN.
Найдём сумму площадей этих треугольников и сравним с площадью трапеции по формуле, где площадь равна половине суммы оснований умноженная на высоту:
SΔAFD+SΔBCF=
=$\frac12\ast BC\ast KF+\;\frac12\ast AD\ast NF=\;\frac12\ast BC\ast NF+\;\frac12\ast AD\ast NF=\\=\frac12\ast NF\;(BC+AD)=\frac12\ast\frac{KN}2\;(BC+AD)$
отсюда как раз и видно, что сумма площадей треугольников равна половине площади трапеции.
7A5DF6
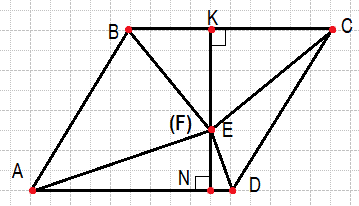
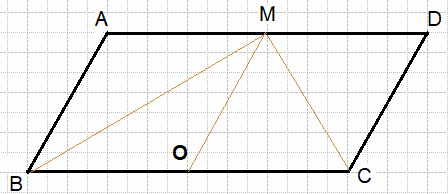
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Решение:
Поставим точку Е и проведем стороны треугольника. Из вершины Е треугольников построим высоты. Площадь параллелограмма равна основание умноженное на высоту. Sabcd = KN*AD, теперь выразим площадь двух треугольников AED и BEC.
$SBEC+SAED=\frac12NE\ast AD+\frac12KE\ast BC=\frac12AD(NE+KE)=\frac12AD\ast KN$
Отсюда собственно и видно, что площадь двух треугольников равна половине площади трапеции.
BD4A4E
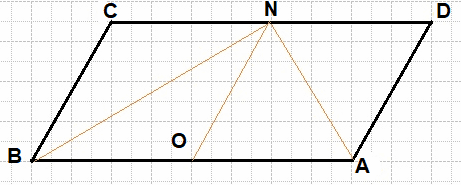
Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
Решение:
Поставим точку Е и проведем стороны треугольника. Из вершины Е треугольников построим высоты. Площадь параллелограмма равна основание умноженное на высоту. Sabcd = KN*AD, теперь выразим площадь двух треугольников AED и BEC.
$SBFC+SAFD=\frac12NF\ast AD+\frac12KF\ast BC=\frac12AD(NF+KF)=\frac12AD\ast KN$
Отсюда собственно и видно, что площадь двух треугольников равна половине площади трапеции.
0796BC
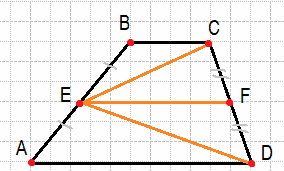
Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
Решение:
Поставим точку Е и проведем среднюю линию трапеции. При этом мы знаем, что площадь трапеции равна сумме оснований, умноженная на высоту и все это поделить на 2, то есть SABCD = 1/2*(BC+AD)*H/
Теперь найдем площадь треугольников DEF и CEF
$SDEF+SCEF=\frac{1\;}2\ast\frac H2\ast EF+\frac{1\;}2\ast\frac H2\ast EF=2\ast\frac{1\;}2\ast\frac H2\ast EF\\=\frac{1\;}2\ast H\ast EF=\frac12\ast H\ast\frac{BC+AD}2$
Из этого равенства видно, что площадь этих двух треугольников как раз и равна площади трапеции.
955204
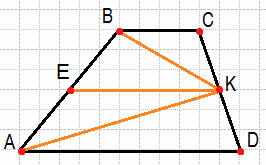
Точка K — середина боковой стороны CD трапеции ABCD. Докажите, что площадь треугольника KAB равна половине площади трапеции.
Решение:
Поставим точку Е и проведем среднюю линию трапеции. При этом мы знаем, что площадь трапеции равна сумме оснований, умноженная на высоту и все это поделить на 2, то есть SABCD = 1/2*(BC+AD)*H/
Теперь найдем площадь треугольников DEF и CEF
$SBKE+SAKE=\frac{1\;}2\ast\frac H2\ast EK+\frac{1\;}2\ast\frac H2\ast EK=2\ast\frac{1\;}2\ast\frac H2\ast EK\\=\frac{1\;}2\ast H\ast EK=\frac12\ast H\ast\frac{BC+AD}2$
Из этого равенства видно, что площадь этих двух треугольников как раз и равна площади трапеции.
ABC508
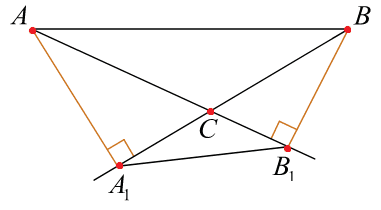
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы AA1B1 и ABB1 равны.
Решение:
Если отрезок AB имеет лучи отрезки исходящие из его концов к точкам А1 и B1, лежащих по одну сторону от прямой AB, под одним и тем же углом (90°), то точки A, B, А1, B1 лежат на одной окружности:
Тогда углы ∠AA1B1 и ∠ABB1 вписанные в окружность, опираются на одну и туже дугу ‿AB1, значит они равны:
∠AA1B1 = ∠ABB1
Что и требовалось доказать.
6B3568
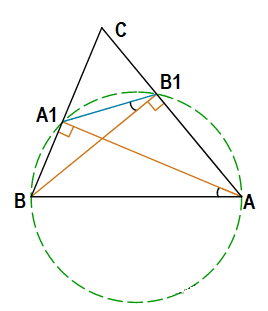
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
Решение:
Если отрезок AB имеет лучи отрезки исходящие из его концов к точкам А1 и B1, лежащих по одну сторону от прямой AB, под одним и тем же углом (90°), то точки A, B, А1, B1 лежат на одной окружности:
Тогда углы ∠BB1А1 и ∠BАА1 вписанные в окружность, опираются на одну и туже дугу ‿A1B, значит они равны:
∠BB1А1 = ∠BАА1
Что и требовалось доказать.
1B07A7
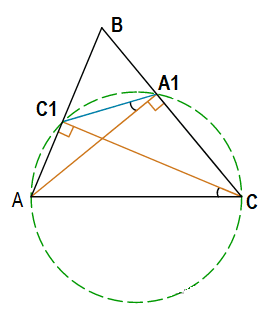
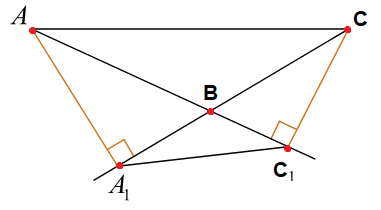
В остроугольном треугольнике ABC проведены высоты AA1 и CC1. Докажите, что углы AA1C1 и ACC1 равны.
Решение:
Если отрезок AC имеет лучи отрезки исходящие из его концов к точкам А1 и C1, лежащих по одну сторону от прямой AC, под одним и тем же углом (90°), то точки A, C, А1, C1 лежат на одной окружности:
Тогда углы ∠AA1C1 и ∠ACC1 вписанные в окружность, опираются на одну и туже дугу ‿AC1, значит они равны:
∠AA1C1 = ∠ACC1
Что и требовалось доказать.
37CCE6
В остроугольном треугольнике ABC проведены высоты AA1 и CC1. Докажите, что углы CC1A1 и CAA1 равны.
Решение:
Если отрезок AC имеет лучи отрезки исходящие из его концов к точкам А1 и C1, лежащих по одну сторону от прямой AC, под одним и тем же углом (90°), то точки A, C, А1, C1 лежат на одной окружности:
Тогда углы ∠CC1A1 и ∠CAA1 вписанные в окружность, опираются на одну и туже дугу ‿A1C, значит они равны:
∠CC1A1 = ∠CAA1
Что и требовалось доказать.
DFBC4D
В остроугольном треугольнике ABC проведены высоты BB1 и CC1. Докажите, что углы BB1C1 и BCC1 равны.
Решение:
Если отрезок BC имеет лучи отрезки исходящие из его концов к точкам B1 и C1, лежащих по одну сторону от прямой AC, под одним и тем же углом (90°), то точки B, C, B1, C1 лежат на одной окружности:
Тогда углы ∠BB1C1 и ∠BCC1 вписанные в окружность, опираются на одну и туже дугу ‿A1C, значит они равны:
∠BB1C1 = ∠BCC1
Что и требовалось доказать.
39A131
В остроугольном треугольнике ABC проведены высоты BB1 и CC1. Докажите, что углы CC1B1 и CBB1 равны.
Решение:
Треугольники CBB1 и CC1B имеют общую гипотенузу BC. Поэтому точки C,B, C1, B1 лежат на одной окружности. Углы CC1B1 и CBB1 опираются на одну дугу, и поэтому равны.
DE7034
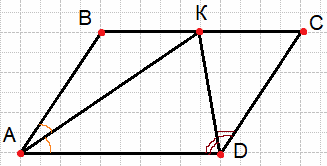
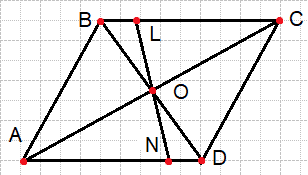
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке K, лежащей на стороне BC. Докажите, что K — середина BC.
Решение:
По определению параллелограмма основание BC параллельно AD, AК — секущая при параллельных прямых, следовательно, углы BКA и КAD равны как накрест лежащие. Поскольку ∠BКA=∠BAК, треугольник ABК — равнобедренный, откуда AB=BК. Аналогично, треугольник CКD — равнобедренный и КC=CD. Стороны AB и CD равны, как противоположные стороны параллелограмма, следовательно:
AB=BК=КC=CD. Таким образом, точка E — середина стороны BC.
B14289
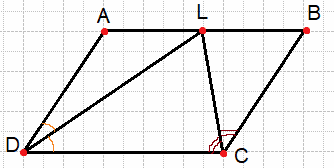
Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке L, лежащей на стороне AB. Докажите, что L — середина AB.
Решение:
По определению параллелограмма основание BC параллельно AD, DL — секущая при параллельных прямых, следовательно, углы ALD и LDC равны как накрест лежащие. А так как ∠ADL=∠ALD, треугольник DAL — равнобедренный, откуда DA=AL. Аналогично, треугольник LCB — равнобедренный и LB=BC. Стороны AB и CD равны, как противоположные стороны параллелограмма, следовательно:
AD=AL=LB=BC. Таким образом, точка L — середина стороны AB.
36C482
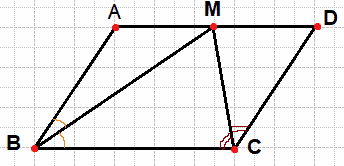
Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M, лежащей на стороне AD. Докажите, что M — середина AD.
Решение:
По определению параллелограмма основание BC параллельно AD, BM — секущая при параллельных прямых, следовательно, углы AMD и MBC равны как накрест лежащие. А так как ∠ABM=∠MBC, треугольник BAM — равнобедренный, откуда BA=AM. Аналогично, треугольник MCD — равнобедренный и MD=DC. Стороны AB и CD равны, как противоположные стороны параллелограмма, следовательно:
BA=AM=MD=DC. Таким образом, точка M — середина стороны AD.
E3F9F8
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N, лежащей на стороне CD. Докажите, что N — середина CD.
Решение:
По определению параллелограмма основание BC параллельно AB, DC — секущая при параллельных прямых, следовательно, углы DNA и NAB равны как накрест лежащие. А так как ∠DAN=∠NAB, треугольник ADN — равнобедренный, откуда AD=DN. Аналогично, треугольник NCB — равнобедренный и NC=CB. Стороны AD и CB равны, как противоположные стороны параллелограмма, следовательно:
AD=DN=NC=CB. Таким образом, точка N — середина стороны CD.
C7AA3F
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.
Решение:
Проведём высоты BH и CK, они равны. Площадь треугольника ABD равна дробь:
1/2*AD*BH
Площадь треугольника ACD равна дробь:
1/2*AD*CK
Поскольку высоты BH и CK равны, равны и площади треугольников ABD и CAD. Однако в этих треугольниках есть общая составляющая, это треугольник AOD, то есть если из площади треугольника ABD вычесть площадь треугольник AOD, то будет получена площадь треугольника ABO. И также если из площади треугольника ACD вычесть площадь AOD, то будет площадь COD. Из этого можно сделать заключение, что треугольники ABO и COD равны.
SAOB=SABD - SAOD=SCAD - SAOD=SCOD.
DAEC5D
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P. Докажите, что площади треугольников APB и CPD равны.
Решение:
Проведём высоты BH и CK, они равны. Площадь треугольника ABD равна дробь:
1/2*AD*BH
Площадь треугольника ACD равна дробь:
1/2*AD*CK
Поскольку высоты BH и CK равны, равны и площади треугольников ABD и CAD. Однако в этих треугольниках есть общая составляющая, это треугольник APD, то есть если из площади треугольника ABD вычесть площадь треугольник APD, то будет получена площадь треугольника ABP. И также если из площади треугольника ACD вычесть площадь APD, то будет площадь CPD. Из этого можно сделать заключение, что треугольники ABP и CPD равны.
SAPB=SABD - SAPD=SCAD - SAPD=SCPD.
2EF3D2
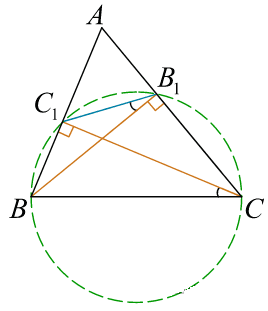
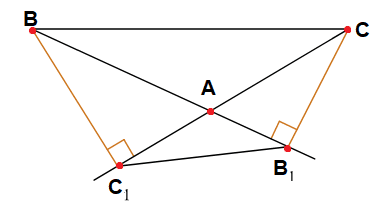
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Решение:
Поскольку угол ACB тупой, основания высот A1 и B1 будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA1B1B пересекаются, поэтому он выпуклый. Поскольку ∠AA1B = ∠AB1B = 90°, каждый из прямоугольных треугольников AA1B и AB1B вписан в окружность с диаметром AB. Это означает, что все вершины четырёхугольника AA1B1B лежат на одной окружности. Тогда углы ∠AB1A1 и ∠ABA1 равны как вписанные углы, опирающиеся на дугу A1A. Аналогично, ∠BA1B1 = ∠BAB1. Значит, указанные треугольники подобны по двум углам.
Приведем решение 2
Поскольку угол ACB тупой, основания высот A1 и B1 будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA1B1B пересекаются, поэтому он выпуклый. Треугольники ACA1 и BCB1 подобны по двум углам, поскольку ∠AA1C = ∠BB1C = 90°, ∠ACA1 = ∠BCB1 равны как вертикальные. Значит, указанные треугольники подобны по двум углам.
A57F97
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Решение:
Поскольку угол ABC тупой, основания высот A1 и C1 будут лежать на продолжениях сторон CA1 и AC1 соответственно. Диагонали четырёхугольника AA1C1C пересекаются, поэтому он выпуклый. Поскольку ∠AA1B = ∠BC1C = 90°, каждый из прямоугольных треугольников AA1B и BC1C вписан в окружность с диаметром AC. Это означает, что все вершины четырёхугольника AA1C1C лежат на одной окружности. Тогда углы ∠ACA1 и ∠AC1C1 равны как вписанные углы, опирающиеся на дугу A1A. Аналогично, ∠CAC1 = ∠CA1C1. Значит, указанные треугольники A1BC1 и ABC подобны по двум углам.
Приведем решение 2
Поскольку угол ACB тупой, основания высот A1 и C1 будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA1C1C пересекаются, поэтому он выпуклый. Треугольники A1BC1 и ABC подобны по двум углам, поскольку ∠AA1B = ∠BC1C = 90°, ∠ABA1 = ∠CBC1 равны как вертикальные. Значит, указанные треугольники A1BC1 и ABC подобны по двум углам.
B35E5A
В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
Решение:
Поскольку угол BAC тупой, основания высот B и C будут лежать на продолжениях сторон B1B и C1C соответственно. Диагонали четырёхугольника BC1B1C пересекаются, поэтому он выпуклый. Поскольку ∠BC1A = ∠CB1A = 90°, каждый из прямоугольных треугольников BC1A и CB1A вписан в окружность с диаметром BC. Это означает, что все вершины четырёхугольника BC1B1C лежат на одной окружности. Тогда углы ∠BCC1 и ∠BB1C1 равны как вписанные углы, опирающиеся на дугу BC1. Аналогично, ∠CC1B1 = ∠B1BC. Значит, указанные треугольники AB1C1 и ABC подобны по двум углам.
Приведем решение 2
Поскольку угол ACB тупой, основания высот B и C будут лежать на продолжениях сторон B1B и C1C соответственно. Диагонали четырёхугольника BC1B1C пересекаются, поэтому он выпуклый. Треугольники AB1C1 и ABC подобны по двум углам, поскольку ∠BC1A = ∠CB1A = 90°, ∠BAC1 = ∠CAB1 равны как вертикальные. Значит, указанные треугольники AB1C1 и ABC подобны по двум углам.
2FEF51
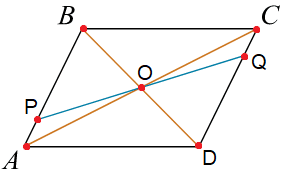
Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и Q соответственно. Докажите, что отрезки BP и DQ равны.
Решение:
Треугольники BOP и DOQ равны по стороне и двум прилежащим к ней углам: BO = OD, поскольку диагонали параллелограмма точкой пересечения делятся пополам, ∠BOP=∠DOQ как вертикальные, ∠PBO= ∠ODQ как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей BD. Из равенства треугольников следует равенство их сходственных сторон: BP = DQ. Что и требовалось доказать.
B609A6
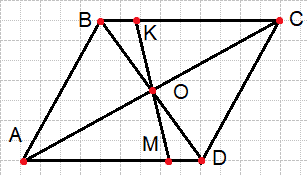
Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны BC и AD в точках K и M соответственно. Докажите, что отрезки BK и DM равны.
Решение:
Треугольники BOK и MOD равны по стороне и двум прилежащим к ней углам: BO = OD, поскольку диагонали параллелограмма точкой пересечения делятся пополам, ∠BOK= ∠MOD как вертикальные, ∠ODM=∠OBK как накрест лежащие углы при пересечении параллельных прямых BC и AD секущей BD. Из равенства треугольников следует равенство их сходственных сторон: BK = DM. Что и требовалось доказать.
18E434
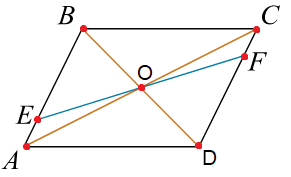
Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках E и F соответственно. Докажите, что отрезки AE и CF равны.
Решение:
Треугольники AOE и COF равны по стороне и двум прилежащим к ней углам: AO = CO, поскольку диагонали параллелограмма точкой пересечения делятся пополам, ∠AOE=∠COF как вертикальные, ∠OAE= ∠OCF как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей AC. Из равенства треугольников следует равенство их сходственных сторон: AE = CF. Что и требовалось доказать.
D2ED10
Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны BC и AD в точках L и N соответственно. Докажите, что отрезки CL и AN равны.
Решение:
Треугольники LOC и AON равны по стороне и двум прилежащим к ней углам: AO = CO, поскольку диагонали параллелограмма точкой пересечения делятся пополам, ∠LOC=∠AON как вертикальные, ∠LCO= ∠AON как накрест лежащие углы при пересечении параллельных прямых BC и AD секущей BD. Из равенства треугольников следует равенство их сходственных сторон: CL = AN. Что и требовалось доказать.
3842C4
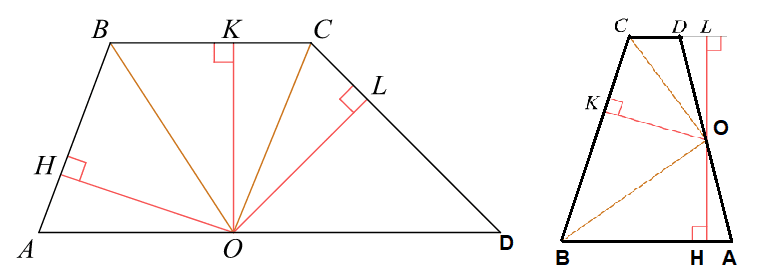
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Решение:
В задаче возможны два случая.
Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
Вариант задачи 2
Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
632804
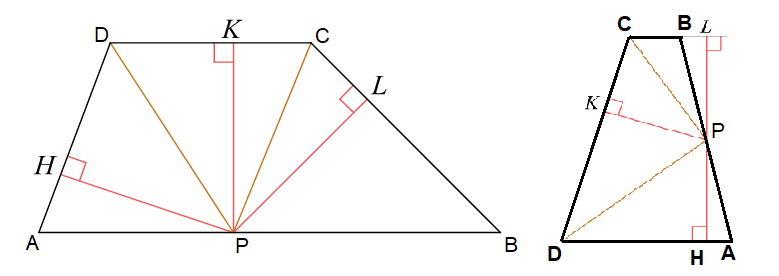
Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
Решение:
В задаче возможны два случая.
Первый случай, AB — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники DPH и DPK, они прямоугольные, углы HDP и KDP равны, DP — общая, следовательно, треугольники равны. Откуда HP = KP. Аналогично из треугольников KPC и CPL получаем, что KP = PL. Таким образом, HP = KP = PL.
Вариант задачи 2
Второй случай, AB — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
D57685
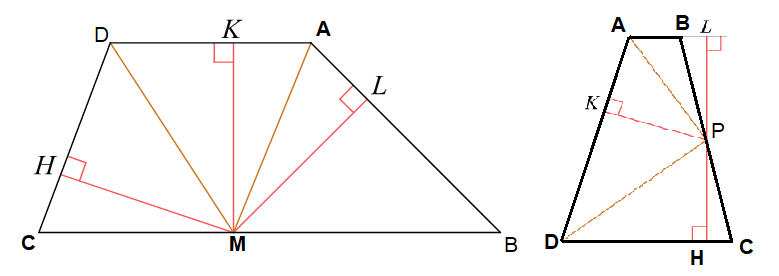
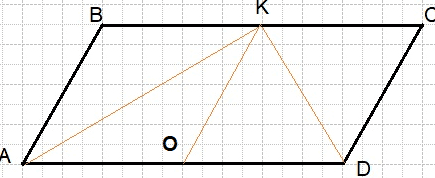
Биссектрисы углов A и D трапеции ABCD пересекаются в точке M, лежащей на стороне BC. Докажите, что точка M равноудалена от прямых AB, AD и CD.
Решение:
В задаче возможны два случая.
Первый случай, CB — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники DMH и DMK, они прямоугольные, углы HDM и KDM равны, DM — общая, следовательно, треугольники равны. Откуда HM = KM. Аналогично из треугольников KMA и AML получаем, что KM = ML. Таким образом, HM = KM = LM.
Вариант задачи 2
Второй случай, CB — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
991A27
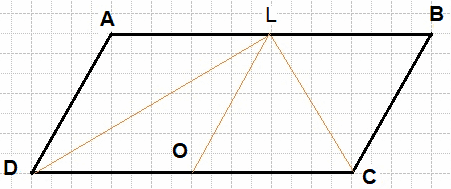
Биссектрисы углов A и B трапеции ABCD пересекаются в точке K, лежащей на стороне CD. Докажите, что точка K равноудалена от прямых AB, BC и AD.
Решение:
В задаче возможны два случая.
Первый случай, CD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники HMB и BMK, они прямоугольные, углы HBM и KBM равны, BM — общая, следовательно, треугольники равны. Откуда HM = KM. Аналогично из треугольников KMA и AML получаем, что KM = ML. Таким образом, HM = KM = LM.
Вариант задачи 2
Второй случай, CD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
730010
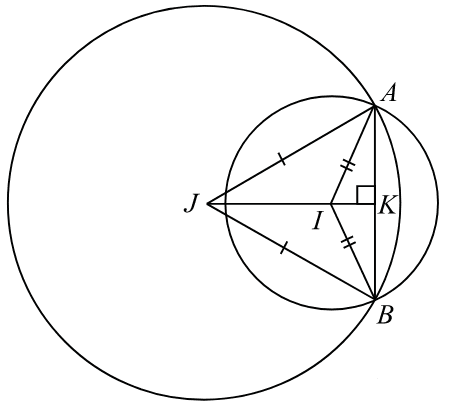
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что прямые AB и IJ перпендикулярны.
Решение:
Проведём медиану JK треугольника AJB. Стороны AJ и BJ равны как радиусы окружности, поэтому треугольник ABJ — равнобедренный, следовательно, медиана JK является также высотой. Проведём медиану IK. Стороны AI и BI равны как радиусы окружности, поэтому треугольник ABI — равнобедренный, следовательно, медиана IK является также высотой. Прямые JK и IM перпендикулярны одной и той же прямой AB, следовательно, они параллельны. Эти прямые проходят через одну и ту же точку M, значит, они совпадают. Таким образом, прямая AB перпендикулярна прямой IJ.
C60AED
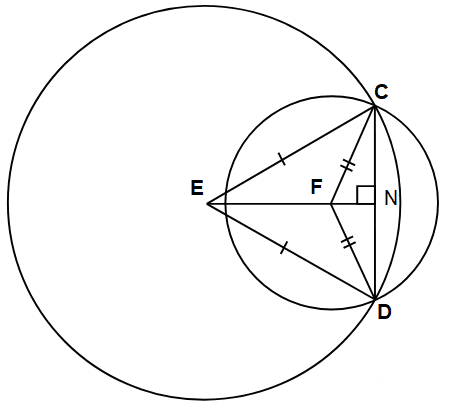
Окружности с центрами в точках E и F пересекаются в точках C и D, причём точки E и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.
Решение:
Проведём медиану EN треугольника CED. Стороны CE и ED равны как радиусы окружности, поэтому треугольник CED — равнобедренный, следовательно, медиана EN является также высотой. Проведём медиану IN. Стороны CF и FD равны как радиусы окружности, поэтому треугольник CFD — равнобедренный, следовательно, медиана IN является также высотой. Прямые EF (лежит на EN) и FN перпендикулярны одной и той же прямой CD, следовательно, они параллельны. Эти прямые проходят через одну и ту же точку N, значит, они совпадают. Таким образом, прямая CD перпендикулярна прямой EF.
B32AEC
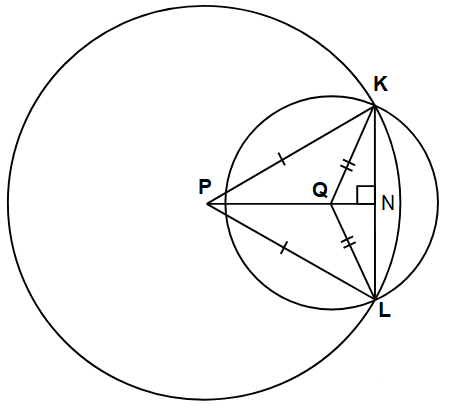
Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по одну сторону от прямой KL. Докажите, что прямые PQ и KL перпендикулярны.
Решение:
Проведём медиану PN треугольника KPL. Стороны PK и PL равны как радиусы окружности, поэтому треугольник KPL — равнобедренный, следовательно, медиана PN является также высотой. Проведём медиану QN. Стороны QN и QL равны как радиусы окружности, поэтому треугольник KQL — равнобедренный, следовательно, медиана QN является также высотой. Прямые PN и QN перпендикулярны одной и той же прямой KL, следовательно, они параллельны. Эти прямые проходят через одну и ту же точку N, значит, они совпадают. Таким образом, прямая PQ (лежит на PN) перпендикулярна прямой KL.
40EA31
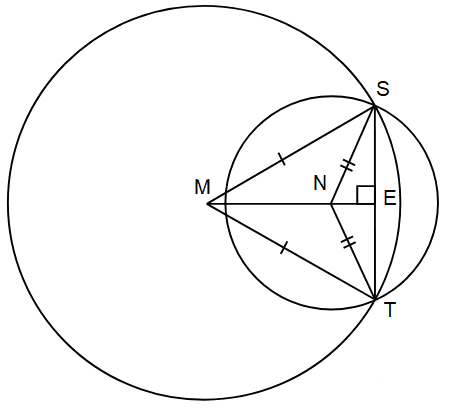
Окружности с центрами в точках M и N пересекаются в точках S и T, причём точки M и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
Решение:
Проведём медиану ME треугольника SMT. Стороны SM и MT равны как радиусы окружности, поэтому треугольник SMT — равнобедренный, следовательно, медиана PN является также высотой. Проведём медиану NE. Стороны SN и NT равны как радиусы окружности, поэтому треугольник SNT — равнобедренный, следовательно, медиана NE является также высотой. Прямые ME и NE перпендикулярны одной и той же прямой ST, следовательно, они параллельны. Эти прямые проходят через одну и ту же точку E, значит, они совпадают. Таким образом, прямая MN (лежит на ME) перпендикулярна прямой ST.
6BB457
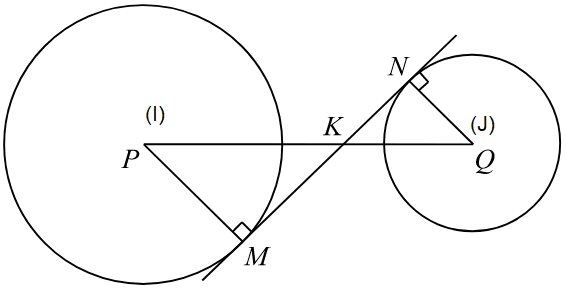
Окружности с центрами в точках I и J не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.
Решение:
Проведём построения и введём обозначения, как показано на рисунке. Пусть
$\frac{PQ}{QK}=\frac mn$
Рассмотрим треугольники PKM и QKN, они прямоугольные, углы PKM и NKQ равны как вертикальные, следовательно, треугольники подобны, откуда
$\frac{PM}{QN}=\frac{PQ}{QK}=\frac mn$
Отношение радиусов равно отношению m:n.
04B467
Окружности с центрами в точках P и Q не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
Решение:
Проведём построения и введём обозначения, как показано на рисунке. Пусть
$\frac{PQ}{QK}=\frac ab$
Рассмотрим треугольники PKM и QKN, они прямоугольные, углы PKM и NKQ равны как вертикальные, следовательно, треугольники подобны, откуда
$\frac{PM}{QN}=\frac{PQ}{QK}=\frac ab$
Отношение радиусов равно отношению a:b.
51ABBB
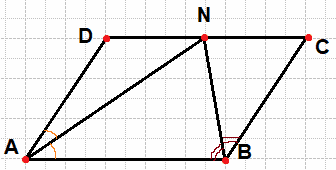
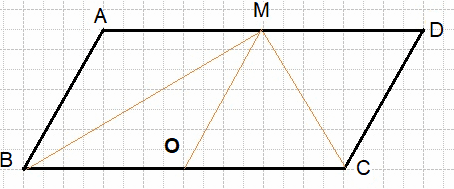
Сторона BC параллелограмма ABCD вдвое больше стороны AB. Точка K — середина стороны BC. Докажите, что AK — биссектриса угла BAD.
Решение:
Проведём KO параллельно AB (см. рис.). Тогда AB = BK = KC. Следовательно, параллелограмм ABKO является ромбом. Диагональ AK ромба ABKO является биссектрисой угла BAO.
079233
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка L — середина стороны AB. Докажите, что DL — биссектриса угла ADC.
Решение:
Проведём LO параллельно AD (см. рис.). Тогда AD = LO = AL. Следовательно, параллелограмм ADOL является ромбом. Диагональ DL ромба ADOL является биссектрисой угла ADC.
13AC23
Сторона AD параллелограмма ABCD вдвое больше стороны CD. Точка M — середина стороны AD. Докажите, что CM — биссектриса угла BCD.
Решение:
Проведём MO параллельно AB (см. рис.). Тогда MD = DC = MO. Следовательно, параллелограмм MOCD является ромбом. Диагональ CM ромба MOCD является биссектрисой угла BCD.
FA5D37
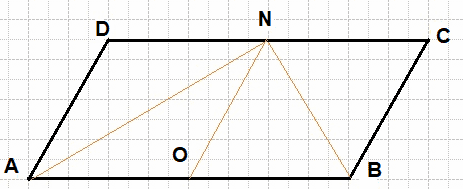
Сторона CD параллелограмма ABCD вдвое больше стороны AD. Точка N — середина стороны CD. Докажите, что AN — биссектриса угла BAD.
Решение:
Проведём NO параллельно AD (см. рис.). Тогда AD = NO = DN. Следовательно, параллелограмм DAON является ромбом. Диагональ AN ромба DAON является биссектрисой угла BAD.
E90E86
Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка K — середина стороны BC. Докажите, что DK — биссектриса угла ADC.
Решение:
Проведём KO параллельно CD (см. рис.). Тогда KC = CD = KO. Следовательно, параллелограмм KCDO является ромбом. Диагональ KD ромба KCDO является биссектрисой угла ADC.
4E334E
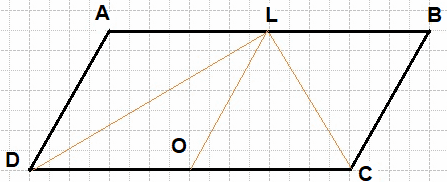
Сторона AB параллелограмма ABCD вдвое больше стороны BC. Точка L — середина стороны AB. Докажите, что CL — биссектриса угла BCD.
Решение:
Проведём LO параллельно BC (см. рис.). Тогда LB = BC = CO. Следовательно, параллелограмм LBCO является ромбом. Диагональ LC ромба LBCO является биссектрисой угла BCD.
9A9096
Сторона AD параллелограмма ABCD вдвое больше стороны AB. Точка M — середина стороны AD. Докажите, что BM — биссектриса угла ABC.
Решение:
Проведём MO параллельно AB (см. рис.). Тогда AB = AM = MO. Следовательно, параллелограмм ABOM является ромбом. Диагональ MO ромба ABOM является биссектрисой угла ABC.
006642
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка N — середина стороны CD. Докажите, что BN — биссектриса угла ABC.
Решение:
Проведём NO параллельно BC (см. рис.). Тогда BC = CN = NO. Следовательно, параллелограмм CBON является ромбом. Диагональ BN ромба CBON является биссектрисой угла ABC.
367AFE