Среди заданий на нахождение площади трапеции есть те, которые требуют развернутого решения, и те, для которых достаточно в ответе лишь числа. Рассмотрим их типы, имеющиеся в открытом банке заданий ФИПИ. Любое из заданий ниже может вам попасться на ОГЭ по математике в этом году в разделе геометрии.

Вспоминаем, что площадь трапеции равна произведению полусуммы оснований на высоту:
$S=\frac{a+b}2\ast h$

Реальные задания по геометрии из банка ФИПИ 

Основания трапеции равны 4 и 10, а высота равна 5. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{4+10}2\ast5=35$

Ответ: 35

3E05A1

Основания трапеции равны 3 и 5, а высота равна 9. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{3+5}2\ast9=36$

Ответ: 36

FB21B9

Основания трапеции равны 4 и 12, а высота равна 6. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{4+12}2\ast6=48$

Ответ: 48

DC3C24

Основания трапеции равны 7 и 11, а высота равна 7. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{7+11}2\ast7=63$

Ответ: 63

A3751A

Основания трапеции равны 2 и 4, а высота равна 11. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{2+4}2\ast11=33$

Ответ: 33

6839CB

Основания трапеции равны 6 и 14, а высота равна 8. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{6+14}2\ast8=80$

Ответ: 80

822BB2

Основания трапеции равны 7 и 19, а высота равна 6. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{7+19}2\ast6=78$

Ответ: 78

F70300

Основания трапеции равны 8 и 14, а высота равна 5. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{8+14}2\ast5=55$

Ответ: 55

444775

Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{5+13}2\ast9=81$

Ответ: 81

39FB77

Основания трапеции равны 13 и 23, а высота равна 5. Найдите площадь этой трапеции.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{13+23}2\ast5=90$

Ответ: 90

FEC9A6

---

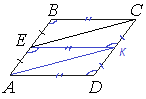
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение 2-мя способами:

1 способ


Так как ABCD - параллелограмм, то AВ = CD.
Пусть точка К - середина стороны CD.
Так как по условию точка Е - середина стороны АВ, то
AE = BE = DK = KC .
ВС  = АD = ЕК (средняя линия)
∠В = ∠АЕК - соответственные углы
∠В = ∠D - противолежащие углы параллелограмма
∠D = ∠ЕКС - соответственные ⇒
отрезки AK, KE и EC разбивают параллелограмм на 4 равновеликих треугольника (по двум сторонам и углу между ними) ⇒
S_DAK = S_АКЕ = S_КЕС = S_ВСЕ = 180 / 4 = 45
Площадь трапеции состоит из трёх равновеликих треугольников ⇒
S_DAEC = 45 * 3 = 135 кв.ед.

Ответ: 135

Лайфхак для быстрого решения: площадь параллелограмма разделим на 4 и умножим на 3

S_{трапеции} = S_{паралл.} : 4 * 3

2 способ


Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 180 / 2 = 90.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 90 / 2 = 45. Следовательно,

S_AECD = S_ABCD - S_CDE = 180 - 45 = 135.

Ответ: 135

40519C

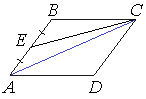
Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 60 / 2 = 30.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 30 / 2 = 15. Следовательно,

S_AECD = S_ABCD - S_CDE = 60 - 15 = 45.

Ответ: 45

41DF2E

Площадь параллелограмма ABCD равна 32. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 32 / 2 = 16.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 16 / 2 = 8. Следовательно,

S_AECD = S_ABCD - S_CDE = 32 - 8 = 24.

Ответ: 24

FD1877

Площадь параллелограмма ABCD равна 76. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 76 / 2 = 38.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 38 / 2 = 19. Следовательно,

S_AECD = S_ABCD - S_CDE = 76 - 19 = 57.

Ответ: 57

87D35B

Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 96 / 2 = 48.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 48 / 2 = 24. Следовательно,

S_AECD = S_ABCD - S_CDE = 96 - 24 = 72.

Ответ: 72

EFCEB8

Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 104 / 2 = 52.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 52 / 2 = 26. Следовательно,

S_AECD = S_ABCD - S_CDE = 104 - 26 = 78.

Ответ: 78

5A41E8

Площадь параллелограмма ABCD равна 92. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 92 / 2 = 46.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 46 / 2 = 23. Следовательно,

S_AECD = S_ABCD - S_CDE = 92 - 23 = 69.

Ответ: 69

CE80A9

Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 132 / 2 = 66.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 66 / 2 = 33. Следовательно,

S_AECD = S_ABCD - S_CDE = 132 - 33 = 99.

Ответ: 99

0D5AAC

Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 28 / 2 = 14.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 14 / 2 = 7. Следовательно,

S_AECD = S_ABCD - S_CDE = 28 - 7 = 21.

Ответ: 21

9CE80E

Площадь параллелограмма ABCD равна 128. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 128 / 2 = 64.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 64 / 2 = 32. Следовательно,

S_AECD = S_ABCD - S_CDE = 128 - 32 = 96.

Ответ: 96

18E5DD

С подобным рисунком есть задачи и на нахождение площади второй части параллелограмма - треугольника. Их решение можно посмотреть в статье "Найдите площадь треугольника", но на эту страничку тоже продублируем:

Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 132 / 2 = 66.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 66 / 2 = 33

Ответ: 33

9A5992

Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 68 / 2 = 34.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 34 / 2 = 17

Ответ: 17

795F61

Площадь параллелограмма ABCD равна 44. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 44 / 2 = 22.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 22 / 2 = 11

Ответ: 11

1ABE2A

Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 84 / 2 = 42.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 42 / 2 = 21

Ответ: 21

A6BEE2

Площадь параллелограмма ABCD равна 196. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 196 / 2 = 98.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 98 / 2 = 49

Ответ: 49

ADA977

Площадь параллелограмма ABCD равна 112. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 112 / 2 = 56.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 56 / 2 = 28

Ответ: 28

4DB6C1

Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 104 / 2 = 52.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 52 / 2 = 26

Ответ: 26

CDB192

Площадь параллелограмма ABCD равна 148. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 148 / 2 = 74.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 74 / 2 = 37

Ответ: 37

E2BFC0

Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 140 / 2 = 70.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 70 / 2 = 35

Ответ: 35

20E710

Площадь параллелограмма ABCD равна 136. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Решение:

Диагональ параллелограмма делит его на два равных треугольника, поэтому
S_ACВ= 136 / 2 = 68.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
S_CВE = ¹/₂ S_ACВ = 68 / 2 = 34

Ответ: 34

2373D8

---

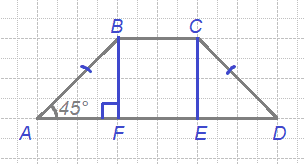
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

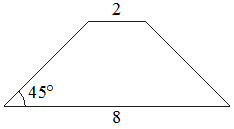
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (8 - 2) / 2 = 3

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 3

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (2 + 8) : 2 * 3 = 15

Ответ: 15

AC6781

В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

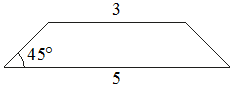
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (5 - 3) / 2 = 1

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 1

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (3 + 5) : 2 * 1 = 4

Ответ: 4

A002C2

В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

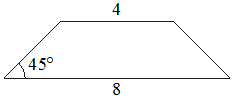
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (8 - 4) / 2 = 2

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (4 + 8) : 2 * 2 = 12

Ответ: 12

03F9DB

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

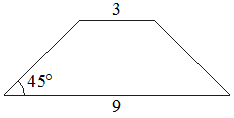
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (9 - 3) / 2 = 3

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 3

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (3 + 9) : 2 * 3 = 18

Ответ: 18

D2652B

В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

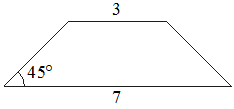
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (7 - 3) / 2 = 2

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (3 + 7) : 2 * 2 = 10

Ответ: 10

1CEEC4

В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

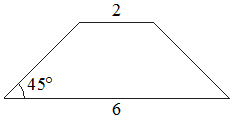
Решение:

Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.

Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (6 - 2) / 2 = 2

Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2

$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
S_АВСD = (2 + 6) : 2 * 2 = 8

Ответ: 8

24CEEC

Задания второй части ОГЭ с развернутым ответом

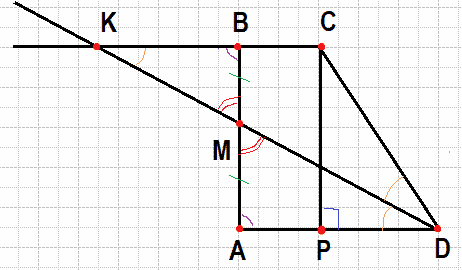
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK будут равны как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CDK  — равнобедренный:
KC = CD = 41.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 41 - 16 = 25.

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD = AD - BC = 25 - 16 = 9

По построению BCPA - параллелограмм, значит
CP=AB=40

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=41²-9²
CP=√(1681-81)=√ 1600=40

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 25, 16 и высота 40. Можем найти площадь трапеции:

$S_{BCAD}=\frac{BC+AD}2\ast CP=\frac{25+16}2\ast40=\frac{41}2\ast40=20,5\ast20=820$

Ответ: 820

0A23B5

Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 25, а основание BC равно 9. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK будут равны как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CDK  — равнобедренный:
KC = CD = 25.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 25 - 9 = 16.

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 16

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=16-9=7

По построению BCPA - параллелограмм, значит
CP = AB = 24

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=25²-7²
CP=√ (625-49)=√ 576=24

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 9, 16 и высота 24. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{9+16}2\ast24=\frac{25}2\ast24=12.5\ast24=300$

Ответ: 300

954230

Боковые стороны AB и CD трапеции ABCD равны соответственно 10 и 26, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=26.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 26 - 1 = 25

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=25-1=24

По построению BCPA - параллелограмм, значит
CP = AB = 10

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=26²-24²
CP=√ (676-576)=√ 100=10

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 25 и высота 10. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+25}2\ast10=\frac{26}2\ast10=13\ast10=130$

Ответ: 130

096495

Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 29, а основание BC равно 4. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=29.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 29 - 4 = 25

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=25-4=21

По построению BCPA - параллелограмм, значит
CP = AB = 20

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=29²-21²
CP=√ (841-576)=√ 400=20

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 25 и высота 20. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{4+25}2\ast20=\frac{29}2\ast20=14.5\ast20=290$

Ответ: 290

5AF0E1

Боковые стороны AB и CD трапеции ABCD равны соответственно 6 и 10, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=10.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 10 - 1 = 9

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 9

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=9-1=8

По построению BCPA - параллелограмм, значит
CP = AB = 6

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=10²-8²
CP=√ (100-64)=√ 36=6

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 8 и высота 6. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+8}2\ast6=\frac{9}2\ast6=4.5\ast6=27$

Ответ: 27

7E8F98

Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 13, а основание BC равно 4. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=13.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 13 - 4 = 9

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 9

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=9-4=5

По построению BCPA - параллелограмм, значит
CP = AB = 12

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=13²-5²
CP=√ (169-25)=√ 144=12

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{4+9}2\ast12=\frac{13}2\ast12=6.5\ast12=78$

Ответ: 78

D9CD8D

Боковые стороны AB и CD трапеции ABCD равны соответственно 16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=34.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 34 - 2 = 32

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 32

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=32-2=30

По построению BCPA - параллелограмм, значит
CP = AB = 16

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=34²-30²
CP=√ (1156-900)=√ 256=16

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{2+32}2\ast16=\frac{34}2\ast16=17\ast16=272$

Ответ: 272

3FECDD

Боковые стороны AB и CD трапеции ABCD равны соответственно 4 и 5, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC = CD = 5.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 5 - 1 = 4

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 4

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=4-1=3

По построению BCPA - параллелограмм, значит
CP = AB = 4

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=5²-3²
CP=√ (25-9)=√ 16=4

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 3 и высота 4. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+3}2\ast4=\frac{4}2\ast4=2\ast4=8$

Ответ: 8

F8F38E

Боковые стороны AB и CD трапеции ABCD равны соответственно 28 и 35, а основание BC равно 7. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=35.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 35 - 7 = 28

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 28

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=28-7=21

По построению BCPA - параллелограмм, значит
CP = AB = 28

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=35²-21²
CP=√ (1225-441)=√ 784=28

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 28, 7 и высота 28. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{7+28}2\ast28=\frac{35}2\ast28=17.5\ast28=490$

Ответ: 490

9CA354

Боковые стороны AB и CD трапеции ABCD равны соответственно 8 и 10, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Решение:

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=10.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 10 - 2 = 8

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 8

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=8-2=6

По построению BCPA - параллелограмм, значит
CP = AB = 8

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=10²-6²
CP=√ (100-36)=√ 64=8

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 8, 2 и высота 8. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{2+8}2\ast8=\frac{10}2\ast8=5\ast8=40$

Ответ: 40

8D9E03