В самом разгаре ЕГЭ по математике, а мы собираем задания, которые были на экзамене. Базовая математика в этом году проще простого, так что, если вам сдавать именно ее, не переживайте, вы справитесь.
Задания с ЕГЭ по базовой математике
1. Задание про билеты.
Шоколадка стоит 20 р. В воскресенье в супермаркете действует специальное предложение: заплатив за 2 шоколадки, покупатель получает 3 (1 в подарок). Сколько шоколадок можно получить на 150 р. (или 135 в др. варианте) в воскресенье?
Было 750 людей +25 членов экипажа, сколько шлюпок нужно для всех людей? какое наименьшее количество?
Яхта вмещает 730 пассажиров и 35 экипажа. В спасательную шлюпку вмещается 60 человек. Какое мин. количество шлюпок надо? (СПБ)
Стоимость полугодовой подписки на журнал 600 р., а стоимость 1 номера журнала в киоске - 28 р. За полгода Аня купила 25 номеров журнала. На сколько р. меньше она бы потратила, если бы подписалась? (74 регион, ответ на 100)
Стоимость полугодовой подписки на журнал составляет 640 рублей, а стоимость одного номера журнала — 29 рублей. За полгода Аня купила 25 номеров журнала. На сколько рублей меньше она бы потратила, если бы подписалась на журнал?
Про шлюпки, 13 (регион 50)
2. а) обороты земли б) вспышка фотоаппарата в) длительность песни г) длительность фильма (47 регион)
А) масса мобильного телефона Б) масса одной ягоды клубники В) масса взрослого слона Г) масса курицы 1) 12,5 г 2) 4 т 3) 3 кг 4) 100 г (74 регион)
масса холодильника, трамвая, новорождённого и карандаша
Продолжительность фильма, длительность одной песни, оборот земли вокруг солнца, вспышка фотоаппарата (СПБ)
3. Среднемесячная температура, найти наибольшую.
Максимальная температура за год. (СПБ)
Графики с количеством осадков.
График с ростом температуры.
4. 182 : 6 ;
Закон Гука можно записать в виде f=kx, где f – сила (в ньютонах), с которой сжимают пружину, х – абсолютное удлинение (сжатие) пружины (в метрах), а к – коэффициент упругости. Пользуясь этой формулой, найдите х (в метрах), если f = 38 Н и к = 2 Н/м.
Закон гука. f=kx, найти x. если f=42 и k=7 (74 регион)
p=u2/R найдите p (СПБ)
5. В основном насосы.
300 насосов не бракованные, 60 из них бракованные, найти вероятность того, что попадется бракованный (ответ 0,2, регион 50, 47).
В партии 200 насосов, 20 из них подтекают, найдите вероятность, что случайно выбранный насос подтекает. (СПБ)
В сборнике билетов по физике всего 40 билетов, в 6 из них встречается вопрос по теме «Термодинамика». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Термодинамика».
6. Давление.
В городском парке имеется пять аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся шесть видов билетов, каждый из которых позволяет посетить один или два аттракциона. Сведения о стоимости билетов представлены в таблице.
| Вид билета | Набор аттракционов | Стоимость (руб.) |
|---|---|---|
| 1 | Колесо обозрения, «Весёлый тир» | 500 |
| 2 | «Ромашка», карусель | 350 |
| 3 | Карусель, колесо обозрения | 150 |
| 4 | Автодром, «Весёлый тир» | 500 |
| 5 | «Ромашка» | 250 |
| 6 | Автодром, «Ромашка» | 450 |
Андрей хочет посетить все пять аттракционов, но имеет в наличии только 900 рублей. Какие виды билетов он должен купить? В ответе укажите номера, соответствующие видам билетов, без пробелов, запятых и других дополнительных символов. (Ответ 345)
Составить вариант экскурсии, чтобы посетить все места и уложиться в лимит. (СПБ)
7. В магазине продаётся 50 шлангов, 4 из них могут оказаться бракованными. Найдите вероятность того, что может попасться НЕБРАКОВАННЫЙ шланг (ответ 0,92).
8. В доме Маши меньше этажей, чем в доме Стаса, в доме Ксюши больше этажей, чем в доме Стаса, а в доме Нади больше этажей, чем в Машином доме, но меньше, чем в Ксюшином доме. Выберите утверждения, которые верны при указанных условиях. 1) В доме Маши меньше этажей, чем в доме Нади. 2) Дом Ксюши самый многоэтажный среди перечисленных четырёх. 3) Среди этих четырёх домов есть три дома с одинаковым количеством этажей. 4) В Надином доме один этаж.
9. Треугольник, плана местности не было.
Площадь трапеции.
10. задание - средняя линия;
11. Посчитать объем куба, перевести ответ в литры.
Аквариум, где все дано и нужно просто перемножить.
Дана цилиндрическая фигура, высота равна 60, а площадь основания 150 см. Найти объем. (74 регион)
В бак, имеющий форму правильной четырехугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 2,6 раза. Найдите объем детали. Ответ дайте в кубических см.
12. Найти высоту пирамиды объемом 40, сторона 30; дан четырехугольник, угол В 77, угол С 141, найдите угол А.
13. Пирамида. Стороны основания правильной треугольной пирамиды равны 6, а боковые ребра равны 5. Найдите площадь боковой поверхности этой пирамиды. (Ответ 36)
14. 6,8+3,5*2,1
1/6*0,72 +2
log⁸(2x+3)=1
log3(2x-5)=2
15. Налоговый вычет; налоги; задача: у Ивана Кузьмича з/п 16000, налог 13%, найти з/п с налогом.
В сентябре сливы стоили 80 рублей, в октябре подорожали на 10 процентов.
В сентября сливы стоили 90 рублей, а в октябре подорожали на 10%. Сколько стали стоить сливы в октябре. (СПБ)
Тариф стоит 400р. В следующем году увеличится на 7% . Сколько будет стоить тариф?
16. 35
33*3
log3(729)-log3(9)
17. неполное квадратное уравнение;
Решите уравнение х2 + 5х = 0. Если 2 корня, укажите меньший.
18. линейные
19. Найти пятизначное число, кратное 15, любые 2 цифры которого отличаются на 2 (соседние и на 3 в другом варианте).
Найдите четырехзначное число, кратное 12, произведение чисел которого больше 40, но меньше 45 (66 регион).
Найти четырёхзначное число кратное 12, произведение чисел которых больше 50, но не больше 55.
На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
Шестизначное число из двоек и единиц кратное 24 (10 регион)
Четырёхзначное число A состоит из цифр 2, 3, 7, 8, а четырёхзначное число B — из цифр 4, 5, 6, 7. Известно, что B=2A. Найдите число A. В ответе укажите какое-нибудь одно такое число, большее 2500.
6тизначное целое число из цифр 1 и 2, делящееся на 24 (Ответ: 221112)
Семизначное число состоит из 1 и 2, делится на 72. (СПБ)
20. Сплавы, почти у всех был никель; первый сплав 50% никеля, второй 15% никеля, из них получился третий 25% никеля.
1ый сплав весит 20 кг и он состоит из 40% меди, 2ой сплав состоит из 25% меди. Из этих двух получился 3ий сплав, который состоит из 35% меди. Узнать сколько весит 3ий сплав. Вроде так. Проценты точно не помню
Растворы (66 регион)
К 5 кг 27% добавили 4 кг воды, найдите концентрацию полученного раствора. (СПБ)
Первый насос наполняет бак за 20 минут второй за 42 а третий за 1 час 45 мин. За сколько наполнят бак три насоса, работая одновременно?
21. Почти у всех этажи.
Петя живет в 12 подъезде в 465 кв., найти этаж;
Саша живет в 10-м подъезде в кв.333, дом девятиэтажный, на каком этаже?
Число этажей больше числа квартир на этаже, квартир на этаже больше, чем подъездов, а подъездов больше 1. Сколько этажей в доме, если в нем 110 квартир (ответ 11), 105 квартир?
В корзине лежит 32 гриба: рыжики и грузди. Известно, что среди любых 23 грибов имеется хотя бы один рыжик, а среди любых 11 грибов хотя бы один груздь. Сколько груздей в корзине?
Красные линии делят ленту на 5 кусков, жёлтые на 7, а зелёные на 11. Сколько кусков, если разрезать по всем линиям?
На палке синие, жёлтые и красные полоски. Если разрезать по синим, получится 5 кусков если по жёлтым- 7, если по красным -11. Сколько кусков получится, если разрезать по всем (СПБ)
А вот в профильной сложнее, но так и должно быть, на то она и профильная. Итак, какие задания были у Дальнего востока.
Формулировки не ЕГЭшные, а по словам учеников.
Профиль
Задания с ЕГЭ по профильной математике с ДВ
1. Трапеция ABCD с площадью, равной 24 (в другом варианте 12). BM - медиана. Найдите площадь BCDM.
2. Объем конуса 9 (в др. варианте 6). Найдите объем цилиндра.
3. 70 спортсменов: 6 из Польши, 7 из Чехии. Какова вероятность того, что спортсмен из Чехии будет выступать четвертым?
4. Биатлонист 4 раза стреляет по мишени. Вероятность попадания 0,9. Найдите вероятность того, что 3 раза попадет, 1 раз промахнется.
5. 5х+4 = 125
6. log12 10 + log2 8/5
log12 2
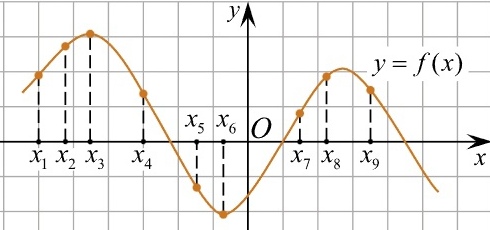
7. Дана функция обычная, надо найти, в каких х производная отрицательная.
8. Задание про линзу, f = 36, расстояние d1 о линзы до лампочки от 30 до 50. Расстояние d2 от линзы до экрана от 160 до 180. Соотношение 1/d1 + 1/d2 = 1/6. Укажите наименьшее расстояние d1.
9. Трубы
10. Дано 2 графика, найти общие точки.
11. Укажите наибольшее значение функции на отрезке [3,21].
у = 12 + 9х - 2х √х
12. 2 cos3x = √3 sin2x + 2 cos x ; [-3π; -5π/2] (Промежуток неправильный, кто помнит точнее, напишите в комментах)
13. Призма, где на серединах сторон были отмечены две точки, одна точка делила сторону в отношении 1:3. В основании призмы равнобедренный треугольник. Доказать, что полученное сечение параллельно стороне АВ.
14. (log20,25(х+3) - log4(х2 + 6х +9) + 1 ) * log4(х + 2) ≤ 0
15. В июле 2025 года планируется взять кредит в банке на сумму 700 тысяч рублей на 10 лет. Условия его возврата таковы:
- в январе 2026,2027,2028,2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
- в январе 2031,2032,2033,2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть погашен полностью.
Найдите общую сумму выплат после полного погашения кредита.
16. Ромб, у которого к одной стороне была проведена прямая, перпендикулярная данной стороне, которая проходит сквозь нее и пересекает две диагонали. Одну диагональ АС пересекает в точке М, где АМ : МС = 1 : 2. BD пересекает в точке N, где BN : ND = 1 : 3. Доказать, что cos А = 1/5
17. Найти значение параметра а, при котором равно 2 значения
{(ху - х + 8) * √у - х + 8 = 0
у = 2х + а
18. На доске написано трехзначное число А. Сережа зачеркивает одну цифру и получает двухзначное число В. Затем Коля записывает число А и зачеркивает одну цифру (может ту же, что и Сережа), получает число С.
а) Может ли быть верным уравнение А = В * С, если А > 140?
б) Может ли быть верным уравнение А = В * С, если 440 ≤ А < 500?
в) Найдите наибольшее число А до 900, чтобы было верным уравнение А = В * С
75 регион профиль
(все цифры в задачах полностью совпадают с тем, что было в КИМе, задачи написаны своими словами)
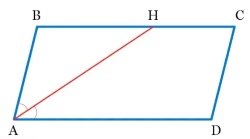
1. площадь параллелограмма 12, найдите площадь трапеции AHCD ( BH = CH; AH - биссектриса) (рисунок в ниже)
2. конус вписан в цилиндр, объем конуса 3, найдите объем цилиндра
3. в соревнованиях учувствуют 70 спортсменов, в том числе 7 поляков. Найдите вероятность, что поляк будет выступать 4
4. стрелок попадает в мишень с вероятностью 0,7 найдите вероятность что он сначала 3 раза попадет а потом 1 раз промахнется
5. 8(9 – x) = 64 , найдите x
6. (log2 21 / log2 3) + log3 9/7
7. на рисунке изображен график функции, укажите в скольких точках производная равна 0 (рисунок похожий на тот что был на экзамене)
8. задание про линзу(второй рисунок) f = 36 , d1 может изменятся в пределах от 30 до 50, d2 в пределах от 160 до 180, найдите минимально возможное d1
1/d1 + 1/d2 = 1/f
9. первая труба пропускает в минуту на 3 литра воды меньше, чем вторая. Первая труба заполняет резервуар объемом 208 литров на 3 минуты дольше. Найдите пропускную способность первой трубы
10. не нашел такого же рисунка, но была дана прямая и парабола, необходимо было найти точку абсцисс пересечения параболы и прямой
11. найдите наибольшее значение функции 12 – 9x – 2x√x на промежутке [3; 21]
18. На доске написано трёхзначное число A. Сережа зачеркивает одну цифру и получает число В, затем Коля записывает число А и зачеркивает одну цифру (может ту же что и Сережа) и получает число С.
1) Может ли быть верным уравнение A=B*C при A>140;
2) Может ли быть верным уравнение A=B*C при 340<=A<400;
3) Найдите наибольшее число A до 800, чтобы уравнение A=B*C было верным.
Другие задания профильной математики, которые удалось вспомнить сдавшим ЕГЭ
1. Мск +1 Дан треугольник. У него средняя линия. Дана площадь треугольника и нужно найти площадь нижней трапеции
Треугольник АБС = 24, DE - средняя линия и нужно было найти площадь трапеции ABED
Четырехугольник.
Треугольник abc с площадью 12, проведена средняя линия mn, найти площадь треугольника man.
мск+0 В треугольнике АВС DЕ - средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника АВС.
мск+0 Площадь треугольника АВС равна 36. DЕ - средняя линия, || АВ. Найдите площадь трапеции АВЕD. (ответ 27)
Средняя линия, площадь большого треугольника 24, а найти надо площадь трапеции. (ответ 18 получился)
+6 от мск Задание с трапецией. Проведен отрезок из угла в середину одного из оснований, найти s этого треугольника, s фигуры = 12.
мск +4 Параллелограмм, в нём проведена медиана. Площадь параллелограмма 60, надо найти площадь отсеченного треугольника. (ответ 15)
Высоты, опущенные к двум сторонам треугольника. 2 стороны и одна высота даны, нужно найти вторую высоту.
Треугольник с площадью 60, средняя линия, и нужно найти площадь трапеции. (ответ 45)
Дан параллелограмм, его площадь равна 36. Точка Е делит сторону параллелограмма пополам. Найдите площадь треугольника. 36:4=9 (регион 54)
Дан параллелограмм стороны которого 12 и 15,высота,проведенная к меньшей стороне равна 10,найдите высоту, проведенную к большей стороне. мск
2. Объём цилиндра = 30 (18 в др. варианте) и нужно найти объём шара, вписанного в цилиндр.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
3. Участвовало 4 страны, 9 из Латвии, 7 из Литвы, и 6 и 8 из каких-то ещё 2 стран, нужно было найти, чтобы Латвия первая начала...
50 участников 7 откуда-то, 13 откуда-то, найти вероятность того что один из оставшихся будет первым.
4. Про батарейки. Сломанная батарейка - 0,01, что её забракуют - 0,94. Норм батарейка - 0,99, что ее забракуют - 0,04. Найти вероятность что рандом батарейку забракуют.
5. 5х-2=125
5-8-x =25
9x-1 = 81 (вроде такая степень была у 9-тки)
4х-7=1/64 мск
6. log0.8(50) - log0,8(32) (ответ -2)
log 12,25 по основанию 7 + log 4 по основанию 7
"было гробовое задание тригонометрическое"
log(16)21/log(16)7+log(3)7/9
log5 73 - log5 3
4 log4√15 (15) (ответ 16)
7. Дан график производной и нужно было найти количество точек, где обычная функция возрастает.
Точки минимума на производной функции. мск
8. +6 от мск "сложное задание с линзами" 1/d1+1/d2=1/f, найти d1
мск Перед отправкой тепловоз издал гудок с частотой f0 = 192 Гц. Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f (Гц) больше первого: она зависит от скорости тепловоза v (в м/с) по закону f(v) = f0 / (1 - v/с), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее, чем на 8 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 300 м/с. Ответ выразите в м/с.
R=R1R2/R1+R2 больше или равно 40, R1=65 мск
9. Заказ на 306 деталей первый рабочий выполняет на 1 ч быстрее, чем второй. Сколько деталей за час делает второй рабочий, если известно, что первый делает за час на одну деталь больше второго? (ответ 17)
Заказ на 140 деталей первый рабочий выполняет на 4 ч быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый делает за час на 4 детали больше второго? +2 мск
Заказ на 198 деталей первый рабочий выполняет на 7 часов быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 7 деталей больше?
мск+0 Первая труба пропускает на 7 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 228 литра она заполняет на 7 минут дольше, чем вторая труба?
мск+0 9 Трубы. Задача была точно такая же, только резервуар 600 с чем-то и вторая труба на 4 минуты быстрее.
+6 от мск Задача на производительность с трубами.
Два велосипедиста одновременно отправились в 220-километровый пробег. Первый ехал со скоростью, на 9 км/ч большей, чем скорость второго, и прибыл к финишу на 9 часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. мск
10. Прямая y = 1/2x - 4 и гипербола 10/x
11. Найти наименьшее значение функции. y=3✓3-6x+3 на отрезке [0;40]
... x✓x - 3x + 9 [1;10]
... f(x)=x√x - 9x + 18, наим. значение, [1; 60] (ответ -89)
у=хкореньх-6х+23 найти наименьшее
Найти точку максимума в функции 6+12x-x√x. (ответ 64)
Найдите наименьшее значение функции у = 2/3 х√х - 6х - 5 на отрезке [9;36]
f(x)=6 + 12х - х√х
y=12+12x-2x^3/2 найти точку максимума
12. 2sin3х - √3 cos2x = 2sin x
2sin3х = √2 cos2x + sin x [-4π; -5π/2]
2cos3x = √2 sin2х + 2cos х
13.
14. log100((x-2)(x2 + 5x - 14)) + 1 ≥ 0,5 lg(x-2)2
log25((x-4)(x2 - 2x - 8)) + 1 ≥ 0,5 lоg5(x-4)2 Мск+3
log4((x - 5)(x2 - 2x - 15)) + 1 ≥ 0,5 log2(x-5)2 мск +4, +2
log100((x-2)(x2+5x-14)) ≥ 1/2 lg(x - 2)2
log0,5(x3 - 9x2 - 3x + 27) ≤ log0,25(x - 3)4
log0,5(x3 - 3x2 - 9x + 24) ≤ log0,25(x - 3)4
log0,1(x3 - 5x2 - 25x + 125) ≤ log0,1((x - 5)4)
log8(x3 - 3x2 + 3x - 1) ≥ log2(x2 - 1) - 5 (ответ (1; 31]) регионы 62,67
log27(x3 - 9x2 + 27x - 27) ≥ log3(x2 - 9) - 4
log2(2-х) - log2(х-1) ≥ 0 МСК + 0
log22х2 + log2х4 + 1
log3(х2) - log5(х2) ≥ 0 МСК + 0
log215(2х2 - 6х + 4,5) + 1
log3(х2) - log2(х2) ≥ 0 МСК + 0
log6(2х2 - 10х + 12,5)2 + 1
log2(х2) - log3(х2) ≥ 0 МСК + 0 ответ (-беск;-1] U [1;2,5) U (2,5; +беск)
log6(2х2 - 10х + 12,5)2 + 1
log8((x-1)(x2-2x+1)) ≥ log2(x2-1) -32 Было кубическое свернул Мск+0
15. екб мск +2, 15 Кредит на 10 лет в июле, с 25 по 35 год. В январе кредит растëт на 30%, в период с февраля по июнь происходит выплата. В июле с 25 по 30 включительно разница между суммой кредита в июле прошлого года с июлем нынешнего года одна, а с 30 по 35 год другая. Известно сумма выплаченная по долгу за всё время. (400к был сам кредит, сумма выплат 910к)
Часовой пояс +2. Брали на 10 лет: первые 5 лет один повышающий коэффициент, остальные 5-другой. Сумма выплат =1420т.р., причем выплаты равномерно растут (взяла за х, 2х, 3х и тд, потом у, 2у, 3у..) нужно найти первую выплату (х)
В долг взяли 400к. Долг равномерно уменьшался 5 лет. Потом снова равномерно, но уже отлично от прошлых пяти лет, в течение 5 лет. Общая выплата долга 910к. Надо найти значение первого платежа. (Ответ: 180к, возможно неправильный)
В июле 2025 года планируется взять кредит на сумму 1400 тыс.руб еа 10 лет
- каждый январь долг возрастает на 10%
- в 2025-2030 годах долг каждый год уменьшается на одну и ту же сумму
- в оставшиеся 5 лет на другую одну и ту же сумму
В июле 2035 долг равен 0.
После выплаты кредита выяснилось, что сумма всех платежей по кредиту составила 2140 тыс.руб. Чему равнялась выплата в 2026 году?
Мск+2 В июле 2025 года планируется взять кредит в банке на сумму 400 тыс. рублей на 10 лет. Условия его возврата таковы:
- в январе каждого года долг увеличивается на 30%
- в июле 2026, 2027, 2028, 2029 и 2030 годов долг уменьшается на одну какую-то величину по сравнению с концом предыдущего года;
- в июле 2031, 2032, 2033, 2034 и 2035 годов долг уменьшается на другую величину по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга одним платежом
- к июлю 2035 года кредит должен быть полностью погашен.
Найдите платеж в 2026 году, если общая сумма выплат после полного погашения кредита составила 910 тыс. рублей
мск +4 Кредит на 10 лет взяли сумму 400 тыс руб, каждый январь на 30%, первые 5 лет в июле долг должен быть на одну и ту же сумму меньше, чем в июле предыдущего, а в остальные 5 лет на какую-то другую сумму долг должен быть меньше, чем в июль предыдущего года. Известна сумма выплат (не помню сколько) найдите выплату в 2026 году (это первый год после изначального)
18. мск+0 В классе не менее 10 и не более 26 учеников. Доля девочек в классе не больше 46%
а) может ли быть 9 девочек в классе?
б) если в класс придёт ещё одна девочка, то сможет ли их доля стать 55%?
в) какая максимальная целая доля девочек может быть после прихода одной девочки?
Пара натуральных чисел (а;б) а>б. За один ход делаются такие действия: (а+б); (а-б) и получается другая пара чисел.
А) можно ли за несколько ходов сделать так, чтобы наибольшим числом из пары было 400, если считать что начальная пара была (100;1)
Б) можно ли за несколько ходов сделать так, чтобы получилась пара (806;788)?
В) какое наименьшее число а может быть в паре, которая за несколько ходов образует пару (806;788)
Сдали ЕГЭ? Какие попались задания? Знаете ответы? Пишите в комментариях.

