Задания ко второй части ОГЭ по математике из открытого банка заданий ФИПИ с развернутым ответом. Эти задачи могут вам попасться на реальном ОГЭ, и нужно уметь их решать. Все решения под катом.
КЭС 7.2.10 Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 0о до 180о 7.3.2 Прямоугольник, квадрат, ромб, их свойства и признаки.
Задания ко второй части ОГЭ с развернутым ответом
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.
Решение:
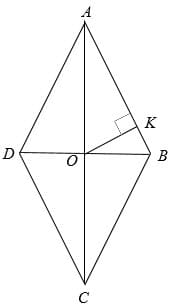
Cделаем рисунок: ромб ABCD
Пусть AC = 60.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 15
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 60/2 = 30.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
D9E6CA
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 40.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 10
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 40/2 = 20.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
987228
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 44.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 11
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 44/2 = 22.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
40D431
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 48.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 12
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 48/2 = 24.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EBA29F
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 52.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 13
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 52/2 = 26.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
D01FBF
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 56.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 14
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 56/2 = 28.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EFC57B
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 64.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 16
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 64/2 = 32.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
9C2D65
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 68.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 17
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 68/2 = 34.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
0247D6
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 18, а одна из диагоналей ромба равна 72. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 72.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 18
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 72/2 = 36.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
2FCCDB
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Решение:

Cделаем рисунок: ромб ABCD
Пусть AC = 76.
Расстояние от точки пересечения диагоналей до одной из его сторон OK = 19
Диагонали ромба точкой пересечения делятся пополам, поэтому AO = 76/2 = 38.
В получившемся прямоугольном треугольнике AOK гипотенуза AO в 2 раза больше катета OK, значит угол против этого катета равен 30º – это половина острого угла ромба.
Тогда острый угол ромба равен 60º.
Тупой угол будет равен 180º – 60º = 120º
Ответ: 60º и 120º
EEF3FC
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Решение:
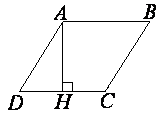
AB=BC=CD=AD=DH+CH=8+2=10 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2=AH2+DH2
AH2=AD2-DH2
AH2=102-82
AH2=100-64
AH2=36
AH=6
Ответ: AH=6
DAF765
Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=1. Найдите высоту ромба.
Решение:
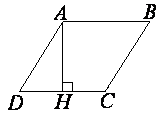
AB=BC=CD=AD=DH+CH= 12 + 1 = 13 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 132 - 122
AH2 = 169 - 144
AH2 = 25
AH = 5
Ответ: AH = 5
C5C26D
Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=3. Найдите высоту ромба.
Решение:
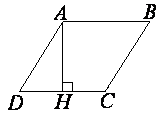
AB=BC=CD=AD=DH+CH= 12 + 3 = 15 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 152 - 122
AH2 = 225 - 144
AH2 = 81
AH = 9
Ответ: AH = 9
F69509
Высота AH ромба ABCD делит сторону CD на отрезки DH=15 и CH=2. Найдите высоту ромба.
Решение:
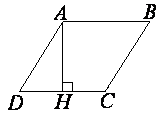
AB=BC=CD=AD=DH+CH= 15 + 2 = 17 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 172 - 152
AH2 = 289 - 225
AH2 = 64
AH = 8
Ответ: AH = 8
F47774
Высота AH ромба ABCD делит сторону CD на отрезки DH=16 и CH=4. Найдите высоту ромба.
Решение:
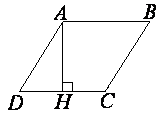
AB=BC=CD=AD=DH+CH= 16 + 4 = 20 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 202 - 162
AH2 = 400 - 256
AH2 = 144
AH = 12
Ответ: AH = 12
8E9764
Высота AH ромба ABCD делит сторону CD на отрезки DH=20 и CH=5. Найдите высоту ромба.
Решение:
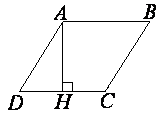
AB=BC=CD=AD=DH+CH= 20 + 5 = 25 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 252 - 202
AH2 = 625 - 400
AH2 = 225
AH = 15
Ответ: AH = 15
F80C88
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=1. Найдите высоту ромба.
Решение:
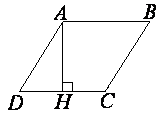
AB=BC=CD=AD=DH+CH= 24 + 1 = 25 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 252 - 242
AH2 = 625 - 576
AH2 = 49
AH = 7
Ответ: AH = 7
FDB483
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Решение:
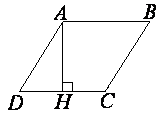
AB=BC=CD=AD=DH+CH= 24 + 2 = 26 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 262 - 242
AH2 = 676 - 576
AH2 = 100
AH = 10
Ответ: AH = 10
745683
Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Решение:
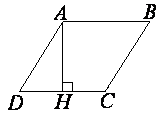
AB=BC=CD=AD=DH+CH=21+8=29 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2=AH2+DH2
292=AH2+212
841=AH2+441
AH2=400
AH=20
Ответ: AH=20
B5384B
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=6. Найдите высоту ромба.
Решение:
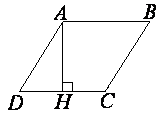
AB=BC=CD=AD=DH+CH= 24 + 6 = 30 (по определению ромба).
Рассмотрим треугольник AHD.
AHD - прямоугольный (т.к. AH - высота), тогда по теореме Пифагора:
AD2 = AH2+DH2
AH2 = AD2-DH2
AH2 = 302 - 242
AH2 = 900 - 576
AH2 = 324
AH = 18
Ответ: AH = 18
8C5FB4

