Алгоритм действий для решения задания №18
1. Читаем задание и подчеркиваем:
Какие команды перемещения робота?
Из какой ячейки таблицы начинается перемещение?
Есть ли условие, при котором робот берет монету (четность, номинал)?
Какие ячейки считаются итоговыми?
В каком порядке выдавать ответ?
Примеры «особенных условий»:
Робот берет только те монеты, которые кратны 2 и не кратны 5, если достоинство монеты не кратно 2 или кратно 5, то Робот монету не берет; это также относится к начальной и конечной клетке маршрута Робота.
В «удобных» клетках поля - тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
2. Копируем формат таблицы чуть ниже таблицы по образцу: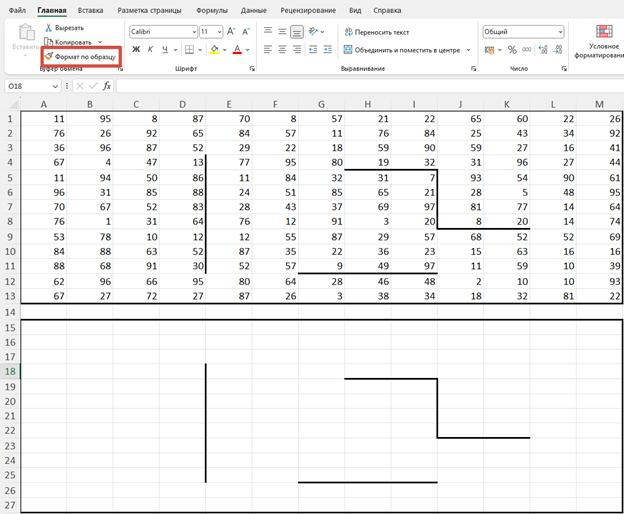
3. В ячейке, с которой начинается движение робота, переписываем значение из таблицы выше в соответствии с условием.
4. В соседних ячейках, в соответствии с условием (например, справа и снизу), записываем формулу.
Пример: робот берет только те монеты, которые красные 2 и не красные 5. Если достоинство монеты не красной 2 или красной 5, то не берет. Это так же относится к начальной и конечной точке маршрута.
Из таблицы выше получаются формулы:
A15=ЕСЛИ(И(ОСТАТ(A1;2)=0;ОСТАТ(A1;5)>0);A1;0)
A16=ЕСЛИ(И(ОСТАТ(A2;2)=0;ОСТАТ(A2;5)>0);A2;0) + A15
B15=ЕСЛИ(И(ОСТАТ(B1;2)=0;ОСТАТ(B1;5)>0);B1;0) + A15
5. Копируем ячейки в соответствующих направлениях вдоль стены (тянем за квадратик в правом нижнем углу ячейки).
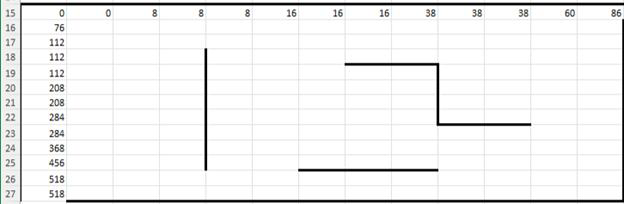
6. В угловой ячейке от начальной записываем формулу.
Для задачи из примера:
B16=ЕСЛИ(И(ОСТАТ(B2;2)=0;ОСТАТ(B2;5)<>0);B2;0) + МАКС(B15;A16)
7. Дублируем значение этой ячейки на всю оставшуюся таблицу и возвращаем формат таблицы из шаблона выше.
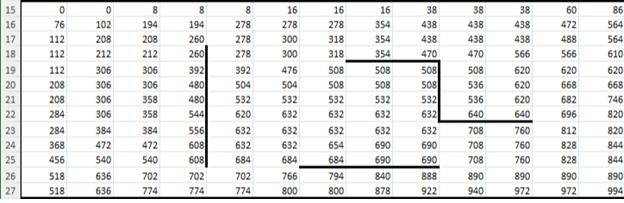
8. В соответствии с движением заменяем значение ячеек у стен. Формулы можно скопировать у соответствующих стен с края таблицы.
Пример: если движение вправо и вниз, то справа и снизу от стен меняем формулы на формулы у левого и верхнего края таблицы.
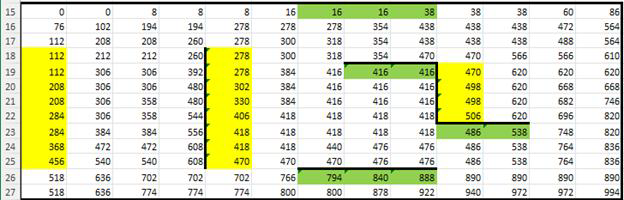
9. Записываем в ответ значение МАКС ячейки из итоговых.
10. Открываем поле замены элементов с помощью комбинации клавиш CTRL+H или CTRL+F и заменяем МАКС на МИН.
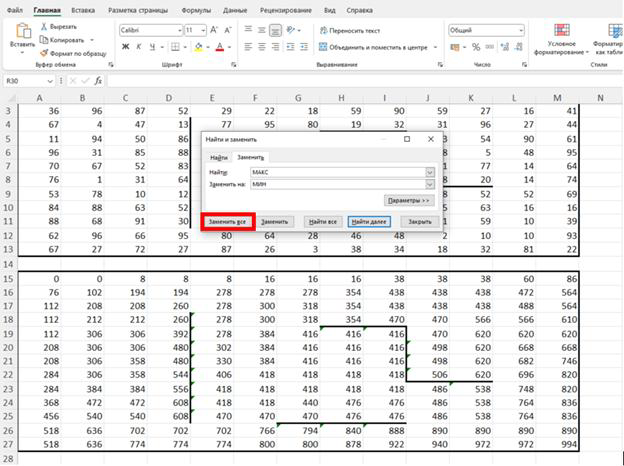
11. Записываем в ответ значение МИН ячейки из итоговых.
Основные комбинации клавиш:
| Сочетания клавиш |
Инструменты |
|
| Описание | CTRL+H или CTRL+F Открывается поле для поиска и замены элементов |
«Формат по образцу» Копирует формат (без содержания) выделенных ячеек в другую обозначенную область |
| Применение | Замена МАКС на МИН во всех формулах таблицы |
Если в задании есть стенки то после внесения всех формул они стираются и их нужно вернуть в исходное положение |
Прототипы с ЕГЭ
Задача №1 Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Ответ: 1099 1026
Задача №2 Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля - тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута. В ответе укажите два числа - сначала минимальную сумму, затем максимальную. Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Ответ: 758 2176
Задания уровня ЕГЭ
Задача №1 Квадрат разлинован на N×N клеток (2 < N < 19). В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 10. Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый имеет две команды – вверх и вправо, второй – вниз и вправо, которые, соответственно, перемещают исполнитель на одну клетку вверх, вниз или вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке, исполнитель НИЗ – в левой верхней.
Какой из исполнителей соберет большее количество монет в результате своей работы, если известно, что каждый из них запрограммирован собрать максимальной количество монет? Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Пример входных данных:
| 1 | 8 | 8 | 4 | 10 |
| 10 | 1 | 1 | 3 | 2 |
| 1 | 3 | 12 | 2 | 8 |
| 2 | 3 | 5 | 6 | 11 |
| 3 | 19 | 14 | 11 | 5 |
Для указанных входных данных ответом является комбинация из названия исполнителя и количества собранных монет
ВЕРХ 84
Ответ: ВЕРХ 1743
Задача №2 Исходные данные для Робота записаны в файле в виде электронной таблицы прямоугольной формы. Робот может двигаться только вверх на соседнюю клетку и вправо на соседнюю клетку. Робот может брать монеты только с тех клеток, где количество монет чётно. Если количество монет нечётно, то Робот не берёт в этой клетке ни одной монеты.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Ответ: 974 306
Задача №3 Квадрат разлинован на NxN клеток (2 < N < 19). В каждой клетке записано целое положительное число, соответствующее значению в ячейке таблицы в файле 18-1.xls. Исполнитель Робот имеет три команды ВПРАВО, ВВЕРХ и ДИАГОНАЛЬ, которые, соответственно, перемещают его на одну клетку вправо, на одну клетку вверх или на одну клетку вверх и право по диагонали. Робот двигается только в рамках поля, выход за границы запрещен. Начало движения робота – левая нижняя клетка, конец – верхняя правая клетка. При прохождении клетки к счету Робота прибавляется число, записанное в соответствующей ячейки таблицы.
Какой максимальный и минимальный счет может быть получен в результате работы исполнителя? В ответе запишите два числа – сначала максимально возможный счет Робота, затем минимальный. Пример входных данных:
| 5 | 1 | 21 | 7 | 11 |
| 6 | 2 | 7 | 13 | 8 |
| 6 | 3 | 18 | 10 | 5 |
| 5 | 8 | 5 | 15 | 3 |
| 2 | 4 | 14 | 11 | 6 |
В качестве ответа необходимо привести сначала максимальное полученное значение, затем наименьшее.
Ответ: 721 272
Задача №4 (16265) Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вниз. По команде влево Робот перемещается в соседнюю левую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля - тех, которые слева и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая левую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из правой верхней клетки в конечную клетку маршрута. В ответе укажите два числа - сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Ответ: 1723 477

