🍓 Задание №4 ЕГЭ по информатике с ответами, ФИПИ. Двоичное кодирование

КЭС 2.1 Двоичное кодирование. Равномерные и неравномерные коды. Декодирование сообщений, записанных с помощью неравномерных кодов. Условие Фано. Построение однозначно декодируемых кодов с помощью дерева

Равномерный двоичный код - кодовые слова одинаковой длины (00, 01,11 и т.п), неравномерный - разной (00, 01, 100).

Алгоритмы и подробные разборы прототипов тут >>

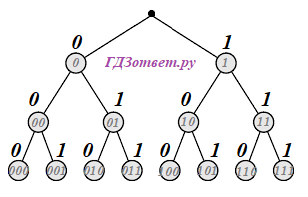Везде сначала строим бинарное дерево. Уровней столько, сколько знаков в самом длинном коде для буквы. Расставляем известные буквы. Где стоит буква, ветка обрывается. На свободных ветках можно разместить искомые буквы.

Тут встречаются задания на выбор ответа, это устаревшая формулировка. Но на ЕГЭ могут дать такое же задание, но без выбора ответа, а с кратким ответом.

Обязательно прямо в условии подчеркивайте, что конкретно надо найти: с наименьшим или наибольшим числовым значением, кратчайшее или самое длинное, сумму, сколько букв в закодированном алфавите (надо, чтобы все буквы влезли на дерево). Может быть несколько условий в задании, например кратчайшее с наибольшим числовым значением.

Задания 2-й линейки ЕГЭ по информатике, ФИПИ

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:

В 00
Г 10
Д 010
Е 110
Ж 0110
З 111

Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: А, Б.

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

КЭС: 2.1 Двоичное кодирование. Равномерные и неравномерные коды. Декодирование сообщений, записанных с помощью неравномерных кодов. Условие Фано. Построение однозначно декодируемых кодов с помощью дерева
2.2 Теоретические подходы к оценке количества информации. Единицы измерения количества информации. Алфавитный подход к оценке количества информации. Закон аддитивности информации. Формула Хартли. Информация и вероятность. Формула Шеннона

Решение:

только восемь букв, удовлетворяющий условию Фано, наименьшее количество двоичных знаков двух оставшихся букв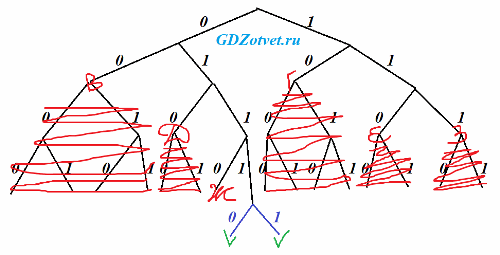

Свободно 2 места самое малое на 5-м уровне (01110 и 01111), то есть каждое кодовое слово по 5 знаков.
Ответ: 10

Номер: 734D40

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, B, C, D, E, F, S, X, Y, Z; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
A	00	F	1001
B	1000	S	1100
C	010	X	1010
D	011	Y	1101
E		Z	111

Укажите кратчайшее кодовое слово для буквы E, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

только десять букв, кратчайшее кодовое слово для буквы E с наименьшим числовым значением, удовлетворяет условию Фано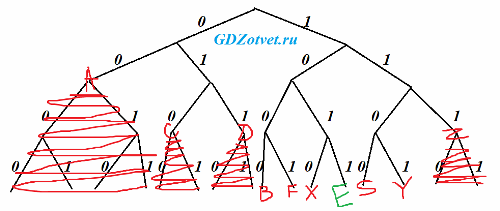

Ответ: 1011

Номер: 566A47

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г. Для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В используются такие кодовые слова: А – 1010; Б – 1100; В – 0.

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Решение:

только четыре буквы, удовлетворяющий условию Фано, кратчайшее кодовое слово для буквы Г с наибольшим числовым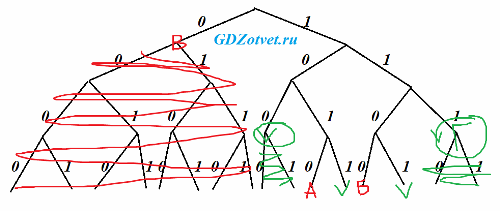

Свободно 4 места, но нам нужно кратчайшее кодовое слово, значит выбор из 100 и 111 (они оба по 3 знака), из них НАИБОЛЬШЕЕ числовое значение у 111 (оно правее на дереве).
Ответ: 111

Номер: 858F4B

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.

Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б		Р	1010
Е	010	С	1110
И	011	Т	1011
К	1111	У	100

Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

только десять букв, кратчайшее кодовое слово для буквы Б с наименьшим числовым, удовлетворять условию Фано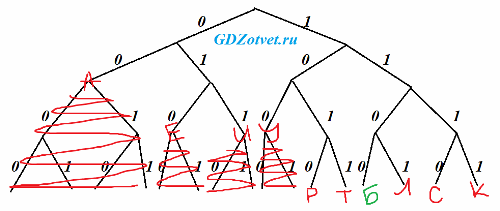

Ответ: 1100

Номер: B8EB09

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р	1110
Е	010	С	1010
И	011	Т	1111
К	1011	У

Укажите кратчайшее кодовое слово для буквы У, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

только десять букв, удовлетворять Фано, кратчайшее кодовое слово для буквы У с наименьшим числовым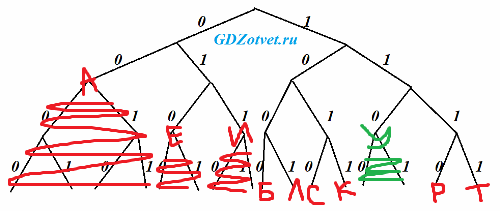

Кратчайшее - 1 место 110, нам и надо всего для 1 буквы.
Ответ: 110

Номер: 882400

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 000, 001, 10, 11 соответственно. Для двух оставшихся букв – Д и Е – кодовые слова неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Решение:

состоящей из букв А, Б, В, Г, Д, Е (6 шт.), удовлетворяющий Фано, кратчайшее кодовое слово для буквы Д с наибольшим числовым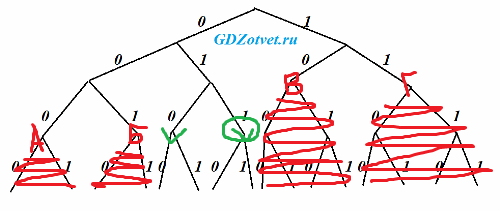

2 места свободны, наибольшее числовое у 011 (оно правее).
Ответ: 011

Номер: 460D7D

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только шесть букв: А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код. Для букв А, Б, В и Г используются кодовые слова 000, 010, 100, 1110 соответственно.

Укажите минимальную сумму длин кодовых слов для букв Д и Е, при котором код будет удовлетворять условию Фано.

Решение:

только шесть букв: А, Б, В, Г, Д, Е, минимальную сумму длин кодовых слов для букв Д и Е, удовлетворять Фано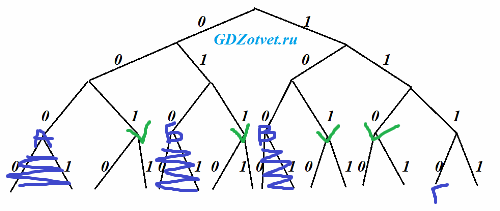

4 места на 3-м уровне, выше разместить невозможно (Фано мешает). Разместить надо 2 буквы, каждый код по 3 знака, итого 6.
Ответ: 6

Номер: 0D5D7E

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

только четыре буквы: А, Б, В, Г, удовлетворяющий Фано, кратчайшее кодовое слово для буквы Г с наименьшим числовым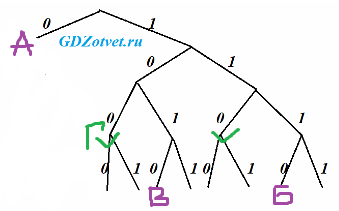

Наименьшее числовое левее на дереве.
Ответ: 100

Номер: 7AD871

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только 10 букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р	1110
Е	010	С
И	011	Т	1111
К	1011	У	110

Укажите кратчайшее кодовое слово для буквы С, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

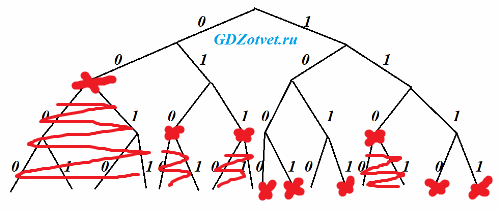
Ответ: 1010

Номер: 29A87E

Укажите минимальную сумму длин кодовых слов для букв Д и Е, при котором код будет удовлетворять условию Фано.

Решение:

минимальную сумму длин, удовлетворять условию Фано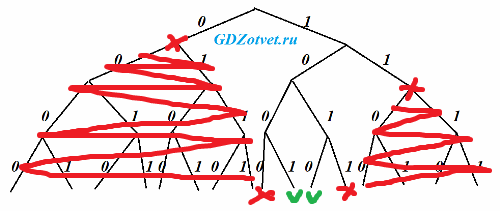

4+4
Ответ: 8

Номер: CE447D

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б		Р	1000
Е	010	С	1110
И	011	Т	1001
К	1111	У	101

Укажите кратчайшее кодовое слово для буквы Б, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ: 1100

Номер: 01AEBA

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р
Е	010	С	1110
И	011	Т	1011
К	1111	У	100

Укажите кратчайшее кодовое слово для буквы Р, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

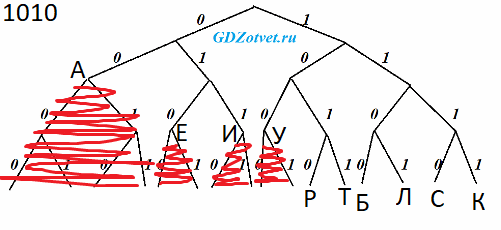
Ответ: 1010

Номер: EE7DB0

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 100, 101, 00, 01 соответственно. Для двух оставшихся букв – Д и Е – коды неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

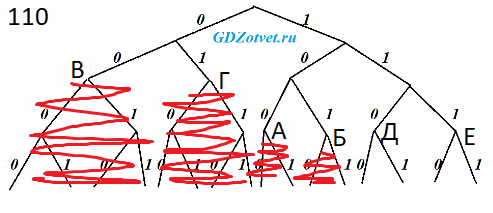
Ответ: 110

Номер: 67E8B4

Впишите правильный ответ.
Для кодирования растрового рисунка, напечатанного с использованием шести красок, применили неравномерный двоичный код. Для кодирования цветов используются кодовые слова.

Цвет	Кодовое слово	Цвет	Кодовое слово
Белый	10	Синий	1110
Зелёный	11110	Фиолетовый	11111
Красный		Чёрный	0

Укажите кратчайшее кодовое слово для кодирования красного цвета, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

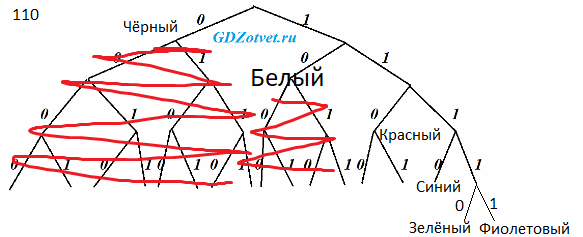
Ответ: 110

Номер: 3A22BB

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

только буквы из набора: А, З, К, Н, Ч (5 шт.), удовлетворяющий условию Фано, количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, минимально возможным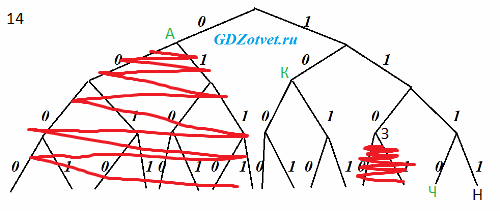

Строим дерево, размещаем известные буквы Р и З. Расставляем буквы А, К и Ч так, чтобы наиболее часто встречающиеся в слове были выше (меньше знаков).
А 0 - один знак
К 10 - два знака
Ч 1110 - 4 знака
К А З А Ч К А
2 1 3 1 4 2 1 = 14
Прорабатываем и другие варианты.
А 00, К 01, Ч 10 - все по 2
К А З А Ч К А = 2 * 6 + 3 = 15
14 меньше
Ответ: 14

Номер: 04FD12

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: К – 1, Н – 001. Для трёх оставшихся букв А, З и Т кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАНТАТА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

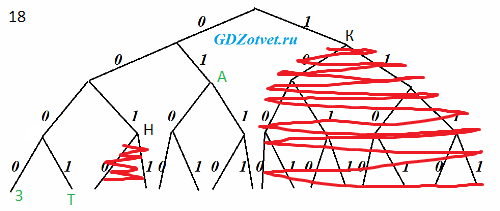
К А Н Т А Т А
1 2 3 4 2 4 2
Ответ: 18

Номер: B17711

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв A, B, C, D, E, F, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы A использовали кодовое слово 0; для буквы B – кодовое слово 10. Какова наименьшая возможная сумма длин кодовых слов для букв C, D, E, F?

Решение:

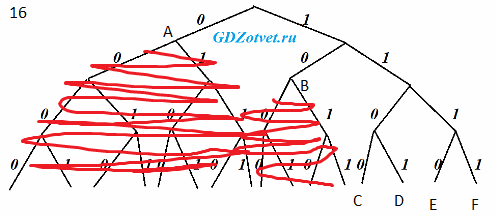
Ответ: 16

Номер: 349C1D

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б		Р	1110
Е	010	С	1010
И	011	Т	1111
К	1011	У	110

Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

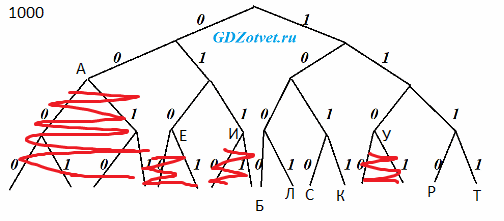
Ответ: 1000

Номер: 38AA15

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.

Буква	Кодовое слово
А	00
Б	1000
Е	010
И	011
К	1011
Л	1001
Р	1100
С	1010
Т	1101
У

Укажите кратчайшее кодовое слово для буквы У, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ: 111

Номер: FEFB2F

Цвет	Кодовое слово	Цвет	Кодовое слово
Белый	0	Синий
Зелёный	11111	Фиолетовый	11110
Красный	1110	Чёрный	10

Укажите кратчайшее кодовое слово для кодирования синего цвета, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

0 занят, значит начинаться будет с 1.
10 занят
11 - начало от зел, кр и фиол
111 - начало от зел, кр и фиол
110 не занято
Ответ: 110

Номер: 504F2E

Укажите минимальную сумму длин кодовых слов для букв Д и Е, при которых код будет удовлетворять условию Фано.

Решение:

Занятые префиксы: 1, 00, 0100, 0111.
Слова для Д и Е должны начинаться с 0 (так как 1 занят).
Проверка длин:
- Длина 1: "0" — префикс 00, 0100, 0111 → не подходит.
- Длина 2:
  - "00", "01" — "00" занято; "01" — префикс 0100, 0111 → не подходят.
- Длина 3:
  - "000", "001" — начинаются с 00 (кодовое слово) → не подходят.
  - "010", "011" — префиксы 0100, 0111 → не подходят.
  - "10", "11" — начинаются с 1 → не подходят.
Длина 4:
- Варианты: "0101", "0110".
- Проверка:
  - "0101": не префикс 0100; 0100 не префикс "0101" → подходит.
  - "0110": не префикс 0111; 0111 не префикс "0110" → подходит.
- Сумма длин: 4 + 4 = 8.

Ответ: 8

Номер: CF8A23

Впишите правильный ответ.

Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв К, Л, М, Н использовали соответственно кодовые слова 000, 001, 010, 11. Для двух оставшихся букв – П и Р – длины кодовых слов неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Занятые префиксы: 000, 001, 010, 11.
Слово для П должно:
- Не конфликтовать с существующими кодами.
Проверка длин:
- Длина 1: "0" — префикс 000, 001, 010; "1" — префикс 11 → не подходят.
- Длина 2:
  - "00" — префикс 000, 001 → не подходит.
  - "01" — префикс 010 → не подходит.
  - "10" — не является префиксом существующих слов; ни одно слово не является его префиксом → подходит.
  - "11" — занято.

Ответ: 10

Номер: 40E3DC

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р	1010
Е	010	С	1110
И	011	Т	1011
К		У	100

Укажите кратчайшее кодовое слово для буквы К, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Занятые префиксы: 00, 010, 011, 100, 1010, 1011, 1100, 1101, 1110.
Проверка длин:
- Длина 1: "0" — префикс 00, 010, 011; "1" — префикс 100, 1010, 1011, 1100, 1101, 1110 → не подходят.
- Длина 2: Все варианты ("00", "01", "10", "11") — заняты или являются префиксами → не подходят.
- Длина 3: Все варианты содержат занятые префиксы (например, "101" — префикс 1010, 1011) → не подходят.
- Длина 4:
  - Занятые коды: 010, 011, 100, 1010, 1011, 1100, 1101, 1110.
  - Свободные: "1111".
  - Проверка "1111": не является префиксом существующих слов; ни одно слово не является его префиксом → подходит.

Ответ: 1111

Номер: 2A35D3

Цвет	Кодовое слово
Белый	0
Зелёный	11111
Красный	110
Синий
Фиолетовый	11110
Чёрный	10

Укажите кратчайшее кодовое слово для кодирования синего цвета, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ: 1110

Номер: 6859DE

Кодовые слова для некоторых букв известны:

А	000
Б	001
В	0101
Г	0100
Д	011
Е	101

Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: Ж, З.

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

Решение:

00, 01 - нельзя по Фано, 11 свободно
100 свободно
2+3=5
Ответ: 5

Номер: 3528DB

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1; для буквы Б – кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е?

Решение:

Ветки 1 и 01 закрыты, значит начинаются остальные с 00. На 00 можем повесть 2 буквы на третьем уровне, но надо 4 ⇒ это будет уже 4-й уровень и 4 знака
4 буквы по 4 знака = 16 знаков
Ответ: 16

Номер: 8171DA

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р	1000
Е	010	С	1110
И	011	Т	1001
К		У	101

Решение:

...
Ответ: 1111

Номер: 1C1557

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У.
Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р
Е	010	С	1010
И	011	Т	1101
К	1011	У	111

Решение:

...
Ответ: 1100

Номер: 501859

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: В, Д, К, Н, О, Р. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 0, К – 1001. Для четырёх оставшихся букв В, Д, О и Р кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КОНОВОД, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

к о н о в о д
4+2+1+2+4+2+4=19
Ответ: 19

Номер: 36D956

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только пять букв: А, Б, В, Г, Д. Для передачи используется неравномерный двоичный код. Для букв А, Б и В используются кодовые слова 001, 010, 0111 соответственно.

Укажите минимальную сумму длин кодовых слов для букв Г и Д, при которых код будет удовлетворять условию Фано.

Решение:

Свободна ветка 1, код 10 и 11 ⇒ длина 2+2=4
Ответ: 4

Номер: 76E4A0

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв A, B, C, D, E, F, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы A использовали кодовое слово 00; для буквы B – кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв C, D, E, F?

Решение:

Свободна ветка 1, на нее надо повесить 4 буквы, это 3-й уровень
3*4=12
Ответ: 12

Номер: 543CA7

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е?

Решение:

Свободна ветка 11, на нее надо повесить 4 буквы, получится 4-й уровень
4*4=16
Ответ: 16

Номер: DA3FC4

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л
Б	1100	Р	1010
Е	010	С	1110
И	011	Т	1011
К	1111	У	100

Укажите кратчайшее кодовое слово для буквы Л, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Ветка 0 тупиковая, смотрим на ветку 1. Свободно 1101
Ответ: 1101

Номер: 5E06CD

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р	1000
Е	010	С	1110
И	011	Т	1001
К	1111	У

Укажите кратчайшее кодовое слово для буквы У, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код
с наименьшим числовым значением.

Решение:

Ветка с 0 тупиковая, смотрим с 1.
101 свободно
Ответ: 101

Номер: A1A6CB

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только четыре буквы: З, А, Р, Я; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв Я, Р, З используются такие кодовые слова: Я – 0, Р – 101; З – 110.

Укажите кратчайшее кодовое слово для буквы А, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Решение:

...
Ответ:

Номер: CCB0C5

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: А, В, Д, К, Р, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Р – 1, К – 0000. Для четырёх оставшихся букв А, В, Д и Н кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАРАВАН, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

...
Ответ:

Номер: 9AF5CD

В	00
Г	1000
Д	111
Е	1001
Ж	01
З	110

Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: А, Б.

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

Решение:

...
Ответ:

Номер: 32DCC7

Укажите кратчайшее кодовое слово для буквы А, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код
с наибольшим числовым значением.

Решение:

...
Ответ:

Номер: 8A6CC1

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р
Е	010	С	1010
И	011	Т	1101
К	1011	У	111

Укажите кратчайшее кодовое слово для буквы Р, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код
с наименьшим числовым значением.

Решение:

...
Ответ:

Номер: 42D598

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв К, Л, М, Н использовали соответственно кодовые слова 00, 01, 100, 110. Для двух оставшихся букв – П и Р – кодовые слова неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы П, при котором код допускает однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ:

Номер: 087792

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р
Е	010	С	1010
И	011	Т	1111
К	1011	У	110

Решение:

...
Ответ:

Номер: 7DAF92

Впишите правильный ответ.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова.

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л
Б	1000	Р	1110
Е	010	С	1010
И	011	Т	1111
К	1011	У	110

Решение:

...
Ответ:

Номер: 72A796

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: А, Б, К, Р, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: К – 01, Р – 001. Для трёх оставшихся букв Б, Н и А кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова БАРАБАН, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

...
Ответ:

Номер: B85498

А	00
Б	1000
В	101
Г	1001
Д	01
Е	110

Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: Ж, З.

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

Решение:

...
Ответ:

Номер: 9A6792

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 100, 101, 00, 01 соответственно. Для двух оставшихся букв – Д и Е – коды неизвестны.

Решение:

...
Ответ:

Номер: 326395

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Л, Ч. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Ч – 1, Л – 011. Для трёх оставшихся букв А, З и К кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЧАЛКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

...
Ответ:

Номер: 038AED

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только буквы из набора: Г, Д, К, С, О, Р. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: С – 0, К – 1011. Для четырёх оставшихся букв Г, Д, О и Р кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КОСОГОР, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение:

...
Ответ:

Номер: B2EEE9

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 00; для буквы Б – кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е?

Решение:

...
Ответ:

Номер: 13BAE9

Укажите минимальную сумму длин кодовых слов для букв Г и Д, при котором код будет удовлетворять условию Фано.

Решение:

...
Ответ:

Номер: A98AE0

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р	1010
Е	010	С	1110
И	011	Т
К	1111	У	100

Укажите кратчайшее кодовое слово для буквы Т, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ:

Номер: 98B3E7

Впишите правильный ответ.
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв Б, В, Г используются такие кодовые слова: Б – 101; В – 110; Г – 0.

Укажите кратчайшее кодовое слово для буквы А, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Решение:

...
Ответ:

Номер: 3D61E7

Цвет	Кодовое слово	Цвет	Кодовое слово
Белый	0	Синий	1110
Зелёный	11111	Фиолетовый
Красный	110	Чёрный	10

Укажите кратчайшее кодовое слово для кодирования фиолетового цвета, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ:

Номер: FD2F65

Буква	Кодовое слово	Буква	Кодовое слово
A		F	0110
B	0111	S	0011
C	100	X	0101
D	101	Y	0010
E	0100	Z	000

Укажите кратчайшее кодовое слово для буквы А, при котором код удовлетворяет условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

...
Ответ:

Номер: B21E6B

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р	1110
Е	010	С	1010
И	011	Т	1111
К		У	110

Решение:

...
Ответ:

Номер: 54C568

Укажите минимальную сумму длин кодовых слов для букв Г и Д, при котором код будет удовлетворять условию Фано.

Решение:

...
Ответ:

Номер: F4F332

Впишите правильный ответ.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0. Какова наименьшая возможная сумма длин всех пяти кодовых слов?

Решение:

...
Ответ:

Номер: 15013A

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1101
Б	1100	Р	1010
Е	010	С	1110
И	011	Т	1011
К	1111	У

Решение:

...
Ответ:

Номер: 6D433E

Буква	Кодовое слово	Буква	Кодовое слово
А	00	Л	1001
Б	1000	Р	1110
Е	010	С	1010
И	011	Т
К	1011	У	110

Решение:

...
Ответ:

Номер: 364539

Укажите минимальную сумму длин кодовых слов для букв Д и Е, при которых код будет удовлетворять условию Фано.

Решение:

...
Ответ:

Номер: 883C3B

А	011
Б	0100
В	10
Г	0101

Какое наименьшее количество двоичных знаков потребуется для кодирования четырёх оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: Д, Е, Ж, З.

Решение:

...
Ответ:

Номер: F9598B

А	10
Б	011
В	110
Г	1110

Какое наименьшее количество двоичных знаков потребуется для кодирования четырёх оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: Д, Е, Ж, З.

Решение:

...
Ответ:

Номер: 3B9384

Задания устаревших формулировок

Выберите правильный ответ.
Для 5 букв русского алфавита заданы их двоичные коды (для некоторых букв ‑ из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

В	К	А	Р	Д
000	11	01	001	10

Из четырех полученных сообщений в этой кодировке, только одно прошло без ошибки и может быть корректно декодировано. Найдите его:

1) 110100000100110011
2) 111010000010010011
3) 110100001001100111
4) 110110000100110010

Решение:

11 01 000 01 001 10 01 11
Ответ: 3

Номер: 5E2DB4

Выберите правильный ответ.
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБВА и записать результат шестнадцатеричным кодом, то получится:

1) 138
2) DBCA
3) D8
4) 3120

Решение:

Закодируем двоичным кодом каждую букву:
А — 00
Б — 01
В — 10
Г — 11
Закодируем последовательность букв ГБВА, используя кодировку букв:
11011000
11011000₂=D8₁₆
Ответ: 3

Номер: E5CC26

: Обновлено: 10 июня 2025

ЕГЭ по информатике 2025. Теория и задания ФИПИ с ответами