Задание 13 ЕГЭ база по математике с ответами: стереометрия

Стереометрия. Тип ответа: краткий ответ. Раздел КЭС геометрия

Все задания ЕГЭ база по математике к линейке 13 по геометрии (стереометрия) из открытого банка ФИПИ с ответами.

Варианты задания 13 ЕГЭ база по математике, ФИПИ

Параллелепипед

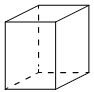
Два ребра прямоугольного параллелепипеда равны 1 и 2, а объём параллелепипеда равен 6. Найдите площадь поверхности этого параллелепипеда.

Решение:

22

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
1*2*x=6
x=3 третье ребро
Считаем площадь
2(2*1)+2(2*3)+2(3*1)=4+12+6=22
Ответ:22

Номер: CDF902

Два ребра прямоугольного параллелепипеда равны 6 и 4, а объём параллелепипеда равен 240. Найдите площадь поверхности этого параллелепипеда.

Решение:

248

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
6*4*x=240
x=10 третье ребро
Считаем площадь
2(6*4)+2(6*10)+2(4*10)=248
Ответ:248

Номер: EA8675

Два ребра прямоугольного параллелепипеда равны 1 и 5, а объём параллелепипеда равен 30. Найдите площадь поверхности этого параллелепипеда.

Решение:

82

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
1*5*x=30
x=6 третье ребро
Считаем площадь
2(1*5)+2(5*6)+2(1*6)=82
Ответ:82

Номер: 8C2DDF

Два ребра прямоугольного параллелепипеда равны 10 и 2, а объём параллелепипеда равен 100. Найдите площадь поверхности этого параллелепипеда.

Решение:

160

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
10*2*x=100
x=5 третье ребро
Считаем площадь
2(10*2)+2(10*5)+2(5*2)=160
Ответ:160

Номер: E2AFC0

Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найдите площадь поверхности этого параллелепипеда.

Решение:

166

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
7*4*x=140
x=5 третье ребро
Считаем площадь
2(7*4)+2(7*5)+2(5*4)=166
Ответ:166

Номер: 90139D BE2DEA

Два ребра прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.

Решение:

262

Объем параллелепипеда высчитывается как произведение трех его ребер, тогда:
8*5*x=280
x=7 третье ребро
Считаем площадь
2(8*5)+2(7*5)+2(8*7)=262
Ответ:262

Номер: F87A44

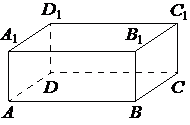
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 2, 6 и 2√10. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

72

Находим 3 ребро
(2√10)²=x²+2²
x²=4*10-4
x=6
Находим объем
2*6*6=72
Ответ:72

Номер: CEB64B

В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

75

Находим 3 ребро
√34²=x²+3²
x²=34-9
x=5
Находим объем
3*5*5=75
Ответ:75

Номер: C1234A

В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра BC, BA и диагональ BC1 боковой грани равны соответственно 5, 7 и √34. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

105

Находим 3 ребро
√34²=x²+5²
x²=34-25
x=3
Находим объем
5*7*3=105
Ответ:105

Номер: 39FAF5

В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ боковой грани CD1 равны соответственно 3, 4 и 5. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

48

Находим 3 ребро
5²=x²+3²
x²=25-9
x=4
Находим объем
3*4*4=48
Ответ:48

Номер: 9A89B4

В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра AB, AD и диагональ AB1 боковой грани равны соответственно 6, 4 и 3√5. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

72

Находим 3 ребро
3√5²=x²+6²
x²=45-36
x=3
Находим объем
6*4*3=72
Ответ:72

Номер: 696914

В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 боковой грани равны соответственно 5, 5 и √29. Найдите объём параллелепипеда ABCDA1B1C1D1.

Решение:

50

Находим 3 ребро
√29²=x²+5²
x²=29-25
x=2
Находим объем
2*5*5=50
Ответ:50

Номер: F87C20

Призма

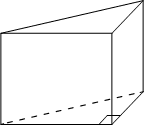
В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 5 и 7. Найдите объём призмы, если её высота равна 4.

Решение:

70

Находим площадь основания
5*7/2=17,5
Находим объем призмы
17,5*4=70
Ответ:70

Номер: 44AF0E 21D1AA

В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 3 и 16. Найдите объём призмы, если её высота равна 3.

Решение:

72

Находим площадь основания
3*16/2=24
Находим объем призмы
24*3=72
Ответ:72

Номер: C60E1D

В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 13 и 4. Найдите объём призмы, если её высота равна 5.

Решение:

130

Находим площадь основания
13*4/2=26
Находим объем призмы
26*5=130
Ответ:130

Номер: 36B123

В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 2 и 18. Найдите объём призмы, если её высота равна 3.

Решение:

54

Находим площадь основания
2*18/2=18
Находим объем призмы
18*3=54
Ответ:54

Номер: 255CC5

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3, а гипотенуза равна 3√5. Найдите объём призмы, если её высота равна 5.

Решение:

45

Находим катет
x²=3√5²-3²
x²=45-9=36
x=6
Находим площадь основания
3*6/2=9
Находим объем призмы
9*5=45
Ответ:45

Номер: 490442

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 6, а гипотенуза равна √85. Найдите объём призмы, если её высота равна 3.

Решение:

63

Находим катет
x²=√85²-6²
x²=85-36=49
x=7
Находим площадь основания
7*6/2=21
Находим объем призмы
21*3=63
Ответ:63

Номер: 4B9A4C

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3, а гипотенуза равна √34. Найдите объём призмы, если её высота равна 6.

Решение:

45

Находим катет
x²=√34²-3²
x²=34-9=25
x=5
Находим площадь основания
3*5/2=7,5
Находим объем призмы
7,5*6=45
Ответ:45

Номер: 905345

В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 5, а гипотенуза равна 5√2. Найдите объём призмы, если её высота равна 4.

Решение:

50

Находим катет
x²=5√2²-5²
x²=50-25=25
x=5
Находим площадь основания
5*5/2=12,5
Находим объем призмы
12,5*4=50
Ответ:50

Номер: DA2102

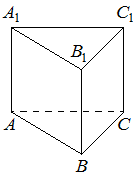
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.

Решение:

12

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(2²√3)/4*4√3=4*3=12
Ответ:12

Номер: FBD845

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 1, а высота этой призмы равна 5√3. Найдите объём призмы ABCA1B1C1.

Решение:

3.75

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(1²√3)/4*5√3=15/4=3.75
Ответ:3.75

Номер: CF0E4E

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна √3. Найдите объём призмы ABCA1B1C1.

Решение:

3

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(2²√3)/4*√3=12/4=3
Ответ: 3

Номер: 14C40A

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 2√3. Найдите объём призмы ABCA1B1C1.

Решение:

6

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(2²√3)/4*2√3=24/4=6
Ответ: 6

Номер: D80603

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 4, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.

Решение:

48

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(4²√3)/4*4√3=192/4=48
Ответ: 48

Номер: C84607

Сторона основания правильной треугольной призмы ABCA1B1C1 равна 5, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.

Решение:

75

В правильной призме в основании правильный треугольник. Находим площадь треугольника, который является основанием
Площадь такого треугольника можно найти по формуле
`S=(a^2*sqrt3)/4`
Тогда объем призмы равен
V=Sh=(5²√3)/4*4√3=300/4=75
Ответ: 75

Номер: 489FB3

Пирамида

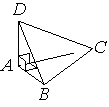
В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=3, AC=18 и AD=7.

Решение:

63

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
3*7/2=10,5
Находим объем
`V=1/3*10.5*18=63`
Ответ:63

Номер: FE7FF2

В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=5, AC=24 и AD=3.

Решение:

60

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
5*24/2=60
Находим объем
`V=1/3*60*3=60`
Ответ:60

Номер: 8F31F8 B4D06A

В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=2, AC=15 и AD=11.

Решение:

55

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
2*15/2=15
Находим объем
`V=1/3*15*11=55`
Ответ:55

Номер: AA43B5

В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=3, AC=14 и AD=8.

Решение:

56

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
3*14/2=21
Находим объем
`V=1/3*21*8=56`
Ответ:56

Номер: DCF59A 3A9F92

В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=2, AC=15 и AD=7.

Решение:

35

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
2*15/2=15
Находим объем
`V=1/3*15*7=35`
Ответ:35

Номер: AFAAEB

В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=8, AC=12 и AD=10.

Решение:

160

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это прямоугольный треугольник
8*12/2=48
Находим объем
`V=1/3*48*10=160`
Ответ:160

Номер: 2FD042

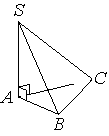
В основании пирамиды SABC лежит правильный треугольник ABC со стороной 4, а боковое ребро SA перпендикулярно основанию и равно 3√3. Найдите объём пирамиды SABC.

Решение:

12

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=4√3
Находим объем
`V=1/3*4sqrt3*3sqrt3=12`
Ответ:12

Номер: 362D41

В основании пирамиды SABC лежит правильный треугольник ABC со стороной 6, а боковое ребро SA перпендикулярно основанию и равно 2√3. Найдите объём пирамиды SABC.

Решение:

18

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=9√3
Находим объем
`V=1/3*9sqrt3*2sqrt3=18`
Ответ:18

Номер: A6C17A

В основании пирамиды SABC лежит правильный треугольник ABC со стороной 4, а боковое ребро SA перпендикулярно основанию и равно 5√3. Найдите объём пирамиды SABC.

Решение:

20

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=4√3
Находим объем
`V=1/3*4sqrt3*5sqrt3=20`
Ответ:20

Номер: D6FE52

В основании пирамиды SABC лежит правильный треугольник ABC со стороной 2, а боковое ребро SA перпендикулярно основанию и равно 4√3.
Найдите объём пирамиды SABC.

Решение:

4

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=√3
Находим объем
`V=1/3*sqrt3*4sqrt3=4`
Ответ:4

Номер: 4F4889

В основании пирамиды SABC лежит правильный треугольник ABC со стороной 10, а боковое ребро SA перпендикулярно основанию и равно 7√3. Найдите объём пирамиды SABC.

Решение:

175

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=25√3
Находим объем
`V=1/3*25sqrt3*7sqrt3=175`
Ответ:175

Номер: E6240F

В основании пирамиды SABC лежит правильный треугольник ABC со стороной 2, а боковое ребро SA перпендикулярно основанию и равно √3. Найдите объём пирамиды SABC.

Решение:

1

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=√3
Находим объем
`V=1/3*sqrt3*sqrt3=1`
Ответ:1

Номер: 66719D

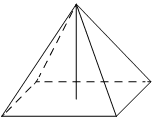
Основанием четырёхугольной пирамиды является прямоугольник со сторонами 9 и 4. Найдите высоту этой пирамиды, если её объём равен 48.

Решение:

4

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=9*4=36
Находим высоту
`48=1/3*36*h`
h=48*3/36=4
Ответ:4

Номер: 8BB444

Основанием четырёхугольной пирамиды является прямоугольник со сторонами 3 и 12. Найдите высоту этой пирамиды, если её объём равен 60.

Решение:

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=3*12=36
Находим высоту
`60=1/3*36*h`
h=5
Ответ:5

Номер: A98E2B

Основанием четырёхугольной пирамиды является прямоугольник со сторонами 3 и 9. Найдите высоту этой пирамиды, если её объём равен 72.

Решение:

8

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=9*3=27
Находим высоту
`72=1/3*27*h`
h=72*3/27=8
Ответ:8

Номер: 4AA2D6

Основанием четырёхугольной пирамиды является прямоугольник со сторонами 12 и 5. Найдите высоту этой пирамиды, если её объём равен 60.

Решение:

3

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=12*5=60
Находим высоту
`60=1/3*60*h`
h=60*3/60=3
Ответ:3

Номер: 5D2839

Основанием четырёхугольной пирамиды является прямоугольник со сторонами 7 и 3. Найдите высоту этой пирамиды, если её объём равен 42.

Решение:

6

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=7*3=21
Находим высоту
`42=1/3*21*h`
h=42*3/21=6
Ответ:6

Номер: DC44FD

Основанием четырёхугольной пирамиды является прямоугольник со сторонами 5 и 12. Найдите высоту этой пирамиды, если её объём равен 100.

Решение:

5

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Отсюда зная объем можно узнать высоту.
Находим площадь основания из условия, что это прямоугольник:
S=5*12=60
Находим высоту
`100=1/3*60*h`
h=100*3/60=5
Ответ:5

Номер: 8CD4FE

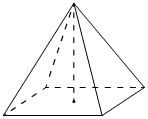
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно 2√11.

Решение:

32

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=4²+4²
x=√32
x=4√2
тогда половина диагонали равна 2√2
Находим высоту (по теореме Пифагора)
h²=2√11²-2√2²
h²=4*11-4*2
h²=44-8=36
h=6
Находим объем
`V=1/3*S*h=1/3*4*4*6`=32
Ответ:32

Номер: FB0748

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.

Решение:

64

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=8²+8²
x=√128
x=8√2
тогда половина диагонали равна 4√2
Находим высоту (по теореме Пифагора)
h²=√41²-4√2²
h²=41-16*2
h²=41-32=9
h=3
Находим объем
`V=1/3*S*h=1/3*8*8*3`=64
Ответ:64

Номер: 73E8F3 CA65F9

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно √43.

Решение:

60

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=6²+6²
x=√72
x=6√2
тогда половина диагонали равна 3√2
Находим высоту (по теореме Пифагора)
h²=√43²-3√2²
h²=43-9*2
h²=43-18=25
h=5
Находим объем
`V=1/3*S*h=1/3*6*6*5`=60
Ответ:60

Номер: A02AB1

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.

Решение:

16

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=4²+4²
x=√32
x=4√2
тогда половина диагонали равна 2√2
Находим высоту (по теореме Пифагора)
h²=√17²-2√2²
h²=17-4*2
h²=17-8=9
h=3
Находим объем
`V=1/3*S*h=1/3*4*4*3`=16
Ответ:16

Номер: 9945BE

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно 3√6.

Решение:

72

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=6²+6²
x=√72
x=6√2
тогда половина диагонали равна 3√2
Находим высоту (по теореме Пифагора)
h²=3√6²-3√2²
h²=54-9*2
h²=54-18=36
h=6
Находим объем
`V=1/3*S*h=1/3*6*6*6`=72
Ответ:72

Номер: 05ED1C

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно √67.

Решение:

84

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим диагональ основания (по теореме Пифагора)
x²=6²+6²
x=√72
x=6√2
тогда половина диагонали равна 3√2
Находим высоту (по теореме Пифагора)
h²=√67²-3√2²
h²=67-9*2
h²=67-18=49
h=7
Находим объем
`V=1/3*S*h=1/3*6*6*7`=84
Ответ:84

Номер: 3BB030

Сторона основания правильной треугольной пирамиды равна 2, а высота пирамиды равна 3√3. Найдите объём этой пирамиды.

Решение:

3

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4`=√3
Находим объем
`V=1/3*sqrt3*3sqrt3=3`
Ответ:3

Номер: 1B20B4

Сторона основания правильной треугольной пирамиды равна 4, а высота пирамиды равна 2√3. Найдите объём этой пирамиды.

Решение:

8

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4 = 4sqrt3`
Находим объем
`V=1/3*4sqrt3*2sqrt3=8`
Ответ:8

Номер: 4B8B1B

Сторона основания правильной треугольной пирамиды равна 5, а высота пирамиды равна 4√3. Найдите объём этой пирамиды.

Решение:

25

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4 = 6.25sqrt3`
Находим объем
`V=1/3*6.25sqrt3*4sqrt3=25`
Ответ:25

Номер: D1811B

Сторона основания правильной треугольной пирамиды равна 2, а высота пирамиды равна 6√3. Найдите объём этой пирамиды.

Решение:

6

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4 = sqrt3`
Находим объем
`V=1/3*sqrt3*6sqrt3=6`
Ответ:6

Номер: BE0CA4

Сторона основания правильной треугольной пирамиды равна 2, а высота пирамиды равна 4√3. Найдите объём этой пирамиды.

Решение:

4

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4 = sqrt3`
Находим объем
`V=1/3*sqrt3*4sqrt3=4`
Ответ:4

Номер: E9EFAE

Сторона основания правильной треугольной пирамиды равна 1, а высота пирамиды равна 32√3. Найдите объём этой пирамиды.

Решение:

8

Объем пирамиды можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
Находим площадь основания из условия, что это правильный треугольник (равносторонний). По формуле площади равностороннего треугольника получаем:
`S=(a^2*sqrt3)/4 = 0.25sqrt3`
Находим объем
`V=1/3*0.25sqrt3*32sqrt3=8`
Ответ:8

Номер: E58000

Стороны основания правильной треугольной пирамиды равны 10, а боковые рёбра равны 13. Найдите площадь боковой поверхности этой пирамиды.

Решение:

180

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(18(18-10)(18-13)(18-13))=sqrt(18*5*5*8)`=60
Узнаем площадь боковых поверхностей
60*3=180
Ответ:180

Номер: BD79F1 1387BB

Стороны основания правильной треугольной пирамиды равны 14, а боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.

Решение:

504

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(32(32-14)(32-25)(32-25))=sqrt(32*18*7*7)`=168
Узнаем площадь боковых поверхностей
168*3=504
Ответ:504

Номер: F71F02

Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды.

Решение:

144

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(18(18-16)(18-10)(18-10))=sqrt(18*2*8*8)`=48
Узнаем площадь боковых поверхностей
48*3=144
Ответ:144

Номер: 40D922

Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 20. Найдите площадь боковой поверхности этой пирамиды.

Решение:

576

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(32(32-24)(32-20)(32-20))=sqrt(32*8*12*12)`=192
Узнаем площадь боковых поверхностей
192*3=576
Ответ:576

Номер: 60D404

Стороны основания правильной треугольной пирамиды равны 42, а боковые рёбра равны 29. Найдите площадь боковой поверхности этой пирамиды.

Решение:

1260

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(50(50-42)(50-29)(50-29))=sqrt(50*8*21*21)`=420
Узнаем площадь боковых поверхностей
420*3=1260
Ответ:1260

Номер: 0DEC6B

Стороны основания правильной треугольной пирамиды равны 18, а боковые рёбра равны 15. Найдите площадь боковой поверхности этой пирамиды.

Решение:

324

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной из боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`S=sqrt(24(24-18)(24-15)(24-15))=sqrt(24*6*9*9)`=108
Узнаем площадь боковых поверхностей
108*3=324
Ответ:324

Номер: C16131

Стороны основания правильной шестиугольной пирамиды равны 12, боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды.

Решение:

288

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь площади боковых сторон по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`p = (12+10+10)/2=32/2=16`
`S=sqrt(16(16-12)(16-10)(16-10))=sqrt(16*4*6*6)`=48
Узнаем площадь боковых поверхностей
48*6=288
Ответ:288

Номер: 514C0F

Стороны основания правильной шестиугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.

Решение:

1008

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной боковой стороны по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
p = 14+25+25=64/2=32
`S=sqrt(32(32-14)(32-25)(32-25))=sqrt(32*18*7*7)`=168
Узнаем площадь боковых поверхностей
168*6=1008
Ответ:1008

Номер: 8209EF 65AFAE

Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.

Решение:

2520

Так как основание правильный треугольник, то все стороны пирамиды равнобедренные треугольники.
Найдем площадь одной боковой стороны по формуле Герона:
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
p = 24+37+37=98/2=49
`S=sqrt(49(49-24)(49-37)(49-37))=sqrt(49*25*12*12)`=420
Узнаем площадь боковых поверхностей
420*6=2520
Ответ:2520

Номер: F979BD

Цилиндр

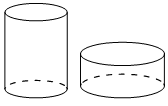
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?

Решение:

6

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·2²·6=24π
Для второго
V = π·6²·4=144π
Находим отношения
144/24=6
Ответ:6

Номер: 0EF144 19D0E6

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 1, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого цилиндра?

Решение:

9

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·4²·1=16π
Для второго
V = π·6²·4=144π
Находим отношения
144/16=9
Ответ:9

Номер: 335304 C59471

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 8, а второго — 8 и 9. Во сколько раз объём второго цилиндра больше объёма первого?

Решение:

18

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·2²·8=32π
Для второго
V = π·8²·9=576π
Находим отношения
576/32=18
Ответ:18

Номер: 360E23

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?

Решение:

10.5

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·2²·6=24π
Для второго
V = π·6²·7=252π
Находим отношения
252/24=10.5
Ответ:10.5

Номер: 3CA1A2

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 3 и 2, а второго — 8 и 9. Во сколько раз объём второго цилиндра больше объёма первого цилиндра?

Решение:

32

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·3²·2=18π
Для второго
V = π·8²·9=576π
Находим отношения
576/18=32
Ответ:32

Номер: 0D4B34

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 3, а второго — 8 и 3. Во сколько раз объём второго цилиндра больше объёма первого цилиндра?

Решение:

16

Для цилиндра объем находится по формуле:
V = π·r²·h
Так для первого цилиндра
V = π·2²·3=12π
Для второго
V = π·8²·3=192π
Находим отношения
192/12=16
Ответ:16

Номер: 3518B4

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго цилиндра?

Решение:

12

Площадь боковой поверхности цилиндра вычисляется по формуле
Sбок = 2πR * H, где R — радиус основания, H — высота цилиндра.

Находим для первого
Sбок = 2π*4*18=144π
Для второго
Sбок = 2π*2*3=12π
Находим соотношения
144π/12π=12
Ответ: 12

Номер: 346AF2 703717

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго цилиндра?

Решение:

4

Площадь боковой поверхности цилиндра вычисляется по формуле
Sбок = 2πR * H, где R — радиус основания, H — высота цилиндра.

Находим для первого
Sбок = 2π*6*14=168π
Для второго
Sбок = 2π*7*3=42π
Находим соотношения
168/42=4
Ответ: 4

Номер: 7B3009 0B04B4

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 15 и 6, а второго — 2 и 5. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго цилиндра?

Решение:

9

Площадь боковой поверхности цилиндра вычисляется по формуле
Sбок = 2πR * H, где R — радиус основания, H — высота цилиндра.

Находим для первого
Sбок = 2π*15*6=180π
Для второго
Sбок = 2π*2*5=20π
Находим соотношения
180π/20π=9
Ответ: 9

Номер: 66D402 F6826F

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 9 и 8, а второго — 12 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

Решение:

2

Площадь боковой поверхности цилиндра вычисляется по формуле
Sбок = 2πR * H, где R — радиус основания, H — высота цилиндра.

Находим для первого
Sбок = 2π*9*8=144π
Для второго
Sбок = 2π*12*3=72π
Находим соотношения
144π/72π=2
Ответ: 2

Номер: 6AEA05 666C6D

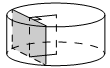
Радиус основания цилиндра равен 25, а его образующая равна 7. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 20. Найдите площадь этого сечения.

Решение:

210

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 20, это расстояние до сечения, 25 это гипотенуза-радиус и x, это это катет и половина второй стороны, которую нам надо найти.
x²=25²-20²
x²=625-400
x = √225
х = 15
Находим площадь сечения
15*2*7=210
Ответ:210

Номер: 1DD343

Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.

Решение:

252

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 12, это расстояние до сечения, 15 это гипотенуза-радиус и x, это это катет и половина второй стороны, которую нам надо найти.
x²=15²-12²
x²=225-144
x = √81
х = 9
Находим площадь сечения
9*2*14=252
Ответ:252

Номер: CBA441

Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 9. Найдите площадь этого сечения.

Решение:

336

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 9, это расстояние до сечения, 15 это гипотенуза-радиус и x, это это катет и половина второй стороны сечения, которую нам надо найти.
x²=15²-9²
x²=225-81
x = √144
х = 12
Находим площадь сечения
12*2*14=336
Ответ:336

Номер: 587608

Радиус основания цилиндра равен 17, а его образующая равна 10. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.

Решение:

300

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 8, это расстояние до сечения, 17 это гипотенуза-радиус и x, это это катет и половина второй стороны сечения, которую нам надо найти.
x²=17²-8²
x²=289-64
x = √225
х = 15
Находим площадь сечения
15*2*10=300
Ответ:300

Номер: BE94F3

Радиус основания цилиндра равен 17, а его образующая равна 5. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.

Решение:

150

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 5, это расстояние до сечения, 17 это гипотенуза-радиус и x, это это катет и половина второй стороны сечения, которую нам надо найти.
x²=17²-8²
x²=289-64
x = √225
х = 15
Находим площадь сечения
15*2*5=150
Ответ:150

Номер: 22FD72

Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.

Решение:

180

Образующая равна высоте цилиндра и равна одной из сторон сечения. Теперь находим вторую сторону. Для этого условно проведем диагональ для перпендикулярного треугольника, где стороны равны 26, это расстояние до сечения, 26 это гипотенуза-радиус и x, это это катет и половина второй стороны сечения, которую нам надо найти.
x²=26²-24²
x²=676-576
x = √100
х = 10
Находим площадь сечения
10*2*9=180
Ответ:18

Номер: 3BC472

Конус

Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.

Решение:

5

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем r
`r = sqrt((3*V)/(π*h))`
`r = sqrt((3*25*π)/(π*3))`
r=√25=5
Ответ:5

Номер: FD1543

Объём конуса равен 96π, а его высота равна 8. Найдите радиус основания конуса.

Решение:

6

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем r
`r = sqrt((3*V)/(π*h))`
`r = sqrt((3*96*π)/(π*8))`
r=√36=6
Ответ:6

Номер: 34E2FF

Объём конуса равен 162π, а его высота равна 6. Найдите радиус основания конуса.

Решение:

9

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем r
`r = sqrt((3*V)/(π*h))`
`r = sqrt((3*162*π)/(π*6))`
r=√81=9
Ответ:9

Номер: 7A4C03

Объём конуса равен 60π, а его высота равна 5. Найдите радиус основания конуса.

Решение:

Номер: C43D78

Объём конуса равен 84π, а его высота равна 7. Найдите радиус основания конуса.

Решение:

Номер: 44E8B4

Объём конуса равен 50π, а его высота равна 6. Найдите радиус основания конуса.

Решение:

Номер: 8B57BD

Объём конуса равен 9π, а радиус его основания равен 3. Найдите высоту конуса.

Решение:

3

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем h
`h = (3*V)/(π*r^2)`
`h = (3*9*π)/(π*r^2)`=3
Ответ:3

Номер: C4C408 95DD7C

Объём конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.

Решение:

18

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем h
`h = (3*V)/(π*r^2)`
`h = (3*24*π)/(π*2^2)`=18
Ответ:18

Номер: 0DEC6D B6673A

Объём конуса равен 6π, а радиус его основания равен 1. Найдите высоту конуса.

Решение:

Номер: 2608D2

Объём конуса равен 16π, а радиус его основания равен 2. Найдите высоту конуса.

Решение:

12

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h` из этой формулы найдем h
`h = (3*V)/(π*r^2)`
`h = (3*16*π)/(π*2^2)`=12
Ответ:12

Номер: 6D758D

Даны два конуса. Радиус основания и высота первого конуса равны соответственно 2 и 9, а второго — 2 и 2. Во сколько раз объём первого конуса больше объёма второго конуса?

Решение:

4,5

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*2^2*9` = 12π
Для второго
`V2=1/3*π*2^2*2` = 8/3π
Соотнесем объемы.
12:8/3=36/8=4,5
Ответ:4,5

Номер: 568EF9

Даны два конуса. Радиус основания и высота первого конуса равны соответственно 9 и 6, а второго — 6 и 3. Во сколько раз объём первого конуса больше объёма второго?

Решение:

4,5

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*9^2*6` = 162π
Для второго
`V2=1/3*π*6^2*3` = 36π
Соотнесем объемы.
162/36=4,5
Ответ:4,5

Номер: 28D803

Даны два конуса. Радиус основания и высота первого конуса равны соответственно 6 и 5, а второго — 3 и 2. Во сколько раз объём первого конуса больше объёма второго?

Решение:

10

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*6^2*5` = 60π
Для второго
`V2=1/3*π*3^2*2` = 6π
Соотнесем объемы.
60/6=10
Ответ:10

Номер: E6F312

Даны два конуса. Радиус основания и высота первого конуса равны соответственно 4 и 9, а второго — 6 и 8. Во сколько раз объём второго конуса больше объёма первого?

Решение:

2

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*4^2*9` = 48π
Для второго
`V2=1/3*π*6^2*8` = 96π
Соотнесем объемы.
96/48=2
Ответ:2

Номер: 621D7C

Решение:

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*4^2*9` = 48π
Для второго
`V2=1/3*π*6^2*8` = 96π
Соотнесем объемы.
96/48=2
Ответ:2

Номер: 1ADCB9

Даны два конуса. Радиус основания и высота первого конуса равны соответственно 2 и 3, а второго — 8 и 6. Во сколько раз объём второго конуса больше объёма первого?

Решение:

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Подсчитаем объем для первого конуса
`V1=1/3*π*2^2*3` = 4π
Для второго
`V2=1/3*π*8^2*6` = 128π
Соотнесем объемы.
128/4=32
Ответ:32

Номер: 3B50BA

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 4 и 6, а второго — 2 и 8. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

Решение:

1,5

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 4 * 6 = 24π
Для второго
Sбок = π * r * l = π * 2 * 8 = 16π
Соотнесем площади
24π:16π=1,5
Ответ:1,5

Номер: 7B394C

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 7 и 9, а второго — 2 и 9. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго конуса?

Решение:

3,5

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 7 * 9 = 63π
Для второго
Sбок = π * r * l = π * 2 * 9 = 18π
Соотнесем объемы.
63:18=3,5
Ответ:3,5

Номер: 35044E

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 5 и 6, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

Решение:

5

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 5 * 6 = 30π
Для второго
Sбок = π * r * l = π * 2 * 3 = 6π
Соотнесем объемы.
30:6=5
Ответ:5

Номер: E1EFFB

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 5 и 9, а второго — 3 и 5. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

Решение:

3

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 5 * 9 = 45π
Для второго
Sбок = π * r * l = π * 3 * 5 = 15π
Соотнесем объемы.
45:15=3
Ответ:3

Номер: 2D270B

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 3, а второго — 2 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого конуса?

Решение:

3

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 2 * 3 = 6π
Для второго
Sбок = π * r * l = π * 2 * 9 = 18π
Соотнесем объемы.
18:6=3
Ответ:3

Номер: A6DE08

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 4 и 6, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

Решение:

4

Sбок = π * r * l, где Sбок — площадь боковой поверхности, r — радиус основания конуса, l — образующая конуса.

Подсчитаем боковую поверхность для первого конуса
Sбок = π * r * l = π * 4 * 6 = 24π
Для второго
Sбок = π * r * l = π * 2 * 3 = 6π
Соотнесем объемы.
24:6=4
Ответ:4

Номер: 8DD670

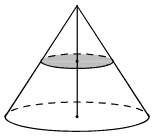
Объём конуса равен 192. Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

3

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является третьей частью (1:3), то есть всего 4 части и 1/4 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/4*r)^2*1/4*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/4*r)^2*1/4*h` =
=`1/3*π*r^2*h (1-1/16*1/4) = 1/3*π*r^2*h*63/64`
Тогда мы видим, что это 63/64 от нашего объема конуса (то есть получили формулу выше с коэффициентом 63/64) и высчитываем Vотсеч.
192*63/64=189 это объем отсеченного. При этом
192-189=3 это объем отсеченного маленького конуса
Ответ: 3

Номер: F7C4F4

Объём конуса равен 375. Через точку, делящую высоту конуса в отношении 1:4, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

3

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:4), то есть всего 5 части и 1/5 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/5*r)^2*1/5*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/5*r)^2*1/5*h` =
=`1/3*π*r^2*h (1-1/25*1/5) = 1/3*π*r^2*h*124/125`
Тогда мы видим, что это 124/125 от нашего объема конуса (то есть получили формулу выше с коэффициентом 124/125) и высчитываем Vотсеч.
375*124/125=372 это объем отсеченного. При этом
375-372=3 это объем отсеченного маленького конуса
Ответ: 3

Номер: 7F13FC

Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

1

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:2), то есть всего 3 части и 1/3 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/3*r)^2*1/3*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/3*r)^2*1/3*h` =
=`1/3*π*r^2*h (1-1/9*1/3) = 1/3*π*r^2*h*26/27`
Тогда мы видим, что это 26/27 от нашего объема конуса (то есть получили формулу выше с коэффициентом 26/27) и высчитываем Vотсеч.
27*26/27=26 это объем отсеченного. При этом
27-26=1 это объем отсеченного маленького конуса
Ответ: 1

Номер: DD8909

Объём конуса равен 256. Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

4

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является третьей частью (1:3), то есть всего 4 части и 1/4 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/4*r)^2*1/4*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/4*r)^2*1/4*h` =
=`1/3*π*r^2*h (1-1/16*1/4) = 1/3*π*r^2*h*63/64`
Тогда мы видим, что это 63/64 от нашего объема конуса (то есть получили формулу выше с коэффициентом 63/64) и высчитываем Vотсеч.
256*63/64=252 это объем отсеченного. При этом
256-252=4 это объем отсеченного маленького конуса
Ответ: 4

Номер: D68C09

Объём конуса равен 8. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

1

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:1), то есть всего 2 части и 1/2 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/2*r)^2*1/2*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/2*r)^2*1/2*h` =
=`1/3*π*r^2*h (1-1/4*1/2) = 1/3*π*r^2*h*7/8`
Тогда мы видим, что это 7/8 от нашего объема конуса (то есть получили формулу выше с коэффициентом 7/8) и высчитываем Vотсеч.
8*7/8=7 это объем отсеченного. При этом
8-7=1 это объем отсеченного маленького конуса
Ответ: 1

Номер: 5A6C02

Объём конуса равен 24. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Решение:

3

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:1), то есть всего 2 части и 1/2 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/2*r)^2*1/2*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/2*r)^2*1/2*h` =
=`1/3*π*r^2*h (1-1/4*1/2) = 1/3*π*r^2*h*7/8`
Тогда мы видим, что это 7/8 от нашего объема конуса (то есть получили формулу выше с коэффициентом 7/8) и высчитываем Vотсеч.
24*7/8=21 это объем отсеченного. При этом
24-21=3 это объем отсеченного маленького конуса
Ответ: 3

Номер: 8A41F5

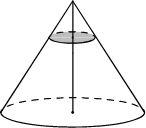
Через точку, делящую высоту конуса в отношении 1 : 2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 10.

Решение:

270

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:2), то есть всего 3 части и 1/3 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/3*r)^2*1/3*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/3*r)^2*1/3*h` =
=`1/3*π*r^2*h (1-1/9*1/3) = 1/3*π*r^2*h*26/27`
...мы видим, что это 26/27 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 26/27) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 10 это 1 часть из 27, а 26 частей отсекается, то есть объем большого конуса будет 10*(26+1)=270
Ответ: 270

Номер: 31CA99

Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 10.

Решение:

640

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:3), то есть всего 4 части и 1/4 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/4*r)^2*1/4*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/4*r)^2*1/4*h` =
=`1/3*π*r^2*h (1-1/16*1/4) = 1/3*π*r^2*h*63/64`
...мы видим, что это 63/64 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 63/64) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 10 это 1 часть из 64, а 63 части отсекается, то есть объем большого конуса будет 10*(63+1)=640
Ответ: 640

Номер: 8DA962 F45E84

Решение:

540

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:2), то есть всего 3 части и 1/3 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/3*r)^2*1/3*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/3*r)^2*1/3*h` =
=`1/3*π*r^2*h (1-1/9*1/3) = 1/3*π*r^2*h*26/27`
...мы видим, что это 26/27 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 26/27) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 20 это 1 часть из 27, а 26 частей отсекается, то есть объем большого конуса будет 20*(26+1)=540
Ответ: 540

Номер: BD1B32

Решение:

320

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:3), то есть всего 4 части и 1/4 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/4*r)^2*1/4*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/4*r)^2*1/4*h` =
=`1/3*π*r^2*h (1-1/16*1/4) = 1/3*π*r^2*h*63/64`
...мы видим, что это 63/64 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 63/64) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 5 это 1 часть из 64, а 63 частей отсекается, то есть объем большого конуса будет 5*(63+1)=320
Ответ: 320

Номер: 9F3B35

Через точку, делящую высоту конуса в отношении 1:4, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 8.

Решение:

1000

Объем конуса можно найти по формуле
`V=1/3*S*h`, где S площадь основания, а h - высота.
С учетом площади круга S=π*r²
`V=1/3*π*r^2*h`
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:4), то есть всего 5 части и 1/5 часть приходится на высоту маленького конуса.
`V2=1/3*π*(1/5*r)^2*1/5*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`Vотсеч.=1/3*π*r^2*h - 1/3*π*(1/5*r)^2*1/5*h` =
=`1/3*π*r^2*h (1-1/25*1/5) = 1/3*π*r^2*h*124/125`
...мы видим, что это 124/125 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 124/125) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 8 это 1 часть из 124, а 125 частей отсекается, то есть объем большого конуса будет 8*(124+1)=1000
Ответ: 1000

Номер: 518FB1 F445CD

Шар

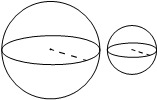
Даны два шара с радиусами 9 и 1. Во сколько раз объём большего шара больше объёма меньшего?

Решение:

729

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=729/1=729

Ответ:729

Номер: BE0C42

Даны два шара с радиусами 3 и 1. Во сколько раз объём большего шара больше объёма меньшего?

Решение:

27

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=27/1=27

Ответ:27

Номер: FE65F4

Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма меньшего шара?

Решение:

64

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=64/1=64

Ответ:64

Номер: BB83FF 148474

Даны два шара с радиусами 2 и 1. Во сколько раз объём большего шара больше объёма меньшего?

Решение:

8

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=8/1=8

Ответ:8

Номер: 410202

Даны два шара с радиусами 5 и 1. Во сколько раз объём большего шара больше объёма меньшего?

Решение:

125

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=125/1=125

Ответ:125

Номер: 53C672

Даны два шара с радиусами 7 и 1. Во сколько раз объём большего шара больше объёма меньшего?

Решение:

343

Объем шара находится по формуле:
`V=3/4*π*r^3`
Тогда объемы шаров будут являться отношением кубов радиусов
`V_1/V_2=r_1^3/r_2^3`=343/1=343

Ответ:343

Номер: 98E870

Даны два шара с радиусами 8 и 1. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Решение:

64

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=64/1=64
Ответ:64

Номер: 68DF40

Даны два шара с радиусами 4 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Решение:

4

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=16/4=4
Ответ:4

Номер: 03B8FA

Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Решение:

9

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=81/9=9
Ответ:9

Номер: 01C37A

Даны два шара с радиусами 5 и 1. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Решение:

25

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=25/1=25
Ответ:25

Номер: 8F397E

Даны два шара с радиусами 6 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Решение:

9

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=36/4=9
Ответ:9

Номер: 5F3ABC

Даны два шара с радиусами 8 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности другого?

Решение:

16

Площадь сферы шара находится по формуле:
`S=4*π*r^2`
Тогда отношение сфер будет отношением квадратов радиусов
`S_1/S_2=r_1^2/r_2^2`=64/4=16
Ответ:16

Номер: BAE81E

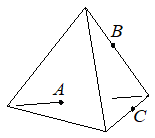
Плоскость, проходящая через точки A, B и C (см. рисунок), разбивает тетраэдр на два многогранника. Сколько рёбер у получившегося многогранника с большим числом вершин?

Решение:

Плоскость отсекает справа треугольную пирамиду, а слева остается многогранник с 6 вершинами и 9 ребрами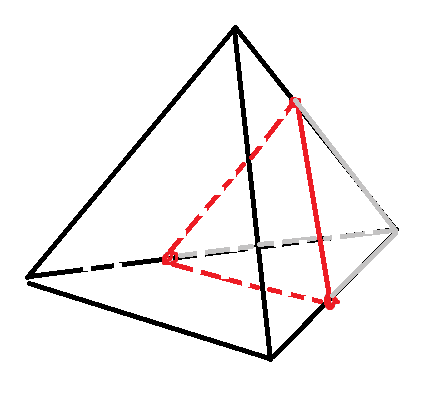

Ответ: 9

Номер: A4660E

: Обновлено: 19 мая 2024

ЕГЭ по математике база 2025, все задания ФИПИ с ответами