Разделы КЭС: геометрия, фигуры на плоскости. Все задания ЕГЭ база по математике к линейке 12 по геометрии (планиметрия) из открытого банка ФИПИ с ответами.
Варианты задания 12 ЕГЭ база по математике, ФИПИ
Впишите правильный ответ.
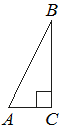
В треугольнике ABC угол C равен 90°, AB=20, AC=2√19. Найдите cosB.
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=20^2-(2sqrt(19))^2`
`BC^2=400-4*19`
`BC^2=400-76`
BC=18
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=18/20=0,9
Ответ:0,9
Номер: 47F947
Впишите правильный ответ.
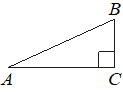
В треугольнике ABC угол C равен 90°, AB=5, AC=√21. Найдите sinA.
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=5^2-(sqrt(21))^2`
`BC^2=25-21`
`BC^2=4`
BC=2
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=4/5=0,8
Ответ:
Номер: 48DE4D
Впишите правильный ответ.
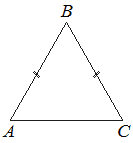
В треугольнике ABC известно, что AB=BC=25 , AC=14. Найдите площадь треугольника ABC.
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=25^2-7^2`
`h^2=625-49`
`h^2=576`
h=24
Найдем площадь:
S= 24*14*0.5=168
Ответ: 168
Номер: 43F64A
Впишите правильный ответ.
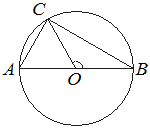
На окружности с центром O и диаметром AB отмечена точка C так, что угол COB равен 120°, AC=23 . Найдите диаметр окружности.
Решение:
∠COB = 120°, тогда ∠OСB = ∠OСB = (180-120)/2 = 30° так как треугольник равнобедренный, стороны являются радиусами.
Получается АС катет в прямоугольном треугольнике напротив угла в 30°, а значит он равен половине гипотенузы.
То есть диаметр равен гипотенузе и двум катетам: 2*23=46
Ответ:46
Номер: 07F341
Впишите правильный ответ.
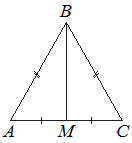
В равнобедренном треугольнике ABC медиана BM , проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
Решение:
BM является также и высотой.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
Тогда из соотношения тангенса AM = 5
Находим сторону треугольника:
`AB^2=BM^2+AМ^2`
`AB^2=12^2+5^2`
`AB^2=144+25`
`AB^2=169`
AB=13
Ответ:13
Номер: E6C947
Номер: BC7D4F
Впишите правильный ответ.
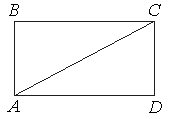
Площадь прямоугольника ABCD равна 300, сторона AB=9 . Найдите тангенс угла CAD .
Решение:
Найдем вторую сторону прямоугольника.
300/9=100/3
Тангенс угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
tg∠CAD=9/(100/3)=0,27
Ответ:
Номер: 16844F
Впишите правильный ответ.
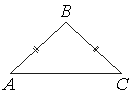
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
Решение:
Проведем высоту для треугольника ABC.
Получим катет противолежащий и гипотенуза с соотношением 3/5. Найдем по теореме Пифагора катет.
`5^2 = 3^2+x^2`
`x^2 =25-9`
`x = sqrt(16)`
x = 4
То есть соотношения всех сторон 3, 4 и 5 в частях. Если гипотенуза 5 частей и 25 в значении, то 1 часть равна 25/5= 5
Высота равна 3*5=15
Основание 4*5=20, а все основание треугольника 20*2=40
`S_(треугольника) = (40*15)/2` = 300
Ответ:300
Номер: C9A789
Номер: 255A4D
Впишите правильный ответ.
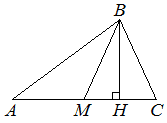
В треугольнике ABC сторона AC=88 , BM — медиана, BH — высота, BC=BM. Найдите длину отрезка AH.
Решение:
АM=MC так как BM — медиана, при этом МН=НС так как это основание равнобедренного треугольника, где H точка пересечения с высотой.
При этом соотношение МС к МH как 1/2, получается все основание треугольника ABC условно можно разделить на 4 части, где одна часть будет равна HC. Тогда AH это 3/4 от всего основания.
88*3/4=66
Ответ:
Номер: E1662A
Номер: D1694D
Впишите правильный ответ.
Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
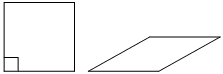
Решение:
Находим сторону квадрата и ромба
L = √64
L = 8
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
8*(8/2)=8*4=32
Ответ:32
Номер: 4720CB
Номер: DC1608
Номер: 502941
Впишите правильный ответ.
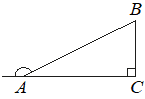
В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Катет BC=30. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-150=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
30*2=60
Ответ:60
Номер: 5D014C
Впишите правильный ответ.
Обе диагонали параллелограмма равны 13. Одна из сторон параллелограмма равна 5. Найдите сторону параллелограмма, соседнюю с данной.
Решение:
Если обе диагонали равны, то этот параллелограмм является прямоугольником. Причем диагональ делит его на два прямоугольных треугольника, где является гипотенузой, один из катетов известен, остается найти второй катет.
`13^2 = 5^2+x^2`
`x^2 =169-25`
`x = sqrt(144)`
x = 12
Ответ:12
Номер: A41548
Впишите правильный ответ.
Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30° , а площадь квадрата равна 16.

Решение:
Находим сторону квадрата и ромба
L = √16
L = 4
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
4*(4/2)=4*2=8
Ответ:
Номер: CA3040
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=12 , ВС=CD=13 (см. рисунок). Найдите среднюю линию трапеции.
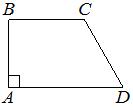
Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`13^2 = 12^2+x^2`
`x^2 =169-144`
`x = sqrt(25)`
x = 5
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
5/2=2.5 средняя линия треугольника.
13+2.5=15,5
Ответ:15,5
Номер: C94728
Номер: CAAB4B
Впишите правильный ответ.
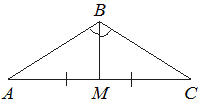
В треугольнике ABC угол B равен 120° . Медиана BM делит угол B пополам и равна 32. Найдите длину стороны AB .
Решение:
Если медиана является в том числе и биссектрисой, то треугольник равнобедренный. Причем ВМ является также и высотой. Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
32*2=64
Ответ:64
Номер: 2135E9
Номер: 33B04F
Впишите правильный ответ.

В треугольнике ABC угол B равен 120° . Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB .
Решение:
Если медиана является в том числе и биссектрисой, то треугольник равнобедренный. Причем ВМ является также и высотой. Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
27*2=54
Ответ:
Номер: 0265FC
Номер: 3BF440
Впишите правильный ответ.
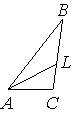
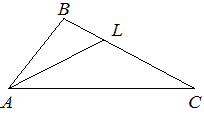
В треугольнике ABC проведена биссектриса AL , угол ALC равен 48° , угол ABC равен 41° . Найдите угол ACB. Ответ дайте в градусах.
Решение:
Если взять за x градусов ∠LAC=∠LAB=xº и рассмотреть два треугольника ABC и ALC у которых один угол общий ∠ACL, то оставшиеся углы должны быть равны между собой:
2x+∠ABC = x+∠ALC
2x+41° = x+48°
x=7°
Теперь вычислим ACB:
ACB = 180-7-48=125°
Ответ:125
Номер: 3F0E43
Впишите правильный ответ.
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30° .
Решение:
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
6*2=12
S = 12*6=72
Ответ: 72
Номер: 2332E0
Номер: FC63F9
Впишите правильный ответ.
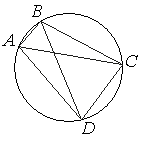
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134° , угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
В любом вписанном четырехугольнике сумма противоположных углов равна 180.
∠ABC = 134°, тогда ∠ADC = 180 - 134 = 46º
Можем найти ∠ACD 180 -81 - 46 = 53º
Так как ∠ACD и ∠ABD опираются на одну секущую по одну сторону, то они равны ∠ACD = ∠ABD = 53º
Ответ:53
Номер: 63B321
Номер: 0CC1F1
Впишите правильный ответ.
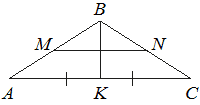
В равнобедренном треугольнике ABC медиана BK=10 , боковая сторона BC=26 . Найдите длину отрезка MN , если известно, что он соединяет середины боковых сторон.
Решение:
В равнобедренном треугольнике медиана является высотой, тогда получаем прямоугольный треугольник и находим неизвестный катет в нем.
`26^2 = 10^2+x^2`
`x^2 =676-100`
`x = sqrt(576)`
x = 24
Средняя линия равна половине основания, но так как треугольника два одинаковых, то мы должны взять среднюю линию два раза. В итоге
она и равна 24.
Ответ:24
Номер: EADEB1
Номер: 0E58FE
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=17, sinA=15/17. Найдите длину стороны AC.

Решение:
Синус это отношение противолежащего катета к гипотенузе. Тогда:
BC/AB=15/17
BC/17=15/17
BC=15
Находим AC по теореме Пифагора
`17^2 = 15^2+x^2`
`x^2 =289-225`
`x = sqrt(64)`
x = 8
Ответ:8
Номер: 03B1F3
Впишите правильный ответ.

Найдите площадь ромба, если его высота равна 24, а острый угол равен 30° .
Решение:
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
24*2=48
S = 24*48=1152
Ответ:
Номер: 7A79F7
Впишите правильный ответ.

На окружности с центром O и диаметром AB отмечена точка C так, что угол COB равен 120° , AC=34 . Найдите диаметр окружности.
Решение:
∠COB = 120°, тогда ∠OСB = ∠OСB = (180-120)/2 = 30° так как треугольник равнобедренный, стороны являются радиусами.
Получается АС катет в прямоугольном треугольнике (угол прямой так как опирается на диаметр) напротив угла в 30°, а значит он равен половине гипотенузы.
То есть диаметр равен гипотенузе или двум катетам АС: 2*34=68
Ответ:
Номер: EE35D7
Номер: B951F0
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB .
Решение:
Проводим высоту. Высота делит треугольник на два прямоугольных треугольника, где известна их площадь и основание.
300/2=150 - площадь
40/2=20 - основание
Тогда высота
(20*h)/2=150
h=300/20=15
Теперь по теореме Пифагора найдем AB
`x^2 = 20^2+15^2`
`x^2 =400+225`
`x = sqrt(625)`
x = 25
Ответ:25
Номер: 74BD4A
Номер: 1FF2FA
Впишите правильный ответ.
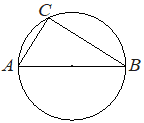
На окружности радиусом 15 отмечена точка C. Отрезок AB — диаметр окружности, AC=12. Найдите cos∠ BAC.
Решение:
cos ∠BAC = AC/AB
При этом гипотенуза 15*2=30
cos ∠BAC = 12/30=0,4
Ответ:0,4
Номер: 2A0BF9
Впишите правильный ответ.
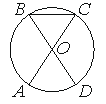
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 88° . Найдите угол ACB . Ответ дайте в градусах.
Решение:
∠BOC = ∠AOD = 88° как накрест лежащие.
Углы у основания равнобедренного треугольника равны, тогда:
(180-88)/2=46°
Ответ:46
Номер: E570C0
Номер: D68DFA
Впишите правильный ответ.
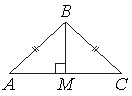
В равнобедренном треугольнике ABC высота BM , проведённая к основанию, равна 6, а tgA=0,3. Найдите площадь треугольника ABC.
Решение:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету. Найдем второй катет.
6/x=3/10
x=20
Находим площадь ABC
20*2*6/2=120
Ответ:120
Номер: 7DF916
Номер: 5076F5
Впишите правильный ответ.
В равнобедренном треугольнике ABC боковые стороны AB=BC=5 , медиана BM=3. Найдите cos∠BAC .
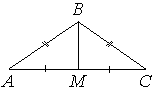
Решение:
Медиана равна высоте
cos ∠BAC = AM/AB
Найдем AM по теореме Пифагора:
`x^2 = 5^2-3^2`
`x^2 =25-9`
`x = sqrt(16)`
x = 4
cos ∠BAC = 4/5=0,8
Ответ:0,8
Номер: A0B7F9
Впишите правильный ответ.
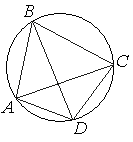
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 56° , угол CAD равен 42° . Найдите угол ABD . Ответ дайте в градусах.
Решение:
В любом вписанном четырехугольнике сумма противоположных углов равна 180.
∠ABC = 56°, тогда ∠ADC = 180 - 56 = 124º
Можем найти ∠ACD 180 - 124 - 42 = 98º
Так как ∠ACD и ∠ABD опираются на одну секущую по одну сторону, то они равны ∠ACD = ∠ABD = 98º
Ответ:
Номер: 12C334
Номер: 6467FA
Впишите правильный ответ.

В треугольнике ABC сторона AC=56 , BM — медиана, BH — высота, BC=BM . Найдите длину отрезка AH .
Решение:
АM=MC так как BM — медиана, при этом МН=НС так как это основание равнобедренного треугольника, где H точка пересечения с высотой.
При этом соотношение МС к МH как 1/2, получается все основание треугольника ABC условно можно разделить на 4 части, где одна часть будет равна HC. Тогда AH это 3/4 от всего основания.
56*3/4=42
Ответ:
Номер: 438700
Впишите правильный ответ.
В параллелограмме ABCD диагонали делят его углы пополам и равны 40 и 42. Найдите периметр параллелограмма ABCD .
Решение:
Этот параллелограмм является ромбом. Он состоит из 4 прямоугольных треугольников, с катетами 20 и 21. Найдем гипотенузу для треугольника.
По теореме Пифагора:
`x^2 = 20^2+21^2`
`x^2 =400+441`
`x = sqrt(841)`
x = 29
Найдем периметр, равный 4 гипотенузам. 29*4=116
Ответ:116
Номер: 7D4C05
Впишите правильный ответ.

Площадь прямоугольника ABCD равна 400, сторона AB=14 . Найдите тангенс угла CAD .
Решение:
Найдем вторую сторону прямоугольника.
400/14=200/7
Тангенс угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
tg∠CAD=14/(200/7)=0,49
Ответ:0,49
Номер: 71F20C
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=12 , ВС=CD=15 (см. рисунок). Найдите среднюю линию трапеции.

Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`15^2 = 12^2+x^2`
`x^2 =225-144`
`x = sqrt(81)`
x = 9
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
9/2=4.5 средняя линия треугольника.
15+4.5=19,5
Ответ:
Номер: B45A00
Впишите правильный ответ.
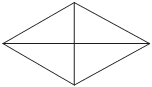
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 22. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с катетами 22/2=11. Найдем гипотенузу для треугольника.
Сумма двух углов равна 120, то есть это углы напротив меньших катетов, 120/2=60° та как углы острые. При этом в треугольнике это углы 60/2=30°, а катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
Тогда периметр ромба 11*2*4=88
Ответ: 88
Номер: BC6D0E
Впишите правильный ответ.

На окружности с центром O и диаметром AB отмечена точка C так, что угол COB равен 120°, AC=29. Найдите длину диаметра окружности.
Решение:
∠COB = 120°, тогда ∠OСB = ∠OСB = (180-120)/2 = 30° так как треугольник равнобедренный, стороны являются радиусами.
Получается АС катет в прямоугольном треугольнике (угол прямой так как опирается на диаметр) напротив угла в 30°, а значит он равен половине гипотенузы.
То есть диаметр равен гипотенузе или двум катетам АС: 2*29=58
Ответ:
Номер: 8CCD03
Впишите правильный ответ.
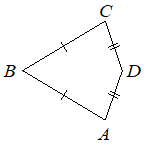
В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=61°, ∠D=151°. Найдите величину угла A. Ответ дайте в градусах.
Решение:
Если провести отрезок СА, то он будет образовывать основание с двумя равнобедренными треугольниками. Углы у основания таких треугольников равны.
При этом угол A равен сумме двух таких одиночных углов у основания от разных треугольников:
(180-61)/2+(180-151)/2=59,5+14,5=74º
Ответ:74
Номер: 886003
Впишите правильный ответ.
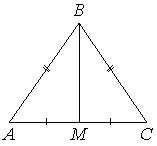
В равнобедренном треугольнике ABC боковые стороны AB=BC=5 , медиана BM=4 .
Найдите cos∠BAC .
Решение:
Медиана равна высоте
cos ∠BAC = AM/AB
Найдем AM по теореме Пифагора:
`x^2 = 5^2-4^2`
`x^2 =25-16`
`x = sqrt(9)`
x = 3
cos ∠BAC = 3/5=0,6
Ответ:0,6
Номер: 438870
Впишите правильный ответ.
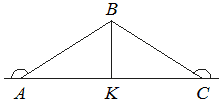
В треугольнике ABC внешние углы при вершинах A и C равны 150° , AB=26 . Найдите длину биссектрисы BK .
Решение:
Углы у основания равны 180-150=30º. Образуется равнобедренный треугольник, у которого медиана в том числе и высота. Эта высота катет для прямоугольного треугольника, где катет равен половине гипотенузы, так как расположен напротив угла в 30º
Тогда BK = AB/2=26/2=13
Ответ:
Номер: 79F4C3
Номер: 08E67B
Впишите правильный ответ.
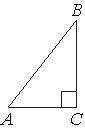
В треугольнике ABC угол C равен 90° , AB=12 , AC=3√7 . Найдите sinA .
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=12^2-(3sqrt(7))^2`
`BC^2=144-9*7`
`BC^2=81`
BC=9
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=9/12=0,75
Ответ:
Номер: 0BD875
Впишите правильный ответ.
В треугольнике АВС угол С равен 90° , АВ=√29 , ВС=2 . Найдите tgA .
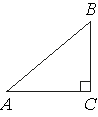
Решение:
Тангенс это отношение противолежащего катета к прилежащему.
Найдем катет AC по теореме Пифагора.
`AC^2=AB^2-AC^2`
`AC^2=(sqrt(29))^2-2^2`
`AC^2=29-5`
`AC^2=25`
AC=5
tgA = 2/5=0,4
Ответ:0,4
Номер: 0CDD7C
Впишите правильный ответ.
Сумма двух углов ромба равна 240°, а его периметр равен 36. Найдите длину меньшей диагонали ромба.

Решение:
Ромб состоит из 4 прямоугольных треугольников, с гипотенузами 36. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° та как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
36/4=9 - гипотенуза.
Тогда меньшая диагональ ромба 9/2*2=9
Ответ:
Номер: 2EE070
Впишите правильный ответ.

На окружности радиусом 10 отмечена точка C. Отрезок AB — диаметр окружности, AC=6. Найдите sin∠ ABC.
Решение:
sin∠ ABC = AC/AB = 6/(2*10)=6/20=0,3
Ответ:0,3
Номер: A7337D
Впишите правильный ответ.
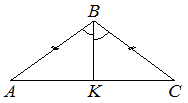
В треугольнике ABC известно, что AB=BC=12, ∠ABC=120°, BK — биссектриса. Найдите длину отрезка BK.
Решение:
Биссектриса в равнобедренном треугольнике является также и высотой. Если угол у вершины 120° то у основания, (180-120)/2=30°
Рассмотрим два прямоугольных треугольника. В них катет являющейся биссектрисой равнобедренного треугольника является стороной лежащей напротив угла в 30°, то есть равен половине гипотенузы AB=BC=12
BK = AB/2 = 12/2 = 6
Ответ:6
Номер: CFD17A
Впишите правильный ответ.
В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=77°, ∠D=141°. Найдите величину угла A. Ответ дайте в градусах.

Решение:
Если провести отрезок СА, то он будет образовывать основание с двумя равнобедренными треугольниками. Углы у основания таких треугольников равны.
При этом угол A равен сумме двух таких одиночных углов у основания от разных треугольников:
(180-77)/2+(180-141)/2=51,5+19,5=71º
Ответ:
Номер: 6C0579
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=4 , AC=2√3 . Найдите sinA .

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=4^2-(2sqrt(3))^2`
`BC^2=16-4*3`
`BC^2=4`
BC=2
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=2/4=0,5
Ответ:
Номер: 887970
Впишите правильный ответ.

В равнобедренном треугольнике ABC с основанием AC медиана BK=9 , отрезок MN , соединяющий середины боковых сторон, равен 40. Найдите боковую сторону AB .
Решение:
МN является средней линией для прямоугольных треугольников. Основание каждого такого прямоугольного треугольника равно MN, так как средняя линия в два раза меньше основания, но здесь две средних линии одинаковых треугольников.
По теореме Пифагора находим гипотенузу.
`AB^2=BK^2+AK^2`
`AB^2=40^2+9^2`
`AB^2=1600+81`
`AB^2=1681`
AB=41
Ответ:41
Номер: B9943D
Номер: 89BC79
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , AB=20 , AC=2√51 . Найдите sinA .
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=20^2-(2sqrt(51))^2`
`BC^2=400-4*51`
`BC^2=196`
BC=14
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=14/20=0,7
Ответ:
Номер: 0FCDB7
Впишите правильный ответ.

В равнобедренном треугольнике ABC медиана BM , проведённая к основанию, равна 7, а tgA=7/24 . Найдите длину боковой стороны треугольника ABC .
Решение:
BM является также и высотой.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
Тогда из соотношения тангенса AM = 24
Находим сторону треугольника:
`AB^2=BM^2+AМ^2`
`AB^2=24^2+7^2`
`AB^2=576+49`
`AB^2=625`
AB=25
Ответ:
Номер: 0552B9
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=13 , AC=10 . Найдите площадь треугольника ABC .
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=13^2-5^2`
`h^2=169-25`
`h^2=144`
h=12
Найдем площадь:
S= 12*10*0.5=60
Ответ:
Номер: 74F2BF
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=15, AC=9. Найдите sinA.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=15^2-9^2`
`BC^2=225-81`
`BC^2=144`
BC=12
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=12/15=0,8
Ответ:
Номер: 1AFCB1
Впишите правильный ответ.

В треугольнике ABC угол B равен 120° . Медиана BM делит угол B пополам и равна 22. Найдите длину стороны AB .
Решение:
Если медиана является в том числе и биссектрисой, то треугольник равнобедренный. Причем ВМ является также и высотой. Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
22*2=44
Ответ:
Номер: 1FD45C
Номер: 28F5B4
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=50 , sinA=24/25 . Найдите длину стороны AC .

Решение:
Синус это отношение противолежащего катета к гипотенузе. Тогда:
BC/AB=24/25
BC/50=24/25
BC=48
Находим AC по теореме Пифагора
`50^2 = 48^2+x^2`
`x^2 =2500-2304`
`x = sqrt(196)`
x = 14
Ответ:
Номер: 831FA8
Номер: 22E0BD
Впишите правильный ответ.
В треугольнике ABC проведена биссектриса AL , угол ALC равен 160° , угол ABC равен 148° . Найдите угол ACB . Ответ дайте в градусах.
Решение:
Если взять за x градусов ∠LAC=∠LAB=xº и рассмотреть два треугольника ABC и ALC у которых один угол общий ∠ACL, то оставшиеся углы должны быть равны между собой:
2x+∠ABC = x+∠ALC
2x+148° = x+160°
x=12°
Теперь вычислим ACB:
ACB = 180-12-160=8°
Ответ:8
Номер: 21CFB8
Впишите правильный ответ.

В равнобедренном треугольнике ABC медиана BK=16 , боковая сторона BC=34 . Найдите длину отрезка MN , если известно, что он соединяет середины боковых сторон.
Решение:
МN является средней линией для прямоугольных треугольников. Основание каждого такого прямоугольного треугольника равно MN, так как средняя линия в два раза меньше основания, но здесь две средних линии одинаковых треугольников.
По теореме Пифагора находим катет АК, который и равен MN.
`АК^2=AB^2-BK^2`
`АК^2=34^2-16^2`
`АК^2=1156-256`
`АК^2=900`
AB=30
Ответ:30
Номер: F8B2D7
Номер: 5B51B2
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=30, AC=24. Найдите cosB.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=30^2-24^2`
`BC^2=900-576`
`BC^2=324`
BC=18
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=18/30=0,6
Ответ:
Номер: 5695BD
Впишите правильный ответ.

Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 21. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с катетами 21/2=10,5. Найдем гипотенузу для треугольника.
Сумма двух углов равна 120, то есть это углы напротив меньших катетов, 120/2=60° та как углы острые. При этом в треугольнике это углы 60/2=30°, а катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
Тогда периметр ромба 10,5*2*4=84
Ответ:
Номер: 50A4BA
Впишите правильный ответ.
На окружности по разные стороны от диаметра AB отмечены точки D и C . Известно, что ∠DBA=41° . Найдите угол DCB . Ответ дайте в градусах.
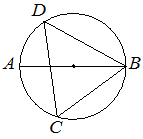
Решение:
Угол DBA=41° — вписанный и опирается на дугу AD, градусная мера которой в 2 раза больше самого угла и равна
2*41 = 82° — градусная мера дуги АD;
Градусная мера для любого угла опирающегося на дугу AB = 180° (так как АВ – это диаметр окружности), следовательно, дуга DB равна:
180°-82°=98° — градусная мера дуги DB;
А вписанный угол DCB, которой опирается на дугу DB, равен половине значения дуги:
98:2 = 49° равен угол DCB
Ответ:49
Номер: 5AA1BE
Впишите правильный ответ.

На окружности радиусом 10 отмечена точка C. Отрезок AB — диаметр окружности, AC=11. Найдите cos∠ BAC.
Решение:
cos ∠BAC = AC/AB
При этом гипотенуза 10*2=20
cos ∠BAC = 11/20=0,55
Ответ:0,55
Номер: 9F8DBF
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , AB=20 , AC=2√51 . Найдите sinA .
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=20^2-(2sqrt(51))^2`
`BC^2=400-4*51`
`BC^2=196`
BC=14
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=14/20=0,7
Ответ:
Номер: 9D59B2
Впишите правильный ответ.
Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30° , а площадь квадрата равна 36.

Решение:
Находим сторону квадрата и ромба
L = √36
L = 6
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
6*(6/2)=6*3=18
Ответ:
Номер: 609CB0
Впишите правильный ответ.

Сумма двух углов ромба равна 120°, а его периметр равен 88. Найдите длину меньшей диагонали ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с гипотенузами 36. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° та как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
88/4=22 - гипотенуза.
Тогда меньшая диагональ ромба 22/2*2=22
Ответ:
Номер: 3308B1
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=20, cosA=0,6. Найдите длину стороны BC.

Решение:
Косинус это отношение прилежащего катета к гипотенузе.
cosA=AC/AB=0,6
AC/20=0,6
AC=0,6*20=12
ВС можно найти по теореме Пифагора
`ВС^2=AB^2-AC^2`
`BC^2=20^2-12^2`
`BC^2=400-144`
`BC^2=256`
BC=16
Ответ:16
Номер: 895DB2
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=4 , AC=√15 . Найдите sinA .

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=4^2-(sqrt(15))^2`
`BC^2=16-15`
`BC^2=1`
BC=1
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=1/4=0,2
Ответ:
Номер: 440410
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=10, AC=√91. Найдите sinA.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=10^2-(sqrt(91))^2`
`BC^2=100-91`
`BC^2=9`
BC=3
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=3/10=0,3
Ответ:
Номер: F48314
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC равно 30, площадь треугольника равна 120. Найдите длину боковой стороны AB .
Решение:
Проводим высоту. Высота делит треугольник на два прямоугольных треугольника, где известна их площадь и основание.
120/2=60 - площадь
30/2=15 - основание
Тогда высота
(15*h)/2=60
h=120/15=8
Теперь по теореме Пифагора найдем AB
`x^2 = 8^2+15^2`
`x^2 =64+225`
`x = sqrt(289)`
x = 17
Ответ:
Номер: FA7BDA
Номер: FCB712
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Катет BC=41. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-150=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
41*2=82
Ответ:
Номер: 05C91B
Впишите правильный ответ.
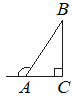
В прямоугольном треугольнике ABC внешний угол при вершине A равен 120°. Катет AC=15. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-(180-120)-90=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
15*2=30
Ответ:
Номер: 053311
Впишите правильный ответ.
На окружности по разные стороны от диаметра AB отмечены точки D и C . Известно, что ∠DBA=39° . Найдите угол DCB . Ответ дайте в градусах.

Решение:
Угол DBA=41° — вписанный и опирается на дугу AD, градусная мера которой в 2 раза больше самого угла и равна
2*39 = 78° — градусная мера дуги АD;
Градусная мера для любого угла опирающегося на дугу AB = 180° (так как АВ – это диаметр окружности), следовательно, дуга DB равна:
180°-78°=102° — градусная мера дуги DB;
А вписанный угол DCB, которой опирается на дугу DB, равен половине значения дуги:
102:2 = 51° равен угол DCB
Ответ:51
Номер: F12E16
Номер: 077B1D
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC=32 , tgA=5/4. Найдите площадь треугольника ABC.
Решение:
Проведем высоту и получим два прямоугольных треугольника.
tgA=5/4=h/(AC/2)
h = 5*(32/2)/4=20
Площадь треугольника ABC
32*20/2=320
Ответ:320
Номер: CE1425
Номер: 760217
Впишите правильный ответ.

В равнобедренном треугольнике ABC боковые стороны AB=BC=12 , медиана BM=6√3 .
Найдите cos∠BAC .
Решение:
Медиана равна высоте
cos ∠BAC = AM/AB
Найдем AM по теореме Пифагора:
`x^2 = 12^2-(6sqrt3)^2`
`x^2 =144-36*3`
`x = sqrt(36)`
x = 6
cos ∠BAC = 6/12=0,5
Ответ:0.5
Номер: 222219
Впишите правильный ответ.
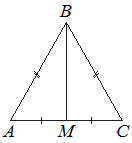
В равнобедренном треугольнике ABC медиана BM , проведённая к основанию, равна 15, а tgA=15/8 . Найдите длину боковой стороны треугольника ABC .
Решение:
BM является также и высотой.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
Тогда из соотношения тангенса AM = 8
Находим сторону треугольника:
`AB^2=BM^2+AМ^2`
`AB^2=8^2+15^2`
`AB^2=64+225`
`AB^2=289`
AB=17
Ответ:
Номер: 9E6F17
Номер: D05F1B
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC равно 32, площадь треугольника равна 192. Найдите длину боковой стороны AB .
Решение:
Проводим высоту. Высота делит треугольник на два прямоугольных треугольника, где известна их площадь и основание.
192/2=96 - площадь
32/2=16 - основание
Тогда высота
(16*h)/2=96
h=192/16=12
Теперь по теореме Пифагора найдем AB
`x^2 = 16^2+12^2`
`x^2 =256+144`
`x = sqrt(400)`
x = 20
Ответ:
Номер: 584313
Впишите правильный ответ.
Стороны параллелограмма равны 10 и 12. Высота, опущенная на меньшую сторону, равна 6. Найдите высоту, опущенную на большую сторону параллелограмма.
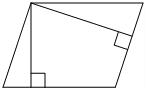
Решение:
Площадь параллелограмма это произведение высоты на сторону. Получаем два варианта нахождения площади, их и приравниваем друг к другу, чтобы найти вторую высоту.
10*6 = 12*h
h = 60/12=5
Ответ:5
Номер: 950310
Впишите правильный ответ.
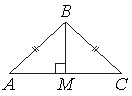
В равнобедренном треугольнике ABC высота BM , проведённая к основанию, равна 2, а tgA=0,4 . Найдите площадь треугольника ABC .
Решение:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету. Найдем второй катет.
2/x=4/10
x=20/4=5
Находим площадь ABC
S = 5*2*2/2=10
Ответ:
Номер: 8E69A3
Номер: 37AA1B
Впишите правильный ответ.
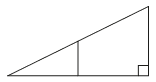
Катет прямоугольного треугольника равен 24, одна из средних линий равна 3,5. Найдите гипотенузу этого треугольника.
Решение:
Средняя линия в прямоугольном треугольнике равна половине основания.
3,5*2=7 основание.
Найдем гипотенузу по теореме Пифагора:
`x^2=7^2+24^2`
`x^2=49+576`
`x^2=625`
x=25
Ответ:25
Номер: 5A6BAB
Номер: 87AC1A
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Гипотенуза AB=28. Найдите длину катета BC.
Решение:
Внутренний острый угол будет равен:
180-150=30°
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы.
28/2=14
Ответ:14
Номер: 75E628
Впишите правильный ответ.
В треугольнике АВС угол С равен 90° , АВ=√101 , ВС=1 . Найдите tgA .

Решение:
Тангенс это отношение противолежащего катета к прилежащему.
Найдем катет AC по теореме Пифагора.
`AC^2=AB^2-AC^2`
`AC^2=(sqrt(101))^2-1^2`
`AC^2=101-1`
`AC^2=100`
AC=10
tgA = 2/10=0,1
Ответ:0,1
Номер: 267626
Впишите правильный ответ.
Стороны параллелограмма равны 9 и 12. Высота, опущенная на меньшую сторону, равна 8. Найдите высоту, опущенную на большую сторону параллелограмма.

Решение:
Площадь параллелограмма это произведение высоты на сторону. Получаем два варианта нахождения площади, их и приравниваем друг к другу, чтобы найти вторую высоту.
9*8 = 12*h
h = 72/12=6
Ответ:6
Номер: A66E22
Впишите правильный ответ.

Катет прямоугольного треугольника равен 12, одна из средних линий равна 2,5. Найдите гипотенузу этого треугольника.
Решение:
Средняя линия в прямоугольном треугольнике равна половине основания.
2,5*2=5 основание.
Найдем гипотенузу по теореме Пифагора:
`x^2=5^2+12^2`
`x^2=25+144`
`x^2=169`
x=13
Ответ:13
Номер: 92B1ED
Номер: 91C825
В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Гипотенуза AB=20. Найдите длину катета BC.

Решение:
Внутренний острый угол будет равен:
180-150=30°
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы.
20/2=10
Ответ:
Номер: 3F4327
Впишите правильный ответ.

В треугольнике ABC внешние углы при вершинах A и C равны 150° , AB=54 . Найдите длину биссектрисы BK .
Решение:
Углы у основания равны 180-150=30º. Образуется равнобедренный треугольник, у которого медиана в том числе и высота. Эта высота катет для прямоугольного треугольника, где катет равен половине гипотенузы, так как расположен напротив угла в 30º
Тогда BK = AB/2=54/2=27
Ответ:
Номер: A36934
Номер: 33502E
Впишите правильный ответ.
В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=69°, ∠D=125°. Найдите величину угла A. Ответ дайте в градусах.

Решение:
Если провести отрезок СА, то он будет образовывать основание с двумя равнобедренными треугольниками. Углы у основания таких треугольников равны.
При этом угол A равен сумме двух таких одиночных углов у основания от разных треугольников:
(180-69)/2+(180-125)/2=55,5+27,5=83º
Ответ:
Номер: FD51DC
Впишите правильный ответ.

В треугольнике ABC сторона AC=96, BM — медиана, BH — высота, BC=BM. Найдите длину отрезка AH.
Решение:
АM=MC так как BM — медиана, при этом МН=НС так как это основание равнобедренного треугольника, где H точка пересечения с высотой.
При этом соотношение МС к МH как 1/2, получается все основание треугольника ABC условно можно разделить на 4 части, где одна часть будет равна HC. Тогда AH это 3/4 от всего основания.
96*3/4=72
Ответ:
Номер: 081DD0
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=20 , AC=32 . Найдите синус угла BAC .
Решение:
Если провести высоту, то она будет и медианой (делит основание пополам). Тогда можно найти из теоремы Пифагора эту высоту.
32/2=16
`x^2=20^2-16^2`
`x^2=400+256`
`x^2=144`
x=12
sin∠BAC = 12/20=0,6
Ответ:0,6
Номер: BBC5D9
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=20, ∠ ABC=120°, BK — биссектриса. Найдите длину отрезка BK.
Решение:
Биссектриса в равнобедренном треугольнике является также и высотой. Если угол у вершины 120° то у основания, (180-120)/2=30°
Рассмотрим два прямоугольных треугольника. В них катет являющейся биссектрисой равнобедренного треугольника является стороной лежащей напротив угла в 30°, то есть равен половине гипотенузы AB=BC=20
BK = AB/2 = 20/2 = 10
Ответ:
Номер: 1583D7
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Гипотенуза AB=34. Найдите длину катета BC.
Решение:
Внутренний острый угол будет равен:
180-150=30°
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы.
34/2=17
Ответ:
Номер: D7BBDD
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC равно 24, площадь треугольника равна 60. Найдите длину боковой стороны AB .
Решение:
Проводим высоту. Высота делит треугольник на два прямоугольных треугольника, где известна их площадь и основание.
60/2=30 - площадь
24/2=12 - основание
Тогда высота
(12*h)/2=30
h=60/12=5
Теперь по теореме Пифагора найдем AB
`x^2 = 12^2+5^2`
`x^2 =144+25`
`x = sqrt(169)`
x = 13
Ответ:
Номер: 7368AF
Номер: 5EBBD2
Впишите правильный ответ.
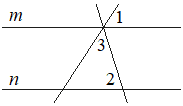
Прямые m и n параллельны (см. рисунок). Найдите величину угла 3, если ∠ 1=74°, ∠ 2=39°. Ответ дайте в градусах.
Решение:
В образовавшемся треугольнике безымянный угол и угол 1 равны, как соответственные углы.
В итоге угол 3 = 180 - (74+39) = 67°
Ответ:67
Номер: AA39D5
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC=25 , tgA=8/5 . Найдите площадь треугольника ABC .
Решение:
Проведем высоту и получим два прямоугольных треугольника.
tgA=8/5=h/(AC/2)
h = 8*(25/2)/5=20
Площадь треугольника ABC
25*20/2=250
Ответ:250
Номер: 12AF53
Номер: A610DA
Впишите правильный ответ.

В треугольнике ABC внешние углы при вершинах A и C равны 150° , AB=42 . Найдите длину биссектрисы BK .
Решение:
Углы у основания равны 180-150=30º. Образуется равнобедренный треугольник, у которого медиана в том числе и высота. Эта высота катет для прямоугольного треугольника, где катет равен половине гипотенузы, так как расположен напротив угла в 30º
Тогда BK = AB/2=42/2=21
Ответ:
Номер: 7D0FA6
Номер: CBE3D7
Впишите правильный ответ.

Сумма двух углов ромба равна 240° , а его меньшая диагональ равна 14. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° так как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
14:2*2=14 - гипотенуза.
Периметр: 14*4=56
Ответ:56
Номер: CFBFDB
Впишите правильный ответ.
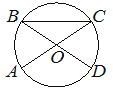
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 114° . Найдите угол ACB . Ответ дайте в градусах.
Решение:
∠BOC = ∠AOD = 114° как накрест лежащие.
Углы у основания равнобедренного треугольника равны, тогда:
(180-114)/2=33°
Ответ:
Номер: 2799A4
Номер: C921DB
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , сторона BC равна 15. Тангенс угла A равен 5/12 . Найдите длину стороны AB .
Решение:
tgA = BC/AC
5/12 = 15/AC
AC = (15*12)/5 = 36
по теореме Пифагора
`AB^2=BC^2+AC^2`
`AB^2=225+1296`
`AB^2=1521`
AB=39
Ответ:39
Номер: 958CDB
Впишите правильный ответ.
В треугольнике АВС угол С равен 90° , АВ=√41 , ВС=4 . Найдите tgA .

Решение:
Тангенс это отношение противолежащего катета к прилежащему.
Найдем катет AC по теореме Пифагора.
`AC^2=AB^2-AC^2`
`AC^2=(sqrt(41))^2-4^2`
`AC^2=41-16`
`AC^2=25`
AC=5
tgA = 4/5=0,8
Ответ:0,8
Номер: 3564DD
Впишите правильный ответ.
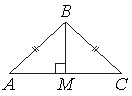
В равнобедренном треугольнике ABC высота BM , проведённая к основанию, равна 2, а tgA=0,2 . Найдите площадь треугольника ABC .
Решение:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету. Найдем второй катет.
2/x=2/10
x=10
Находим площадь ABC
S = 10*2*2/2=20
Ответ:
Номер: 9EBA8C
Номер: 3DB5D9
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 120°. Катет AC=23. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-(180-120)-90=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
23*2=46
Ответ:
Номер: 468055
Впишите правильный ответ.
В трапеции ABCD известно, что AB=CD , ∠BDA=52° и ∠BDC=26° . Найдите угол ABD . Ответ дайте в градусах.
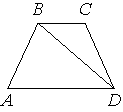
Решение:
Так как трапеция равнобедренная, а углы у основания равны, а прилежащих к боковой стороне равны 180°, то напротив лежащие углы тоже равны 180°:
BAD = 52+26 = 78º
ABD = 180 - 78 - 52 = 50º
Ответ:50
Номер: 4CC65E
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 150°. Катет BC=22. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-150=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
22*2=44
Ответ:
Номер: 475A56
Впишите правильный ответ.

В равнобедренном треугольнике ABC с основанием AC медиана BK=7 , отрезок MN , соединяющий середины боковых сторон, равен 24. Найдите боковую сторону AB .
Решение:
МN является средней линией для прямоугольных треугольников. Основание каждого такого прямоугольного треугольника равно MN, так как средняя линия в два раза меньше основания, но здесь две средних линии одинаковых треугольников.
По теореме Пифагора находим гипотенузу.
`AB^2=BK^2+AK^2`
`AB^2=24^2+7^2`
`AB^2=576+49`
`AB^2=625`
AB=25
Ответ:25
Номер: 8690A5
Номер: F3135C
Впишите правильный ответ.

В трапеции ABCD известно, что AB=CD , ∠BDA=49° и ∠BDC=13° . Найдите угол ABD . Ответ дайте в градусах.
Решение:
Так как трапеция равнобедренная, а углы у основания равны, а прилежащих к боковой стороне равны 180°, то напротив лежащие углы тоже равны 180°:
BAD = 49+13 = 62º
ABD = 180 - 62 - 49 = 69º
Ответ:
Номер: FDBE5E
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=10 , AC=12 . Найдите площадь треугольника ABC .
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=10^2-6^2`
`h^2=100-36`
`h^2=64`
h=8
Найдем площадь:
S= 12*8*0.5=48
Ответ:
Номер: D92055
Впишите правильный ответ.

В равнобедренном треугольнике ABC медиана BM , проведённая к основанию, равна 9, а tgA=3/4 . Найдите длину боковой стороны треугольника ABC .
Решение:
BM является также и высотой.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
Тогда из соотношения тангенса:
9/AM = 3/4,
АМ = 12
Находим сторону треугольника:
`AB^2=BM^2+AМ^2`
`AB^2=12^2+9^2`
`AB^2=144+81`
`AB^2=225`
AB=15
Ответ:
Номер: DBCBE2
Номер: DFC059
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=40, cosA=0,8. Найдите длину стороны BC.

Решение:
Косинус это отношение прилежащего катета к гипотенузе.
cosA=AC/AB=0,8
AC/40=0,8
AC=0,8*40=32
ВС можно найти по теореме Пифагора
`ВС^2=AB^2-AC^2`
`BC^2=40^2-32^2`
`BC^2=1600-1024`
`BC^2=576`
BC=24
Ответ:24
Номер: DC4858
Впишите правильный ответ.
В треугольнике ABC сторона AC=12 , BM — медиана, BH — высота, BC=BM . Найдите длину отрезка AH .

Решение:
АM=MC так как BM — медиана, при этом МН=НС так как это основание равнобедренного треугольника, где H точка пересечения с высотой.
При этом соотношение МС к МH как 1/2, получается все основание треугольника ABC условно можно разделить на 4 части, где одна часть будет равна HC. Тогда AH это 3/4 от всего основания.
12*3/4=9
Ответ:
Номер: E6B651
Впишите правильный ответ.

В треугольнике ABC угол B равен 120° . Медиана BM делит угол B пополам и равна 29. Найдите длину стороны AB .
Решение:
Если медиана является в том числе и биссектрисой, то треугольник равнобедренный. Причем ВМ является также и высотой. Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
29*2=58
Ответ:
Номер: 7838A9
Номер: 6EAC5B
Впишите правильный ответ.

На окружности по разные стороны от диаметра AB отмечены точки D и C . Известно, что ∠DBA=23° . Найдите угол DCB . Ответ дайте в градусах.
Решение:
Угол DBA=41° — вписанный и опирается на дугу AD, градусная мера которой в 2 раза больше самого угла и равна
2*23 = 46° — градусная мера дуги АD;
Градусная мера для любого угла опирающегося на дугу AB = 180° (так как АВ – это диаметр окружности), следовательно, дуга DB равна:
180°-46°=134° — градусная мера дуги DB;
А вписанный угол DCB, которой опирается на дугу DB, равен половине значения дуги:
134:2 = 67° равен угол DCB
Ответ:67
Номер: 620656
Впишите правильный ответ.

В равнобедренном треугольнике ABC медиана BM , проведённая к основанию, равна 7, а tgA=7/24 . Найдите длину боковой стороны треугольника ABC .
Решение:
BM является также и высотой.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету.
Тогда из соотношения тангенса AM = 24
Находим сторону треугольника:
`AB^2=BM^2+AМ^2`
`AB^2=24^2+7^2`
`AB^2=576+49`
`AB^2=625`
AB=25
Ответ:
Номер: 809C54
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , сторона BC равна 9. Тангенс угла A равен 0,75. Найдите длину стороны AB .
Решение:
tgA = BC/AC
75/100 = 9/AC
AC = (9*100)/75 = 12
по теореме Пифагора
`AB^2=BC^2+AC^2`
`AB^2=81+144`
`AB^2=225`
AB=15
Ответ:
Номер: 8A9A5E
Впишите правильный ответ.

В треугольнике АВС известно, что АВ=ВС=18, ∠ АВС=120°, BK — биссектриса. Найдите длину отрезка BK.
Решение:
Биссектриса в равнобедренном треугольнике является также и высотой. Если угол у вершины 120° то у основания, (180-120)/2=30°
Рассмотрим два прямоугольных треугольника. В них катет являющейся биссектрисой равнобедренного треугольника является стороной лежащей напротив угла в 30°, то есть равен половине гипотенузы AB=BC=18
BK = AB/2 = 18/2 = 9
Ответ:
Номер: B7BCAF
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=20, AC=12. Найдите cosB.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=20^2-12^2`
`BC^2=400-144`
`BC^2=256`
BC=16
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=16/20=0,8
Ответ:
Номер: B08DA8
Впишите правильный ответ.
На прямой AB отмечена точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC=63°. Найдите величину угла CMA. Ответ дайте в градусах.
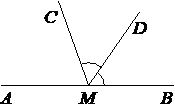
Решение:
∠CMA = 180-63*2=54º
Ответ:54
Номер: 2B38A3
Впишите правильный ответ.

Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с катетами 25/2=12,5. Найдем гипотенузу для треугольника.
Сумма двух углов равна 120, то есть это углы напротив меньших катетов, 120/2=60° та как углы острые. При этом в треугольнике это углы 60/2=30°, а катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
Тогда периметр ромба 12,5*2*4=100
Ответ:
Номер: C0BDAD
Впишите правильный ответ.
В прямоугольной трапеции основания равны 3 и 8, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
8-3=5
Ответ:5
Номер: 9F52AB
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=28, ∠ ABC=120°, BK — биссектриса. Найдите длину отрезка BK.
Решение:
Биссектриса в равнобедренном треугольнике является также и высотой. Если угол у вершины 120° то у основания, (180-120)/2=30°
Рассмотрим два прямоугольных треугольника. В них катет являющейся биссектрисой равнобедренного треугольника является стороной лежащей напротив угла в 30°, то есть равен половине гипотенузы AB=BC=28
BK = AB/2 = 28/2 = 14
Ответ:
Номер: E5EDAC
Впишите правильный ответ.

В равнобедренном треугольнике ABC боковая сторона AB=30 , sinA=4/5 . Найдите площадь треугольника ABC .
Решение:
Проведем высоту для треугольника ABC.
Получим катет противолежащий и гипотенуза с соотношением 4/5. Найдем по теореме Пифагора катет.
`5^2 = 4^2+x^2`
`x^2 =25-16`
`x = sqrt(9)`
x = 3
То есть соотношения всех сторон 3, 4 и 5 в частях. Если гипотенуза 5 частей и 30 в значении, то 1 часть равна 30/5= 6
Высота равна 4*5=20
Основание 3*5=15, а все основание треугольника 15*2=30
`S_(треугольника) = (30*20)/2` = 300
Ответ:
Номер: 9F22C7
Номер: E626A6
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC=30 , tgA=4/3 . Найдите площадь треугольника ABC .
Решение:
Проведем высоту и получим два прямоугольных треугольника.
tgA=4/3=h/(AC/2)
h = 4*(30/2)/3=20
Площадь треугольника ABC
30*20/2=300
Ответ:
Номер: 3D0FAC
Номер: 6E39AF
Впишите правильный ответ.

Сумма двух углов ромба равна 240°, а его меньшая диагональ равна 9. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° так как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
9:2*2=9 - гипотенуза.
Периметр: 9*4=36
Ответ:36
Номер: 62D2A6
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , сторона BC равна 28. Тангенс угла A равен 7/24 . Найдите длину стороны AB .
Решение:
tgA = BC/AC
7/24 = 28/AC
AC = (28*24)/7 = 96
по теореме Пифагора
`AB^2=BC^2+AC^2`
`AB^2=784+9216`
`AB^2=10000`
AB=100
Ответ:
Номер: F6BEC2
Впишите правильный ответ.

Прямые m и n параллельны (см. рисунок). Найдите величину угла 3, если ∠ 1=65°, ∠ 2=51°. Ответ дайте в градусах.
Решение:
В образовавшемся треугольнике безымянный угол и угол 1 равны, как соответственные углы.
В итоге угол 3 = 180 - (65+51) = 64°
Ответ:
Номер: 71C4C9
Впишите правильный ответ.

Сумма двух углов ромба равна 240°, а его меньшая диагональ равна 12. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° так как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
12:2*2=12 - гипотенуза.
Периметр: 12*4=48
Ответ:
Номер: BAE5CC
Впишите правильный ответ.
В прямоугольной трапеции основания равны 3 и 5, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
5-3=2
Ответ:
Номер: B38FC3
Впишите правильный ответ.

В равнобедренном треугольнике ABC боковая сторона AB=34 , sinA=8/17 . Найдите площадь треугольника ABC .
Решение:
Проведем высоту для треугольника ABC.
Получим катет противолежащий и гипотенуза с соотношением 8/17. Найдем по теореме Пифагора катет.
`17^2 = 8^2+x^2`
`x^2 =289-64`
`x = sqrt(225)`
x = 15
То есть соотношения всех сторон 8, 15 и 17 в частях. Если гипотенуза 17 частей и 34 в значении, то 1 часть равна 34/17= 2
Высота равна 8*2=16
Основание 15*2=30, а все основание треугольника 30*2=60
`S_(треугольника) = (60*16)/2` = 480
Ответ:
Номер: B9B49A
Номер: 1F2EC3
Впишите правильный ответ.

Сумма двух углов ромба равна 240°, а его меньшая диагональ равна 15. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° так как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
15:2*2=15 - гипотенуза.
Периметр: 15*4=60
Ответ:
Номер: 5EE2C7
Впишите правильный ответ.
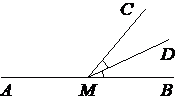
На прямой AB отмечена точка M. Луч MD — биссектриса угла CMB. Известно, что ∠CMA=124°. Найдите величину угла DMB. Ответ дайте в градусах.
Решение:
(180-124)/2=28º
Ответ:28
Номер: A45BCC
Впишите правильный ответ.
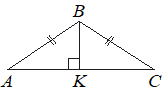
В равнобедренном треугольнике ABC угол ABC равен 120°. Высота BK, проведённая к основанию AC, равна 17. Найдите длину стороны AB.
Решение:
Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
17*2=34
Ответ:
Номер: 96A0C4
Впишите правильный ответ.
На прямой AB отмечена точка M. Луч MD — биссектриса угла CMB. Известно, что ∠CMA=122°. Найдите величину угла DMB. Ответ дайте в градусах.

Решение:
(180-122)/2=29º
Ответ:29
Номер: 8513C7
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , AB=12 , AC=3√7 . Найдите sinA .
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=12^2-(3sqrt(7))^2`
`BC^2=144-9*7`
`BC^2=81`
BC=9
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=9/12=0,75
Ответ:
Номер: 4ACB9B
Впишите правильный ответ.
Стороны параллелограмма равны 10 и 15. Высота, опущенная на меньшую сторону, равна 12. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.

Решение:
Площадь параллелограмма это произведение высоты на сторону. Получаем два варианта нахождения площади, их и приравниваем друг к другу, чтобы найти вторую высоту.
10*12 = 15*h
h = 120/15=8
Ответ:8
Номер: 44C79D
Впишите правильный ответ.

На окружности с центром O и диаметром AB отмечена точка C так, что угол COB равен 120°, AC=23. Найдите длину диаметра окружности.
Решение:
∠COB = 120°, тогда ∠OСB = ∠OСB = (180-120)/2 = 30° так как треугольник равнобедренный, стороны являются радиусами.
Получается АС катет в прямоугольном треугольнике (угол прямой так как опирается на диаметр) напротив угла в 30°, а значит он равен половине гипотенузы.
То есть диаметр равен гипотенузе или двум катетам АС: 2*23=46
Ответ:
Номер: 4FF69E
Впишите правильный ответ.

В треугольнике ABC внешние углы при вершинах A и C равны 150° , AB=56 . Найдите длину биссектрисы BK .
Решение:
Углы у основания равны 180-150=30º. Образуется равнобедренный треугольник, у которого медиана в том числе и высота. Эта высота катет для прямоугольного треугольника, где катет равен половине гипотенузы, так как расположен напротив угла в 30º
Тогда BK = AB/2=56/2=28
Ответ:
Номер: 9DE5EE
Номер: 00C295
Впишите правильный ответ.
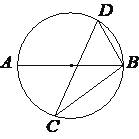
На окружности по разные стороны от диаметра AB отмечены точки D и C. Известно, что ∠DBA=49°. Найдите угол DCB. Ответ дайте в градусах.
Решение:
Угол DBA=49° — вписанный и опирается на дугу AD, градусная мера которой в 2 раза больше самого угла и равна
2*49 = 98° — градусная мера дуги АD;
Градусная мера для любого угла опирающегося на дугу AB = 180° (так как АВ – это диаметр окружности), следовательно, дуга DB равна:
180°-98°=82° — градусная мера дуги DB;
А вписанный угол DCB, которой опирается на дугу DB, равен половине значения дуги:
82:2 = 41° равен угол DCB
Ответ:41
Номер: 28D997
Впишите правильный ответ.
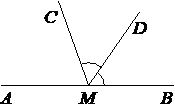
На прямой AB отмечена точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC=65°. Найдите величину угла CMA. Ответ дайте в градусах.
Решение:
∠CMA = 180-65*2=50º
Ответ:50
Номер: DAC895
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=50 , cosA=7/25 . Найдите длину стороны BC .

Решение:
Косинус это отношение прилежащего катета к гипотенузе.
cosA=AC/AB=7/25
AC/50=7/25
AC=350/25=14
ВС можно найти по теореме Пифагора
`ВС^2=AB^2-AC^2`
`BC^2=50^2-14^2`
`BC^2=2500-196`
`BC^2=2304`
BC=48
Ответ:48
Номер: 644E9B
Впишите правильный ответ.
В треугольнике каждая из двух сторон равна 5, а третья сторона равна 8. Найдите длину медианы, проведённой к третьей стороне треугольника.
Решение:
8/2=4 основание прямоугольного треугольника.
По теореме Пифагора
`x^2=5^2-4^2`
`x^2=25-16`
`x^2=9`
x=3
Ответ:3
Номер: 36C997
Впишите правильный ответ.

В прямоугольнике ABCD сторона BC равна 27, tg∠CAD=4/9 . Найдите площадь прямоугольника.
Решение:
tg∠CAD=4/9=CD/AD
AD=BC=27, тогда
4/9=CD/27
CD=4*27/9=12
S=12*27=324
Ответ:324
Номер: 397791
Впишите правильный ответ.
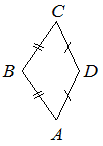
В выпуклом четырехугольнике ABCD известно, что AB=BC , AD=CD , ∠B=94° , ∠D=120° . Найдите угол A . Ответ дайте в градусах.
Решение:
(360-(94+120))/2=73º
Ответ:73
Номер: 05ACE4
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=17 , AC=16 . Найдите площадь треугольника ABC .
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=17^2-8^2`
`h^2=289-64`
`h^2=225`
h=15
Найдем площадь:
S= 16*15*0.5=120
Ответ:
Номер: CC6AE9
Номер: 04C4EA
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=51 , cosA=15/17 . Найдите длину стороны BC .

Решение:
Косинус это отношение прилежащего катета к гипотенузе.
cosA=AC/AB=15/17
AC/51=15/17
AC=765/17=45
ВС можно найти по теореме Пифагора
`ВС^2=AB^2-AC^2`
`BC^2=51^2-45^2`
`BC^2=2601-2025`
`BC^2=576`
BC=26
Ответ:26
Номер: D040E9
Впишите правильный ответ.

В прямоугольном треугольнике ABC внешний угол при вершине A равен 120°. Катет AC=47. Найдите длину гипотенузы AB.
Решение:
Угол ABC = 180-(180-120)-90=30° Гипотенуза в два раза больше катета лежащего в прямоугольном треугольнике напротив угла в 30 градусов.
47*2=94
Ответ:
Номер: D9D9E9
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=10 , AC=12. Найдите площадь треугольника ABC.
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=10^2-6^2`
`h^2=100-36`
`h^2=64`
h=8
Найдем площадь:
S = 12*8*0,5=48
Ответ:
Номер: AE18E5
Впишите правильный ответ.

Прямые m и n параллельны (см. рисунок). Найдите величину угла 3, если ∠ 1=42°, ∠ 2=73°. Ответ дайте в градусах.
Решение:
В образовавшемся треугольнике безымянный угол и угол 1 равны, как соответственные углы.
В итоге угол 3 = 180 - (42+73) = 65°
Ответ:
Номер: 96BEEE
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , AB=8 , AC=2√15 . Найдите cosB .
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=8^2-(2sqrt(15))^2`
`BC^2=64-4*15`
`BC^2=4`
BC=2
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=2/8=0,25
Ответ:
Номер: E891E8
пишите правильный ответ. В треугольнике ABC угол C равен 90°, AB=25, AC=20. Найдите sinA.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=25^2-20^2`
`BC^2=625-400`
`BC^2=225`
BC=15
Косинус это отношение противолежащего катета к гипотенузе
cosB = BC/AB=15/20=0,8
Ответ:
Номер: 04AD6D
Впишите правильный ответ.

Сумма двух углов ромба равна 120°, а его периметр равен 24. Найдите длину меньшей диагонали ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с гипотенузами 36. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° та как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
24/4=6 - гипотенуза.
Тогда меньшая диагональ ромба 6/2*2=6
Ответ:
Номер: 70446B
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=13 , sinA=12/13 . Найдите длину стороны AC.

Решение:
Синус это отношение противолежащего катета к гипотенузе. Тогда:
BC/AB=12/13
BC/13=12/13
BC=12
Находим AC по теореме Пифагора
`13^2 = 12^2+x^2`
`x^2 =169-144`
`x = sqrt(25)`
x = 5
Ответ:
Номер: 74656B
Впишите правильный ответ.

В равнобедренном треугольнике ABC угол ABC равен 120°. Высота BK, проведённая к основанию AC, равна 11. Найдите длину стороны AB.
Решение:
Получаем прямоугольные треугольники, основание у основания которых углы 180-(120/2)-90=30º
В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Гипотенуза равна AB, тогда:
11*2=22
Ответ:
Номер: 7A6D6B
Впишите правильный ответ.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124° . Найдите угол ACB . Ответ дайте в градусах.

Решение:
∠BOC = ∠AOD = 124° как накрест лежащие.
Углы у основания равнобедренного треугольника равны, тогда:
(180-124)/2=28°
Ответ:
Номер: 1FCB6F
Впишите правильный ответ.

Найдите площадь ромба, если его высота равна 22, а острый угол равен 30° .
Решение:
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
22*2=44
S = 22*44=968
Ответ:
Номер: 23A065
Впишите правильный ответ.
В треугольнике ABC угол C равен 90°, AB=5, AC=2√6. Найдите cosB.

Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=5^2-(2sqrt(6))^2`
`BC^2=25-4*6`
`BC^2=1`
BC=1
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=1/5=0,2
Ответ:
Номер: 2CD863
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=12 , AC=12√3 . Найдите синус угла BAC .
Решение:
Если провести высоту, то она будет и медианой (делит основание пополам). Тогда можно найти из теоремы Пифагора эту высоту.
12√3/2=6√3
`x^2=12^2-(6sqrt(3))^2`
`x^2=144-36*3`
`x^2=36`
x=6
sin∠BAC = 6/12=0,5
Ответ:0,5
Номер: D7BD68
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=25 , sinA=7/25 . Найдите длину стороны AC .

Решение:
Синус это отношение противолежащего катета к гипотенузе. Тогда:
BC/AB=7/25
BC/25=7/25
BC=7
Находим AC по теореме Пифагора
`25^2 = 7^2+x^2`
`x^2 =625-49`
`x = sqrt(576)`
x = 24
Ответ:
Номер: A10D60
Впишите правильный ответ.
В прямоугольной трапеции основания равны 2 и 6, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
6-2=4
Ответ:
Номер: EF126E
Впишите правильный ответ.

В треугольнике ABC угол C равен 90°, AB=14 , AC=7√3. Найдите cosB.
Решение:
Найдем катет прямоугольного треугольника
`AB^2=BC^2+AC^2`
`BC^2=AB^2-AC^2`
`BC^2=14^2-(7sqrt(3))^2`
`BC^2=196-49*3`
`BC^2=49`
BC=7
Косинус это отношение прилежащего катета к гипотенузе
cosB = BC/AB=7/14=0,5
Ответ:
Номер: 66DD6C
Впишите правильный ответ.

В треугольнике ABC угол C равен 90° , сторона BC равна 32. Тангенс угла A равен 8/15 . Найдите длину стороны AB .
Решение:
tgA = BC/AC
8/15 = 32/AC
AC = (32*15)/8 = 60
по теореме Пифагора
`AB^2=BC^2+AC^2`
`AB^2=1024+3600`
`AB^2=4624`
AB=68
Ответ:
Номер: FA243C
Впишите правильный ответ.
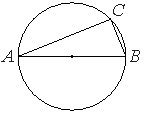
На окружности радиусом 10 отмечена точка C. Отрезок AB — диаметр окружности, AC=18. Найдите sin∠ ABC.
Решение:
sin∠ ABC = AC/AB = 18/(2*10)=18/20=0,9
Ответ:0,9
Номер: 0A9736
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=13 , AC=10. Найдите площадь треугольника ABC.
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=13^2-5^2`
`h^2=169-25`
`h^2=144`
h=12
Найдем площадь:
S= 12*10*0.5=60
Ответ:
Номер: 25793B
Впишите правильный ответ.
Прямые m и n параллельны (см. рисунок). Найдите величину угла 3, если ∠ 1=32°, ∠ 2=77°. Ответ дайте в градусах.

Решение:
В образовавшемся треугольнике безымянный угол и угол 1 равны, как соответственные углы.
В итоге угол 3 = 180 - (32+77) = 71°
Ответ:
Номер: DD763A
Впишите правильный ответ.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70° , угол CAD равен 49° . Найдите угол ABD . Ответ дайте в градусах.

Решение:
В любом вписанном четырехугольнике сумма противоположных углов равна 180.
∠ABC = 70°, тогда ∠ADC = 180 - 70 = 110º
Можем найти ∠ACD 180 - 110 - 49 = 21º
Так как ∠ACD и ∠ABD опираются на одну секущую по одну сторону, то они равны ∠ACD = ∠ABD = 21º
Ответ:
Номер: 546339
Впишите правильный ответ.

В треугольнике АВС известно, что АВ=ВС=20 , АС=24. Найдите синус угла ВАС.
Решение:
Проведем высоту. Она делит АС пополам.
24/2=12
sin ВАС = h/АВ
найдем h по теореме Пифагора
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=20^2-12^2`
`h^2=400-144`
`h^2=256`
h=16
sin ВАС = 16/20=0,8
Ответ:0,8
Номер: CBA43D
Впишите правильный ответ.
В прямоугольной трапеции основания равны 5 и 9, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
9-5=4
Ответ:
Номер: 9E7F3B
Впишите правильный ответ.
В выпуклом четырёхугольнике ABCD известно, что AB=BC , AD=CD , ∠B=59° , ∠D=147° . Найдите угол A . Ответ дайте в градусах.

Решение:
(360-(59+147))/2=77º
Ответ:77
Номер: EDAA35
Впишите правильный ответ.

В прямоугольнике ABCD сторона BC равна 48, tg∠CAD=5/16 . Найдите площадь прямоугольника.
Решение:
tg∠CAD=5/16=CD/AD
AD=BC=48, тогда
5/16=CD/48
CD=5*48/16=15
S=15*48=720
Ответ:720
Номер: 3EE23C
Впишите правильный ответ.
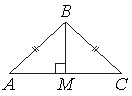
В равнобедренном треугольнике ABC высота BM , проведённая к основанию, равна 3, а tgA=0,6 . Найдите площадь треугольника ABC .
Решение:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему катету. Найдем второй катет.
3/x=6/10
x=30/6=5
Находим площадь ABC
S = 5*2*2/2=10
Ответ:
Номер: 1CF889
Номер: 8F8A3C
Впишите правильный ответ.

Найдите площадь ромба, если его высота равна 18, а острый угол равен 30° .
Решение:
Площадь ромба равна произведению основания на высоту. При этом высота равна половине стороны, так как это катет прямоугольного треугольника напротив угла в 30 градусов, где сторона ромба и является гипотенузой.
18*2=36
S = 18*36=648
Ответ:
Номер: 412A85
Впишите правильный ответ.

В треугольнике ABC известно, что AB=BC=25 , AC=14 . Найдите площадь треугольника ABC .
Решение:
Находим высоту треугольника:
`AB^2=h^2+(AC/2)^2`
`h^2=AB^2-(AC/2)^2`
`h^2=25^2-7^2`
`h^2=625-49`
`h^2=576`
h=24
Найдем площадь:
S= 14*24*0.5=168
Ответ:
Номер: 08FF8F
Впишите правильный ответ.

Сумма двух углов ромба равна 120°, а его периметр равен 48. Найдите длину меньшей диагонали ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников, с гипотенузами 36. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° та как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
48/4=12 - гипотенуза.
Тогда меньшая диагональ ромба 12/2*2=12
Ответ:
Номер: 0FC08C
Впишите правильный ответ.
Сумма двух углов ромба равна 120° , а его меньшая диагональ равна 8. Найдите периметр ромба.

Решение:
Ромб состоит из 4 прямоугольных треугольников, с катетами 8/2=4. Найдем гипотенузу для треугольника.
Сумма двух углов равна 120, то есть это углы напротив меньших катетов, 120/2=60° та как углы острые. При этом в треугольнике это углы 60/2=30°, а катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
Тогда периметр ромба 4*2*4=32
Ответ:
Номер: 2E7580
Впишите правильный ответ.

Сумма двух углов ромба равна 240°, а его меньшая диагональ равна 30. Найдите периметр ромба.
Решение:
Ромб состоит из 4 прямоугольных треугольников. Найдем катет для треугольника.
Сумма двух углов равна 240, то есть это углы напротив больших катетов, 240/2=120° так как углы тупые. При этом в треугольнике это углы 120/2=60°, а второй угол у прямоугольного треугольника 180-60-90=30º. Катеты в прямоугольных треугольниках напротив углов в 30º равны половине гипотенузы.
30:2*2=30 - гипотенуза.
Периметр: 30*4=120
Ответ:
Номер: 20EA85
Впишите правильный ответ.
В треугольнике ABC угол C равен 90° , AB=39 , cosA=5/13 . Найдите длину стороны BC .

Решение:
Косинус это отношение прилежащего катета к гипотенузе.
cosA=AC/AB=5/13
AC/39=5/13
AC=195/13=15
ВС можно найти по теореме Пифагора
`ВС^2=AB^2-AC^2`
`BC^2=39^2-15^2`
`BC^2=1521-225`
`BC^2=1296`
BC=36
Ответ:36
Номер: D8538F
Впишите правильный ответ.
В треугольнике АВС угол С равен 90° , АВ=√26 , ВС=1 . Найдите tgA .

Решение:
Тангенс это отношение противолежащего катета к прилежащему.
Найдем катет AC по теореме Пифагора.
`AC^2=AB^2-AC^2`
`AC^2=(sqrt(26))^2-1^2`
`AC^2=26-1`
`AC^2=25`
AC=5
tgA = 1/5=0,2
Ответ:0,2
Номер: 57A58F
Впишите правильный ответ.
В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=55°, ∠D=137°. Найдите величину угла A. Ответ дайте в градусах.

Решение:
Если провести отрезок СА, то он будет образовывать основание с двумя равнобедренными треугольниками. Углы у основания таких треугольников равны.
При этом угол A равен сумме двух таких одиночных углов у основания от разных треугольников:
(180-55)/2+(180-137)/2=62,5+21,5=84º
Ответ:
Номер: 950C88
Впишите правильный ответ.
На стороне BC прямоугольника ABCD , у которого AB=12 и AD=17 , отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED .
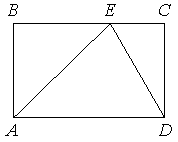
Решение:
EC=17-12=5
CD=BA=12
по теореме Пифагора
`ED^2=EC^2+CD^2`
`ED^2=5^2+12^2`
`ED^2=25+144`
`ED^2=169`
ED=13
Ответ:13
Номер: 4E4948
Впишите правильный ответ.
Основания равнобедренной трапеции равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции.

Решение:
Находим разницу оснований и делим на два. Узнаем основание прямоугольных треугольников, образованных если провести высоту из точек пересечения меньшего основания и боковых сторон.
(24-10)/2=7
Высоту можно найти по теореме Пифагора:
`h^2=25^2-7^2`
`h^2=625-49`
`h^2=576`
h=24
Ответ:24
Номер: D149FE
Впишите правильный ответ.
На окружности радиуса 3 отмечена точка С. Отрезок АВ — диаметр окружности, АС=4√2 . Найдите ВС.

Решение:
Диаметр равен двум радиусам
3*2=6
Образовавшийся треугольник прямоугольный, так как его катеты опираются на диаметр.
Находим катет ВС
`ВС^2=6^2-(4sqrt(2))^2`
`ВС^2=36-16*2`
`ВС^2=4`
ВС=2
Ответ:2
Номер: 5862FF
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС, медиана ВМ равна 2. Площадь треугольника АВС равна 2√21. Найдите длину стороны АВ .

Решение:
Медиана равна высоте. Площадь прямоугольного треугольника:
S = 1/2 * BM * AM
2√21/2 = 1/2 * 2 * AM
AM = √21
Найдем АВ по теореме Пифагора:
`АВ^2=2^2+sqrt(21)^2`
`АВ^2=4+21`
`АВ^2=25`
АВ=5
Ответ:5
Номер: 31F2FB
Впишите правильный ответ.
В параллелограмме АВСD отмечена точка M — середина стороны ВС . Отрезки ВD и AM пересекаются в точке K . Найдите длину отрезка ВK , если ВD=15 .
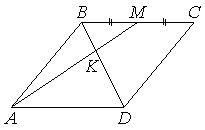
Решение:
Рассмотрим треугольник BMK и AKD они подобны, так как стороны параллелограмма параллельные, АМ секущая, где у вершины K углы равны и накрест лежащие также равны. При этом меньший треугольник соотносится как 1 к 2, как и его основание к большему треугольнику. То есть если BD = 15, то там 3 части, 2 из которых приходится на больший треугольник, и 1 часть на меньший.
Тогда 15/3=5
Ответ:5
Номер: 733A09
Впишите правильный ответ.
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17 , а один из катетов равен 1.
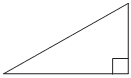
Решение:
Найдем второй катет по теореме Пифагора.
`x^2=sqrt(17)^2-1^2`
`x^2=17-1`
`x^2=16`
x=4
Площадь:
S=1/2*4*1=2
Ответ:2
Номер: DF3909
Впишите правильный ответ.
На окружности радиуса 3 отмечена точка С . Отрезок АВ — диаметр окружности, АС=2√5 . Найдите ВС.

Решение:
Диаметр равен двум радиусам
3*2=6
Образовавшийся треугольник прямоугольный, так как его катеты опираются на диаметр.
Находим катет ВС
`ВС^2=6^2-(2sqrt(5))^2`
`ВС^2=36-4*5`
`ВС^2=16`
ВС=4
Ответ:4
Номер: C3830D
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , медиана ВМ равна 5. Площадь треугольника АВС равна 10√6 . Найдите длину стороны АВ .

Решение:
Медиана равна высоте. Площадь прямоугольного треугольника:
S = 1/2 * BM * AM
10√6/2 = 1/2 * 5 * AM
AM = 5√6:2,5=2√6
Найдем АВ по теореме Пифагора:
`АВ^2=5^2+(2sqrt(6))^2`
`АВ^2=25+4*6`
`АВ^2=49`
АВ=7
Ответ:7
Номер: 3B2200
Впишите правильный ответ.
В параллелограмме АВСD отмечена точка M — середина стороны ВС . Отрезки ВD и AM пересекаются в точке K . Найдите длину отрезка ВK , если ВD=18 .

Решение:
Рассмотрим треугольник BMK и AKD они подобны, так как стороны параллелограмма параллельные, АМ секущая, где у вершины K углы равны и накрест лежащие также равны. При этом меньший треугольник соотносится как 1 к 2, как и его основание к большему треугольнику. То есть если BD = 18, то там 3 части, 2 из которых приходится на больший треугольник, и 1 часть на меньший.
Тогда 18/3=6
Ответ:
Номер: 4C5E77
Впишите правильный ответ.
Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение:
Проведем высоту из тупого известного угла. Получим прямоугольный треугольник с углами 90 и 150-90=60 и 180 -60-90 = 30 градусов.
Катет против угла в 30 градусов равен половине гипотенузы. 6/2=3. Он же является высотой трапеции. Найдем площадь трапеции.
S = (8+16)/2*3 = 12*3=36
Ответ:36
Номер: 33F078
Впишите правильный ответ.
В параллелограмме АВСD отмечена точка M — середина стороны ВС . Отрезки ВD и AM пересекаются в точке K . Найдите длину отрезка ВK , если ВD=12 .

Решение:
Рассмотрим треугольник BMK и AKD они подобны, так как стороны параллелограмма параллельные, АМ секущая, где у вершины K углы равны и накрест лежащие также равны. При этом меньший треугольник соотносится как 1 к 2, как и его основание к большему треугольнику. То есть если BD = 15, то там 3 части, 2 из которых приходится на больший треугольник, и 1 часть на меньший.
Тогда 12/3=4
Ответ:
Номер: 0DFEBE
Впишите правильный ответ.

В равнобедренном треугольнике ABC основание AC равно 48, площадь треугольника равна 168. Найдите длину боковой стороны AB .
Решение:
Проводим высоту. Высота делит треугольник на два прямоугольных треугольника, где известна их площадь и основание.
168/2=84 - площадь
48/2=24 - основание
Тогда высота
(24*h)/2=84
h=168/24=7
Теперь по теореме Пифагора найдем AB
`x^2 = 24^2+7^2`
`x^2 =576+49`
`x = sqrt(625)`
x = 25
Ответ:
Номер: CD30B9
Впишите правильный ответ.
В равнобедренной трапеции одно из оснований равно 3, а другое — 7. Высота трапеции равна 4. Найдите тангенс острого угла трапеции.
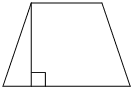
Решение:
Найдем разницу оснований трапеции и поделим пополам. Это будет катет треугольника.
(7-3)/2=2
Тангенс острого угла трапеции равен отношению высоты трапеции к найденному катету.
4/2=2
Ответ:2
Номер: 98DFB4
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , АС=10 , tg∠ВАС=√11/5 . Найдите длину стороны АВ .

Решение:
Проведем высоту h из вершины В. Тангенс равен отношению катетов (противолежащего к прилежащему), где противолежащий катет это высота, а прилежащий половина основания.
tg∠ВАС=√11/5 = h/(AC/2)
AC/2 = 10/2=5, тогда h = √11
По теореме Пифагора найдем гипотенузу.
`АВ^2 = sqrt(11)^2+5^2`
`АВ^2 =11+25`
`АВ = sqrt(36)`
АВ = 6
Ответ:6
Номер: FD7112
Впишите правильный ответ.
Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30° , а площадь квадрата равна 16.

Решение:
Сторона равна √16=4. Площадь ромба равна сторона умноженная на высоту. Высота напротив угла в 30 градусов в прямоугольном треугольнике равна половине гипотенузы (стороны).
S ромба = 4*(4/2)=8
Ответ:8
Номер: B10013
Впишите правильный ответ.
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √13 , а один из катетов равен 2.

Решение:
Найдем второй катет по теореме Пифагора.
`x^2=sqrt(13)^2-2^2`
`x^2=13-4`
`x^2=9`
x=3
Площадь:
S=1/2*3*1=1.5
Ответ:1.5
Номер: DDCA29
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , АС=8 , tg∠ВАС=3/4 . Найдите длину стороны АВ .

Решение:
Проведем высоту h из вершины В. Тангенс равен отношению катетов (противолежащего к прилежащему), где противолежащий катет это высота, а прилежащий половина основания.
tg∠ВАС=3/4 = h/(AC/2)
AC/2 = 8/2=4, тогда h = 3
По теореме Пифагора найдем гипотенузу.
`АВ^2 = 3^2+4^2`
`АВ^2 =9+16`
`АВ = sqrt(25)`
АВ = 5
Ответ:5
Номер: 856025
Впишите правильный ответ.
Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.

Решение:
Находим разницу оснований и делим на два. Узнаем основание прямоугольных треугольников, образованных если провести высоту из точек пересечения меньшего основания и боковых сторон.
(21-11)/2=5
Высоту можно найти по теореме Пифагора:
`h^2=13^2-5^2`
`h^2=169-25`
`h^2=144`
h=12
Ответ:
Номер: 94FBDF
Впишите правильный ответ.
Основания равнобедренной трапеции равны 7 и 13, боковая сторона равна 5. Найдите высоту трапеции.

Решение:
Находим разницу оснований и делим на два. Узнаем основание прямоугольных треугольников, образованных если провести высоту из точек пересечения меньшего основания и боковых сторон.
(13-7)/2=3
Высоту можно найти по теореме Пифагора:
`h^2=5^2-3^2`
`h^2=25-9`
`h^2=16`
h=4
Ответ:
Номер: 7BF3A8
Впишите правильный ответ.
Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение:
Проведем высоту из тупого известного угла. Получим прямоугольный треугольник с углами 90 и 150-90=60 и 180 -60-90 = 30 градусов.
Катет против угла в 30 градусов равен половине гипотенузы. 8/2=4. Он же является высотой трапеции. Найдем площадь трапеции.
S = (10+20)/2*4 = 15*4=60
Ответ:
Номер: 2840A6
Впишите правильный ответ.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130° . Найдите угол ACB . Ответ дайте в градусах.

Решение:
∠BOC = ∠AOD = 130° как накрест лежащие.
Углы у основания равнобедренного треугольника равны, тогда:
(180-130)/2=25°
Ответ:
Номер: 5702A4
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=3 , ВС=CD=5 . Найдите среднюю линию трапеции.

Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`5^2 = 3^2+x^2`
`x^2 =25-9`
`x = sqrt(16)`
x = 4
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
4/2=2 средняя линия треугольника.
5+2=7
Ответ:
Номер: 6CBDA1
Впишите правильный ответ.
Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30° , а площадь квадрата равна 36.

Решение:
Сторона равна √36=6. Площадь ромба равна сторона умноженная на высоту. Высота напротив угла в 30 градусов в прямоугольном треугольнике равна половине гипотенузы (стороны).
S ромба = 6*(6/2)=18
Ответ:
Номер: 04CFC3
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , АС=6 , tg∠ВАС=√7/3 . Найдите длину стороны АВ .

Решение:
Проведем высоту h из вершины В. Тангенс равен отношению катетов (противолежащего к прилежащему), где противолежащий катет это высота, а прилежащий половина основания.
tg∠ВАС=√7/3 = h/(AC/2)
AC/2 = 6/2=3, тогда h = √7
По теореме Пифагора найдем гипотенузу.
`АВ^2 = sqrt(7)^2+3^2`
`АВ^2 =7+9`
`АВ = sqrt(16)`
АВ = 4
Ответ:
Номер: 2DCDCD
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , АС=12 , tg∠ВАС=√13/6 . Найдите длину стороны АВ .

Решение:
Проведем высоту h из вершины В. Тангенс равен отношению катетов (противолежащего к прилежащему), где противолежащий катет это высота, а прилежащий половина основания.
tg∠ВАС=√13/6 = h/(AC/2)
AC/2 = 12/2=6, тогда h = √13
По теореме Пифагора найдем гипотенузу.
`АВ^2 = sqrt(13)^2+6^2`
`АВ^2 =16+36`
`АВ = sqrt(49)`
АВ = 7
Ответ:
Номер: F75093
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=12 , ВС=CD=15 (см. рисунок). Найдите среднюю линию трапеции.

Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`15^2 = 12^2+x^2`
`x^2 =225-144`
`x = sqrt(81)`
x = 9
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
9/2=4.5 средняя линия треугольника.
15+4.5=19,5
Ответ:
Номер: 0B5C97
Впишите правильный ответ.
Стороны параллелограмма равны 10 и 15. Высота, опущенная на меньшую сторону, равна 12. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Решение:
Площадь параллелограмма равна высота умноженная на основание.
12*10=15*h
h=120/15= 8
Ответ:
Номер: 7B929A
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , медиана ВМ равна 4. Площадь треугольника АВС равна 8√5. Найдите длину стороны АВ .

Решение:
Медиана равна высоте. Площадь прямоугольного треугольника:
S = 1/2 * BM * AM
8√5/2 = 1/2 * 4 * AM
AM = 4√5:2=2√5
Найдем АВ по теореме Пифагора:
`АВ^2=4^2+(2sqrt(5))^2`
`АВ^2=16+4*5`
`АВ^2=36`
АВ=6
Ответ:6
Номер: B45194
Впишите правильный ответ.
В треугольнике АВС известно, что АВ=ВС , медиана ВМ равна 3. Площадь треугольника АВС равна 18√2 . Найдите длину стороны АВ .

Решение:
Медиана равна высоте. Площадь прямоугольного треугольника:
S = 1/2 * BM * AM
18√2/2 = 1/2 * 3 * AM
AM = 9√2:1,5=6√2
Найдем АВ по теореме Пифагора:
`АВ^2=3^2+(6sqrt(2))^2`
`АВ^2=9+36*2`
`АВ^2=81`
АВ=9
Ответ:9
Номер: A52D9F
Впишите правильный ответ.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 112° . Найдите угол ACB . Ответ дайте в градусах.

Решение:
∠BOC = ∠AOD = 112° как накрест лежащие.
Углы у основания равнобедренного треугольника равны, тогда:
(180-112)/2=34°
Ответ:
Номер: B89AEE
Впишите правильный ответ.
В прямоугольной трапеции основания равны 3 и 5, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
5-3=2
Ответ:2
Номер: 207DE7
Впишите правильный ответ.
В равнобедренной трапеции одно из оснований равно 5, а другое — 9. Высота трапеции равна 6. Найдите тангенс острого угла трапеции.

Решение:
Найдем разницу оснований трапеции и поделим пополам. Это будет катет треугольника.
(9-5)/2=2
Тангенс острого угла трапеции равен отношению высоты трапеции к найденному катету.
6/2=3
Ответ:
Номер: CF1FE7
Впишите правильный ответ.
На стороне BC прямоугольника ABCD , у которого AB=15 и AD=23 , отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED .

Решение:
EC=23-15=8
CD=BA=15
по теореме Пифагора
`ED^2=EC^2+CD^2`
`ED^2=8^2+15^2`
`ED^2=64+225`
`ED^2=289`
ED=17
Ответ:17
Номер: 6F29E1
Впишите правильный ответ.
Стороны параллелограмма равны 10 и 12. Высота, опущенная на меньшую сторону, равна 6. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Решение:
Площадь параллелограмма равна высота умноженная на основание.
6*10=12*h
h=5
Ответ:5
Номер: 49126A
Впишите правильный ответ.
В прямоугольной трапеции основания равны 4 и 7, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
7-4=3
Ответ:
Номер: 201C6D
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=8 , ВС=CD=10 . Найдите среднюю линию трапеции.

Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`10^2 = 8^2+x^2`
`x^2 =100-64`
`x = sqrt(36)`
x = 6
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
6/2=3 средняя линия треугольника.
10+3=13
Ответ:
Номер: F4BE37
Впишите правильный ответ.
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=15 , ВС=CD=17 . Найдите среднюю линию трапеции.

Решение:
Если провести высоту из точки С, то она равна АВ=12, получаем также прямоугольный треугольник, где неизвестен один катет. Находим его.
`17^2 = 15^2+x^2`
`x^2 =289-225`
`x = sqrt(64)`
x = 8
При этом средняя линия трапеции будет равна средней линии этого треугольника и основания BC.
8/2=4 средняя линия треугольника.
17+4=21
Ответ:
Номер: D3C13A
Впишите правильный ответ.
На окружности радиуса 3 отмечена точка С . Отрезок АВ — диаметр окружности, АС=3√3 . Найдите ВС.

Решение:
Диаметр равен двум радиусам
3*2=6
Образовавшийся треугольник прямоугольный, так как его катеты опираются на диаметр.
Находим катет ВС
`ВС^2=6^2-(3sqrt(3))^2`
`ВС^2=36-9*3`
`ВС^2=9`
ВС=3
Ответ:3
Номер: CECE3B
Впишите правильный ответ.
В прямоугольной трапеции основания равны 5 и 9, а один из углов равен 135° . Найдите меньшую боковую сторону.

Решение:
Проведем высоту из тупого угла и найдем углы у треугольника.
135-90=45° Получается треугольник равнобедренный и прямоугольный.
Разность оснований и будет высотой, и она равна меньшей стороне.
9-5=4
Ответ:
Номер: A0838E
Впишите правильный ответ.
Стороны параллелограмма равны 9 и 12. Высота, опущенная на меньшую сторону, равна 8. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Решение:
Площадь параллелограмма равна высота умноженная на основание.
9*8=12*h
h=72/12= 6
Ответ:
Номер: 92F78E

