Алгоритм выполнения задания 22 (минимальное время/с параметром t)
1. Считаем итоговое время каждого процесса по формуле:
Итоговое время процесса = время текущего процесса + итоговое время процесса, от которого зависит текущий процесс.
Примечание: если процессов, от которых зависит текущий, несколько, то ко времени текущего прибавляем итоговое время самого долгого процесса.
2. Выбираем самое большое значение среди итоговых времен, записываем его в ответ.
З. Если время одного из процессов не известно (обозначено как t), то стираем значение этой ячейки и выделяем её цветом. После проделанных шагов 1 и 2 подбираем значение t, подходящее по условию.
Алгоритм выполнения задания 22 (нахождение макс. отрезка)
1. Внимательно читаем условие и выделяем для себя сколько процессов должно выполняться одновременно.
2. Строим таблицу количество процессов / мс возле основной таблицы зависимостей, чтобы в дальнейшем визуализировать все процессы. Также рекомендуется уменьшить ширину столбца.

3. Ячейки помечаем любым цветом, что означает количество мс, которые необходимы для завершения этого процесса. Процессы, зависимые от других, начинаем помечать после выполнения зависимых процессов. Далее в каждую закрашенную ячейку помещаем единицу для дальнейшего анализа.

4. Для удобства раскашиваем блоки зависимых процессов разными цветами.
Пример. Для задания выше процессы 1-8 зависят от выполнения первых двух процессов; процесс 11 зависим только от 9 процесса; процесс 12 зависим от 10. Поэтому помечаем эти три блока разными цветами, как на рисунке ниже.

5. Под получившейся таблицей считаем сумму одновременно выполняемых процессов в данную мс.
Для примера, описанного выше, воспользуемся формулой: =СУММ(F2:F13) для всех ячеек, в которых есть хотя бы 1 выполняемый процесс.
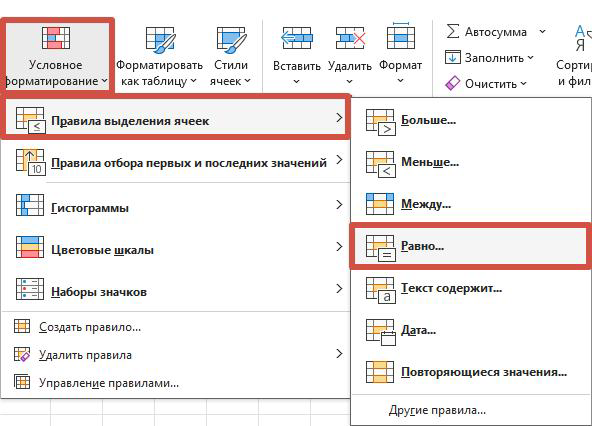
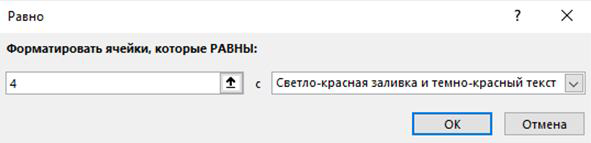
Дополнение: с помощью условного форматирования можно выделить цветом подходящее количество процессов для большей наглядности. В Условном форматировании Нажимаем на «Правила выделения ячеек» - «Равно» и выставляем параметр «4»
6. Смотрим на процессы и передвигаем их в соответствии с их зависимостями. Так, например, можно передвигать независимые процессы в любое «место» на таблице, а зависимые процессы ставить на любые «места» после выполнения зависимых процессов. В случае, если от вторых далее идут зависимые процессы, то их также необходимо передвинуть дальше по таблице.
7. Находим самую выгодную позицию, чтобы под таблицей было как можно больше выделенных цветом цифр без прерывания.

8. Записываем ответ.
Пример: ответ 13
Прототипы с ЕГЭ
Задача №1 В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Ответ: 656
Задача №2 В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0. Определите максимальную продолжительность отрезка времени (в мс), в течение которого возможно одновременное выполнение четырёх процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Ответ: 7

