В задании 22 ОГЭ по математике нужно построить график функции и определить, при каких значениях заданная прямая имеет с графиком ровно одну/ две/три общие точки или не имеет с графиком общих точек. Это задания с развернутым ответом, так что важно оформление.
За это задание можно заработать 2 балла, если выполнено 2 условия: график построен верно; верно найдены искомые значения параметра.
В открытом банке заданий ФИПИ находятся следующие задания, которые могут попасться вам на экзамене в этом году.
КЭС 5.1 Функция, способы задания функции. График функции. Область определения и множество значений функции. Нули функции. Промежутки знакопостоянства. Промежутки монотонности функции. Максимумы и минимумы функции. Наибольшее и наименьшее значение функции на промежутке
Задания про графики функций из банка ФИПИ
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2+6x+7\\x+10\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-4,\\x<-4.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 90FF4E
Постройте график функции y=x2+14x−3|x+8|+48 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 675547
Постройте график функции
y=|x|⋅(x−1)−6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
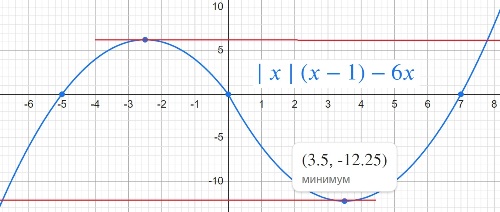
y=6,25
y=-12,25
Ответ: 6,25 -12,25
Номер: 6DCB49
Постройте график функции
y=4|x−3|−x2+8x−15.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: F98AF0
Постройте график функции
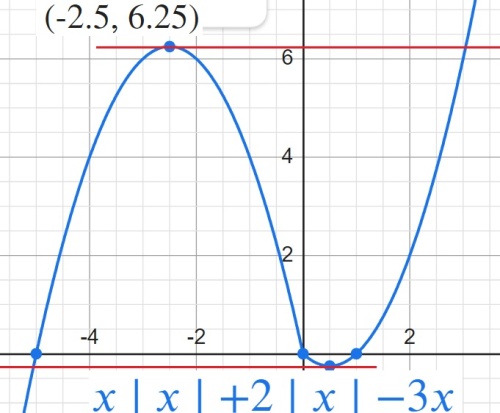
y=x|x|+2|x|−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: F486F7
Постройте график функции
y=4|x+6|−x2−11x−30.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: A58BF6
Постройте график функции
y=|x|⋅(x−1)−2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
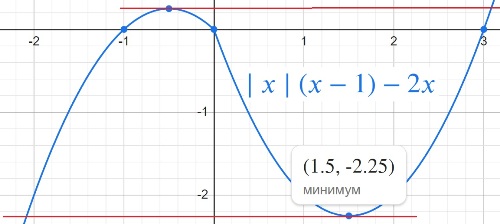
y=0,25
y=-2,25
Ответ: 0,25 -2,25
Номер: 1D2900
Постройте график функции
y=|x|⋅(x+1)−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
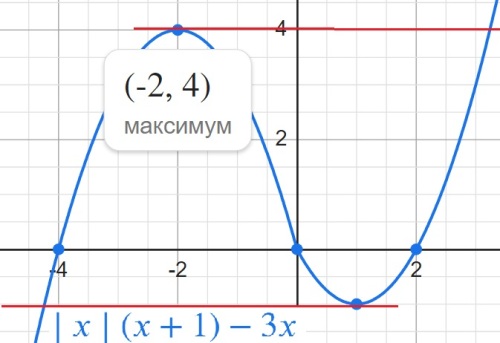
y=4
y=-1
Ответ: 4 -1
Номер: 5A5902
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2+8x-17\\-x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq2,\\x<2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 447D77
Постройте график функции
y=|x|⋅(x−1)−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
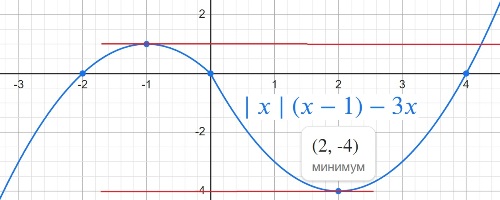
y=1
y=-4
Ответ: 1 -4
Номер: E4D078
Постройте график функции y=x2−9x−2|x−4|+20 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: F708B3
Постройте график функции
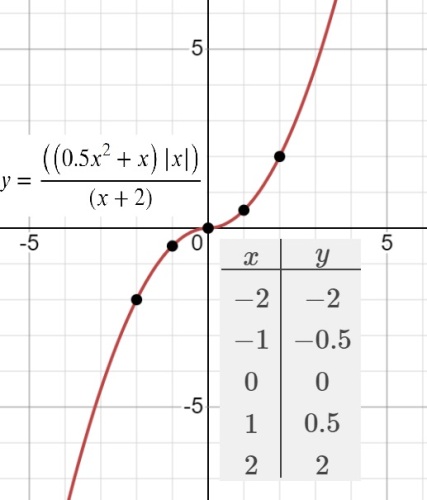
$y=\frac{{(0,5x^2+x)}⋅{\vert x\vert}}{x+2}$
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
...
Ответ: ...
Номер: D35EB0
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2+2x+3\\-x+1\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-1,\\x<-1.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 5BD2BC
Постройте график функции
$y=\left\{\begin{array}{l}x^2-6x+10\;\text{при }x\geq1,\\x+2\;\text{при }x<1.\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 9E02BA
Постройте график функции
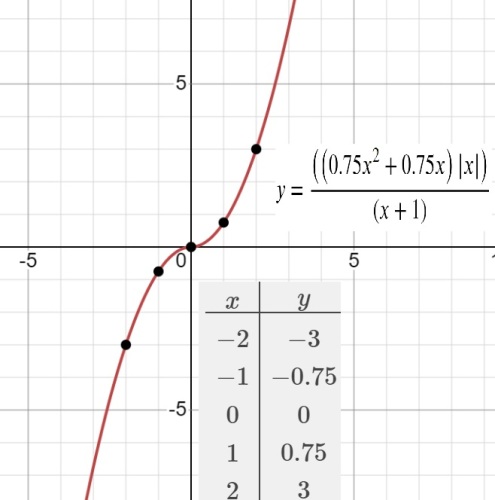
$y=\frac{{(0,75x^2+0,75x)}⋅{\vert x\vert}}{x+1}$
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 9600B6
Постройте график функции y=x2−5x−5|x−2|+6 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 6E2FBC
Постройте график функции
y=|x|⋅(x+3)−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
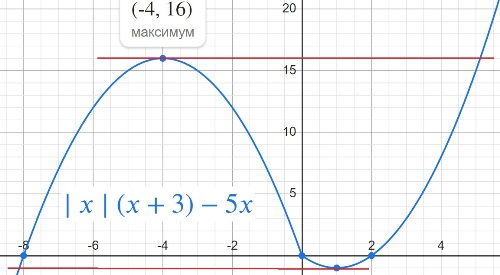
y=16
y=-1
Ответ: 16 -1
Номер: 85AFB6
Постройте график функции
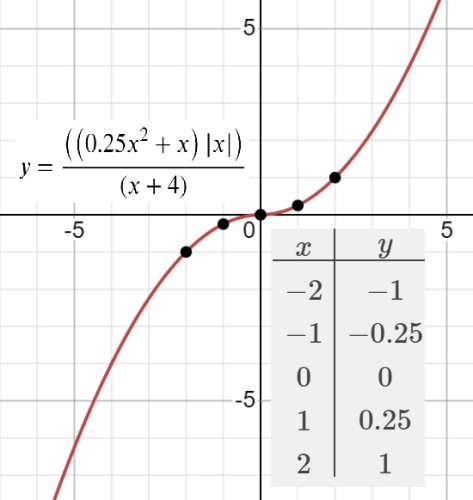
$y=\frac{{(0,25x^2+x)}⋅{\vert x\vert}}{x+4}$
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 43A519
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-8x+14\\x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq3,\\x<3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 68001C
Постройте график функции
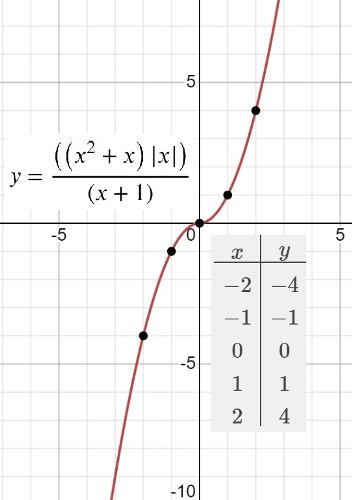
$y=\frac{{(x^2+x)}⋅{\vert x\vert}}{x+1}$
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 32AB12
Постройте график функции
y=3|x+2|−x2−3x−2.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
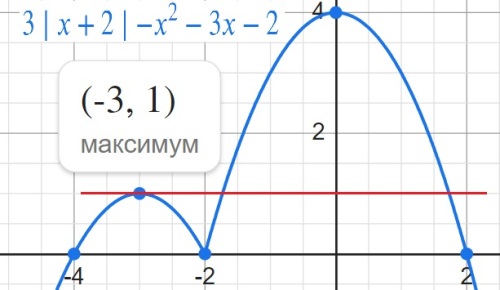
y=1
Прямая y = m имеет с графиком ровно три общие точки, если она проходит через вершину первой параболы и пересекает вторую или если она проходит через точку (-2; 0) . Получаем, что m = 0 или m =1
Ответ: m = 0, m =1
Номер: 36C01E
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-6x+6\\x-3\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq2,\\x<2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: DB3225
Постройте график функции
y=4|x+2|−x2−3x−2.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
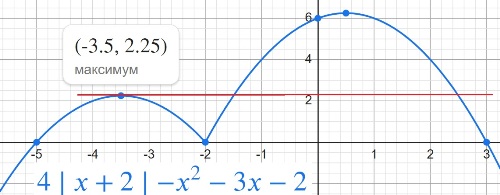
y=2,25
Прямая y = m имеет с графиком ровно три общие точки, если она проходит через вершину первой параболы и пересекает вторую или если она проходит через точку (-2; 0) . Получаем, что m = 0 или m =2,25.
Ответ: m = 0, m =2,25
Номер: B817D5
Постройте график функции
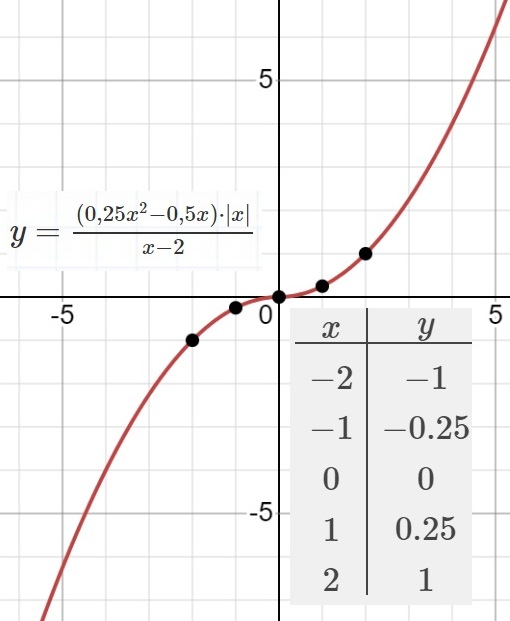
$y=\frac{{(0,25x^2-0,5x)}⋅{\vert x\vert}}{x-2}$
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: AD9AD9
Постройте график функции
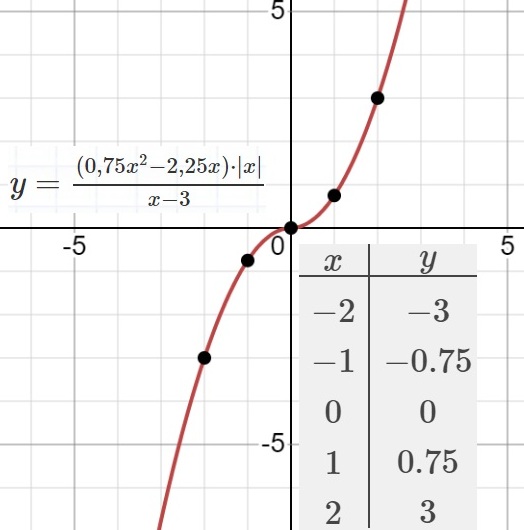
$y=\frac{{(0,75x^2-2,25x)}⋅{\vert x\vert}}{x-3}$
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 880BD7
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2+4x-1\\x\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-4,\\x<-4.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 89C3D3
Постройте график функции
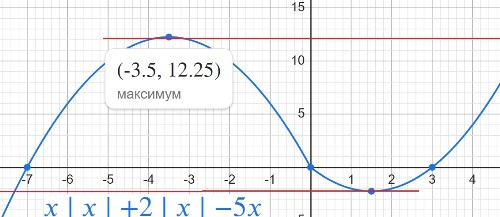
y=x|x|+2|x|−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 5E5852
Постройте график функции y=x2−7x−5|x−3|+12 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 91BF55
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-4x-1\\-x-3\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-3,\\x<-3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: E1EE5C
Постройте график функции
y=x|x|+|x|−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
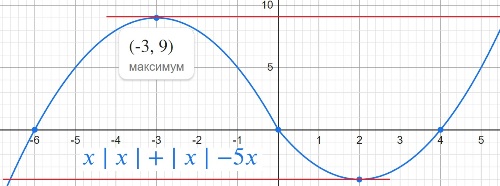
y=9
y=-4
Ответ: 9 -4
Номер: 5C9FAE
Дайте развернутый ответ. 2025
Постройте график функции `y=(x^4-13x^2+36)/((x-3)(x+2))` и определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Решение:
...
Ответ:
Номер: C344AD
Постройте график функции
y=2|x−5|−x2+11x−30.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
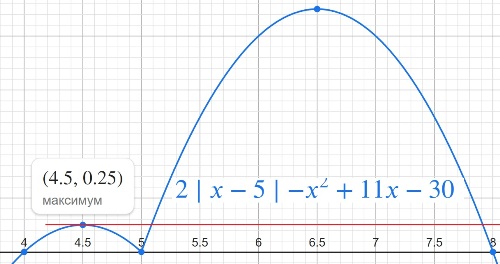
y=0,25
Прямая y = m имеет с графиком ровно три общие точки, если она проходит через вершину первой параболы и пересекает вторую или если она проходит через точку (5; 0) . Получаем, что m = 0 или m =0,25
Ответ: m = 0, m =0,25
Номер: 32C5AB
Постройте график функции
$y=\frac{{(0,75x^2-1,5x)}⋅{\vert x\vert}}{x-2}$
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...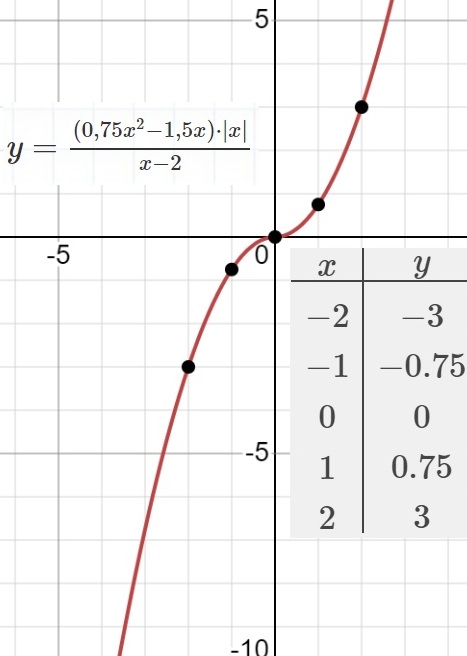
Ответ: ...
Номер: A2BECD
Постройте график функции
y=x|x|+|x|−6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
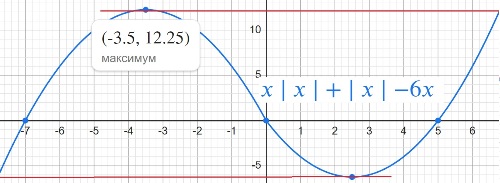
y=12,25
y=-6,25
Ответ: 12,25 -6,25
Номер: D89894
Постройте график функции
$y=\frac{{(0,5x^2+0,5x)}⋅{\vert x\vert}}{x+1}$
Определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
...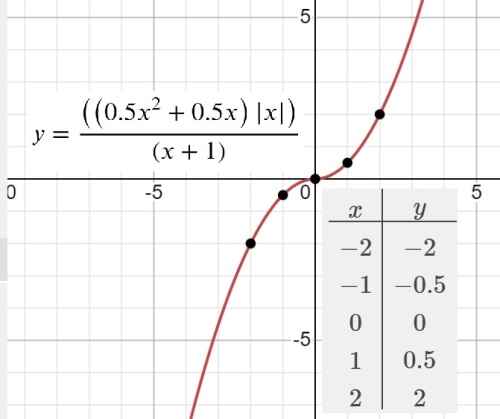
Ответ: ...
Номер: C7E39A
Постройте график функции y=x2+13x−3|x+7|+42 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 7D78E6
Постройте график функции
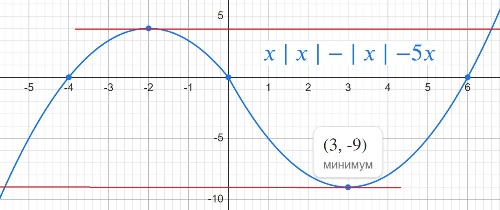
y=x|x|−|x|−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 7B9160
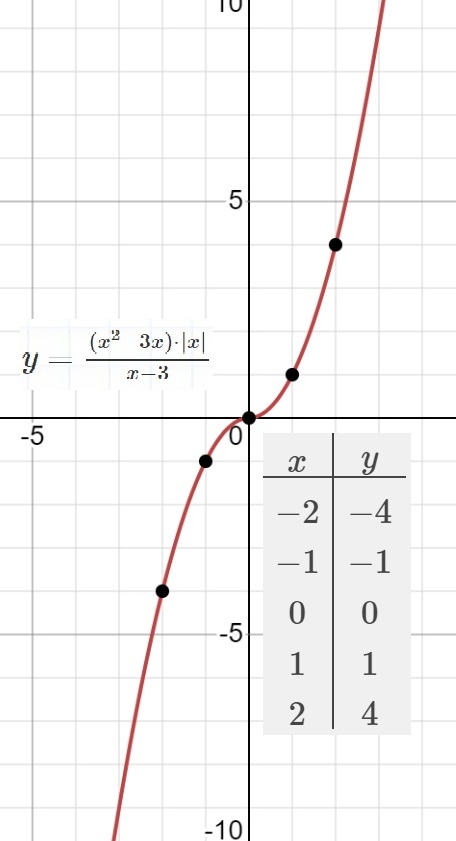
Постройте график функции
$y=\frac{{(x^2-3x)}⋅{\vert x\vert}}{x-3}$
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: A8A167
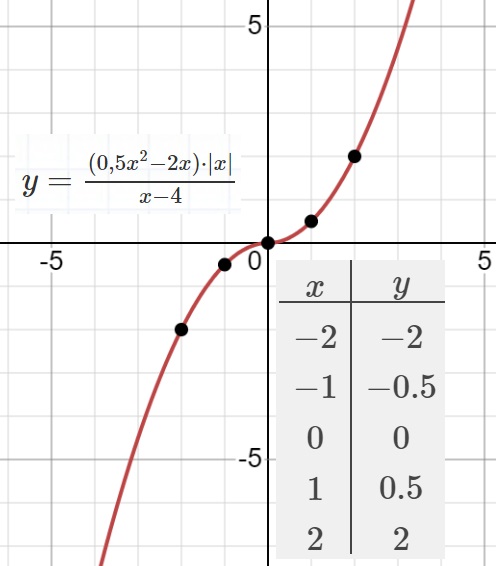
Постройте график функции
$y=\frac{{(0,5x^2-2x)}⋅{\vert x\vert}}{x-4}$
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: C6653F
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2+6x-9\\-x\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq2,\\x<2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: E05C3B
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-2x+2\\-x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-3,\\x<-3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: E73835
Постройте график функции
y=x2 +3x−4|x+2|+2.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 0B2341
Постройте график функции
$y=\frac{2,5{\vert x\vert}-1}{{\vert x\vert}-2,5x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 772C4F
Постройте график функции
y=x|x|+3|x|−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
y=x|x|+3|x|−5x
1. Рассмотрим две параболы. Составив систему возможных функций
y=x2+3x−5x
y=-x2+3|x|−5x
2. Найдем корни
y=x2−2x (0; 2)
y=-x2−8x (0; -8)
3. Найдем точки вершин парабол
Находим абсциссу вершины для первой функции x0=-b/2a = 2/2=1
Находим абсциссу вершины для второй функции x0=-b/2a = 8/-2=-4
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=1+(-2*1)=-1
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-16+(-8*-4)=16
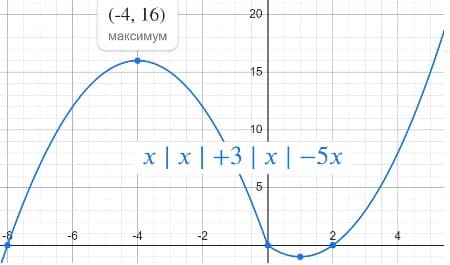
Две общие точки будут в случае если прямые проходят параллельно оси абсцисс и через вершины парабол.
m = -1 и m = 16
Ответ: -1 16
Номер: B4CE4A
Постройте график функции
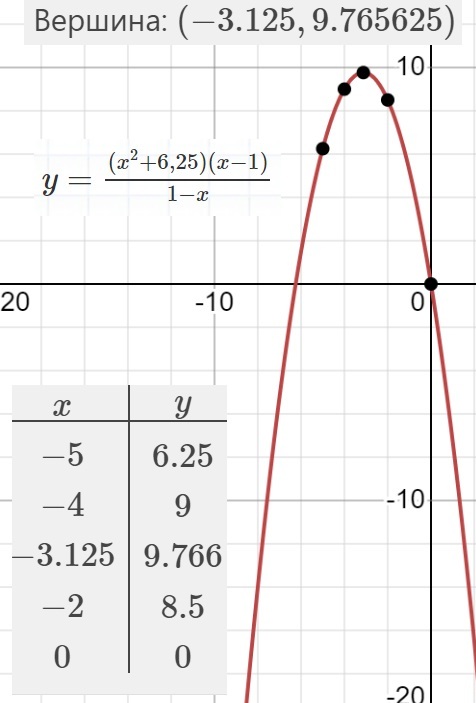
$y=\frac{{(x^2+6,25)}{(x-1)}}{1-x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 152E49
Постройте график функции
$y=\frac{{(0,5x^2-0,5x)}⋅{\vert x\vert}}{x-1}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 2A2D4E
Постройте график функции
$y=\frac{{(x^2+1)}{(x-2)}}{2-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: DF7E4D
Постройте график функции
y=∣x2 +5x+6∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: C0BD4C
Постройте график функции
$y=-2-\frac{x+4}{x^2+4x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 632946
Постройте график функции
$y=\left\{\begin{array}{l}x^2+2x+1\text{ при }x\geq-4,\\-\frac{36}x\text{ при }x<-4.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 46EEF6
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}2,5x-1\\-3,5x+11\\x-1\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<2,\\2\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 13A5FD
Постройте график функции
$y=\frac{2{\vert x\vert}-1}{{\vert x\vert}-2x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: AB4DF3
Постройте график функции
$y=\frac{{(0,5x^2-x)}⋅{\vert x\vert}}{x-2}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: CB85F6
Постройте график функции
$y=\frac{{(x^2+6,25)}{(x+1)}}{-1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: EB0FF0
Постройте график функции
$y=\frac{{(x^2-x)}⋅{\vert x\vert}}{x-1}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: E993F3
Постройте график функции
$y=\frac{{(0,5x^2+2x)}⋅{\vert x\vert}}{x+4}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 625FF0
Постройте график функции
$y=\frac{{(x^2+4)}{(x+1)}}{-1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 6250F0
Постройте график функции
y=x|x|−|x|−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Рассмотрим две параболы. Составив систему возможных функций
y=x|x|−|x|−3x.
y=x2−4x.
y=-x2−2x.
2. Находим корни
y=x2−4x (0; 4)
y=-x2−2x (0; -2)
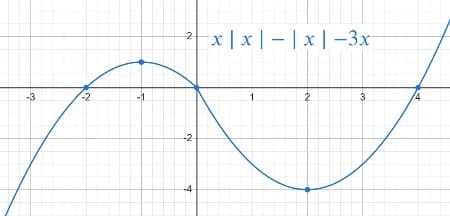
3.
Находим абсциссу вершины для первой функции x0=-b/2a = 4/2=2
Находим абсциссу вершины для второй функции x0=-b/2a = 2/-2=-1
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=1*4+(-4*2)=-4
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-1*1+(-2*-1)=-1+2=1
Ответ: -4 1
Номер: 6D7DF6
Постройте график функции
$y=\left\{\begin{array}{l}x^2-4x+4\text{ при }x\geq-1,\\-\frac9x\text{ при }x<-1.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 46800C
Постройте график функции
$y=\frac{{\vert x\vert}-1}{{\vert x\vert}-x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 768602
Постройте график функции
$y=\frac{4{\vert x\vert}-1}{{\vert x\vert}-4x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: B3D80F
Постройте график функции
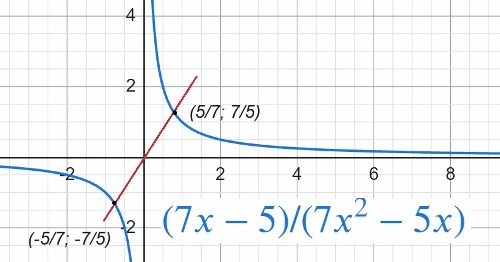
$y=\frac{7x-5}{7x^2-5x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 20CD08
Постройте график функции
$y=\left\{\begin{array}{l}x-0,5,\text{ если }x<-2,\\-2x-6,5,\text{ если }-2\leq x\leq-1,\\x-3,5,\text{ если }x>-1,\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: C1600B
Постройте график функции
$y=3-\frac{x+2}{x^2+2x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: C69602
Постройте график функции
$y=5-\frac{x+5}{x^2+5x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 68EB0C
Постройте график функции
y=5|x−2|−x2 +5x−6.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 35020B
Постройте график функции
y=|x|⋅(x+2)−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Рассмотрим две параболы. Составив систему возможных функций
y=|x|⋅(x+2)−5x.
y=x2 +2x−5x
y=-x2-7x.
2. Находим корни, строим график
y=x2 - 3x (0;3)
y=-x2-7x (0; -7)
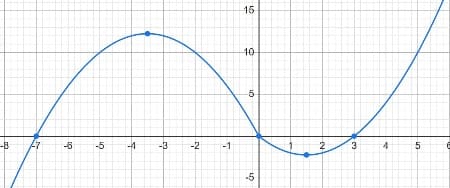
3.
Находим абсциссу вершины для первой функции x0=-b/2a = 3/2=1.5
Находим абсциссу вершины для второй функции x0=-b/2a = 7/-2=-3.5
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=2.25+(-3*1,5)=-2.25
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-12.25+(-7*-3,5)=-12,25+25=12,25
Ординаты и будут значением m
Ответ: -2.25 12,25
Номер: 3D9A0A
Постройте график функции
$y=\left\{\begin{array}{l}x^2+6x+9\text{ при }x\geq-5,\\-\frac{20}x\text{ при }x<-5.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: FCB77C
Постройте график функции
y=|x|⋅(x+1)−6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Раскроем модуль, тем самым у нас получится система из двух возможных функций.
y=x2-5x
y=-x2 - 7x
2. Строим график функций.
для первой корни 0; 5
для второй 0; -7
Поэтому отсекаем функции на областях, где они перекрываются по значениям, то есть в 0
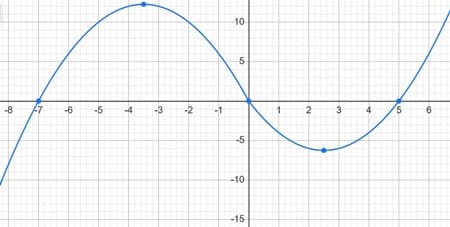
3. Две общие точки будут в вершинах функций.
Находим абсциссу вершины для первой функции x0=-b/2a = 5/2=2.5
Находим абсциссу вершины для второй функции x0=-b/2a = 7/-2=-3.5
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=6.25+(-5*2.5)=-6.25
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-12.25+(-7*-3.5)=-12.25+24.5=12.25
Ординаты и будут значением m
-6,25 12,25
Ответ: -6,25 12,25
Номер: 0D3070
Постройте график функции
y=x|x|+|x|−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
y=x|x|+|x|−3x
1. Рассмотрим две параболы. Составив систему возможных функций
y=x2+x−3x
y=x2-x−3x
2. Найдем корни.
y=x2 - 2x (0; 2)
y=-x2-4x (0; -4)
3. Найдем точки вершин парабол
Находим абсциссу вершины для первой функции x0=-b/2a = 2/2=1
Находим абсциссу вершины для второй функции x0=-b/2a = 4/-2=-2
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=1+(-2*1)=-1
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=4+(-4*-2)=4
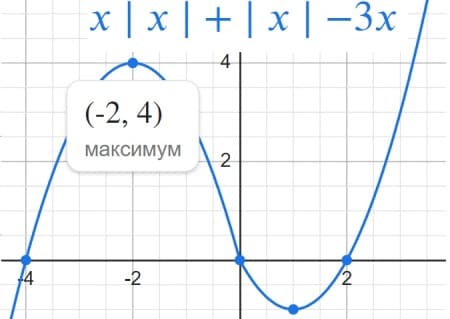
Две общие точки будут в случае если прямые проходят параллельно оси абсцисс и через вершины парабол.
m = -1 и m = 4
Ответ: -1 4
Номер: 076977
Постройте график функции
$y=\frac{3{\vert x\vert}-1}{{\vert x\vert}-3x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 7AC574
Постройте график функции
y=∣x2 −4x+3∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: B80D72
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-2x+3\\-x-1\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-2,\\x<-2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 1CE27B
Постройте график функции
$y=\frac12{(\left|\frac x{4,5}-\frac{4,5}x\right|+\frac x{4,5}+\frac{4,5}x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 158C7B
Постройте график функции
$y=\frac{4,5{\vert x\vert}-1}{{\vert x\vert}-4,5x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 381A79
Постройте график функции
$y=\frac12{(\left|\frac x{2,5}-\frac{2,5}x\right|+\frac x{2,5}+\frac{2,5}x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 4773B7
Постройте график функции
y=|x|⋅(x+2)−3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Рассмотрим две параболы. Составив систему возможных функций
y=|x|⋅(x+2)−3x
y=x2+2x−3x
y=-x2-2x−3x
2. Находим корни
y=x2−x (Корни 0;1)
y=-x2-5x (Корни 0;-5)
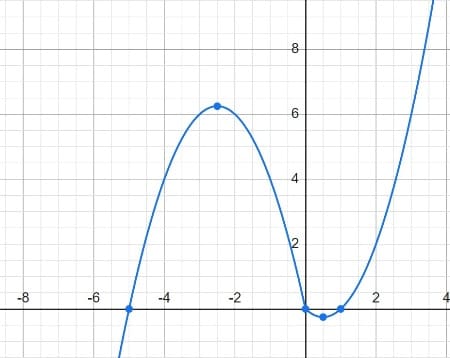
3.
Находим абсциссу вершины для первой функции x0=-b/2a = 1/2=0.5
Находим абсциссу вершины для второй функции x0=-b/2a = 5/-2=-2.5
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=0.25-0.5=0.25
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-6.25-5*-2.5=6.25
Ординаты и будут значением m
Ответ: 0.25 6.25
Номер: F0A0B3
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x-4\\-1,5x+4,5\\1,5x-7,5\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<3,\\3\leq x\leq4,\\x>4.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 7493BA
Постройте график функции
y=∣x2 +2x−3∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: EF61B5
Постройте график функции
$y=\frac12{(\left|\frac x3-\frac3x\right|+\frac x3+\frac3x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 4FBE10
Постройте график функции
$y=-4-\frac{x+1}{x^2+x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 4CB11B
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-4x+1\\-x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-3,\\x<-3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: F3131F
Постройте график функции
y=x2 +3x−3|x+2|+2.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 02F213
Постройте график функции
$y=\frac12{(\left|\frac x4-\frac4x\right|+\frac x4+\frac4x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: D69F19
Постройте график функции
$y=\frac{{(x^2+0,25)}{(x-1)}}{1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 929B17
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}2x-2\\-3x+13\\1,5x-7\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<3,\\3\leq x\leq4,\\x>4.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: E23414
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2+10x-21\\-x+5\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq3,\\x<3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: E88E19
Постройте график функции
y=5|x−3|−x2 +7x−12.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 6DF71A
Постройте график функции
$y=-1-\frac{x-4}{x^2-4x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 396E17
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}x-2,5\\-x+1,5\\x-5\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<2,\\2\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 41D023
Постройте график функции
$y=\left\{\begin{array}{l}2,5x-3,5\\-3x+7,5\\x-6\end{array}\begin{array}{cc}\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<2,\\2\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 0DC82F
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}4x-5\\-2,5x+5\\x-9\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<1,\\1\leq x\leq4,\\x>4.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 03E125
Постройте график функции
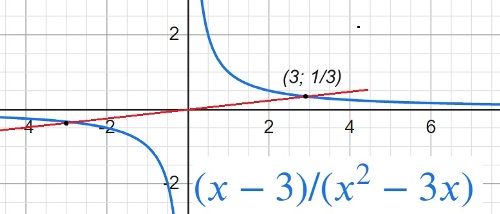
$y=\frac{x-3}{x^2-3x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 70822B
Постройте график функции
$y=\frac{{(0,75x^2+1,5x)}⋅{\vert x\vert}}{x+2}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 2C1121
Постройте график функции
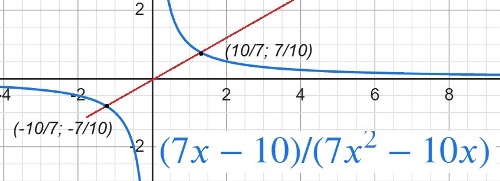
$y=\frac{7x-10}{7x^2-10x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: DE232E
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-2x+1\\-x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-3,\\x<-3.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: C16D27
Постройте график функции
$y=\frac12{(\left|\frac x2-\frac2x\right|+\frac x2+\frac2x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: C1F62D
Постройте график функции
$y=2-\frac{x-5}{x^2-5x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: CC5028
Постройте график функции
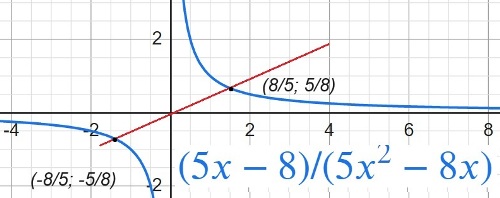
$y=\frac{5x-8}{5x^2-8x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 90DE2C
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}-x^2-2x-3\\-x-7\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-2,\\x<-2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 693B2F
Постройте график функции
y=3|x+8|−x2 −14x−48.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
1. Раскроем модуль, тем самым у нас получится система из двух возможных функций.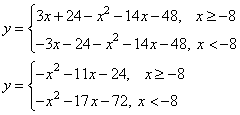
2. Строим график функций.
для первой корни -3;-8
для второй -8; -9
Поэтому отсекаем функции на областях, где они перекрываются по значениям, отсюда и -8 является критерием для наших вычислений в системе.
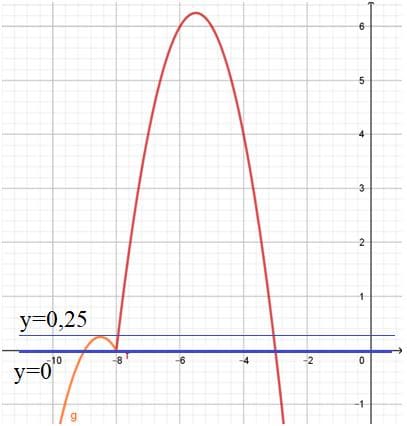
3. При этом прямая будет иметь три точки по вершине второй функции и параллельно оси x и по оси x.
![]()
вычисляем
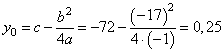
Ответ: 0 и 0,25
Номер: 8A552E
Постройте график функции
y=∣x2 +5x+4∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: B745DE
Постройте график функции
$y=\frac{3x+5}{3x^2+5x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
При решении уравнения знаменатель не должен быть равен 0. Значит
x(3x+5) ≠ 0
То есть получаем две точки, которые должны быть исключены из графика функции
х ≠ 0
х ≠ – 5/3
При этом линейная функция y=kx предполагает, что в любом случае ордината и абсцисса сойдутся в центре координат (0; 0)
Строим график
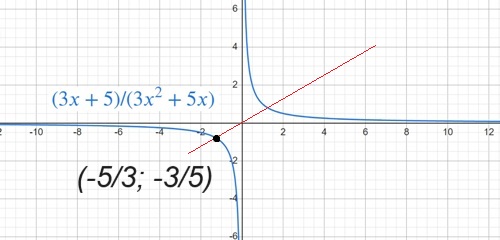
Переносим на него точку на абсциссе х = – 5/3, дабы исключить ее. В итоге получаем ординату -3/5
То есть появилось соотношение абсциссы и ординаты, дабы провести прямую через выколотую точку на графике и через координаты 0 и 0.
(3/5) /(5/3) = 9/25 = 0,36
Это и есть k
Ответ: 0.36
Номер: DA94D8
Постройте график функции
$y=\frac{{(x^2+4)}{(x-1)}}{1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 942ADF
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-10x+25\\x-2\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq4,\\x<4.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 67EDD6
Постройте график функции
y=3|x+7|−x2 −13x−42.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 34C6D0
Постройте график функции
$y=\frac{{(0,25x^2-x)}⋅{\vert x\vert}}{x-4}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 38C1D6
Постройте график функции
$y=\frac{2x+5}{2x^2+5x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
При решении уравнения знаменатель не должен быть равен 0. Значит
исключаем x ≠ 0
2x+5 ≠ 0
x ≠ -5/2.
При этом линейная функция y=kx предполагает, что в любом случае ордината и абсцисса сойдутся в центре координат (0; 0)
Строим график
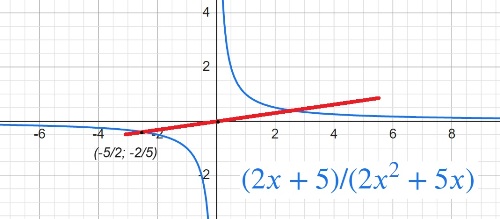
То есть появилось соотношение абсциссы и ординаты, дабы провести прямую через выколотую точку на графике и через координаты 0 и 0.
(2/5)/(5/2) = 4/25=0.16
Ответ: 0.16
Номер: 8E25DC
Постройте график функции
y=∣x2 +x−2∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: 8D22D9
Постройте график функции
$y=\frac12{(\left|\frac x{3,5}-\frac{3,5}x\right|+\frac x{3,5}+\frac{3,5}x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: F92250
Постройте график функции
y=∣x2 −9∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: B50355
Постройте график функции
y=x2 −11x−2|x−5|+30.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 1D555C
Постройте график функции
y=∣x2 −6x+5∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: 2E135D
Постройте график функции
$y=\frac{3,5{\vert x\vert}-1}{{\vert x\vert}-3,5x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 92985D
Постройте график функции
$y=\left\{\begin{array}{l}x^2+4x+4\text{ при }x\geq-3,\\-\frac3x\text{ при }x<-3.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 64F750
Постройте график функции
$y=\left\{\begin{array}{l}x^2-2x+1\text{ при }x\geq-2,\\-\frac{18}x\text{ при }x<-2.\end{array}\right.$.
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: FE4FAA
Постройте график функции
y=2|x−4|−x2 +9x−20.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 2F87A2
Постройте график функции
$y=\frac{{(x^2+0,25)}{(x+1)}}{-1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: E4E1A2
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}2,5x-3,5\\-2,5x+4\\1,5x-8\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<1,\\1\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 8228A6
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}3x-3\\-3x+8,5\\3,5x-11\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<2,\\2\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 4296C4
Постройте график функции
y=|x|⋅(x+1)−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
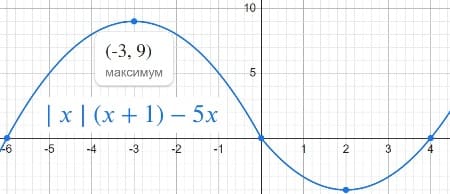
Две общие точки в вершине парабол
при х >0 y=x (x+1)−5x = x2 + x – 5x = x2 – 4x
х0 = – b/2a = 4/2 = 2
у0 = 22 – 4(2) = 4 – 8 = – 4
при x<0 y= – x (x+1)−5x = – x2 – x – 5x = – x2 – 6x
х0 = – b/2a = 6/( – 2) = – 3
у0 = –( – 3)2 – 6( – 3) = – 9 + 18 = 9
Ответ: – 4; 9
Номер: FD51C3
Постройте график функции
y=x|x|−|x|−2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Рассмотрим две параболы. Составив систему возможных функций
y=x|x|−|x|−2x
y=x2−x−2x
y=-x2+x−2x
y=x2−3x
y=-x2−x
2. Найдем корни
y=x2−3x (0; 3)
y=-x2−x (0; -1)
3. Найдем точки вершин парабол
Находим абсциссу вершины для первой функции x0=-b/2a = 3/2=1,5
Находим абсциссу вершины для второй функции x0=-b/2a = 1/-2=-0,5
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=2,25+(-3*1,5)=-2,25
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-0,25+(-1*-0,5)=-0,25+0,5=0,25
4. Строим график по получившимся значениям.
Две общие точки будут в случае если прямые проходят параллельно оси абсцисс и через вершины парабол.
m = -2,25 и m = 0,25
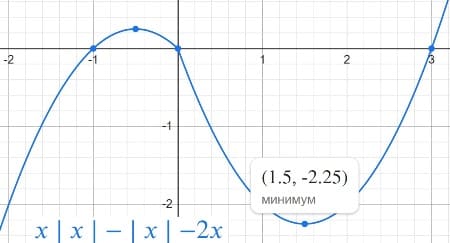
Ответ: -2,25 0,25
Номер: B6A5C4
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2+2x+1\\x+6\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq-2,\\x<-2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: BCD2CD
Постройте график функции
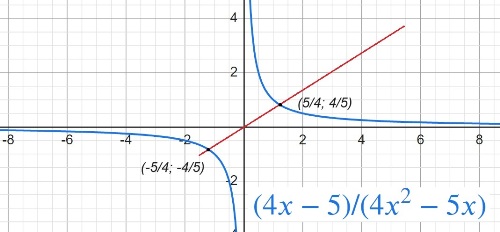
$y=\frac{4x-5}{4x^2-5x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 2939C4
Постройте график функции
$y=1-\frac{x+5}{x^2+5x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 2029CA
Постройте график функции
$y=\frac{6x+7}{6x^2+7x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
При решении уравнения знаменатель не должен быть равен 0. Значит
исключаем x ≠ 0
6x +7 ≠ 0
x ≠ -7/6.
При этом линейная функция y=kx предполагает, что в любом случае ордината и абсцисса сойдутся в центре координат (0; 0)
Строим график
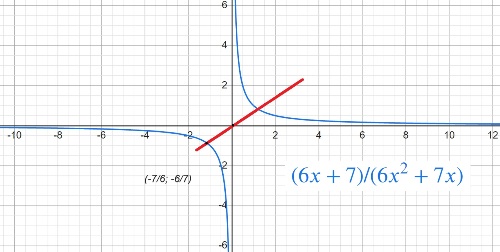
То есть появилось соотношение абсциссы и ординаты, дабы провести прямую через выколотую точку на графике и через координаты 0 и 0.
(6/7)/(7/6) = 36/49
Ответ: 36/49
Номер: DC01C3
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-4x+5\\x+3\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq1,\\x<1.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: 93A1CB
Постройте график функции
$y=\frac12{(\left|\frac x{1,5}-\frac{1,5}x\right|+\frac x{1,5}+\frac{1,5}x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 644EC3
Постройте график функции
y=|x|⋅(x−1)−5x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
1. Рассмотрим две параболы. Составив систему возможных функций
y=|x|⋅(x−1)−5x.
y=x2−x−5x
y=-x2−4x
2. Находим корни
y=x2−6x (0; 6)
y=-x2−4x (0; -4)
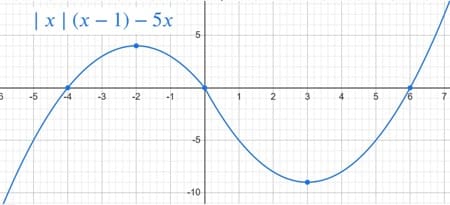
3.
Находим абсциссу вершины для первой функции x0=-b/2a = 6/2=3
Находим абсциссу вершины для второй функции x0=-b/2a = 4/-2=-2
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=9+(-6*3)=-9
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=-4+(-4*-2)=4
Ординаты и будут значением m
Ответ: -9 4
Номер: B1979C
Постройте график функции
$y=\left\{\begin{array}{l}x^2+2x+1\text{ при }x\geq-2,\\-\frac2x\text{ при }x<-2.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 2C6E96
Постройте график функции
$y=\left\{\begin{array}{ccc}\begin{array}{l}1,5x-1\\-1,5x+3\\3x-10,5\end{array}&\begin{array}{l}\text{при}\\\text{при}\\\text{при}\end{array}&\begin{array}{l}x<2,\\2\leq x\leq3,\\x>3.\end{array}\end{array}\begin{array}{l}\\\\\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ: ...
Номер: DCCD98
Постройте график функции
$y=\frac{{(x^2+2,25)}{(x-1)}}{1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: F8D6E6
Постройте график функции
$y=\frac{{(0,75x^2+2,25x)}⋅{\vert x\vert}}{x+3}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 59A6E0
Постройте график функции
$y=\frac{{(x^2+3x)}⋅{\vert x\vert}}{x+3}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: C415E2
Постройте график функции
$y=\frac{1,5{\vert x\vert}-1}{{\vert x\vert}-1,5x^2}$.
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 95BEE9
Постройте график функции
$y=\left\{\begin{array}{l}x^2+4x+4\text{ при }x\geq-5,\\-\frac{45}x\text{ при }x<-5.\end{array}\right.$
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 333EE6
Постройте график функции
$y=\frac12{(\left|\frac x{5,5}-\frac{5,5}x\right|+\frac x{5,5}+\frac{5,5}x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 3B00E8
Постройте график функции
$y=-5-\frac{x-1}{x^2-x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: 769468
Постройте график функции
$y=\frac{{(x^2+2,25)}{(x+1)}}{-1-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: B0AF6B
Постройте график функции
y=∣x2 +3x+2∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: 1A7E63
Постройте график функции
$y=-5-\frac{x-2}{x^2-2x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: C1266B
Постройте график функции
$y=\left\{\begin{array}{l}x^2+1\;\text{при }x\geq-1,\\-\frac4x\;\text{при }x<-1.\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: EFF36A
Постройте график функции
$y=\frac{{(x^2+1)}{(x+2)}}{-2-x}$.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 7FE635
Постройте график функции
$y=\frac{{(0,25x^2+0,5x)}⋅{\vert x\vert}}{x+2}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: D22637
Постройте график функции
y=∣x2 −x−2∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: D28F33
Постройте график функции
y=x|x|−|x|−6x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
y=x|x|−|x|−6x
1. Рассмотрим две параболы. Составив систему возможных функций
y=x2−7x
y=-x2−5x
2. Найдем корни.
y=x2−7x (0; 7)
y=-x2−5x (0; -5)
3. Найдем точки вершин парабол
Находим абсциссу вершины для первой функции x0=-b/2a = 7/2=3,5
Находим абсциссу вершины для второй функции x0=-b/2a = 5/-2=-2,5
Находим ординату вершины для первой функции y0=a(x02)+bx0+c=12,25+(-7*3,5)=-12,25
Находим ординату вершины для второй функции y0=a(x02)+bx0+c=6,25+(-5*-2,5)=6,25
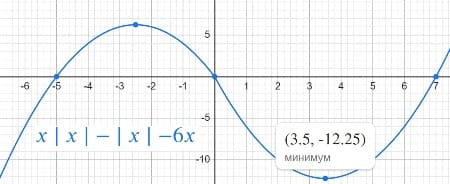
Две общие точки будут в случае если прямые проходят параллельно оси абсцисс и через вершины парабол.
m = -12,25 и m = 6,25
Ответ: -12,25 6,25
Номер: CE2631
Постройте график функции
$y=\left\{\begin{array}{l}x^2+2\;\text{при }x\geq-2,\\-\frac6x\;\text{при }x<-2.\end{array}\right.$
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: EC2E37
Постройте график функции
$y=\frac{9x+1}{9x^2+x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
При решении уравнения знаменатель не должен быть равен 0. Значит
исключаем x ≠ 0
и
9x +1 ≠ 0
x ≠ -1/9.
При этом линейная функция y=kx предполагает, что в любом случае ордината и абсцисса сойдутся в центре координат (0; 0)
Строим график
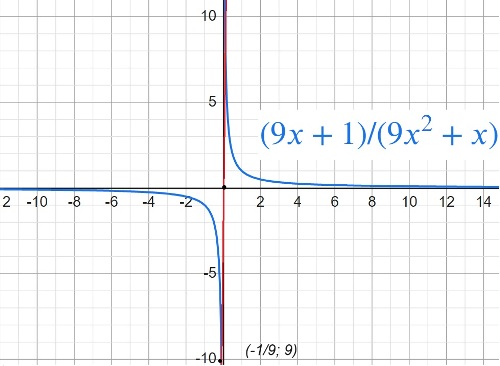
То есть появилось соотношение абсциссы и ординаты, дабы провести прямую через выколотую точку на графике и через координаты 0 и 0.
9/(1/9) = 81
Это и есть k
Ответ: 81
Номер: E34C3B
Постройте график функции
$y=3-\frac{x+5}{x^2+5x}$.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
...
Ответ: ...
Номер: E13E3C
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-6x+11\\x+3\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq2,\\x<2.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 38ED33
Постройте график функции
$y=\left\{\begin{array}{l}x^2+4x+4\text{ при }x\geq-4,\\-\frac{16}x\text{ при }x<-4.\end{array}\right.$.
и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
...
Ответ: ...
Номер: 83223D
Постройте график функции
y=∣x2 +4x−5∣.
Какое наибольшее число общих точек может иметь график данной функции
с прямой, параллельной оси абсцисс?
Решение:
...
Ответ: ...
Номер: 778885
Постройте график функции
$y={\{\begin{array}{ccc}\begin{array}{l}x^2-10x+27\\x\end{array}&\begin{array}{l}\text{при}\\\text{при}\end{array}&\begin{array}{l}x\geq4,\\x<4.\end{array}\end{array}}$
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
...
Ответ:
Номер: 7AC286
Постройте график функции
y=x2 −8x−4|x−3|+15.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 2CBB87
Постройте график функции
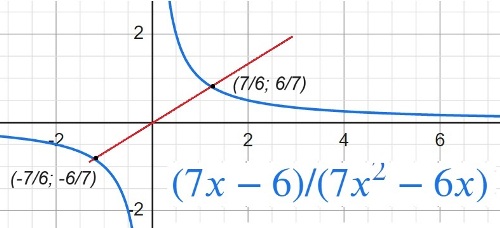
$y=\frac{7x-6}{7x^2-6x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: 24E78D
Постройте график функции
$y=\frac{{(0,75x^2-0,75x)}⋅{\vert x\vert}}{x-1}$.
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Решение:
...
Ответ: ...
Номер: 5A6286
Постройте график функции
$y=\frac12{(\left|\frac x6-\frac6x\right|+\frac x6+\frac6x)}$.
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
...
Ответ: ...
Номер: E0478E
Постройте график функции
y=x2 +11x−4|x+6|+30.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 6B948F
Убрали из банка ФИПИ:
![]() Постройте график функции
Постройте график функции
y=x2 −|4x+3|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 3EDA10
![]() Постройте график функции
Постройте график функции
y=x2 −|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 08081C
![]() Постройте график функции
Постройте график функции
y=x2 −|6x+5|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: D87710
![]() Постройте график функции
Постройте график функции
y=x2 −|4x+5|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: C1D0CF
![]() Постройте график функции
Постройте график функции
y=x2 −|4x+1|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 8AEE4B
![]() Постройте график функции
Постройте график функции
y=x2 −|8x+1|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 0DD22C
![]() Постройте график функции
Постройте график функции
y=x2 −|4x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: F745D2
![]() Постройте график функции
Постройте график функции
y=x2 −|2x+1|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: 950696
![]() Постройте график функции
Постройте график функции
y=x2 −|6x+1|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: D7A6CB
![]() Постройте график функции
Постройте график функции
y=x2 −|8x+3|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
...
Ответ: ...
Номер: A450AB

