В задании 20 на ОГЭ по математике нужно решить уравнение. Задание с развернутым ответом, решение записывается подробно. Задания разноплановые, если повезет - достанется простое, а не повезет - какая-нибудь дичь.
Варианты задания 20 из раздела ФИПИ алгебраические выражения дублируют задания из раздела уравнения и неравенства, так что их отдельно писать нет смысла. Вообще, много заданий у ФИПИ дублируется и находится не на своем месте. Этот бардак мы превратили в порядок у себя на ГДЗответ ру. Пользуйтесь!
Варианты задания 20 из раздела ФИПИ уравнения и неравенства, развернутый ответ
2026 год 10 прототипов + 60 заданий
Дайте развернутый ответ.
Решите неравенство ![]()
Решение:
...
Ответ:
Номер: F5A849
Решите неравенство 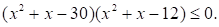
Решение:
...
Ответ:
Номер: 166F42
Решите неравенство 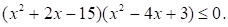
Решение:
...
Ответ:
Номер: 2A0B4A
Решите неравенство 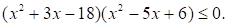
Решение:
...
Ответ:
Номер: 7585FE
Решите неравенство 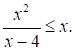
Решение:
...
Ответ:
Номер: D842F6
Решите неравенство 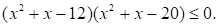
Решение:
...
Ответ:
Номер: A2F1F4
Решите неравенство 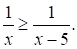
Решение:
...
Ответ:
Номер: A5ABF3
Решите неравенство 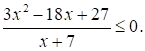
Решение:
...
Ответ:
Номер: CDC8F5
Решите неравенство 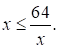
Решение:
...
Ответ:
Номер: 6FF9F5
Решите неравенство 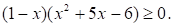
Решение:
...
Ответ:
Номер: 678BFE
Решите неравенство 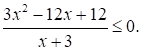
Решение:
...
Ответ:
Номер: C7CC09
Решите неравенство 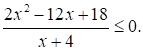
Решение:
...
Ответ:
Номер: 7DD37C
Решите неравенство 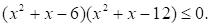
Решение:
...
Ответ:
Номер: E31F7D
Решите неравенство 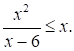
Решение:
...
Ответ:
Номер: 8CC574
Решите неравенство 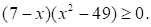
Решение:
...
Ответ:
Номер: F05EB9
Решите неравенство 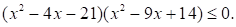
Решение:
...
Ответ:
Номер: 6F56B0
Решите неравенство 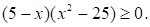
Решение:
...
Ответ:
Номер: 04A113
Решите неравенство 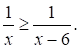
Решение:
...
Ответ:
Номер: 6CE616
Решите неравенство 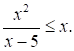
Решение:
...
Ответ:
Номер: 0B532B
Решите неравенство 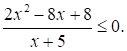
Решение:
...
Ответ:
Номер: 0B612B
Решите неравенство 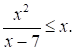
Решение:
...
Ответ:
Номер: 736422
Решите неравенство 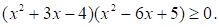
Решение:
...
Ответ:
Номер: C03D26
Решите неравенство 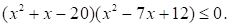
Решение:
...
Ответ:
Номер: 61CB27
Решите неравенство 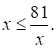
Решение:
...
Ответ:
Номер: F9C4D8
Решите неравенство 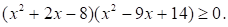
Решение:
...
Ответ:
Номер: 05B7D9
Решите неравенство ![]()
Решение:
...
Ответ:
Номер: 7B31DA
Решите неравенство 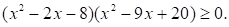
Решение:
...
Ответ:
Номер: B59AD9
Решите неравенство 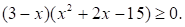
Решение:
...
Ответ:
Номер: 110FD7
Решите неравенство 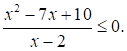
Решение:
...
Ответ:
Номер: A510D6
Решите неравенство 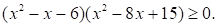
Решение:
...
Ответ:
Номер: 8E13D9
Решите неравенство 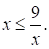
Решение:
...
Ответ:
Номер: 78A058
Решите неравенство 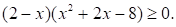
Решение:
...
Ответ:
Номер: BCC653
Решите неравенство 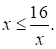
Решение:
...
Ответ:
Номер: AF5155
Решите неравенство 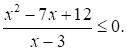
Решение:
...
Ответ:
Номер: 6E7950
Решите неравенство 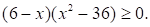
Решение:
...
Ответ:
Номер: 679557
Решите неравенство 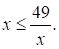
Решение:
...
Ответ:
Номер: 80E8AF
Решите неравенство 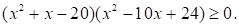
Решение:
...
Ответ:
Номер: 0982C0
Решите неравенство 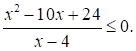
Решение:
...
Ответ:
Номер: 35E1C0
Решите неравенство 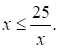
Решение:
...
Ответ:
Номер: B62A96
Решите неравенство 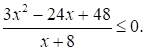
Решение:
...
Ответ:
Номер: D9F592
Решите неравенство 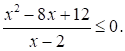
Решение:
...
Ответ:
Номер: 614C93
Решите неравенство 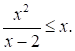
Решение:
...
Ответ:
Номер: 0DB1E0
Решите неравенство 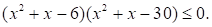
Решение:
...
Ответ:
Номер: AD29E3
Решите неравенство 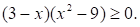
Решение:
...
Ответ:
Номер: 9329E9
Решите неравенство 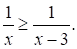
Решение:
...
Ответ:
Номер: E5C8E9
Решите неравенство 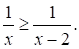
Решение:
...
Ответ:
Номер: 06106A
Решите неравенство 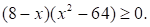
Решение:
...
Ответ:
Номер: 728662
Решите неравенство 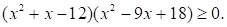
Решение:
...
Ответ:
Номер: 999165
Решите неравенство 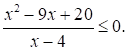
Решение:
...
Ответ:
Номер: 83EB65
Решите неравенство 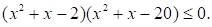
Решение:
...
Ответ:
Номер: 225137
Решите неравенство 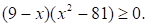
Решение:
...
Ответ:
Номер: C7733C
Решите неравенство 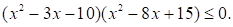
Решение:
...
Ответ:
Номер: E7C13F
Решите неравенство 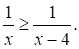
Решение:
...
Ответ:
Номер: E18C35
Решите неравенство 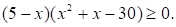
Решение:
...
Ответ:
Номер: 88833C
Решите неравенство 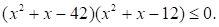
Решение:
...
Ответ:
Номер: 805539
Решите неравенство 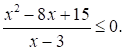
Решение:
...
Ответ:
Номер: 111583
Решите неравенство 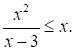
Решение:
...
Ответ:
Номер: 2FEB86
Решите неравенство 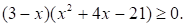
Решение:
...
Ответ:
Номер: 248786
Решите неравенство 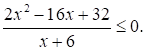
Решение:
...
Ответ:
Номер: D0878B
Решите неравенство 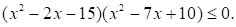
Решение:
...
Ответ:
Номер: 878188
2025 год
Решите неравенство `-12/(x^2-7x-8)≤0`
Решение:
`-12/(x^2-7x-8)≤0` x≠-1, x≠8
: (-1)
`12/(x^2-7x-8)≥0`, знаменатель должен быть больше 0
`x^2-7x-8>0`
Найдем нули
`x^2-7x-8=0`
`x*(x+1)-8*(x+1)=0`
`(x+1)(x-8)=0`
`x_1=-1`
`x_2=8`
График квадратного уравнения - парабола, ветви направлены вверх (отмечаем нули и знаки промежутков на числовой прямой), значит положительные значения в промежутках (-∞;-1) и (8;+∞)
Ответ: (-∞;-1) ⋃ (8;+∞)
Номер: AB3F33
Решите уравнение $\frac1{x^2}+\frac2x-3=0$.
Решение:
1 способ
`1/(x^2)+2/x-3=0`
x≠0
Пусть `t=1/x` , тогда уравнение принимает вид `t^2+2t-3=0`, находим корни
D=b2-4ac=4-4*1*-3=4+12=16
`t1=(-2+4)/(2*1)=1 `
`t2=(-2-4)/(2*1)=-6/2=-3`
Уравнение вида `1/x=1` имеет корень x=1
Уравнение вида `1/x=-3` имеет корень `x=-1/3`
Ответ: 1 -1/3
2 способ
`1/(x^2)+2/x-3=0`
x≠0
`(1+2х)/(x^2)=3`
`1+2х = 3*x^2`
`3*x^2-2х-1 = 0`
D=b2-4ac=4-4*3*-1=4+12=16
`x1=(2+4)/(2*3)=6/6=1 `
`x2=(2-4)/(2*3)=-2/6=- 1/3`
Ответ: 1 -1/3
Номер: E5318F
Решите уравнение $\frac1{{(x-1)}^2}+\frac2{x-1}-3=0$.
Решение:
1 способ
`1/(x-1)^2+2/(x-1)-3=0`
x≠1
Пусть `t=1/(x-1)` , тогда уравнение принимает вид `t^2+2t-3=0`, находим корни
D=b2-4ac=4-4*1*-3=4+12=16
`t1=(-2+4)/(2*1)=1 `
`t2=(-2-4)/(2*1)=-6/2=-3`
Уравнение вида `1/(x-1)=1` имеет корень x=2
Уравнение вида `1/(x-1)=-3`
`(x-1)=-1/3`
`x=1-1/3`
`x=2/3`
имеет корень `x=2/3`
Ответ: 2 2/3
2 способ
`1/(x-1)^2+(2(x-1))/(x-1)^2-3=0`
x≠1
`(1+2(x-1))/(x-1)^2=3`
`1+2(x-1)=3*(x-1)^2`
`1+2x-2=3*(x^2-1x-1x+1)`
`1+2x-2= 3*x^2-6x+3`
`3*x^2-8x+4=0`
D=b2-4ac=64-4*3*4=64-48=16
`x1=(8+4)/(2*3)=2 `
`x2=(8-4)/(2*3)=4/6=2/3`
Ответ: 2 2/3
Номер: 29978C
Решите уравнение $\frac1{x^2}-\frac1x-6=0$.
Решение:
1 способ
`1/x^2-1/x-6=0`
x≠0
Пусть `t=1/x` , тогда уравнение принимает вид `t^2+t-6=0`, , находим корни
D=b2-4ac=1-4*1*-6=1+24=25
`t1=(-1+5)/(2*1)=2`
`t2=(-1-5)/(2*1)=-6/2=-3`
Уравнение вида `1/x=2` имеет корень x=0,5
Уравнение вида `1/x=-3` имеет корень `x=-1/3`
Ответ: 1/3 -0.5
2 способ
`1/x^2-1/x-6=0`
x≠0
`(1-x))/x^2=6`
`6x^2+x-1=0`
D=b2-4ac=1--4*6*-1=25
`x1=(-1+5)/(2*6)=4/12=1/3 `
`x2=(-1-5)/(2*6)=-6/12=-0.5`
Ответ: 1/3 -0.5
Номер: 7033CA
Решите уравнение $\frac1{{(x-2)}^2}-\frac1{x-2}-6=0$.
Решение:
1 способ
`1/(x-2)^2-1/(x-2)-6=0`
x≠2
Пусть `t=1/(x-2)`, тогда уравнение принимает вид `t^2-t-6=0`, находим корни
D=b2-4ac=1-4*1*-6=1+24=25
`t1=(1+5)/(2*1)=3`
`t2=(1-5)/(2*1)=-4/2=-2`
Уравнение вида `1/(x-2)=3` имеет корень
`x-2=1/3`
x=2 1/3
Уравнение вида `1/(x-2)=-2` имеет корень
`x-2=-1/2`
x=1,5
Ответ: 2 1/3 1,5
2 способ
`1/(x-2)^2-1/(x-2)-6=0`
x≠2
`(1-(x-2))/(x-2)^2=6`
`1-x+2 = 6x^2-24x+24`
`6x^2-23x+21=0`
D=b2-4ac=529-4*6*21=529-504=25
`x1=(23+5)/(2*6)=2 1/3 `
`x2=(23-5)/(2*6)=18/12=1.5`
Ответ: 2 1/3, 1,5
Номер: 758215
Решите уравнение $\frac1{x^2}+\frac3x-10=0$.
Решение:
`1/(x^2) + 3/x -10 = 0`
`1/(x^2) + (3x)/(x^2) - (10x^2)/(x^2) = 0` ОДЗ: x ≠ 0
`1 + 3x – 10x^2 = 0`
`-10x^2 + 3x + 1=0 *-1`
`10x^2 – 3x -1 = 0`
`D = (-3^2) – 4 * 10 * (-1) = 49`
X1 = `(3-7)/(10*2) = (-1)/5 = -0, 2`
X2 = `(3+7)/(10*2) = 1/2 = 0, 5`
Ответ: -0,2 0,5
Номер: DA1518
Решите уравнение $\frac1{{(x-1)}^2}+\frac3{x-1}-10=0$.
Решение:
`1/(x-1)^2+3/(x-1)-10=0`
x≠1
Пусть `t=1/(x-1)`, тогда уравнение принимает вид `t^2+3t-10=0`, находим корни
D=b2-4ac=9-4*1*-10=9+40=49
`t1=(-3+7)/(2*1)=2`
`t2=(-3-7)/(2*1)=-5`
Уравнение вида `1/(x-1)=2` имеет корень
`x-1=1/2`
x=1,5
Уравнение вида `1/(x-1)=-5` имеет корень
`x-1=-1/5`
x=0,8
Ответ: 0,8 1,5
Номер: 61F9E5
Решите уравнение $\frac1{x^2}-\frac3x-4=0$.
Решение:
`1/(x^2) - 3/x - 4 = 0`
x≠0
`1/(x^2) - (3x)/(x^2) - (4x^2)/(x^2) = 0` ОДЗ: x ≠ 0
`1 - 3x – 4x^2 = 0`
`-4x^2 - 3x + 1=0 *-1`
`4x^2 + 3x - 1 = 0`
`D = 3^2 – 4 * 4 * (-1) = 25`
X1 = `(-3-5)/(4*2) = (-8)/8 = -1`
X2 = `(-3+5)/(4*2) = 2/8 = 0, 25`
Ответ: -1 0,25
Номер: 74F954
Решите уравнение $\frac1{{(x-3)}^2}-\frac3{x-3}-4=0$.
Решение:
`1/(x-3)^2-3/(x-3)-4=0`
x≠3
Пусть `t=1/(x-3)`, тогда уравнение принимает вид `t^2-3t-4=0`, находим корни
D=b2-4ac=9-4*1*-4=9+16=25
`t1=(3+5)/(2*1)=4`
`t2=(3-5)/(2*1)=-1`
Уравнение вида `1/(x-3)=4` имеет корень
`x-3=1/4`
x=3,25
Уравнение вида `1/(x-3)=1` имеет корень
`x-3=-1`
x=2
Ответ: 2 3,25
Номер: C0319F
Решите уравнение $\frac1{x^2}+\frac4x-12=0$.
Решение:
`1/(x^2) + 4/x - 12 = 0`
x≠0
`1/(x^2) + (4x)/(x^2) - (12x^2)/(x^2) = 0` ОДЗ: x ≠ 0
`1 + 4x – 12x^2 = 0`
`-12x^2 + 4x + 1=0 *-1`
`12x^2 - 4x - 1 = 0`
`D = (-42) – 4 * 12 * (-1) = 64`
X1 = `(4-8)/(12*2) = (-4)/24 = (-1)/6`
X2 = `(4+8)/(12*2) = 12/24 = 0, 5`
Ответ: -1/6 0,5
Номер: 7A30BC
Решите уравнение $\frac1{{(x-1)}^2}+\frac4{x-1}-12=0$.
Решение:
`1/(x-1)^2+4/(x-1)-12=0`
x≠1
Пусть `t=1/(x-1)`, тогда уравнение принимает вид `t^2+4t-12=0`, находим корни
D=b2-4ac=16-4*1*-12=16+48=64
`t1=(-4+8)/(2*1)=2`
`t2=(-4-8)/(2*1)=-6`
Уравнение вида `1/(x-1)=2` имеет корень
`x-1=1/2`
x=1,5
Уравнение вида `1/(x-1)=-6` имеет корень
`x-1=-1/6`
x=5/6
Ответ: 5/6 1,5
Номер: 605EEE
Решите уравнение x(x2 +2x+1)=2(x+1).
Решение:
х3 + 2х2 + х = 2х + 2
х3 + 2х2 + х - 2х - 2 = 0
х3 + 2х2 - х - 2 = 0
х2(х+2) - (х+2) = 0
(х+2)(х2 - 1) = 0
(х+2) = 0 х2 - 1 = 0
х = -2 х = ±1
Ответ: -2 -1 1
Номер: FCC5F4
Решите уравнение (x-1)(x2 +4x+4)=4(x+2).
Решение:
Преобразуем уравнение:
(x-1)(x2 +4x+4)=4(x+2)
(x-1)(x +2)2=4(x+2)
(x-1)(x +2)(x +2)-4(x+2) = 0
Вынесем за скобки (x+2)
(x+2)((x-1)(x +2)-4)=0
(x+2)(x2+2x-x-2-4)=0
(x+2)(x2+x-6)=0
Теперь найдем корни из двух множителей (x+2) и (x2+x-6)
x+2 = 0
x1=-2
x2+x-6=0
D=b2-4ac=1-4*1*-6=1+24=25
x2=(-1+5)/(2*1)=4/2=2
x3=(-1-5)/(2*1)=-6/2=-3
Ответ: -3 -2 2
Номер: 344BE0
Решите уравнение x(x2 +6x+9)=4(x+3).
Решение:
Преобразуем уравнение:
x(x+3)2=4(x+3)
x(x+3)(x+3)-4(x+3)=0
(x+3)(x(x+3)-4)=0
(x+3)(x2+3x-4)=0
Теперь найдем корни из двух множителей (x+3) и (x2+3x-4)
x+3 = 0
x1=-3
x2+3x-4 = 0
D=b2-4ac=9-4*1*-4=9+16=25
x2=(-3+5)/(2*1)=2/2=1
x3=(-3-5)/(2*1)=-8/2=-4
Ответ: -4 -3 1
Номер: 176E9F
Решите уравнение (x-1)(x2 +8x+16)=6(x+4).
Решение:
х3 + 8х2 + 16х - х2 - 8х - 16 = 6х + 24
х3 + 8х2 + 16х - х2 - 8х - 16 - 6х - 24 = 0
х3 + 7х2 + 2х - 40 = 0
х3 - 2х2 + 9х2 - 18х +20х - 40 = 0
х2 (х-2) + 9х (х-2) + 20 (х-2) = 0
(х-2)(х2 + 9х + 20) = 0
(х-2)(х2 + 5х + 4х + 20) = 0
(х-2)(х(х+5) + 4(х+5)) = 0
(х-2)(х+5)(х+4) = 0
(х-2) = 0 (х+5) = 0 (х+4) = 0
х = 2 х = -5 х = -4
Ответ: -5 -4 2
Номер: 541E78
Решите уравнение x(x2 +2x+1)=6(x+1).
Решение:
x(x+1)2=6(x+1)
x(x+1)(x+1)-6(x+1)=0
(x+1)(x(x+1)-6)=0
(x+1)(x2+x-6)=0
Теперь найдем корни из двух множителей (x+1) и (x2+x-6)
x+1 = 0
x2=-1
x2+x-6 = 0
D=b2-4ac=1-4*1*-6=1+24=25
x2=(-1+5)/(2*1)=4/2=2
x3=(-1-5)/(2*1)=-6/2=-3
Ответ: -3 -1 2
Номер: 8FB942
Решите уравнение (x-1)(x2 +6x+9)=5(x+3).
Решение:
`(x-1)(x^2 +6x+9)=5(x+3)`
`(x-1)(x+3)^2= 5(x+3)`
`(x-1)(x+3)^2-5(x+3)=0`
`(x+3)((x-1)(x+3)-5)=0`
`(x+3)(x^2+3x-x-3-5)=0`
`(x+3)(x^2+2x-8)=0`
`x+3=0` или `x^2+2x-8=0`
`x=-3`
`D=2^2-4*1*(-8)=4+32=36>0`, 2 корня
`x_1= (-2- sqrt36)/2 = (-2-6)/2 = -8/2= -4`
`x_2= (-2+6)/2 = 4/2 = 2`
Ответ: -4 -3 2
Номер: 9947F1
Решите уравнение (x-2)(x2 +8x+16)=7(x+4).
Решение:
`(x-2)(x^2 +8x+16)=7(x+4)`
`(x-2)(x+4)^2= 7(x+4)`
`(x+4)((x-2)(x+4)-7)=0`
`(x+4)(x^2+4x-2x-8-7)=0`
`(x+4)(x^2+2x-15)=0`
`x+4=0` или `x^2+2x-15=0`
`x=-4`
`D=2^2-4*1*(-15)=4+60=64>0`, 2 корня
`x_1= (-2- sqrt64)/2 = (-2-8)/2 = -10/2= -5`
`x_2= (-2+8)/2 = 62 = 3`
Ответ: -5 -4 3
Номер: 0DC884
Решите уравнение x(x2 +4x+4)=3(x+2).
Решение:
x(x+2)2=3(x+2)
x(x+2)(x+2)-3(x+2)=0
(x+2)(x(x+2)-3)=0
(x+2)(x2+2x-3)=0
Теперь найдем корни из двух множителей (x+2) и (x2+2x-3)
x+2 = 0
x1=-2
x2+2x-3 = 0
D=b2-4ac=4-4*1*-3=4+12=16
x2=(-2+4)/(2*1)=2/2=1
x3=(-2-4)/(2*1)=-6/2=-3
Ответ: -3 -2 1
Номер: 984D22
Решите уравнение (x-2)(x2 +2x+1)=4(x+1).
Решение:
(x-2)(x+1)2=4(x+1)
(x-2)(x+1)(x+1)-4(x+1)=0
(x-2)(x+1)((x+1)-4)=0
(x+2)(x+1)(x-3)=0
Теперь найдем корни из двух множителей (x+2), (x+1) и (x-3)
x+2 = 0
x1=-2
x+1 = 0
x2=-1
x-3 = 0
x3=3
Ответ: -2 -1 3
Номер: C63018
Решите уравнение (x-2)(x2 +6x+9)=6(x+3).
Решение:
(x-2)(x+1)2=4(x+1)
(x-2)(x+1)(x+1)-4(x+1)=0
(x-2)(x+1)((x+1)-4)=0
(x+2)(x+1)(x-3)=0
Теперь найдем корни из двух множителей (x+2), (x+1) и (x-3)
x+2 = 0
x1=-2
x+1 = 0
x2=-1
x-3 = 0
x3=3
Ответ: -4 -3 3
Номер: AF5B2C
Решите уравнение (x+2)4 -4(x+2)2 -5=0.
Решение:
(x+2)4 -4(x+2)2 -5=0
Пусть t=(x+2)2 , тогда уравнение принимает вид `t^2-4t-5=0`, находим корни
D=b2-4ac=16-4*1*-5=16+20=36
t1 = (4+6)/(2*1)=10/2=5
t2 = (4-2)/(2*1)=-2/2=-1
Находим корни для уравнений:
-1=(x+2)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
5=(x+2)2
(x+2)(x+2)-5=0
x2+2x+2x+4-5=0
x2+4x-1=0
D=b2-4ac=16-4*1*-1=16+4=20
x1=(-4+√20)/(2*1)=(-4+2√5)/(2*1)=-2+√5
x2=(-4-√20)/(2*1)=(-4-2√5)/(2*1)=-2-√5
Ответ: -√5-2 √5 -2
Номер: 8941C2
Решите уравнение (x+1)4 +(x+1)2 -6=0.
Решение:
t2 + t - 6 = 0
t1 = -3
t2 = 2
(x+1)2 = -3
(x+1)2 = 2
x ∉ R
x1 = -√2-1
x2 = √2-1
Ответ: -√2-1 √2-1
Номер: 5DDDE2
Решите уравнение (x+3)4 +2(x+3)2 -8=0.
Решение:
(x+3)4 +2(x+3)2 -8=0
Пусть t=(x+3)2 , тогда уравнение принимает вид `t^2+2t-8=0`, находим корни
D=b2-4ac=4-4*1*-8=4+32=36
t1 = (-2+6)/(2*1)=4/2=2
t2 = (-2-6)/(2*1)=-8/2=-4
Находим корни для уравнений:
-4=(x+3)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
2=(x+3)2
(x+3)(x+3)-2=0
x2+3x+3x+9-2=0
x2+6x+7=0
D=b2-4ac=36-4*1*7=36+28=8
x1=(-6+√8)/(2*1)=(-6+2√2)/(2*1)=-3+√2
x2=(-6-√8)/(2*1)=(-6-2√2)/(2*1)=-3-√2
Ответ: -√2-3 √2-3
Номер: 571126
Решите уравнение (x-1)4 -2(x-1)2 -3=0.
Решение:
(x-1)4 -2(x-1)2 -3=0
Пусть t=(x-1)2 , тогда уравнение принимает вид `t^2-2t-3=0`, находим корни
D=b2-4ac=4-4*1*-3=4+12=16
t1=(2+√16)/(2*1)=(2+4)/2=3
t2=(2-√16)/(2*1)=(2-4)/2=-1
Находим корни для уравнений:
-1=(x-1)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
3=(x-1)2
(x-1)(x-1)-3=0
x2-x-x+1-3=0
x2-2x-2=0
D=b2-4ac=4-4*1*-2=12
x1=(2+√12)/(2*1)=(2+2√3)/(2*1)=1+√3
x2=(2-√12)/(2*1)=(2-2√3)/(2*1)=1-√3
Ответ: -√3+1 √3+1
Номер: EDFB3F
Решите уравнение (x-2)4 -(x-2)2 -6=0.
Решение:
(x-2)4 -(x-2)2 -6=0
Пусть t=(x-2)2 , тогда уравнение принимает вид `t^2-t-6=0`, находим корни
D=b2-4ac=1-4*1*-6=1+24=25
t1=(1+√25)/(2*1)=(1+5)/2=3
t2=(1-√25)/(2*1)=(1-5)/2=-2
Находим корни для уравнений:
-2=(x-2)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
3=(x-2)2
(x-2)(x-2)-3=0
x2-2x-2x+4-3=0
x2-4x+1=0
D=b2-4ac=16-4*1*1=12
x1=(4+√12)/(2*1)=(4+2√3)/(2*1)=2+√3
x2=(4-√12)/(2*1)=(4-2√3)/(2*1)=2-√3
Ответ: -√3+2 √3+2
Номер: 154A3F
Решите уравнение (x-3)4 -3(x-3)2 -10=0.
Решение:
(x-3)4 -3(x-3)2 -10=0
Пусть t=(x-3)2 , тогда уравнение принимает вид `t^2-3t-10=0`, находим корни
D=b2-4ac=9-4*1*-40=9+40=49
t1=(3+√49)/(2*1)=(3+7)/2=5
t2=(3-√49)/(2*1)=(3-7)/2=-2
Находим корни для уравнений:
-2=(x-3)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
5=(x-3)2
(x-3)(x-3)-5=0
x2-3x-3x+9-5=0
x2-6x+4=0
D=b2-4ac=36-4*1*4=20
x1=(6+√20)/(2*1)=(6+2√5)/(2*1)=3+√5
x2=(6-√20)/(2*1)=(6-2√5)/(2*1)=3-√5
Ответ: -√5+3 √5+3
Номер: 93098E
Решите уравнение (x+4)4 -6(x+4)2 -7=0.
Решение:
(x+4)4 -6(x+4)2 -7=0
Пусть t=(x+4)2 , тогда уравнение принимает вид `t^2-6t-7=0`, находим корни
D=b2-4ac=36-4*1*-7=36+28=64
t1=(6+√64)/(2*1)=(6+8)/2=7
t2=(6-√64)/(2*1)=(6-8)/2=-1
Находим корни для уравнений:
-1=(x+4)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
7=(x+4)2
(x+4)(x+4)-7=0
x2+4x+4x+16-7=0
x2+8x+9=0
D=b2-4ac=64-4*1*9=28
x1=(-8+√28)/(2*1)=(-8+2√7)/(2*1)=-4+√7
x2=(-8-√28)/(2*1)=(-8-2√7)/(2*1)=-4-√7
Ответ: -√7-4 √7-4
Номер: 27B06C
Решите уравнение (x-4)4 -4(x-4)2 -21=0.
Решение:
(x-4)4 -4(x-4)2 -21=0
Пусть t=(x-4)2 , тогда уравнение принимает вид `t^2-4t-21=0`, находим корни
D=b2-4ac=16-4*1*-21=100
t1=(4+√100)/(2*1)=(4+10)/2=7
t2=(4-√100)/(2*1)=(4-10)/2=-3
Находим корни для уравнений:
-3=(x-4)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
7=(x-4)2
(x-4)(x-4)-7=0
x2-4x-4x+16-7=0
x2-8x+9=0
D=b2-4ac=64-4*1*9=28
x1=(8+√28)/(2*1)=(8+2√7)/(2*1)=4+√7
x2=(8-√28)/(2*1)=(8-2√7)/(2*1)=4-√7
Ответ: -√7+4 √7+4
Номер: CC11F7
Решите уравнение (x+2)4 +(x+2)2 -12=0.
Решение:
(x+2)4 +(x+2)2 -12=0
Пусть t=(x+2)2 , тогда уравнение принимает вид `t^2+t-12=0`, находим корни
D=b2-4ac=1-4*1*-12=49
t1=(-1+√49)/(2*1)=(-1+7)/2=3
t2=(-1-√49)/(2*1)=(-1-7)/2=-4
Находим корни для уравнений:
-4=(x+2)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
3=(x+2)2
(x+2)(x+2)-3=0
x2+2x+2x+4-3=0
x2+4x+1=0
D=b2-4ac=16-4*1*1=12
x1=(-4+√12)/(2*1)=(-4+2√3)/(2*1)=-2+√3
x2=(-4-√12)/(2*1)=(-4-2√3)/(2*1)=-2-√3
Ответ: -√3-2 √3-2
Номер: 9C0922
Решите уравнение (x-2)4 +3(x-2)2 -10=0.
Решение:
(x-2)4 +3(x-2)2 -10=0
Пусть t=(x-2)2 , тогда уравнение принимает вид `t^2+3t-10=0`, находим корни
D=b2-4ac=9-4*1*-10=49
t1=(-3+√49)/(2*1)=(-3+7)/2=2
t2=(-3-√49)/(2*1)=(-3-7)/2=-5
Находим корни для уравнений:
-5=(x-2)2
не имеет корней так как квадрат не может быть отрицательным числом. Рассмотрим второе уравнение.
2=(x-2)2
(x-2)(x-2)-2=0
x2-2x-2x+4-2=0
x2-4x+2=0
D=b2-4ac=16-4*1*2=8
x1=(4+√8)/(2*1)=(4+2√2)/(2*1)=2+√2
x2=(4-√8)/(2*1)=(4-2√2)/(2*1)=2-√2
Ответ: -√2+2 √2+2
Номер: 06F70C
Решите неравенство $\frac{-12}{{(x-1)}^2-2}\geq0$.
Решение:
x ≠ -√2 + 1, x ≠ √2 + 1
$\frac{-12}{x^2-2x+1-2}\geq0$
$\frac{-12}{x^2-2x-1}\geq0$
$\frac1{x^2-2x-1}\leq0$
x2 - 2x - 1 < 0
Запишем соответствующее квадратное уравнение
x2 - 2x - 1 = 0
х1 = 1+√2
х2 = 1-√2
Разложим выражение на множители, используя х1 и х2.
(х-(1+√2))(х-(1-√2)) < 0
(х - 1-√2)(х - 1+√2) < 0
Рассмотрим все возможные случаи
$\left\{\begin{array}{l}(х-1-\sqrt2)<0\\(х-1+\sqrt2)>0\end{array}\right.$
$\left\{\begin{array}{l}(х-1-\sqrt2)>0\\(х-1+\sqrt2)<0\end{array}\right.$
$\left\{\begin{array}{l}х<1+\sqrt2\\х>1-\sqrt2\end{array}\right.$
$\left\{\begin{array}{l}х>1+\sqrt2\\х<1-\sqrt2\end{array}\right.$
x∈{1-√2, 1+√2>
∅
Ответ: x∈(1-√2, 1+√2)
Номер: 131EDB
Решите неравенство $\frac{-11}{{(x-2)}^2-3}\geq0$.
Решение:
- 11 ≥ 0
х2 - 4х + 1
- 11 ≥ 0
(х - 2 + √3) (х - 2 - √3)
То есть знаменатель х2 - 4х + 1 должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
х2 - 4х + 1 = 0
D=b2-4ac=16-4*1*1=12
x1=(4+√12)/(2*1)=(4+2√3)/(2*1)=2+√3
x2=(4-√12)/(2*1)=(4-2√3)/(2*1)=2-√3
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(2-√3, 2+√3)
альтернативный вид: (х| 2-√3 < x < 2+√3)
Номер: 8CCFF9
Решите неравенство $\frac{-10}{{(x-3)}^2-5}\geq0$.
Решение:
`(-10)/((x-3)^2-5)≥0`
То есть знаменатель `(x-3)^2-5` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x-3)(x-3)-5=0
x2-3x-3x+9-5=0
x2-6x+4=0
D=b2-4ac=36-4*1*4=20
x1=(6+√20)/(2*1)=(6+2√5)/(2*1)=3+√5
x2=(6-√20)/(2*1)=(6-2√5)/(2*1)=3-√5
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(3-√5, 3+√5)
Номер: C62D48
Решите неравенство $\frac{-13}{{(x-4)}^2-6}\geq0$.
Решение:
`(-13)/((x-4)^2-6)≥0`
То есть знаменатель `(x-4)^2-6` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x-4)(x-4)-6=0
x2-4x-4x+16-6=0
x2-8x+10=0
D=b2-4ac=64-4*1*10=24
x1=(8+√24)/(2*1)=(8+2√6)/(2*1)=4+√6
x2=(8-√24)/(2*1)=(8-2√6)/(2*1)=4-√6
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(4-√6, 4+√6)
Номер: 3F88F1
Решите неравенство $\frac{-14}{{(x-5)}^2-2}\geq0.$.
Решение:
`(-14)/((x-5)^2-2)≥0`
То есть знаменатель `(x-5)^2-2` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x-5)(x-5)-2=0
x2-5x-5x+25-2=0
x2-10x+23=0
D=b2-4ac=100-4*1*23=8
x1=(10+√8)/(2*1)=(10+2√2)/(2*1)=5+√2
x2=(10-√8)/(2*1)=(10-2√2)/(2*1)=5-√2
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(5-√2, 5+√2)
Номер: 41D970
Решите неравенство $\frac{-15}{{(x+1)}^2-3}\geq0$.
Решение:
`(-15)/((x+1)^2-3)≥0`
То есть знаменатель `(x+1)^2-3` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x+1)(x+1)-3=0
x2+x+x+1-3=0
x2+2x-2=0
D=b2-4ac=4-4*1*-2=12
x1=(-2+√12)/(2*1)=(-2+2√3)/(2*1)=-1+√3
x2=(-2-√12)/(2*1)=(-2-2√3)/(2*1)=-1-√3
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(-1-√3, -1+√3)
Номер: 2D3686
Решите неравенство $\frac{-16}{{(x+2)}^2-5}\geq0.$.
Решение:
`(-16)/((x+2)^2-5)≥0`
То есть знаменатель `(x+2)^2-5` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x+2)(x+2)-5=0
x2+2x+2x+4-5=0
x2+4x-1=0
D=b2-4ac=16-4*1*-1=20
x1=(-4+√20)/(2*1)=(-4+2√5)/(2*1)=-2+√5
x2=(-4-√20)/(2*1)=(-4-2√5)/(2*1)=-2-√5
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(-2-√5, -2+√5)
Номер: FD43BD
Решите неравенство $\frac{-17}{{(x+3)}^2-7}\geq0.$.
Решение:
`(-17)/((x+3)^2-7)≥0`
То есть знаменатель `(x+3)^2-7` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x+3)(x+3)-7=0
x2+3x+3x+9-7=0
x2+6x+2=0
D=b2-4ac=36-4*1*2=28
x1=(-6+√28)/(2*1)=(-6+2√7)/(2*1)=-3+√7
x2=(-6-√28)/(2*1)=(-6-2√7)/(2*1)=-3-√7
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(-3-√7, -3+√7)
Номер: 6CEBED
Решите неравенство $\frac{-18}{{(x+4)}^2-10}\geq0.$.
Решение:
`(-18)/((x+4)^2-10)≥0`
То есть знаменатель `(x+3)^2-7` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x+4)(x+4)-10=0
x2+4x+4x+16-10=0
x2+8x+6=0
D=b2-4ac=64-4*1*6=40
x1=(-8+√40)/(2*1)=(-8+2√10)/(2*1)=-4+√10
x2=(-8-√40)/(2*1)=(-8-2√10)/(2*1)=-4-√10
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(-4-√10, -4+√10)
Номер: 484B3D
Решите неравенство $\frac{-19}{{(x+5)}^2-6}\geq0.$.
Решение:
`(-19)/((x+5)^2-6)≥0`
То есть знаменатель `(x+5)^2-6` должен быть меньше нуля, чтобы при делении на отрицательное число был положительный результат.
(x+5)(x+5)-6=0
x2+5x+5x+25-6=0
x2+10x+19=0
D=b2-4ac=100-4*1*19=24
x1=(-10+√24)/(2*1)=(-10+2√6)/(2*1)=-5+√6
x2=(-10-√24)/(2*1)=(-10-2√6)/(2*1)=-5-√6
Так как a>0, то ветви параболы направлены вверх, то есть отрицательные значения находятся на промежутки между этими корнями.
Ответ: x∈(-5-√6, -5+√6)
Номер: 517272
Решите неравенство ${(x-1)}^2<\sqrt2{(x-1)}$.
Решение:
`(x-1)^2<sqrt2(x-1)`
`(x-1)^2-sqrt2(x-1)<0`
`(x-1)(x-1)-sqrt2(x-1)<0`
`(x-1)((x-1)-sqrt2)<0`
`(x-1)((x-1-sqrt2)<0`
`(x-1)(x-(1+sqrt2))<0`
Следовательно находится между корнями множителей
x-1=0
x=1
x-(1+√2)=0
x=1+√2
1<x<1+√2
Ответ: x∈(1, 1+√2)
Номер: D24A93
Решите неравенство ${(x-2)}^2<\sqrt3{(x-2)}$.
Решение:
`(x-2)^2<sqrt3(x-2)`
`(x-2)^2-sqrt3(x-2)<0`
`(x-2)(x-2)-sqrt3(x-2)<0`
`(x-2)((x-2)-sqrt3)<0`
`(x-2)((x-2-sqrt3)<0`
`(x-2)(x-(2+sqrt3))<0`
Следовательно находится между корнями множителей
x-2=0
x=2
x-(2+√3)=0
x=2+√3
Ответ: x∈{2, 2+√3}
Номер: 314727
Решите неравенство ${(x-3)}^2<\sqrt5{(x-3)}$.
Решение:
`(x-3)^2<sqrt5(x-3)`
`(x-3)^2-sqrt5(x-3)<0`
`(x-3)(x-3)-sqrt5(x-3)<0`
`(x-3)((x-3)-sqrt5)<0`
`(x-3)((x-3-sqrt5)<0`
`(x-3)(x-(3+sqrt5))<0`
Следовательно находится между корнями множителей
x-3=0
x=3
x-(3+√5)=0
x=3+√5Ответ: x∈{3, 3+√5}
Номер: 190CD6
Решите неравенство ${(x-4)}^2<\sqrt6{(x-4)}$.
Решение:
`(x-4)^2<sqrt6(x-4)`
`(x-4)^2-sqrt6(x-4)<0`
`(x-4)(x-4)-sqrt6(x-4)<0`
`(x-4)((x-4)-sqrt6)<0`
`(x-4)((x-4-sqrt6)<0`
`(x-4)(x-(4+sqrt6))<0`
Следовательно находится между корнями множителей
x-4=0
x=4
x-(4+√6)=0
x=4+√6
Ответ: x∈{4, 4+√6}
Номер: DA9FF9
Решите неравенство ${(x-5)}^2<\sqrt7{(x-5)}$.
Решение:
`(x-5)^2<sqrt7(x-5)`
`(x-5)^2-sqrt7(x-5)<0`
`(x-5)(x-5)-sqrt7(x-5)<0`
`(x-5)((x-5)-sqrt7)<0`
`(x-5)((x-5-sqrt7)<0`
`(x-5)(x-(5+sqrt7))<0`
Следовательно находится между корнями множителей
x-5=0
x=5
x-(5+√7)=0
x=5+√7
Ответ: x∈{5, 5+√7}
Номер: B86D7F
Решите неравенство ${(x-6)}^2<\sqrt{10}{(x-6)}$.
Решение:
`(x-6)^2<sqrt10(x-6)`
`(x-6)^2-sqrt10(x-6)<0`
`(x-6)(x-6)-sqrt10(x-6)<0`
`(x-6)((x-6)-sqrt10)<0`
`(x-6)((x-6-sqrt10)<0`
`(x-6)(x-(6+sqrt10))<0`
Следовательно находится между корнями множителей
x-6=0
x=6
x-(6+√10)=0
x=6+√10
Ответ: x∈{6, 6+√10}
Номер: 3AD023
Решите неравенство ${(x-7)}^2<\sqrt{11}{(x-7)}$.
Решение:
`(x-7)^2<sqrt11(x-7)`
`(x-7)^2-sqrt11(x-7)<0`
`(x-7)(x-7)-sqrt11(x-7)<0`
`(x-7)((x-7)-sqrt11)<0`
`(x-7)((x-7-sqrt11)<0`
`(x-7)(x-(7+sqrt11))<0`
Следовательно находится между корнями множителей
x-7=0
x=7
x-(7+√11)=0
x=7+√11
Ответ: x∈{7, 7+√11}
Номер: D2F0FF
Решите неравенство ${(x-8)}^2<\sqrt3{(x-8)}$.
Решение:
`(x-8)^2<sqrt3(x-8)`
`(x-8)^2-sqrt3(x-8)<0`
`(x-8)(x-8)-sqrt3(x-8)<0`
`(x-8)((x-8)-sqrt3)<0`
`(x-8)((x-8-sqrt3)<0`
`(x-8)(x-(8+sqrt3))<0`
Следовательно находится между корнями множителей
x-8=0
x=8
x-(8+√3)=0
x=8+√3
Ответ: x∈{8, 8+√3}
Номер: 2AC60B
Решите неравенство ${(x-9)}^2<\sqrt2{(x-9)}$.
Решение:
`(x-9)^2<sqrt2(x-9)`
`(x-9)^2-sqrt2(x-9)<0`
`(x-9)(x-9)-sqrt2(x-9)<0`
`(x-9)((x-9)-sqrt2)<0`
`(x-9)((x-9-sqrt2)<0`
`(x-9)(x-(9+sqrt2))<0`
Следовательно находится между корнями множителей
x-9=0
x=9
x-(9+√2)=0
x=9+√2
Ответ: x∈{9, 9+√2}
Номер: 735E34
Решите неравенство ${(x-11)}^2<\sqrt5{(x-11)}$.
Решение:
`(x-11)^2<sqrt5(x-11)`
`(x-11)^2-sqrt5(x-11)<0`
`(x-11)(x-11)-sqrt5(x-11)<0`
`(x-11)((x-11)-sqrt5)<0`
`(x-11)((x-11-sqrt5)<0`
`(x-11)(x-(11+sqrt5))<0`
Следовательно находится между корнями множителей
x-11=0
x=11
x-(11+√5)=0
x=11+√5
Ответ: x∈{11, 11+√5}
Номер: 536E9B
Решите уравнение x3 +3x2 =16x+48.
Решение:
x3 +3x2 =16x+48
x3 +3x2 -(16x+48)=0
x2(x +3) -16(x+3)=0
(x +3) (x2-16)=0
(x +3) (x-4)(x+4)=0
Находим корни для множителей
x +3=0
x=-3
x-4=0
x=4
x+4=0
x=-4
Ответ: -4 -3 4
Номер: 750F66
Решите уравнение x3 +4x2 =4x+16.
Решение:
`x^3 +4x^2=4x+16`
`x^2(x +4)=4(x+4)`
`x^2(x +4)-4(x+4)=0`
`(x+4)(x^2-4)=0`
(x+4)(x-2)(x+2)=0
Находим корни для множителей
x +4=0
x=-4
x-2=0
x=2
x+2=0
x=-2
Ответ: -4 -2 2
Номер: A60833
Решите уравнение x3 +6x2 =4x+24.
Решение:
x3 +6x2 =4x+24
x2(x +6)=4(x+6)
x2(x +6)-4(x+6)=0
(x+6)(x2-4)=0
(x+6)(x-2)(x+2)=0
Находим корни для множителей
x +6=0
x=-6
x-2=0
x=2
x+2=0
x=-2
Ответ: -6 -2 2
Номер: 91510C
Решите уравнение x3 +6x2 =9x+54.
Решение:
x3 +6x2 =9x+54
x2(x +6)=9(x+6)
x2(x +6)-9(x+6)=0
(x+6)(x2-9)=0
(x+6)(x-3)(x+3)=0
Находим корни для множителей
x +6=0
x=-6
x-3=0
x=3
x+3=0
x=-3
Ответ: -6 -3 3
Номер: A06C64
Решите уравнение x3 +3x2 =4x+12.
Решение:
x3 +3x2 =4x+12
x2(x +3)-4(x+3)=0
(x +3)(x2-4)=0
(x +3)(x-2)(x+2)=0
Находим корни для множителей
x +3=0
x=-3
x-2=0
x=2
x+2=0
x=-2
Ответ: -3 -2 2
Номер: 1FD0B1
Решите уравнение x3 +2x2 =9x+18.
Решение:
x3 +2x2 =9x+18
x2(x +2)-9(x+2)=0
(x +2)(x2-9)=0
(x +2)(x-3)(x+3)=0
Находим корни для множителей
x +2=0
x=-2
x-3=0
x=3
x+3=0
x=-3
Ответ: -3 -2 3
Номер: 8B4010
Решите уравнение x3 +7x2 =4x+28.
Решение:
x3 +7x2 =4x+28
x2(x +7)-4(x+7)=0
(x +7)(x2-4)=0
(x +7)(x-2)(x+2)=0
Находим корни для множителей
x +7=0
x=-7
x-2=0
x=2
x+2=0
x=-2
Ответ: -7 -2 2
Номер: 3D7F40
Решите уравнение x3 +4x2 =9x+36.
Решение:
x3 +4x2 =9x+36
x2(x +4)-9(x+4)=0
(x +4)(x2-9)=0
(x +4)(x-3)(x+3)=0
Находим корни для множителей
x +4=0
x=-4
x-3=0
x=3
x+3=0
x=-3
Ответ: -4 -3 3
Номер: 4AF24D
Решите уравнение x3 +5x2 =4x+20.
Решение:
x3 +5x2 =4x+20
x2(x +5)-4(x+5)=0
(x +5)(x2-4)=0
(x +5)(x-2)(x+2)=0
Находим корни для множителей
x +5=0
x=-5
x-2=0
x=2
x+2=0
x=-2
Ответ: -5 -2 2
Номер: 5AAE7A
Решите уравнение x3 +5x2 =9x+45.
Решение:
x3 +5x2 =9x+45
x2(x +5)-9(x+5)=0
(x +5)(x2-9)=0
(x +5)(x-3)(x+3)=0
Находим корни для множителей
x +5=0
x=-5
x-3=0
x=3
x+3=0
x=-3
Ответ: -5 -3 3
Номер: 52CAF6
Решите уравнение x3 +3x2 -x-3=0.
Решение:
x3 +3x2 -x-3=0
x2(x +3)-1(x-3)=0
(x +3)(x2-1)=0
(x +3)(x-1)(x+1)=0
Находим корни для множителей
x +3=0
x=-3
x-1=0
x=1
x+1=0
x=-1
Ответ: -3 -1 1
Номер: 35233A
Решите уравнение x3 +4x2 -4x-16=0.
Решение:
x3 +4x2 -4x-16=0
x2(x +4)-4(x+4)=0
(x +4)(x2-4)=0
(x +4)(x-2)(x+2)=0
Находим корни для множителей
x +4=0
x=-4
x-2=0
x=2
x+2=0
x=-2
Ответ: -4 -2 2
Номер: F4C4E0
Решите уравнение x3 +5x2 -x-5=0.
Решение:
x3 +5x2 -x-5=0
x2(x +5)-1(x+5)=0
(x +5)(x2-1)=0
(x +5)(x-1)(x+1)=0
Находим корни для множителей
x +5=0
x=-5
x-1=0
x=1
x+1=0
x=-1
Ответ: -5 -1 1
Номер: C0EC49
Решите уравнение x3 +2x2 -x-2=0.
Решение:
x3 +2x2 -x-2=0
x2(x +2)-1(x+2)=0
(x +2)(x2-1)=0
(x +2)(x-1)(x+1)=0
Находим корни для множителей
x +2=0
x=-2
x-1=0
x=1
x+1=0
x=-1
Ответ: -2 -1 1
Номер: 8AA84C
Решите уравнение x3 +3x2 -4x-12=0.
Решение:
x3 +3x2 -4x-12=0
x2(x +3)-4(x+3)=0
(x +3)(x2-4)=0
(x +3)(x-2)(x+2)=0
Находим корни для множителей
x +3=0
x=-3
x-2=0
x=2
x+2=0
x=-2
Ответ: -3 -2 2
Номер: 98D489
Решите уравнение x3 +2x2 -9x-18=0.
Решение:
x3 +2x2 -9x-18=0
x2(x +2)-9(x+2)=0
(x +2)(x2-9)=0
(x +2)(x-3)(x+3)=0
Находим корни для множителей
x +2=0
x=-2
x-3=0
x=3
x+3=0
x=-3
Ответ: -3 -2 3
Номер: 8DED97
Решите уравнение x3 +4x2 -x-4=0.
Решение:
x3 +4x2 -x-4=0
x2(x +4)-1(x+4)=0
(x +4)(x2-1)=0
(x +4)(x-1)(x+1)=0
Находим корни для множителей
x +4=0
x=-4
x-1=0
x=1
x+1=0
x=-1
Ответ: -4 -1 1
Номер: 202FFC
Решите уравнение x3 +4x2 -9x-36=0.
Решение:
x3 +4x2 -9x-36=0
x2(x +4)-9(x+4)=0
(x +4)(x2-9)=0
(x +4)(x-3)(x+3)=0
Находим корни для множителей
x +4=0
x=-4
x-3=0
x=3
x+3=0
x=-3
Ответ: -4 -3 3
Номер: 97D599
Решите уравнение x3 +5x2 -4x-20=0.
Решение:
x3 +5x2 -4x-20=0
x2(x +5)-4(x+5)=0
(x +5)(x2-4)=0
(x +5)(x-2)(x+2)=0
Находим корни для множителей
x +5=0
x=-5
x-2=0
x=2
x+2=0
x=-2
Ответ: -5 -2 2
Номер: C96480
Решите уравнение x3 +5x2 -9x-45=0.
Решение:
x3 +5x2 -9x-45=0
x2(x +5)-9(x+5)=0
(x +5)(x2-9)=0
(x +5)(x-3)(x+3)=0
Находим корни для множителей
x +5=0
x=-5
x-3=0
x=3
x+3=0
x=3
Ответ: -5 -3 3
Номер: 4F75FE
Решите уравнение x4 =(x-20)2.
Решение:
x4 =(x-20)2
x4 -(x-20)2=0
(x2 -(x-20))(x2 +(x-20))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -x+20 = 0
D=b2-4ac=1-4*1*20=-81 нет корней.
второе:
x2 +x-20 = 0
D=b2-4ac=1-4*1*-20=81
x1=(-1+√81)/(2*1)=(-1+9)/(2*1)=4
x2=(-1-√81)/(2*1)=(-1-9)/(2*1)=-5
Ответ: -5 4
Номер: BA23E9
Решите уравнение x4 =(2x-15)2.
Решение:
x4 =(2x-15)2
x4 -(2x-15)2=0
(x2 -(2x-15))(x2 +(2x-15))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -2x+15 = 0
D=b2-4ac=4-4*1*15=-56 нет корней.
второе:
x2 +2x-15 = 0
D=b2-4ac=4-4*1*-15=64
x1=(-2+√64)/(2*1)=(-2+8)/(2*1)=3
x2=(-2-√64)/(2*1)=(-2-8)/(2*1)=-5
Ответ: -5 3
Номер: 727066
Решите уравнение x4 =(3x-10)2.
Решение:
x4 =(3x-10)2
x4 -(3x-10)2=0
(x2 -(3x-10))(x2 +(3x-10))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -3x+10 = 0
D=b2-4ac=9-4*1*10=-31 нет корней.
второе:
x2 +3x-10 = 0
D=b2-4ac=9-4*1*-10=49
x1=(-3+√49)/(2*1)=(-3+7)/(2*1)=2
x2=(-3-√49)/(2*1)=(-3-7)/(2*1)=-5
Ответ: -5 2
Номер: 94AF92
Решите уравнение x4 =(4x-5)2.
Решение:
x4 =(4x-5)2
x4 -(4x-5)2=0
(x2 -(4x-5))(x2 +(4x-5))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -4x+5 = 0
D=b2-4ac=16-4*1*5=-4 нет корней.
второе:
x2 +4x-5 = 0
D=b2-4ac=16-4*1*-5=36
x1=(-4+√36)/(2*1)=(-4+6)/(2*1)=1
x2=(-4-√36)/(2*1)=(-4-6)/(2*1)=-5
Ответ: -5 1
Номер: 424AC9
Решите уравнение x4 =(x-12)2.
Решение:
x4 =(x-12)2
x4 -(x-12)2=0
(x2 -(x-12))(x2 +(x-12))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -x+12 = 0
D=b2-4ac=1-4*1*12=-47 нет корней.
второе:
x2 +x-12 = 0
D=b2-4ac=1-4*1*-12=49
x1=(-1+√49)/(2*1)=(-1+7)/(2*1)=3
x2=(-1-√49)/(2*1)=(-1-7)/(2*1)=-4
Ответ: -4 3
Номер: 4DCE6B
Решите уравнение x4 =(2x-8)2.
Решение:
x4 =(2x-8)2
x4 -(2x-8)2=0
(x2 -(2x-8))(x2 +(2x-8))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -2x+8 = 0
D=b2-4ac=4-4*1*8=-28 нет корней.
второе:
x2 +2x-8 = 0
D=b2-4ac=4-4*1*-8=36
x1=(-2+√36)/(2*1)=(-2+6)/(2*1)=2
x2=(-2-√36)/(2*1)=(-2-6)/(2*1)=-4
Ответ: -4 2
Номер: 4FB09D
Решите уравнение x4 =(3x-4)2.
Решение:
x4 =(3x-4)2
x4 -(3x-4)2=0
(x2 -(3x-4))(x2 +(3x-4))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -3x+4 = 0
D=b2-4ac=9-4*1*4=-5 нет корней.
второе:
x2 +3x-4 = 0
D=b2-4ac=3-4*1*-4=25
x1=(-3+√25)/(2*1)=(-3+5)/(2*1)=1
x2=(-3-√25)/(2*1)=(-3-5)/(2*1)=-4
Ответ: -4 1
Номер: 1BBDA9
Решите уравнение x4 =(x-6)2.
Решение:
x4 =(x-6)2
x4 -(x-6)2=0
(x2 -(x-6))(x2 +(x-6))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -x+6 = 0
D=b2-4ac=1-4*1*6=-23 нет корней.
второе:
x2 +x-6 = 0
D=b2-4ac=1-4*1*-6=25
x1=(-1+√25)/(2*1)=(-1+5)/(2*1)=2
x2=(-1-√25)/(2*1)=(-1-5)/(2*1)=-3
Ответ: -3 2
Номер: 0260D6
Решите уравнение x4 =(2x-3)2.
Решение:
x4 =(2x-3)2
x4 -(2x-3)2=0
(x2 -(2x-3))(x2 +(2x-3))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -2x+3 = 0
D=b2-4ac=4-4*1*3=-8 нет корней.
второе:
x2 +2x-3 = 0
D=b2-4ac=4-4*1*-3=16
x1=(-2+√16)/(2*1)=(-2+4)/(2*1)=1
x2=(-2-√16)/(2*1)=(-2-4)/(2*1)=-3
Ответ: -3 1
Номер: 193429
Решите уравнение x4 =(x-2)2.
Решение:
x4 =(x-2)2
x4 -(x-2)2=0
(x2 -(x-2))(x2 +(x-2))=0 (разность квадратов, по формуле сокращенного умножения)
Находим корни для уравнений:
x2 -x+2 = 0
D=b2-4ac=1-4*1*2=-7 нет корней.
второе:
x2 +x-2 = 0
D=b2-4ac=1-4*1*-2=9
x1=(-1+√9)/(2*1)=(-1+3)/(2*1)=1
x2=(-1-√9)/(2*1)=(-1-3)/(2*1)=-2
Ответ: -2 1
Номер: 478148
Решите уравнение $x^2-6x+\sqrt{6-x}=\sqrt{6-x}+7$.
Решение:
При x≤6 исходное уравнение приводится к виду
`x^2-6x+sqrt(6-x)=sqrt(6-x)+7`
`x^2-6x+sqrt(6-x)-sqrt(6-x)-7=0`
`x^2-6x-7=0`
D=b2-4ac=36-4*1*-7=64
x1=(6+√64)/(2*1)=(6+8)/(2*1)=7
x2=(6-√64)/(2*1)=(6-8)/(2*1)=-1
Условию x≤6 удовлетворяет только решение x=−1
Ответ: -1
Номер: DC6888
Решите уравнение $x^2-2x+\sqrt{2-x}=\sqrt{2-x}+3$.
Решение:
При x≤2 исходное уравнение приводится к виду
`x^2-2x+sqrt(2-x)=sqrt(2-x)+3`
`x^2-2x+sqrt(2-x)-sqrt(2-x)-3=0`
`x^2-2x-3=0`
D=b2-4ac=4-4*1*-3=16
x1=(2+√16)/(2*1)=(2+4)/(2*1)=3
x2=(2-√16)/(2*1)=(2-4)/(2*1)=-1
Условию x≤2 удовлетворяет только решение x=−1
Ответ: -1
Номер: C8CB59
Решите уравнение $x^2-2x+\sqrt{3-x}=\sqrt{3-x}+8$.
Решение:
При x≤3 исходное уравнение приводится к виду
`x^2-2x+sqrt(3-x)=sqrt(3-x)+8`
`x^2-2x+sqrt(3-x)-sqrt(3-x)-8=0`
`x^2-2x-8=0`
D=b2-4ac=4-4*1*-8=36
x1=(2+√36)/(2*1)=(2+6)/(2*1)=4
x2=(2-√36)/(2*1)=(2-6)/(2*1)=-2
Условию x≤3 удовлетворяет только решение x=−2
Ответ: -2
Номер: 4BCAFD
Решите уравнение $x^2-3x+\sqrt{3-x}=\sqrt{3-x}+10$.
Решение:
При x≤3 исходное уравнение приводится к виду
`x^2-3x+sqrt(3-x)=sqrt(3-x)+10`
`x^2-3x+sqrt(3-x)-sqrt(3-x)-10=0`
`x^2-3x-10=0`
D=b2-4ac=9-4*1*-10=49
x1=(3+√49)/(2*1)=(3+7)/(2*1)=5
x2=(3-√49)/(2*1)=(3-7)/(2*1)=-2
Условию x≤3 удовлетворяет только решение x=−2
Ответ: -2
Номер: F0A811
Решите уравнение $x^2-3x+\sqrt{5-x}=\sqrt{5-x}+18$.
Решение:
При x≤5 исходное уравнение приводится к виду
`x^2-3x+sqrt(5-x)=sqrt(5-x)+18`
`x^2-3x+sqrt(5-x)-sqrt(5-x)-18=0`
`x^2-3x-18=0`
D=b2-4ac=9-4*1*-10=49
x1=(3+√49)/(2*1)=(3+7)/(2*1)=5
x2=(3-√49)/(2*1)=(3-7)/(2*1)=-2
Условию x≤5 удовлетворяет только решение x=−2
Ответ: -2
Номер: 602723
Решите уравнение $x^2-2x+\sqrt{4-x}=\sqrt{4-x}+15$.
Решение:
При x≤4 исходное уравнение приводится к виду
`x^2-2x+sqrt(4-x)=sqrt(4-x)+15`
`x^2-2x+sqrt(4-x)-sqrt(4-x)-15=0`
`x^2-2x-15=0`
D=b2-4ac=9-4*1*-15=64
x1=(2+√64)/(2*1)=(2+8)/(2*1)=5
x2=(2-√64)/(2*1)=(2-8)/(2*1)=-3
Условию x≤4 удовлетворяет только решение x=−3
Ответ: -3
Номер: F66235
Решите уравнение $x^2-3x+\sqrt{6-x}=\sqrt{6-x}+28$.
Решение:
При x≤6 исходное уравнение приводится к виду
`x^2-3x+sqrt(6-x)=sqrt(6-x)+28`
`x^2-3x+sqrt(6-x)-sqrt(6-x)-28=0`
`x^2-3x-28=0`
D=b2-4ac=9-4*1*-28=121
x1=(3+√121)/(2*1)=(3+11)/(2*1)=7
x2=(3-√121)/(2*1)=(3-11)/(2*1)=-4
Условию x≤6 удовлетворяет только решение x=−4
Ответ: -4
Номер: 27B07D
Решите уравнение $x^2-2x+\sqrt{5-x}=\sqrt{5-x}+24$.
Решение:
При x≤5 исходное уравнение приводится к виду
`x^2-2x+sqrt(5-x)=sqrt(5-x)+24`
`x^2-2x+sqrt(5-x)-sqrt(5-x)-24=0`
`x^2-2x-24=0`
D=b2-4ac=4-4*1*-24=100
x1=(2+√100)/(2*1)=(2+10)/(2*1)=6
x2=(2-√100)/(2*1)=(2-10)/(2*1)=-4
Условию x≤5 удовлетворяет только решение x=−4
Ответ: -4
Номер: C1DBE5
Решите уравнение $x^2-2x+\sqrt{6-x}=\sqrt{6-x}+35$.
Решение:
При x≤6 исходное уравнение приводится к виду
`x^2-2x+sqrt(6-x)=sqrt(6-x)+35`
`x^2-2x+sqrt(6-x)-sqrt(6-x)-35=0`
`x^2-2x-35=0`
D=b2-4ac=4-4*1*-35=144
x1=(2+√144)/(2*1)=(2+12)/(2*1)=7
x2=(2-√144)/(2*1)=(2-12)/(2*1)=-5
Условию x≤6 удовлетворяет только решение x=−5
Ответ:-5
Номер: F38DEF
Решите уравнение $x^2-3x+\sqrt{6-x}=\sqrt{6-x}+40$.
Решение:
При x≤6 исходное уравнение приводится к виду
`x^2-3x+sqrt(6-x)=sqrt(6-x)+40`
`x^2-3x+sqrt(6-x)-sqrt(6-x)-40=0`
`x^2-3x-40=0`
D=b2-4ac=9-4*1*-40=169
x1=(3+√169)/(2*1)=(3+13)/(2*1)=8
x2=(3-√169)/(2*1)=(3-13)/(2*1)=-5
Условию x≤6 удовлетворяет только решение x=−5
Ответ: -5
Номер: A69BB1
Решите уравнение (x2 -25)2 +(x2 +3x-10)2 =0.
Решение:
(x2 -25)2 +(x2 +3x-10)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -25 =0
x2 =25
x1=5
x2=-5
x2 +3x-10 =0
D=b2-4ac=9-4*1*-10=49
x1=(-3+√49)/(2*1)=(-3+7)/(2*1)=2
x2=(-3-√49)/(2*1)=(-3-7)/(2*1)=-5
Общие корни -5
Ответ: -5
Номер: C7A037
Решите уравнение (x2 -16)2 +(x2 +x-12)2 =0.
Решение:
(x2 -16)2 +(x2 +x-12)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -16 =0
x2 =16
x1=4
x2=-4
x2 +x-12 =0
D=b2-4ac=1-4*1*-12=49
x1=(-1+√49)/(2*1)=(-1+7)/(2*1)=3
x2=(-1-√49)/(2*1)=(-1-7)/(2*1)=-4
Общие корни -4
Ответ: -4
Номер: 3CCDCA
Решите уравнение (x2 -9)2 +(x2 -2x-15)2 =0.
Решение:
(x2 -9)2 +(x2 -2x-15)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -9 =0
x2 =9
x1=3
x2=-3
x2 -2x-15 =0
D=b2-4ac=4-4*1*-15=64
x1=(2+√64)/(2*1)=(2+8)/(2*1)=5
x2=(2-√64)/(2*1)=(2-8)/(2*1)=-3
Общие корни -3
Ответ: x = -3,
Номер: 4CA219
Решите уравнение (x2 -4)2 +(x2 -6x-16)2 =0.
Решение:
(x2 -4)2 +(x2 -6x-16)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -4 =0
x2 =4
x1=2
x2=-2
x2 -6x-16 =0
D=b2-4ac=36-4*1*-16=100
x1=(6+√100)/(2*1)=(6+10)/(2*1)=8
x2=(6-√100)/(2*1)=(6-10)/(2*1)=-2
Общие корни -2
Ответ: x = -2
Номер: 5D3C80
Решите уравнение (x2 -1)2 +(x2 -6x-7)2 =0.
Решение:
(x2 -1)2 +(x2 -6x-7)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -1 =0
x2 =1
x1=1
x2=-1
x2 -6x-7 =0
D=b2-4ac=36-4*1*-7=64
x1=(6+√64)/(2*1)=(6+8)/(2*1)=7
x2=(6-√64)/(2*1)=(6-8)/(2*1)=-1
Общие корни -1
Ответ: x = -1
Номер: 35AF32
Решите уравнение (x2 -36)2 +(x2 +4x-12)2 =0.
Решение:
(x2 -36)2 +(x2+4x-12)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -36 =0
x2 =36
x1=6
x2=-6
x2+4x-12 =0
D=b2-4ac=16-4*1*-12=64
x1=(-4+√64)/(2*1)=(-4+8)/(2*1)=2
x2=(-4-√64)/(2*1)=(-4-8)/(2*1)=-6
Общие корни -6
Ответ: x = -6
Номер: D6770A
Решите уравнение (x2 -49)2 +(x2 +4x-21)2 =0.
Решение:
(x2 -49)2 +(x2+4x-21)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -49 =0
x2 =49
x1=7
x2=-7
x2+4x-21 =0
D=b2-4ac=16-4*1*-21=100
x1=(-4+√100)/(2*1)=(-4+10)/(2*1)=3
x2=(-4-√100)/(2*1)=(-4-10)/(2*1)=-7
Общие корни -7
Ответ: x = -7
Номер: B3F219
Решите уравнение (x2 -4)2 +(x2 -3x-10)2 =0.
Решение:
(x2 -4)2 +(x2-3x-10)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -4 =0
x2 =4
x1=2
x2=-2
x2-3x-10 =0
D=b2-4ac=9-4*1*-10=49
x1=(3+√49)/(2*1)=(3+7)/(2*1)=5
x2=(3-√49)/(2*1)=(3-7)/(2*1)=-2
Общие корни -2
Ответ: х = -2
Номер: 11EC1E
Решите уравнение (x2 -9)2 +(x2 +x-6)2 =0.
Решение:
(x2 -9)2 +(x2+x-6)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -9 =0
x2 =9
x1=3
x2=-3
x2+x-6 =0
D=b2-4ac=1-4*1*-6=25
x1=(-1+√25)/(2*1)=(-1+5)/(2*1)=2
x2=(-1-√25)/(2*1)=(-1-5)/(2*1)=-3
Общие корни -3
Ответ: х = -3
Номер: 2E0EEA
Решите уравнение (x2 -25)2 +(x2 +2x-15)2 =0.
Решение:
(x2 -25)2 +(x2+2x-15)2 =0
Получается у нас есть два уравнения. Если мы найдем корни, а потом выберем для каждого из них одинаковые корни (корень), то это и будет решением нашего главного уравнения. При этом важным условием является то, обстоятельство что уравнения должны быть по факту равны 0, так как 0+0=0, и лишь 0 во второй степени и будет нулем. Именно это условие удовлетворяет нашему уравнению. То есть решаем каждое из них самостоятельно, выбирая впоследствии корни.
x2 -25 =0
x2 =25
x1=5
x2=-5
x2+2x-15 =0
D=b2-4ac=4-4*1*-15=64
x1=(-2+√64)/(2*1)=(-2+8)/(2*1)=3
x2=(-2-√64)/(2*1)=(-2-8)/(2*1)=-5
Общие корни -5
Ответ: х = -5
Номер: 681B15
Решите систему уравнений
Решите систему уравнений $\left\{\begin{array}{l}3x^2+y=4,\\2x^2-y=1.\end{array}\right.$.
Решение:
`3x^2+y=4`
`y=4-3x^2`
Тогда
`2x^2-y=1`
`2x^2-(4-3x^2)=1`
`2x^2-4+3x^2=1`
`5x^2-5=0`
`5(x^2-1)=0`
x^2-1=0
`x_1=1`
`x_2=-1`
При x1=1
`y=4-3*1^2`
y=1
При x2=-1
`y=4-3*(-1)^2`
y=1
Ответ:
(x1, y1) = (-1,1)
(x2, y2) = (1,1)
Номер: E5E7B8
Решите систему уравнений $\left\{\begin{array}{l}2x^2+y=4,\\4x^2-y=2.\end{array}\right.$.
Решение:
`2x^2+y=4`
`y=4-2x^2`
Тогда
`4x^2-y=2`
`4x^2-(4-2x^2)=2`
`4x^2-4+2x^2=2`
`6x^2-4=2`
`6x^2=6`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`y=4-2*1^2`
y=2
При x2=-1
`y=4-2*(-1)^2`
y=2
Ответ:
(x1, y1) = (-1,2)
(x2, y2) = (1,2)
Номер: 3E1CF4
Решите систему уравнений $\left\{\begin{array}{l}3x^2+y=6,\\4x^2-y=1.\end{array}\right.$.
Решение:
`3x^2+y=6`
`y=6-3x^2`
Тогда
`4x^2-y=1`
`4x^2-(6-3x^2)=1`
`4x^2-6+3x^2=1`
`7x^2-6=1`
`7x^2=7`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`4x^2-y=1`
`y = 4x^2-1`
y=3
При x2=-1
`4x^2-y=1`
`y = 4x^2-1`
y=3
Ответ:
(x1, y1) = (-1,3)
(x2, y2) = (1,3)
Номер: F2373A
Решите систему уравнений $\left\{\begin{array}{l}x^2+y=5,\\6x^2-y=2.\end{array}\right.$.
Решение:
`x^2+y=5`
`y=5-x^2`
Тогда
`6x^2-y=2`
`6x^2-(5-x^2)=2`
`6x^2-5+x^2=2`
`7x^2-5=2`
`7x^2=7`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`6x^2-y=2`
`y = 6x^2-2`
y=4
При x2=-1
`6x^2-y=2`
`y = 6x^2-2`
y=4
Ответ:
(x1, y1) = (-1,4)
(x2, y2) = (1,4)
Номер: 7CB2F7
Решите систему уравнений $\left\{\begin{array}{l}4x^2+y=9,\\8x^2-y=3.\end{array}\right.$.
Решение:
`4x^2+y=9`
`y=9-4x^2`
Тогда
`8x^2-y=3`
`8x^2-(9-4x^2)=3`
`8x^2-9+4x^2=3`
`12x^2-9=3`
`12x^2=12`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`8x^2-y=3`
`y = 8x^2-3`
y=5
При x2=-1
`8x^2-y=3`
`y = 8x^2-3`
y=5
Ответ:
(x1, y1) = (-1,5)
(x2, y2) = (1,5)
Номер: D0D6A3
Решите систему уравнений $\left\{\begin{array}{l}x^2+y=7,\\2x^2-y=5.\end{array}\right.$.
Решение:
`x^2+y=7`
`y=7-x^2`
Тогда
`2x^2-y=5`
`2x^2-(7-x^2)=5`
`2x^2-7+x^2=5`
`3x^2-7=5`
`3x^2=12`
`x^2=4`
`x_1=2`
`x_2=-2`
При x1=2
`2x^2-y=5`
`y = 2x^2-5`
y=8-5=3
При x2=-2
`2x^2-y=5`
`y = 2x^2-5`
y=8-5=3
Ответ:
(x1, y1) = (-2,3)
(x2, y2) = (2,3)
Номер: B5C26E
Решите систему уравнений $\left\{\begin{array}{l}3x^2+y=9,\\7x^2-y=1.\end{array}\right.$.
Решение:
`3x^2+y=9`
`y=9-3x^2`
Тогда
`7x^2-y=1`
`7x^2-(9-3x^2)=1`
`7x^2-9+3x^2=1`
`10x^2-9=1`
`10x^2=10`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`7x^2-y=1`
`y = 7x^2-1`
y=6
При x2=-1
`7x^2-y=1`
`y = 7x^2-1`
y=6
Ответ:
(x1, y1) = (-1,6)
(x2, y2) = (1,6)
Номер: 290154
Решите систему уравнений $\left\{\begin{array}{l}5x^2+y=12,\\9x^2-y=2.\end{array}\right.$.
Решение:
`5x^2+y=12`
`y=12-5x^2`
Тогда
`9x^2-y=2`
`9x^2-(12-5x^2)=2`
`9x^2-12+5x^2=2`
`14x^2-12=2`
`14x^2=14`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`9x^2-y=2`
`y = 9x^2-2`
y=7
При x2=-1
`9x^2-y=2`
`y = 9x^2-2`
y=7
Ответ:
(x1, y1) = (-1,7)
(x2, y2) = (1,7)
Номер: 2E988B
Решите систему уравнений $\left\{\begin{array}{l}6x^2+y=14,\\12x^2-y=4.\end{array}\right.$.
Решение:
`6x^2+y=14`
`y=14-6x^2`
Тогда
`12x^2-y=4`
`12x^2-(14-6x^2)=4`
`12x^2-14+6x^2=4`
`18x^2-14=4`
`18x^2=18`
`x^2=1`
`x_1=1`
`x_2=-1`
При x1=1
`12x^2-y=4`
`y = 12x^2-4`
y=8
При x2=-1
`12x^2-y=4`
`y = 12x^2-4`
y=8
Ответ:
(x1, y1) = (-1,8)
(x2, y2) = (1,8)
Номер: 6BB1B0
Решите систему уравнений $\left\{\begin{array}{l}2x^2+y=9,\\3x^2-y=11.\end{array}\right.$.
Решение:
`2x^2+y=9`
`y=9-2x^2`
Тогда
`3x^2-y=11`
`3x^2-(9-2x^2)=11`
`3x^2-9+2x^2=11`
`5x^2-9=11`
`5x^2=20`
`x^2=4`
`x_1=2`
`x_2=-2`
При x1=-2
`3x^2-y=11`
`y = 3x^2-11`
y=1
При x2=2
`3x^2-y=11`
`y = 3x^2-11`
y=1
Ответ:
(x1, y1) = (-2,1)
(x2, y2) = (2,1)
Номер: 149938
Решите систему уравнений $\left\{\begin{array}{l}3x^2-2x=y,\\3x-2=y.\end{array}\right.$.
Решение:
`3x^2-2x=y`
Тогда
`3x-2=3x^2-2x`
`3x^2-2x-3x+2=0`
`3x^2-5x+2=0`
D=b2-4ac=25-4*3*2=1
x1=(5-1)/(2*3)=4/6=2/3
x2=(5+1)/(2*3)=1
При x1=2/3
`3x-2=y`
y=0
При x2=1
`3x-2=y`
y=1
Ответ:
(x1, y1) = (2/3, 0)
(x2, y2) = (1,1)
Номер: 417E79
Решите систему уравнений $\left\{\begin{array}{l}3x^2-4x=y,\\3x-4=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`3x^2-4x=3x-4`
`3x^2-7x+4=0`
D=b2-4ac=49-4*3*4=1
x1=(7+1)/(2*3)=4/3
x2=(7-1)/(2*3)=1
При x1=4/3
`3x-4=y`
y=0
При x2=1
`3x-4=y`
y=-1
Ответ:
(x1, y1) = (4/3, 0)
(x2, y2) = (1, -1)
Номер: 8E6FA9
Решите систему уравнений $\left\{\begin{array}{l}2x^2-5x=y,\\2x-5=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`2x^2-5x=2x-5`
`2x^2-7x+5=0`
D=b2-4ac=49-4*2*5=9
x1=(7+3)/(2*2)=5/2
x2=(7-3)/(2*2)=1
При x1=5/2
`2x-5=y`
y=0
При x2=1
`2x-5=y`
y=-3
Ответ:
(x1, y1) = (5/2, 0)
(x2, y2) = (1, -3)
Номер: FA4684
Решите систему уравнений $\left\{\begin{array}{l}2x^2-x=y,\\2x-1=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`2x^2-x=2x-1`
`2x^2-3x+1=0`
D=b2-4ac=9-4*2*1=1
x1=(3-1)/(2*2)=1/2
x2=(3+1)/(2*2)=1
При x1=1/2
`2x-1=y`
y=0
При x2=1
`2x-1=y`
y=1
Ответ:
(x1, y1) = (1/2, 0)
(x2, y2) = (1,1)
Номер: 4BBE8B
Решите систему уравнений $\left\{\begin{array}{l}4x^2-3x=y,\\8x-6=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`4x^2-3x=8x-6`
`4x^2-11x+6=0`
D=b2-4ac=121-4*4*6=25
x1=(11-5)/(2*4)=6/8=3/4
x2=(11+5)/(2*4)=2
При x1=3/4
`8x-6=y`
y=0
При x2=2
`8x-6=y`
y=10
Ответ:
(x1, y1) = (3/4, 0)
(x2, y2) = (2, 10)
Номер: EC6ABC
Решите систему уравнений $\left\{\begin{array}{l}4x^2-5x=y,\\8x-10=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`4x^2-5x=8x-10`
`4x^2-13x+10=0`
D=b2-4ac=169-4*4*10=9
x1=(13-3)/(2*4)=10/8=5/4
x2=(13+3)/(2*4)=2
При x1=5/4
`8x-10=y`
y=0
При x2=2
`8x-10=y`
y=6
Ответ:
(x1, y1) = (5/4, 0)
(x2, y2) = (2, 6)
Номер: 801B6A
Решите систему уравнений $\left\{\begin{array}{l}5x^2-9x=y,\\5x-9=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`5x^2-9x=5x-9`
`5x^2-14x+9=0`
D=b2-4ac=196-4*5*9=16
x1=(14+4)/(2*5)=18/10=9/5
x2=(14-4)/(2*5)=1
При x1=9/5
`5x-9=y`
y=0
При x2=2
`5x-9=y`
y=-4
Ответ:
(x1, y1) = (9/5, 0)
(x2, y2) = (1, -4)
Номер: AF0F2A
Решите систему уравнений $\left\{\begin{array}{l}5x^2-11x=y,\\5x-11=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`5x^2-11x=5x-11`
`5x^2-16x+11=0`
D=b2-4ac=256-4*5*11=36
x1=(16+6)/(2*5)=22/10=11/5
x2=(16-6)/(2*5)=1
При x1=11/5
`5x-11=y`
y=0
При x2=2
`5x-11=y`
y=-6
Ответ:
(x1, y1) = (11/5, 0)
(x2, y2) = (1, -6)
Номер: 5EA9CF
Решите систему уравнений $\left\{\begin{array}{l}7x^2-5x=y,\\7x-5=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`7x^2-5x=7x-5`
`7x^2-12x+5=0`
D=b2-4ac=144-4*7*5=4
x1=(12-2)/(2*7)=10/14=5/7
x2=(12+2)/(2*7)=1
При x1=5/7
`7x-5=y`
y=0
При x2=2
`7x-5=y`
y=2
Ответ:
(x1, y1) = (5/7, 0)
(x2, y2) = (1, 2)
Номер: 3CA76F
Решите систему уравнений $\left\{\begin{array}{l}9x^2-14x=y,\\9x-14=y.\end{array}\right.$.
Решение:
Тогда приравниваем два уравнения между собой
`9x^2-14x=9x-14`
`9x^2-23x+14=0`
D=b2-4ac=529-4*9*14=25
x1=(23+5)/(2*9)=28/18=14/9
x2=(23-5)/(2*9)=1
При x1=14/9
`9x-14=y`
y=0
При x2=1
`9x-14=y`
y=-5
Ответ:
(x1, y1) = (14/9, 0)
(x2, y2) = (1, -5)
Номер: C73C78
Решите систему уравнений $\left\{\begin{array}{l}2x^2+3y^2=11,\\4x^2+6y^2=11x.\end{array}\right.$.
Решение:
1 способ
`2x^2+3y^2=11`
`3y^2=11-2x^2`
Тогда
`4x^2+2(11-2x^2)=11x`
`4x^2+22-4x^2=11x`
`11x=22`
x=2
При x=2 (для 1 уравнения)
`2x^2+3y^2=11`
`2*4+3y^2=11`
`3y^2=11-8`
`3y^2=3`
y^2=1
y1=1
y2=-1
При x=2 (для второго уравнения)
`4x^2+6y^2=11x`
`4*4+6y^2=11*2`
`6y^2=22-16`
y^2=1
y1=1
y2=-1
Ответ:
(x1, y1) = (2, -1)
(x2, y2) = (2, 1)
2 способПеренесем переменную в левую часть равенства
`{(2x^2 +3y^2=11),(4x^2+6y^2-11x=0):}`
Умножим обе части на -2
`{(-4x^2 -6y^2=-22),(4x^2+6y^2-11x=0):}`
Исключим одну из переменных путем сложения уравнений
`-11x=-22`
`x=2`
Подставим значение x в `2x^2 +3y^2=11`
`2*2^2 +3y^2=11`
`y=±1`
Решения системы уравнений: (2; − 1) и (2; 1).
Ответ:
(x1, y1) = (2, -1)
(x2, y2) = (2, 1)
Номер: F821AB
Решите систему уравнений $\left\{\begin{array}{l}2x^2+4y^2=24,\\4x^2+8y^2=24x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(2x^2 +4y^2=24),(4x^2+8y^2-24x=0):}`
Разделим обе части на -2 в нижнем уравнении
`{(2x^2 +4y^2=24),(-2x^2-4y^2+12x=0):}`
Исключим одну из переменных путем сложения уравнений
`12x=24`
`x=2`
Подставим значение x в `2x^2+4y^2=24`
`2*2^2 +4y^2=24`
`4y^2=24-8`
`y^2=4`
`y=±2`
Решения системы уравнений: (2; − 2) и (2; 2).
Ответ:
(x1, y1) = (2, -2)
(x2, y2) = (2, 2)
Номер: 50AC99
Решите систему уравнений $\left\{\begin{array}{l}x^2+3y^2=31,\\2x^2+6y^2=31x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(x^2+3y^2=31),(2x^2+6y^2-31x=0):}`
Разделим обе части на -2 в нижнем уравнении
`{(x^2+3y^2=31),(-x^2-3y^2-15,5x=0):}`
Исключим одну из переменных путем сложения уравнений
`15,5x=31`
`x=2`
Подставим значение x в `x^2+3y^2=31`
`2^2 +3y^2=31`
`3y^2=31-4`
`y^2=9`
`y=±3`
Решения системы уравнений: (2; −3) и (2; 3).
Ответ:
(x1, y1) = (2, -3)
(x2, y2) = (2, 3)
Номер: 116114
Решите систему уравнений $\left\{\begin{array}{l}5x^2+y^2=36,\\10x^2+2y^2=36x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(5x^2+y^2=36),(10x^2+2y^2-36x=0):}`
Разделим обе части на -2 в нижнем уравнении
`{(5x^2+y^2=36),(-5x^2-y^2+18x=0):}`
Исключим одну из переменных путем сложения уравнений
`18x=36`
`x=2`
Подставим значение x в `5x^2+y^2=36`
`5*2^2+y^2=36`
`3y^2=36-20`
`y^2=16`
`y=±4`
Решения системы уравнений: (2; −4) и (2; 4).
Ответ:
(x1, y1) = (2, -4)
(x2, y2) = (2, 4)
Номер: 5A9DFE
Решите систему уравнений $\left\{\begin{array}{l}2x^2+3y^2=21,\\6x^2+9y^2=21x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(2x^2+3y^2=21),(6x^2+9y^2-21x=0):}`
Разделим обе части на -3 в нижнем уравнении
`{(2x^2+3y^2=21),(-2x^2-3y^2+7x=0):}`
Исключим одну из переменных путем сложения уравнений
`7x=21`
`x=3`
Подставим значение x в `2x^2+3y^2=21`
`2*3^2+3y^2=21`
`3y^2=21-18`
`y^2=1`
`y=±1`
Решения системы уравнений: (3; −1) и (3; 1).
Ответ:
(x1, y1) = (3, -1)
(x2, y2) = (3, 1)
Номер: 9102C8
Решите систему уравнений $\left\{\begin{array}{l}x^2+4y^2=25,\\3x^2+12y^2=25x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(x^2+4y^2=25),(3x^2+12y^2-25x=0):}`
Разделим обе части на -3 в нижнем уравнении
`{(x^2+4y^2=25),(-x^2-4y^2+(25/3)x=0):}`
Исключим одну из переменных путем сложения уравнений
`(25/3)x=25`
`x=3`
Подставим значение x в `x^2+4y^2=25`
`3^2+4y^2=25`
`4y^2=25-9`
`4y^2=16`
`y=±2`
Решения системы уравнений: (3; −2) и (3; 2).
Ответ:
(x1, y1) = (3, -2)
(x2, y2) = (3, 2)
Номер: 546FEF
Решите систему уравнений $\left\{\begin{array}{l}3x^2+2y^2=45,\\9x^2+6y^2=45x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(3x^2+2y^2=45),(9x^2+6y^2-45x=0):}`
Разделим обе части на -3 в нижнем уравнении
`{(3x^2+2y^2=45),(-3x^2-2y^2+15x=0):}`
Исключим одну из переменных путем сложения уравнений
`15x=45`
`x=3`
Подставим значение x в `3x^2+2y^2=45`
`3*3^2+2y^2=45`
`2y^2=45-27`
`2y^2=18`
`y^2=9`
`y=±3`
Решения системы уравнений: (3; −3) и (3; 3).
Ответ:
(x1, y1) = (3, -3)
(x2, y2) = (3, 3)
Номер: 817AD0
Решите систему уравнений $\left\{\begin{array}{l}5x^2+y^2=61,\\15x^2+3y^2=61x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(5x^2+y^2=61),(15x^2+3y^2-61x=0):}`
Разделим обе части на -3 в нижнем уравнении
`{(5x^2+y^2=61),(-5x^2-y^2+(61/3)x=0):}`
Исключим одну из переменных путем сложения уравнений
`(61/3)x=61`
`x=3`
Подставим значение x в `5x^2+y^2=61`
`5*3^2+y^2=61`
`y^2=61-46`
`y^2=16`
`y=±4`
Решения системы уравнений: (3; −4) и (3; 4).
Ответ:
(x1, y1) = (3, -4)
(x2, y2) = (3, 4)
Номер: 11667F
Решите систему уравнений $\left\{\begin{array}{l}3x^2+2y^2=50,\\12x^2+8y^2=50x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(3x^2+2y^2=50),(12x^2+8y^2-50x=0):}`
Разделим обе части на -4 в нижнем уравнении
`{(3x^2+2y^2=50),(-3x^2-2y^2+(50/4)x=0):}`
Исключим одну из переменных путем сложения уравнений
`(50/4)x=50`
`x=4`
Подставим значение x в `3x^2+2y^2=50`
`3*4^2+2y^2=50`
`y^2=50-48`
`2y^2=2`
`y=±1`
Решения системы уравнений: (4; −1) и (4; 1).
Ответ:
(x1, y1) = (4, -1)
(x2, y2) = (4, 1)
Номер: F0912F
Решите систему уравнений $\left\{\begin{array}{l}2x^2+y^2=36,\\8x^2+4y^2=36x.\end{array}\right.$.
Решение:
Перенесем переменную в левую часть равенства
`{(2x^2+y^2=36),(8x^2+4y^2-36x=0):}`
Разделим обе части на -4 в нижнем уравнении
`{(2x^2+y^2=36),(-2x^2-y^2+9x=0):}`
Исключим одну из переменных путем сложения уравнений
`9x=36`
`x=4`
Подставим значение x в `2x^2+y^2=36`
`2*4^2+y^2=36`
`y^2=4`
`y=±2`
Решения системы уравнений: (4; −2) и (4; 2).
Ответ:
(x1, y1) = (4, -2)
(x2, y2) = (4, 2)
Номер: 253706
Найдите значение выражения
Найдите значение выражения 61a−11b+50, если $\frac{2a-7b+5}{7a-2b+5}=9$
Решение:
2a−7b+5 = 9 (7a−2b+5)
2a−7b+5 = 63a - 18b + 45
63a - 18b + 45 - 2a + 7b - 5 = 0
61a - 11b + 40 = 0
61a−11b+50 = (61a−11b+40)+10 = 0 + 10 = 10
Ответ: 10
Номер: 272B07
Найдите значение выражения 39a−15b+25, если $\frac{3a-6b+4}{6a-3b+4}=7$
Решение:
3a−6b+4 = 7 (6a−3b+4)
3a−6b+4 = 42a - 21b + 28
42a - 21b + 28 - 3a + 6b - 4 = 0
39a - 15b + 24 = 0
39a−15b+25 = (39a−15b+24)+1 = 0 + 1 = 1
Ответ: 1
Номер: E06DFB
Найдите значение выражения 31a−4b+55, если $\frac{a-4b+7}{4a-b+7}=8$
Решение:
a−4b+7 = 8 (4a−b+7)
a−4b+7 = 32a - 8b + 56
32a - 8b + 56 - a + 4b - 7 = 0
31a - 4b + 49 = 0
31a−4b+55 = (31a−4b+49)+6 = 0 + 6 = 6
Ответ: 6
Номер: 105F79
Найдите значение выражения 41a−11b+15, если $\frac{4a-9b+3}{9a-4b+3}=5$
Решение:
4a−9b+3 = 5 (9a−4b+3)
4a−9b+3 = 45a - 20b + 15
45a - 20b + 15 - 4a + 9b - 3 = 0
41a - 11b + 12 = 0
41a−11b+15 = (41a−11b+12)+3 = 0 + 3 = 3
Ответ: 3
Номер: 120B5C
Найдите значение выражения 19a−7b+12, если $\frac{5a-8b+2}{8a-5b+2}=3$
Решение:
5a−8b+2 = 3 (8a−5b+2)
5a−8b+2 = 24a - 15b + 6
24a - 15b + 6 - 5a + 8b - 2 = 0
19a - 7b + 4 = 0
19a−7b+12 = (19a−7b+4)+8 = 0 + 8 = 8
Ответ: 8
Номер: D6B729
Найдите значение выражения 25a−5b+22, если $\frac{3a-7b+6}{7a-3b+6}=4$
Решение:
a−7b+6 = 4 (7a−3b+6)
3a−7b+6 = 28a - 12b + 24
28a - 12b + 24 - 3a + 7b - 6 = 0
25a - 5b + 18 = 0
25a−5b+22 = (25a−5b+18)+4 = 0 + 4 = 4
Ответ: 4
Номер: E18558
Найдите значение выражения 28a−7b+40, если $\frac{2a-5b+7}{5a-2b+7}=6$
Решение:
2a−5b+7 = 6 (5a−2b+7)
2a−5b+7 = 30a - 12b + 42
30a - 12b + 42 - 2a + 5b - 7 = 0
28a - 7b + 35 = 0
28a−7b+40 = (28a−7b+35)+5 = 0 + 5 = 5
Ответ: 5
Номер: 125CD4
Найдите значение выражения 33a−23b+71, если $\frac{3a-4b+8}{4a-3b+8}=9$
Решение:
3a−4b+8 = 9 (4a−3b+8)
3a−4b+8 = 36a - 27b + 72
36a - 27b + 72 - 3a + 4b - 8 = 0
33a - 23b + 64 = 0
33a−23b+71 = (33a−23b+64)+7 = 0 + 7 = 7
Ответ: 7
Номер: 1A8DA9
Найдите значение выражения 41a−b+45, если $\frac{a-6b+5}{6a-b+5}=7$
Решение:
41а-b+45, если `(а-6b+5)/(6a-b+5)=7`
Переписываем часть после если и получаем:
`(а-6b+5)/(6a-b+5)=7/1` (пропорция)
7(а-6b+5)=1(6a-b+5)
42a-a-7b+6b=5-35
41a-b=-30, тогда
41a-b+45=-30+45=15
Ответ: 15
Номер: C7B10B
Найдите значение выражения 11a−7b+21, если $\frac{4a-5b+6}{5a-4b+6}=3$
Решение:
Чтобы найти значение выражения, преобразуем равенство;
(4a-5b+6)/(5a-4b+6)=3;
(4a-5b+6)=3*(5a-4b+6);
4a-5b+6=15a-12b+18;
4a-5b+6-15a+12b-18=0;
-11a+7b-12=0 (*-1);
11a-7b+12=0;
11a-7b+21-9=0 представим 12 в виде разности 21-9, тогда;
11a-7b+21=9.
Ответ: 9
Номер: F64A87

