Один из видов заданий из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, которые могут вам попасться на реальном экзамене в этом году.
Вспоминаем, что центральный угол окружности — это угол, образованный двумя радиусами окружности, вершина которого совпадает с центром окружности. Дуга, лежащая во внутренней области угла, называется дугой, соответствующей этому центральному углу. Дугу окружности можно измерять в градусах. Градусная мера дуги — это градусная мера соответствующего ей центрального угла. Сумма градусных мер двух дуг с общими концами равна 360°.
Реальные задания по геометрии из банка ФИПИ
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
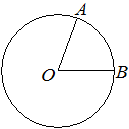
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 66°.
Значит градусная мера большей дуги равна
360° - 66° = 294°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
66° - 99
294° - х
66 = 99
294 х
x = 294*99
66
x = 294*3
2
х = 441
Ответ: 441
7F142F
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=140°. Длина меньшей дуги AB равна 98. Найдите длину большей дуги AB.
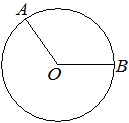
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 98°.
Значит градусная мера большей дуги равна
360° - 140° = 220°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
140° - 98
220° - х
140 = 98
220 х
x = 220*98
140
x = 21560
140
х = 154
Ответ: 154
BDEBC5
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=122°. Длина меньшей дуги AB равна 61. Найдите длину большей дуги AB.
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 122°.
Значит градусная мера большей дуги равна
360° - 122° = 238°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
122° - 61
238° - х
122 = 61
238 х
x = 238*61
122
x = 14518
122
х = 119
Ответ: 119
A18BFC
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=18°. Длина меньшей дуги AB равна 5. Найдите длину большей дуги AB.
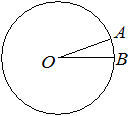
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 18°.
Значит градусная мера большей дуги равна
360° - 18° = 342°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
18° - 5
342° - х
18 = 5
342 х
x = 342*5
18
x = 1710
18
х = 95
Ответ: 95
7057F4
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=45°. Длина меньшей дуги AB равна 91. Найдите длину большей дуги AB.
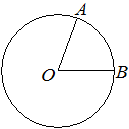
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 45°.
Значит градусная мера большей дуги равна
360° - 45° = 315°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
45° - 91
315° - х
45 = 91
315 х
x = 315*91
45
x = 28665
45
х = 637
Ответ: 637
F9F4CA
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги AB.
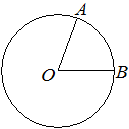
Решение:
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 40°.
Значит градусная мера большей дуги равна
360° - 40° = 320°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
40° - 50
320° - х
40 = 50
320 х
x = 8320*50
40
х = 8*50
х = 400
Ответ: 400
5A934C
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=80°. Длина меньшей дуги AB равна 58. Найдите длину большей дуги AB.
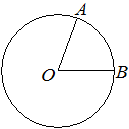
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 80°.
Значит градусная мера большей дуги равна
360° - 80° = 280°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
80° - 58
280° - х
80 = 58
280 х
x = 280*58
80
x = 16240
80
х = 203
Ответ: 203
41B474
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=20°. Длина меньшей дуги AB равна 88. Найдите длину большей дуги AB.
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 20°.
Значит градусная мера большей дуги равна
360° - 20° = 340°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
20° - 88
340° - х
20 = 88
340 х
x = 340*88
20
x = 29920
20
х = 1496
Ответ: 1496
0F64A4
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=15°. Длина меньшей дуги AB равна 48. Найдите длину большей дуги AB.
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 15°.
Значит градусная мера большей дуги равна
360° - 15° = 345°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
15° - 48
345° - х
15 = 48
345 х
x = 345*48
15
x = 16560
15
х = 1104
Ответ: 1104
86C060
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=120°. Длина меньшей дуги AB равна 67. Найдите длину большей дуги AB.
Решение:
Мы знаем, что номинал отрезка по периметру окружности зависит от градусной меры. Какой-либо сектор этой окружности по градусам и размер дуги для этого сектора, будет пропорционален градусам ко всей окружности и размер дуги и также будет пропорционален ко всему периметру этой окружности.
∠AOB является центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 120°.
Значит градусная мера большей дуги равна
360° - 120° = 240°
Пусть х - длина большей дуги, тогда получаем пропорцию:
градусы длина
120° - 67
240° - х
120 = 67
240 х
x = 240*67
120
x = 16080
120
х = 134
Ответ: 134
9C53BA
