Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
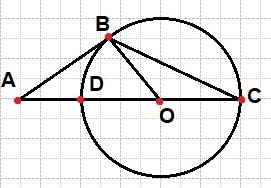
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=9, AC=12.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем AB2=AC*AD, при этом неизвестное здесь AD, которое и выражаем.
AD=AB2/AC=92/12=81/12=6,75
Теперь остается из AC вычесть AD и найдем диаметр.
12-6,75=5,25
Ответ: 5,25
EFA5CC
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=3, AC=5.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем AB2=AC*AD, при этом неизвестное здесь AD, которое и выражаем.
AD=AB2/AC=32/5=9/5=1,8
Теперь остается из AC вычесть AD и найдем диаметр.
5-1,8=3,2
Ответ: 3,2
631164
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=2, AC=8.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем AB2=AC*AD, при этом неизвестное здесь AD, которое и выражаем.
AD=AB2/AC=22/8=4/8=0,5
Теперь остается из AC вычесть AD и найдем диаметр.
8-0,5=7,5
Ответ: 7,5
0A90C5
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=1, AC=5.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем AB2=AC*AD, при этом неизвестное здесь AD, которое и выражаем.
AD=AB2/AC=12/5=1/5=0,2
Теперь остается из AC вычесть AD и найдем диаметр.
5-0,2=4,8
Ответ: 4,8
6D4E75
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=3, AC=9.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем AB2=AC*AD, при этом неизвестное здесь AD, которое и выражаем.
AD=AB2/AC=32/9=9/9=1
Теперь остается из AC вычесть AD и найдем диаметр.
9-1=8
Ответ: 8
118EC8
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB=8.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. При этом по свойству касательной и секущей, так как AB касательная до проведенный радиус к ней будет перпендикуляром, то есть треугольник ABO прямоугольным. Из этого утверждения по теореме Пифагора можно найти AO, прибавим половину диаметра, то есть радиус и найдем необходимое нам AC.
$AO^2=\sqrt{AB^2+OB^2}=\sqrt{8^2+1.8^2}\;=\sqrt{64+3.24}\;=\;\sqrt{67,24}=\;8,2$
8.2+1.8=10
Ответ: 10
F0C3BD
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 6,4, а AB=6.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. При этом по свойству касательной и секущей, так как AB касательная до проведенный радиус к ней будет перпендикуляром, то есть треугольник ABO прямоугольным. Из этого утверждения по теореме Пифагора можно найти AO, прибавим половину диаметра, то есть радиус и найдем необходимое нам AC.
$AO=\sqrt{AB^2+OB^2}=\sqrt{6^2+3.2^2}\;=\sqrt{36+10.24}\;=\;\sqrt{46,24}=\;6.8$
6.8+3.2=10
Ответ: 10
F6CC6F
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. При этом по свойству касательной и секущей, так как AB касательная до проведенный радиус к ней будет перпендикуляром, то есть треугольник ABO прямоугольным. Из этого утверждения по теореме Пифагора можно найти AO, прибавим половину диаметра, то есть радиус и найдем необходимое нам AC.
$AO=\sqrt{AB^2+OB^2}=\sqrt{4^2+4.2^2}\;=\sqrt{16+17.64}\;=\;\sqrt{33.64}=\;5.8$
5.8+4.2=10
Ответ: 10
D5F808
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 15, а AB=4.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. При этом по свойству касательной и секущей, так как AB касательная до проведенный радиус к ней будет перпендикуляром, то есть треугольник ABO прямоугольным. Из этого утверждения по теореме Пифагора можно найти AO, прибавим половину диаметра, то есть радиус и найдем необходимое нам AC.
$AO=\sqrt{AB^2+OB^2}=\sqrt{4^2+7.5^2}\;=\sqrt{16+56.25}\;=\;\sqrt{72.25}=\;8.5$
8.5+7.5=16
Ответ: 16
19BB60
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB=15.
Решение:
Пусть окружность второй раз пересекает прямую AC в точке D. При этом по свойству касательной и секущей, так как AB касательная до проведенный радиус к ней будет перпендикуляром, то есть треугольник ABO прямоугольным. Из этого утверждения по теореме Пифагора можно найти AO, прибавим половину диаметра, то есть радиус и найдем необходимое нам AC.
$AO=\sqrt{AB^2+OB^2}=\sqrt{15^2+8^2}\;=\sqrt{225+64}\;=\;\sqrt{289}=\;17$
17+8=25
Ответ: 25
C911B9