Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
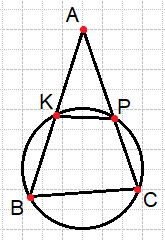
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=6, а сторона AC в 1,5 раза больше стороны BC.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.5\ast BC}=\frac{AK}{1.5}$
6:1,5=4
Ответ: 4
3A4E2D
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=14, а сторона AC в 2 раза больше стороны BC.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{2\ast BC}=\frac{AK}{2}$
14:2=7
Ответ: 7
23F177
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.2\ast BC}=\frac{AK}{1.2}$
18:1,2=15
Ответ: 15
27E2F1
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=7, а сторона AC в 1,4 раза больше стороны BC.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.4\ast BC}=\frac{AK}{1.4}$
7:1,4=5
Ответ: 5
3BDDCB
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=16, а сторона AC в 1,6 раза больше стороны BC.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.6\ast BC}=\frac{AK}{1.6}$
16:1,6=10
Ответ: 10
E847C5
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=36, а сторона BC в 1,8 раза меньше стороны AB.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов. Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов. Из приведённых равенств, получаем, что ∠KBC=∠APK. Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.8\ast BC}=\frac{AK}{1.8}$
36:1,8=20
Ответ: 20
9A2CC6
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=21, а сторона BC в 1,5 раза меньше стороны AB.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.8\ast BC}=\frac{AK}{1.8}$
36:1,8=20
Ответ: 20
AD1CCC
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=9, а сторона BC в 3 раза меньше стороны AB.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{3\ast BC}=\frac{AK}{3}$
9:3=3
Ответ: 3
853489
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=34, а сторона BC в 2 раза меньше стороны AB.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{2\ast BC}=\frac{AK}{2}$
34:2=17
Ответ: 17
DDE606
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=30, а сторона BC в 1,2 раза меньше стороны AB.
Решение:
Поскольку четырёхугольник KPCB вписан в окружность, сумма противоположных углов равна 180°, следовательно, ∠KBC + ∠KPC=180 градусов.
Углы APK и KPC — смежные, следовательно, ∠APK + ∠KPC=180 градусов.
Из приведённых равенств, получаем, что ∠KBC=∠APK.
Рассмотрим треугольники ABC и AKP, угол A — общий, углы APK и KBC равны, следовательно, треугольники подобны, откуда:
KP/BC = AK/AC = AP/AB
AK/AC = KP/BC, найдём KP:
$\frac{AK}{AC}=\frac{KP}{BC}\\KP=\frac{AK\ast BC}{AC}\\KP=\frac{AK\ast BC}{1.2\ast BC}=\frac{AK}{1.2}$
30:1,2=25
Ответ: 25
A39656