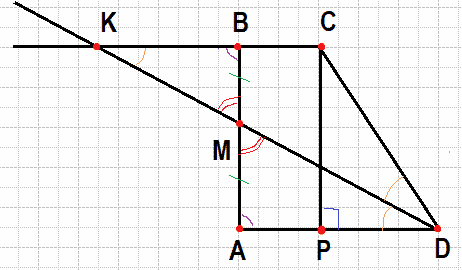
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK будут равны как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CDK  — равнобедренный:
KC = CD = 41.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 41 - 16 = 25.

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD = AD - BC = 25 - 16 = 9

По построению BCPA - параллелограмм, значит
CP=AB=40

Теперь надо догадаться, что △CPD прямоугольный. Если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=41²-9²
CP=√(1681-81)=√ 1600=40 . Точно, прямоугольный.

Но записываем так:

По теореме, ОБРАТНОЙ теореме Пифагора, если PD²+CP²=CD² , то треугольник прямоугольный.

(Кто не в курсе, обратная теорема Пифагора:
Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.
Если a² + b² = c², то треугольник ABC — прямоугольный.)

PD² + CP² = 9² + 40² = 1681
CD² = 41² = 1681 ,
1681 = 1681, следовательно PD²+CP²=CD²  и треугольник CPD прямоугольный.

Значит, CP является высотой трапеции.

В итоге нам известны основания 25, 16 и высота 40. Можем найти площадь трапеции:

$S_{BCAD}=\frac{BC+AD}2\ast CP=\frac{25+16}2\ast40=\frac{41}2\ast40=20,5\ast20=820$

Ответ: 820

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK будут равны как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CDK  — равнобедренный:
KC = CD = 25.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 25 - 9 = 16.

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 16

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=16-9=7

По построению BCPA - параллелограмм, значит
CP = AB = 24

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=25²-7²
CP=√ (625-49)=√ 576=24

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 9, 16 и высота 24. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{9+16}2\ast24=\frac{25}2\ast24=12.5\ast24=300$

Ответ: 300

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=26.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 26 - 1 = 25

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=25-1=24

По построению BCPA - параллелограмм, значит
CP = AB = 10

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=26²-24²
CP=√ (676-576)=√ 100=10

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 25 и высота 10. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+25}2\ast10=\frac{26}2\ast10=13\ast10=130$

Ответ: 130

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=29.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 29 - 4 = 25

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 25

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=25-4=21

По построению BCPA - параллелограмм, значит
CP = AB = 20

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=29²-21²
CP=√ (841-576)=√ 400=20

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 25 и высота 20. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{4+25}2\ast20=\frac{29}2\ast20=14.5\ast20=290$

Ответ: 290

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=10.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 10 - 1 = 9

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 9

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=9-1=8

По построению BCPA - параллелограмм, значит
CP = AB = 6

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=10²-8²
CP=√ (100-64)=√ 36=6

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 8 и высота 6. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+8}2\ast6=\frac{9}2\ast6=4.5\ast6=27$

Ответ: 27

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=13.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 13 - 4 = 9

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 9

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=9-4=5

По построению BCPA - параллелограмм, значит
CP = AB = 12

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=13²-5²
CP=√ (169-25)=√ 144=12

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{4+9}2\ast12=\frac{13}2\ast12=6.5\ast12=78$

Ответ: 78

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=34.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 34 - 2 = 32

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 32

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=32-2=30

По построению BCPA - параллелограмм, значит
CP = AB = 16

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=34²-30²
CP=√ (1156-900)=√ 256=16

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{2+32}2\ast16=\frac{34}2\ast16=17\ast16=272$

Ответ: 272

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC = CD = 5.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 5 - 1 = 4

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 4

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=4-1=3

По построению BCPA - параллелограмм, значит
CP = AB = 4

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=5²-3²
CP=√ (25-9)=√ 16=4

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 1, 3 и высота 4. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{1+3}2\ast4=\frac{4}2\ast4=2\ast4=8$

Ответ: 8

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=35.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 35 - 7 = 28

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 28

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=28-7=21

По построению BCPA - параллелограмм, значит
CP = AB = 28

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=35²-21²
CP=√ (1225-441)=√ 784=28

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 28, 7 и высота 28. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{7+28}2\ast28=\frac{35}2\ast28=17.5\ast28=490$

Ответ: 490

Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD  — равнобедренный:
KC=CD=10.

Найдём KB, вычитая известное основание из известной стороны по условиям задачи:
KB = KC - BC = 10 - 2 = 8

Рассмотрим треугольники KMB и AMD. Углы KMB и AMD равны как вертикальные; углы KBM и MAD равны как накрест лежащие при параллельных прямых; AM=BM по условию. Значит, эти треугольники равны по стороне и 2-м прилежащим к ней углам (2-й признак равенства треугольников). Отсюда 
AD = KB = 8

Проведем отрезок CP от одного основания к другому параллельно BA. Получится, что BC = AP, из этого мы сможем найти отрезок PD:
PD=AD-BC=8-2=6

По построению BCPA - параллелограмм, значит
CP = AB = 8

Теперь, если бы треугольник CPD был бы прямоугольным, то по теореме Пифагора было бы верно утверждение CD²=PD²+CP²
Подставим известные нам значения для PD и СD:
CP²=CD²-PD²
CP²=10²-6²
CP=√ (100-36)=√ 64=8

Получившееся значение CP равно AB, значит для треугольника CPD действует теорема Пифагора и он прямоугольный. То есть CP является высотой трапеции.

В итоге нам известны основания 8, 2 и высота 8. Можем найти площадь трапеции:

$\;S_{BCAD}=\frac{2+8}2\ast8=\frac{10}2\ast8=5\ast8=40$

Ответ: 40