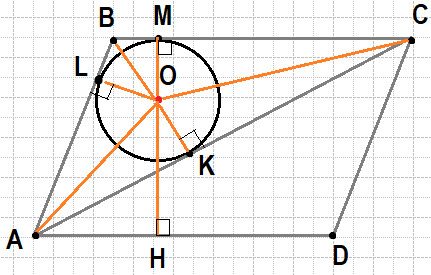
Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{25-9}$ = 4

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 4.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{4+4+2BM+2MC}2\ast3=3\ast(4+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(3+4)\ast(BM+MC)=7\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{7\ast(BM+MC)}2=3\;\ast\;(\;4\;+\;B\;M\;+\;M\;C)\\7\ast(BM+MC)\;=\;6\;\ast\;(\;4\;+\;B\;M\;+\;M\;C)\\7\ast(BM+MC)\;=\;24\;+\;6\;\ast\;(B\;M\;+\;M\;C)\\7\ast(BM+MC)\;-\;6\;\ast\;(B\;M\;+\;M\;C)\;=\;24\\B\;M\;+\;M\;C\;=\;24\\\\\\$

 То есть основание BC = 24.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(3+4)*24=168

Ответ:  168

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(6+5)\ast(BM+MC)=11\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{11\ast(BM+MC)}2=5\ast(12+BM+MC)\\11\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\11\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\11\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\B\;M+M\;C\;=\;120\\\\\\$

 То есть основание BC = 120.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+6)*120=1320

Ответ:  1320

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(7+5)\ast(BM+MC)=12\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{12\ast(BM+MC)}2=5\ast(12+BM+MC)\\12\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\12\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\12\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\2\ast(BM+MC)\;=\;120\\BM+MC\;=\;60\\\\\\\\$

 То есть основание BC = 60.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(7+5)*60=720

Ответ:  720

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(8+5)\ast(BM+MC)=13\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{13\ast(BM+MC)}2=5\ast(12+BM+MC)\\13\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\13\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\13\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\3\ast(BM+MC)\;=\;120\\BM+MC\;=\;40\\\\\\\\$

 То есть основание BC = 40.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+8)*40=520

Ответ:  520

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(9+5)\ast(BM+MC)=14\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{14\ast(BM+MC)}2=5\ast(12+BM+MC)\\14\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\14\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\14\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\4\ast(BM+MC)\;=\;120\\BM+MC\;=\;30\\\\\\\\$

 То есть основание BC = 30.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+9)*30=420

Ответ:  420

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(13+7)\ast(BM+MC)=20\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{20\ast(BM+MC)}2=7\ast(24+BM+MC)\\20\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\20\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\20\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\6\ast(BM+MC)\;=\;336\\BM+MC\;=\;56\\\\\\\\$

 То есть основание BC = 56.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(13+7)*56=1120

Ответ:  1120

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(14+7)\ast(BM+MC)=21\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{21\ast(BM+MC)}2=7\ast(24+BM+MC)\\21\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\21\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\21\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\7\ast(BM+MC)\;=\;336\\BM+MC\;=\;48\\\\\\\\$

 То есть основание BC = 48.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(14+7)*48=1008

Ответ:  1008

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(15+7)\ast(BM+MC)=22\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{22\ast(BM+MC)}2=7\ast(24+BM+MC)\\22\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\22\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\22\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\8\ast(BM+MC)\;=\;336\\BM+MC\;=\;42\\\\\\\\$

 То есть основание BC = 42.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(15+7)*42=924

Ответ:  924

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(17+7)\ast(BM+MC)=24\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{24\ast(BM+MC)}2=7\ast(24+BM+MC)\\24\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\24\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\24\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\10\ast(BM+MC)\;=\;336\\BM+MC\;=\;33,6\\\\\\\\$

 То есть основание BC = 33,6.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(17+7)*33,6=806,4

Ответ:  806,4

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(19+7)\ast(BM+MC)=26\ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$\frac{26\ast(BM+MC)}2=7\ast(24+BM+MC)\\26\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\26\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\26\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\12\ast(BM+MC)\;=\;336\\BM+MC\;=28\\\\\\\\$

 То есть основание BC = 28.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(19+7)*28=728

Ответ:  728

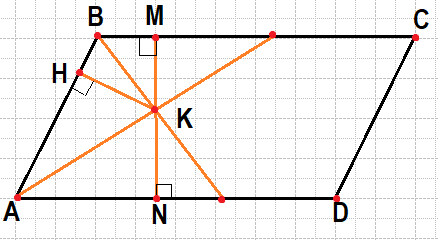
Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=7.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=7. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =19*(7+7)=19*14=266.

Ответ: 266

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=3.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=3. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =11*(3+3)=11*6=66.

Ответ: 66

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=9.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=9. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =12*(9+9)=12*18=216.

Ответ: 216

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =19*(10+10)=19*20=380.

Ответ: 380

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =17*(10+10)=17*20=340.

Ответ: 340.

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =18*(1+1)=18*2=36.

Ответ: 36

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=4.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=4. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =7*(4+4)=7*8=56.

Ответ: 56

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=8.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=8. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =2*(8+8)=2*16=32.

Ответ: 32

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=6.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=6. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =6*(6+6)=6*12=72.

Ответ: 72

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =2*(1+1)=2*2=4.

Ответ: 4