| операция | Формулировка в задании | Python |
| Конъюнкция | A ∧ B | A and B |
| Дизъюнкция | A ∨ B | A or B |
| Инверсия | ¬A | not(A) |
| Импликация | A → B | A <= B |
| Эквиваленция | A ≡ B | A == B |
| Число n делится без остатка на число m | ДЕЛ(n,m) | n%m==0 |
| Поразрядная конъюнкция | m&n | m&n==0 m&n !=0 |
Программное решение №15 (не включая множества и отрезки)
forA in range(1, 1000): #если указано А – натуральное число, то диапазон начинается с 1
flag = True #флаг показывает, подходит нам параметр или нет
forх in range(1, 500): #если указано, что переменные натуральные числа, то с 1
forу in range(1, 500): #количество циклов зависит, от количества переменных в задании
if(<выражение из условия>) == 0:
flag = False #изменяем переменную-флаг, чтобы показать, что параметр не подходит
break #прерываем цикл, дальше перебирать значения нет смысла
if flag == True: #проверяем, что выражение всегда было равно истине
print(A) #выводим ответ
#если в задании просят найти наименьшее значение А, можно поставить break
Аналитический метод решения 15 задания с отрезками
- Упростить данное выражение с помощью равносильных выражений и логических законов.
- Если в итоге получилась дизъюнкция трех элементов, то решаем одним из способов:
- Сопоставить А логическую 1, остальным элементам — 0. Сделать обратную замену и составить систему. Нарисовать получившиеся отрезки на одной числовой прямой. А — в пересечении.
- Нарисовать на одной числовой прямой отрезки в выражении. А — на «свободном» промежутке.
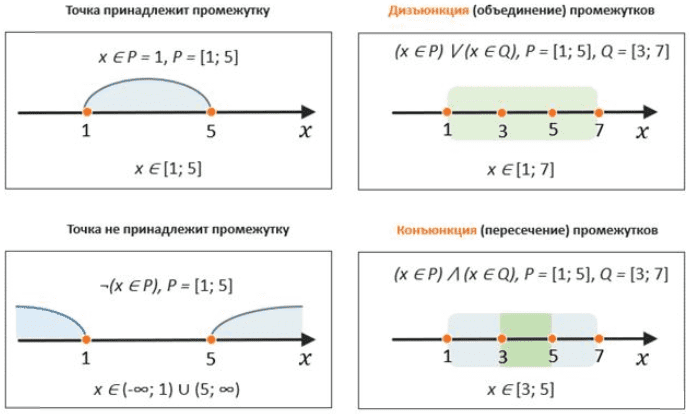
Законы логики
| Формулы де-Моргана | Тавтология |
| ¬(A ∧ B)=¬A ∨ ¬B ¬(A ∨ B)=¬A ∧ ¬B |
A ∧ A=A A ∨ A=A |
| Закон исключенного третьего | Сочетательный закон |
| ¬A ∧ A=0 ¬A ∨ A=1 |
(A ∧ B) ∧ C=A ∧ (B ∧ C) (A ∨ B) ∨ C=A ∨ (B ∨ C) |
| Правила 0 | Распределительный закон |
| 0 ∧ A=0 0 ∨ A=A |
A ∧ (B ∨ C)=(A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C)=(A ∨ B) ∧ (A ∨ C) |
| Правила 1 | Закон поглощения |
| 1 ∧ A=A 1 ∨ A=1 |
A ∧ (A ∨ B)=A A ∨ (A ∨ B)=A |
Прототипы с ЕГЭ
Задача №1 Определите наибольшее целое значение A, при котором выражение
(2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A)
истинно для любых целых положительных значений х и у.
Ответ: 26
Задача №2 Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 6) → ¬ДЕЛ(x, 10)) \/ (x + A > 121)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
Ответ: 92
Задача №3 Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102&01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x&39 = 0 ∨ (x&11 = 0 → ¬(x&А = 0))
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Ответ: 36
Задача №4 Для какого наименьшего целого неотрицательного числа A выражение
(x+2y<A)∨(y>x)∨(x>60)
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?
Ответ: 181
Задача №5 На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что формула
(x∈P)→(((x∈Q)∧¬(x∈A))→¬(x∈P))
истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х
Ответ: 20
Задача №6 Для какого наибольшего целого числа А формула
((x ≤ 9) →(x⋅x ≤ A)) ⋀ ((y⋅y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
Ответ: 99
Задачи уровня ЕГЭ
Задача №1 Обозначим как БОЛЬ(х, А) утверждение, что число х больше А. Сколько существует целых положительных значений параметра А, при которых приведенное ниже выражение истинно для любых натуральных х и у.
(БОЛЬ(x2, 60) ∨ ¬БОЛЬ(x, A)) ∧ (¬БОЛЬ(y2, 90) ∨ БОЛЬ(y, A))
Ответ: 3
Задача №2 Укажите минимальное количество целых чисел, которые принадлежат отрезку А, когда выражение
((x2 + x – 20 ≥ 0) ˅ (х ∉ А)) ˄ ((x2 – 3x – 18 ≤ 0) ˅ (x ∈ A))
тождественно истинно (то есть принимает значение 1) хотя бы для 10 целых значений х?
Ответ: 0
Задача №3 Обозначим через div(n, m) результат целочисленного деления n на m. Для какого наименьшего натурального числа А формула
(div(x,50)>3) ˅ ¬(div(x,13)>3) ˅ (div(x,A)>6)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 1
Задача №4 Обозначим утверждение «х делится на А без остатка», как ДЕЛ(х, А). Сколько целых значений параметра А таковы, что выражение
ДЕЛ(А, 25) /\ (ДЕЛ(х, 24) /\ ДЕЛ(х, 75) → ДЕЛ(х, А))
истинно, т.е. принимает значение 1 при любом целом значении переменной х.
Ответ: 16
Задача №5 На числовой прямой задана пара отрезков P = [254;800] и Q = [410; 823]. Известно, что значение выражения
((x∈P) ˄(x∉A)) → (x∈Q)
истинно на всей числовой прямой. Укажите минимальную длину отрезка А, для которого данное условие соблюдается.
Ответ: 156
Задача №6 Обозначим ПЛОЩ(a, b, c) утверждение «Площадь прямоугольника со сторонами a и b больше c». Найдите наибольшее целое значение А, при котором выражение
¬ПЛОЩ(x, y, A+13) → ПЛОЩ(28, y, 520) ∨ ПЛОЩ(x, 25, 800)
тождественно истинно, то есть принимает значение 1 при любых натуральных значениях x и y.
Ответ: -13
Задача №7 Обозначим через ТРЕУГ(n, m, k) утверждение «существует невырожденный треугольник с длинами сторон n, m и k». Для какого наибольшего натурального числа А формула
¬((ТРЕУГ(х, 11, 18) ≡ (¬(MAKC(x, 5) > 68))) ⋀ ТРЕУГ(х, А, 5))
тождественно истинна (т. е. принимает значение 1) при любом натуральном значении переменной х?
Примечание. МАКС(а, b) = а, если а > b и МАКС(а, b) = b, если а ≤ b.
Ответ: 64

