Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
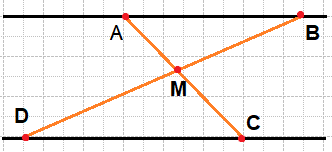
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=14, DC=42, AC=52.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
42/14=3/1, значит в общей длине сторон AC = AM + MC будет 4 части, где одна сторона в три раза больше другой (это три части) и 1 часть - это длина меньшей стороны (катета). А так как МС - катет большего треугольника, тогда:
52:4*3=39
Ответ: 39
A9B305
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=13, DC=65, AC=42.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
65/13=5, тогда в общей длине сторон AC = AM + MC будет 6 частей, где одна сторона в 5 раз больше другой (это 5 частей) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
42:6*5=35
Ответ: 35
2A556B
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=12, DC=48, AC=35.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
48/12=4, тогда в общей длине сторон AC = AM + MC будет 5 частей, где одна сторона в 4 раза больше другой (это 4 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
35:5*4=28
Ответ: 28
D6ACF3
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=11, DC=22, AC=27.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
22/11=2, тогда в общей длине сторон AC = AM + MC будет 3 части, где одна сторона в 2 раза больше другой (это 2 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
27:3*2=18
Ответ: 18
FDCAEE
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=10, DC=25, AC=56.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
25/10=2,5, тогда в общей длине сторон AC = AM + MC будет 3,5 части, где одна сторона в 2,5 раза больше другой (это 2,5 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
56:3,5*2,5=40
Ответ: 40
ACAF91
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
24/16=1,5, тогда в общей длине сторон AC = AM + MC будет 2,5 части, где одна сторона в 1,5 раза больше другой (это 1,5 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
25:2,5*1,5=15
Ответ: 15
2DD84F
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
30/15=2, тогда в общей длине сторон AC = AM + MC будет 3 части, где одна сторона в 2 раза больше другой (это 2 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
39:3*2=26
Ответ: 26
13C50A
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=18, DC=54, AC=48.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
54/18=3, тогда в общей длине сторон AC = AM + MC будет 4 части, где одна сторона в 3 раза больше другой (это 3 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
48:4*3=36
Ответ: 36
105572
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=14, DC=56, AC=40.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
56/14=4, тогда в общей длине сторон AC = AM + MC будет 5 частей, где одна сторона в 4 раза больше другой (это 4 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
40:5*4=32
Ответ: 32
B5852E
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=11, DC=55, AC=30.
Решение:
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные. Следовательно, треугольники DMC и BMA подобны по двум углам.
Значит, их стороны относятся друг другу пропорционально.
Зная их гипотенузу и соотношение между гипотенузами, можно найти и соответственные стороны, зная их общую длину как в нашем случае или одну из сторон в одном из треугольников.
Гипотенузы треугольников относятся как
55/11=5, тогда в общей длине сторон AC = AM + MC будет 6 частей, где одна сторона в 5 раз больше другой (это 5 части) и 1 часть - это длина меньшей стороны ( катета). А так как МС - катет большего треугольника, тогда:
30:6*5=25
Ответ: 25
214395