Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
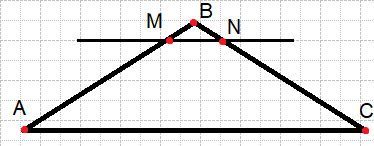
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=51/17=3 - коэффициент подобия.
Значит BC/BN=3, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 2, тогда получается так
BN=32/2=16
Ответ: 16
E208B7
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=11, AC=44, NC=18.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=44/11=4 - коэффициент подобия.
Значит BC/BN=4, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 3, тогда получается так
BN=18/3=6
Ответ: 6
740FCC
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=13, AC=65, NC=28.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=65/13=5 - коэффициент подобия.
Значит BC/BN=5, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 4, тогда получается так
BN=28/4=7
Ответ: 7
75F77A
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=14, AC=21, NC=10.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=21/14=1,5 - коэффициент подобия.
Значит BC/BN=1,5, при этом BC=NC+BN, однако так как BN одна часть, то NC будет половина от этой части 0,5, чтобы получилось 1,5
BN=10/0,5=20
Ответ: 20
F5E152
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=22, AC=55, NC=36.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=55/22=2,5 - коэффициент подобия.
Значит BC/BN=2,5, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 1,5, чтобы получилось 2,5
BN=36/1,5=24
Ответ: 24
D344E8
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=25/15=1 10/15 - коэффициент подобия.
Значит BC/BN=1 10/15, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 10/15, чтобы получилось 1 10/15
BN=(22*15)/10=330/10=33
Ответ: 33
9A0CCB
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=16, AC=20, NC=15.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=20/16=1 4/16 - коэффициент подобия.
Значит BC/BN=1 4/16, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 4/16, чтобы получилось 1 4/16
BN=(15*16)/4=240/4=60
Ответ: 60
591A99
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=42/12=3,5 - коэффициент подобия.
Значит BC/BN=3,5, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 2,5, чтобы получилось 3,5
BN=25/2,5=10
Ответ: 10
5BE0F9
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=18, AC=42, NC=40.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=42/18=2 1/3 - коэффициент подобия.
Значит BC/BN=2 1/3, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 1 1/3, чтобы получилось 2 1/3
BN=40*3/4=120/4=30
Ответ: 30
68B434
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=20, AC=35, NC=39.
Решение:
Рассмотрим треугольники ABC и MBN. В этих треугольниках углы BMN и BAC равны как соответственные, также равны и углы BNM и BCA. Значит, треугольники ABC и MBN подобные по 1 признаку подобия треугольников (по двум углам).
AC/MN=35/20=1,75 - коэффициент подобия.
Значит BC/BN=1,5, при этом BC=NC+BN, однако так как BN одна часть, то NC будет 0,5, чтобы получилось 1,5
BN=39/0,75=52
Ответ: 52
7E7A22