Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

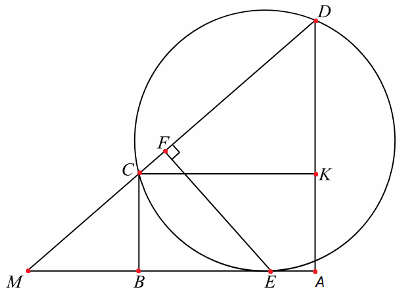
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=14 -12=2. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac2{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{12}2=6CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (6CD + CD)* 6CD=42CD² 

Откуда ME= CD√42. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=2ME/CD=2CD√42/CD=2√42

Ответ: 2√42

CE1DA2

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=14 - 7=7. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac7{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{7}7=CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (CD + CD)* CD=2CD² 

Откуда ME= CD√2. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*7/CD = (7*CD√2)/CD

Ответ: 7√2

C6F56B

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=8, BC=4.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=8 - 4 = 4. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac4{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{4}4=CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (CD + CD)* CD=2CD² 

Откуда ME= CD√2. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*4/CD = (4*CD√2)/CD

Ответ: 4√2

26D14E

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=8, BC=7.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=8 - 7 = 1. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac1{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac71$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (CD  ⁷/₁ + CD)* CD  ⁷/₁ =CD ⁸/₁ *  CD  ⁷/₁ = ⁵⁶/₁ CD²

Откуда ME= CD√56. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*1/CD = (CD√56)/CD = √56

Ответ: √56

EBE71A

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=4, BC=2.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=4 - 2 = 2. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac2{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{2}2=CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (CD + CD)* CD=2CD² 

Откуда ME= CD√2. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*2/CD = (2*CD√2)/CD

Ответ: 2√2

9E2A56

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=12, BC=9.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=12 - 9 = 3. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac3{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{9}3=3CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (3CD + CD)* 3CD=12CD² 

Откуда ME= CD√12. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*3/CD = (3*CD√12)/CD

Ответ: 3√12

8A2B5A

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=20, BC=15.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=20 - 15 = 5. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac5{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{15}5=3CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (3CD + CD)* 3CD=12CD² 

Откуда ME= CD√12. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*5/CD = (5*CD√12)/CD

5√12 = 5*2√3

Ответ: 10√3

57D6A3

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=12, BC=10.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=12 - 10 = 2. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac2{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{10}2=5CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (5CD + CD)* 5CD=30CD² 

Откуда ME= CD√30. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*2/CD = (2*CD√30)/CD

Ответ: 2√30

BD3655

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=6, BC=5.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=6 - 5 = 1. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac2{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{10}2=5CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (5CD + CD)* 5CD=30CD² 

Откуда ME= CD√30. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*2/CD = (2*CD√30)/CD

Ответ: 2√30

D035F7

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=20, BC=10.

Решение:

Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD  — отрезок EF. Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный AB. Рассмотрим четырёхугольник ABCK прямая BC  параллельна AK, прямая AB параллельна прямой CK, угол BAK  — прямой, следовательно, ABCK  — прямоугольник. Откуда AB=KC. Значит, KD=AD - BC=20 - 10 = 10. Из прямоугольного треугольника:

$\cos\angle CDK=\frac{KD}{CD}\;=\;\frac10{CD}$

Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:

$\frac{BC}{KD}=\frac{MC}{CD}\;откуда\\MC=CD\frac{BC}{KD}=CD\frac{10}10=CD$

По теореме о касательной и секущей:

ME² =MD * MC= (MC + CD) * MC= (CD + CD)* CD=2CD² 

Откуда ME= CD√2. Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC  — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  cos∠MEF= cos∠ADM. Найдём EF из прямоугольного треугольника MEF:

EF=ME*cos∠MEF=ME*cos∠ADM=ME*DK/CD=ME*10/CD = (10*CD√2)/CD

Ответ: 10√2

A79D29