На этой странице мы собрали задания ЕГЭ по профильной математике с кратким ответом восьмой линейки - задания с графиками производных различных функций. Все эти задания есть в новом банке ФИПИ, все они выпадали на ЕГЭ по профильной математике в прошлые годы, так что огромные шансы, что и в этом году у вас на ЕГЭ попадется нечто подобное. В старом банке те же типы заданий, только больше примеров.
СТАРЫЙ и НОВЫЙ БАНК.
КЭС : Начала математического анализа Тип ответа: Краткий ответ 36 заданий из нового банка, остальные из старого
Что нужно знать: Если функция возрастает, то производная положительна; если функция убывает, то производная отрицательна; в точках, где функция не возрастает и не убывает (стационарные точки), производная равна 0.
Типы заданий:
- На рисунке изображён график функции y=f(x). На оси абсцисс отмечено _ точек: _. Найдите количество отмеченных точек, в которых производная функции f(x) отрицательна/положительна/равна 0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (_; _). Найдите количество точек экстремума/минимума функции f(x), принадлежащих отрезку [_; _].
- На рисунке изображён график функции y=f(x), определённой на интервале (_; _). Найдите количество корней уравнения f'(x)=0, принадлежащих отрезку [_; _].
- На рисунке изображён график функции y=f(x), определённой на интервале (_; _). Найдите корень уравнения f'(x)=0.
- На рисунке изображён график y=f'(x) — производной функции f(x). На оси абсцисс отмечено _ точек: _. Сколько из этих точек принадлежит промежуткам убывания/возрастания функции f(x)?
- На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены точки − _. В какой из этих точек значение производной наибольшее/наименьшее? В ответе укажите эту точку.
Все варианты задания ЕГЭ мат профи про график производной из нового банка
Впишите правильный ответ.
На рисунке изображён график функции y=f(x). На оси абсцисс отмечено девять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9. Найдите количество отмеченных точек, в которых производная функции f(x) отрицательна.
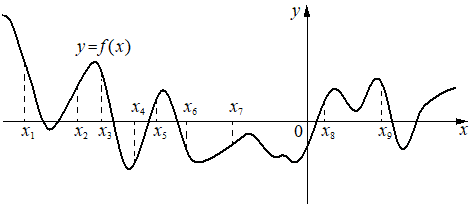
Решение:
Производная отрицательна, если функция убывает.
х1, х3, х6, х9 - функция убывает, 4 точки
Ответ: 4
Номер: 71BC43
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
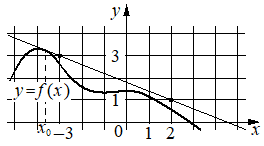
Решение:
-0.4
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-3;3) и (2;1) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (3−1)/(-3-2) ` = -2/5 = -0.4
Ответ: -0.4
Номер: D13540
Впишите правильный ответ.
На рисунке изображён график функции y=f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Найдите количество отмеченных точек, в которых производная функции f(x) положительна.
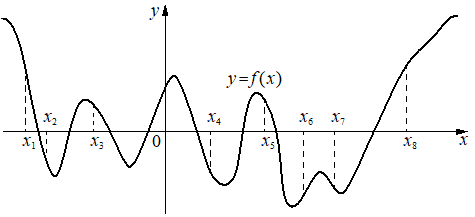
Решение:
2
Производная будет положительной на возрастающей функции
x6, x8 - 2 точки
Ответ:2
Номер: 28FA05
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
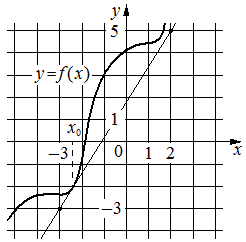
Решение:
1.6
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-3;-3) и (2;5) . Если прямая проходит через точки (x1;y1) и (x2;y2), то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (-3−5)/(-3-2) ` = -8/-5 = 1.6
Ответ: 1.6
Номер: 57C40E
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 19; 3). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [− 17; − 4].
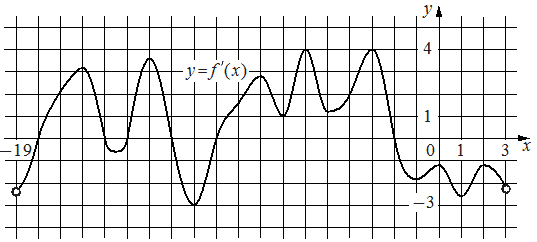
Решение:
4
Рассмотрим график производной y=f'(x) на отрезке [− 17; − 4], проанализируем. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции.
| Области | [− 17; − 15) | -15 | (-15;-14) | -14 | (-14;12) | -12 | (-12;-10) | -10 | (-10; -4) |
| Значение производной (динамика функции) |
+ | 0 | - | 0 | + | 0 | - | 0 | + |
| Что с функцией? | растет↑ | макс | убывает↓ | мин | растет↑ | макс | убывает↓ | мин | растет↑ |
Получается 4 точки где производная равна 0 и меняет свой знак, а значит функция имеет "горбы" максимум или минимум, - точек экстремума.
Универсальное правило, - корни производной являются точками экстремума для самой функции!
Ответ:4
Номер: 0ED279
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
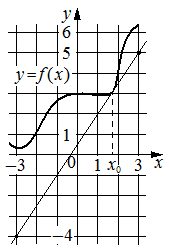
Решение:
1.5
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-3;-4) и (3;5) . Если прямая проходит через точки (x1;y1) и (x2;y2), то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (-4−5)/(-3-3) ` = -9/-6 = 1,5
Ответ: 1.5
Номер: 626B77
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x). На оси абсцисс отмечено одиннадцать точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?
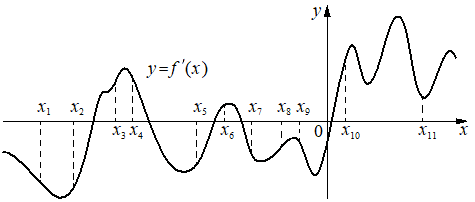
Решение:
6
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции.
| Области | x1, x2 | x2, x3 | x3, x4 | x4, x5 | x5, x6 | x6, x7 | x7 x8 x9 | x9, x10 | x10, x11 |
| Производная (динамика функции) |
- | -0+ | + | +0- | -0+ | +0- | - | -0+ | + |
| Что с функцией | убывает | убывала, вышла на мин., начинается рост |
растет | росла, вышла на макс., началось падение |
убывала, вышла на мин., начался рост |
росла, вышла на макс., началось падение |
было падение | падала, вышла на мин., начался рост |
растет |
| Точки на убывающей функции |
x1, x2 | x5 | x5 | x7 | x7 x8 x9 |
Итого точки на убывающей функции: x1, x2, x5, x7, x8, x9
То есть все отрицательные точки (отрицательные значения y) расположены на убывающем участке функции! Это можно считать за универсальное правило для данной задачи.
Ответ: 6
Номер: D143BD
Впишите правильный ответ.
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены точки − 1 , 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
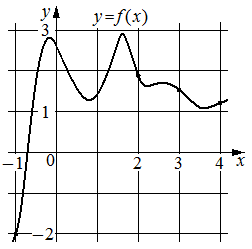
Решение:
-1
Производная функции положительна при возрастании функции. Причем чем выше рост функции, тем больше производная, тогда это точка x= -1.
Ответ:-1
Номер: 56EA1A
Впишите правильный ответ.
На рисунке изображён график y=f '(x) —производной функции f(x).
На оси абсцисс отмечено семь точек: x1, x2, x3, x4, x5, x6, x7. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?
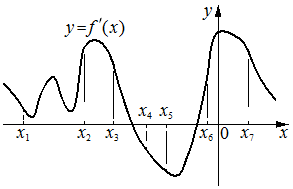
Решение:
2
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции.
| Области | x1, x2, x3 | x3, x4, x5 | x5, x6 | x6, x7 |
| Производная (динамика функции) |
+ | +0- | -0+ | + |
| Что с функцией? | возрастает | растет, выходит на макс., убывает |
убывает, выходит на мин., растет |
растет |
| Точки на области убывания |
x4, x5 | x5 |
Итого: точки на убывающей функции: x4, x5
То есть все отрицательные точки (отрицательные значения y) расположены на убывающем участке функции! Это можно считать за универсальное правило для данной задачи.
Ответ: 2
Номер: C0261C
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
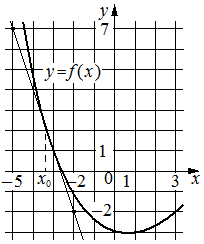
Решение:
-3
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-5;7) и (-2;-2) . Если прямая проходит через точки (x1;y1) и (x2;y2), то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (7+2)/(-5+2) ` = 9/-3 = -3
Ответ: -3
Номер: F9EA20
Впишите правильный ответ.
На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
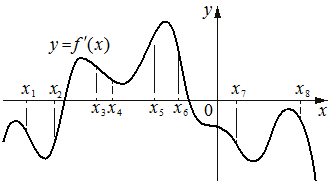
Решение:
4
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции.
| Области | x1, x2 | x2, x3 | x3, x4, x5, x6 | x6, x7, x8 |
| Производная (динамика функции) |
- | -0+ | + | +0- |
| Что с функцией? | убывает | убывает, мин., растет |
растет | растет, макс., убывает |
| Точки | x3 | x3, x4, x5, x6 |
Получаются точки x3, x4, x5, x6 находятся на возрастающей функции.
То есть все положительные точки (положительные значения y) расположены на возрастающем участке функции! Это можно считать за универсальное правило для данной задачи.
Ответ: 4
Номер: 026E2D
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 9; 3). В какой точке отрезка [− 7; − 5] функция f(x) принимает наибольшее значение?
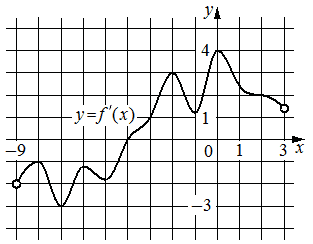
Решение:
-7
Дан график производной, а надо найти значение функции.
В итоге, где производная минимальная, значит там идет самый большой спад функции, а значит можно говорить о ее пике.
Ответ:-7
Номер: 966E26
Впишите правильный ответ.
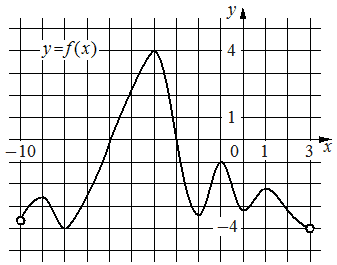
На рисунке изображён график функции y=f(x), определённой на интервале (− 10; 3). Найдите количество корней уравнения f'(x)=0, принадлежащих отрезку [− 7; 2].
Решение:
5
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0- положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции.
Считаем эти точки для координаты x: -4, -2, -1, 0, 1. Всего 5 точек.
Ответ: 5
Номер: BE1DDB
Впишите правильный ответ.
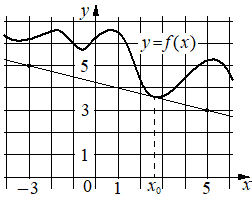
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение:
-0,25
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-3;5) и (5;3) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (5−3)/(-3-5) ` = 2/-8 = -0,25
Ответ: -0,25
Номер: 497F54
Впишите правильный ответ.
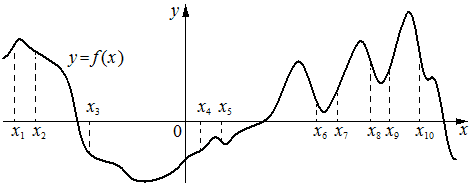
На рисунке изображён график функции y=f(x). На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Найдите количество отмеченных точек, в которых производная функции f(x) отрицательна.
Решение:
6
При убывающей функции ее динамика которая и является производной будет отрицательной. То есть точки в которых производная отрицательная:
x2, x3, x5, x6, x8, x10 Всего 6 точек.
Ответ:6
Номер: FFE757
Впишите правильный ответ.
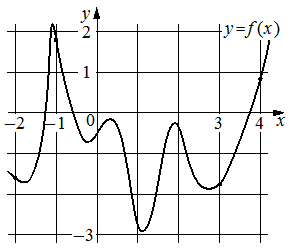
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены точки − 2 , − 1 , 3, 4. В какой из этих точек значение производной наименьшее?
В ответе укажите эту точку.
Решение:
-1
Производная максимально отрицательная при максимальном убывании функции, это точка -1
Ответ: -1
Номер: 099555
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [1; 6].
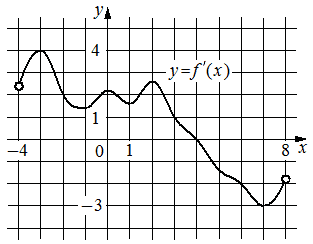
Решение:
4
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции. Производная равна нулю, это и есть точка экстремума функции, x = 4
Ответ: 4
Номер: B81155
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 5; 14). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 4; 9].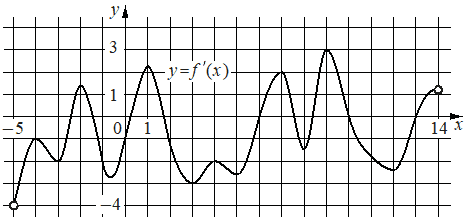
Решение:
4
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции, но нам надо найти из них минимальные.
| Области | -4;-2 | -2; 1 | 1; 6 | 6;9 |
| Производная (динамика функции) |
-0+ | +0-0+ | +0-0 | +0-0+ |
| Что с функцией? | убывает, имеет мин., растет |
растет, имеет макс., убывает, имеет мин., растет |
растет, точка макс., убывает, точка мин. |
растет, точка макс., убывает, точка мин., растет |
| Точки | -2,5 примерно | 0,3 примерно | 5 | 8,5 примерно |
Количество областей функций находящихся ниже оси x и возвращающихся в 0 точно такое же как и количество точек минимума функции!
Ответ: 4
Номер: 4849A6
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 15; 5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 11; 4].
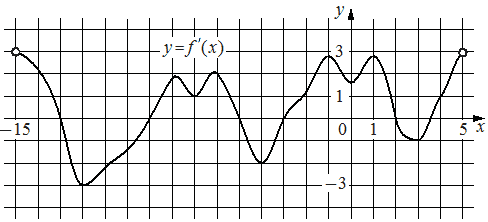
Решение:
2
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции, но нам надо найти из них максимальные.
| Области | -11;-4 | -4; 2 | 2; 4 |
| Производная (динамика функции) |
-0+0 | -0+0 | -0+ |
| Что с функцией? | убывает, имеет мин., растет имеет макс. |
убывает, имеет мин., растет, имеет макс. |
убывает, имеет мин., растет |
| Точки | есть макс | есть макс |
Количество областей функций находящихся выше оси x и возвращающихся в 0 точно такое же как и количество точек максимума функции!
Ответ:2
Номер: 162BAA
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x).
На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?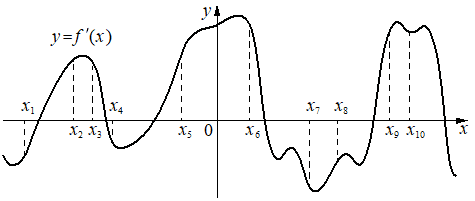
Решение:
6
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции, после которых функция либо растет, либо уменьшается. Находим минимумы и смотрим за точками которые находятся от них и до максимумов.
| Области | x1 x2 x3 | x3 x4 x5 | x5 x6 x7 x8 x9 x 10 |
| Производная (динамика функции) |
-0+ | +0-0+ | +0-0+ |
| Что с функцией? | убывает, мин., растет (x2 x3) |
растет, макс, убывает, мин., растет (x5 x6) |
растет (x6), макс., убывает, мин., растет (x9, x10) |
| Точки | x2 x3 | x5 x6 | x9, x10 |
То есть все положительные точки расположены на возрастающем участке функции! Это можно считать за универсальное правило для данной задачи.
Ответ: 6
Номер: 6796AE
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
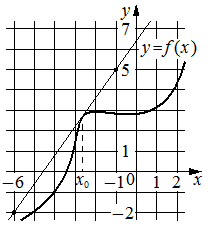
Решение:
1,4
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-1;5) и (-6;-2) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (5+2)/(-1+6) ` = 7/5 = 1,4
или тоже самое если точки взять в другом порядке (поменять первую со второй)
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (-2-5)/(-6+1) `= -7/-5 = 1,4
Ответ: 1,4
Номер: FEE4C3
Впишите правильный ответ.
На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 4). Найдите корень уравнения f'(x)=0.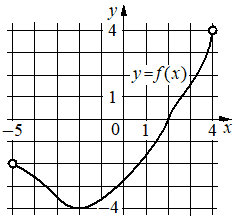
Решение:
-2
В точке минимум производная поменяет свое значение, а значит перейдет через ось абсцисс, что и станет корнем производной
Ответ:-2
Номер: FFF1E1
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.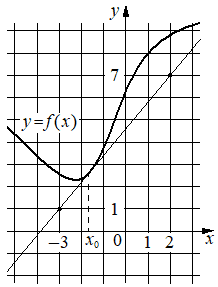
Решение:
1,2
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (2;7) и (-3;1) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (7-1)/(2+3) ` 6/5 = 1,2
Ответ: 1,2
Номер: C380E8
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
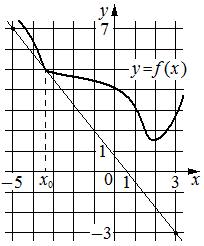
Решение:
-1,25
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-5;7) и (3;-3) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (7+3)/(-5-3) ` 10/-8 = -1,25
Ответ: -1,25
Номер: F25161
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
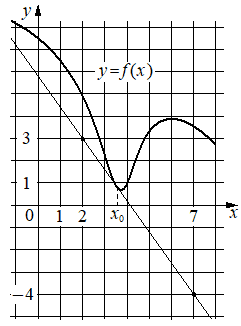
Решение:
-1,4
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (2;3) и (7;-4) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (3+4)/(2-7) ` 7/-5 = -1,4
Ответ: -1,4
Номер: D00D6F
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
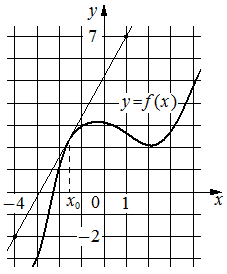
Решение:
1,8
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-4;-2) и (1;7) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (-2-7)/(-4-1) ` -9/-5 = 1,8
Ответ: 1,8
Номер: D79C6E
Впишите правильный ответ.
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки 1, 2, 3, 4. В какой из этих точек значение производной функции f(x) наименьшее? В ответе укажите эту точку.
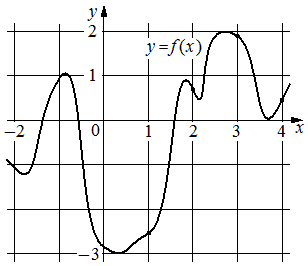
Решение:
2
Производная максимально отрицательная при максимальном убывании функции, это точка 2
Ответ:2
Номер: A2E26B
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
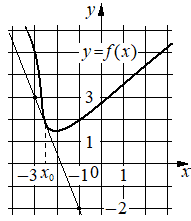
Решение:
-2,5
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-3;3) и (-1;-2) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (3+2)/(-3+1) ` = 5/-2 = -2,5
Ответ: -2,5
Номер: 093E32
Впишите правильный ответ.
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 2, 1, 3, 4. В какой из этих точек значение производной функции f(x) наибольшее? В ответе укажите эту точку.
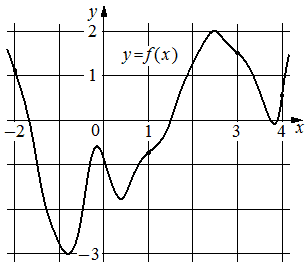
Решение:
4
Производная максимально положительная при максимальном прибавлении функции, это точка 4
Ответ:4
Номер: B65F3D
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 12; 11). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 11; 5].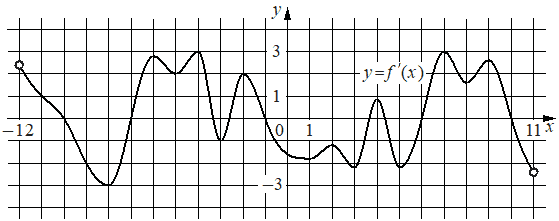
Решение:
4
Рассмотрим график y=f'(x) — производной функции. Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная- 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни.
Делаем вывод, что корни производной образовываются на всех пиках функции, но нам надо найти из них максимальные.
| Области | -11; -10 | -10; -7 | -7;-1 | -1;5 |
| Производная (динамика функции) |
+0 | -0 | +0-0+0 | -0+0- |
| Что с функцией? | растет, макс |
убывает, минимум |
растет, макс, убывает, минимум, растет, макс |
убывает, мин., растет, макс, убывает |
| Точки | -10 | -3,5 примерно -1 |
4,5 примерно |
Количество областей функций находящихся выше оси x и возвращающихся в 0 точно такое же как и количество точек максимума функции!
Ответ:4
Номер: D65930
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
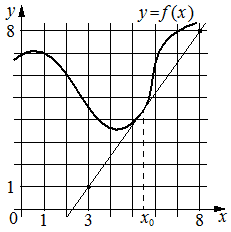
Решение:
1,4
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (3;1) и (8;8) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (1-8)/(3-8) ` = -7/-5 = 1,4
Ответ: 1,4
Номер: DDC830
Впишите правильный ответ.
На рисунке изображён график y=f'(x) — производной функции f(x) , определённой на интервале (− 6; 5). В какой точке отрезка [− 5; − 2] функция f(x) принимает наименьшее значение?
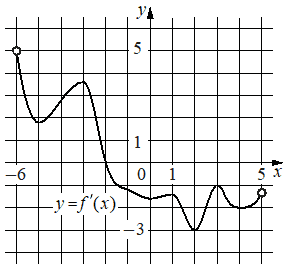
Решение:
-5
Функция от - 5 до -2 имеет положительную производную, а значит функция на всем этом промежутке растет, то есть минимальное значение само функции будет в начальной точке в x=-5
Ответ:-5
Номер: 4DB285
Впишите правильный ответ.
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
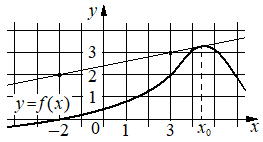
Решение:
0,2
Производная функции f(x) в точке x0 равна тангенсу угла наклона касательной к графику функции в этой точке. По условию эта касательная проходит через точки (-2;2) и (3;3) . Если прямая проходит через точки (x1;y1) и (x2;y2) , то тангенс угла её наклона равен
tg α= `(y1−y2)/(x1-x2)`
Тогда мы может вычислить производную функции f(x) в точке x0:
f`(x0) =tgα = `(y1−y2)/(x1-x2) = (2-3)/(-2-3) ` = -1/-5 = 0,2
Ответ: 0,2
Номер: 7F208A
Впишите правильный ответ.
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечено десять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 . В ответе укажите количество точек (из отмеченных), в которых производная функции f(x) отрицательна.
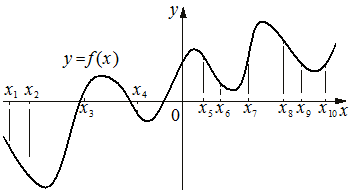
Решение:
7
При убывающей функции динамика отрицательная, то есть производная функции будет отрицательной.
x1 x2 x4 x5 x6 x8 x9 - 7 точек
Ответ: 7
Номер: A62F87
Впишите правильный ответ.
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечено восемь точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В ответе укажите количество точек (из отмеченных), в которых производная функции f(x) положительна.
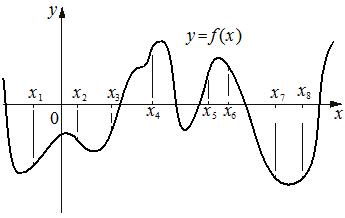
Решение:
5
При возрастающей функции динамика положительная, то есть производная функции будет положительной.
x1 x3 x4 x5 x8 - 5 точек
Ответ: 5
Номер: 655F85
Впишите правильный ответ.
На рисунке изображён график функции y=f(x). На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Найдите количество отмеченных точек, в которых производная функции f(x) положительна.
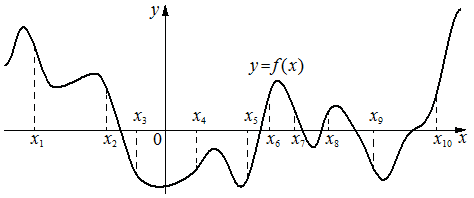
Решение:
5
При возрастающей функции динамика положительная, то есть производная функции будет положительной.
x4 x5 x6 x8 x10 - 5 точек
Ответ: 5
Номер: 875A8A
Задания из старого банка
КЭС: Начала математического анализа. Типы заданий те же, что и в новом банке.
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены восемь точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) отрицательна?
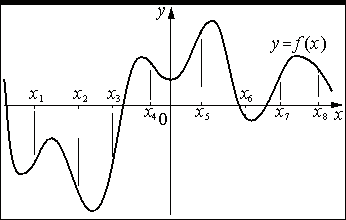
Номер: A2CAD3
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены шесть точек: x1 , x2 , x3 , x4 , x5 , x6 . В скольких из этих точек производная функции f(x) отрицательна?
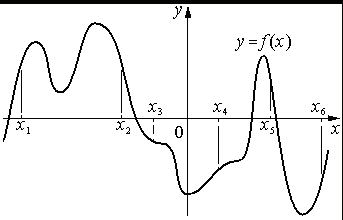
Номер: 3374CF
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены одиннадцать точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 , x11 . В скольких из этих точек производная функции f(x) отрицательна?
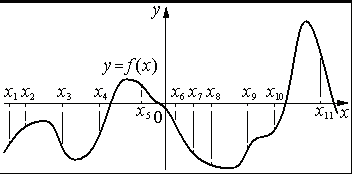
Номер: 77298F
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены семь точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) положительна?
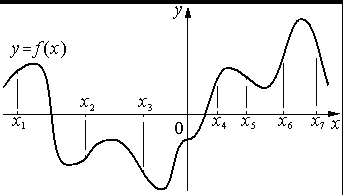
Номер: A5894A
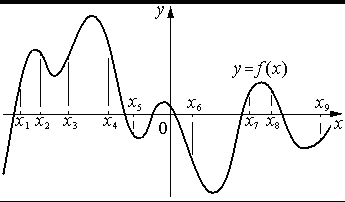
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены девять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) положительна?
Номер: F946BA
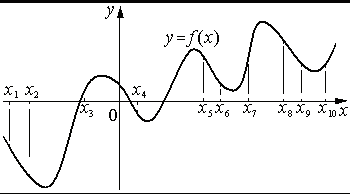
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены десять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 . В скольких из этих точек производная функции f(x) положительна?
Номер: 927992
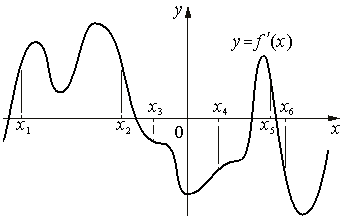
На рисунке изображён график y=f '(x) — производной функции f(x) . На оси абсцисс отмечены шесть точек: x1 , x2 , x3 , x4 , x5 , x6 . Сколько из этих точек лежит на промежутках возрастания функции f(x) ?
Номер: A9FB0A
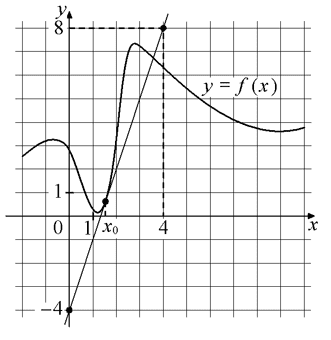
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: 56F47A
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
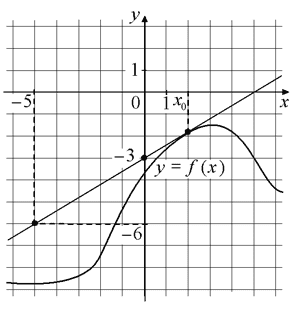
Номер: 0CF013
На рисунке изображён график y=f′(x) — производной функции f(x) , определённой на интервале (−9; 8) . Найдите точку экстремума функции f(x) на отрезке [−3; 3] .
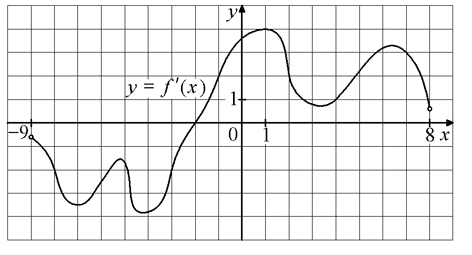
Номер: 720371
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) положительна?
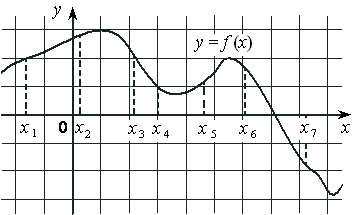
Номер: DFA6D7
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
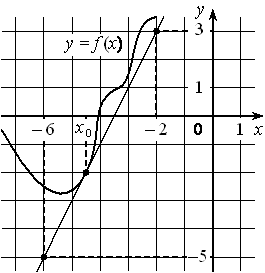
Номер: EB3D0A
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
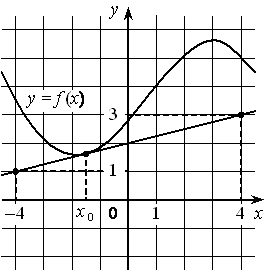
Номер: C70016
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (− 3 ; 8) . Найдите точку минимума функции f(x) .
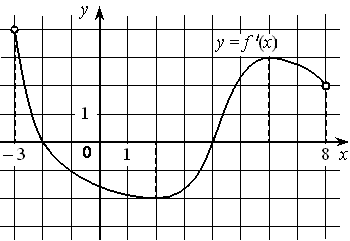
Номер: 453C87
На рисунке изображён график функции y=f(x) , определённой на интервале (− 9; 5) . Найдите количество точек, в которых производная функции f(x) равна 0.
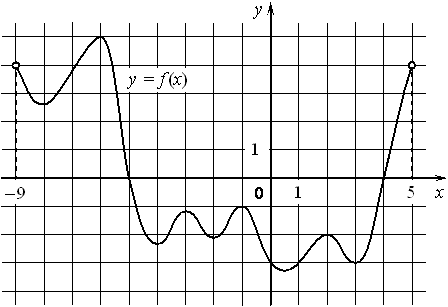
Номер: 8E93FF
На рисунке изображён график функции y=f(x) , определённой на интервале (− 5; 9) . Найдите количество точек, в которых производная функции f(x) равна 0.
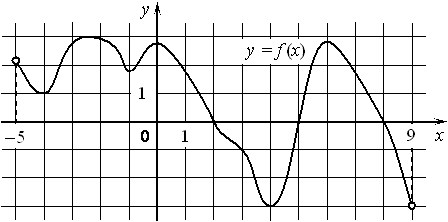
Номер: 9F59EB
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 2; 9) . В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?
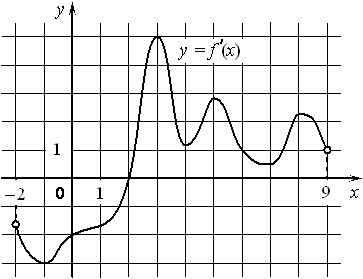
Номер: 12659F
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 8; 4) . В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
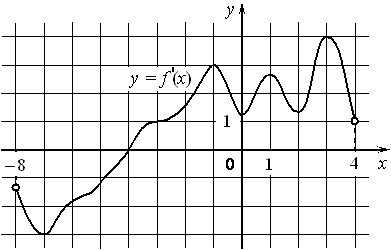
Номер: 88A22A
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
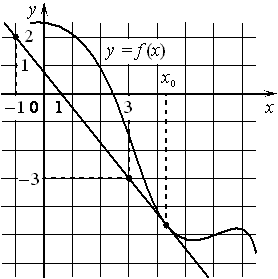
Номер: 5D7FC4
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
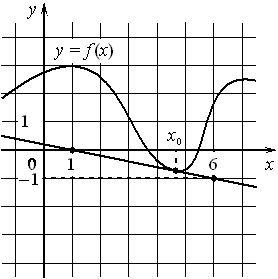
Номер: D2A14A
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
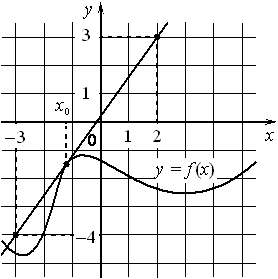
Номер: E58E8A
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
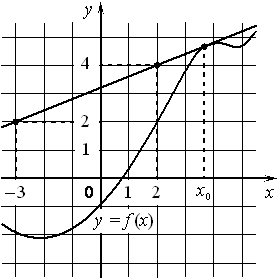
Номер: 854220
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
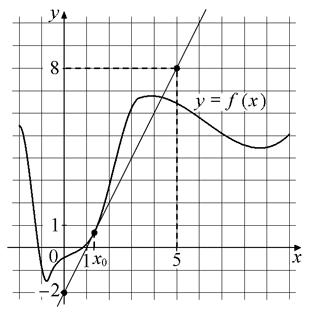
Номер: 4002C5
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
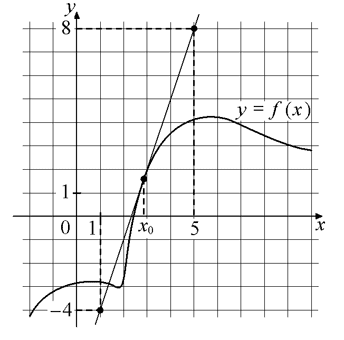
Номер: FDFD5A
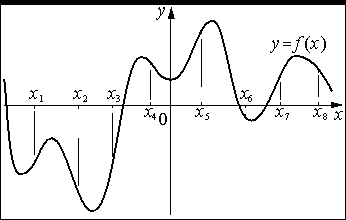
На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены восемь точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) отрицательна?
Номер: 20047E
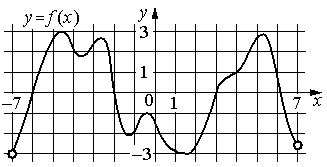
На рисунке изображён график функции y=f(x) , определённой на интервале (− 7 ; 7) . Определите количество целых точек, в которых производная функции положительна.
Номер: 2E361B
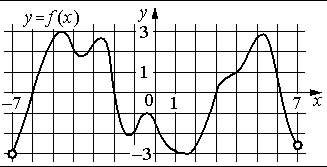
На рисунке изображён график функции y=f(x) , определённой на интервале (− 7 ; 7) . Определите количество целых точек, в которых производная функции отрицательна.
Номер: 55112C
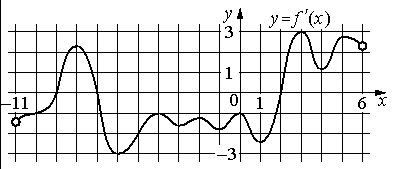
На рисунке изображён график y=f '(x) — производной функции f(x) , определённой на интервале (− 11 ; 6) . Найдите количество точек минимума функции f(x) , принадлежащих отрезку [− 6 ; 4] .
Номер: 7D7A50
На рисунке изображён график функции y=f(x) , определённой на интервале (− 6 ; 6) . Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5] .
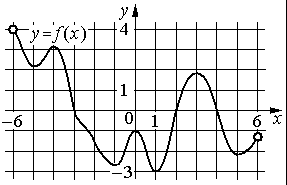
Номер: 9933A1
На рисунке изображён график y=f '(x) — производной функции f(x) . На оси абсцисс отмечены девять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . Сколько из этих точек лежит на промежутках убывания функции f(x) ?
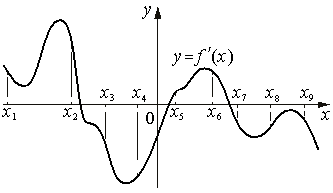
Номер: 8FD3A4
На рисунке изображён график y=f '(x) — производной функции f(x) , определённой на интервале (− 3 ; 19) . Найдите количество точек максимума функции f(x) , принадлежащих отрезку [− 2 ; 15] .
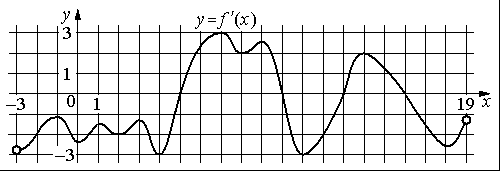
Номер: 25CE62
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (− 3 ; 8) . Найдите точку максимума функции f(x) .
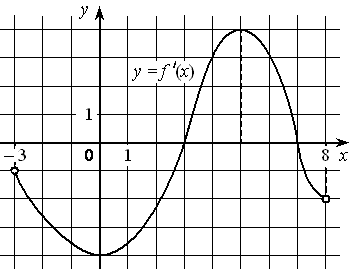
Номер: FFD023
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: AFF52F
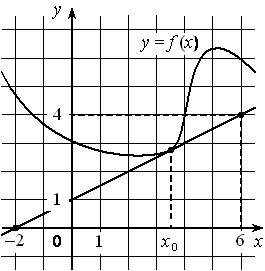
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: E0C82C
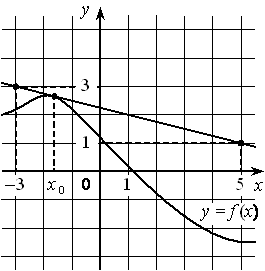
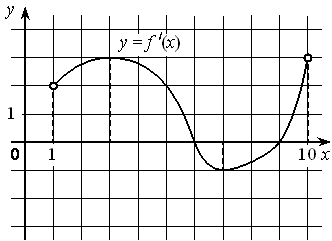
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (1 ; 10) . Найдите точку минимума функции f(x) .
Номер: 51E6D7
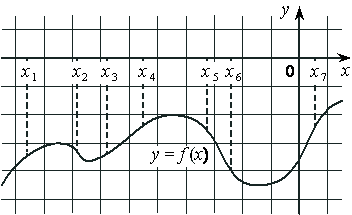
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) отрицательна?
Номер: A919D4
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 3 ; 8) . Найдите точку из отрезка [− 2 ; 5] , в которой производная функции f(x) равна 0.
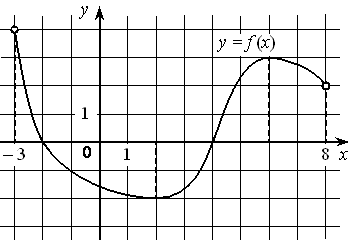
Номер: 55F759
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) положительна?
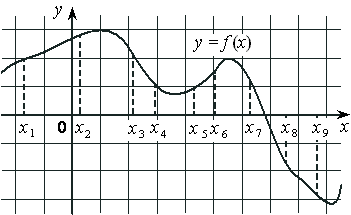
Номер: 789DA0
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (− 9 ; 3) . Найдите точку минимума функции f(x) .
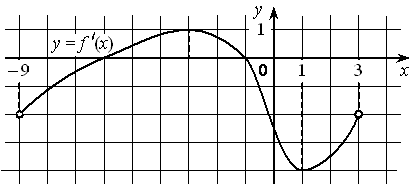
Номер: B633AD
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (− 5 ; 5) . Найдите точку максимума функции f(x) .
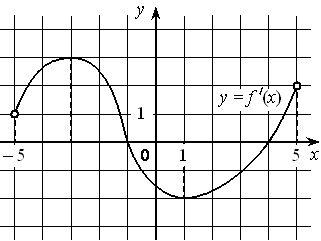
Номер: 22DEAE
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) положительна?
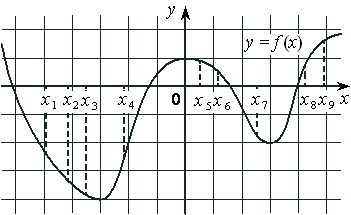
Номер: D2EEA3
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
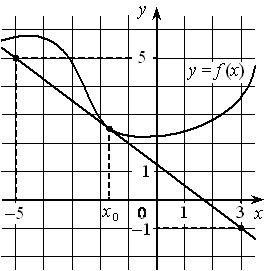
Номер: A4A3C5
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) отрицательна?
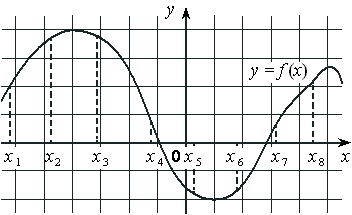
Номер: 3C39C5
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 11 ; − 1) . Найдите точку из отрезка [− 7 ; − 2] , в которой производная функции f(x) равна 0.
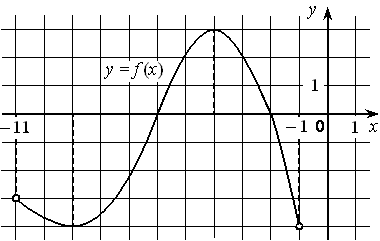
Номер: 393CC9
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) положительна?
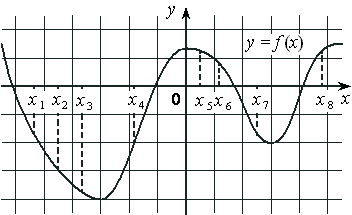
Номер: F64897
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: 78A09D
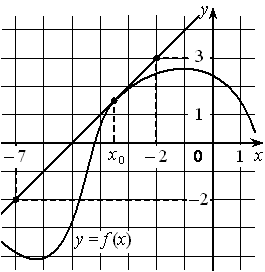
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены шесть точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 . В скольких из этих точек производная функции f(x) положительна?
Номер: 57FC91
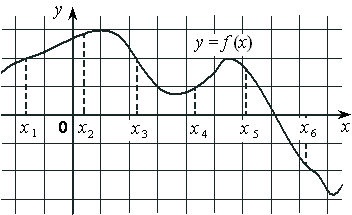
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (2 ; 13) . Найдите точку из отрезка [8 ; 12] , в которой производная функции f(x) равна 0.
Номер: 69F391
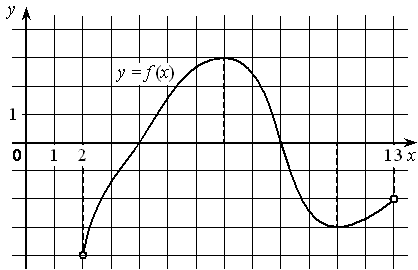
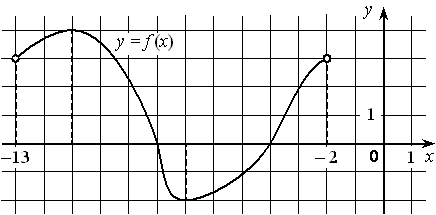
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 13 ; − 2) . Найдите точку из отрезка [− 10 ; − 3] , в которой производная функции f(x) равна 0.
Номер: BB73E9
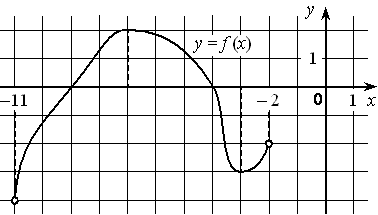
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 11 ; − 2) . Найдите точку из отрезка [− 10 ; − 4] , в которой производная функции f(x) равна 0.
Номер: 23CAEB
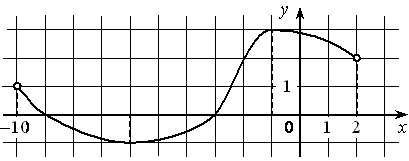
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 10 ; 2) . Найдите точку из отрезка [− 9 ; − 2] , в которой производная функции f(x) равна 0.
Номер: 778D65
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены шесть точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 . В скольких из этих точек производная функции f(x) отрицательна?
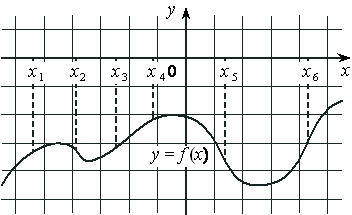
Номер: 2CC167
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) отрицательна?
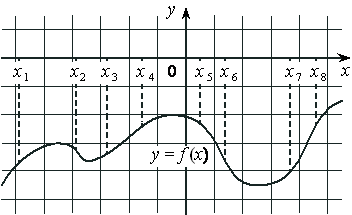
Номер: EEA96D
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) положительна?
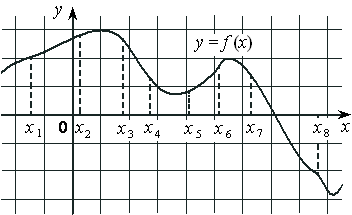
Номер: 448B37
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) отрицательна?
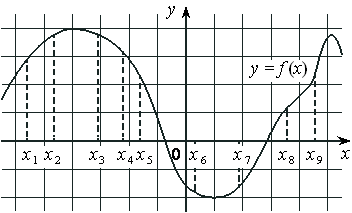
Номер: 4BE931
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (2 ; 13) . Найдите точку из отрезка [7 ; 12] , в которой производная функции f(x) равна 0.
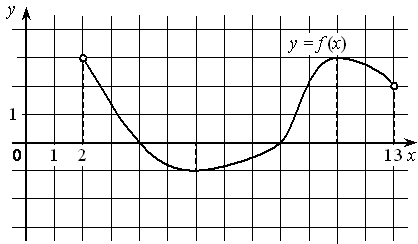
Номер: 530D3A
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (2 ; 13) . Найдите точку максимума функции f(x) .
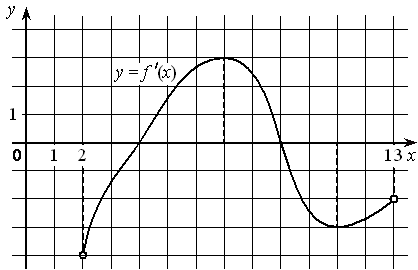
Номер: C10D3C
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
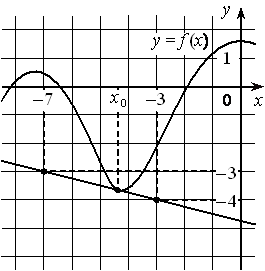
Номер: 95503D
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 3 ; 8) . Найдите точку из отрезка [2 ; 7] , в которой производная функции f(x) равна 0.
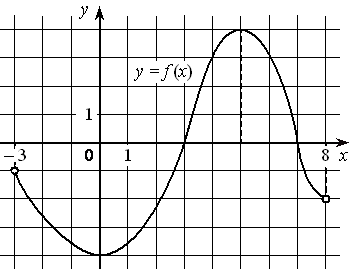
Номер: 5C7B8B
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 9 ; 3) . Найдите точку из отрезка [− 8 ; 0] , в которой производная функции f(x) равна 0.
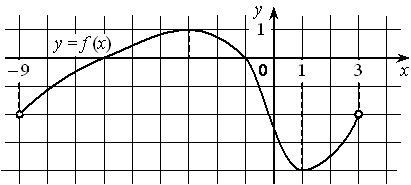
Номер: A7FFFB
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 5 ; 5) . Найдите точку из отрезка [− 2 ; 4] , в которой производная функции f(x) равна 0.
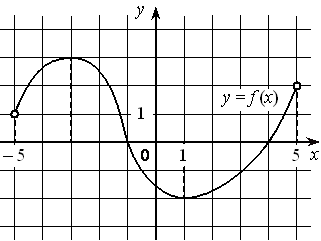
Номер: BA9C0F
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
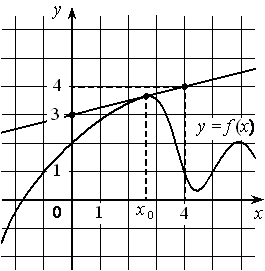
Номер: D08F0A
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (− 6 ; 3) . Найдите точку минимума функции f(x) .
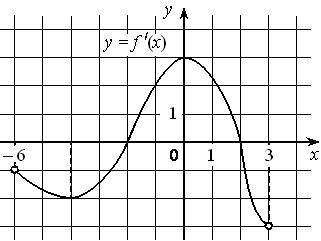
Номер: D6390E
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (− 6 ; 3) . Найдите точку из отрезка [− 5 ; − 1] , в которой производная функции f(x) равна 0.
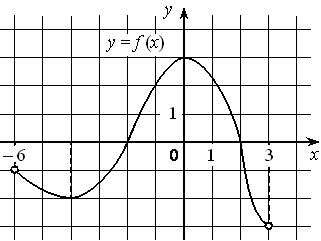
Номер: 6EE100
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) отрицательна?
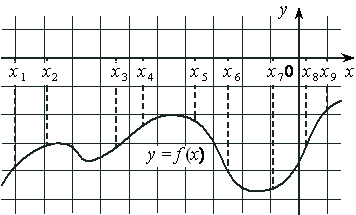
Номер: 0AC579
На рисунке изображён график функции y=f′(x) — производной функции f(x) , определённой на интервале (2 ; 13) . Найдите точку максимума функции f(x) .

Номер: BE7F78
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены шесть точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 . В скольких из этих точек производная функции f(x) отрицательна?
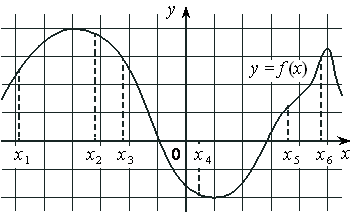
Номер: 263F70
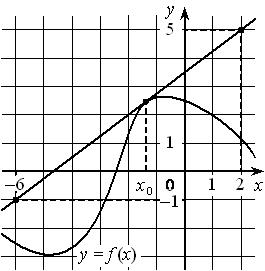
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: 93E07A
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) положительна?
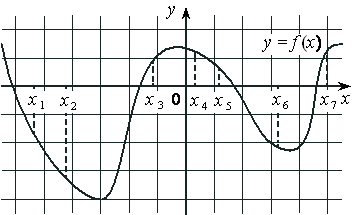
Номер: 77F0BF
На рисунке изображён график дифференцируемой функции y=f(x) , определённой на интервале (1 ; 10) . Найдите точку из отрезка [2 ; 6] , в которой производная функции f(x) равна 0.
Номер: C6EBB5
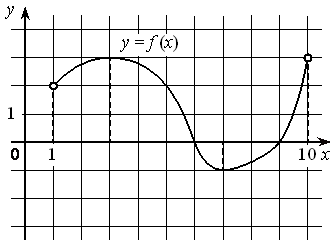
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
Номер: A6D310
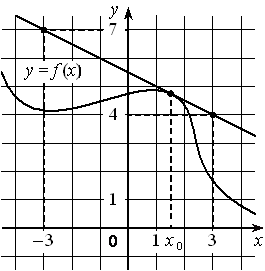
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены шесть точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 . В скольких из этих точек производная функции f(x) положительна?
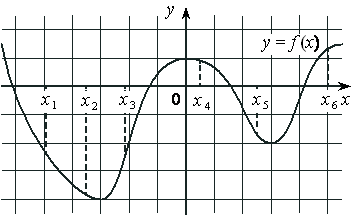
Номер: AEF41E
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) отрицательна?
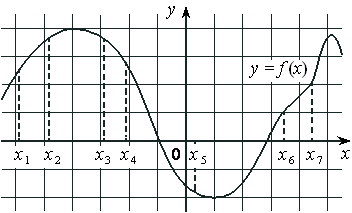
Номер: 6A5D13
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 3; 8) . В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?

Номер: 16B2FF
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) , определённой на интервале (− 7; 5) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2] .
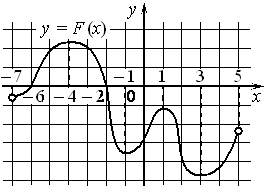
Номер: 1E2DFC
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
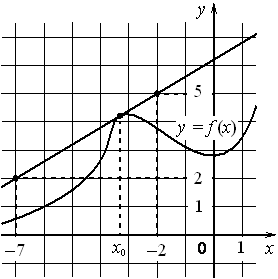
Номер: 9622F2
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
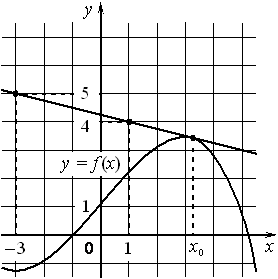
Номер: 8F90FD
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 . В скольких из этих точек функция f(x) положительна?
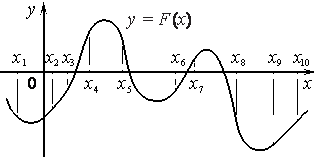
Номер: 42A509
На рисунке изображён график функции y=f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек производная функции f(x) отрицательна?
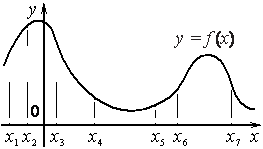
Номер: E1A601
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) , определённой на интервале (− 8; 7) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 5] .
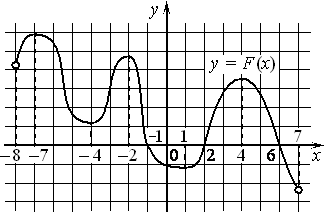
Номер: ECF906
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены семь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 . В скольких из этих точек функция f(x) положительна?

Номер: 103C75
На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) отрицательна?
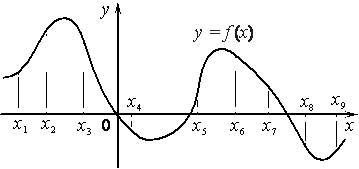
Номер: 7B49B6
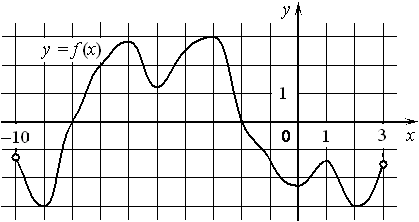
На рисунке изображён график функции y=f(x) , определённой на интервале (− 10; 3) . Найдите количество точек, в которых производная функции f(x) равна 0.
Номер: 182916
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
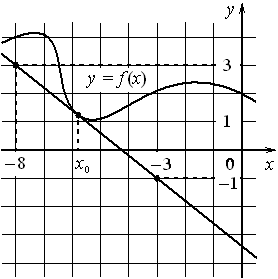
Номер: 6E4A20
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 3; 8) . В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
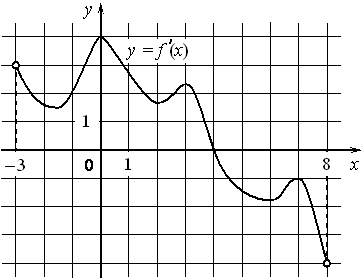
Номер: 508AD7
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) , определённой на интервале (− 7; 8) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [0; 5] .
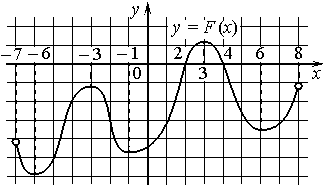
Номер: C996DA
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 . В скольких из этих точек функция f(x) положительна?

Номер: 3E43DA
На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . В скольких из этих точек производная функции f(x) отрицательна?
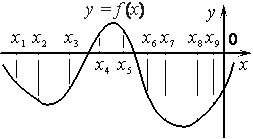
Номер: 406350
На рисунке изображён график y=F (x) одной из первообразных некоторой функции f (x), определённой на интервале (1;13). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [2;11].
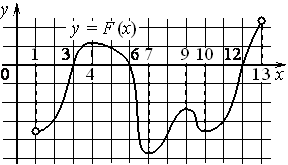
Номер: 47915D
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 6; 5) . В какой точке отрезка [− 5; −1] функция f(x) принимает наименьшее значение?

Номер: 50A3AB
На рисунке изображён график функции y=f(x) , определённой на интервале (− 5; 8) . Найдите количество точек, в которых производная функции f(x) равна 0.
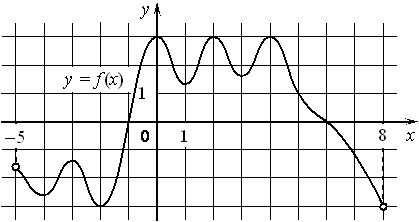
Номер: EC5AA8
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
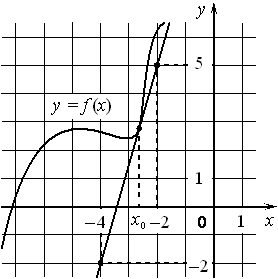
Номер: 071D93
На рисунке изображён график функции y=f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек производная функции f(x) положительна?
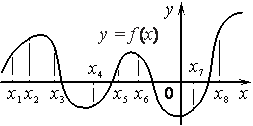
Номер: 6C9E9B
На рисунке изображён график y=f′(x) производной функции f(x) , определённой на интервале (− 8; 3) . В какой точке отрезка [− 6; −1] функция f(x) принимает наименьшее значение?
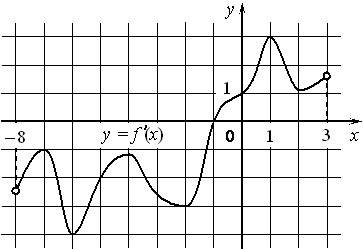
Номер: 45CAE1
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
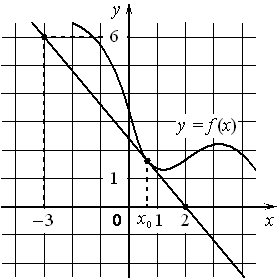
Номер: BC1BE4
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 . В скольких из этих точек функция f(x) отрицательна?
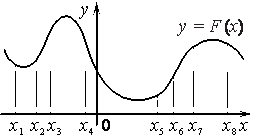
Номер: DD57EB
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
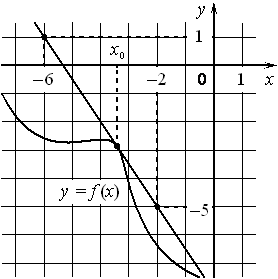
Номер: 9686E0
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
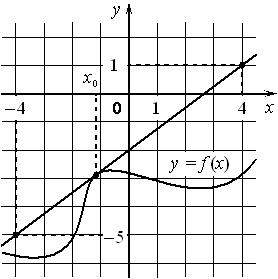
Номер: FEA331
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
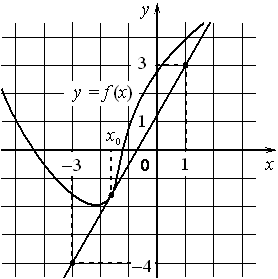
Номер: C7603A
На рисунке изображён график функции y=f(x) , определённой на интервале (− 3; 8) . Найдите количество точек, в которых производная функции f(x) равна 0.
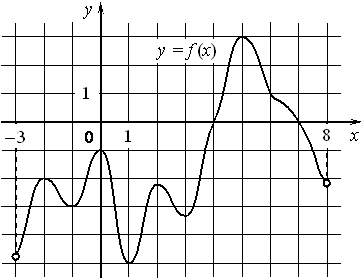
Номер: AF0A83
На рисунке изображён график функции y=f(x) , определённой на интервале (− 6; 5) . Найдите количество точек, в которых производная функции f(x) равна 0.
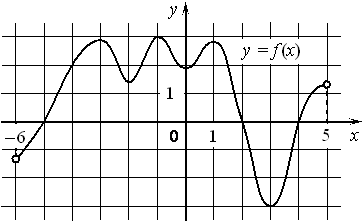
Номер: 9A008B
На рисунке изображён график y=f '(x) — производной функции f(x) , определённой на интервале (− 2 ; 11) . Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.
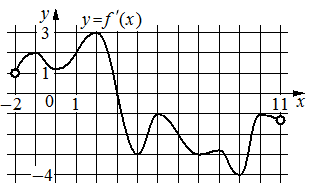
Номер: 7C42F8
На рисунке изображён график y=f '(x) — производной функции f(x) . На оси абсцисс отмечено одиннадцать точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 , x10 , x11 . Сколько из этих точек принадлежит промежуткам убывания функции f(x) ?
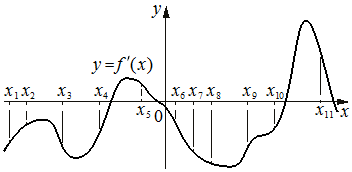
Номер: AB9C7F
На рисунке изображён график y=f '(x) — производной функции f(x) . На оси абсцисс отмечено девять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . Сколько из этих точек принадлежит промежуткам убывания функции f(x) ?
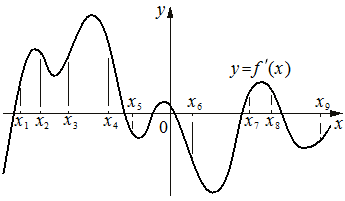
Номер: 59DF1F
На рисунке изображён график y=f '(x) — производной функции f(x) , определённой на интервале (− 4 ; 13) . Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=− 2x−10 или совпадает с ней.
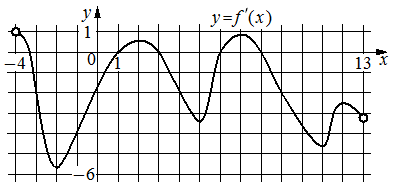
Номер: ADB310
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
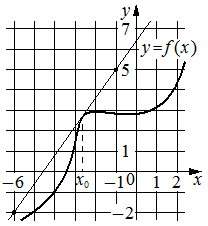
Номер: 4ECF20
На рисунке изображён график функции y=f(x) , определённой на интервале (− 4 ; 13) . Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14 .
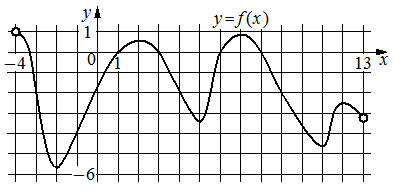
Номер: 935729
На рисунке изображён график y=f '(x) — производной функции f(x) , определённой на интервале (− 4 ; 6) . Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней.
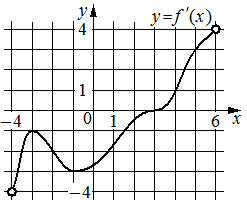
Номер: 345AAE
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .
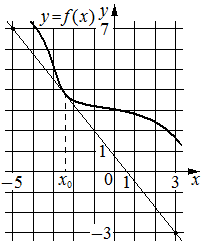
Номер: 3FBE88

