КЭС: Геометрия. Тип ответа: Развернутый ответ. Мы для вас перебрали весь новый и весь старый банк, оставили дубли в единичном экземпляре, ничего лишнего и, в то же время, полный комплект заданий по геометрии с развернутым ответом ко второй части ЕГЭ по профильной математике.
ВСЕ задания из ОБОИХ банков ФИПИ.
Ответы в процессе подготовки. Наш проект волонтерский. Если вы можете помочь с ответами, прикрепляйте их в комментариях в печатном виде.
Все задания с развернутым ответом по геометрии из нового банка ФИПИ
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А= 30° , В1С1 = 5 и площадь треугольника АВ1С1 в пять раз меньше площади четырёхугольника ВСВ1С1.
КЭС: 5 Геометрия
Решение:
а) Заметим, что `∠AB_1C_1 +∠C_1B_1C = 180º`
Четырехугольник BCB1C1 вписан в окружность, отсюда:
`∠C_1BC=∠C_1B_1C=180º`
Значит, `∠AB_1C_1=∠C_1BC=∠ABC`.
Следовательно, треугольники `ABC` и `AB_1C_1` подобны.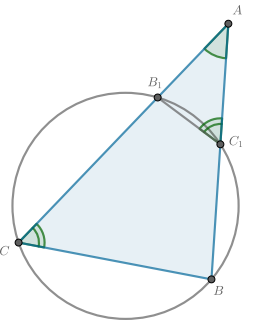
б) Пусть коэффициент подобия треугольников `ABC` и `AB_1C_1` равен `k`. Тогда имеем:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
`S_(ABC): S_(AB_1C_1) = (S+5S)/S= k^2`
`k = sqrt6`
Из подобия получаем
`BC = sqrt6B_1C_1 = 5sqrt6`
Пусть `AB_1=x`, тогда `АВ=xsqrt6`
По теореме косинусов для `ΔABB_1`:
`В_1В^2 = АВ_1^2+АВ^2-2АВ_1*cosA`
`В_1В^2 = x^2+(xsqrt6)^2-2*x*xsqrt6 cos30=7x^2-x^2sqrt18`
`ВВ_1 = xsqrt(7-3sqrt2)`
По теореме синусов для `ΔABB_1`:
`(AB)/(sin∠AB_1B) = (BB_1)/(sin∠A)`
`sinAB_1B =(AB sin∠A)/(BB_1)`
Но `sin∠AB_1B = sin∠BB_1C`, поскольку синусы смежных углов равны. Получаем
`sinBB_1C=(AB sin∠A)/(BB_1)=(xsqrt6*1/2)/(xsqrt(7-3sqrt2))`
`sinBB1C=(sqrt6)/(2(7-3sqrt2))`
Тогда радиус окружности, описанной около треугольника BB1C:
`2R = (BC)/(sin∠BB_1C)`
`R =(BC)/(sin∠BB_1C) : 2= (5sqrt6 * 2 sqrt (7-3sqrt2))/(2*sqrt6)=5sqrt(7-3sqrt2)`
Ответ:
б) `5sqrt6`; `5sqrt(7-3sqrt2)`
Номер: AA7FF7
Дайте развернутый ответ.
Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N . Отрезки AM и CN пересекаются в точке P .
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC=7 , AD=23 .
КЭС: 5 Геометрия
Решение:
а) Пусть O — точка пересечения диагоналей трапеции. Докажем, что точка P лежит на OD.
Углы ∠AMD = ∠CND = 90º, так как это вписанные углы, опирающиеся на диаметры соответствующих окружностей. Тогда точка P — ортоцентр (пересечение высот) треугольника ACD. Угол AOD между диагоналями прямой по условию, значит, DO — третья высота в треугольнике ACD и тоже проходит через точку P.
Трапеция ABCD равнобокая, следовательно, треугольники DBC и ACB равны, откуда ∠DBC =∠ACB и OB = OC. Угол ∠BOC = 90° по условию, тогда треугольник BOC — прямоугольный равнобедренный, а ∠OBC = 45°. Углы
∠CND = ∠BCN = 90° как накрест лежащие.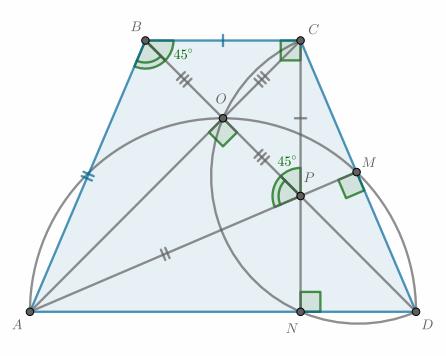
Тогда по сумме углов треугольника BCP:
∠CP B =180º− 90º− 45º = 45º = ∠CBP ⇒ CB = CP
Прямая OC — серединный перпендикуляр к отрезку BP, точка A лежит на прямой OC, следовательно, AB = AP. Получили, что в выпуклом четырехугольнике ABCP суммы противоположных сторон равны:
AB + CP = BC + AP
Значит в четырехугольник ABCP можно вписать окружность.
б) Рассмотрим равнобедренные прямоугольные треугольники AOD и BOC:
∠OBC =∠OAD = 45º ⇒ BO = BC = `7/(sqrt2)`, AO = OD = `23/(sqrt2)`
Тогда по теореме Пифагора для треугольника ABO:
`AB = sqrt(BO^2+AO^2) =sqrt(24,5+264,5) = 17 = AP`
Площадь четырехугольника ABCP из соображений симметрии равна удвоенной площади треугольника ABC:
`S_ABCP =2S_ABC=
=2*1/2(AO+OC)*BO=
=2*1/2(23/(sqrt2)+7/(sqrt2))*7/(sqrt2)=
=30/(sqrt2)*7/(sqrt2)=105`
Площадь описанного четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p⋅r, значит
`r=S_(ABCP)/p=105/((17+17+7+7)/2)=105/24=35/8`
Ответ:
б) 35/8
Номер: B45F0C
Дайте развернутый ответ.
Дана трапеция ABCD с основаниями AD и BC . Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD .
а) Докажите, что луч AC — биссектриса угла BAD .
б) Найдите CD, если известны диагонали трапеции: AC=12 и BD=6,5 .
КЭС: 5 Геометрия
Решение:
Номер: 5CBC00
Дайте развернутый ответ. стереометрия
В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре AD отмечена точка T так, что AT:TD=2:1 . Через точку Т параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
КЭС: 5 Геометрия
Решение:
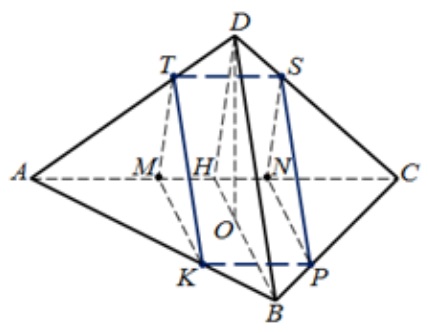
а) Так как плоскость, проведенная через точку Т параллельна АС, то линия пересечения TS этой плоскости с гранью ADC параллельна AC, а так как плоскость параллельна BD, то линия пересечения TK этой плоскости с гранью ABD параллельна BD. AC лежит в плоскости основания ABC, поэтому линия пересечения KP основания ABC и плоскости TSPK параллельна AC, наконец, BD принадлежит грани BDC, и поэтому линия пересечения SP плоскости TSPK и грани BDC параллельна BD.
TS||AC и KP||AC ⇒ TS||KP, TK||BD и SP||BD ⇒ TK||SP получается TSPK - параллелограмм. Докажем что какой-либо угол прямой.
Точка H середина AC. Так как AD = DC, то DH⊥AC, так как AB = BC, то BH⊥AC, и DHB⊥AC. Через прямую ТK, параллельную BD, проведем плоскость, параллельную DHB, которая пересечет AC в точке М,
TMK||DHB ⇒ TMK⊥AC ⇒ TK⊥AC. TK⊥AC и TS||AC ⇒ TS⊥TK и TSPK - прямоугольник.
б) AT:TD=2:1 и AD=3x, тогда TD = x, AT = 2x TD:AD=1:3 AT:AD=2:3
ΔATK ∼ ΔADB ⇒ `TK/BD=AT/AD=2/3 ⇒ TK=2/3 BD = 2/3 * 5 = 10/3 `
ΔTDS ∼ ΔADC ⇒ `TS/AC=TD/AD=1/3 ⇒ TS=1/3 *AC = 1/3 * 6 = 2 `
`S_(TSPK)= TK*TS=10/3 * 2 = 20/3`
Ответ:20/3
Номер: 30ED04
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А= 45∘ , В1С1= 6 и площадь треугольника АВ1С1 в восемь раз меньше площади четырёхугольника ВСB1C1.
КЭС: 5 Геометрия
Решение:
а) Четырехугольник `BCB_1C_1` вписанный, отсюда имеем:
`∠BCB_1 +∠B_1C_1B = 180º = ∠B_1C_1B + ∠B_1C_1A`
`∠BCB_1 =∠B_1C_1A` так как: `180º - ∠B_1C_1B = ∠B_1C_1A`
Тогда `△ ABC ∼ △AB_1C_1` по двум углам, так как `∠BCA = ∠B_1C_1A` и ∠A — общий.
б) Пусть коэффициент подобия треугольников ABC и `AB_1C_1` равен k. Тогда имеем:
`S_ABC : S_AB_1C_1 = (S+8S)/S= k^2`
`k = 3`
Из подобия получаем
`BC = 3B_1C_1 = 18`
По условию ∠A = 45∘. Обозначим угол CC1B через α. Так как он внешний в треугольнике CAC1, то имеем:
`∠ACC_1 =∠CC_1B − ∠CAC_1 = α − 45°`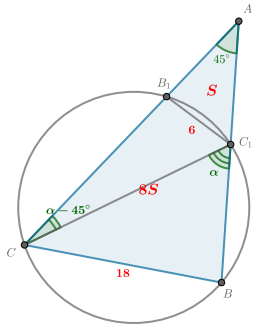
Обозначим искомый радиус через R. Запишем теорему синусов для треугольников CB1C1 и CC1B с учетом того, что у них общая описанная окружность:
`(B_1C_1)/(sin∠B_1C C_1) = 2R = (CB)/(sin∠C C_1B)`
`6/(sin (α − 45°)) = 2R = 18/(sinα)`
`sin (α − 45°) = (sin α)/3`
`sin α cos(−45°) + sin(−45°) cos α = (sin α)/3`
`sin α - cos α = (sqrt2)/3 * sin α`
`sin α (1 - (sqrt2)/3) = cos α`
Далее имеем:
α < 180° тогда sin α > 180°
`sqrt(1-cos^2 α) (1 - (sqrt2)/3) = cos α cos α≥180°`
`(1-cos^2 α) (1 - (2sqrt2)/3 +2/9) = cos^2 α `
`(11 - 6sqrt2) = cos^2 α(20 - 6sqrt2)`
`cos^2 α = 1-9/(20 - 6sqrt2)`
`sin^2 α = 9/(20 - 6sqrt2)`
`sin α = 3/(sqrt(20 - 6sqrt2))`
Отсюда окончательно получаем
`R = 9/(sinα)= 3sqrt(20− 6sqrt2)`
Ответ:
б) 18; `3sqrt(20− 6sqrt2)`
Номер: 2EBDBF
Дайте развернутый ответ.
Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M , а окружность с диаметром CD пересекает основание AD в точке N . Отрезки AM и CN пересекаются в точке P .
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC=7 , AD=17 .
КЭС: 5 Геометрия
Решение:
а) Пусть O — точка пересечения диагоналей трапеции. Докажем, что точка P лежит на OD.
Углы ∠AMD = ∠CND = 90º, так как это вписанные углы, опирающиеся на диаметры соответствующих окружностей. Тогда точка P — ортоцентр (пересечение высот) треугольника ACD. Угол AOD между диагоналями прямой по условию, значит, DO — третья высота в треугольнике ACD и тоже проходит через точку P.
Трапеция ABCD равнобокая, следовательно, треугольники DBC и ACB равны, откуда ∠DBC =∠ACB и OB = OC. Угол ∠BOC = 90° по условию, тогда треугольник BOC — прямоугольный равнобедренный, а ∠OBC = 45°. Углы
∠CND = ∠BCN = 90° как накрест лежащие.
Тогда по сумме углов треугольника BCP:
∠CP B =180º− 90º− 45º = 45º = ∠CBP ⇒ CB = CP
Прямая OC — серединный перпендикуляр к отрезку BP, точка A лежит на прямой OC, следовательно, AB = AP. Получили, что в выпуклом четырехугольнике ABCP суммы противоположных сторон равны:
AB + CP = BC + AP
Значит в четырехугольник ABCP можно вписать окружность.
б) Рассмотрим равнобедренные прямоугольные треугольники AOD и BOC:
∠OBC =∠OAD = 45º ⇒ BO = BC = `7/(sqrt2)`, AO = OD = `17/(sqrt2)`
Тогда по теореме Пифагора для треугольника ABO:
`AB = sqrt(BO^2+AO^2) =sqrt(24,5+144,5) = 13 = AP`
Площадь четырехугольника ABCP из соображений симметрии равна удвоенной площади треугольника ABC:
`S_ABCP =2S_ABC=
=2*1/2(AO+OC)*BO=
=2*1/2(17/(sqrt2)+7/(sqrt2))*7/(sqrt2)=
=24/(sqrt2)*7/(sqrt2)=84`
Площадь описанного четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p⋅r, значит
`r=S_(ABCP)/p=84/((13+13+7+7)/2)=84/20=21/5`
Ответ:
б) 21/5
Номер: D57CB9
Дайте развернутый ответ. стереометрия
В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 5. Боковое ребро пирамиды равно 9. На ребре AD отмечена точка T так, что AT:TD=1:2 . Через точку Т параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
КЭС: 5 Геометрия
Решение:

а) Так как плоскость, проведенная через точку Т параллельна АС, то линия пересечения TS этой плоскости с гранью ADC параллельна AC, а так как плоскость параллельна BD, то линия пересечения TK этой плоскости с гранью ABD параллельна BD. AC лежит в плоскости основания ABC, поэтому линия пересечения KP основания ABC и плоскости TSPK параллельна AC, наконец, BD принадлежит грани BDC, и поэтому линия пересечения SP плоскости TSPK и грани BDC параллельна BD.
TS||AC и KP||AC ⇒ TS||KP, TK||BD и SP||BD ⇒ TK||SP получается TSPK - параллелограмм. Докажем что какой-либо угол прямой.
Точка H середина AC. Так как AD = DC, то DH⊥AC, так как AB = BC, то BH⊥AC, и DHB⊥AC. Через прямую ТK, параллельную BD, проведем плоскость, параллельную DHB, которая пересечет AC в точке М,
TMK||DHB ⇒ TMK⊥AC ⇒ TK⊥AC. TK⊥AC и TS||AC ⇒ TS⊥TK и TSPK - прямоугольник.
б) AT:TD=1:2 и AD=3x, тогда TD = 2x, AT = x AT:AD=1:3 TD:AD=2:3
ΔATK ∼ ΔADB ⇒ `TK/BD=AT/AD=1/3 ⇒ TK=1/3 BD = 1/3 * 9 = 3 `
ΔTDS ∼ ΔADC ⇒ `TS/AC=TD/AD=2/3 ⇒ TS=2/3 AC = 2/3 * 5 = 10/3 `
`S_(TSPK)= TK*TS=10/3 * 3 = 10`
Ответ:10
Номер: 149319
Дайте развернутый ответ.
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=3:4 , радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12 , угол PWQ — острый.
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD .
КЭС: 5 Геометрия
Решение:
Смотреть ответ аналогичного задания где AP:PB=CQ:QB=CW:WD=1:4 (A96557)
Номер: 56C211
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А= 135∘ , B1C1=10 и площадь треугольника АВ1С1 в семь раз меньше площади четырёхугольника ВСB1C1.
КЭС: 5 Геометрия
Решение:
а) Четырехугольник BCB1C1 вписанный, отсюда имеем:
∠BCB1 +∠B1C1B = 180º = ∠B1C1B + ∠B1C1A
∠BCB1 =∠B1C1A так как: 180º - ∠B1C1B = ∠B1C1A
Тогда △ ABC ∼ △AB1C1 по двум углам, так как ∠BCA = ∠B1C1A и ∠A — общий.
б) Пусть коэффициент подобия треугольников ABC и AB1C1 равен k. Тогда имеем:
`SABC: S_AB1C1 = (S+7S)/S= k^2`
k = √8
///
Номер: 3CDB1B
Дайте развернутый ответ.
Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC , перпендикулярна CM и пересекает катет AC в точке K . При этом AK:KC=1:2 .
а) Докажите, что ∠BAC=30° .
б) Пусть прямые MK и BC пересекаются в точке P , а прямые AP и BK — в точке Q . Найдите KQ , если BC=√21 .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: 5E7BDE
Дайте развернутый ответ.
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4 , радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12 , угол PWQ — острый.
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
КЭС: 5 Геометрия
Решение:
Номер: A96557
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠А= 45° , В1С1= 6 и площадь треугольника АВ1С1 в восемь раз меньше площади четырёхугольника ВСВ1С1.
КЭС: 5 Геометрия
Решение:
а) Четырехугольник BCB1C1 вписанный, отсюда имеем:
∠BCB1 +∠B1C1B = 180º = ∠B1C1B + ∠B1C1A
∠BCB1 =∠B1C1A так как: 180º - ∠B1C1B = ∠B1C1A
Тогда △ ABC ∼ △AB1C1 по двум углам, так как ∠BCA = ∠B1C1A и ∠A — общий.
б) Пусть коэффициент подобия треугольников ABC и AB1C1 равен k. Тогда имеем:
`SABC: S_AB1C1 = (S+8S)/S= k^2`
k = √9 = 3
Из подобия получаем
BC = 3B1C1 = 3*6=18
Пусть AB1=x, тогда АВ=x*3
По теореме косинусов для ΔABB1:
В1В2 = АВ2+АВ12-2АВ1*cosA
В1В2 = (3x)2+x2-2*x*3x cos45
`ВВ_1^2 = 10x^2 - 6x^2/(sqrt2)` cos 45 =`1/sqrt2`
`ВВ_1 = xsqrt(10-6/sqrt2)`
По теореме синусов для ΔABB1:
`(AB)/(sinAB1B) = (BB1)/(sinA)=(AB1)/(sinABB1)`
`sinAB1B =(AB sinA)/(BB1)`
sinAB1B = sinBB1C
`sinBB1C=(3x(1/sqrt2))/(xsqrt(10-6/sqrt2))`
`sinBB1C=3/(sqrt(20-12/sqrt2))`
Тогда радиус
`2R = (BC)/(sinBB1C)`
`2R = (18)/(3/(sqrt(20-12/sqrt2))`
`R = (18sqrt(20-12/sqrt2))/(2*3)`
`R = 3sqrt(20-12/sqrt2)`
Ответ:
б) 18; `3sqrt(20-12/sqrt2)`
Номер: 829956
Дайте развернутый ответ. стереометрия
В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный (AB=BC) треугольник ABC . Точка K — середина ребра A1B1 , а точка M делит ребро AC в отношении AM:MC=1:3 .
а) Докажите, что KM⊥AC .
б) Найдите угол между прямой KM и плоскостью ABB1 , если AB=6 , AC=8 и AA1=3 .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: F7B7A1
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1
б) Вычислите длину стороны В1С1 и радиус данной окружности, если ∠A=150° , BC=√55 и площадь треугольника АВ1С1 в четыре раза меньше площади четырёхугольника ВСВ1С1.
КЭС: 5 Геометрия
Решение:
а) Четырехугольник BCB1C1 вписанный, отсюда имеем:
∠BCB1 +∠B1C1B = 180º = ∠B1C1B + ∠B1C1A
∠BCB1 =∠B1C1A так как: 180º - ∠B1C1B = ∠B1C1A
Тогда △ ABC ∼ △AB1C1 по двум углам, так как ∠BCA = ∠B1C1A и ∠A — общий.
б) Пусть коэффициент подобия треугольников ABC и AB1C1 равен k. Тогда имеем:
`SABC: S_AB1C1 = (S+4S)/S= k^2`
k = √5
Из подобия получаем
B1C1 = BC/√5 = √55/√5=√11
Пусть AB1=x, тогда АВ=x*√5
По теореме косинусов для ΔABB1:
В1В2 = АВ2+АВ12-2АВ1*cosA
В1В2 = (√5 x)2+x2-2*x*√5 x cos150
`ВВ_1^2 = 6x^2 + 2sqrt5sqrt3x^2/2` cos 120 =`-√3/2`
`ВВ_1^2 = 6x^2 + sqrt15x^2`
`ВВ_1 = xsqrt(6+sqrt15)`
По теореме синусов для ΔABB1:
`(AB)/(sinAB1B) = (BB1)/(sinA)=(AB1)/(sinABB1)`
`sinAB1B =(AB sinA)/(BB1)`
sinAB1B = sinBB1C
`sinBB1C=(xsqrt5*(sqrt(3)/2))/(xsqrt(6+sqrt15))`
`sinBB1C=(sqrt15)/(2sqrt(6+sqrt15))`
Тогда радиус
`2R = (BC)/(sinBB1C)`
`R = (sqrt55*2sqrt(6+sqrt15))/(2sqrt15)`
`R = sqrt825*sqrt(6+sqrt15)`
`R = 5sqrt(198+33sqrt15)`
Ответ:
б) √11; `5sqrt(198+33sqrt15)`
Номер: 8F66A4
Дайте развернутый ответ.
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1
б) Вычислите длину стороны В1С1 и радиус данной окружности, если ∠A=120° , BC=10√7 и площадь треугольника АВ1С1 в три раза меньше площади четырёхугольника ВСВ1С1.
КЭС: 5 Геометрия
Решение:
а) Четырехугольник BCB1C1 вписанный, отсюда имеем:
∠BCB1 +∠B1C1B = 180º = ∠B1C1B + ∠B1C1A
∠BCB1 =∠B1C1A так как: 180º - ∠B1C1B = ∠B1C1A
Тогда △ ABC ∼ △AB1C1 по двум углам, так как ∠BCA = ∠B1C1A и ∠A — общий.
б) Пусть коэффициент подобия треугольников ABC и AB1C1 равен k. Тогда имеем:
`SABC: S_AB1C1 = (S+3S)/S= k^2`
k = √4 = 2
Из подобия получаем
B1C1 = BC/2 = (10√7)/2=5√7
Пусть AB1=x, тогда АВ=x*2
По теореме косинусов для ΔABB1:
В1В2 = АВ2+АВ12-2АВ1*cosA
В1В2 = (2x)2+x2-2*x*2x cos120
`ВВ_1^2 = 5x^2 + 4x^2/2` cos 120 =`-1/2`
`ВВ_1^2 = 5x^2 + 2x^2`
`ВВ_1 = xsqrt7`
По теореме синусов для ΔABB1:
`(AB)/(sinAB1B) = (BB1)/(sinA)=(AB1)/(sinABB1)`
`sinAB1B =(AB sinA)/(BB1)`
sinAB1B = sinBB1C
`sinBB1C=(2x((sqrt3)/2))/(xsqrt7)`
`sinBB1C=(sqrt3)/(sqrt7)`
Тогда радиус
`2R = (BC)/(sinBB1C)`
`R = (5sqrt7sqrt7)/(sqrt3)`
Ответ:
б) 18; `35/sqrt3`
Номер: 2B52E7
Дайте развернутый ответ.
Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC , пересекает сторону AD в точке M , равноудалённой от вершин B и D .
а) Докажите, что ∠ABM=∠DBС=30° .
б) Найдите расстояние от центра прямоугольника до прямой CM , если BC=9 .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: FAAE63
Дайте развернутый ответ. стереометрия
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E:EA=1:2 , на ребре BB1 — точка F так, что B1F:FB=1:5 , а точка Т — середина ребра B1C1 . Известно, что AB=2 , AD=6 , AA1=6 .
а) Докажите, что плоскость EFT проходит через вершину D1 .
б) Найдите угол между плоскостью EFT и плоскостью AA1B1 .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: E95564
Дайте развернутый ответ.
Дана трапеция ABCD с основаниями AD и BC . Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD .
а) Докажите, что луч AC — биссектриса угла BAD .
б) Найдите CD , если известны диагонали трапеции: AC=15 и BD=8,5 .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: 00E23C
Дайте развернутый ответ. стереометрия
В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9 . Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E , а на ребре AS — точка F так, что SF=BE=4 .
а) Докажите, что плоскость CEF параллельна ребру SB .
б) Плоскость CEF пересекает ребро SD в точке Q . Найдите расстояние от точки Q до плоскости ABC .
КЭС: 5 Геометрия
Решение:
...
Ответ:
Номер: EA6B32
Дайте развернутый ответ.
На сторонах AB, BC и AC треугольника ABC отмечены точки C1, A1 и B1 соответственно, причём AC1:C1B=8:3, BA1:A1C=1:2, AB1:B1C=1:3. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что четырёхугольник ADA1B1 — параллелограмм.
б) Найдите радиус окружности, описанной около треугольника ABC, если отрезки AD иBC перпендикулярны, AC=16, BC=15.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 4F4F44
Дайте развернутый ответ. стереометрия
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM=2, SK=1.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
КЭС: 5.2.5 Перпендикулярность плоскостей, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 03B44B
Дайте развернутый ответ. 2024 стереометрия
В правильной четырёхугольной пирамиде SABCD с основанием ABCD точка O — центр основания пирамиды, точка M — середина ребра SC, точка K делит ребро BC в отношении BK:KC=3:1, а AB=2 и SO=√14.
а) Докажите, что плоскость OMK параллельна прямой SA.
б) Найдите длину отрезка, по которому плоскость OMK пересекает грань SAD.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: 04294C
Дайте развернутый ответ.
В треугольнике ABC точки A1 , B1 и C1 — середины сторон BC , AC и AB соответственно, AH — высота, ∠BAC=60° , ∠BCA=45° .
а) Докажите, что точки A1 , B1 , C1 и H лежат на одной окружности.
б) Найдите A1H , если BC=2√3 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 2AE241
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A , B и C , а на окружности другого основания — точка C1 , причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=45° , AB=2√3 , CC1=2√6 .
а) Докажите, что угол между прямыми AC1 и BC равен 60° .
б) Найдите расстояние от точки B до прямой AC1 .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.4 Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными и скрещивающимися прямыми; расстояние между параллельными плоскостями
Решение:
...
Ответ:
Номер: C84642
Дайте развернутый ответ.
Четырёхугольник ABCD вписан в окружность радиуса R=8 . Известно, что AB=BC=CD=12 .
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD .
КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: C5B743
Дайте развернутый ответ. стереометрия
Различные точки A, B и C лежат на окружности основания конуса с вершиной S так, что отрезок AB является её диаметром. Угол между образующей конуса и плоскостью основания равен 60°. а) Докажите, что cos∠ ASC+cos∠ BSC=1,5. б) Найдите объём тетраэдра SABC, если SC=1, cos∠ ASC=2/3.
КЭС: 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 6B5C41
Дайте развернутый ответ. стереометрия
В основании пирамиды SABCD лежит трапеция ABCD с основаниями AD и BC, равными 8 и 3 соответственно. Точки M и N лежат на рёбрах SD и BC соответственно, причём SM:MD=3:2, BN:NC=1:2.
Плоскость AMN пересекает ребро SC в точке K. а) Докажите, что SK:KC=6:1. б) Плоскость AMN делит пирамиду SABCD на два многогранника. Найдите отношение их объёмов.
КЭС: 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.3.4 Сечения куба, призмы, пирамиды 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 8EEB4F
Дайте развернутый ответ. стереометрия
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α , содержащей прямую BD1 и параллельной прямой AC , является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями α и BCC1 , если AA1=10 , AB=12 .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 8A0B46
Дайте развернутый ответ.
В трапеции ABCD основание AD в два раза больше основания BC . Внутри трапеции взяли точку M так, что углы ABM и DCM прямые.
а) Докажите, что AM=DM .
б) Найдите угол BAD , если угол ADC равен 70° , а расстояние от точки M до прямой AD равно стороне BC .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 4E19FD
Дайте развернутый ответ.
В треугольнике ABC угол A равен 120° . Прямые, содержащие высоты BM и CN треугольника ABC , пересекаются в точке H . Точка O — центр окружности, описанной около треугольника ABC .
а) Докажите, что AH=AO .
б) Найдите площадь треугольника AHO , если BC=√15 , ∠ABC=45° .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 41A5F8
Дайте развернутый ответ.
Окружность проходит через вершины A , B и C параллелограмма ABCD , пересекает продолжение стороны AD за точку D в точке E и пересекает продолжение стороны CD за точку D в точке K .
а) Докажите, что BK=BE .
б) Найдите отношение KE:AC , если ∠BAD=30° .
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: 0BC5F1
Дайте развернутый ответ.
Биссектрисы углов BAD и BCD равнобедренной трапеции ABCD пересекаются в точке O. На боковых сторонах AB и CD отмечены точки M и N соответственно так, что AM=MO, CN=NO.
а) Докажите, что точки M, O и N лежат на одной прямой.
б) Найдите отношение AM:MB, если AO=CO и BC:AD=17:31.
КЭС: 5.1.3 Трапеция 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: B58CFA
Дайте развернутый ответ. стереометрия
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали трапеции пересекаются в точке O. Точки M и N — середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO. а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α , если AD=10, BC=8, SO=8, а прямая SO перпендикулярна прямой AD.
КЭС: 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.3.4 Сечения куба, призмы, пирамиды 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 182CF4
16. Дайте развернутый ответ.
На стороне BC параллелограмма ABCD выбрана точка M такая, что AM=MC.
а) Докажите, что центр вписанной в треугольник AMD окружности лежит на диагонали AC.
б) Найдите радиус вписанной в треугольник AMD окружности, если AB=5, BC=10, ∠ BAD=60°.
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
а) Треугольник АМС — равнобедренный, следовательно. ∠МАС = ∠МСА.
Прямые AD и BС — параллельны, следовательно, накрест лежащие углы BCA и CAD при секущей АС равны. Получаем, что ∠MAC=∠MCA=∠CAD, а значит, луч АС является биссектрисой угла МАD, на которой лежит центр вписанной в треугольник AMD окружности.
Ответ: б) `(17sqrt3-3sqrt13)/10`
Смотреть полное решение
Номер: 2412FA
Дайте развернутый ответ. стереометрия
В правильной шестиугольной пирамиде SABCDEF сторона основания AB равна 2, а боковое ребро SA равно 8. Точка M — середина ребра AB . Плоскость a перпендикулярна плоскости ABC и содержит точки M и D . Прямая SC пересекает плоскость a в точке K .
а) Докажите, что KM=KD .
б) Найдите объём пирамиды CDKM .
КЭС: 5.2.5 Перпендикулярность плоскостей, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 9A3AF9
02. Дайте развернутый ответ. 2024
Окружность с центром в точке O касается сторон угла с вершиной N в точках A и B. Отрезок BC — диаметр этой окружности.
а) Докажите, что прямая AC параллельна биссектрисе угла ANB.
б) Найдите длину отрезка NO, если известно, что AC=10 и AB=24.
КЭС: 7.1 Фигуры на плоскости
Решение:
Номер: 6B82FF
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B , а на окружности другого основания — точки B1 и C1 , причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB=20 , BB1=15 , B1C1=21 .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 416B0F
Дайте развернутый ответ.
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC .
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD , если AD=15 и AC=2√61 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 060A0A
Дайте развернутый ответ. стереометрия
В правильной шестиугольной пирамиде SABCDEF сторона основания AB равна 5, а боковое ребро SA равно 9. Точка M лежит на ребре AB , AM=1 , а точка K лежит на ребре SC . Известно, что MK=KD .
а) Докажите, что плоскость DKM перпендикулярна плоскости ABC .
б) Найдите площадь треугольника DKM .
КЭС: 5.2.5 Перпендикулярность плоскостей, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 065E0A
Дайте развернутый ответ.
В трапеции ABCD угол BAD прямой. Окружность, построенная на большем основании AD как на диаметре, пересекает меньшее основание BC в точках C и M .
а) Докажите, что ∠BAM=∠CAD .
б) Диагонали трапеции ABCD пересекаются в точке O . Найдите площадь треугольника AOB , если AB=√10 , а BC=2BM .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: B3890A
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B , а на окружности другого основания — точки B1 и C1 , причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите объём цилиндра, если AB=7 , BB1=24 , B1C1=10 .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 13D60B
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCDA1B1C1D1 лежит параллелограмм ABCD с углом 60° при вершине A. На рёбрах A1B1, B1C1 и BC отмечены точки M, K и N соответственно так, что четырёхугольник AMKN — равнобедренная трапеция с основаниями 1 и 2.
а) Докажите, что точка M — середина ребра A1B1.
б) Найдите высоту призмы, если её объём равен 5 и известно, что точка K делит ребро B1C1 в отношении B1K:KC1=2:3.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: ED4407
Дайте развернутый ответ. стереометрия
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM=2, SK=1. Плоскость a перпендикулярна плоскости ABC и содержит точки M и K.
а) Докажите, что плоскость a содержит точку C.
б) Найдите площадь сечения пирамиды SABCD плоскостью a.
КЭС: 5.2.5 Перпендикулярность плоскостей, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.3.4 Сечения куба, призмы, пирамиды 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 3C8708
Дайте развернутый ответ.
Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK=15 , KL=6 , LB=5 .
КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: D9D771
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A , B и C , а на окружности другого основания — точка C1 , причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=30° , AB=√2 , CC1=2 .
а) Докажите, что угол между прямыми AC1 и BC равен 45° .
б) Найдите объём цилиндра.
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: D7147A
Дайте развернутый ответ.
В треугольнике ABC продолжения высоты CC1 и биссектрисы BB1 пересекают описанную окружность в точках N и M соответственно, ∠ ABC=40°, ∠ ACB=85°.
а) Докажите, что BM=CN.
б) Прямые BC и MN пересекаются в точке D. Найдите площадь треугольника BDN, если его высота BH равна 6.
КЭС: 5.1.1 Треугольник 5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 54E571
Дайте развернутый ответ. стереометрия
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно √21. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM=4, SK:KB=1:3.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
КЭС: 5.2.5 Перпендикулярность плоскостей, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 4679B2
Дайте развернутый ответ.
На стороне AC равностороннего треугольника ABC отмечена точка M. Серединный перпендикуляр к отрезку BM пересекает стороны AB и BC в точках E и K соответственно.
а) Докажите, что треугольники AEM и CMK подобны.
б) Найдите отношение AM:MC, если площади треугольников AEM и CMK равны 4 и 9 соответственно.
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: B5D2B2
Дайте развернутый ответ. 2024
Пятиугольник ABCDE вписан в окружность. Диагонали AD и BE пересекаются в точке M. Известно, что BCDM — параллелограмм.
а) Докажите, что BC=DE.
б) Найдите длину стороны AB, если известно, что DE=4, AD=7, BE=8 и AB>BC.
КЭС: 7.1 Фигуры на плоскости
Решение:
...
Ответ:
Номер: AC39B7
Дайте развернутый ответ. 2024
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠BB1C1=∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1=18 и ∠BAC=30°.
КЭС: 7.1 Фигуры на плоскости
Решение:
...
Ответ:
Номер: 10D010
Дайте развернутый ответ. 2024 стереометрия
Дана правильная четырёхугольная призма ABCDA1B1C1D1.
Плоскость α проходит через вершины B1 и D и пересекает рёбра AA1 и CC1 в точках M и K соответственно. Известно, что четырёхугольник MB1KD — ромб.
а) Докажите, что точка M — середина ребра AA1.
б) Найдите высоту призмы ABCDA1B1C1D1, если площадь её основания ABCD равна 3, а площадь ромба MB1KD равна 6.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: 16C715
Дайте развернутый ответ. стереометрия
В пирамиде ABCD рёбра DA , DB и DC попарно перпендикулярны, а AB=BC=AC=6√2 .
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=1:2 . Найдите расстояние от точки D до плоскости MNB .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 5D991D
Дайте развернутый ответ.
Окружность проходит через вершины A , B и D параллелограмма ABCD , пересекает сторону BC в точках B и E и пересекает продолжение стороны CD за точку D в точке K .
а) Докажите, что AE=AK .
б) Найдите отношение KE:BD , если ∠BAD=60° .
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: 813416
Дайте развернутый ответ.
В треугольнике ABC точки M и N лежат на сторонах AB и BC соответственно так, что AM:MB=CN:NB=2:3. Окружность, вписанная в треугольник ABC, касается отрезка MN в точке L.
а) Докажите, что AB+BC=4AC.
б) Найдите радиус окружности, вписанной в треугольник ABC, если ML=9/5, LN=3.
КЭС: 5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 7C842B
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCDA1B1C1D1 лежит равнобедренная трапеция ABCD с основаниями AD=3 и BC=2. Точка M делит ребро A1D1 в отношении A1M:MD1=1:2, а точка K — середина ребра DD1.
а) Докажите, что плоскость MKC параллельна прямой BD.
б) Найдите тангенс угла между плоскостью MKC и плоскостью основания призмы, если ∠MKC=90°, ∠ADC=60°.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.2 Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями
Решение:
...
Ответ:
Номер: 72412D
Дайте развернутый ответ.
Окружность проходит через вершины A , B и D параллелограмма ABCD , пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D .
а) Докажите, что AE=AK .
б) Найдите AD , если CE=10 , DK=9 и cos∠BAD=0,2 .
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: 73BE23
Дайте развернутый ответ.
В треугольнике ABC точки A1 , B1 и C1 — середины сторон BC , AC и AB соответственно, AH — высота, ∠BAC=120° , ∠BCA=45° .
а) Докажите, что точки A1 , B1 , C1 и H лежат на одной окружности.
б) Найдите A1H , если BC=6√3 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: EA7D2B
Дайте развернутый ответ.
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE=CE.
а) Докажите, что AL⋅BC=AB⋅AC.
б) Найдите EL, если AC=8, tg∠ BCA=1/2.
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: FC6FD7
Дайте развернутый ответ. 2024 стереометрия
В правильном тетраэдре ABCD точки M и N — середины рёбер AB и CD соответственно. Плоскость α перпендикулярна прямой MN и пересекает ребро BC в точке K.
а) Докажите, что прямая MN перпендикулярна рёбрам AB и CD.
б) Найдите площадь сечения тетраэдра ABCD плоскостью α, если известно, что BK=1, KC=3.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: 0E8DDE
Дайте развернутый ответ. стереометрия
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 6, а боковое ребро SA равно 7. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC=SK:KC=1:2 . Плоскость α содержит прямую KN и параллельна прямой BC .
а) Докажите, что плоскость α параллельна прямой SA .
б) Найдите угол между плоскостями α и SBC .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.2 Параллельность прямой и плоскости, признаки и свойства 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.2 Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями
Решение:
...
Ответ:
Номер: 142CDC
Дайте развернутый ответ. стереометрия
Основанием четырёхугольной пирамиды SABCD является прямоугольник ABCD , причём AB=2√2 , BC=4 . Основанием высоты пирамиды является центр прямоугольника. Из вершин A и C опущены перпендикуляры AP и CQ на ребро SB .
а) Докажите, что P — середина отрезка BQ .
б) Найдите угол между гранями SBA и SBC , если SD=4 .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: C185DD
Дайте развернутый ответ. стереометрия
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=6√2 , AD=10 , AA1=16 . На рёбрах AA1 и BB1 отмечены точки E и F соответственно, причём A1E:EA=5:3 и B1F:FB=5:11 . Точка T — середина ребра B1C1 .
а) Докажите, что плоскость EFT проходит через точку D1 .
б) Найдите площадь сечения параллелепипеда плоскостью EFT .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: C300DC
Дайте развернутый ответ.
В прямоугольном треугольнике ABC точка M лежит на катете AC , а точка N лежит на продолжении катета BC за точку C , причём CM=BC и CN=AC .
а) Отрезки CP и CQ — медианы треугольников ABC и NCM соответственно. Докажите, что прямые CP и CQ перпендикулярны.
б) Прямые MN и AB пересекаются в точке K , а прямые BM и AN — в точке L . Найдите KL , если BC=1 , а AC=5 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: EF3DDA
Дайте развернутый ответ. 2024 стереометрия
Все рёбра правильной четырёхугольной пирамиды SABCD с основанием ABCD равны 4. Точка O — центр основания пирамиды. Плоскость, параллельная прямой SA и проходящая через точку O, пересекает рёбра SC и SD в точках M и N соответственно. Точка N делит ребро SD в отношении SN:ND=1:3.
а) Докажите, что точка M — середина ребра SC.
б) Найдите длину отрезка, по которому плоскость OMN пересекает грань SBC.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: 616CD3
Дайте развернутый ответ. стереометрия
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 7. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC=SK:KC=1:3 . Плоскость α содержит прямую KN и параллельна прямой BC .
а) Докажите, что плоскость α параллельна прямой SA .
б) Найдите угол между плоскостями α и SBC .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.2 Параллельность прямой и плоскости, признаки и свойства 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.2 Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями
Решение:
...
Ответ:
Номер: 876DD3
Дайте развернутый ответ. стереометрия
В пирамиде ABCD рёбра DA , DB и DC попарно перпендикулярны, а AB=BC=AC=5√2 .
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=2:3 . Найдите площадь сечения MNB .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
Все грани правильной пирамиды – равнобедренные треугольники, а все её боковые ребра равны между собой.
Решение из демо 2024: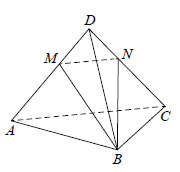 а) Прямоугольные треугольники ABD и ACD равны, поскольку катет AD общий, а AB = AC. Прямоугольные треугольники ABD и BCD равны, поскольку катет BD общий, а AB = BC.
а) Прямоугольные треугольники ABD и ACD равны, поскольку катет AD общий, а AB = AC. Прямоугольные треугольники ABD и BCD равны, поскольку катет BD общий, а AB = BC.
Значит, BD = CD = AD.
AB = BC = AC по условию,
следовательно, пирамида правильная, ч.т.д.
б) Найдём боковые рёбра. Треугольник BCD – равнобедренный и прямоугольный, поэтому
`BD=CD=(BC)/sqrt2=5`.
Аналогично, AD = 5 .
Найдём стороны треугольника MNB:
`MB=NB=sqrt(ND^2+DB^2)=sqrt29`,
`MN=sqrt(MD^2+DN^2)=2sqrt2`.
Площадь равнобедренного треугольника MNB равна
`1/2⋅MN⋅sqrt(MB^2-((MN)/2)^2)=3sqrt6 `
Ответ: б) `3sqrt6 `
Номер: 429E53
Дайте развернутый ответ. 2024
Пятиугольник ABCDE вписан в окружность. Известно, что AB=CD=3, BC=DE=4.
а) Докажите, что AC=CE.
б) Найдите длину диагонали BE, если AD=6.
КЭС: 7.1 Фигуры на плоскости
Решение:
...
Ответ:
Номер: D8C152
Дайте развернутый ответ. стереометрия
В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 6, а боковое ребро AA1 равно 4. На рёбрах AA1 и BB1 отмечены точки M и N соответственно, причём AM=BN=3 .
а) Точки O и O1 — центры окружностей, описанных около треугольников ABC и A1B1C1 соответственно. Докажите, что прямая OO1 содержит точку пересечения медиан треугольника CMN .
б) Найдите расстояние от точки C1 до плоскости CMN .
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.4 Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными и скрещивающимися прямыми; расстояние между параллельными плоскостями
Решение:
...
Ответ:
Номер: F416AF
Дайте развернутый ответ. стереометрия
В прямоугольном параллелепипеде ABCDA1B1C1D1 через середину M диагонали AC1 проведена плоскость α перпендикулярно этой диагонали, AB=5, BC=3, AA1=4. а) Докажите, что плоскость α содержит точку D1. б) Найдите отношение, в котором плоскость α делит ребро A1B1.
КЭС: 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 0B28A5
Дайте развернутый ответ.
Сумма оснований трапеции равна 10, а её диагонали равны 6 и 8.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 5259A1
Дайте развернутый ответ.
Две окружности касаются внутренним образом в точке C. Вершины A и B равнобедренного прямоугольного треугольника ABC с прямым углом C лежат на меньшей и большей окружностях соответственно. Прямая AC вторично пересекает бо́льшую окружность в точке E, а прямая BC вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите AC, если радиусы окружностей равны 3 и 4.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: A7A4AB
Дайте развернутый ответ.
В треугольнике ABC точки A1 , B1 и C1 — середины сторон BC , AC и AB соответственно, AH — высота, ∠BAC=30° , ∠BCA=45° .
а) Докажите, что точки A1 , B1 , C1 и H лежат на одной окружности.
б) Найдите A1H , если BC=4√3 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 9595A4
Дайте развернутый ответ. стереометрия
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=2√2 , AD=6 , AA1=10 . На рёбрах AA1 и BB1 отмечены точки E и F соответственно, причём A1E:EA=3:2 и B1F:FB=3:7 . Точка T — середина ребра B1C1 .
а) Докажите, что плоскость EFT проходит через точку D1 .
б) Найдите площадь сечения параллелепипеда плоскостью EFT .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: E8E9A7
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A , B и C , а на окружности другого основания — точка C1 , причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=30° , AB=1 , CC1=2√2 .
а) Докажите, что угол между прямыми AC1 и BC равен 60° .
б) Найдите площадь боковой поверхности цилиндра.
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: E8FAA5
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCA1B1C1 лежит равнобедренный треугольник ABC с основанием AB. Точка P делит ребро AB в отношении AP:PB=1:3, а точка Q — середина ребра A1C1. Через середину M ребра BC провели плоскость α, перпендикулярную отрезку PQ. а) Докажите, что плоскость α параллельна ребру AB. б) Найдите отношение, в котором плоскость α делит отрезок PQ, считая от точки P, если известно, что AB=AA1, AB:BC=2:5.
КЭС: 5.2.2 Параллельность прямой и плоскости, признаки и свойства 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 82F7A1
Дайте развернутый ответ. 2024
Окружность с центром в точке O касается сторон угла с вершиной N в точках A и B. Отрезок BC — диаметр этой окружности.
а) Докажите, что ∠ANB=2∠ABC.
б) Найдите расстояние от точки N до прямой AB, если известно, что AC=14 и AB=36.
КЭС: 7.1 Фигуры на плоскости
Решение:
...
Ответ:
Номер: 8377A1
Дайте развернутый ответ.
Прямая, перпендикулярная стороне BC ромба ABCD, пересекает его диагональ AC в точке M, а диагональ BD в точке N, причём AM:MC=1:2, BN:ND=1:3.
а) Докажите, что cos∠BAD=1/5 .
б) Найдите площадь ромба, если MN=5.
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 78A6C2
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B , а на окружности другого основания — точки B1 и C1 , причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите угол между прямыми BB1 и AC1 , если AB=6 , BB1=15 , B1C1=8 .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.2 Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 77C190
Дайте развернутый ответ.
В треугольнике ABC точки A1 , B1 и C1 — середины сторон BC , AC и AB соответственно, AH — высота, ∠BAC=120° , ∠BCA=15° .
а) Докажите, что точки A1 , B1 , C1 и H лежат на одной окружности.
б) Найдите A1H , если BC=4√3 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: BAD790
Дайте развернутый ответ. стереометрия
Основанием четырёхугольной пирамиды PABCD является трапеция ABCD , причём ∠BAD+∠ADC=90° . Плоскости PAB и PCD перпендикулярны плоскости основания, K — точка пересечения прямых AB и CD .
а) Докажите, что плоскости PAB и PCD перпендикулярны.
б) Найдите объём пирамиды KBCP , если AB=BC=CD=4 , а высота пирамиды PABCD равна 9.
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 9B8297
Дайте развернутый ответ. 2024
Периметр треугольника ABC равен 36. Точки E и F — середины сторон AB и BC соответственно. Отрезок EF касается окружности, вписанной в треугольник ABC.
а) Докажите, что AC=9.
б) Найдите площадь треугольника ABC, если ∠ACB=90°.
КЭС: 7.1 Фигуры на плоскости
Решение:
...
Ответ:
Номер: 92699C
Дайте развернутый ответ. стереометрия
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B , а на окружности другого основания — точки B1 и C1 , причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите расстояние от точки B до прямой AC1 , если AB=21 , BB1=12 , B1C1=16 .
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх перпендикулярах 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 8EBB9F
Дайте развернутый ответ.
В квадрате ABCD точки M и N — середины сторон AB и BC соответственно. Отрезки CM и DN пересекаются в точке K.
а) Докажите, что ∠ BKM=45°.
б) Найдите радиус окружности, описанной около треугольника ABK, если сторона AB=2√10.
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: 86B99A
Дайте развернутый ответ.
На стороне AC равностороннего треугольника ABC отмечена точка M. Серединный перпендикуляр к отрезку BM пересекает стороны AB и BC в точках E и K соответственно.
а) Докажите, что ∠AEM=∠CMK.
б) Найдите отношение площадей треугольников AEM и CMK, если AM:MC=1:4.
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: F2A2EB
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCDA1B1C1D1 лежит параллелограмм ABCD. На рёбрах A1B1, B1C1 и BC отмечены точки M, K и N соответственно, причём B1K:KC1=1:2. Четырёхугольник AMKN — равнобедренная трапеция с основаниями 2 и 3.
а) Докажите, что точка N — середина ребра BC.
б) Найдите площадь трапеции AMKN, если объём призмы равен 12, а высота призмы равна 2.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: 0549EB
Дайте развернутый ответ.
В остроугольном треугольнике ABC высоты AA1, BB1 и CC1 пересекаются в точке H . Через точку C1 параллельно высоте BB1 проведена прямая, пересекающая высоту AA1 в точке K.
а) Докажите, что AB⋅KH=BC⋅C1H.
б) Найдите отношение площадей треугольников C1HK и ABC, если AB=6, BC=4, AC=5.
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 0063ED
Дайте развернутый ответ.
Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L — точка пересечения отрезков KM и AP. Найдите длину отрезка AL, если радиус большей окружности равен 34, а BC=32.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: BE8FE4
Дайте развернутый ответ. стереометрия
Точка M — середина ребра SA правильной четырёхугольной пирамиды SABCD с основанием ABCD. Точка N лежит на ребре SB, SN:NB=1:2.
а) Докажите, что плоскость CMN параллельна прямой SD.
б) Найдите площадь сечения пирамиды SABCD плоскостью CMN, если все рёбра пирамиды равны 6.
КЭС: 5.2.2 Параллельность прямой и плоскости, признаки и свойства 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.3.4 Сечения куба, призмы, пирамиды 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: 1D76E2
Дайте развернутый ответ. стереометрия
На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM:MB=CN:NB=1:2 . Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P , Q , M и N лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 1F7CE6
Дайте развернутый ответ. стереометрия
В кубе ABCDA1B1C1D1 точки M и N — середины рёбер AB и AD соответственно.
а) Докажите, что прямые B1N и CM перпендикулярны.
б) Плоскость α проходит через точки N и B1 параллельно прямой CM. Найдите расстояние от точки C до плоскости α, если B1N=6.
КЭС: 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых 5.2.2 Параллельность прямой и плоскости, признаки и свойства 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.4 Сечения куба, призмы, пирамиды 5.5.4 Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными и скрещивающимися прямыми; расстояние между параллельными плоскостями
Решение:
...
Ответ:
Номер: A47BE8
14. Дайте развернутый ответ.
На стороне BC треугольника ABC отмечена точка D так, что AB=BD. Биссектриса BF треугольника ABC пересекает прямую AD в точке E. Из точки C на прямую AD опущен перпендикуляр CK.
а) Докажите, что AB:BC=AE:EK.
б) Найдите отношение площади треугольника ABE к площади четырёхугольника CDEF, если BD:DC=5:2.
КЭС: 5.1.1 Треугольник 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
а) В равнобедренном треугольнике ABD биссектриса ВЕ является медианой и высотой.
Следовательно, — прямые BF и СК перпендикулярны прямой АК, а значит, параллельны. По — свойству биссектрисы треугольника ДВ:ВС=лЕ:ЕС, а по теореме Фалеса AF:FC=AE:EK. Таким образом,
АВ: ВС = АЕ: EK.
Ответ: б) 30/19
Смотреть полное решение
Номер: 003F6E
Дайте развернутый ответ. стереометрия
Точка M — середина бокового ребра SC правильной четырёхугольной пирамиды SABCD. Точка N лежит на стороне основания BC. Плоскость α проходит через точки M и N параллельно боковому ребру SA.
а) Плоскость α пересекает боковое ребро SD в точке L. Докажите, что BN:NC=DL:LS.
б) Плоскость α делит пирамиду SABCD на два многогранника. Найдите отношение их объёмов, если BN:NC=1:3.
КЭС: 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.3.4 Сечения куба, призмы, пирамиды 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
...
Ответ:
Номер: DE9364
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCDA1B1C1D1 лежит равнобедренная трапеция ABCD с основаниями AD=3 и BC=2. Точка M делит ребро A1D1 в отношении A1M:MD1=1:2, а точка K — середина ребра DD1.
а) Докажите, что плоскость MKC делит отрезок BB1 пополам.
б) Найдите площадь сечения призмы плоскостью MKC, если ∠MKC=90°, ∠ADC=60°.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: C87061
Дайте развернутый ответ.
Прямая, перпендикулярная стороне BC ромба ABCD, пересекает его диагональ AC в точке M, а диагональ BD в точке N, причём AM:MC=1:2, BN:ND=1:3.
а) Докажите, что прямая MN делит сторону ромба BC в отношении 1:4.
б) Найдите сторону ромба, если MN=√6.
КЭС: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: E80769
Дайте развернутый ответ. стереометрия
На ребре SD правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка M , причём SM:MD=2:1 . Точки P и Q — середины рёбер BC и AD соответственно.
а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 6F3F6D
Дайте развернутый ответ.
Две окружности разных радиусов касаются внешним образом в точке C . Вершины A и B равнобедренного прямоугольного треугольника ABC с прямым углом C лежат на меньшей и большей окружностях соответственно. Прямая AC вторично пересекает бо́льшую окружность в точке E , а прямая BC вторично пересекает меньшую окружность в точке D .
а) Докажите, что прямые AD и BE параллельны.
б) Найдите BC , если радиусы окружностей равны √15 и 15.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 7E3432
Дайте развернутый ответ.
Окружность с центром O1 касается оснований BC и AD и боковой стороны AB трапеции ABCD . Окружность с центром O2 касается сторон BC , CD и AD . Известно, что AB=10 , BC=9 , CD=30 , AD=39 .
а) Докажите, что прямая O1O2 параллельна основаниям трапеции ABCD .
б) Найдите O1O2 .
КЭС: 5.1.1 Треугольник 5.1.3 Трапеция 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: 7EEB3E
Дайте развернутый ответ. стереометрия
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α , содержащей прямую BD1 и параллельной прямой AC , является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями α и BCC1 , если AA1=6 , AB=4 .
КЭС: 5.2 Прямые и плоскости в пространстве 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
...
Ответ:
Номер: 17B23F
Дайте развернутый ответ.
Точка E — середина боковой стороны CD трапеции ABCD . На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O .
а) Докажите, что CO=KO .
б) Найдите отношение оснований трапеции BC и AD , если площадь треугольника BCK составляет 9/100 площади трапеции ABCD .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 15EF35
Дайте развернутый ответ. 2024 стереометрия
На рёбрах AC, AD, BD и BC тетраэдра ABCD отмечены точки K, L, M и N соответственно, причём AK:KC=2:3. Четырёхугольник KLMN — квадрат со стороной 2.
а) Докажите, что прямые AB и CD перпендикулярны.
б) Найдите расстояние от вершины B до плоскости KLM, если объём тетраэдра ABCD равен 25.
КЭС: 7.3 Многогранники
Решение:
...
Ответ:
Номер: A2B731
Дайте развернутый ответ.
Окружность проходит через вершины A , B и D параллелограмма ABCD , пересекает сторону BC в точках B и M и пересекает продолжение стороны CD за точку D в точке N .
а) Докажите, что AM=AN .
б) Найдите отношение CD:DN , если AB:BC=1:2 , а cos∠BAD=2/3 .
КЭС: 5.1.1 Треугольник 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат 5.1.4 Окружность и круг
Решение:
...
Ответ:
Номер: 909839
Дайте развернутый ответ.
В равнобедренной трапеции ABCD основание AD в два раза больше основания BC .
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O — точка пересечения диагоналей трапеции ABCD . Найдите расстояние от вершины C до середины отрезка OD , если BC=16 и AB=10 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 832C34
Дайте развернутый ответ. стереометрия
В основании прямой призмы ABCA1B1C1 лежит равнобедренный треугольник ABC с основанием AB. Точка P делит ребро AB в отношении AP:PB=1:3, а точка Q — середина ребра A1C1. Через середину M ребра BC провели плоскость α, перпендикулярную отрезку PQ. а) Докажите, что плоскость α делит ребро AC пополам.
б) Найдите отношение, в котором плоскость α делит ребро A1C1, считая от точки A1, если известно, что AB=AA1, AB:BC=2:5.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.4 Сечения куба, призмы, пирамиды 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
...
Ответ:
Номер: FA228B
Дайте развернутый ответ. 2024 стереометрия
В правильной треугольной пирамиде SABC с основанием ABC точки M и K — середины рёбер AB и SC соответственно, а точки N и L отмечены на рёбрах SA и BC соответственно так, что отрезки MK и NL пересекаются, а AN=3NS.
а) Докажите, что прямые MN, KL и SB пересекаются в одной точке.
б) Найдите отношение BL:LC.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: BCEB84
Дайте развернутый ответ.
На сторонах AB , BC и AC треугольника ABC отмечены точки C1 , A1 и B1 соответственно, причём AC1:C1B=21:10 , BA1:A1C=2:3 , AB1:B1C=2:5 . Отрезки BB1 и CC1 пересекаются в точке D .
а) Докажите, что четырёхугольник ADA1B1 — параллелограмм.
б) Найдите CD , если отрезки AD и BC перпендикулярны, AC=63 , BC=25 .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: AC2684
Дайте развернутый ответ.
Биссектрисы углов BAD и BCD равнобедренной трапеции ABCD пересекаются в точке O. Через точку O провели прямую, параллельную основаниям BC и AD. а) Докажите, что отрезок этой прямой внутри трапеции равен её боковой стороне.
б) Найдите отношение длин оснований трапеции, если AO=CO и данная прямая делит сторону AB в отношении AM:MB=1:2.
КЭС: 5.1.3 Трапеция 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение:
...
Ответ:
Номер: E87882
Дайте развернутый ответ. 2024 стереометрия
В правильной треугольной пирамиде SABC с основанием ABC точки M и K — середины рёбер AB и SC соответственно. На продолжении ребра SB за точку S отмечена точка R.
Прямые RM и RK пересекают рёбра AS и BC в точках N и L соответственно, причём BL=3LC.
а) Докажите, что отрезки MK и NL пересекаются.
б) Найдите отношение AN:NS.
КЭС: 7.2 Прямые и плоскости в пространстве 7.3 Многогранники
Решение:
...
Ответ:
Номер: 637C89
Дайте развернутый ответ.
В треугольнике ABC угол A равен 120° . Прямые, содержащие высоты BM и CN треугольника ABC , пересекаются в точке H . Точка O — центр окружности, описанной около треугольника ABC .
а) Докажите, что AH=AO .
б) Найдите площадь треугольника AHO , если BC=3 , ∠ABC=15° .
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 3B468E
Дайте развернутый ответ.
Окружность, вписанная в равнобедренную трапецию ABCD , касается её боковой стороны CD в точке M . Луч AM вторично пересекает окружность в точке N , а прямую BC — в точке K , причём AN=4 , MN=12 .
а) Докажите, что ∠AMD=∠MCK .
б) Найдите основания трапеции.
КЭС: 5.1 Планиметрия
Решение:
...
Ответ:
Номер: 8C8D87
Все задания по геометрии 2-й части ЕГЭ из старого банка (без дублей нового)
Дана равнобедренная трапеция ABCD с основаниями AD и BC . Окружность с центром O , построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H , точка Q — середина CD .
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD , если ∠BAD=60° и BC=2 .
Решение:
...
Ответ:
Номер: E16AF4
Дана равнобедренная трапеция ABCD с основаниями AD и BC . Окружность с центром O , построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H , точка Q — середина CD .
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD , если ∠BAD=67,5° и BC=3 .
Решение:
...
Ответ:
Номер: B81100
Дана равнобедренная трапеция ABCD с основаниями AD и BC . Окружность с центром O , построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H , точка Q — середина CD .
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD , если ∠BAD=75° и BC=1 .
Решение:
...
Ответ:
Номер: DDB7A7
К окружности, вписанной в квадрат ABCD , проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P . В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM:MB=1:2 ?
Решение:
...
Ответ:
Номер: 6B7451
К окружности, вписанной в квадрат ABCD , проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P . В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM:MB=1:3 ?
Решение:
...
Ответ:
Номер: C131C9
К окружности, вписанной в квадрат ABCD , проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P . В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM:MB=1:4 ?
Решение:
...
Ответ:
Номер: EE3463
Диагонали AC и BD четырёхугольника ABCD , вписанного в окружность, пересекаются в точке P , причём BC=CD .
а) Докажите, что AB:BC=AP:PD .
б) Найдите площадь треугольника COD , где O — центр окружности, вписанной в треугольник ABD , если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB=5 , а BC=52–√ .
Решение:
...
Ответ:
Номер: D81F46
Дан прямоугольный треугольник ABC с прямым углом C . На катете AC взята точка M . Окружность с центром O и диаметром CM касается гипотенузы в точке N .
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN , если CN=4 и AM:MC=1:3 .
Решение:
...
Ответ:
Номер: 76AFB6
Две окружности касаются внутренним образом в точке A , причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P . Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L — точка пересечения отрезков KM и AP . Найдите AL , если радиус большей окружности равен 10, а BC=16 .
Решение:
...
Ответ:
Номер: C4A623
Точка B лежит на отрезке AC . Прямая, проходящая через точку A , касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K . Продолжение отрезка MB пересекает окружность с диаметром AB в точке D .
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC , если AK=3 и MK=12 .
Решение:
...
Ответ:
Номер: 1549DC
Точка M лежит на стороне BC выпуклого четырёхугольника ABCD , причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD .
б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD , если известно, что BM:MC=1:3 , а площадь четырёхугольника, стороны которого лежат на прямых AM , DM , BN и CN , равна 18.
Решение:
...
Ответ:
Номер: 2CAEDB
Две окружности касаются внутренним образом в точке K , причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C . Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L .
а) Докажите, что CN:CM=LB:LA .
б) Найдите MN , если LB:LA=2:3 , а радиус малой окружности равен √23 .
Решение:
...
Ответ:
Номер: AB1F55
54. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD , вторая — боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что `(AP)/(PD)=sinD`.
б) Найдите площадь трапеции, если радиусы окружностей равны 4/3 и 1/3 .
Решение:
Номер: 999FC4
Дана равнобедренная трапеция ABCD с основаниями AD и BC . Окружность с центром O , построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H , точка Q — середина CD .
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD , если ∠BAD=75° и BC=1 .
Решение:
...
Ответ:
Номер: F6716D
В остроугольном треугольнике ABC проведены высоты AK и CM . На них из точек M и K опущены перпендикуляры ME и KH соответственно.
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH к AC , если ∠ABC=30° .
Решение:
...
Ответ:
Номер: 250B4D
В трапеции ABCD точка E — середина основания AD , точка M — середина боковой стороны AB . Отрезки CE и DM пересекаются в точке O .
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE , если BC=3 , AD=4 .
Решение:
...
Ответ:
Номер: C5C4F4
Точка O — центр окружности, описанной около остроугольного треугольника ABC , I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB .
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC .
б) Найдите угол OHI , если ∠ABC=40° .
Решение:
...
Ответ:
Номер: BF1575
В выпуклом четырёхугольнике ABCD точки K , L , M и N — середины сторон AB , BC , CD и AD соответственно.
Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11:17 .
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD .
Решение:
...
Ответ:
Номер: A0FD25
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH . Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK , если AB=5 , AC=8 .
Решение:
...
Ответ:
Номер: AAF5C4
В трапеции ABCD боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH . На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED , если ∠BCD=120° .
Решение:
...
Ответ:
Номер: BD119B
В треугольнике ABC угол ABC равен 60° . Окружность, вписанная в треугольник, касается стороны AC в точке M .
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin∠BMC , если известно, что отрезок BM в 2,5 раза больше радиуса вписанной в треугольник окружности.
Решение:
...
Ответ:
Номер: 6FC99C
Точка O — центр окружности, описанной около остроугольного треугольника ABC , I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB .
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC .
б) Найдите угол OHI , если ∠ABC=70° .
Решение:
...
Ответ:
Номер: A74E6D
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 5. На его ребре BB1 отмечена точка K так, что KB=4 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=3:1 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C .
Решение:
...
Ответ:
Номер: 132142
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 3. На его ребре BB1 отмечена точка K так, что KB=2 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что плоскость α проходит через середину ребра A1B1 .
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C .
Решение:
...
Ответ:
Номер: 9DEFF7
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB=3 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=2:1 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C .
Решение:
...
Ответ:
Номер: 39C879
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 5. На его ребре BB1 отмечена точка K так, что KB=3 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=1:2 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α .
Решение:
...
Ответ:
Номер: 474248
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 7. На его ребре BB1 отмечена точка K так, что KB=4 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=1:3 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α .
Решение:
...
Ответ:
Номер: AC96DF
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 6. На его ребре BB1 отмечена точка K так, что KB=5 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=4:1 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α .
Решение:
...
Ответ:
Номер: 639055
стереометрия В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB=3 . Через точки K и C1 проведена плоскость α , параллельная прямой BD1 .
а) Докажите, что A1P:PB1=2:1 , где P — точка пересечения плоскости α с ребром A1B1 .
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C .
Решение:
...
Ответ:
Номер: 039761
стереометрия В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1 , считая от точки C .
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α .
Решение:
...
Ответ:
Номер: 64597E
стереометрия В правильной треугольной пирамиде SABC сторона основания AB равна 60, а боковое ребро SA равно 37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1 , считая от точки C .
б) Найдите расстояние от вершины A до плоскости α .
Решение:
...
Ответ:
Номер: 257425
стереометрия В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1 , считая от точки C .
б) Найдите объём пирамиды, вершиной которой является точка C , а основанием — сечение пирамиды SABC плоскостью α .
Решение:
...
Ответ:
Номер: 29565E
стереометрия В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 13. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1 , считая от точки C .
б) Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью α .
Решение:
...
Ответ:
Номер: 32528E
стереометрия В правильной треугольной пирамиде SABC сторона AB основания равна 12, а высота пирамиды равна 1. На рёбрах AB , AC и AS отмечены точки M , N и K соответственно, причём AM=AN=3 и AK=74 .
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC .
Решение:
...
Ответ:
Номер: 0E2FD2
стереометрия В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 6, а боковое ребро AA1 равно 3. На рёбрах AB и B1C1 отмечены точки K и L соответственно, причём AK=B1L=2 . Точка M — середина ребра A1C1 . Плоскость γ параллельна прямой AC и содержит точки K и L .
а) Докажите, что прямая BM перпендикулярна плоскости γ .
б) Найдите объём пирамиды, вершина которой — точка M , а основание — сечение данной призмы плоскостью γ .
Решение:
...
Ответ:
Номер: 0BDC03
стереометрия В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 3, а боковое ребро AA1 равно √2 . На рёбрах AB , A1B1 и B1C1 отмечены точки M , N и K соответственно, причём AM=B1N=C1K=1 .
а) Пусть L — точка пересечения плоскости MNK с ребром AC . Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK .
Решение:
...
Ответ:
Номер: 025013
стереометрия В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно 2√2 . На рёбрах AB , A1B1 и B1C1 отмечены точки M , N и K соответственно, причём AM=B1N=C1K=2 .
а) Пусть L — точка пересечения плоскости MNK с ребром AC . Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK .
Решение:
...
Ответ:
Номер: F5A762
стереометрия В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 6, а боковое ребро AA1 равно 3. На ребре AB отмечена точка K так, что AK=1 . Точки M и L — середины рёбер A1C1 и B1C1 соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L .
а) Докажите, что прямая BM перпендикулярна плоскости γ .
б) Найдите расстояние от точки C до плоскости γ .
Решение:
...
Ответ:
Номер: 3B7532
стереометрия В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6 . Длины боковых рёбер пирамиды SA=3 , SB=5 , SD=3√5 .
а) Докажите, что SA — высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC .
Решение:
...
Ответ:
Номер: DCA9B6
стереометрия В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6 . Длины боковых рёбер пирамиды SA=√21 , SB=√85 , SD=√57 .
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD .
Решение:
...
Ответ:
Номер: A885B6
стереометрия В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=3 . Длины боковых рёбер пирамиды SA=√11 , SB=3√3 , SD=2√5 .
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB .
Решение:
...
Ответ:
Номер: CB3CC8
стереометрия В правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 6, а боковое ребро AA1 равно 2√3 . На рёбрах BC и C1D1 отмечены точки K и L соответственно, причём BK=C1L=2 . Плоскость γ параллельна прямой BD и содержит точки K и L .
а) Докажите, что прямая A1C перпендикулярна плоскости γ .
б) Найдите объём пирамиды, вершина которой — точка A1 , а основание — сечение данной призмы плоскостью γ .
Решение:
...
Ответ:
Номер: 779E17
стереометрия В правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 8, а боковое ребро AA1 равно 4√2 . На рёбрах BC и C1D1 отмечены точки K и L соответственно, причём BK=C1L=2 . Плоскость γ параллельна прямой BD и содержит точки K и L .
а) Докажите, что прямая A1C перпендикулярна плоскости γ .
б) Найдите расстояние от точки B до плоскости γ .
Решение:
...
Ответ:
Номер: C29114
стереометрия В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 16, а высота пирамиды равна 4. На рёбрах AB , CD и AS отмечены точки M , N и K соответственно, причём AM=DN=4 и AK=3 .
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки K до плоскости SBC .
Решение:
...
Ответ:
Номер: 859A67
Реальные задания ЕГЭ с официальными ключами
1. Дайте развернутый ответ. 2024
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB1=∠ACB.
б) Найдите длину стороны BC, если AH=6 и ∠BAC=45°.
Решение:
2 см. в новом банке
3. Дайте развернутый ответ. 2024
В треугольнике ABC длина стороны AC равна 4. Точки E и F - середины сторон AB и BC соответственно. Отрезок EF касается окружности, вписанной в треугольник ABC.
а) Докажите, что периметр треугольника ABC равен 16.
б) Найдите площадь четырехугольника AEFC, если ∠ACB=90°.
Решение:
4. В остроугольном треугольнике АВС поведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН к АС, если ∠АВС = 60°.
Решение:
5. На сторонах ВС и СD квадрата АВСD отмечены точки Е и К соответственно. Известно, что АЕ = 2, ЕК = 1, АК = `sqrt5`.
а) Докажите, что ∠ВАЕ = ∠СЕК.
б) Найдите площадь квадрата АВCD.
Решение:
6. Стороны АВ и АD квадрата АВСD касаются окружности, радиус которой втрое меньше стороны квадрата.
а) Докажите, что эта окружность разбивает диагональ ВD на три равных отрезка.
б) Касательная к окружности, проведенная через точку В, пересекает сторону СD в точке Е. Найдите длину отрезка DE, если сторона квадрата равна 12.
Решение:
6-2. Стороны АВ и АD квадрата АВСD касаются окружности, радиус которой втрое меньше стороны квадрата.
а) Докажите, что эта окружность разбивает диагональ ВD на три равных отрезка.
б) Касательная к окружности, проведенная через точку В, пересекает сторону СD в точке Е. Найдите длину отрезка DE, если сторона квадрата равна 18.
Решение:
7. На стороне АС равностороннего треугольника АВС отмечена точка М. Серединный перпендикуляр к отрезку ВМ пересекает стороны АВ и ВС в точках Е и К соответственно.
а) Докажите, что ∠АЕМ = ∠СМК.
б) Найдите отношение площадей треугольников АЕМ и СМК, если АМ:МС = 1:4.
Решение:
8. Биссектриса АМ острого угла А равнобедренной трапеции АВСD делит боковую сторону СD пополам. Отрезок DN перпендикулярен отрезку АМ и делит сторону АВ в отношении AN:NB = 5:1.
а) Докажите, что прямые ВМ и СN перпендикулярны.
б) Найдите длину отрезка MN, если площадь трапеции равна `3sqrt2`.
Решение:
9. Точка В лежит на отрезке АС. Прямая, проходящая через точку А, касается окружности с диаметром ВС в точке М и второй раз пересекает окружность с диаметром АВ в точке К. Продолжение отрезка МВ пересекает окружность с диаметром АВ в точке D.
а) Докажите, что прямые AD и МС параллельны.
б) Найдите площадь треугольника DBC, если АК = 5 и МК = 25.
Решение:
10. Прямая, перпендикулярная стороне ВС ромба АВСD, пересекает его диагональ АС в точке М, а диагональ BD в точке N, причем АМ:МС = 1:2, BN:ND = 1:3.
а) Докажите, что прямая MN делит сторону ромба ВС в отношении 1:4.
б) Найдите сторону ромба, если MN = `2sqrt3`.
Решение:
11. Биссектрисы углов BAD и BCD равнобедренной трапеции АВСD пересекаются в точке О. На боковых сторонах АВ и СD отмечены точки М и N соответственно так, что АМ = МО, CN = NO.
а) Докажите, что точки М, О и N лежат на одной прямой.
б) Найдите отношение АМ:МВ, если АО = СО и ВС:АD = 1:7.
Решение:
12. Окружность касается одной из сторон прямого угла с вершиной D в точке Е и пересекает вторую сторону в точках А и В (точка А лежит между В и D). В окружности проведен диаметр АС.
а) Докажите, что отрезок ВС вдвое больше отрезка DЕ.
б) Найдите расстояние от точки Е до прямой АС, если AD = 4 и АВ = 5.
Решение:
13. Точка М - середина стороны АВ треугольника АВС. Окружность вписанная в треугольник АВС, касается стороны АВ в точке Р.
а) Докажите, что `МР = (|BC - AC|)/ 2`.
б) Известно, что МС = МА, ВС>АС, а отрезок МР относится к радиусу окружности, вписанной в треугольник АВС, как 7 : 4. Найдите углы треугольника АВС.
Решение:
14. Есть в новом банке ФИПИ
15. На стороне острого угла с вершиной A отмечена точка В. Из точки В на биссектрису и другую сторону угла опущены перпендикуляры ВС и BD соответственно.
а) Докажите, что AC2 +CD2 =AD2 +BD2.
0) Прямые АС и BD пересекаются в точке T. Найдите отношение AT: TC, если cos ∠ABC = 3/8
Решение:
а) Углы BCA и BDA прямые, значит, точки С и D лежат на окружности с диаметром АB.
Биссектриса AC вписанного угла BAD делит дугу ВСD пополам, значит, хорды ВС и СD,
стягивающие равные дуги, равны. Следовательно,
AC2 +CD2 = AC2 + ВС2 =AD2 +BD2.
Ответ: б) 46:9
Смотреть полное решение
16. Есть в новом банке ФИПИ
17. В треугольнике АВС точки М и N — середины сторон AB и ВС соответственно. Известно, что около четырёхугольника АМNС можно описать окружность.
а) Докажите, что треугольник ABC равнобедренный.
6) На стороне АС отмечена точка F такая, что ∠ АFВ=135°. Отрезок ВF пересекает отрезок МN в точке Е. Найдите радиус окружности, описанной около четырёхугольника AMNC, если ∠ АВС =120°, EF = 6√2.
Решение:
а) Отрезок MN — средняя линия треугольника АВС, значит, прямые AC и ММ параллельны, а четырёхугольник АМNС является трапецией (ММ< АС).
Поскольку окружность можно описать только около равнобедренной трапеции,
АМ =СN, то есть АВ=ВС, а значит, треугольник АВС равнобедренный.
Ответ: б) 12√7.
Смотреть полное решение
18. Точка D лежит на основании AC равнобедренного треугольника ABC.
Точки I и J — центры окружностей, описанных около треугольников ABD и CBD соответственно.
а) Докажите, что прямые BI и DJ параллельны.
6) Найдите IJ, если АС =12, cos ∠ BDC =3/7.
Решение:
а) Радиусы окружностей, описанных около треугольников ABD и СВО, равны
`(AB)/(2sin∠ADB)` и `(BC)/(2sin ∠BDC)` соответственно.
Поскольку ∠ ADB =180°- ∠ВDС и АВ=ВС, радиусы окружностей, описанных около треугольников ABD и CBD, равны. Следовательно, четырёхугольник BIDJ является ромбом.
Значит, прямые BI и DJ параллельны.
Ответ: б) `(21sqrt10)/10`.
Смотреть полное решение
19. Дана трапеция ABCD с основаниями АР и ВС. Окружность, описанная около треугольника АВС, пересекает боковую сторону CD в точке Ё, а основание AD в точке F, причём АВ = FD.
а) Докажите, что ∠EAD = ∠EDA.
6) Найдите площадь трапеции ABCD, если АВ=5, ВС =3, а прямые АЕ и CF перпендикулярны.
Решение:
а) Трапеция АВСF вписана в окружность, поэтому CF = АВ = FD. Значит, треугольник CFD равнобедренный и
∠EDA = ∠CDF = ∠FCD = ∠FCE = ∠FAE = ∠ЕАD.
Ответ: б) `20sqrt3`.
Смотреть полное решение
20. Окружность с центром О, построенная на катете AC прямоугольного треугольника АВС как на диаметре, пересекает гипотенузу АВ в точках A и D. Касательная, проведённая к этой окружности в точке D, пересекает катет ВС в точке М.
а) Докажите, что ВМ =СМ.
6) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К. Найдите ВК : КР, если `соs∠BAC=(2sqrt5)/5`.
Решение:
а) Отрезок CD является высотой треугольника АВС, поскольку вписанный угол АDС опирается на диаметр окружности.
Прямая ВС касается окружности с диаметром АС в точке С, поскольку радиус окружности ОС перпендикулярен ВС.
Следовательно, СМ = MD как отрезки касательных, проведённых из одной точки.
Значит,
∠MBD =90°- ∠MCD =90°- ∠МDС = ∠MDB,
поэтому ВМ =MD=CM.
Ответ: б) 3:5.
Смотреть полное решение
21. Аналогично 41 Ященко.
22. Высоты ВВ1 и СС1 остроугольного треугольника АВС пересекаются в точке H. Отрезок АР — диаметр окружности, описанной около треугольника ABC.
а) Докажите, что прямая HP пересекает отрезок BC в его середине.
б) Луч PH вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка MC1, если расстояние от центра этой окружности до прямой BC равно 4, ∠BPH=120°.
Решение:
а) Пусть (ВС) ∩ (PH)=G;
РСА = 90°(опирается на диаметр) =>
РС ⊥ АС, но BH ⊥ АС => РС || ВН;
аналогично СН || ВР =>
СРВН — параллелограмм, диагонали которого пересекаются в их середине => С — середина ВС
Ответ: б) `4sqrt3`.
Смотреть полное решение
23. В равнобедренной трапеции ABCD меньшее основание BC равно боковой стороне. На плоскости выбрали точку Е такую, что прямая ВЕ перпендикулярна прямой AD, а прямая CE перпендикулярна прямой BD.
а) Докажите, что ∠AEB = ∠ADB.
6) Найдите площадь трапеции ABCD, если AB=32, cos∠AEB= 3/4.
Решение:
а) Обозначим точку пересечения прямых AD и ВЕ через H, a точку пересечения прямых BD и СЕ через I.
В равнобедренной трапеции ABCD сумма противоположных углов равна 180°, следовательно, около неё можно описать окружность.
В равнобедренном треугольнике BCD
∠CBD = ∠CDB. E
В прямоугольном треугольнике BCE
∠ВЕС =90°— ∠IBE = ∠СВD = ∠CDB.
Следовательно, точка E лежит на окружности, описанной около треугольника BCD, то есть точки A, В, С, D и Е лежат на одной окружности.
Значит, ∠AEB = ∠АDВ.
Ответ: б) `432sqrt7`.
Смотреть полное решение
24. Отрезок СН — высота прямоугольного треугольника АВС с прямым углом С. На катетах АС и ВС выбраны точки М и N соответственно такие, что ∠МNH =90°.
а) Докажите, что треугольник МNH подобен треугольнику ABC.
6) Найдите СN, если BC =2, АС=4, СМ =1.
Решение:
а) В четырёхугольнике СМНN углы NCM и МНN равны 90°. Следовательно, около этого четырёхугольника можно описать окружность.
Значит,
∠NMH = ∠NCH =90°— ∠HBC = ∠ВАС.
Таким образом, прямоугольные треугольники ABC и МNH подобны по острому углу.
Ответ: б) `3/2`.
Смотреть полное решение
25. В треугольнике АВС угол А равен 120°. Прямые, содержащие высоты BM и CN треугольника АВС, пересекаются в точке Н. Точка О — центр окружности, описанной около треугольника АВС.
а) Докажите, что AH = АО.
0) Найдите площадь треугольника АНО . если ВС = √15, ∠ABC =45°.
Решение:
Ответ: б) `5/4`.
Смотреть полное решение
26. В прямоугольном треугольнике АВС точка М лежит Ha катете АС, а точка N лежит на продолжении катета ВС за точку С, причём СМ =ВС и СN=АС.
а) Отрезки СН и СF — высоты треугольников ACB и NCM соответственно. Докажите, что прямые СН и СF перпендикулярны.
6) Прямые ВМ и АМ пересекаются в точке L. Найдите LM, если ВС =4, а АС =6.
Решение:
а) Прямоугольные треугольники АВС и NМС равны по двум катетам. Пусть ∠BAC =α, тогда по свойству высоты в прямоугольном треугольнике:
∠ACH =90°-α, ∠FСМ = ∠CNM = ∠САВ=α,
откуда
∠FCH = ∠FСМ + ∠ACH =α+(90°-α)=90°.
Ответ: б) √2.
Смотреть полное решение
27. На сторонах АВ, ВС и AC треугольника АВС отмечены точки C1, A1 и B1 соответственно, причём АС1:С1В= 21:10, BA1:A1C =2:3, AB1: B1C =2:5. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что четырёхугольник ADA1B1 — параллелограмм.
6) Найдите CD, если отрезки AD и ВС перпендикулярны, АС = 63, ВС =25.
Решение:
Ответ: б) 27.
Смотреть полное решение
28. В остроугольном треугольнике АВС проведены высота CC1 и медиана AA1, причём точки A, С, А1 и С1 лежат на одной окружности.
а) Докажите, что треугольник АВС равнобедренный.
6) Найдите площадь треугольника АВС, если АА1 :СС1 =3:2 и A1C1 =2.
Решение:
а) Вписанные углы АС1С и AA1C опираются на одну дугу АС, значит, они равны, то есть
∠AA1C =90°. В треугольнике АВС медиана AA1 является высотой, значит, треугольник ABC равнобедренный, АВ = АС
Ответ: б) 8√2.
Смотреть полное решение
29. Биссектрисы острых углов A и В прямоугольного треугольника ABC пересекают окружность, описанную около этого треугольника, в точках A1 и В1 соответственно.
а) Докажите, что угол А1ВВ1 равен 45°
6) Биссектриса угла с пересекает окружность, описанную около треугольника АВС, точке C1. Найдите В1С1 если АВ = 2√3, ∠BAC = 60°
Решение:
Ответ: б) 3.
Смотреть полное решение
30. Две окружности касаются внутренним образом в точке С. Вершины A и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат большей и меньшей окружностях соответственно.
Прямая AC вторично пересекает меньшую окружность в точке D.
Прямая ВС вторично пересекает большую окружность в точке E.
а) Докажите, что AE параллельно BD.
6) Найдите АС. если радиусы окружностей равны 8 и 15.
Решение:
а) ∠АСВ = 90° => BD и AE — диаметры меньшей и большей окружностей соответственно.
△BOC — равнобедренный,
∠OBC = ∠OCB =a;
△ESC — равнобедренный,
∠SCE = ∠SEC =a
=> ∠SEC = ∠OBC, a это соответственные углы при прямых BD и AE и секущей CE. Следовательно, AE || BD.
Ответ: б) 240/17.
Смотреть полное решение
31. Биссектриса прямого угла прямоугольного треугольника ABC вторично
пересекает окружность, описанную около этого треугольника, в точке L.
Прямая, проходящая через точку L и середину N гипотенузы AB,
пересекает катет ВС в точке М.
а) Докажите, что ∠BML= ∠ВАС.
6) Найдите площадь треугольника АВС ‚если АВ =20 и СМ = 3√5.
Решение:
а) Поскольку луч CL — биссектриса угла АСВ, дуги AL и BL равны, а значит, стягивающие их соответственные одноимённые хорды равны.
Следовательно, треугольник ALB равнобедренный, a прямая LN — серединный перпендикуляр к отрезку АВ. Прямоугольные треугольники АВС и МВN имеют общий угол АВС.
Значит, они подобны, откуда получаем, что ∠BML = ∠ВАС.
Ответ: б) 80.
Смотреть полное решение
32. Дана трапеция ABCD с основаниями AD и ВС. Точки М и N — середины сторон АВ и CD соответственно. Окружность проходит через точки В и С и пересекает отрезки ВМ и СN в точках Р и Q, отличных от концов отрезков, соответственно.
а) Докажите, что точки M, N, Р и Q лежат на одной окружности.
6) Найдите QN, если отрезки DР и РС перпендикулярны, АВ=26, ВС =4,5, CD=25, AD=21,5.
Решение:
а) Четырёхугольник ВСQР вписан в окружность, а средняя линия МN трапеции ABCD параллельна её основанию ВС, значит.
∠MPQ =180° - ∠BPQ = ∠BCQ =180°- ∠МNQ.
Таким образом, сумма противоположных углов четырёхугольника МРQN равна 180°, значит, около него можно описать окружность.
Ответ: б) 182/25.
Смотреть полное решение
33. Две окружности разных радиусов касаются внешним образом в точке К.
Прямая касается первой окружности в точке A, а второй окружности в точке В.
Луч ВК пересекает первую окружность в точке D, луч АК пересекает вторую окружность в точке С.
а) Докажите, что четырёхугольник ABCD — трапеция.
6) Найдите радиус окружности, описанной около треугольника BCD, если радиус первой окружности равен 1, а радиус второй окружности равен 4.
Решение:
а) Пусть прямая KM — общая касательная двух окружностей, причём точка М лежит на отрезке АВ. Тогда по свойству отрезков касательных, проведённых из одной точки к окружности, AM = KМ = ВМ . Следовательно, точка К лежит на окружности диаметром AB, а значит, ∠АКВ =90°.
Углы АКD и ВКС прямые, поэтому AD и ВС — диаметры первой и второй окружностей соответственно. Значит, неравные отрезки AD и ВС перпендикулярны касательной АВ, следовательно, они параллельны. Таким образом, четырёхугольник ABCD — трапеция.
Ответ: б) `sqrt65/2`.
Смотреть полное решение
34. Точка О — центр вписанной в треугольник АВС окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Р.
а) Докажите, что ∠РОА = ∠РАО.
б) Найдите площадь треугольника АРО, если радиус описанной около треугольника АВС окружности равен 10, ∠BAC = 75°, ∠АВС= 60°.
Решение:
34-2. Точка О — центр вписанной в треугольник АВС окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Р.
а) Докажите, что ∠РОА = ∠РАО.
б) Найдите площадь треугольника АРО, если радиус описанной около треугольника АВС окружности равен 6, ∠BAC = 75°, ∠АВС= 60°.
Решение:
 а) Поскольку точка О — центр вписанной в треугольник АВС окружности, лучи АО и ВО являются биссектрисами углов треугольника АВС. Угол РОА является внешним углом треугольника АОВ. Следовательно,
а) Поскольку точка О — центр вписанной в треугольник АВС окружности, лучи АО и ВО являются биссектрисами углов треугольника АВС. Угол РОА является внешним углом треугольника АОВ. Следовательно,
∠РОА = ∠ВАО + ∠АВО = 1/2 ∠BAC + 1/2 ∠АВС.
Углы РАС и РВС равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника АВС, поэтому
∠РАО = ∠РАС + ∠ОАС = ∠РВС + ∠ОАС = 1/2 ∠АВС + 1/2 ∠BAC.
Таким образом, ∠РОА = ∠РАО.
б) Пусть В = 6 — радиус окружности, описанной около треугольника АВС.
Поскольку ∠РОА = ∠РАО, треугольник АРО равнобедренный, следовательно,
ОР = АР = 2R sin∠АВР = 2R sin30° = 6.
Таким образом, площадь треугольника АРО равна
`(AP*OP*sin∠APO)/2=(AP^2*sin∠ACB)/2=(AP^2*sin45°)/2=9sqrt2`
Ответ: б) `9sqrt2`.
35. Точка О — центр вписанной в треугольник АВС окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке Р.
а) Докажите, что OP =СР.
6) Найдите радиус описанной около треугольника АВС окружности, если расстояние от точки Р до прямой АС равно 18, ∠АВC= 60 °.
Решение:
Ответ: б) 36
Смотреть решение
36. Точка О — центр вписанной в треугольник АВС окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Р.
а) Докажите, что ∠POC = ∠PCO.
6) Найдите площадь треугольника АРС, если радиус описанной около треугольника АВС окружности равен 8, ∠ABC = 60°.
Решение:
Ответ: б) 16√3
Смотреть решение
37. В остроугольном треугольнике АВС угол A равен 60°. Высоты BN и СМ треугольника АВС пересекаются в точке М. Точка О — центр окружности, описанной около треугольника АВС.
а) Докажите, что АН = AO.
6) Найдите площадь треугольника AHO, если BC =6√3, ∠ABC =45°.
Решение:
Ответ: б) 9
Смотреть решение
38. Из вершины С прямого угла прямоугольного треугольника АВС проведена высота СН.
а) Докажите, что отношение площадей кругов, построенных на отрезках АН и ВН соответственно как на диаметрах, равно (tg АВС)4.
6) Пусть точка О1 — центр окружности диаметром АН, вторично пересекающей отрезок АС в точке Р, а точка О2 — центр окружности диаметром BH, вторично пересекающей отрезок ВС в точке Q. Найдите площадь четырёхугольника O1 PQO2, если АС =12, ВС =10.
Решение:
Ответ: б) 30
Смотреть решение
Задания из сборников Ященко
34-2 из сборника и была на реальном ЕГЭ.
39. Две окружности касаются внутренним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите АС, если радиусы окружностей равны 3 и 4.
Решение:
 а) Пусть CL — общая касательная двух окружностей, причём точки L и В лежат по одну сторону от прямой АС.
а) Пусть CL — общая касательная двух окружностей, причём точки L и В лежат по одну сторону от прямой АС.
Тогда по теореме об угле между касательной и хордой
∠CAD = ∠LCB = ∠СЕВ.
Значит, прямые AD и BE параллельны, поскольку соответственные углы CAD и СЕВ при пересечении этих прямых прямой АЕ равны.
б) Поскольку угол АСВ прямой, AD и BE — диаметры меньшей и большей окружностей соответственно.
Прямоугольные треугольники ACD и ЕСВ подобны по острому углу (∠CAD = ∠СЕВ) с коэффициентом подобия `(AD)/(BE)=3/4`.
Пусть АС = ВС = х, тогда `CD = 3/4 BC =(3x)/4`.
В прямоугольном треугольнике ACD:
`AD^2=AC^2 + CD^2`, `36 = x^2 + (9x^2)/16`,
откуда `х = 24/5`
Ответ: 4,8.
40. Точки 𝐴1, 𝐵1, 𝐶1 – середины сторон соответственно 𝐵𝐶, 𝐴𝐶 и 𝐴𝐵 остроугольного треугольника 𝐴𝐵𝐶.
а) Докажите, что окружности, описанные около треугольников 𝐴1𝐶𝐵1, 𝐴1𝐵𝐶1 и 𝐵1𝐴𝐶1, пересекаются в одной точке.
б) Известно, что 𝐴𝐵 = 𝐴𝐶 = 13 и 𝐵𝐶 = 10. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников 𝐴1𝐶𝐵1, 𝐴1𝐵𝐶1 и 𝐵1𝐴𝐶1.
Решение:
41. Точки 𝐴, 𝐵, 𝐶, 𝐷 и 𝐸 лежат на окружности в указанном порядке, причем 𝐴𝐸 = 𝐸𝐷 = 𝐶𝐷, а прямые 𝐴𝐶 и 𝐵𝐸 перпендикулярны. Отрезки 𝐴𝐶 и 𝐵𝐷 пересекаются в точке 𝑇.
а) Докажите, что прямая 𝐸𝐶 пересекает отрезок 𝑇𝐷 в его середине.
б) Найдите площадь треугольника 𝐴𝐵𝑇, если 𝐵𝐷 = 6, 𝐴𝐸 =√6.
Решение:
42. Окружность с центром в точке 𝐶 касается гипотенузы 𝐴𝐵 прямоугольного треугольника
𝐴𝐵𝐶 и пересекает его катеты 𝐴𝐶 и 𝐵𝐶 в точках 𝐸 и 𝐹. Точка 𝐷 – основание высоты,
опущенной из вершины 𝐶. 𝐼 и 𝐽 – центры окружностей, вписанных в треугольники
𝐵𝐶𝐷 и 𝐴𝐶𝐷.
а) Докажите, что 𝐼 и 𝐽 лежат на отрезке 𝐸𝐹.
б) Найдите расстояние от точки 𝐶 до прямой 𝐼𝐽, если 𝐴𝐶 = 15, 𝐵𝐶 = 20.
Решение:
43. В параллелограмме 𝐴𝐵𝐶𝐷 угол 𝐵𝐴𝐶 вдвое больше угла 𝐶𝐴𝐷. Биссектриса угла 𝐵𝐴𝐶 пересекает отрезок 𝐵𝐶 в точке 𝐿. На продолжении стороны 𝐶𝐷 за точку 𝐷 выбрана такая точка 𝐸, что 𝐴𝐸 = 𝐶𝐸.
а) Докажите, что 𝐴𝐿 : 𝐴𝐶 = 𝐴𝐵 : 𝐵𝐶.
б) Найдите 𝐸𝐿, если 𝐴𝐶 = 21, tg∠𝐵𝐶𝐴 = 0,4.
Решение:
44. На стороне 𝐵𝐶 ромба 𝐴𝐵𝐶𝐷 отметили точку 𝐸 так, что 𝐵𝐸 : 𝐸𝐶 = 1 : 4. Через точку 𝐸 перпендикулярно 𝐵𝐶 провели прямую, которая пересекает диагонали 𝐵𝐷 и 𝐴𝐶 в точках 𝑅 и 𝑀 соответственно , при этом 𝐵𝑅 : 𝑅𝐷 = 1 : 3.
a) Докажите, что точка 𝑀 делит отрезок 𝐴𝐶 в отношении 2 : 1, считая от вершины 𝐶.
б) Найдите периметр ромба 𝐴𝐵𝐶𝐷, если 𝑀𝑅 = 2√3.
Решение:
45. Прямая, перпендикулярная стороне 𝐵𝐶 ромба 𝐴𝐵𝐶𝐷, пересекает его диагональ 𝐴𝐶 в точке 𝑀, а диагональ 𝐵𝐷 в точке 𝑁, причём 𝐴𝑀 : 𝑀𝐶 = 1:2, причём 𝐵𝑁 : 𝑁𝐷 = 1:3.
a) Докажите, что прямая 𝑀𝑁 делит сторону ромба 𝐵𝐶 в отношении 1 : 4.
б) Найдите сторону ромба, если 𝑀𝑁 = `sqrt12`.
Решение:
46. На сторонах АС, АВ и ВС прямоугольного треугольника АВС с прямым углом С вне треугольника АВС построены равнобедренные прямоугольные треугольники АКС, ALB и ВМС с прямыми углами К, L и М соответственно.
а) Докажите, что LC — высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LС = 4.
Решение:
 а) По условию ∠АСВ + ∠BLA = 90° + 90° = 180°.
а) По условию ∠АСВ + ∠BLA = 90° + 90° = 180°.
Значит, четырёхугольник LACB вписанный.
Хорды AL и LB описанной около четырёхугольника LACB окружности равны. Значит, равны между собой стягиваемые этими хордами дуги, а также опирающиеся на эти дуги вписанные углы ACL и LCB. Тогда
∠ACL = ∠LCB = 45°.
По условию ∠КСА = ∠МСВ = 45°. Следовательно,
∠KCL = ∠КСА + ∠ACL = 90° и ∠MCL = ∠MCB + ∠LCB - 90°,
а значит, LC — высота треугольника KLM.
б) Пусть ВС = а, АС = b, АВ = с и CL = d, Р — точка пересечения CL и АВ. Тогда по доказанному в пункте а) СР — биссектриса треугольника АВС.
По свойству биссектрисы АР : РВ = АС: СВ = Ь:а, АР + РВ = АВ = с.
Отсюда `AP=(bc)/(a+b)` и `PB=(ac)/(a+b)`.
Поскольку ∠ACL - ∠BAL = 45°, получаем, что треугольники ACL и PAL подобны по двум углам. Отсюда `(AC)/(PA)=(CL)/(AL)`, `b:(bc)/(a+b)=d:c/sqrt2` и `d=(a+b)/sqrt2`.
Площадь треугольника KLM равна половине произведения его высоты LC = d на основание
КМ=КС + СМ = `a/sqrt2 +b/sqrt2=d`
Следовательно, искомая площадь равна
`d^2/2=8`
Ответ: б) 8.
47. На гипотенузе АВ и катетах ВС и АС прямоугольного треугольника АВС отмечены точки М, N и К соответственно, причём прямая NK параллельна прямой АВ и ВМ = BN = 1/2 KN. Точка Р — середина отрезка KN.
а) Докажите, что четырёхугольник ВСРМ — равнобедренная трапеция.
б) Найдите площадь треугольника АВС, если ВМ = 1 и ∠ВСМ = 15°.
Решение:
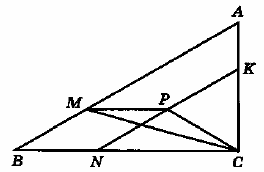 а) Поскольку прямая NP параллельна прямой ВМ и NP = 1/2 KN = ВМ = BN, четырёхугольник BNPM — ромб. Значит, прямая РМ параллельна прямой ВС, а так как СР — медиана прямоугольного треугольника KCN, проведённая из вершины прямого угла, то
а) Поскольку прямая NP параллельна прямой ВМ и NP = 1/2 KN = ВМ = BN, четырёхугольник BNPM — ромб. Значит, прямая РМ параллельна прямой ВС, а так как СР — медиана прямоугольного треугольника KCN, проведённая из вершины прямого угла, то
СР = 1/2 KN = BN = РМ = ВМ.
Следовательно, четырёхугольник ВСРМ — равнобедренная трапеция.
б) Поскольку СР = 1/2 KN = BN = РМ, треугольник СРМ равнобедренный, поэтому
∠РСМ = ∠СМР = ∠ВСМ .
Значит, СМ — биссектриса угла ВСР. Тогда
∠АВС = ∠МВС = ∠ВСР = 2∠ВСМ = 2*15° = 30° ,
∠KNC = ∠АВС = 30° , CN = KN cos30° = 2*`sqrt3/2` = `sqrt3`,
ВС = CN + BN = `sqrt3`+1, АС = ВС tg 30° =`(sqrt3 +1)/sqrt3`.
Следовательно,
`S_(ABC)=1/2AC*BC=1/2(sqrt3 +1)*(sqrt3 +1)/sqrt3=(2sqrt3 +3)/3`
Ответ: `(2sqrt3 +3)/3`
48. Четырёхугольник ABCD вписан в окружность радиуса R=27. Известно, что АВ = ВС = CD = 36.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Решение:
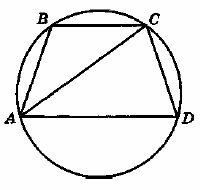 а) Острые углы ВСА и CAD равны, поскольку опираются на равные хорды АВ и CD. Значит, прямые ВС и AD параллельны.
а) Острые углы ВСА и CAD равны, поскольку опираются на равные хорды АВ и CD. Значит, прямые ВС и AD параллельны.
б) Обозначим угол ВСА через α. По теореме синусов
`sinα =(AB)/(2R) = 2/3` .
Треугольник АВС равнобедренный, поэтому
∠ВАС = ∠ВСА = α. Значит, ∠BAD = ∠BAC + ∠CAD = 2α.
Четырёхугольник ABCD — равнобедренная трапеция, поэтому
∠CDA - ∠BAD = 2α.
Значит,
∠ACD = 180° - ∠CAD - ∠CDA = 180° - Зα.
Таким образом, по теореме синусов для треугольников ACD и АСВ получаем:
`(AD)/sin(180-Зα)=(AB)/sinα`;
`AD=sin(Зα)/sinα * AB= (3-4sin^2 α)AB=44`
Ответ: б) 44.
49. В трапеции ABCD основание AD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.
Решение:
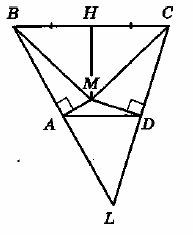
а) Пусть прямые АВ и CD пересекаются в точке L.
Тогда треугольники BLC и ALD подобны с коэффициентом подобия 2, поскольку ВС = 2AD. Значит, А и D — середины BL и CL соответственно. Таким образом, AM и DM — серединные перпендикуляры в треугольнике BLC, а М — центр описанной около этого треугольника окружности, поэтому ВМ = СМ как радиусы этой окружности.
б) Пусть Н — середина ВС, тогда МН — серединный перпендикуляр к стороне ВС. Значит, треугольники ВНМ и СНМ равнобедренные прямоугольные, поэтому ∠ВМС = 90°. По свойству вписанного угла ∠BLC = ∠BMC / 2 =45°, откуда
∠ABC = ∠LBC = 180° - ∠BLC- ∠BCL = 71°.
Ответ: б) 71°.
50. Окружность с центром О1 касается оснований ВС и AD, а также боковой стороны АВ трапеции ABCD. Окружность с центром О2 касается сторон ВС, CD и AD. Известно, что АВ = 9, ВС = 8, CD = 4, AD = 15.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции ABCD.
б) Найдите О1О2.
Решение:
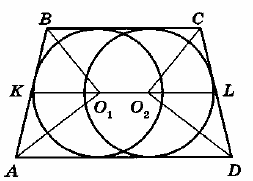 а) Точка O1 равноудалена от прямых AD и ВС.
а) Точка O1 равноудалена от прямых AD и ВС.
Значит, точка О1 лежит на средней линии трапеции ABCD. Аналогично, точка О2 лежит на средней
линии трапеции ABCD. Следовательно, прямая О1О2 содержит среднюю линию трапеции ABCD, а значит, прямая О1О2 параллельна основаниям трапеции ABCD.
б) Пусть К — середина стороны АВ, a L — середина стороны CD. Точка O1 равноудалена от прямых АВ, ВС и AD, поэтому лучи АО1 и ВО1 являются биссектрисами углов DAB и АВС соответственно. Значит,
∠ВАО1 + ∠АВО1 = `(∠BAD + ∠ABC)/2`= 90°,
то есть ∠АО1В = 90°. Следовательно, КО1 — медиана, проведённая к гипотенузе АВ прямоугольного треугольника АО1В.
Аналогично, треугольник CO2D прямоугольный, a LO2 — медиана, проведённая к его гипотенузе CD. Точки К, O1, О2 и L лежат на средней линии трапеции ABCD.
Значит,
O1О2 = KL - KO1 - LO2 = `(AD + BC)/2 - (AB)/2 - (CD)/2`= 5
Ответ: б) 5.
51. Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключенного внутри окружности.
Решение:
52. Окружность с центром О, вписанная в треугольник ABC, касается его сторон AB, AC и BC в точках C1, B1 и A1 соответственно. Биссектриса угла A пересекает эту окружность в точке Q, лежащей внутри треугольника AB1C1.
а) Докажите, что C1Q - биссектриса угла AC1B1.
б) Найдите расстояние от точки O до центра окружности, вписанной в треугольник AC1B1, если известно, что BC=15, AB=13, AC=14.
Решение:
53. Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC=120°.
а) Докажите, что ∠ CBE = ∠COE
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE=40 и CE=24.
Решение:
54 см. в старом банке
55. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в 6 раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону.
Решение:
56. Четырехугольник ABCD вписан в окружность, причем сторона CD - диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность - в точке F, причем H - середина AE.
а) Докажите, что четырехугольник BCFE - параллелограмм.
б) Найдите площадь четырехугольника ABCD, если известно, что AB =5 и AH = 4.
Решение:

